Инфоурок › Геометрия ›Презентации›Презентация по геометрии на тему «Аксиома параллельных прямых»









Описание презентации по отдельным слайдам:
1 слайд
2 слайд Описание слайда:
ЦЕЛЬ УРОКА: Познакомить с понятием аксиомы в геометрии Организация деятельности обучающихся по изучению и первичному закреплению аксиомы параллельных прямых и её следствий.
3 слайд Описание слайда:
Теорема – утверждение , для которого в рассматриваемой теории существует доказательство. Следствие – утверждение, которое выводится из теорем и аксиом. * Теорема и следствие
4 слайд Описание слайда:
АКСИОМА Что это такое? Как произошло?
5 слайд Описание слайда:
Аксиома Это исходные положения, на основе, которых доказываются далее теоремы и строится вся геометрия. Происходит от греческого «аксиос», что означает «ценный, достойный».
6 слайд Описание слайда:
Некоторые аксиомы были сформулированы еще в первой главе (хотя они и не назывались там аксиомами).
7 слайд Описание слайда:
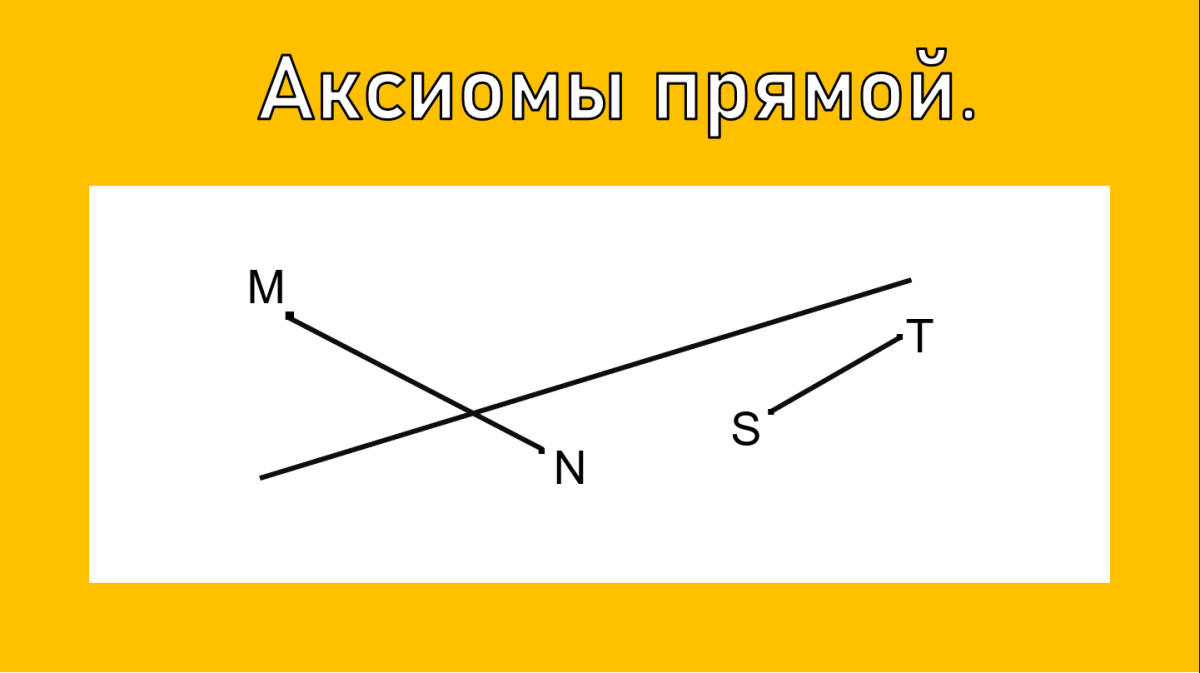
Через любые две точки проходит прямая, и притом только одна
8 слайд Описание слайда:
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один
9 слайд Описание слайда:
От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один
10 слайд Описание слайда:
Сначала формулируются исходные положения — аксиомы На их основе, путём логических рассуждений доказываются другие утверждения Такой подход к построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида 365 – 300 гг. до н.э. Геометрия, изложенная в «Началах», называется евклидовой геометрией Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии
11 слайд Описание слайда:
ЗАДАЧА Всегда ли через точку , не лежащую на данной прямой, можно провести параллельную прямую? Сколько параллельных прямых можно провести через данную точку?
12 слайд Описание слайда:
М а в с Давайте докажем, что через точку М можно провести прямую, параллельную прямой а.
Дано: а, М а Доказать: можно провести прямую через Ма Доказательство: Проведем прямую с, а ┴ с, в ┴ с =>а в (две прямые ┴ к третьей не пересекаются, значит ) Можно ли через т.
М провести еще одну прямую , параллельную прямой а ? в в а М Нам представляется, что через т.М нельзя провести прямую (отличную от прямой в), параллельную прямой а.
13 слайд Описание слайда:
Можно ли это утверждение доказать? Огромную роль в решении этого непростого вопроса сыграл великий русский математик Николай Иванович Лобачевский Он выяснил, что это утверждение доказать нельзя, т.к. само является аксиомой.
14 слайд Описание слайда:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. а b М
15 слайд Описание слайда:
«Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной». «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной». Какое из данных утверждений является аксиомой? Чем отличаются вышеуказанные утверждения ?
16 слайд Описание слайда:
1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Доказательство: (методом от противного) Предположим, что прямая с не пересекает прямую в, значит, с в. Тогда через т.М проходят две прямые а и с параллельные прямой в. 3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.
17 слайд Описание слайда:
2.Если две прямые параллельны третьей прямой, то они параллельны. Доказательство: (методом от противного) Предположим, что прямая а и прямая в пересекаются. 2. Тогда через т.М проходят две прямые а и в параллельные прямой с 3 . Но это противоречит аксиоме параллельных прямых. 4. Значит прямые а и в параллельны.
18 слайд Описание слайда:
Решение задач Задача №197 Через точку, не лежащую на данной прямой p , проведены четыре прямые. Сколько из этих прямых пересекают прямую p ? Рассмотрите все возможные случаи. А р Задача № 199 Прямая р параллельна стороне АВ треугольника АВС. Докажите, что прямые АВ и ВС пересекают прямую р. А В С р
19 слайд Описание слайда:
Исходные утверждения о свойствах геометрических фигур называются … Через точку, не лежащую на данной прямой … Если прямая пересекает одну из двух параллельных прямых, то …. Если две прямые параллельны третьей, то ….
20 слайд Описание слайда:
Домашнее задание: П. 27, 28 стр. 68, вопросы 7 – 11 Решить задачи № 196, 198, 200
Скрыть
Важно! Узнайте, чем закончилась проверка учебного центра «Инфоурок»?
Общая информация
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Источник: https://infourok.ru/prezentaciya-po-geometrii-na-temu-aksioma-parallelnih-pryamih-1761690.html
Параллельные прямые — YouClever.org
Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Параллельные прямые…Прежде всего: что это такое?
| Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали. |
Вот, как рельсы

Принято обозначение:
| – читается как параллельна . |
Самым важным фактом, который нужно принять без доказательства (не только тебе, но и любому математику) для того, чтобы вся геометрия не развалилась и не превратилась в какую-то неузнаваемую теорию, является так называемая «аксиома параллельных прямых».
Часто ее еще называют «пятый постулат Евклида». Формулируем:
Аксиома параллельных прямых
| Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной. |
 |
Смотри: через любую точку проходит только одна прямая , которая параллельна , все остальные будут пересекать прямую . |
Казалось бы: чего проще – ну , одна так одна… Но ты себе просто не представляешь, сколько споров вели математики на протяжении прямо-таки тысячелетий, прежде чем осознали истинную роль этой аксиомы о параллельных прямых. В конце концов , уже в 19-м веке, после открытий Лобачевского, Гаусса и других ученых стало ясно, что можно построить и другие виды геометрии, в которых не выполняется аксиома параллельных прямых, в которых ее можно выбросить, но эти геометрии уже оказываются не геометриями плоскости, а геометриями на каких-то хитрых поверхностях.
А наша привычная плоскость оттого и называется евклидовой, что при построении геометрии на ней, при решении всех задачек и доказательстве теорем мы считаем этот многострадальный пятый постулат Евклида выполнимым.
Ну вот, а теперь возникает два вопроса:
- Если где-то в задаче даны или оказались параллельными две какие-то прямые, то что? Как это использовать?
- А как вообще узнать, что какие-то прямые параллельны?
- Ответ на первый вопрос называется «свойства параллельных прямых», а ответ на второй вопрос называется «признаки параллельных прямых».
- Но прежде нам понадобится много названий, которые нужно запомнить, как таблицу умножения.
- Итак, ситуация: две прямые пересечены третьей (она называется секущей)

Получается куча углов. Целых штук.
Приняты такие названия этих углов:
  |
и называются внутренними накрест лежащими углами и – тоже внутренние накрест лежащие углы. |
Название говорит само за себя: и , так же, как и и лежат «накрест» — по разные стороны от секущей и «внутри», между прямыми и .
  |
и (а еще и ) называются внутренними односторонними углами. Они лежат с одной стороны от секущей и «внутри» между прямыми и . |
  |
и (а еще и ) называются внешними односторонними углами (ты уже догадался, почему?) |
И последнее название: соответственные углы.
 |
Это пары углов: |
Обрати внимание, и лежат в одинаковых «соответственных» местах около точек и . То же можно сказать и об остальных перечисленных парах – посмотри на рисунок.
Свойства параллельных прямых
Напоминаем (а то отвлеклись на названия), что пытаемся ответить на вопрос: если , то что?
И вот что:
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
|
Запомни – все задачи с участием слова «параллельность» решаются с помощью этой теоремы о свойствах параллельных прямых.
А теперь, наоборот, признаки параллельных прямых.
Признаки параллельных прямых
То есть, как бы узнать, что прямые – параллельны?
Если две прямые ( и ) пересечены третьей и оказалось, что
то прямые и – параллельны |
- Заметь, что для того, чтобы установить параллельность прямых, достаточно выяснить, скажем, равенство всего двух углов (или накрест лежащих, или соответственных), а уже все остальное окажется , так сказать, бонусом.
- Смотри-ка, вот схема:
Параллельные прямые. коротко о главном
- Параллельные прямые — это прямые, которые лежат в одной плоскости и не пересекаются, сколько бы их не продолжали: .
- Секущая — прямая, пересекающая две параллельные прямые: .
- Аксиома параллельных прямых: через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.
|
Свойства параллельных прямых:
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
- внутренние накрест лежащие углы равны: , ;
- соответственные углы равны: , , , ;
- сумма любых двух внутренних односторонних углов равна : , ;
- сумма любых двух внешних односторонних углов равна : , .
Признаки параллельных прямых:
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
- Стать учеником YouClever,
- Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
- А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
Источник: https://youclever.org/book/parallelnye-pryamye-1
Геометрия_10-1
- Материалы к зачетной работе по теме
«РћСЃРЅРѕРІРЅС‹Рµ понятия Рё аксиомы стереометрии. Параллельность прямых Рё плоскостей» - Стереометрия — это раздел геометрии, РІ котором изучаются свойства фигур РІ пространстве.
- Слово «стереометрия» РїСЂРѕРёСЃС…РѕРґРёС‚ РѕС‚ греческих слов В«στερεοσВ» — объемный, пространственный Рё В«μετρεοВ» — измерять.
- Простейшие фигуры в пространстве: точка, прямая, плоскость.
| Плоскость. Представление Рѕ плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно РІРѕ РІСЃРµ стороны. |  |
| РќР° рисунках плоскости изображаются РІ РІРёРґРµ параллелограмма или РІ РІРёРґРµ произвольной области Рё обозначаются греческими буквами α, β, γ Рё С‚.Рґ. Точки Рђ Рё Р’ лежат РІ плоскости β (плоскость β РїСЂРѕС…РѕРґРёС‚ через эти точки), Р° точки M, N, P РЅРµ лежат РІ этой плоскости. Коротко это записывают так: Рђ ∈ β, B ∈ β, |
 |
Аксиомы стереометрии и их следствия
| РђРєСЃРёРѕРјР° 1. Через любые три точки, РЅРµ лежащие РЅР° РѕРґРЅРѕР№ РїСЂСЏРјРѕР№, РїСЂРѕС…РѕРґРёС‚ плоскость, Рё притом только РѕРґРЅР°. |  |
| РђРєСЃРёРѕРјР° 2. Если РґРІРµ точки РїСЂСЏРјРѕР№ лежат РІ плоскости, то РІСЃРµ точки РїСЂСЏРјРѕР№ лежат РІ этой плоскости. (Прямая лежит РЅР° плоскости или плоскость РїСЂРѕС…РѕРґРёС‚ через РїСЂСЏРјСѓСЋ). |  |
| Р�Р· аксиомы 2 следует, что если прямая РЅРµ лежит РІ данной плоскости, то РѕРЅР° имеет СЃ ней РЅРµ более РѕРґРЅРѕР№ общей точки. Если прямая Рё плоскость имеют РѕРґРЅСѓ общую точку, то РіРѕРІРѕСЂСЏС‚, что РѕРЅРё пересекаются. |  |
| РђРєСЃРёРѕРјР° 3. Если РґРІРµ различные плоскости имеют общую точку, то РѕРЅРё имеют общую РїСЂСЏРјСѓСЋ, РЅР° которой лежат РІСЃРµ общие точки этих плоскостей. Р’ таком случае РіРѕРІРѕСЂСЏС‚, плоскости пересекаются РїРѕ РїСЂСЏРјРѕР№. Пример: пересечение РґРІСѓС… смежных стен, стены Рё потолка комнаты. |  |
Некоторые следствия из аксиом
| Теорема 1. Через РїСЂСЏРјСѓСЋ a Рё РЅРµ лежащую РЅР° ней точку Рђ РїСЂРѕС…РѕРґРёС‚ плоскость, Рё притом только РѕРґРЅР°. |  |
| Теорема 2. Через РґРІРµ пересекающиеся прямые a Рё b РїСЂРѕС…РѕРґРёС‚ плоскость, Рё РїСЂРё том только РѕРґРЅР°. |  |
Параллельные прямые в пространстве
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
| Теорема Рѕ параллельных прямых. Через любую точку пространства, РЅРµ лежащую РЅР° данной РїСЂСЏРјРѕР№, РїСЂРѕС…РѕРґРёС‚ прямая, параллельная данной, Рё притом только РѕРґРЅР°. |  |
| Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. |
|
|
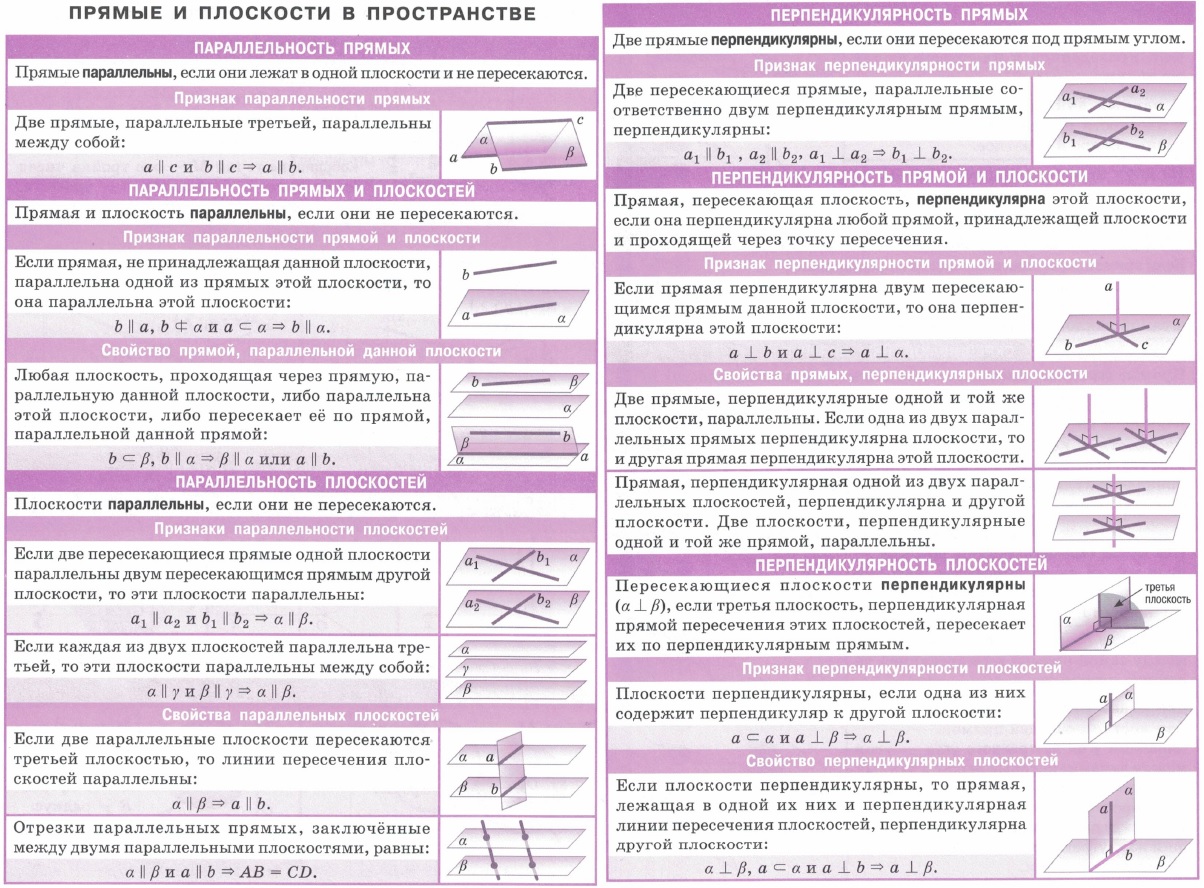
Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек.
| Признак параллельности прямой и плоскости Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. |
| Теорема. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Теорема. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. |
Взаимное расположение прямых в пространстве
| Пересекающиеся прямые: лежат в одной плоскости, имеют одну общую точку. | Параллельные прямые: лежат в одной плоскости, не имеют общих точек (не пересекаются) | Скрещивающиеся прямые: не лежат в одной плоскости, не имеют общих точек (не пересекаются) |
| Параллельность плоскостей Две плоскости называются параллельными, если РѕРЅРё РЅРµ пересекаются, С‚.Рµ. РЅРµ имеют РЅРё РѕРґРЅРѕР№ общей точки. α∥β. |
| Признак параллельности РґРІСѓС… плоскостей Теорема. Если РґРІРµ пересекающиеся прямые РѕРґРЅРѕР№ плоскости параллельны РґРІСѓРј пересекающимся прямым РґСЂСѓРіРѕР№ плоскости , то эти плоскости параллельны.Если Р°∥Р°1 Рё b∥b1, то α∥β. |
Свойства параллельных плоскостей
| Вели α∥β Рё РѕРЅРё пересекаются СЃ γ, то Р°∥b. Если РґРІРµ параллельные плоскости пересечены третьей, то линии РёС… пересечения параллельны. |
|
| вернуться РЅР° страницу «РњР°С‚ематика» | вверх |
Источник: http://osiktakan.ru/mg_10-0.htm
Урок 20. аксиома параллельных прямых — Геометрия — 7 класс — Российская электронная школа
- Геометрия
- 7 класс
- Урок № 20
- Аксиома параллельных прямых
- Перечень рассматриваемых вопросов:
- Аксиомы и теоремы.
- Исторические сведения об аксиоматическом построении евклидовой геометрии.
- Параллельные и перпендикулярные прямые.
- Признаки параллельности прямых.
- Решение задач на доказательство параллельности прямых.
- Тезаурус:
- Аксиома – это утверждение, которое принимается в качестве исходного, без доказательства в рамках данной теории.
- Аксиома параллельных прямых.
- Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
- Следствия из аксиомы.
- Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
- Если две прямые, параллельны третьей прямой, то они параллельны.
- Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
- Теоретический материал для самостоятельного изучения
- Построение геометрии
- Геометрия на плоскости изучает фигуры: сначала даются их определения, затем доказываются свойства или отношения в виде теорем.
Однако есть утверждения, которые принимаются в качестве исходных, они не доказываются. Это аксиомы.
Аксиома – происходит от греческого «аксиос», что означает «ценный, достойный». Изначально имело смысл «самоочевидная истина».
Теорема – греческое слово, означает «зрелище, представление». В математике греков употреблялось в смысле «истина, доступная созерцанию».
- Аксиома параллельных прямых.
- Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
- Следствия из аксиомы.
- Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
- Если две прямые параллельны третьей прямой, то они параллельны.
Впервые аксиоматический подход к изложению геометрии был изложен в знаменитом сочинении Евклида «Начала» в III веке до нашей эры. Геометрию, которую мы изучаем, по сей день, называют евклидовой.
Схема изучения геометрии представлена так: задаются начальные понятия (точка, прямая, плоскость), определения фигур (отрезок, луч, треугольник и др.).
Затем изучаются свойства или отношения между ними в виде аксиом или теорем.
Приведём примеры аксиом, которые уже встречали в предыдущих параграфах, хотя они не назывались аксиомами.
- Через любые две точки проходит прямая, и притом только одна.
- На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
- От любого луча можно отложить угол, равный данному неразвёрнутому углу, и притом только один.
Евклид является автором аксиоматического подхода к построению геометрии.

Аксиома параллельных прямых:
через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
На рисунке через точку М проведены две прямые. Но только одна из них прямая b параллельна прямой а.

Утверждения, которые выводятся из аксиом или теорем, называются следствиями, и они доказываются.
Следствия из аксиомы параллельных прямых.
1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Доказательство методом от противного.
Пусть a ║b, c пересекает прямую a в точке M. Предположим, что прямая c не пересекает b. Тогда через точку M проходит две прямые a и c параллельные b. Это противоречит аксиоме, значит предположение неверно, т. е. прямая c пересекает b.

2. Если две прямые параллельны третьей прямой, то они параллельны.
Доказательство методом от противного.
Пусть a ║ c, b ║ c.
Предположим, что прямые a и b не параллельны, т. е. пересекаются в точке M. Тогда через точку M проходит две прямые a и b параллельные c. Это противоречит аксиоме, значит, предположение неверно, т. е. прямая a параллельна прямой b.

Разбор заданий тренировочного модуля
№ 1. Доказать существование прямой, параллельной данной.
Объяснение:
Доказательство:
- Проведём через точку М прямую c ┴ а.
- Затем проведём прямую b ┴ c.
- Так как прямые a и b перпендикулярны прямой c, то они параллельны.
№ 2. Через точку А, не лежащую на прямой р, проведены четыре различные прямые.
Сколько из них пересекает прямую р?

Объяснение.
1 случай. Если одна из прямых параллельна р. Тогда три других пересекают прямую р, согласно следствию 1 из аксиомы параллельных прямых.
2 случай. Если ни одна из прямых не параллельна р. Тогда все четыре пересекают прямую р.
Ответ: 3 или 4.
Источник: http://resh.in.edu.ru/subject/lesson/7074/conspect/
Свойства параллельных прямых. Аксиома параллельных прямых — урок. Геометрия, 7 класс
Признаки, которые мы рассматривали в первой части теории, и свойства, которые будем рассматривать в этой части, доказываем разными способами.
Признак — это некоторый факт, благодаря которому мы устанавливаем справедливость интересующего нас суждения о некотором объекте.
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти две прямые параллельны.
Свойство — если мы уверены в справедливости суждения, мы формулируем свойство объекта.
Если две прямые параллельны, то при пересечении их с третьей секущей накрест лежащие углы равны.
Аксиома, в свою очередь — такая истина, которую не надо доказывать. В каждой науке есть свои аксиомы, на справедливости которых строят все дальнейшие суждения и их доказательства.
Аксиома параллельных прямых.
В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.
Иногда эту аксиому называют как одно из свойств параллельных прямых, но на справедливости этой аксиомы строятся многие доказательства в геометрии.
Другие свойства параллельных прямых.
1. Если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.
2. Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
Эти свойства в отличие от аксиомы нужно доказать.
Докажем 1. Свойство.
Даны две параллельные прямые (a) и (b). Верно ли, что если прямая (c) параллельна прямой (a), то она параллельна и прямой (b)?
Используем противоположное суждение.
Допустим, что возможна ситуация, когда прямая (c) параллельна одной из параллельных прямых — прямой (a) — пересекает другую прямую (b) в некоторой точке (K).

Получается противоречие с аксиомой параллельных прямых. Мы имеем ситуацию, когда через точку проходят две пересекающиеся прямые, которые параллельны одной и той же прямой (a). Такого не может быть, значит, прямые (b) и (c) пересекаться не могут.
Мы доказали, что верно: если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.
Попробуй доказать самостоятельно 2. Свойство.
Если некая прямая (c) пересекает одну из двух параллельных прямых (a), то она пересекает и вторую параллельную прямую (b).

Таким же методом от противоположного суждения попробуй представить, что возможна ситуация, когда прямая пересекает одну из параллельных прямых, но не пересекает другую.

Свойства углов, которые образуются при пересечении двух параллельных прямых с третьей секущей, мы уже назвали в первой части теории.
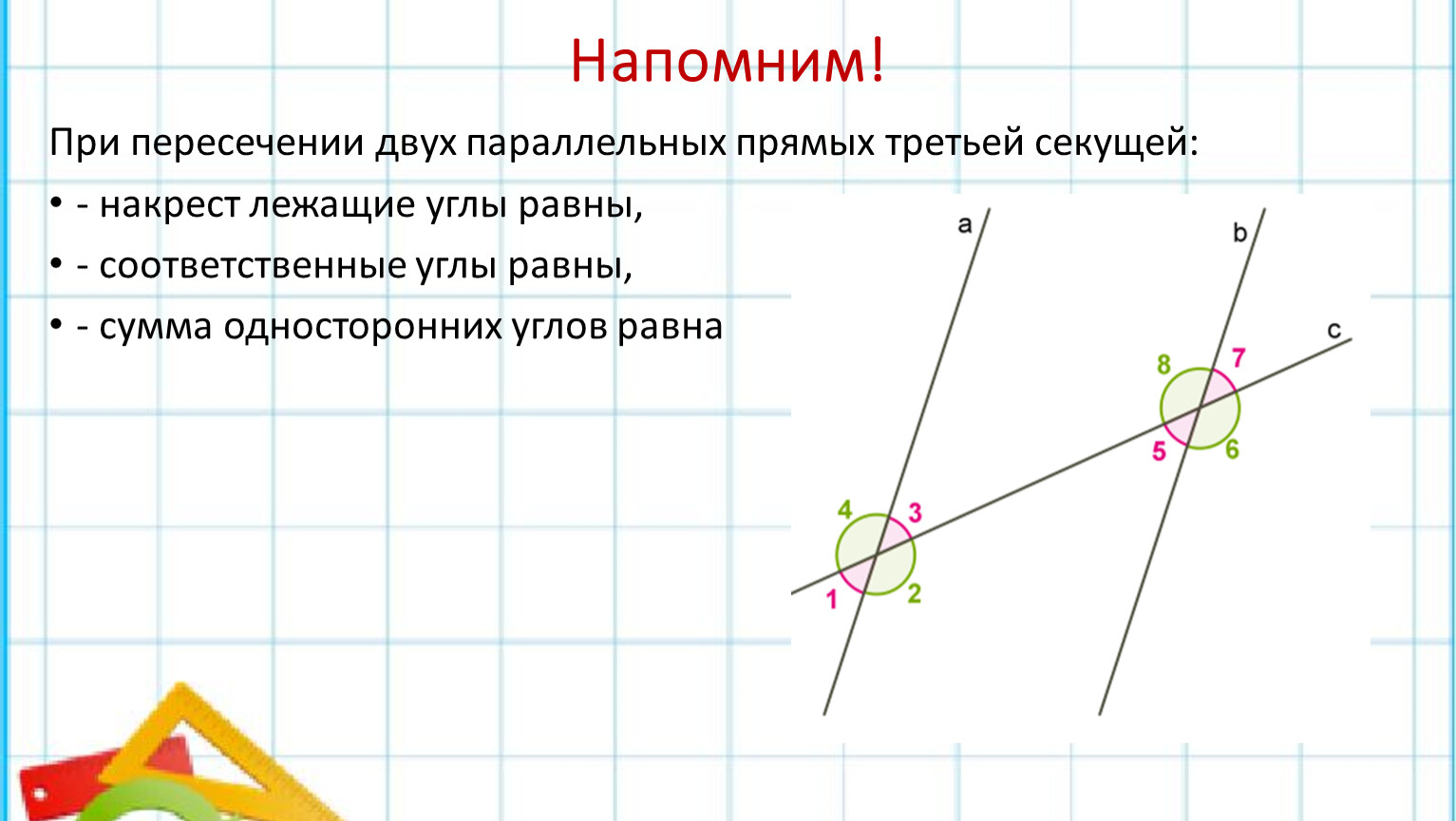
При пересечении двух параллельных прямых третьей секущей:
- — накрест лежащие углы равны,
- — соответственные углы равны,
- — сумма односторонних углов равна (180°).
Источник: https://www.yaklass.ru/p/geometria/7-klass/parallelnye-priamye-9124/priznaki-parallelnosti-dvukh-priamykh-aksioma-parallelnykh-priamykh-9228/re-4ba7ee5b-3478-495b-b7eb-3e4eeb2d9b4c
Об аксиомах геометрии. Аксиома параллельности прямых
Цели урока:
- дать представление о неизвестных учащимся аксиомах геометрии, повторить уже известные им аксиомы;
- ввести аксиому параллельных прямых;
- ввести понятие следствия из аксиом, теорем;
- показать как используются аксиома параллельных прямых и следствия из неё при решении задач;
- воспитание патриотизма, гордости за свою родину на примере великого русского математика Н.И.Лобачевского.
- Оборудование: компьютер, проектор.
- ХОД УРОКА
- 1. Проверка предыдущего домашнего задания
- 2. Повторение уже известных учащимся аксиом планиметрии
Учитель: В знаменитом сочинении Евклида «Начала» (III в. до н.э.) были систематизированы основные известные в то время геометрические сведения.
Главное же − в «Началах» был развит аксиоматический подход к построению геометрии, который состоит в том, что сначала формулируются основные положения, не требующие доказательства (аксиомы), а затем на их основе посредством рассуждений доказываются другие утверждения (теоремы). Некоторые из аксиом, предложенных Евклидом, и сейчас используются в курсах геометрии.
Само слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный». Полный список аксиом планиметрии, принятых в нашем курсе геометрии, приведён в приложениях в конце учебника на страницах 344-348. Эти аксиомы вы рассмотрите дома самостоятельно.
Некоторые из этих аксиом мы уже рассматривали. Вспомните и сформулируйте эти аксиомы.
Учащиеся:
1) Имеются, по крайней мере, три точки, не лежащие на одной прямой. 2) Через любые две точки проходит прямая, и притом только одна. 3) Из трёх точек прямой одна и только одна лежит между двумя другими.
4) Каждая точка О прямой разделяет её на две части (два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.
5) Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.
6) Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки. 7) На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
- 8) От любого луча в заданную полуплоскость можно отложить угол, равный данному неразвёрнутому углу, и притом только один.
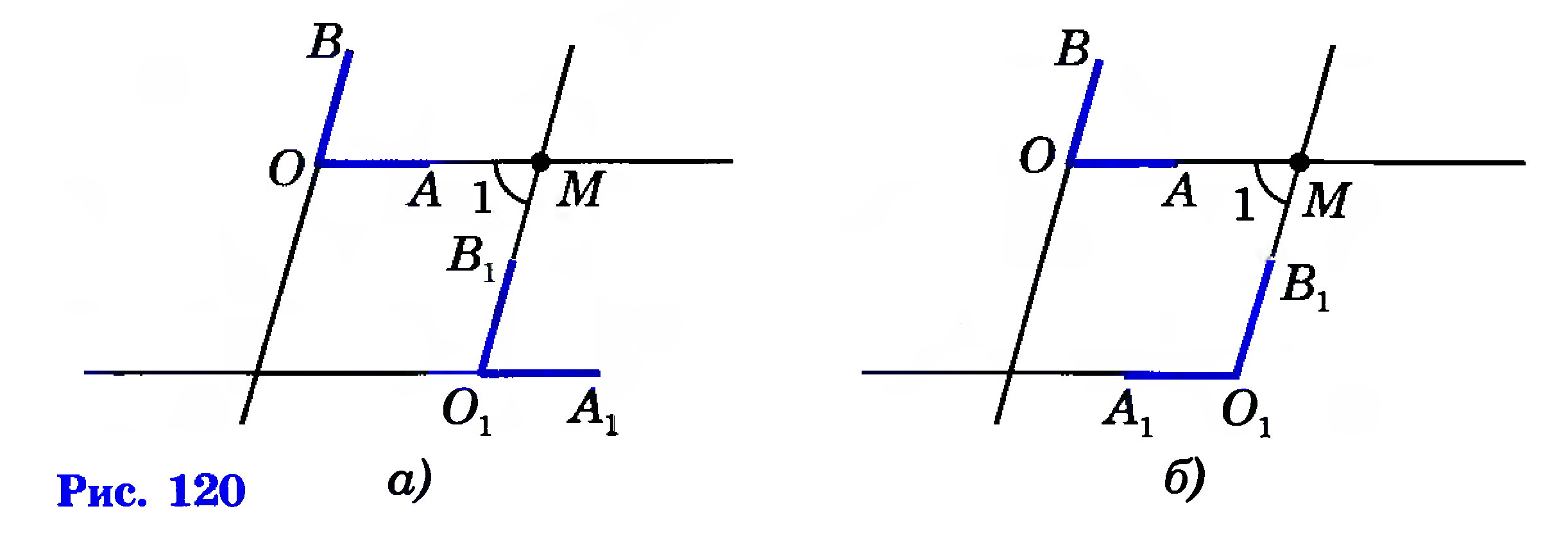 Учитель: Какие прямые называются параллельными на плоскости?
Учитель: Какие прямые называются параллельными на плоскости?- Учащиеся: Две прямые на плоскости называются параллельными, если они не пересекаются.
- Учитель: Сформулируйте признаки параллельности прямых.
- Учащиеся:
1) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 2) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
3) Если при пересечении двух прямых секущей сумма односторонних углов равна 180˚ то прямые параллельны.
3. Новая тема. Аксиома параллельных прямых
Учитель: Решим задачу: «Через точку М, не лежащую на прямой а, проведите прямую, параллельную прямой а».
Решение.
План решения задачи обсуждается всем классом. Один из учащихся записывает решение на доске (без записи в тетрадях).
Учитель: Возникает вопрос: можно ли через точку М провести ещё одну прямую, параллельную прямой а? Этот вопрос имеет большую историю.
В «Началах» Евклида содержится пятый постулат: «И если прямая, падающая на две прямые, образуют внутренние и по одну сторону углы, меньше двух прямых, то продолженные эти прямые неограниченно встретятся с той стороны, где углы меньше двух прямых». Прокл в V в.н.э.
переформулировал постулат Евклида проще и понятнее: «Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной». Это и есть аксиома параллельных прямых. Отсюда видно, что рассмотренная выше задача имеет единственное решение.
Многие математики предпринимали попытки доказать пятый постулат, так как его формулировка слишком напоминала теорему. Все эти попытки каждый раз оказывались неудачными. И лишь в XIX в. было окончательно выяснено, что пятый постулат Евклида нельзя доказать, он сам является аксиомой.
Огромную роль в решении этого вопроса сыграл великий русский математик Николай Иванович Лобачевский (1792-1856).
4. Закрепление изученного. Решение задач
№ 196
Дан ∆АВС. Сколько прямых, параллельных стороне АВ, можно провести через вершину С?
- Решение.
- Согласно аксиоме параллельных прямых, можно провести единственную прямую.
- № 197
Через точку, не лежащую на прямой р, проведены четыре прямые. Сколько из этих прямых пересекают прямую р? Рассмотрите все возможные случаи.
Решение.

Ответ: 3 или 4 прямые.
Следствия из аксиомы параллельных прямых.
Утверждения, которые выводятся непосредственно из аксиом или теорем, называются следствиями. Рассмотрим следствия из аксиомы параллельных прямых.
Следствие 1˚. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Следствие 2˚. Если две прямые параллельны третьей прямой, то они параллельны. (Предлагается доказать учащимся самостоятельно).
- Чертёж тот же.
- Дано: а || b, с || b Доказать: а || с
- Доказательство (метод «от противного»):
Пусть прямые а и с не параллельны. Тогда они пересекаются в некоторой точке М. Через точку М проходят две различные прямые (а и с), параллельные прямой b. Это противоречит аксиоме параллельных. Значит наше предположение не верно. А верно то, что а || с. Ч.т.д. Второе следствие из аксиомы параллельных прямых является по сути дела ещё одним признаком параллельности прямых на плоскости.
5. Решение задач: №№ 217 (устно), 218 (устно), 198, 200, 213.
№ 217 (устно)
Прямые а и b параллельны прямой с. Докажите, что любая прямая, пересекающая прямую а, пересекает также и прямую b.
Решение.
Если а || b и b || с, то а || с (следствие 2˚). Если произвольная прямая d ∩ а, то d ∩ b (следствие 1˚).
№ 218 (устно)
Прямые а и b пересекаются. Можно ли провести такую прямую, которая пересекает прямую а и параллельна прямой b? Ответ обоснуйте.
Решение.
Возьмём на прямой а точку А b. Через точку А можно провести единственную прямую, параллельную прямой b (аксиома параллельных). Построенная прямая будет пересекать прямую а, так как имеет с ней общую точку А.
№ 198
Прямые а и bперпендикулярны к прямой р, прямая с пересекает прямую а. Пересекает ли прямая с прямую b?
- Дано: а р, b р, с ∩ а Найти: пересекает ли с прямую b?
- Решение: если а р и b р, то а || b (теорема).
- Ответ: с ∩ b.
- № 200
Если с ∩ а и а || b, то с ∩ b (следствие 1˚).
На рисунке учебника АD || р и PQ || BC. Докажите, что прямая р пересекает прямые АВ, АЕ, АС, ВС, РQ.

№ 213
На рисунке учебника СЕ = ED, ВЕ = EF и КЕ = AD. Докажите, что КЕ || ВС.
6. Подведение итогов
1) В чём заключается главная заслуга Евклида? 2) Что называется аксиомой? 3) Какие аксиомы мы знаем? 4) Кто из русских учёных построил стройную теорию неевклидовой геометрии? 5) Что называется следствием в математическом смысле слова?
- 6) Какие следствия мы сегодня узнали?
- 7. Задание на дом:
§2, п.27, 28, приложение об аксиомах геометрии стр. 344-348, вопросы 7-11 стр. 68, №199, 214. №199: Прямая р параллельна стороне АВ треугольника АВС. Докажите, что прямые ВС и АС пересекают прямую р.
№214: Прямая, проходящая через середину биссектрисы AD треугольника АВС и перпендикулярная к AD, пересекает сторону АС в точке М. Докажите, что MD¦AB.
Источник: https://multiurok.ru/index.php/files/ob-aksiomakh-geometrii-aksioma-parallelnosti-priam.html
Видеоурок «Аксиома параллельных прямых»
Содержание:
§ 1 Аксиома параллельных прямых
Выясним, какие утверждения называются аксиомами, приведем примеры аксиом, сформулируем аксиому параллельных прямых и рассмотрим некоторые её следствия.
При изучении геометрических фигур и их свойств возникает необходимость в доказательстве различных утверждений – теорем. При их доказательстве часто опираются на ранее доказанные теоремы.
Возникает вопрос: а на чем основаны доказательства самых первых теорем? В геометрии приняты некоторые исходные положения, на их основе и доказываются далее теоремы. Такие исходные положения называются аксиомами. Аксиома принимается без доказательств.
Слово аксиома происходит от греческого слова «аксиос», что означает «ценный, достойный».
С некоторыми аксиомами мы уже знакомы. Например, аксиомой является утверждение: через любые две точки проходит прямая, и притом только одна.
- При сравнении двух отрезков и двух углов мы накладывали один отрезок на другой, а угол накладывали на другой угол. Возможность такого наложения вытекает из следующих аксиом:
- ·на любом луче от его начала можно отложить отрезок, равный данному, и притом только один;
- ·от любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.

Геометрия – древняя наука. Почти два тысячелетия геометрия изучалась по знаменитому сочинению «Начала» древнегреческого ученого Евклида. Евклид сначала формулировал исходные положения – постулаты, а затем на их основе путем логических рассуждений доказывал другие утверждения.
Геометрия, изложенная в «Началах», называется евклидовой геометрией. В рукописях ученого есть утверждение, называемое пятым постулатом, вокруг которого очень долгое время разгорались споры. Многие математики предпринимали попытки доказать пятый постулат Евклида, т.е.
вывести его из других аксиом, но каждый раз доказательства были неполными или заходили в тупик. Лишь в XIX веке было окончательно выяснено, что пятый постулат не может быть доказан на основе остальных аксиом Евклида, и сам является аксиомой.
Огромную роль в решении этого вопроса сыграл русский математик Николай Иванович Лобачевский (1792-1856). Итак, пятый постулат – аксиома параллельных прямых.

Аксиома: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
§ 2 Cледствия из аксиомы параллельных прямых
Утверждения, которые выводятся непосредственно из аксиом или теорем, называются следствиями. Рассмотрим некоторые следствия из аксиомы параллельных прямых.
Следствие 1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Дано: прямые а и b параллельны, прямая с пересекает прямую а в точке А.
Доказать: прямая с пересекает прямую b.
Доказательство: если бы прямая с не пересекала прямую b, то через точку А проходили бы две прямые а и с, параллельные прямой b. Но это противоречит аксиоме параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Значит, прямая с пересекает прямую b.

Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны.
Дано: прямые а и b параллельны прямой с. (а||с, b||с)

Доказать: прямая а параллельна прямой b.
Доказательство: допустим, что прямые а и b не параллельны, т.е. пересекаются в некоторой точке А. Тогда через точку А проходят две прямые а и b, параллельные прямой с. Но по аксиоме параллельных прямых через точку, не лежащую на данной прямой, проходит только одна прямая, параллельна данной. Значит, наше предположение неверно, следовательно, прямые а и b параллельны.

Список использованной литературы:
- Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013. – 383 с.: ил.
- Гаврилова Н.Ф. Поурочные разработки по геометрии 7 класс. — М.: «ВАКО», 2004, 288с. – (В помощь школьному учителю).
- Белицкая О.В. Геометрия. 7 класс. Ч.1. Тесты. – Саратов: Лицей, 2014. – 64 с.
Использованные изображения:
Источник: https://znaika.ru/catalog/7-klass/geometry/Aksioma-parallelnykh-pryamykh.html
Аксиома параллельных прямых
Рассмотрим произвольную прямую и точку М, не лежащую на ней (Рис.1).

Докажем, что через точку М можно провести прямую, параллельную прямой . Для этого проведем через точку М две прямые: сначала прямую перпендикулярно к прямой , а затем прямую перпендикулярно к прямой (Рис.2). А из того, что две прямые и перпендикулярны к третьей прямой следует, что они параллельны ().
Возникает вопрос: можно ли через точку М провести еще одну прямую, параллельную прямой ?
Если прямую «повернуть» на какой-то угол вокруг точки М, то она пересечет прямую (прямая ' на рис.3).
То естьнам кажется, что через точку М нельзяпровести прямую отличную от прямой , параллельную прямой .
Утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой.
| Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. |
Следствия из аксиомы параллельных прямых
| 10. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. |
Дано: , = М (Рис.4).
- Доказать: .
- Доказательство:
Если мы предположим, что прямая не пересекает прямую , то прямая будет параллельна прямой , а по условию через точку М проходит прямая параллельная прямой , значит получим, что черезточку М будут проходить две прямые и параллельные прямой (Рис.5).
Но это противоречит аксиоме параллельных прямых, значит, наше предположение неверно, и прямая пересекает прямую , т.е. . Что и требовалось доказать.
| 20. Если две прямые параллельны третьей прямой, то они параллельны. |
Дано: , (Рис.6).
- Доказать: .
- Доказательство:
Предположим, что прямые и не параллельны, т.е. пересекаются в некоторой точке М (Рис.7).
Тогда получим, что через точку М проходят две прямые и параллельные прямой , т.к. по условию и . Но это противоречит аксиоме параллельных прямых, следовательно, наше предположение неверно, значит, прямые и параллельны, т.е. . Что и требовалось доказать.
Следствие — утверждение, которое выводится непосредственно из аксиом или теорем.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
- Параллельные прямые
- Признаки параллельности двух прямых
- Практические способы построения параллельных прямых
- Аксиомы геометрии
- Теорема о накрест лежащих углах
- Теорема о соответственных углах
- Теорема об односторонних углах
- Теорема об углах с соответственно параллельными сторонами
- Теорема об углах с соответственно перпендикулярными сторонами
- Параллельные прямые
Правило встречается в следующих упражнениях:
- 7 класс
- Задание 196, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- Задание 199, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- Задание 200, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- Задание 217, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- Задание 277, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- Задание 279, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- Задание 281, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- Задание 1148, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
- © budu5.com, 2020
- Пользовательское соглашение
- Copyright
- Нашли ошибку?
- Связаться с нами
Источник: https://budu5.com/manual/chapter/3400




