- «Свойства окружности»
- Оглавление
- Введение
- Свойства касательных к окружности
- Окружность, вписанная в произвольный треугольник
- Окружность, вписанная в трапецию и описанная около трапеции.
- Формула отрезка общей касательной к двум касающимся окружностям
- Ведение
В школьном курсе геометрии уделяется немного уроков для изучения темы «Окружность», учащиеся узнают о взаимном расположении окружностей и многоугольников и окружности, получают формулы для нахождения радиуса окружности, вписанной в правильный треугольник, квадрат и правильный шестиугольник, а также формы для радиусов описанных окружностей около квадрата, правильного треугольника и шестиугольника. Но остается открытым вопрос о том, как же находить радиус окружности, вписанной в произвольный треугольник, как связаны отрезки касательных к окружности с радиусом и углами треугольника.
Из школьного курса геометрии известно, где лежит центр окружности, описанной около треугольника, квадрата, правильного шестиугольника, но ведь в окружность можно вписать и трапецию, где в этом случае будет лежать центр этой окружности? Всякую ли трапеции можно вписать в окружность? На эти вопросы поможет ответить данная проектная работа, в которой изложены теоремы и их доказательства, относящиеся к нахождению элементов окружности и многоугольников, как вписанных в окружность, так и описанных около нее. Полученные формулы помогут при решении задач, упростят нахождение радиуса окружности, элементов многоугольника. К тому же в задании ЕГЭ С4 нередко встречаются задачи с вписанными и описанными окружностями. Приведенные факты и формулы помогут сориентироваться учащимся при решении задач на доказательство и нахождение элементов многоугольника из С4.
- Предмет проекта:
- Окружности, элементы окружностей и многоугольники, вписанные в окружность и описанные около окружности.
- Цели
- — расширить и систематизировать знания об окружностях и многоугольниках, вписанных в окружность и описанных около окружности.
- Задачи:
- — изучить и обобщить свойства касательной и секущей к окружности;
- — вывести: формулы для отрезков касательных к окружности, вписанной в треугольник; формулы радиуса окружности, вписанной в произвольный треугольник; формулу отрезка общей касательной к двум касающимся окружностям;
- — изучить особенности окружности, вписанной в трапецию и описанной около нее.
- Свойства касательной к окружности
В этом разделе общаются и систематизируются сведения о касательной и секущей к окружности. Приводится доказательство дополнительных свойств, о которых не упоминается в учебнике геометрии, но они могут быть полезны при решении олимпиадных задач и подготовки к экзамену.
Напомним определение касательной и секущей. 
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Секущей называется прямая, пересекающая окружность.
Основные свойства касательной к окружности
Данные свойства и их доказательства приводят в учебнике геометрии.
- Отрезки касательных к окружности, проведенные из одной точки, равны.
На рисунке изображены две касательные к окружности. AB и AC – отрезки касательных к окружности. AB = AC.
- Углы, образованные касательными, проведенными из одной точки, и прямой, проходящей через центр окружности и эту точку, равны.
На рисунке выше, прямая AO является биссектрисой , значит,
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
- На рисунке касательная проведена к окружности в точке A, тогда прямая

- Дополнительные свойства.
- Здесь приведем доказательства свойств касательной и секущей к окружности, которые могут быть полезны для вычисления углов и отрезков касательных.
- Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть.
На рисунке МС – касательная, MA – секущая, тогда MC2 = MA·MB.
- Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.
На рисунке МА – касательная, МВ – секущая, тогда МА2=МВ·МС
Доказательство: , и следовательно,. У АМС и ВМА угол при вершине М общий, то эти треугольники подобны по двум углам (первый признак подобия треугольников). Из подобия следует: , значит, МА2=МВ·МС.
- Угол между касательными и хордой.Величина угла, образованного касательной и хордой, имеющими общую точку на окружности, равна половине угловой величины дуги, заключенной между его сторонами.
- ∠NAB — угол между касательной MN и хордой AB, имеющих на окружности общую точку A, тогда ∠NAB== (180о-∠BOC) = ∠АОВ или ∠NAB = .

Доказательство: Дополнительное построение. Проводим диаметр АС. Касательная перпендикулярна радиусу, проведенному в точку касания, а, значит, перпендикулярна диаметру АС, тогда ∠CAN=90о. – вписанный угол, тогда = , ∠NAB=90о-, получаем ∠NAB== (180о-∠BOC) = ∠АОВ или ∠NAB = .
Угол между секущими.
- Если точка пересечения двух секущих к окружности находится внутри окружности, то угол между секущими равен половине суммы градусных мер дуг, которые они стягивают.
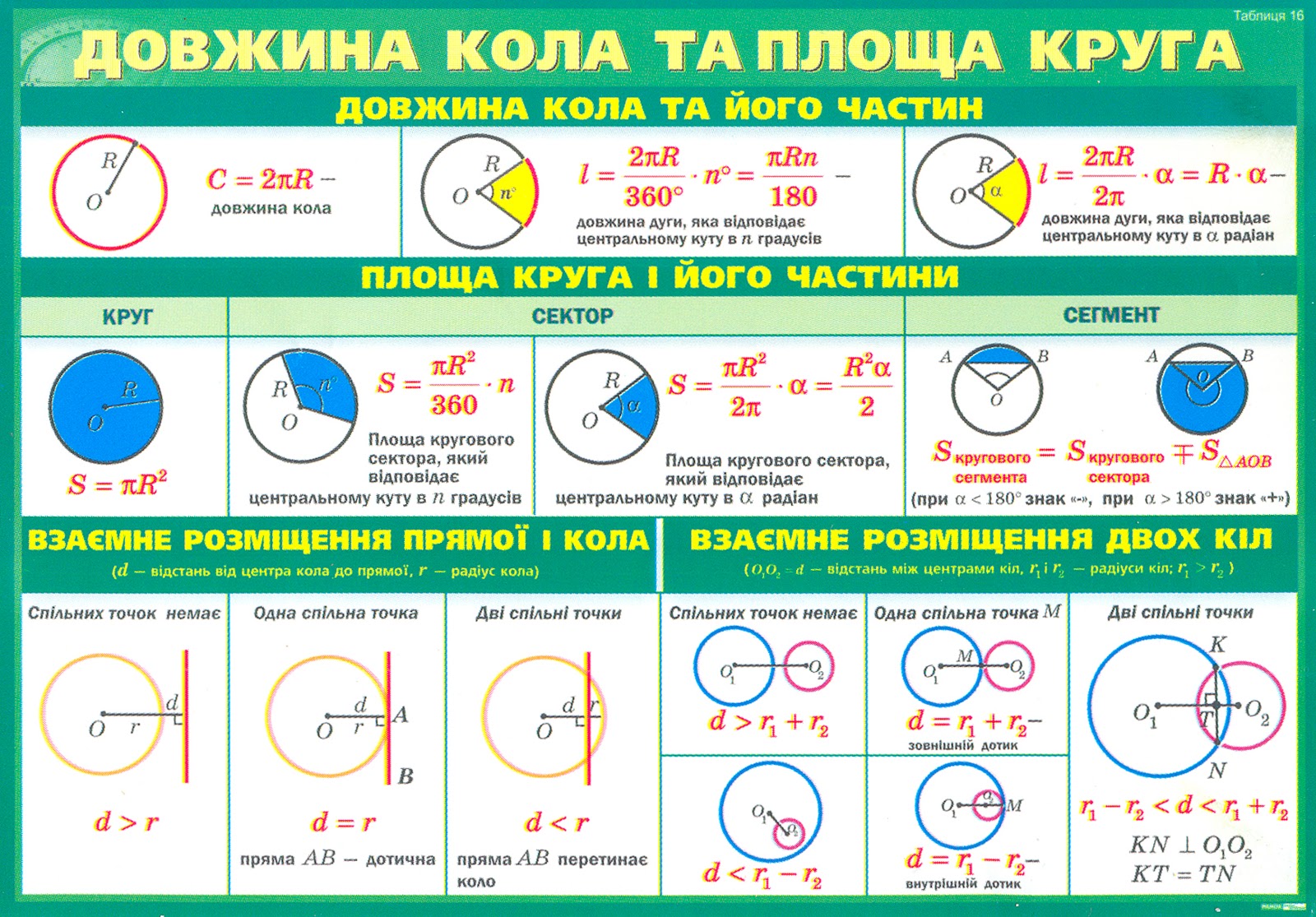
- F
- M
- R
- Доказательство: Дополнительное построение. Проведем хорду FR, треугольника FMR получим: Получаем
- Если точка пересечения двух секущих к окружности находится вне окружности, то угол между секущими равен половине разности градусных мер дуг, которые они стягивают.
- M

- C
- D
- E
- F
- Доказательство: Дополнительное построение. Проведем хорду ED, тогда
- так как они являются вписанными углами. Из треугольника MED: углами, значит, тогда
- Окружность, вписанная в произвольный треугольник
- Для выведения формул отрезков касательных к окружности и радиуса окружности, вписанной в треугольник напомним определение окружности, вписанной в треугольник.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности. 
Формулы для отрезков касательных к окружности, вписанной в треугольник
Пусть точки K, M, N – точки касания окружности со сторонами треугольника. Стороны треугольника, описанного около окружности лежат на касательных к этой окружности, тогда отрезки касательных равны, то есть AK=AN, BK=BM, CN=CM. Обозначим их соответственно буквами x, y, z.
р – полупериметр треугольника ABC. .
BC=y+z ; AC=x+z ; AB=x+y, тогда p= = =x+(y+z) =x+BC p=x+BC
Отсюда х= р — BC, т.е. AK=AN=p — BC.
Аналогично y=p — AC ; z=p — AB т.е. BK=BM=p — AC,CM=CN= p – AB.
- Если окружность вписана в треугольник, то отрезки касательных можно вычислить как разность полупериметра и стороны треугольника, на которой данный отрезок касательной не лежит.
- В формулезаменимpнаa+b+c, где a=BC, b=AC, c=AB, получим:
- BK=BM=y
- CM=CN=z
- В треугольнике со сторонами a, b, c расстояние от вершины А до точек касания вписанной окружности сторон, содержащих эту вершину, равно , расстояние от вершины B до точек касания вписанной окружности сторон, содержащих эту вершину, равно , расстояние от вершины C до точек касания вписанной окружности сторон, содержащих эту вершину, равно .
- Выведем еще одну формулу для вычисления отрезков касательных:
Для доказательства рассмотрим АОN –прямоугольный т.к ONAC (радиус перпендикулярен касательной). AO – отрезок биссектрисы ∠ А => ∠ONA=
- ctg ∠ OAN =, тогда
- Аналогично и
- Окружность, вписанная в трапецию и описанная около трапеции.
Из школьного курса геометрии известно, что в окружность можно вписать любой треугольник, квадрат, правильный шестиугольник. Определим, можно ли в окружность вписать трапецию.
- Теорема.
- Трапеция вписана в некоторую окружность тогда и только тогда, когда она является равнобедренной.
- Доказательство: так как они являются односторонними углами. По теореме Птолемея, если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого
- четырёхугольника можно описать окружность, тогда , значит то есть трапеция должна быть равнобедренной.
- Следующая теорема показывает, как можно вычислить радиус окружности, вписанной в трапецию.
- Теорема.
- Если в трапецию вписана окружность с радиусом r и она делит боковую сторону точкой касания на два отрезка — a и b, то B C
- M
- O
- A D
Доказательство: Если концы боковой стороны соединит с центром окружности, то образуется прямоугольный треугольник ABO, с прямым углом O. Радиус — это высота, опущенная из его прямого угла в точку касания окружности. Из подобия треугольников BOM и AOM, следует что , тогда .
- Теорема.
- Центр окружности, описанной около трапеции, лежит на пересечении серединных перпендикуляров к сторонам трапеции.
- B C
- O
- A D
Доказательство: Проведем диагональ AC, она делит трапецию на два треугольника, вписанных в окружность, значит отрезки AO, BO, CO равны, так как треугольник ABC является вписанным в окружность.
Из школьного курса планиметрии известно, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника ABC.
Но стороны треугольника ABC являются сторонами трапеции ABCD, значит центр окружности, описанной около трапеции, является точкой пересечения серединных перпендикуляров к сторонам трапеции.
Формула отрезка общей касательной к двум касающимся окружностям
Две окружности имеют различное взаимное расположение относительно друг друга, а именно: окружности могут касаться друг друга, пересекаться, не пересекаться, одна окружность может лежать внутри другой. Рассмотрим случай, когда окружности касаются внешним образом. Они имеют общую точку касания.
Рассмотрим понятие внешней касательной к окружности. Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. На рисунке прямая a – внешняя касательная к двум касающимся окружностям.
- Теорема.
- Отрезок общей внешней касательной к двум касающимся окружностям равен ,где R и r –радиусы окружностей.
- Пусть AB – общая касательная к окружностям; O1 и O2 -центры окружностей , тогда
O1A AB и O2B AB так как радиус, проведенный в точку касания, перпендикулярен касательной. O1ABO2 -прямоугольная трапеция. Проведем высоту O1Н.
- O1H=AB, O2H= O2B-HB= O2B- O1A=R-r
- По теореме Пифагора O1O2 = O2H+ O1H
- 1H
- Решив квадратное уравнение, получаем:
Данная формула применяется для вычисления отрезка общей касательной к двум касающимся окружностям через радиусы этих окружностей. Задачи, в которых присутствует окружность и касательная часто встречаются в С4 ЕГЭ. Применяя эту формулу мы упростим вычисления при решении подобных задач.
Заключение
В ходе работы были изучены основные свойства касательной к окружности, доказаны дополнительные свойства, о которых не упоминается в школьном курсе планиметрии. Произведена систематизация этих свойств.
Также были выведены формулы для отрезков касательных к окружности, вписанной в треугольник; формулы радиуса окружности, вписанной в произвольный треугольник; формула отрезка общей касательной к двум касающимся окружностям.
Были изучены особенности окружности вписанной и описанной в трапеции. Выведена формула для вычисления радиуса вписанной в трапецию окружности.
Полученные знания станут существенным подспорьем в понимании свойств касательной и секущей к окружности. Будут необходимы при решении как задач курса планиметрии, так и олимпиадных и экзаменационных задач.
Список литературы
учителям по математике.
-
Полонский В.Б., Рабинович Е.М., Якир М.С. Учимся решать задачи по геометрии. Учеб.-метод. пособие. – К. «Магистр», 1996.
Источник: https://infourok.ru/metodicheskiy-material-po-teme-svoystva-okruzhnosti-3032975.html
Окружность
- Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.

- Центр окръжности

- Радиус: расстояние от центра окружности до его границы.

Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.

$d = 2cdot r$
- Периметр (длина окружности): длина границы окружности.

Длина окружности $= pi cdot$ диаметр $= 2 cdot pi cdot$ радиус - Длина окружности $= pi cdot d = 2 cdot pi cdot r$
$pi$ — pi: число, равное 3,141592… или $approx frac{22}{7}$, то есть отношение $frac{ ext{длины окружности}}{ ext{диаметр}}$ любого окружности.
Дуга: изогнутая линия, которая является частью окружности.

Дуги окружности измеряется в градусах или радианах.
Например: 90° или $frac{pi}{2}$ — четверть круга,
180° или $pi$ — половина круга.
- Сумма всех дуг окружности составляет 360° или $2pi$
- Хорда: отрезок прямой, соединяющей две точки на окружности.

- Сектор: похож на часть пирога (клин).

- Касательная к окружности: прямая, перпендикулярна к радиусу, и имеющая ТОЛЬКО одну общую точку с окуржностью.

Формулы
- Длина окружности $=pi cdot ext{диаметр} = 2cdot pi cdot ext{радиус}$
- Площадь круга $= pi cdot$ радиус2
- Радиус обозначается как r, диаметр как d,
длина окружности как P и площадь как S. - $P = pi cdot d = 2cdot pi cdot r$
$S = pi cdot r^2$
- Площадь сектора круга K: (с центральным углом $ heta$ и радиусом $r$).
Если угол $ heta$ в градусах, тогда площадь = $frac{ heta}{360} pi r^2$ - Если угол $ heta$ в радианах, тогда площадь, тогда площадь = $frac{ heta}{2} r^2$
Углы
Центральный угол
Если длина дуги составляет $ heta$ градуов или радиан, то значение центрального угла также $ heta$ (градусов или радиан).
Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах …) вы можете найти значение её соответствующего центрального угла ($ heta$) по формуле:
$ heta = 360 cdot frac{l}{P} = frac{360 cdot l}{2 cdot pi cdot r} = frac{180 cdot l}{pi cdot r}$
$l$ — длина дуги.
Вписанный угол
Вписанный угол это угол с вершиной на окружности и со сторонами, которые содержат хорды окружности.
На рисунке, угол APB это вписанный угол.
Величина вписанного угла равна половине дуги, на которую он опирается.
- Пример:
$widehat{AB} = 84^circ$ - $angle APB = frac{84}{2} = 42^circ$
- Случай 1: два секущие пересекаются внутри окружности.
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются.
На рисунке дуга AB и дуга CD равны 60° и 50°
тогда углы 1 и 2 равны $frac{1}{2}(60^circ + 50^circ)=55^circ$
Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
$angle ABC =frac{1}{2}(x — y)$
На рисунке дуга AB=80° и дуги CD=30°.
$angle ABC = frac{1}{2}(80 — 30) = frac{1}{2} cdot 50 = 25^circ$
Хорды
-
Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:
- $AX cdot XB = CX cdot XD$
Источник: https://www.math10.com/ru/geometria/krugi.html
Окружность и ее свойства. Длина окружности. :
Окружность в математике является фигурой одной из самых главных и важных. Она необходима для множества расчетов. Знания свойств этой фигуры из школьной программы непременно пригодятся в жизни. Длина окружности требуется при расчете многих материалов с круглым сечением. Заниматься чертежами, строить заборчик возле клумбы – для этого понадобится знание геометрической фигуры и ее свойств.

Понятие окружности и ее основные элементы
Фигура на плоскости, состоящая из многочисленных точек, расположенных на равном расстоянии от центральной, называется окружностью.
Отрезок, выходящий из центра и соединяющий его с одной из точек, образующих окружность, называется радиусом. Хордой является отрезок, который соединяет пару точек, расположенных по периметру круга, между собой.
Если она расположена так, что проходит через центральную точку, то одновременно является диаметром.
Длина радиуса окружности равна длине диаметра, уменьшенной вдвое. Пара несовпадающих точек, находящихся на окружности, делят ее на две дуги. Если отрезок с концами в этих точках проходит через центральную точку (тем самым являясь диаметром), то образуемые дуги будут являться полуокружностями.

Длина окружности
Расчет периметра окружности определяется несколькими способами: через диаметр или через радиус. На практике было выявлено, что длина окружности (l) при делении на ее же диаметр (d) всегда дает одно число. Это число π, которое ровняется 3,141692666… Расчет производится по формуле: π= l/ d. Преобразуя ее, получается длина окружности. Формула такова: l=πd.
Для нахождения радиуса применим следующую формулу: d=2r. Это стало возможным, благодаря делению. Ведь радиус — это половина диаметра. Как только получили вышеуказанные значения, можно вычислить, чему же ровна длина окружности, по формуле следующего вида: l=2πr.
Основные свойства
Площадь круга всегда больше, если сравнивать ее с площадями иных замкнутых кривых. Касательная — это прямая, которая соприкасается с окружностью только в одной точке. Если прямая пересекает ее в двух местах, то она является секущей.
Точка, в которой 2 различные окружности соприкасаются друг с другом, всегда находится на прямой, проходящей через их центральные точки. Пересекающимися на плоскости являются такие окружности, которые имеют 2 общие точки.
Угол между ними рассчитывается как угол, образованный касательными к точкам соприкосновения.
Если через точку, не являющейся точкой окружности, провести две секущиеся к ней прямые, то образованный ими угол будет равен разности длин дуг, уменьшенной вдвое. Данное правило действует и в противоположном случае, когда речь идет о двух хордах.
Две пересекающиеся хорды образуют угол, равный сумме длин дуг, уменьшенной в два раза. Дуги в такой ситуации выбирают в данном углу и углу, расположенному напротив. Оптическое свойство окружности гласит следующее: лучи света, отраженные от зеркал, расставленных по периметру круга, собираются обратно в его центр.
В данном случае источник света должен быть установлен в центральной точке круга.
Источник: https://www.syl.ru/article/271563/new_okrujnost-i-ee-svoystva-dlina-okrujnosti
Окружность — это… Что такое Окружность?
Окружность и её центр
Окружность — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом.
Другие определения
Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.
Окружность — это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы. (см. Окружность Аполлония)
Также фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками.
Связанные определения
- Радиус — не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек.
- Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.
- Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.
- Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Через вершину треугольника проведена касательная к описанной окружности
- Угол, образуемый дугой окружности, равной по длине радиусу, принимается за 1 радиан.
- Длина единичной полуокружности обозначается через .
- Геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое, называется кругом.
- Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
- Прямая, проходящая через две различных точки окружности, называется секущей.
- Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается.
- Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
- Две окружности, имеющие общий центр, называются концентрическими.
- Две окружности, пересекающиеся под прямым углом, называются ортогональными.
Свойства
- Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
- Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
- Касательная к окружности всегда перпендикулярна её диаметру, один из концов которого является точкой касания.
- Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
- Точка касания двух окружностей лежит на прямой, проходящей через их центры.
- Длину дуги окружности радиуса , образованной центральным углом , измеренным в радианах, можно вычислить по формуле .
- Длину окружности с радиусом можно вычислить по формуле .
- Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.
- Угол между двумя секущими, проведёнными из точки, лежащей вне окружности равен полуразности мер дуг, лежащих между секущими.
- Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле и дуги напротив неё.
- Угол между касательной и хордой равен половине градусной меры дуги, стягиваемой хордой.
- Отрезки касательных к окружности, проведённых из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
- При пересечении двух хорд произведение отрезков, на которые делится одна из них точкой пересечения, равно произведению отрезков другой.
- Произведение длин расстояний от выбранной точки до двух точек пересечения окружности и секущей, проходящей через выбранную точку, не зависит от выбора секущей и равно абсолютной величине степени точки относительно окружности.
- Квадрат длины отрезка касательной равен произведению длин отрезков секущей и равен абсолютной величине степени точки относительно окружности.
- Окружность является простой плоской кривой второго порядка.
- Окружность является коническим сечением и частным случаем эллипса.
Основные формулы
Длина окружности:
Радиус окружности:
Диаметр окружности:
Площадь круга радиуса R:
Площадь сектора, ограниченного углом α, измеряемым в градусах, радиусом R:
Площадь сегмента, ограниченного дугой окружности углом α, хордой:
Уравнения
Декартовы координаты
Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)
Общее уравнение окружности записывается как:
или
где
Точка — центр окружности, — её радиус.
Уравнение окружности радиуса с центром в начале координат:
Уравнение окружности, проходящей через три точки (с помощью определителя) и
Окружность также можно описать с помощью параметрического уравнения:
В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:
Если центр окружности совпадает с началом координат, функции принимают вид:
Полярные координаты
Окружность радиуса с центром в точке :
Если полярные координаты центра окружности то проходящая через начало координат окружность описывается уравнением:
Если же центр является началом координат, то уравнение будет иметь вид:
Комплексная плоскость
На комплексной плоскости окружность задаётся формулой:
или в параметрическом виде
Касательные и нормали
Уравнение касательной к окружности в точке определяется уравнением
Уравнение нормали в той же точке можно записать как
Концентрические и ортогональные окружности
Две окружности, заданные уравнениями:
являются концентрическими (то есть имеющими общий центр) в том и только в том случае, когда и
Две окружности являются ортогональными (то есть пересекающиеся под прямым углом) тогда и только тогда, когда выполняется условие
См. также
- Вписанная окружность
- Описанная окружность
- Окружность Аполлония
Литература
- Математическая энциклопедия в пяти томах. — М: Советская энциклопедия, 1983.
- Маркушевич А. И. Замечательные кривые, выпуск 4. — М: Гостехиздат, 1952. — 32 с.
- Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 70.
- Атанасян Л.С., Бутузов В.Ф. Кадомцев С.Б. и др. Дополнительные главы к учебнику 8 класса // Геометрия. — 3-е издание. — М: Вита-Пресс, 2003.
Источник: https://dic.academic.ru/dic.nsf/ruwiki/6756




