Формулы площади треугольника и примеры применения

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Определение площади

Что такое площадь? Странный вопрос – не правда ли? В обычной жизни мы привыкли к тому, что у всяких плоских фигур (таких как поверхность стола, стула, пол наших квартир и т.д.) есть не только длина и ширина, но и какая-то еще характеристика, которую мы, не задумываясь, называем площадью. А теперь вот давай задумаемся: что же все-таки такое площадь?

Давай начнем с самого простого. За основу берется тот факт, что:

Площадь квадрата со стороной, равной   единице длины, равна   единице площади.

Другими словами, площадь квадрата со стороной   метр мы считаем одним «метром площади».

Но писать все время «метр площади» и слишком длинно, и звучит как-то странно. И вот, математики придумали название «метр квадратный» и обозначение « »

Посмотри внимательно на картинку и убедись, что там действительно нарисован – «метр квадратный»! И запомни обозначение.

А вот теперь хитрый вопрос: а что такое  ? Площадь квадрата со стороной  ? А вот и нет!

Смотри: квадрат со стороной  .

Пересчитай-ка сколько в нем квадратных метров? Удивительно, но получается  !

А чтобы получить   квадратных метра (то есть,  ), мы должны нарисовать, например так:

Видишь, здесь действительно нарисовано   квадратных метра?

• А как получить, скажем,  ? Ну например так:
• 
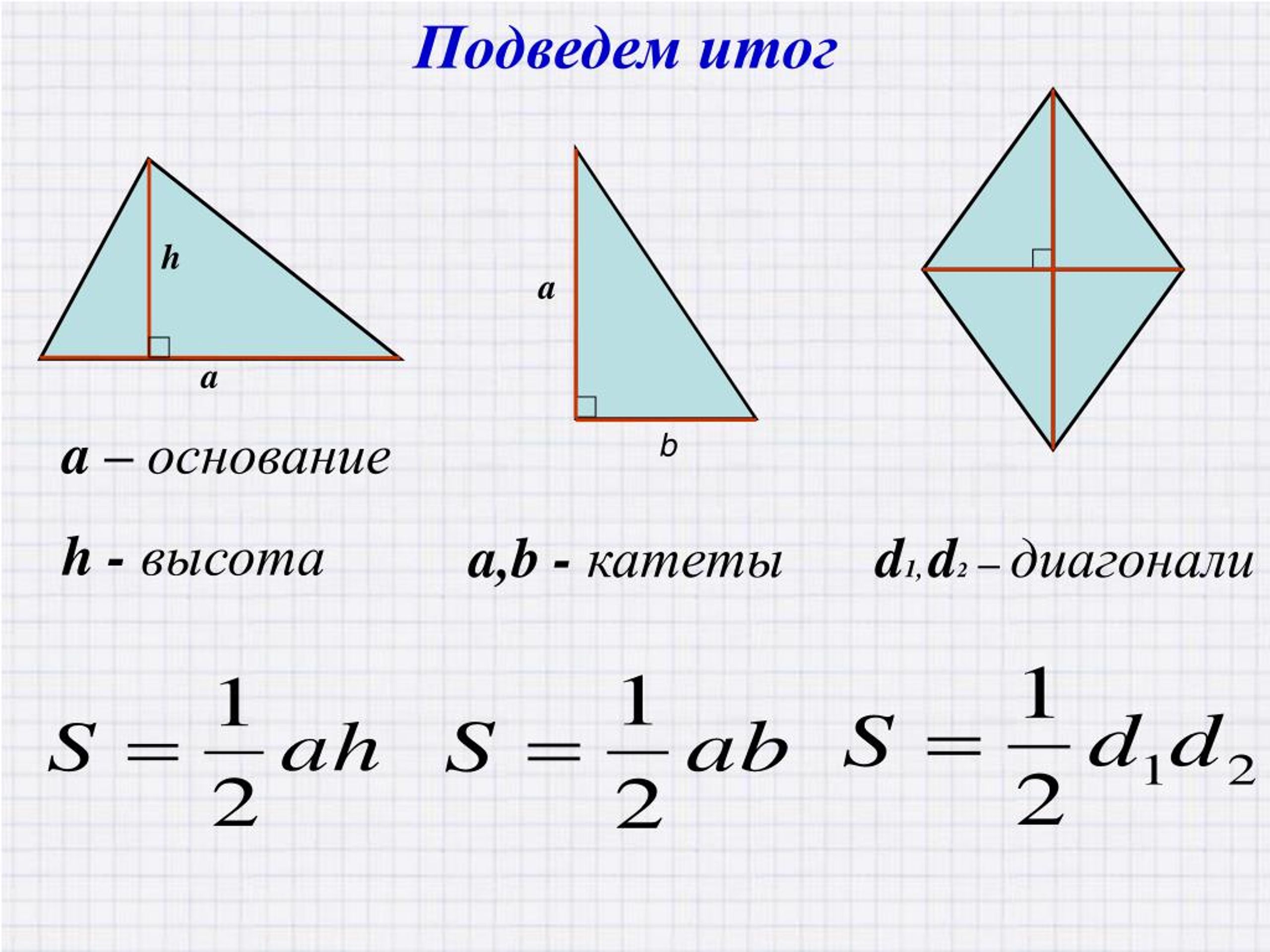
• Да и вообще, если мы возьмем прямоугольник, у которого стороны равны   метров и   метров, то в этом прямоугольнике:

Поместится ровно   квадратных метров. Посмотри внимательно: у нас есть   «слоев», в каждом из которых ровно   квадратных метров.

Значит, всего в прямоугольнике размером  x  поместилось   квадратных метров. Вот это число, сколько квадратных метров поместилось в прямоугольнике, и есть его площадь.

А если фигура – вовсе не прямоугольник, а какая-то абракадабра?

Можно ли узнать, сколько квадратных метров в ней находится? Можно ведь некоторые квадратные метры «порезать» , переставить и т.д….?

Удивлю тебя – бывают такие ужасные абракадабры, для которых совершенно невозможно установить сколько там квадратных метров. Даже приблизительно! К сожалению нарисовать такие фигуры – невозможно.

Но они есть! Они похожи, например, на такую «расческу» с очень мелкими зубьями.

Но мы такими «расческами» орудовать не будем, а будем рассматривать нормальные фигуры.

И вот, для нормальных фигур можно интуитивно (то есть для себя) считать ,что площадь фигуры – это такое число, сколько в этой фигуре «поместится» квадратных единиц (метров, сантиметров и т.д.) Более строгое, «настоящее» определение площади смотри в следующих уровнях теории.

И представь себе, математики для многих фигур научились выражать площади через какие-то линейные (те, что можно измерить линейкой) элементы фигур. Эти выражения называются «формулы площади». Формул этих довольно много – математики долго старались. Ты постарайся запомнить сначала самые простые и основные формулы, а потом уже те, что посложнее.

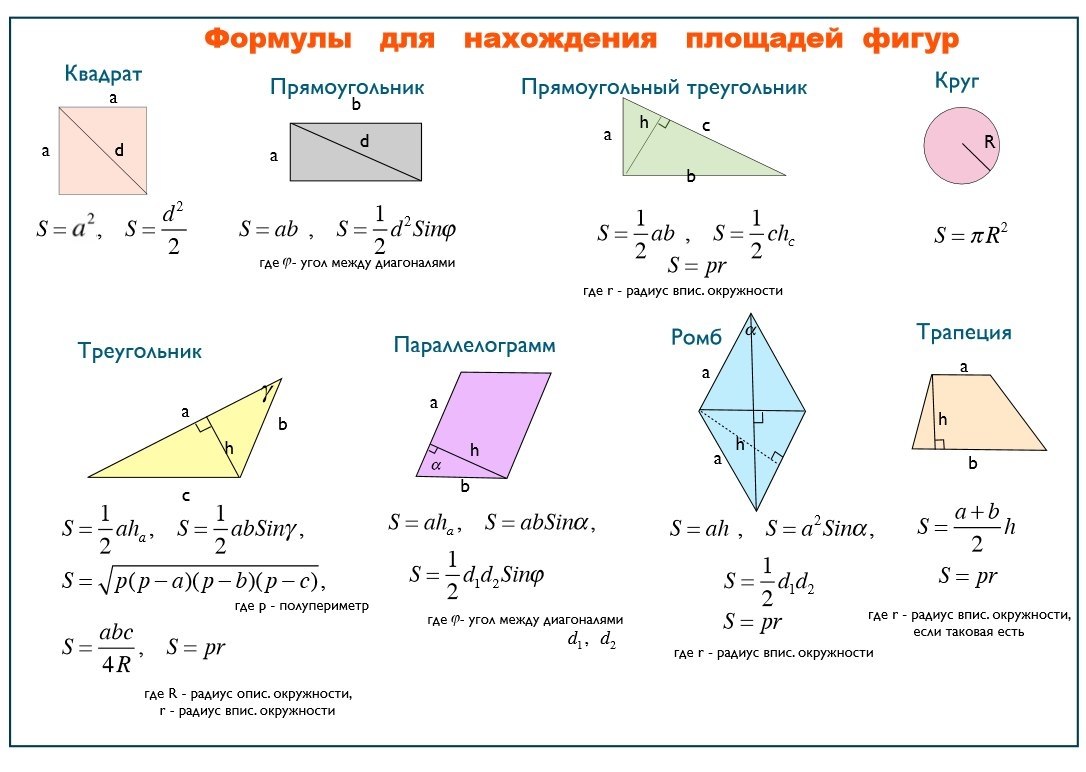
Формулы площади

Квадрат

— это просто, не правда ли?

Прямоугольник

— это мы уже успели обсудить.

Прямоугольный треугольник

Прямоугольный треугольник — ровно половина прямоугольника. Поэтому:    ,   – катеты.

Треугольник (произвольный)

Для треугольника есть сразу несколько формул площади.

Основная формула

– любая сторона,   – высота к этой стороне.

Вторая основная формула

,   – любые две стороны,   — угол между ними.

Третья формула

— полупериметр,   – радиус вписанной окружности.

Формула Герона

, ,  — стороны,   — полупериметр.

Какую же формулу выбрать для твоей задачки? Основными являются формулы 1 и 2. Третью формулу нужно применять, если тебе все дано: и три стороны, и радиус вписанной окружности.

Но так ведь не бывает, верно? Поэтому формулу 3 мы используем, скорее наоборот, для нахождения радиуса вписанной окружности .

Тогда нужно найти площадь по одной из формул 1, 2 или 4, а потом уже радиус:  .

Ну и формула 4 позволяет по  -м сторонам с помощью длиннющей арифметики находить площадь. И не ошибайся в арифметике, когда будешь применять формулу Герона!

Произвольный четырехугольник

— диагонали   — угол между ними

Для произвольного четырехугольника больше ничего нет, а вот для «хороших» четырехугольников – есть другие формулы.

Параллелограмм

Основная формула

— любая сторона,   — высота, опущенная на эту! cторону

Вторая формула

И, как для всякого четырехугольника:     — диагонали,   — угол между ними.

Ромб

У ромба диагонали перпендикулярны, поэтому основной для него становится  формула:

— и никакого   потому что  , и     — как всегда, диагонали

Вторая формула

А дополнительной формулой становится

— сторона,   — высота, опущенная на cторону.

Трапеция

Основная формула

— основания,   — высота.

Вторая формула

— ведь трапеция – тоже четырехугольник.   — диагонали,   — угол между ними.

«Хитрые вопросы о площади»

Кроме задачек, в которых просят просто найти площадь, встречаются еще всякие вопросики. Ну вот например:

Во сколько раз увеличится площадь квадрата, если его сторону увеличить в три раза?

Давай ответим на этот вопрос двумя способами. Первый способ – формальный: используем формулу площади квадрата. Итак, было  , значит   — площадь увеличилась в   раз!

В случае с квадратами есть и второй способ «пощупать» и убедится напрямую в этом числе  .

Рисуем:

Видишь, в квадрате со стороной   уместилось ровно   квадратов со стороной  . Значит формулам действительно можно верить.

Если же у тебя не квадрат, то остается только подставлять новые значения в формулы – и не удивляйся, если вдруг числа получатся довольно большими.

Площадь треугольника и четырехугольника. коротко о главном

Прямоугольник

Прямоугольный треугольник

Треугольник (произвольный)

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

1. Стать учеником YouClever,
2. Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц», 
3. А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.

можно кликнув по этой ссылке.

 

Источник: https://youclever.org/book/ploshhadi-ploskih-figur-1

Площадь треугольника

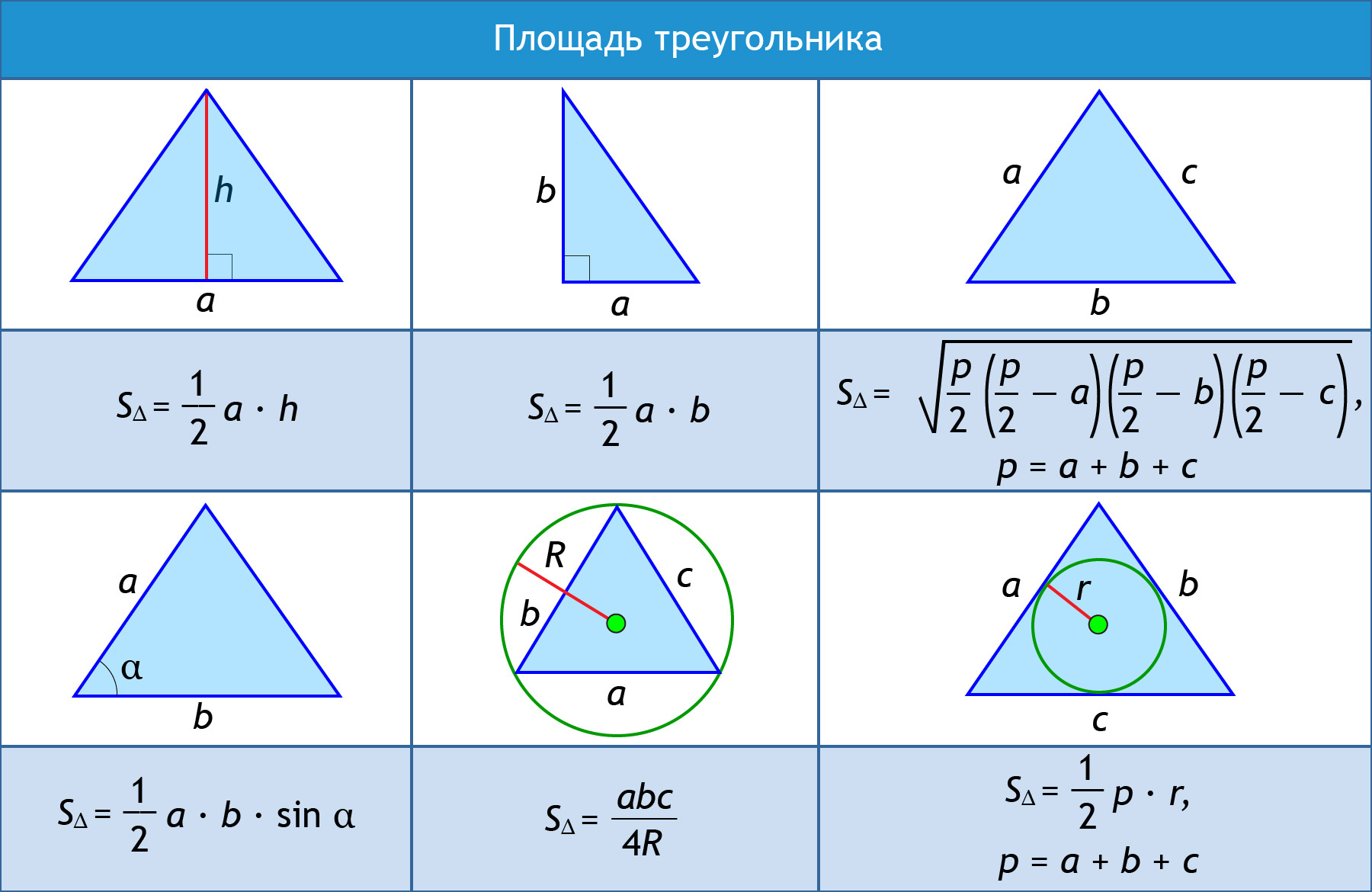
Площадь треугольника. Во многих задачах по геометрии связанных с вычислением площадей используются формулы площади треугольника. Их существует несколько, здесь мы рассмотрим основные. Перечислить эти формулы было бы слишком просто и пользы ни какой. Мы разберём происхождение основных формул, тех что используются наиболее чаще.

Перед тем как ознакомиться с выводом формул обязательно посмотрите статью о площади параллелограмма. После изучения материала вы без труда сможете восстановить формулы в памяти (если вдруг они «вылетят» в нужный вам момент).

• Первая формула
• Диагональ параллелограмма разбивает его на два равных по площади треугольника:
• 
• Следовательно площадь треугольника будет равна половине площади параллелограмма:
• 

Площадь треугольника формула

1. 
2. *То есть если нам будет известна любая сторона треугольника и высота опущенная на эту сторону, то мы всегда сможем вычислить площадь этого треугольника.
3. Формула вторая
4. Как уже было изложено в статье о площади параллелограмма формула имеет вид:
5. 
6. Площадь треугольника равна половине его площади, значит:
7. 
8. *То есть если будут известны любые две стороны в треугольнике и угол между ними, мы всегда сможем вычислить площадь такого треугольника.
9. Формула Герона (третья)
10. 

Данную формулу выводить сложно и вам это ни к чему. Посмотрите какая она красивая, можно сказать, что сама запоминается.

• *Если даны три стороны треугольника, то по данной формуле мы всегда можем вычислить его площадь.
• Формула четвёртая
• 
• где r – радиус вписанной окружности
• *Если известны три стороны треугольника и радиус вписанной в него окружности, то мы всегда можем найти площадь этого треугольника.
• Формула пятая
• 
• где R – радиус описанной окружности.
• *Если известны три стороны треугольника и радиус описанной около него окружности, то мы всегда можем найти площадь такого треугольника.
• Возникает вопрос: если  известны три стороны треугольника, то не проще ли его площадь найти по формуле Герона!

Да, бывает проще, но не всегда, иногда возникает сложность. Это связано с извлечением корня. Кроме того, данные формулы очень удобно применять в задачах, где дана площадь треугольника, его стороны и требуется найти радиус вписанной или описанной окружности. Такие задания имеются  в составе ЕГЭ.

1. Давайте отдельно рассмотрим формулу:
2. 
3. Она является частным случаем формулы площади многоугольника, в который вписана окружность:
4. Рассмотрим её на примере пятиугольника:
5. Соединим центр окружности с вершинами данного пятиугольника и опустим из центра перпендикуляры к его сторонам. Получим пять треугольников, при чём  опущенные перпендикуляры являются радиусами вписанной окружности:
6. Площадь пятиугольника равна:
7. Теперь понятно, что если речь идёт о треугольнике, то данная формула приобретает вид:
8. Формула шестая
9. Пусть сторона треугольника равна a, из противоположной вершины к этой стороне проведён произвольный отрезок образующий с ней угол (фи):
10. Тогда
11. Данная формула используется очень редко на практике, возможно вы её видите впервые, ну так просто написал, чтобы знали. Её ещё можно вывести преобразовав формулу площади четырёхугольника:
12. Также она является следствием из формулы:

Что добавить? Есть ещё формулы треугольника связанные с координатами  вершин, векторами на которых он построен. Об этом будет статья в будущем, не пропустите!

Площадь прямоугольного треугольника. Тут всё просто — она равна половине площади прямоугольника, то есть одной второй произведения катетов.

На этом всё! Успеха Вам!

С уважением, Александр Крутицких 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник: https://matematikalegko.ru/formuli/ploshhad-treugolnika-shest-formul.html

Свойства треугольника. В том числе равенство и подобие, равные треугольники, стороны треугольника, углы треугольника, площадь треугольника — формулы вычисления, прямоугольный треугольник, равнобедренный треугольник, высота треугольника

Навигация по справочнику TehTab.ru:  главная страница  / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.  / / Свойства треугольника. В том числе равенство и подобие, равные треугольники, стороны треугольника, углы треугольника, площадь треугольника — формулы вычисления, прямоугольный треугольник, равнобедренный треугольник, высота треугольника.

Свойства треугольников. Меню Треугольник -это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. Для инженера это еще и единственная «жесткая» плоская фигура на свете. Раздел математики, посвященный изучению закономерностей треугольников — тригонометрия. Сумма всех углов в треугольнике равна 180°. Обозначения в треугольнике. Вершины треугольника обычно обозначаются заглавными латинскими буквами (A, B, C), величины углов при соответственных вершинах — греческими буквами (α, β, γ), а длины противоположных сторон — прописными латинскими буквами (a, b, c). Виды треугольников: (по величине углов) Остроугольный треугольник — это треугольник, в котором все три угла острые, т.е. меньше 90°. Прямоугольный треугольник — это треугольник, содержащий прямой угол. Две стороны, образующие прямой угол, называются катетами (АС и АВ), а сторона, противолежащая прямому углу, называется гипотенузой (ВС). Тупоугольный треугольник — это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°. (по числу равных сторон) (по соотношению сторон) Равносторонний (правильный) треугольник — это треугольник, у которого все стороны и все углы равны (каждый угол равен 60°). Равнобедренный тругольник — это треугольник, у которого два угла и две стороны равны. Разносторонний треугольник — это треугольник, в котором все углы, а значит и все стороны попарно различны. (Разносторонний треугольник может быть остроугольным, прямоугольным и тупоугольным). Рассмотрим рис. ниже. Углы α, β, γ нызываются внутренними углами треугольника. Угол Θ — называется внешним углом треугольника, он равен сумме двух противолежащих ему внутренних углов, т.е. Θ= β+γ (а+с+b) — периметр треугольника. Угол α, называется смежным по отношению к углу Θ. ( α+ Θ)=180° (развернутый угол) Основные свойства треугольников. В любом треугольнике: Против большей стороны лежит больший угол, и наоборот. Против равных сторон лежат равные углы, и наоборот. (В частности, все углы в равностороннем треугольнике равны.) Сумма углов треугольника равна 180 °  (Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60 °). Продолжая одну из сторон треугольника (AВ), получаем внешний угол Θ. Любая сторона треугольника меньше суммы двух других сторон и больше их разности:  a < b + c,  a > b – c;  b < a + c,  b > a – c;  c < a + b,  c > a – b. Два треугольника называются конгруэнтными (равными), если они равны по всем параметрам, т.е. три угла и три стороны одного треугольника равны трем углам и трем сторонам другого треугольника. Признаки равенства треугольников: 1. Три стороны одного треугольника равны трем сторонам другого треугольника (по трем сторонам). 2. Две стороны одного треугольника равны двум сторонам другого треугольника и углы между этими сторонами также равны (по двум сторонам и углу между ними). 3. Три угла одного треугольника равны трем углам другого треугольника (по трем углам).4. Два угла одного треугольника равны двум углам другого треугольника, и любая сторона первого треугольника равна соответствующей стороне другого треугольника. Признаки равенства прямоугольных треугольников: Два прямоугольных треугольника равны, если у них соответственно равны: 1. Гипотенуза и острый угол. 2. Катет и противолежащий угол. 3. Катет и прилежащий угол. 4. Два катета.5. Гипотенуза и катет. Подобные треугольники. Два треугольника являются подобными, если углы одного треугольника равны, углам тругого треугольника, а стороны подобны, т.е. (р/а)=(q/b)=(r/c). Признаки подобия треугольников: Два угла одного треугольника равны двум углам другого треугольника. Две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны. Три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника. Свойства подобных треугольников. Отношение площадей подобных треугольников равно квадрату коэффициента подобия [(р/а)=(q/b)=(r/c)=коэффициент подобия]. Отношение периметров и длин либо биссектрис, либо медиан, либо высот, либо серединных перпендикуляров равно коэффициенту подобия. т.е. в подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны. Подобие в прямоугольных треугольниках. Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит: 1. Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому (Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось.) проекций катетов на гипотенузу. 2. Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу. Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. , т.е. BC2=AB2+AC2 см. рис. выше. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности: Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника AD, CF, BE пересекаются в одной точке O, всегда лежащей внутри треугольника и являющейся центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины. Медиана разбивает треугольник на два треугольника одинаковой площади. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников. Из двух медиан треугольника большая медиана проведена к его меньшей стороне. Биссектриса Биссектриса угла треугольника— это луч, который исходит из вершины треугольника, проходит между его сторонами и делит данный угол пополам. Три биссектрисы треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника. Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам например, на  рис. выше  AE:CE = AB:BC Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. Высота треугольника Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону (или её продолжение). Эта сторона называется основанием треугольника. Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника.Ортоцентр остроугольного треугольника (точка O на рис. выше) расположен внутри треугольника, а ортоцентр тупоугольного треугольника – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла. Прямые, содержащие высоты треугольника пересекаются в одной точке (ортоцентре треугольника). Отрезок, соединяющий основания высот остроугольного треугольника, отсекает от данного треугольника подобный ему с коэффициентом подобия, равным косинусу общего угла этих треугольников. Из двух высот треугольника большая высота проведена к его меньшей стороне. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники. В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны. Срединный перпендикуляр Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка(стороны). Три срединных перпендикуляра треугольника АВС(KO, MO, NO, рис.выше) пересекаются в одной точке О, являющейся центром описанного круга( точки K, M, N – середины сторон треугольника ABC). В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике. 1. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. 2. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника. Средняя линия Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Формулы площади треугольника 1.Произвольный треугольник — формулы площади a, b, c — стороны; α — угол между сторонами a и b; p=(a+b+c) / 2— полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; ha — высота, проведенная к стороне a. S=(1/2)*(a* ha) — по стороне и высоте. S=(1/2) *(a*b*sinα) по двум сторонам и синусу угла между ними — по длинам сторон — формула площади Герона S=p*r — через периметр и радиус вписанной окружности S=(a*b*c) / (4R) — через длины сторон и радиус описанной оружности a, b — катеты; c — гипотенуза; hc — высота, проведенная к стороне c. 1. S=(1/2)*a*b 2. S=(1/2)*c*hc S=(a2*√3)/4 — Синус α — это отношение AB/OB (отношение противолежащего катета к гипотенузе) — Косинус α — это отношение ОА/OB (отношение прилежащего катета к гипотенузе) — Тангенс α — это отношение AB/OA (отношение противолежащего катета к прилежащему) — Котангенс α — это отношение ОА/AB (отношение прилежащего катета к противолежащему)

Источник: https://tehtab.ru/guide/guidemathematics/perimsqvolgradrad/squaresofplainfigures/trianglesproporties/

«Формула Герона и другие формулы для площади треугольника»

• Конспект урока
• Тема: «Формула Герона и другие формулы для площади треугольника».
• Тип урока: урок открытия новых знаний.
• Класс:10.

Цели урока: обеспечить в ходе урока сознательное повторение формул для вычисления площади треугольника, которые изучаются в школьной программе.

Показать необходимость знания II формулы Герона, формулы площади треугольника, заданного в прямоугольной системе координат. Обеспечить сознательное усвоение и применение этих формул при решении задач.

1. Задачи:
2. Развивающие: развитие логического мышления, способности самостоятельно решать учебные задачи; развитие любознательностьучащихся, познавательного интереса к предмету; развитие творческого мышления, математической речи учащихся; 
3. Воспитательные: воспитание интереса к математике; создание условий для формирования коммуникативных навыков и волевых качеств личности.
4. Образовательные: углубление знаний модуля действительного числа; обучить умению решать типовые задачи.
5. Универсальные учебные действия:
6. Личностные: уважение к личности и ее достоинству; устойчивый познавательный интерес; умение вести диалог на основе равноправных отношений и взаимного уважения.
7. Регулятивные: ставить цели деятельности на уроке; планировать пути достижения цели; принимать решения в проблемной ситуации на основе переговоров.
8. Познавательные: владеть общими приемами решения задач, выполнения заданий и вычислений; выполнять задания на основе использования свойств  модуля действительного числа.
9. Коммуникативные: адекватно использовать речь для планирования и регуляции своей деятельности; формулировать собственное мнение.
10. Техническое обеспечение: компьютер, проектор, интерактивная доска.
11. Структура урока

1. Мотивационный этап – 2мин.

2. Домашняя работа – 1 мин.

3. Этап актуализации знаний по предложенной теме и осуществление первого пробного действия – 10 мин.

4. Выявление затруднения: в чем сложность нового материала, что именно создает проблему, поиск противоречия — 4 мин.

5. Разработка проекта, плана по выходу их создавшегося затруднения, рассмотрения множества вариантов, поиск оптимального решения – 2 мин.

6. Реализация выбранного плана по разрешению затруднения- 5 мин.

7. Первичное закрепление нового знания — 10 мин.

8. Самостоятельная работа и проверка по эталону – 5 мин.

9. Рефлексия, включающая в себя и рефлексию учебной деятельности, и самоанализ, и рефлексию чувств и эмоций – 1мин.

Ход урока.

Здравствуйте ребята, присаживайтесь. Сегодня наш урок пройдёт  по следующему плану: в ходе урока мы изучим новую тему: «Формула Герона и другие формулы для площади треугольника»; повторим те формулы, которые вы знаете; научимся применим эти формулы при решении задач. Итак, приступаем к работе.

1. Этап актуализации знаний по предложенной теме и осуществление первого пробного действия.

Слайд 1.

Запишите тему урока. Прежде чем приступить непосредственно к формулам, давайте вспомним какие же формулы для вычисления площади треугольника вы знаете? (учащиеся вспоминает все изученные ими формулы)

• Слайд 2.
• Напишите эти формулы.
• Какие же формулы для вычисления площади треугольника вы знаете? (учащиеся вспоминает все изученные ими формулы)
• Слайд 3.

Площадь прямоугольного треугольника. S=ab. Запишите формулу

Слайд 4.

Площадь любого треугольника. S= а. a= , = Запишите формулу.

Слайд 5. Площадь треугольника по двум сторонам и углу между ними.

S=½·ab·sinα. Запишите формулу.

А теперь мы изучим новые формулы для нахождения площади.

Слайд 6.

Площадь треугольника через радиус вписанной окружности. S = Р r. Запишите формулу.

1. Слайд 7.
2. Площадь треугольника через R-радиус описанной окружности.
3. , Запишите формулу.
4. S =
5. Слайд 8.
6. Формула Герона.
7. Прежде чем приступим к доказательству вспомним две теоремы геометрии — это теорема синусов и теорема косинусов.
8. 1. , a=2R; b=2R; c=2R

2., cos γ = .

Слайд 9- 10

Доказательство формулы Герона. Запишите формулу.

Слайд 11.

Формула площади треугольника по трём сторонам была открыта Архимедом в III в до н.э. Однако соответствующая работа до наших дней не дошла. Эта формула содержится в «Метрике» Герона Александрийского (I в н. э.

) и названа в его честь. Герон интересовался треугольниками с целочисленными сторонами, площади которых также являются целыми. Такие треугольники носят название Героновых треугольников.

Простейшим Героновым треугольником является египетский треугольник

1. Выявление затруднения: в чем сложность нового материала, что именно создает проблему, поиск противоречия.

Слайд 12.

Найдите площадь треугольника с данными сторонами: 4,6,8. Хватает ли сведений для решения задачи? Через какую формулу можно решить данное задание?

1. Разработка проекта, плана по выходу их создавшегося затруднения, рассмотрения множества вариантов, поиск оптимального решения.

Данную задачу можно решить с помощью формулы Герона. Для начало необходимо найти полупериметр треугольника, а затем полученные значения подставить в формулу.

1. Реализация выбранного плана по разрешению затруднения.

• Нахождение р
• p=(13+14+15)/2=21
• p-a=21-13=8
• p-b=21-14=7
• p-c=21-15=6
• S = 21*8*7*6=84
• Ответ:84
• Задача №2
• Найдите стороны треугольника ABC, если площадь треугольников ABO,BCO,ACO ,где О-центр вписанной окружности, равны 17,65,80 дц2.
• Решение:
• S=17+65+80=162 –складываем площади треугольников. По формуле
• SABO=1/2AB*r, следовательно 17=1/2AB*r ; 65=1/2ВС*r; 80=1/2AC*r
• 34/r=AB; 130/r=BC; 160/r=AC
• Находим р
• p= (34+130+160)/2=162/r
• (р-а)=162-34=128 (р-c)=162-160=2
• (р-b)=162-130=32
• По формуле Герона S=128/r*2/r*32/r*162/r=256*5184/r4=1152/r2
• Т.к S=162, следовательно r =1152/162=3128/18
• Ответ:AB=34/3128/18, ВС=130/3128/18, АС=160/3128/18.

1. Первичное закрепление нового знания.

№10(1)

Найдите площадь треугольника с данными сторонами:

№12

1. Самостоятельная работа и проверка по эталону.

№10.(2)

1. Домашнее задание. П.83, №10(3), №15

2. Рефлексия, включающая в себя и рефлексию учебной деятельности, и самоанализ, и рефлексию чувств и эмоций.

Какие формулы вы сегодня повторили?

Какие формулы вы узнали только сегодня?

Источник: https://infourok.ru/formula-gerona-i-drugie-formuli-dlya-ploschadi-treugolnika-2154241.html

Напишите формулу нахождение площади треугольника

Формулы, для нахождения площади треугольника: 1. По стороне и высоте.Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты. Т.е. S = 1/2ah 2. По трем сторонам. S = √p(p — a) (p — b) (p — c). 3. По двум сторонам и углу между ними. Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. Т.е. S = 1/2 * a * b* siny. 4. По трем сторонам и радиусу описанной окружности. S = (a * b * c) / 4R. 5. По трем сторонам и радиусу вписанной окружности. Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. S = p * r.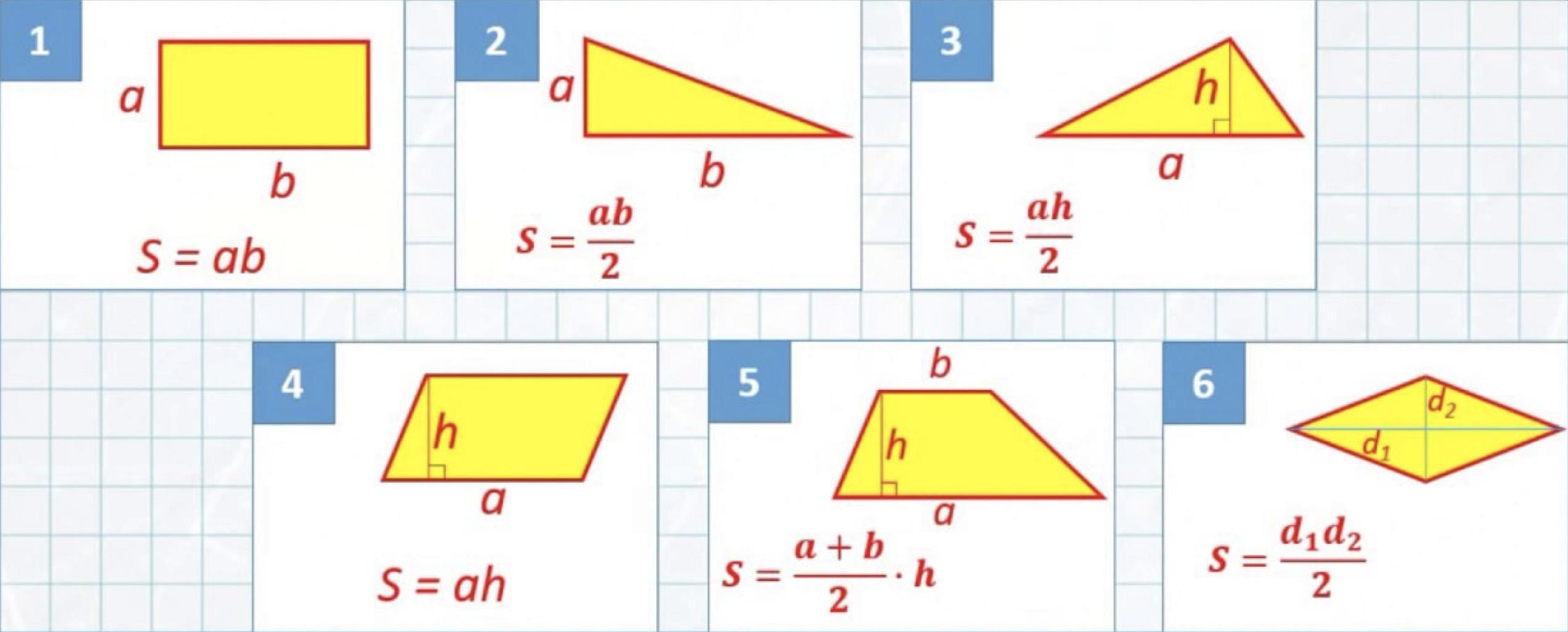

В зависимости от формы треугольника существуют различные формулы для определения его площади.

1. Классическая формула определения площади треугольника.
2. Формула для равностороннего треугольника.
3. Формула для прямоугольного треугольника.
4. Формула площади для равнобедренного треугольника.

Классическая формула площади треугольника

В данной формуле площадь равна произведению половины основания на высоту, где:

• S — площадь треугольника;
• a — основание треугольника;
• h — высота треугольника.

S = 1/2 * a * h.

Площадь равностороннего треугольника

• Можно использовать как классическую формулу, так и данную формулу.
• a — одна из сторон равностороннего треугольника.
• S = √3/4 * a^2.
• Если а = 8 см получим:
• S = √3/4 * 8 * 8 = 27,7 см^2.

Площадь прямоугольного треугольника

1. Площадь равна произведению половины первого катета на второй катет.
2. S = 1/2 * a * b,
3. Где:

• S — площадь;
• a — первый катет;
• b — второй катет.

Площадь равнобедренного треугольника

• Можно использовать классическую формулу и данную:
• S = (b * √(a^2 — b^2/4))/2.
• а — длина бедра;
• b — длина основания.
• Если а = 6 см, b = 4 см, получим:
• S = (4 * √(6^2 — 4^2/4))/2 =(4 * √(36 — 4))/2 = (4 * 5,66) / 2 = 11,32 см^2.

Знаешь ответ?

Как написать хороший ответ?

Будьте внимательны!

• Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. ?
• Публикуются только развернутые объяснения. Ответ не может быть меньше 110 символов!

Источник: https://vashurok.ru/questions/napishite-formulu-nahozhdenie-ploschadi-treugolnika

Площадь треугольника — формулы и примеры решения задач

Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров.

Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности.

Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.

Примечание. Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы: 

  

Формулы площади треугольника

Пояснения к формулам: a, b, c — длины сторон треугольника, площадь которого мы хотим найти r — радиус вписанной в треугольник окружности R — радиус описанной вокруг треугольника окружности h — высота треугольника, опущенная на сторону p — полупериметр треугольника, 1/2 суммы его сторон (периметра) α — угол, противолежащий стороне a треугольника β — угол, противолежащий стороне b треугольника γ — угол, противолежащий стороне c треугольника ha, hb, hc — высота треугольника, опущенная на сторону a, b, c

Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.

• Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на  два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
• Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2 ) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
• Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
• Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
• Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
• Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
• Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
• Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов. (Формула 8)
• Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
• Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
• Формула 11 позволяет вычислить площадь треугольника по координатам его вершин, которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений

См. также площадь равнобедренного треугольника.

Примечание. Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме.

В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение.

 Иногда для простых подкоренных выражений может использоваться символ √

Задача. Найти площадь по двум сторонам и углу между ними

Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника.

• Решение.
• Для решения этой задачи используем формулу номер два из теоретической части урока. Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
• S=1/2 ab sin γ
• Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу: S = 1/2 * 5 * 6 * sin 60   

В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов. Он будет равен корню из трех на два.  S = 15 √3 / 2

Ответ: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)

Задача. Найти площадь равностороннего треугольника

1. Найти площадь равностороннего треугольника со стороной 3см.
2. Решение.

Площадь треугольника можно найти по формуле Герона:

S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )

• Поскольку a = b = c формула площади равностороннего треугольника примет вид:
• S = √3 / 4 * a2
• S = √3 / 4 * 32
• S = 9 √3 / 4
• Ответ: 9 √3 / 4. 

Задача. Изменение площади при изменении длины сторон

Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?

Решение.

Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.

Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.

Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:

1. S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )  (см. первую строку рисунка внизу)
2. Длины сторон произвольного треугольника заданы переменными a, b, c. Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:
3. S2 = 1/4 sqrt( ( 4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c) ) (см. вторую строку на рисунке внизу)
4. Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики. Тогда
5. S2 = 1/4 sqrt( 4 * 4 * 4 * 4 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — на третьей строке рисунка S2 = 1/4 sqrt( 256 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — четвертая строка
6. Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня     S2 = 16 * 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) S2 = 4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) (см. пятую строку рисунка внизу)

Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального. Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.

S2 / S = 16 (см. внизу подробнее запись в виде дроби и ее сокращения — в последней строке)

На рисунке логика вычисления решения, описанного выше, приведена уже в виде формул (одна за другой)

Ответ: Площадь треугольника увеличится в 16 раз

10380.6235  

 Сумма углов треугольника | Описание курса | Медиана треугольника 

Источник: https://profmeter.com.ua/communication/learning/course/course7/lesson133/