Формула емкости конденсатора, с

Если вы рассмотрите печатную плату даже самого простого электронного устройства, то обязательно увидите конденсатор, а чаще всего встретите множество этих элементов. Присутствие этих изделий на различных электронных схемах объясняется свойствами данных радиоэлементов, широким диапазоном функций, которые они выполняют.

В настоящее время промышленность поставляет на рынок конденсаторную продукцию различных видов (рис. 1). Параметры изделий варьируются в широких пределах, что позволяет легко подобрать радиодеталь для конкретной цели.

Рис. 1. Распространённые типы конденсаторов

Рассмотрим более подробно конструкции и основные параметры этих вездесущих радиоэлементов.

Что такое конденсатор?

В классическом понимании конденсатором является радиоэлектронное устройство, предназначенное для накопления энергии электрического поля, обладающее способностью накапливать в себе электрический заряд, с последующей передачей накопленной энергии другим элементам электрической цепи. Устройства очень часто используют в различных электрических схемах.

Конденсаторы способны очень быстро накапливать заряд и так же быстро отдавать всю накопленную энергию. Для их работы характерна цикличность данного процесса. Величина накапливаемого электричества и периоды циклов заряда-разряда определяется характеристиками изделий, которые в свою очередь зависят от типа модели. Параметры этих величин можно определить по маркировке изделий.

Конструкция и принцип работы

Простейшим конденсатором являются две металлические пластины, разделённые диэлектриком. Выступать в качестве диэлектрика может воздушное пространство между пластинами. Модель такого устройства изображена на рис. 2.

Рис. 2. Модель простейшего конденсаторного устройства

Если на конструкцию подать постоянное напряжение, то образуется кратковременная замкнутая электрическая цепь. На каждой металлической пластине сконцентрируются заряды, полярность которых будет соответствоать полярности приложенного тока. По мере накопления зарядов ток будет ослабевать, и в определенный момент цепь разорвётся. В нашем случае это произойдёт молниеносно.

При подключении нагрузки накопленная энергия устремится через нагрузочный элемент в обратном направлении. Произойдёт кратковременный всплеск электрического тока в образованной цепи. Количество накапливаемых зарядов (ёмкость, C) прямо зависит от размеров пластин.

Единицу измерения ёмкости принятоназывать фарадой (Ф). 1 F – очень большая величина, поэтому на практике часто применяют кратные величины: микрофарады (1 мкФ = 10-6 F), нанофарады ( 1 нФ = 10-9 F = 10-3 мкФ), пикофарады (1 пкФ = 10-12 F = 10-6  мкФ). Очень редко применяют величину милифараду (1 мФ = 10-3 Ф).

Конструкции современных конденсаторов отличаются от рассматриваемой нами модели. С целью увеличения ёмкости вместо пластин используют обкладки из алюминиевой, ниобиевой либо танталовой фольги, разделённой диэлектриками. Эти слоеные ленты туго сворачивают в цилиндр и помещают в цилиндрический корпус. Принцип работы не отличается от описанного выше.

Существуют также плоские конденсаторы, конструктивно состоящие из множества тонких обкладок, спрессованных между слоями диэлектрика в форме параллелепипеда. Такие модели можно представить себе в виде стопки пластин, образующих множество пар обкладок, соединённых параллельно.

В качестве диэлектриков применяют:

• бумагу;
• полипропилен;
• тефлон;
• стекло;
• полистирол;
• органические синтетические плёнки;
• эмаль;
• титанит бария;
• керамику и различные оксидные материалы.

Отдельную группу составляют изделия, у которых одна обкладка выполнена из металла, а в качестве второй выступает электролит. Это класс электролитических конденсаторов (пример на рисунке 3 ниже).

Они отличаются от других типов изделий большой удельной ёмкостью. Похожими свойствами обладают оксидно-полупроводниковые модели.

Второй анод у них – это слой полупроводника, нанесённый на изолирующий оксидный слой.

Рис. 3. Конструкция радиального электролитического конденсатора

Электролитические модели, а также большинство оксидно-полупроводниковых конденсаторов имеют униполярную проводимость. Их эксплуатация допустима лишь при наличии положительного потенциала на аноде и при номинальных напряжениях. Поэтому следует строго соблюдать полярность подключения упомянутых радиоэлектронных элементов.

На корпусе такого прибора обязательно указывается полярность (светлая полоска со значками «–», см. рис. 4) или значок «+» со стороны положительного электрода на корпусах старых отечественных конденсаторов.

Рисунок 4. Обозначение полярности выводов

Срок службы электролитического конденсатора ограничен. Эти приборы очень чувствительны к высоким напряжениям. Поэтому при выборе радиоэлемента старайтесь, чтобы его рабочее напряжение было значительно выше номинального.

Свойства

Из описания понятно, что для постоянного тока конденсатор является непреодолимым барьером, за исключением случаев пробоя диэлектрика.

В таких электрических цепях радиоэлемент используется для накопления и сохранения электричества на его электродах. Изменение напряжения происходит лишь в случаях изменений параметров тока в цепи.

Эти изменения могут считывать другие элементы схемы и реагировать на них.

Ещё одно свойство состоит в том, что переменную емкость можно использовать для сдвига фаз. Существуют специальные пусковые конденсаторы (рис.5), применяемые для запусков трёхфазных электромоторов в однофазных электросетях.

Рис. 5. Пусковой конденсатор с проводами

Основные параметры и характеристики

• Ёмкость.
• Важным параметром конденсатора является его номинальная ёмкость. Для плоского конденсатора справедлива формула:
• С = (ε*ε*S) / d,
• где ε – диэлектрическая проницаемость диэлектрика, S – размеры обкладок (площадь пластин), d – расстояние между пластинами (обкладками).

Реальная емкость отдельных элементов обычно невелика, но можно получить конструкцию ёмкостью в несколько фарад, если параллельно соединить огромное число обкладок. В этом случае реальная ёмкость равняется сумме всех ёмкостей обкладок.

Максимальные емкости некоторых конденсаторов могут достигать нескольких фарад.

Удельная ёмкость.

Величина, характеризующая отношение ёмкости к объёму или к массе радиодетали. Данный параметр важен в микроэлектронике, где размеры деталей очень важны.

Номинальное напряжение.

Одной из важных электрических характеристик является номинальное напряжение – значение максимальных напряжений, при которых конденсатор может работать без потери значений других его параметров.

При превышении критической величины равной напряжению пробоя происходит разрушение диэлектрика.

Поэтому номинальное напряжение подбирают заведомо большее любых возможных максимальных амплитуд синусоидального тока в цепи конденсатора.

Существуют характеристики, такие как тангенс угла потерь, температурный коэффициент ёмкости, сопротивление утечки, диэлектрическая абсорбция и др., которые интересны только узким специалистам, а их параметры можно узнать из специальных справочников.

Классификация

Основные параметры конденсаторных изделий определяются типом диэлектрика. От материала зависит стабильность ёмкости, тангенс диэлектрических потерь, пьезоэффект и другие. Исходя из этого, классификацию моделей целесообразно осуществлять именно по виду диэлектрика.

По данному признаку различают следующие типы изделий:

• вакуумные;
• с воздушным диэлектриком;
• радиоэлементы, в которых диэлектриком является жидкость;
• с твёрдым неорганическим диэлектриком (стекло, слюда, керамика). Характеризуются малым током утечки;
• модели с бумажным диэлектриком и комбинированные, бумажно-плёночные;
• масляные конденсаторы постоянного тока;
• электролитические;
• категория оксидных конденсаторов, к которым относятся оксидно-полупроводниковые и танталовые конденсаторы;
• твёрдотельные, у которых вместо жидкого электролита используется органический полимер или полимеризованный полупроводник.

В
твёрдотельных моделях срок службы больший, чем у жидко-электролитических и составляет
около 50 000 часов. У них меньшее внутренне сопротивление, то есть ЭПС почти
не зависит от температуры, они не взрываются.

Классифицируют изделия и по другому важному параметру – изменению ёмкости. По данному признаку различают:

• постоянные конденсаторы, то есть те, которые имеют постоянную емкость;
• переменные, у которых можно управлять изменением ёмкости механическим способом либо с помощью приложенного напряжения (варикапы и вариконды), а также путём изменения температуры (термоконденсаторы);
• класс подстроечных конденсаторов, которые используют для подстройки или выравнивания рабочих ёмкостей при настройке контуров, а также с целью периодической подстройки различных схем.

Все существующие конденсаторы можно условно разделить на общие и специальные. К изделиям общего назначения относятся самые распространённые низковольтные конденсаторы (см. рис. 6). К ним не предъявляют особых требований.

Рис. 6. Конденсаторы общего назначения

Все остальные ёмкостные радиоэлементы принадлежат к классу специального назначения:

• импульсные;
• пусковые;
• высоковольтные (см. рис. 7);
• помехоподавляющие,
• дозиметрические и др.;

Рис. 7. Высоковольтные конденсаторы

Изображённые на фото устройства могут работать в высоковольтных цепях сравнительно низкой частоты.

Маркировка

Для маркировки отечественных изделий применялась буквенная система. Сегодня распространена цифровая маркировка. В буквенной системе применялись символы:

• К – конденсатор;
• Б, К, С, Э и т. д
  – тип диэлектрика, например: К – керамический, Э – электролитический;
• На третьем месте
  стоял символ, обозначающий особенности исполнения.

В данной системе маркировки иногда первую букву опускали.

В новой системе маркировки на первом месте может стоять буква К, а после неё идёт буквенно-цифровой код. Для обозначения номинала, вида диэлектрика и номера разработки используют цифры. Пример такой маркировки показан на рисунке 8. Обратите внимание на то, что на корпусе электролитического конденсатора обозначена полярность включения.

Рис. 8. Маркировка конденсаторов

• Ёмкость от 0 до 999 пФ указывают в пикофарадах, например: 250p:
• от 1000 до 999999 пФ – в нанофарадах: n180;
• от 1 до 999 мкФ – в микрофарадах: 2μ5;
• от 1000 до 999999 мкФ – в миллифарадах: m150;
• ёмкость, больше значения 999999 мкФ, указывают в фарадах.

Обозначение на схемах

Каждое семейство конденсаторов имеет своё обозначение, позволяющее визуально определить его тип (см. рис. 9).

Рис. 9. Обозначение на схемах

Соединение конденсаторов

Существует два способа соединения: параллельное и последовательное. При параллельном соединении общая ёмкость равна сумме ёмкостей отдельных элементов: Собщ. = С1 + С2 + … + Сn.

Для последовательного соединения расчёт ёмкости рассчитывается по формуле: Cобщ. = ( C1* C2 *…* Cm ) / ( C1 + C2+…+Cn )

Чтобы быстро посчитать общую емкость соединенных конденсаторов лучше воспользоваться нашими калькуляторами:

Применение

Конденсаторы применяются почти во всех областях электротехники. Перечислим лишь некоторые из них:

• построение цепей обратной связи, фильтров, колебательных контуров;
• использование в качестве элемента памяти;
• для компенсации реактивной мощности;
• для реализации логики в некоторых видах защит;
• в качестве датчика для измерения уровня жидкости;
• для запуска электродвигателей в однофазных сетях переменного тока.

С
помощью этого радиоэлектронного элемента можно получать импульсы большой
мощности, что используется, например, в фотовспышках, в системах зажигания карбюраторных
двигателей.

Источник: https://www.asutpp.ru/chto-takoe-kondensator.html

Ёмкость конденсатора: в чём измеряется и от чего зависит величина, как её определить, формулы расчёта

История накопителей заряда

Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.

Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.

Первое устройство для хранения полученных зарядов было создано в 1745 г. двумя электриками (так тогда называли людей, изучающих природу статического электричества), работающими независимо друг от друга: Эвальдом фон Клейстом, деканом собора в Пруссии, и Питером ван Мюссенбруком, профессором математики и физики в университете Лейдена.

Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях.

Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни.

Основные даты хронологии появления устройств для хранения зарядов:

• 1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
• 1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
• 1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
• конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
• начало XX в. — изобретение слюдяных и керамических конденсаторов.

Физика ёмкостных характеристик

Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.

Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным.

В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу.

В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.

Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью.

Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства.

Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:

• геометрия пластин;
• расстояние между ними;
• диэлектрический материал между пластинами.

Единица и формулы расчёта

Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.

Математическое выражение фарада

Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:

• пикофарад — 10—12 Ф;
• нанофарад — 10—9 Ф;
• микрофарад — 10—6 Ф.

Диэлектрическая проницаемость

Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:

• А — площадь меньшей пластины;
• d — расстояние между ними;
• ε — абсолютная проницаемость используемого диэлектрического материала.

На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:

• 1,0006 — воздух;
• 2,5—3,5 — бумага;
• 3—10 — стекло;
• 5—7 — слюда.

Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.

Практические измерения

Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.

Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость.

Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат.

Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.

Вам это будет интересно  Киловатт — производная единица измерения мощности

Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность.

Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.

Идея суперконденсатора

Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.

Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них.

При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ.

Основные недостатки аккумуляторов по сравнении и конденсаторами:

• непродолжительный жизненный цикл;
• невысокая удельная мощность;
• узкий диапазон температур зарядки и разрядки;
• неспособность быстро отдать весь запас энергии.

Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.

Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками.

Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.

Источник: https://rusenergetics.ru/praktika/formula-raschyota-yomkosti-kondensatora

Емкость конденсаторов: определение, формулы, примеры

Определение 1

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:

C=qφ1-φ2=qU.

Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика.

Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным.

Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.

Плоский конденсатор

Определение 2

Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.

Формула для расчета электроемкости записывается как

C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε — диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.

Рисунок 1

При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:

C=ε0Sd1ε1+d2ε2+…+dNεN.

Сферический конденсатор

Определение 3

Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.

Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:

C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.

Рисунок 2

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

C=2πεε0llnR2R1, где l — высота цилиндров, R1 и R2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.

Рисунок 3

Определение 4

Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.

Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Электроемкость плоского конденсатора. Формулы

Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:

C=∑i=1NCi.

При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:

Пример 1

Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.

• Решение
• Чтобы рассчитать электроемкость конденсатора, применяется формула:
• C=εε0Sd.
• Значения:
• ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.
• Подставим числовые выражения и вычислим:
• C=8,85·10-12·10-410-3=8,85·10-13 (Ф).
• Ответ: C≈0,9 пФ.

Пример 2

Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения — 103 В.

1. Решение
2. Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
3. E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x — расстояние от центра сферы.
4. Нахождение заряда предполагает применение определения емкости конденсатора С:
5. q=CU.
6. Для сферического конденсатора предусмотрена формула вида
7. C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.
8. Производим подстановку выражений для получения искомой напряженности:
9. E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.
10. Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:
11. E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.
12. Ответ: E=3,45·104 Вм.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Источник: https://Zaochnik.com/spravochnik/fizika/elektricheskoe-pole/emkost-kondensatorov/

Конденсатор: формулы для конденсаторов

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

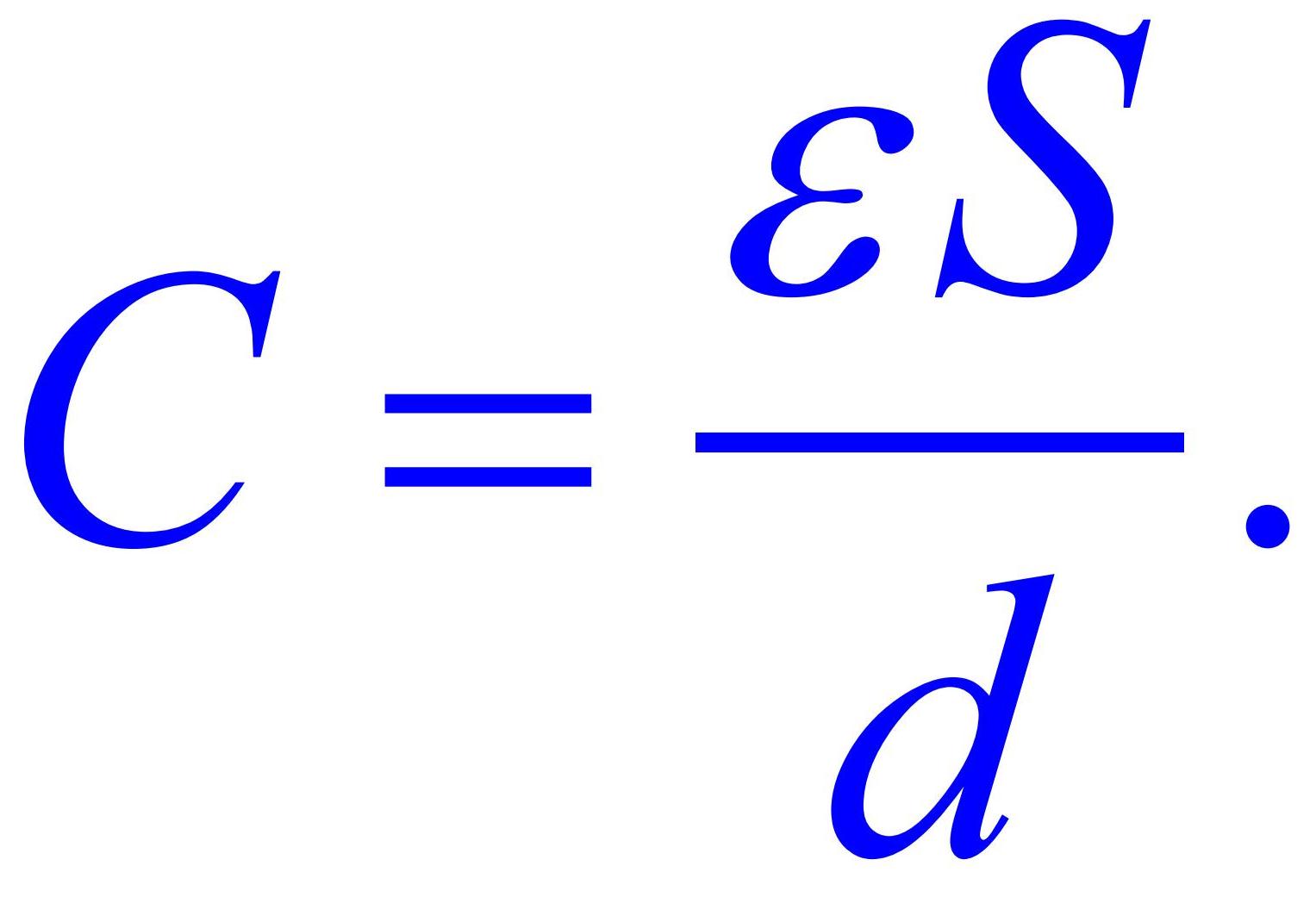
Для расчетов емкости плоского конденсатора используется формула: в которой ε = 8,854187817 х 10-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора.

После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки.

С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

Как перевести киловатты в ватты

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора.

Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами.

Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed.

Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2.

Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU2/2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение.

Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки.

В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции.

В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.

Источник: https://electric-220.ru/news/kondensator_formuly/2016-09-22-1067

Емкость конденсатора: формула

Емкостный показатель является одной из основных характеристик не только батареек и аккумуляторных элементов, но и конденсаторных устройств.

Любому человеку, работающему с электросхемами, необходимо знать, от чего зависит эта величина, может ли она уменьшиться или увеличиться под влиянием внешних факторов (как, например, период времени, зарядка элемента или частота напряжения), и как выглядит выражающая емкость конденсатора формула для разных типов элементов.

Измерение емкостных данных мультиметром

Расчёт конденсаторов

• В общем случае емкостной показатель С определяется по формуле:
• C=q/U,
• где q – заряд конденсатора на одной из его пластин, U – значение напряжения на конденсаторе.
• Из этого выражения можно вывести формулу заряда конденсатора, величину которого можно найти, измерив два других показателя с помощью мультиметра.

Часто возникает вопрос, может ли этот параметр измениться. Он является постоянной величиной, присущей данному элементу и зависящей от его габаритов и устройства.

Узнать емкостное значение можно с помощью мультиметра. Пользуясь этими данными, можно рассчитать целевую индуктивность дросселя для колебательного контура или параметры резистора.

В чем измеряется емкость? За измерительную единицу принимается параметр конденсаторного устройства, который можно зарядить 1 Кл до состояния, когда разница потенциалов будет равной 1 вольту. Название этой единицы – фарад (Ф).

Ниже приведены формулы для конденсаторных элементов разной конфигурации. Рассчитанные по ним значения соответствуют идеальным устройствам, но релевантны и для реальных в тех случаях, когда емкостными потерями можно пренебречь.

Формула электрической емкости плоского конденсатора

В основном электрополе пластин плоского конденсатора бывает однородным, за исключением боковых частей, влиянием которых обычно принято пренебрегать.

Однако, если пространство между обкладками велико в сопоставлении с их габаритами, краевые искажения нужно учитывать.

В общем случае, чтобы высчитать, сколько фарад составит емкость плоского конденсатора, пользуются выражением:

C=E*E0*S/d, где S – площадь меньшей обкладки, E0 – электрическая константа, d – длина пространства между пластинами.

Плоский конденсаторный элемент

Формула электрической емкости цилиндрического изделия

Такой компонент состоит из пары разных по размеру коаксиальных цилиндрических элементов проводника, в пространстве между которыми расположили диэлектрический материал. В этом случае для нахождения емкостной величины не нужно узнавать значение заряда на обкладках конденсатора. Можно воспользоваться следующей формулой емкости:

С=2 π *E*E0*l / ln(R2/R1).

Здесь R1 и R2 – радиусы, соответственно, внутреннего и наружного цилиндров, l – их высота (она одинакова, в то время как радиальные параметры отличаются).

Формула для сферического изделия

1. Сферическая деталь состоит из двух проводниковых сфер с диэлектрическим слоем между ними. Вот как найти емкость круглого конденсатора:
2. C=4 π *E*E0* R1* R2 / R2 – R1.
3. Буквами R обозначены, как и в предыдущем примере, радиусы компонентов.

Ёмкость одиночного проводника

Это характеристика способности твердого проводникового компонента к удержанию электрозаряда.  Она определяется особенностями средового окружения (в частности, диэлектрической проницаемостью), взаиморасположением тел, имеющих на себе заряд, размерами детали. От силы тока и величины заряда она не зависит.

Способы соединения элементов

Монтаж изделия на плату может быть вертикальным или горизонтальным. При использовании нескольких изделий они могут быть соединены между собой разными способами.

Параллельное соединение

Для его организации нужно подключить группу  деталей к электроцепи так, чтобы обкладки всех деталей были подсоединены напрямую к местам включения. Поскольку все компоненты получают заряд от одного источника тока, у них будет одинаковая разность потенциалов.

Но так как заряд копится на каждом изделии отдельно, количество электричества на группе можно выразить как сумму количеств на ее деталях. Это справедливо и для емкостных данных – значение для конфигурации равно сумме значений каждой единицы.

Поэтому такую группу можно считать равной одному конденсатору, емкостной параметр которого равен сумме таковых для всех частей.

Последовательное соединение

Эта схема подразумевает соединение устройств одно за другим, когда к местам подключения к цепи подсоединены только два крайних изделия. Количество электричества для каждой детали будет одинаковым. При этом, чем менее емкое устройство, тем большее значение напряжения на нем будет наблюдаться.

Важно! Емкостной показатель такой системы будет еще меньше, чем у устройства, обладающего наименьшим его значением. Соотношение выглядит так: 1/С = 1/С1 + 1/С2 + 1/С3 + … Опираясь на него, можно произвести вывод непосредственно формулы С. Для двух элементов: С = С1*С2 / С1+С2.

Последовательное подключение

Смешанное соединение

Такая сложная конструкция содержит фрагменты с двумя вышеприведенными типами соединений. Чтобы подсчитать полную емкость, схему делят на простые блоки, состоящие только из деталей, соединенных каким-то одним образом. Находят эквивалентные значения для каждого блока и затем рисуют схему заново в упрощенном виде. Рассчитывают  данные для получившейся системы.

Чтобы суметь подобрать подходящий конденсаторный набор, нужно уметь узнавать емкостные данные. Важно также знать, как рассчитывается показатель для конфигурации из нескольких деталей, соединенных между собой тем или иным образом.

Видео

Сопротивление резистора – формула для рассчета

Источник: https://amperof.ru/teoriya/emkost-kondensatora-formula.html

Диэлектрик в конденсаторе: электричекое поле и плотность энергии

В статье мы расскажем про диэлектрики и их роль в конденсаторе, электрическое поле в диэлектрике и плотность энергии электрического поля в диэлектрике.

Диэлектрик — это газ, жидкость или твердое тело, которое не является проводником электричества. Это означает, что электрические заряды, содержащиеся в каждом теле, связаны в диэлектрике в том смысле, что они могут перемещаться только внутри диэлектрика.

 Если электрическое поле приложено к диэлектрику, смещение нагрузок под этим полем приведет к поляризации диэлектрика, то есть, давая ему ненулевой дипольный момент.

 Это означает, что между крышками заряженного конденсатора поверхность диэлектрика, примыкающая к положительно заряженной крышке, получит отрицательный заряд. И наоборот, отрицательно заряженная крышка будет притягиваться к положительно заряженной поверхности диэлектрика.

 Наиболее важным эффектом диэлектрической поляризации является то, что часть заряда на крышках конденсатора нейтрализуется и больше не способствует генерации электрического поля между крышками.

Частичная, но не полная нейтрализация (компенсация) заряда электрода диэлектрическим слоем связана с тем фактом, что полярность диэлектрика обусловлена ​​ориентацией диполей, существующих внутри диэлектрика. Такие диполи можно условно разделить на постоянные и индуцированные диполи.

 Постоянные диполи встречаются в веществах, молекулы которых имеют стабильный дипольный момент. Здесь наглядным примером является вода, которая подвергается очень сильной поляризации в электрическом поле. Индуцированные диполи не возникают при отсутствии приложенного электрического поля и появляются в атоме или молекуле только под действием этого поля.

 Внешнее поле деформирует электронный заряд атомов и молекул, в результате чего центр отрицательного заряда электронов больше не совпадает с центром положительного заряда ядра и, таким образом, появляется дипольный момент, который сразу исчезает после выключения поля.

 Поляризация ионных кристаллов состоит в том, что положительные и отрицательные ионы смещаются относительно друг друга под воздействием приложенного поля, и в некоторых веществах поляризация движущегося пространственного заряда (например, ионных примесей) также может играть роль. 

Ориентация диполя в диэлектрике никогда не бывает идеальной, и поэтому мы не имеем полной компенсации заряда конденсатора конденсатора, заполненного диэлектриком.

 Причиной отсутствия полной ориентации диполей является, главным образом, дезорганизация тепловых движений, а также ограничения, налагаемые кристаллической структурой диэлектрического слоя и препятствиями при вращении молекул из других молекул.

 Таким образом, полная ориентация диполя, то есть полная поляризация диэлектрика, не достигается до напряжения пробоя диэлектрика.

Роль диэлектрика в конденсаторе

Что происходит с емкостью конденсатора, если пространство между его крышками заполнено диэлектриком?

Оказывается, емкость конденсатора, заполненного диэлектриком, во много раз превышает емкость пустого конденсатора (наполненного воздухом). Давайте посмотрим, в чем причина этого очень важного явления. Емкость зарядного конденсатора С с разностью потенциалов между крышками основана на определении

Хотя все рассуждения, представленные ниже, действительны для каждого типа конденсатора, мы ограничимся далее простейшим случаем плоского конденсатора.

Ранее мы получили, используя закон Гаусса, формулу для емкости такого конденсатора

Если в этом примере плоский конденсатор заряжен постоянным зарядом Q, обозначенным на левом рисунке ниже двумя знаками плюс и двумя минусами (заряды на крышках создаются смещением заряда и должны быть одинаковыми), то интенсивность поля E будет обозначаться двумя векторами, начинающимися с заряда плюс и конец на заряде минус. Количество загрузок на крышках, представленных на рисунке, является только символическим — на самом деле это число исчисляется многими миллиардами.

Натяжение между крышками, удаленными друг от друга, определяется уже известным нам шаблоном («шаговое напряжение»)

 Поле Е уменьшилось вдвое, и поэтому натяжение между крышками также уменьшится вдвое.

 Поскольку конденсатор отключен от источника питания, заряд на электродах не может быть изменен, и при применении формулы, определяющей емкость

Затем мы обнаруживаем, что емкость конденсатора стала вдвое больше. Если мы обозначим емкость левого конденсатора как Сслева , а справа как Ссправа, то мы сразу увидим, что

  и 

другими словами, в этом символическом случае емкость конденсатора с диэлектриком удвоилась

На самом деле работа диэлектрика намного эффективнее, и увеличение емкости конденсатора, заполненного диэлектриком, может достигать нескольких, нескольких десятков или даже нескольких сотен раз.

Совершенно аналогично, мы получаем увеличение емкости конденсатора после заполнения его диэлектриком, когда конденсатор подключен к источнику постоянного напряжения V. Ситуация в «воздушном» конденсаторе показана ниже

На этом символическом рисунке каждый плюс-заряд порождает вектор поля E, который заканчивается минус-зарядом. Если теперь мы поместим диполь между крышками, как на рисунке ниже, то теперь также один из векторов E будет удален из пространства между электродами противоположно направленным дипольным полем.

Возникла ситуация, которую невозможно поддерживать. Когда источник постоянного напряжения V подключен, напряженность поля E должна быть такой, чтобы зависимость выполнялась.

 Для этого от источника напряжения должен вытекать дополнительный заряд, который заменит заряд, компенсируемый наличием диэлектрика.

 С другой стороны, у нас есть три вектора E, как на рисунке ниже, и это столько, сколько необходимо для удовлетворения требования, выраженного в формуле.

Теперь, при неизменном напряжении, на конденсаторе появляется больший заряд, что означает, что емкость конденсатора соответственно увеличилась.

 Чтобы количественно оценить влияние диэлектрика на емкость конденсатора, мы вводим материальную постоянную для этого диэлектрика, которую мы называем относительной электрической проницаемостью ε и которую мы определяем, как отношение емкости конденсатора, заполненного диэлектриком C, к емкости пустого конденсатора C0  

E, D и P векторы

Более точное формальное описание поведения диэлектрика в конденсаторе получается путем введения двух дополнительных векторов: вектора P — поляризации и вектора D — смещения. Вектор P уже появился на скриншоте выше.

 Обратите особое внимание на вектор D, длина которого равна общей плотности заряда σ, накопленной на крышках конденсатора, и которая входит в уравнения Максвелла, записанные в компактной, элегантной форме.

 Когда пустой конденсатор поддерживается под постоянным напряжением V, а плотность заряда на крышках этого конденсатора обозначается σ0, то поле E между крышками таково, что

 Часть нагрузок на покрытиях, имеющих плотность σ0, будет «замаскирована» противоположным индуктивным зарядом с плотностью σi. Затем источник напряжения должен перезарядить конденсатор до такой плотности заряда, чтобы снова напряженность поля между крышками удовлетворяла условию V = Ed.

 Таким образом, σ = σ0 + σi , то есть плотность полного заряда на крышках конденсатора с диэлектриком равна сумме плотности заряда на конденсаторе без диэлектрика и плотности поляризационного заряда.

•             Если мы имеем в виду
• σ 0 = ε 0 E,
• σ i = P
• σ = D
• и мы применим закон Гаусса к конденсатору с диэлектриком, тогда мы сразу получим соединение

Эта связь между векторами D, E и P записана в векторной форме

Напомним, что D — вектор смещения, E — вектор поля, а P — вектор поляризации. Вектор Р (показано ниже обозначена красным) проходит внутри диэлектрика и сделать его в виде стрелки от «негативного» на «позитивный», то есть противоположно вектору Е .

Как уже было сказано, диэлектрическая проницаемость ε определяется как отношение емкости С и диэлектрическим заполнением конденсатора пустых C0.

Помните, что конденсатор постоянно подключен к источнику напряжения, т.е. V = Q/C = const. Емкость конденсатора с диэлектриком будет

и емкость пустого конденсатора будет

Исходя из этого, мы можем написать

Подставив выражение, мы получим эквивалентное определение вектора D: 

Электрическое поле в диэлектрике

Если конденсатор НЕ подключен к источнику питания, заряд Q = CV на его крышках будет оставаться постоянным независимо от того, помещен ли диэлектрик между ними. Если мы обозначим C0 и E0 соответственно, емкость пустого конденсатора и значение электрического поля между его крышками, а C и E аналогичные значения для конденсатора, заполненного диэлектриком, мы можем записать

Отсюда и на основании определения диэлектрической проницаемости ε получаем

Таким образом, видно, что напряженность поля в диэлектрике в ε раз меньше, чем в вакууме.

Это соотношение является общим и применяется в каждом фиксированном поле E, независимо от его источника.

Плотность энергии электрического поля в диэлектрике

Плотность энергии электрического поля E в диэлектрике в ε раз больше, чем в вакууме, и равна

Используя выражение зависимости от плотности энергии, мы можем записать в компактном векторном виде 

Это выражение всегда применимо, в том числе и для кристаллов, где векторы E и D обычно не параллельны друг другу.

2. Плотность заряда на крышке конденсатора, частично заполненного диэлектриком, не постоянна. 

Гауссовский обобщенный закон

Описывая кулоновскую силу между точечными зарядами в диэлектрике, электрическая проницаемость вакуума умножалась на диэлектрическую проницаемость и вместо ε 0 мы использовали произведение ε 0 ε. Мы можем обобщить эту процедуру и применить ее к закону Гаусса, где центром, через который проникает поле, является не вакуум, а диэлектрик. Тогда мы знаем закон Гаусса

мы сможем написать в форме

мы получим окончательную форму обобщенного закона Гаусса

Закон Гаусса в таком виде применяется в вакууме, где ε = 1, и в диэлектриках. Заряд Q в этом уравнении, как и прежде, представляет собой результирующий заряд, содержащийся внутри замкнутой поверхности, после чего происходит интегрирование.

В конденсаторе с диэлектриком результирующий заряд представляет собой разницу между нагрузкой, накопленной на крышке q1 = σA, и поляризационным зарядом (с противоположным знаком), индуцированным в диэлектрике поверхностного слоя q2 = -σ и A.

Если мы используем закон Гаусса для этой структуры, то мы предполагаем, что заряды они накапливаются на соседних поверхностях крышки и диэлектрика, и это поле не выходит за пределы крышек конденсатора. Естественным выбором гауссовой поверхности, после которой мы интегрируем поток, является прямоугольная призма или поверхность цилиндра.

 Основание прямоугольной призмы А параллельно поверхности крышки. Одна база находится снаружи крышки (там, где нет поля), а другая находится внутри диэлектрика.

Закон Гаусса в представленной выше форме является одним из четырех уравнений Максвелла, описывающих все электрические, магнитные и оптические явления. Уравнения Максвелла являются фундаментальными законами электродинамики, и ни одно из них не может быть выведено из более простых законов.

 Если бы существовали еще более фундаментальные права, они, безусловно, были бы представлены здесь. Эти уравнения являются результатом творческого вдохновения, просвещения их создателей Гаусса, Фарадея и Ампера.

 Максвелл представил им гениальную концепцию «тока смещения», о которой мы поговорим чуть позже, которая позволила унифицировать структуру этих уравнений и распространить их на случай электромагнитных и, следовательно, световых волн.

Источник: https://meanders.ru/dijelektrik-v-kondensatore.shtml