Формула напряжённости магнитного поля

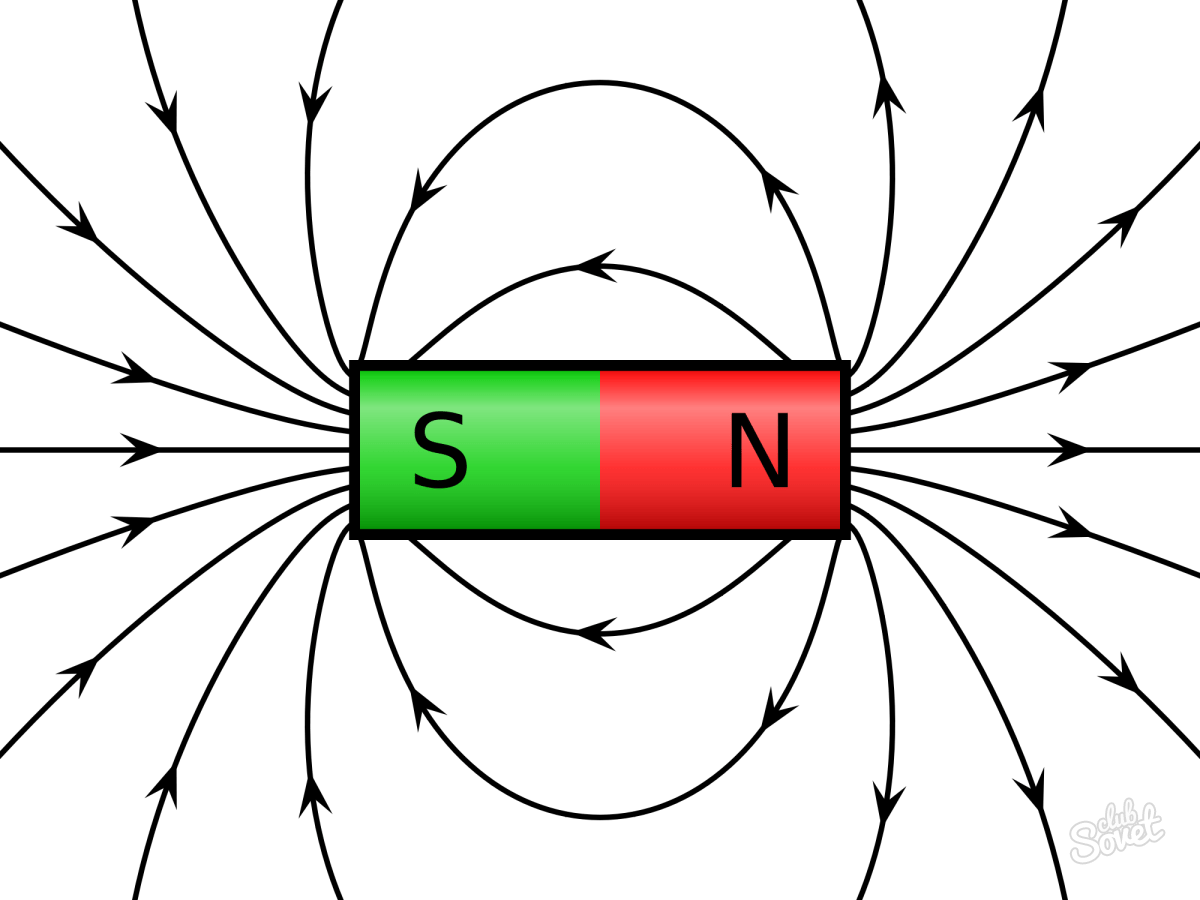
Всем доброго времени суток. В прошлой статье я рассказывал о основной характеристике магнитного поля – магнитной индукции, однако приведённые расчётные формулы соответствуют магнитному полю в вакууме. Что в практической деятельности встречается довольно редко.

Когда проводники с током находятся в какой–либо среде, даже в воздухе, магнитное поле, которое они создают, претерпевает некоторые, а иногда и существенные изменения. Какие изменения происходят с магнитным полем, и от чего это зависит, я расскажу в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Как связана индукция и напряженность магнитного поля?

Магнетиком называется вещество, которое под действием магнитного поля способно намагничиваться (или как говорят физики приобретать магнитный момент). Магнетиками являются практически все вещества.

Намагничивание веществ объясняется тем, что в веществах присутствуют свои собственные микроскопические магнитные поля, которые создаются вращением электронов по своим орбитам.

Когда внешнее магнитное поле отсутствует, то микроскопические поля расположены произвольным образом, а под воздействием внешнего магнитного поля соответствующим образом ориентируются.

Таким образом, под действием внешнего магнитного поля с магнитной индукцией В0, магнетик намагничивается и создает свое магнитное поле с магнитной индукцией В’. В итоге общая индукция В будет состоять из двух слагаемых

Тут возникает проблема вычисления магнитной индукции намагниченного вещества В’, для решения которой необходимо считать электронные микротоки всего вещества, что практически нереально.

Альтернативой данного решения есть ввод вспомогательных параметров, а именно напряженность магнитного поля Н и магнитная восприимчивость χ. Напряженность связывает магнитную индукцию В и намагничивание вещества J следующим выражением

• где В – магнитная индукция,
• μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м.
• В то же время вектор намагничивания J связан с напряженность магнитного поля В параметром, характеризующим магнитные свойства вещества и называемым магнитной восприимчивостью χ

1. где J – вектор намагничивания вещества,
2. μr – относительная магнитная проницаемость вещества.
3. Однако наиболее часто для характеристики магнитных свойств веществ используют относительную магнитную проницаемость μr.
4. Таким образом, связь между напряженностью и магнитной индукцией будет иметь следующий вид

• где μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м,
• μr – относительная магнитная проницаемость вещества.
• Так как намагничивание вакуума равна нулю (J = 0), то напряженность магнитного поля в вакууме будет равна
• Отсюда можно вывести выражения напряженности для магнитного поля, создаваемого прямым проводом с током:

1. где I – ток протекающий по проводнику,
2. b – расстояние от центра провода до точки, в которой считается напряженность магнитного поля.
3. Как видно из данного выражения единицей измерения напряженности является ампер на метр (А/м) или эрстед (Э)

Таким образом, магнитная индукция В и напряженность Н являются основными характеристиками магнитного поля, а магнитная проницаемость μr – магнитной характеристикой вещества.

Намагничивание ферромагнетиков

В зависимости от магнитных свойств, то есть способности намагничиваться под действием внешнего магнитного поля, все вещества делятся на несколько классов. Которые характеризуются разной величиной относительной магнитной проницаемости μr и магнитной восприимчивости χ.

Большинство веществ являются диамагнетиками (χ = -10-8 … -10-7 и μr < 1) и парамагнетиками (χ = 10-7 … 10-6 и   μr > 1), несколько реже встречаются ферромагнетики (χ = 103 … 105 и   μr >> 1).

Кроме данных классов магнетиков существует ещё несколько классов магнетиков: антиферромагнетики, ферримагнетики и другие, однако их свойства проявляются только при определённых условиях.

Особый интерес в радиоэлектронике ферромагнитные вещества. Основным отличием данного класса веществ является нелинейная зависимость намагничивания, в отличие от пара- и диамагнетиков, имеющих линейную зависимость намагничивания J от напряженности Н магнитного поля.

Зависимость намагничивания J ферромагнетика от напряженности Н магнитного поля.

На данном графике показана основная кривая намагничивания ферромагнетика. Изначально намагниченность  J, в отсутствие магнитного поля (Н = 0), равна нулю. По мере возрастания напряженности намагничивание ферромагнетика проходит довольно интенсивно, вследствие того что его магнитная восприимчивость и проницаемость очень велика.

Однако по достижении напряженности магнитного поля порядка H ≈ 100 А/м увеличение намагниченности прекращается, так как достигается точка насыщения JНАС. Данное явление называется магнитным насыщением.

В данном режиме магнитная проницаемость ферромагнетиков сильно падает и при дальнейшем увеличении напряженности магнитного поля стремится к единице.

Гистерезис ферромагнетиков

Еще одной особенностью ферромагнетиков является наличие петли гистерезиса, которая является основополагающим свойством ферромагнетиков.

Для понимания процесса намагничивания ферромагнетика изобразим зависимость индукции В от напряженности Н магнитного поля, где красным цветом выделим основную кривую намагничивания. Данная зависимость довольно неопределенна, так как зависит от предыдущего намагничивания ферромагнетика.

Возьмём образец ферромагнитного вещества, которое не подвергалось намагничиванию (точка 0) и поместим его в магнитное поле, напряженность Н которого начнем увеличивать, то есть зависимость будет соответствовать кривой 0 – 1, пока не будет достигнуто магнитное насыщение (точка 1).

Дальнейшее увеличение напряженности не имеет смысла, потому как намагниченность J практически не увеличивается, а магнитная индукция увеличивается пропорционально напряженности Н.

Если же начинать уменьшать напряженность, то зависимость В(Н) будет соответствовать кривой 1 – 2 – 3, при этом когда напряженность магнитного поля упадёт до нуля (точка 2), то магнитная индукция не упадёт до нуля, а будет равна некоторому значению Br, которое называется остаточной индукцией, а намагничивание будет иметь значение Jr, называемое остаточным намагничиванием.

Для того чтобы снять остаточное намагничивание и уменьшить остаточную индукцию Br до нуля, необходимо создать магнитное поле, противоположное полю, вызвавшему намагничивание, причем напряженность размагничивающего поля должна составлять Нс, называемая коэрцитивной силой. При дальнейшем росте напряженности магнитного поля, которое противоположно первоначальному полю, происходит насыщение ферромагнетика (точка 4).

Таким образом, при действии на ферромагнетик переменного магнитного поля зависимость индукции от напряженности будет соответствовать кривой 1 – 2 – 3 – 4 – 5 – 6 – 1, которая называется петлёй гистерезиса.

Таких петель для ферромагнетика может быть множество (пунктирные кривые), называемые частными циклами.

Однако, если при максимальных значениях напряженности магнитного поля происходит насыщение, то получается максимальная петля гистерезиса (сплошная кривая).

• Так как магнитная проницаемость μr ферромагнетиков имеет довольно сложную зависимость от напряженности магнитного поля, поэтому нормируются два параметра магнитной проницаемости:
• μн – начальная магнитная проницаемость соответствует напряженности Н = 0;
• μmax – максимальная магнитная проницаемость достигается в магнитном поле при приближении магнитного насыщения.
• Таким образом, у ферромагнетиков величины Br, Нс и μн (μmax) являются основными характеристиками, влияющими на выбор вещества в конкретном случае.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник: https://www.electronicsblog.ru/nachinayushhim/magnitnoe-pole-v-veshhestve-chast-1.html

Формула напряженности магнитного поля

Определение

Напряженностью магнитного поля называют векторную физическую величину, направленную по касательной к силовым линиям поля, являющуюся характеристикой магнитного поля, равную:

где – вектор магнитной индукции,
Гн/м(Н/А2)- магнитная постоянная,
– вектор намагниченности среды в исследуемой точке поля.

Для магнитного поля в вакууме напряженность магнитного поля определяется выражением:

В изотропной среде формула (1) преобразуется к виду:

Закон Био-Савара-Лапласа

• Это важнейший в электромагнетизме закон. Он определяет вектор напряженности
  в произвольной точке магнитного поля, которое создает в вакууме элементарный проводник длинны dl с постоянным током I:
• где – вектор элемента проводника, который по модулю равен длине
  проводника, направление совпадает с направлением тока; – радиус–вектор,
  который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля;
  .

Вектор – перпендикулярен плоскости, в которой находятся
векторы и
, и направлен так, что из его конца вращение вектора
по кратчайшему пути до совмещения с вектором
происходило по часовой стрелке. Для нахождения направления вектора
можно использовать правило буравчика (Буравчик (винт) вращаем так,
чтобы его поступательное движение совпадало с направлением тока, тогда направление, по которому вращается ручка винта, совпадает с направлением
вектора напряженности поля, которое создает рассматриваемый ток).

Закон Био-Савара-Лапласа дает возможность вычислять величину полной напряженности магнитного поля, которое создает ток, текущий по проводнику любой формы.

Для нахождения полной напряженности магнитного поля, которое создает в исследуемой точке ток I, который течет по проводнику l, следует
векторно суммировать все элементарные напряженности , порождаемые
элементами проводника и найденные по формуле (4).

Единицы измерения

Основной единицей измерения момента силы в системе СИ является: [H]=А/м

Примеры решения задач

Пример

Задание. Чему равна напряженность (H) в центре кругового витка (R — радиус витка) с током I.

Решение. Каждый элементарный ток витка магнитное поле в центре окружности, напряженность которого направлена по положительной нормали к плоскости контура витка (рис.1). Поэтому, если элементарную напряженность поля найти по закону Био-Савара – Лапласа, то векторное сложение элементарных полей можно будет заменить на алгебраическое.

1. В соответствии с законом Био-Савара – Лапласа dH равно:
2. Применяя выражение (1.1) к нашему случаю, получим:
3. Возьмем интеграл по контуру, получим:
4. Ответ.

Пример

Задание. Какова напряженность магнитного поля, которую создает электрон, движущийся прямолинейно и равномерно со скоростью v? Если точка, в которой исследуется поле, находится на расстоянии r от электрона на перпендикуляре к вектору скорости, если перпендикуляр провести через мгновенное положение частицы.

Решение. Сделаем рисунок.

• Напряженность магнитного поля будем искать, применяя закон Био – Савара – Лапласа:
• Учтем, что:
• Если все заряды одинаковы (q), то плотность тока равна:

заряд отрицательный, следовательно, направления векторов
и
противоположны. n – концентрация зарядов. Подставим формулу (2.3)
в (2.2), результат в (2.1) получаем:

1. где dN=Sdln — количество заряженных частиц в отрезке dl. В таком случае, напряженность поля, которое создает один заряд:
2. По условию задачи , значит модуль напряжённости магнитного поля в точке А (рис.2) будет равен:
3. Ответ.

Читать дальше: Формула напряженности электрического поля.

Вы поняли, как решать? Нет?

Источник: https://www.webmath.ru/poleznoe/formules_21_25_naprjazhennost_magnitnogo_polja.php

Магнитное поле. Индукция и напряженность магнитного поля. Закон Ампера

Проводники с током в магнитном поле. Взаимодействие параллельных токов.

Для определения направления силы, действующей в магнитном поле, применяют правило левой руки: если расположить левую руку так, чтобы магнитные линии входили в ладонь, а вытянутые четыре пальца совпадали с направлением тока проводнике, то большой палец укажет направление действия силы, приложенной к проводнику.

Два параллельных тока одинакового направления притягиваются друг к другу с силой, равной

Если токи имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания, определяемая выражением.

Движение заряженной частицы в магнитном поле. Сила Лоренца.

Формула силы Лоренца дает возможность найти ряд закономерностей движения заряженных частиц в магнитном поле. Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях.

Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля.

Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и Вравен 0 или π.

Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

В случае, если заряженная частица движется в магнитном поле со скоростью v, которая перпендикулярна вектору В, то сила ЛоренцаF=Q[vB] постоянна по модулю и перпендикулярна к траектории частицы. По второму закону Ньютона, сила Лоренца создает центростремительное ускорение. Значит, что частица будет двигаться по окружности, радиус r которой находится из условия QvB=mv2/r , следовательно

Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

Источник: https://infopedia.su/3x289b.html

Вектор напряженности магнитного поля формула — Вместе мастерим

Напряженность магнитного полянеобходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме.

Напряженность магнитного поля (формула)векторная физическая величина, равная:

Напряженность магнитного поля в СИ — ампер на метр (А/м).

Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поляв данной точке, то можно определить индукцию поля в этой точке.

• Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.
• Намагниченность — характеристика магнитного состояния макроскопического физического тела.
• Однородно намагниченное тело:

Любое вещество, помещенное в магнитное поле, приобретает некоторый магнитный момент. Намагниченность J – это магнитный момент единицы объема.

В несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничивание: :

Если же тело намагничено неоднородно (состоит из нескольких частей), то намагниченность определяется для каждого физически малого объема dV

МАГНИТНАЯ ВОСПРИИМЧИВОСТЬ , величина, характеризующая связь намагниченности вещества с магнитным полем в этом веществе. М. в. в статич. полях равна отношению намагниченности вещества М к напряжённости Н намагничивающего поля: ; — величина безразмерная. М. в., рассчитанная на 1 кг (или 1 г) вещества, наз. удельной ( , где р — плотность вещества), а М. в. одного моля — молярной (или атомной): , где т — молекулярная масса вещества. С магнитной проницаемостью . в. в статич. полях (статич. М. в.) связана соотношениями: (в ед. СГС), (в ед. СИ). М. в. может быть как положительной, так и отрицательной. Отрицательной М. в. обладают диамагнетики (ДМ), они намагничиваются против поля; положительной — парамагнетики (ПМ) и ферромагнетики (ФМ), они намагничиваются по полю. М. в. ДМ и ПМ мала по абс. величине , она слабо зависит от Н и то лишь в области очень сильных полей (и низких темп-р).

Физическая величина, показывающая, во сколько раз индукция магнитного поля в однородной среде отличается по модулю от индукции магнитного поля в вакууме, называется магнитной проницаемостью:

18.Диамагнетики,парамагнетики,ферромагнетики.

Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики.

Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля.

Поэтому у парамагнетиковμ > 1, а у диамагнетиков μ –5 , у хлористого железа (FeCl3) μ – 1 ≈ 2,5·10 –3 . К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь(μ – 1 ≈ –3·10 –6 ), вода (μ – 1 ≈ –9·10 –6 ), висмут (μ – 1 ≈ –1,7·10 –3 ) и другие вещества.

Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются (рис. 1.19.1).

Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей.

Возникающее при этом собственное магнитное поле атома оказывается направленным против направления индукции внешнего поля.

Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками. Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах 10 2 –10 5 . Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная проницаемость достигает значений 250000.

К рассматриваемой группе относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.

Ферромагнетиками могут быть различные сплавы, содержащие ферромагнитные элементы. Широкое применение в технике получили керамические ферромагнитные материалы – ферриты.

Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна 770 °C, у кобальта 1130 °C, у никеля 360 °C.

Ферромагнитные материалы делятся на две большие группы – на магнито-мягкие и магнито-жесткие материалы. Магнито-мягкие ферромагнитные материалы почти полностью размагничиваются, когда внешнее магнитное поле становится равным нулю.

Эти материалы применяются в приборах переменного тока, в которых происходит непрерывное перемагничивание, то есть изменение направления магнитного поля (трансформаторы, электродвигатели и т. п.).

Магнито-жесткие материалы в значительной мере сохраняют свою намагниченность и после удаления их из магнитного поля. Примерами магнито-жестких материалов могут служить углеродистая сталь и ряд специальных сплавов. Магнито-жесткие метериалы используются в основном для изготовления постоянных магнитов.

Магнитная проницаемость μ ферромагнетиков не является постоянной величиной; она сильно зависит от индукции B внешнего поля. Типичная зависимость μ (B) приведена на рис. 1.19.2. В таблицах обычно приводятся значения максимальной магнитной проницаемости.

  Автоматическая горелка на отработанном масле

Последнее изменение этой страницы: 2016-06-23; Нарушение авторского права страницы

Она необходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах.Напряженность магнитного поляхарактеризует магнитное поле в вакууме.

Напряженность магнитного поля (формула) векторная физическая величина, равная:

Где u0- магнитная постоянная.Гн/мН/А².

Напряженность магнитного поляв СИ — ампер на метр (А/м).

Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поля в данной точке, то можно определить индукцию поля в этой точке.

1. Напряженность магнитного полязависит только от силы тока, протекающего по проводнику, и его геометрии.
2. С помощью следующей формулы, мы можем сформулировать теорему о циркуляции вектора H:циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром.
3. Напряженность магнитного поля является аналогом электрического смещения.

23)Условия для h и b на границе раздела двух изотропных магнетиков :

Рассмотрим поведение линий векторов магнитной индукции и напряжённости магнитного поля при переходе через границу раздела двух магнетиков.

Представим себе две однородные, изотропные полубесконечные среды с магнитными проницаемостями и, имеющие плоскую горизонтальную границу раздела. Пусть оба магнетика находятся в однородном внешнем магнитном поле.

Чтобы понять, как происходит преломление линий векторов магнитной индукциии напряжённости магнитного полячерез эту границу, рассмотрим проекции этих векторов на саму границу и на направление, перпендикулярное границе и назовём их касательными и нормальными составляющими, соответственно.

Представим себе, что линии вектора преломляются при переходе через границу раздела так, как показано на рис. 1. Рассмотрим при этом преломление пока только одной силовой линии.

Поместим на границе раздела воображаемую цилиндрическую поверхность с высотой h значительно меньшей радиусов оснований S1 и S2, лежащих по обе стороны от границы раздела и параллельных ей. На рисунке также показана нормаль к границе раздела и к обоим основаниям.

• Запишем теорему Гаусса для магнитной индукции:
• или ,
• где S ─ замкнутая поверхность, состоящая из боковой поверхности и оснований цилиндра.
• Этот круговой интеграл можно разбить на 3 интеграла, каждый из которых равен потоку через верхнее и нижнее основания и боковую поверхность

  Заготовки из томатов на зиму золотые рецепты

1. .
2. Здесь и─ нормальные составляющие векторов магнитной индукции в верхнем и нижнем магнетиках, соответственно,─ среднее значение проекции вектора магнитной индукции на нормаль к боковой поверхности.
3. Поскольку оба магнетика помещены в однородное внешнее магнитное поле, то все интегралы можно заменить соответствующими произведениями:
4. .

Как и в предыдущей формуле, здесь первая составляющая магнитного потока положительна, так как силовые линии выходят из поверхности, а вторая составляющая─ отрицательна, так как силовые линии входят в поверхность(вектораиспроектированы на одну и ту же нормаль). Третьей составляющей ─можно пренебречь, так как высота цилиндра выбрана очень малой по сравнению с радиусами оснований, т. е., если, то.

• Учитывая, что , получим:
• . (1)
• Используя связь магнитной индукции и напряжённости магнитного поля
• , (2)
• и, применяя её для первого и второго магнетиков в формуле (1), получим:
• .
• . (3)

Напряженность магнитного полянеобходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме.

Напряженность магнитного поля [H] – это отношение магнитной индукции к магнитной проницаемости среды

Напряженность магнитного поля – величина векторная. За единицу измерения напряженности магнитного поля в Международной системе единиц принят ампер на метр.

1. Напряженность магнитного поля (формула)векторная физическая величина, равная:
2. Напряженность магнитного поля в СИ — ампер на метр (А/м).

Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поляв данной точке, то можно определить индукцию поля в этой точке.

Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.

Обобщая экспериментальные данные французских физиков Био и Савара, Лаплас (французский математик) предложил формулу, по которой можно вычислять напряженность поля, создаваемого элементом тока в точке, расположенной от этого элемента на расстоянии r.

• Теорема Ампера о циркуляции магнитного поля:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10611 — | 7337 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock! и обновите страницу (F5)очень нужно

Источник: https://vmeste-masterim.ru/vektor-naprjazhennosti-magnitnogo-polja-formula.html

22) Напряженность магнитного поля

Она
необходима для определения магнитной
индукции поля, создаваемого токами
различной конфигурации в различных
средах.Напряженность магнитного поляхарактеризует магнитное поле в вакууме.

Напряженность
магнитного поля (формула) векторная
физическая величина, равная:

Где
u0- магнитная постоянная.Гн/мН/А².

Напряженность
магнитного поляв СИ — ампер на метр
(А/м).

Векторы
индукции (В) и напряженности магнитного
поля (Н) совпадают по направлению. Если
знать Напряженность магнитного поля
в данной точке, то можно определить
индукцию поля в этой точке.

• Напряженность
  магнитного полязависит только от
  силы тока, протекающего по проводнику,
  и его геометрии.
• С
  помощью следующей формулы, мы можем
  сформулировать теорему о циркуляции
  вектора H:циркуляция
  вектора напряженности магнитного поля
  по некоторому контуру равна алгебраической
  сумме макроскопических токов, охватываемых
  этим контуром.
• Напряженность
  магнитного поля является аналогом
  электрического смещения.

23)Условия для h и b на границе раздела двух изотропных магнетиков :

Рассмотрим
поведение линий векторов магнитной
индукции и напряжённости магнитного
поля при переходе через границу раздела
двух магнетиков.

Представим
себе две однородные, изотропные
полубесконечные среды с магнитными
проницаемостями и,
имеющие плоскую горизонтальную границу
раздела. Пусть оба магнетика находятся
в однородном внешнем магнитном поле.

Чтобы понять, как происходит преломление
линий векторов магнитной индукциии
напряжённости магнитного поля

png» width=»24″>через
эту границу, рассмотрим проекции этих
векторов на саму границу и на направление,
перпендикулярное границе и назовём их
касательными и нормальными составляющими,
соответственно.

Пусть
и─
нормальные составляющие векторов
магнитной индукции и напряжённости
магнитного поля, а

png» width=»31″>и─
касательные составляющие тех же векторов
в верхней среде, имеющей магнитную
проницаемость.

Аналогичные величины в нижней среде,
имеющей магнитную проницаемость,
обозначим

png» width=»42″>.

Поместим
на границе раздела воображаемую
цилиндрическую поверхность с высотой
h
значительно меньшей радиусов оснований
S1
и S2,
лежащих по обе стороны от границы раздела
и параллельных ей.

На рисунке также
показана нормаль к
границе раздела и к обоим основаниям.

png» width=»297″>

1. Запишем
   теорему Гаусса для магнитной индукции:
2. или
   ,
3. где
   S
   ─ замкнутая поверхность, состоящая из
   боковой поверхности и оснований цилиндра.
4. Этот
   круговой интеграл можно разбить на 3
   интеграла, каждый из которых равен
   потоку через верхнее и нижнее основания
   и боковую поверхность

Здесь
и

png» width=»33″>─
нормальные составляющие векторов
магнитной индукции в верхнем и нижнем
магнетиках, соответственно,

png» width=»43″>─
среднее значение проекции вектора
магнитной индукции на нормаль к боковой
поверхности.

Поскольку
оба магнетика помещены в однородное
внешнее магнитное поле, то все интегралы
можно заменить соответствующими
произведениями:

Как
и в предыдущей формуле, здесь первая
составляющая магнитного потока
положительна,
так как силовые линии выходят из
поверхности,
а вторая составляющая

QHeD/img-CWFnNW.png» width=»49″>─
отрицательна, так как силовые линии
входят в поверхность(вектораи

png» width=»42″>,
то.

Используя
связь магнитной индукции и напряжённости
магнитного поля

и,
применяя её для первого и второго
магнетиков в формуле (1), получим:

Отсюда
следует

Источник: https://studfile.net/preview/2455643/page:12/