Каноническое уравнение, формулы и примеры

или можно встретить следующую форму записи: К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.

Покажем на примере определение значений коэффициентов.

Рассмотрим кривую второго порядка: 

Вычислим определитель из коэффициентов:

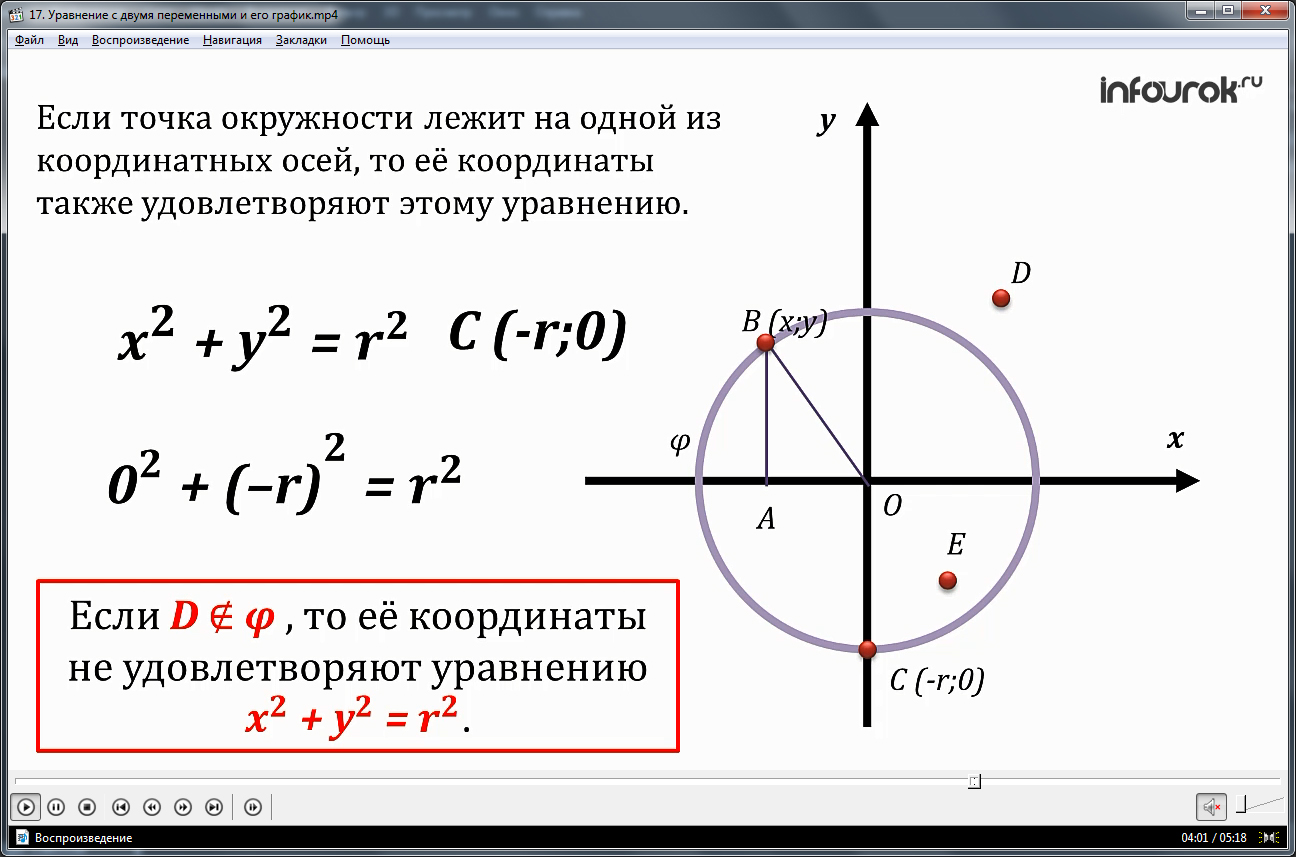
• Если Δ = 0, кривая второго порядка параболического типа,
• если Δ > 0, кривая второго порядка эллиптического типа,
• если Δ < 0, кривая второго порядка гиперболического типа.

Эллипс — множество точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 есть величина постоянная, большая расстояния между этими точками

F1 и F2 — фокусы.  

с — фокальное расстояние, F1(-c;0) — левый фокус, F2(c;0) — правый фокус.

Каноническое уравнение эллипса с центром симметрии в начале координат:

• 2а — большая ось эллипса, 2b — малая ось эллипса.
• а — большая полуось эллипса, b — малая полуось эллипса.
• Если a = b, то имеем окружность с радиусов R = a = b:

Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0),  оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:

Эксцентриситет — число, равное отношению  фокального расстояния к большей полуоси:

Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.

Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками

F1 и F2 — фокусы.

с — фокальное расстояние, F1(-c;0) — левый фокус, F2(c;0) — правый фокус. А1(-а;0),  А2(а;0) — вершины.

• Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
• Каноническое уравнение гиперболы с центром симметрии в начале координат:
• x —  действительная ось,   y — мнимая ось.
• а — действительная полуось,   b —  мнимая полуось.
• Если центр гиперболы находится в некоторой точке C(x0;y0),  оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
• Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.
• Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
• Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
• f1 —  правая директриса,   f2 —  левая директриса.
• Уравнения директрис:
• Порядок построения гиперболы:

1. Строим прямоугольник со сторонами 2a и 2b.

2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.

3. Строим гиперболу с вершинами в точках А1(-а;0),  А2(а;0).

Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f

F — фокус параболы, f — директриса параболы. 

р — фокальное расстояние  Фокус параболы: Директриса параболы:

Пример по теме кривые второго порядка №1

Привести к каноническому виду и построить график кривой второго порядка. 

Источник: http://matecos.ru/mat/matematika/krivye-vtorogo-poryadka.html

Уравнение прямой

Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

• Любую прямую на плоскости можно задать уравнением прямой первой степени вида
• A x + B y + C = 0
• где A и B не могут быть одновременно равны нулю.

1. Общее уравнение прямой при B≠0 можно привести к виду
2. y = k x + b
3. где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
4. k = tg φ

Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках

Если прямая проходит через две точки M(x1, y1) и N(x2, y2), такие что x1 ≠ x2 и y1 ≠ y2, то уравнение прямой можно найти, используя следующую формулу

x — x1	=	y — y1
x2 — x1	y2 — y1

• Параметрические уравнения прямой могут быть записаны следующим образом
• x = l t + x0y = m t + y0
• где N(x0, y0) — координаты точки лежащей на прямой, a = {l, m} — координаты направляющего вектора прямой.

Если известны координаты точки N(x0, y0) лежащей на прямой и направляющего вектора a = {l; m} (l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Пример 1. Найти уравнение прямой проходящей через две точки M(1, 7) и N(2, 3).

1. Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
2. x — 12 — 1 = y — 73 — 7
3. Упростив это уравнение получим каноническое уравнение прямой
4. x — 11 = y — 7-4
5. Выразим y через x и получим уравнение прямой с угловым коэффициентом
6. y — 7 = -4(x — 1)
7. y = -4x + 11

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

• MN = {2 — 1; 3 — 7} = {1; -4}
• Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
• x = t + 1y = -4t + 7

Пример 2. Найти уравнение прямой проходящей через две точки M(1, 3) и N(2, 3).

Решение. Так как My — Ny = 0, то невозможно записать уравнение прямой проходящей через две точки.

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

1. MN = {2 — 1; 3 — 3} = {1; 0}
2. Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
3. x = t + 1y = 3

Если прямая проходит через две точки M(x1, y1, z1) и N(x2, y2, z2), такие что x1 ≠ x2, y1 ≠ y2 и z1 ≠ z2, то уравнение прямой можно найти используя следующую формулу

x — x1	=	y — y1	=	z — z1
x2 — x1	y2 — y1	z2 — z1

Параметрические уравнения прямой могут быть записаны следующим образом

x = l t + x0

y = m t + y0

z = n t + z0

где (x0, y0, z0) — координаты точки лежащей на прямой, {l; m; n} — координаты направляющего вектора прямой.

Если известны координаты точки M(x0, y0, z0) лежащей на прямой и направляющего вектора n = {l; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x — x0	=	y — y0	=	z — z0
l	m	n

Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений

A1x + B1y + C1z + D1 = 0

A2x + B2y + C2z + D2 = 0

при условии, что не имеет место равенство

Источник: https://ru.onlinemschool.com/math/library/analytic_geometry/line/

Что такое канонический вид уравнения?

Это общепринятый стандартный вид уравнения, когда в считанные секунды становится ясно, какой геометрический объект оно определяет. Кроме того, канонический вид очень удобен для решения многих практических заданий. Так, например, по каноническому уравнению «плоской» прямой, во-первых, сразу понятно, что это прямая, а во-вторых – элементарно просматривается принадлежащая ей точка и направляющий вектор .

• Очевидно, что любая линия 1-го порядка представляет собой прямую. На втором же этаже нас ждёт уже не вахтёр, а гораздо более разнообразная компания из девяти статуй:
• Классификация линий второго порядка
• С помощью специального комплекса действий любое уравнение линии второго порядка приводится к одному из следующих видов:
• ( и – положительные действительные числа)

4) – мнимый эллипс;

1. 6) – пара мнимых пересекающихся прямых (с единственной действительной точкой пересечения в начале координат);
2. 7) – пара параллельных прямых;
3. 8) – пара мнимых параллельных прямых;
4. 9) – пара совпавших прямых.

У ряда читателей может сложиться впечатление неполноты списка.

Например, в пункте №7 уравнение задаёт пару прямых , параллельных оси , и возникает вопрос: а где же уравнение , определяющее прямые , параллельные оси ординат? Ответ: оно не считается каноническим.

Прямые представляют собой тот же самый стандартный случай , повёрнутый на 90 градусов, и дополнительная запись в классификации избыточна, поскольку не несёт ничего принципиально нового.

Сначала рассмотрим эллипс. Как обычно, я акцентирую внимание на тех моментах, которые имеют большое значение для решения задач, и если вам необходим подробный вывод формул, доказательства теорем, пожалуйста, обратитесь, например, к учебнику Базылева/Атанасяна либо Александрова..

• Эллипс и его каноническое уравнение
• Правописание… пожалуйста, не повторяйте ошибок некоторых пользователей Яндекса, которых интересует «как построить эллибз», «отличие элипса от овала» и «эксцентриситет элебса».
• Каноническое уравнение эллипса имеет вид , где – положительные действительные числа, причём . Само определение эллипса я сформулирую позже, а пока самое время отдохнуть от говорильни и решить распространённую задачу:
• Как построить эллипс?
• Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:
• Пример 1
• Построить эллипс, заданный уравнением
• Решение: сначала приведём уравнение к каноническому виду:

Зачем приводить? Одно из преимуществ канонического уравнения заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению .

В данном случае : Отрезок называют большой осью эллипса; отрезок – малой осью; число называют большой полуосью эллипса; число – малой полуосью. в нашем примере: .

Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.

Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы. И вы можете выполнить чертёж с помощью какого-либо приложения.

Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше).

Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.

По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями . Как вариант, можно уменьшить масштаб и, соответственно, размеры чертежа. Но в общем случае крайне желательно найти дополнительные точки.

Существует два подхода к построению эллипса – геометрический и алгебраический.

В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса на черновике быстренько выражаем:

Далее уравнение распадается на две функции: – определяет верхнюю дугу эллипса; – определяет нижнюю дугу эллипса.

Любой эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично – симметрия почти всегда предвестник халявы.

Очевидно, что достаточно разобраться с 1-ой координатной четвертью, поэтому нам потребуется функция . Напрашивается нахождение дополнительных точек с абсциссами .

Настукаем три смс-ки на калькуляторе: Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.

Отметим на чертеже точки (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию: Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?

Источник: https://megaobuchalka.ru/6/52352.html

Каноническое уравнение прямой на плоскости

В данной статье мы рассмотрим каноническое уравнение прямой на плоскости. Определим понятие направляющего вектора прямой. Рассмотрим примеры построения канонического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим метод преобразования уравнения в каноническом виде в параметрический и общий виды.

Определение 1. Любой ненулевой вектор, параллельный данной прямой называется направляющим вектором этой прямой.

На рисунке Рис.1 представлена прямая L и векторы q1, q2, q3, q4. Из определения следует, что векторы q1, q2, q4 являются направляющими векторами прямой L, а q3 − нет.

где x1, y1 координаты некоторой точки M1 на прямой L. Вектор q={m, p} является направляющим вектором прямой L.

Надо отметить, что при записи уравнения прямой в каноническом виде, допускается, чтобы один из чисел m и p была равна нулю (одновременно m и p не могут быть равным нулю, т.к.

направляющий вектор прямой не должен быть нулевым вектором). Равенство нулю одного из знаменателей означает равенство нулю соответствующего числителя.

В этом можно убедится, записав уравнение (1) в следующем виде:

Пусть в (2) m=0, p≠0. Тогда мы заключаем, что x−x1=0.

Выше мы отметили, что прямая L проходит через точку M1(x1, y1). В этом можно убедится, подставив x=x1, y=y1 в уравнение (1).

Запишем каноническое уравнение прямой проходящей через две различные точки M1(x1, y1) и M2(x2, y2):

Чтобы убедится, что точки M1(x1, y1) и M2(x2, y2) находятся на прямой L, поочередно подставим в уравнение (3) координаты точек M1 и M2. Получим тождества, следовательно эти точки принадлежат прямой L.

Сравним уравнения (1) и (3). Тогда можно записать q={m, p}={x2−x1, y2−y1}. На рисунке Рис.

Следовательно, для определения направляющего вектора прямой, достаточно взять две точки на данной прямой и найти разность между соответсвующими координатами этих точек.

Таким образом, прямая на плоскости определяется точкой и направляющим вектором или двумя точками.

Онлайн калькулятор, для построения прямой через две точки находится тут.

Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q={−3, 5}. Построить каноническое уравнение прямой.

Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

Ответ:

Пример 2. Прямая проходит через точку M=(2, 2) и имеет направляющий вектор q={0, 3}. Построить каноническое уравнение прямой.

Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

Ответ:

Пример 3. Прямая проходит через точки M1=(−7, 2) и M2=(−4, 4). Построить каноническое уравнение прямой. Воспользуемся формулой (3). Подставим координаты точек в уравнение (3):

• Упростим полученное уравнение:
• Ответ:
• Для приведения канонического уравнения прямой на плоскости к параметрическому виду, обозначим каждую часть уравнения (1) переменным t:
• Выразим переменные x и y через t:
• где t называется параметром, а уравнение (4) называется параметрическим уравнением прямой.

Для построения уравнения прямой, представленной параметрическом виде (4), достаточно задать параметру t любые значения и вычислить из уравнений (4) соответствующие координаты x и y некоторых точек. Затем провести через эти точки прямую.

1. Обратное преобразование смотрите здесь.
2. Пример 4. Каноническое уравнение прямой задана следующим уравнением:
3. Найти параметрическое уравнение прямой.
4. Решение. Обозначим через t левую и правую части уравнения (5):
5. Выразим переменные x и y через t:
6. Ответ:
7. Пусть прямая на плоскости задана каноническим уравнением прямой (1). Преобразовав (1) получим:
8. Сделаем следующие обозначения:
9. Тогда уравнение (6) можно записать в следующем виде:
10. где n={A,B} − называется нормальным вектором прямой.

Нетрудно заметить, что нормальный и направляющий векторы прямой перепендикулярны, т.е. скалярное произведение этих векторов равно нулю:

• Обратное преобразование смотрите здесь.
• Пример 5. Каноническое уравнение прямой задана следующим уравнением:
• Записать общее уравнение прямой.
• Решение. Сделаем преобразования уравнения (7):
• Ответ:

Источник: https://matworld.ru/analytic-geometry/kanonicheskoe-uravnenie-prjamoj.php

Гипербола определение, свойства и виды, каноническое уравнение, формула нахождения фокуса, алгоритмы и примеры построения графика функции

При упоминании термина «гипербола» человек с поэтическим складом мышления подумает о преувеличенном сопоставлении. В крайности доходящем до абсурда.

Близкий к математике представит нечто подобное:

Это родственные кривые, полученные при сечении конуса плоскостью. Парабола, эллипс (окружность), гипербола.

Что такое гипербола в математике

Это геометрическое место точек M, физическая разница расстояний от которых до выбранных (F1, F2), называемых фокусами, постоянна.

Оговоримся, что все сказанное относится к Евклидовой плоскости, где параллельные прямые не пересекаются.

Но если из отрезка |F1F2| соорудить координатную прямую X, за начальную точку взять середину (она же будет центром гиперболы) отрезка, то получим декартову систему координат. Где кривая описывается алгебраическим уравнением II-го порядка. 

• Получим классическую формулу аналитической геометрии:
• где a – действительная полуось, b – мнимая.
• Особенности:

• поскольку x и y связаны квадратной зависимостью, обе оси будут осями симметрии;
• пересечения с осью абсцисс (фокусов) с координатами ±a называются вершинами гиперболы, и расстояние между ними является минимальной дистанцией между ветвями (о последних ниже);
• кратчайший отрезок от фокуса до вершины зовется перицентрическим расстоянием и пишется «rp».

Асимптоты и фокусы гиперболы

Фокусы находятся на оси X (из этого исходили). Расстояние до центра гиперболы (он же центр симметрии C) называется фокальным и обозначается «c». Его формула:

Умозрительно очевидно, что сечение конуса состоит из двух кривых. Называются они ветвями гиперболы. Также не подлежит сомнению то, что ветви ограничены воображаемой поверхностью. Фокусы всегда находятся внутри ветвей.

1. Помучившись с производными и пределами, получим формулы асимптот (прямые, расстояние до которых от кривой стремится к нулю на бесконечном удалении от «0»):
2. Дистанцию от фокуса до асимптоты зовут прицельным параметром и обозначают буквой «b».

Как построить график функции гиперболы

Существует много ресурсов, где можно онлайн наблюдать, как строится функция. Но нужно все уметь самому. Итак, давайте учиться.

Построим для примера график уравнения

Решение:

По формуле выше выстраиваем асимптоты.

Отмечаем вершины х = ±2 (А1, А2). Приблизительный вид уже ясен.

При х = ±3, y = ±3,5 (примерно).

x = ±4, y = ±5,2.

Эксцентриситет гиперболы

• Эксцентриситетом считают величину:
• Или, в иной записи:
• Является параметром, характеризующим отклонение конического сечения от окружности:

Равнобочная (равносторонняя) гипербола

1. Таковой кривая является при условии a = b. Если покрутить систему координат, функцию можно свести к виду:
2. Эксцентриситет данной конструкции составит квадратный корень из 2.

3. Иначе говоря, получаем график обратной пропорциональности:
4. Или «любимую» школьниками.

5. Коль уж речь зашла о школьном курсе, добавим сведений:

• прямые x = 0, y = 0 – асимптоты;
• область определения – все действительные числа, кроме 0;
• область значений – все, за исключением 0;
• функция нечетная, поскольку меняет знак при смене знака аргумента;
• убывающая при положительных и отрицательных x.

Касательная и нормаль

В каждой точке гладкой кривой возможно построить касательную и нормаль (перпендикуляр). Гипербола – не исключение. Касательная – прямая, совпадающая с кривой только в одной точке (в пределах изгиба одного порядка).

• Уравнение касательной в точке с координатами (x0y0) имеет вид:
• В другой форме:
• Для нормали:

Сопряженные гиперболы

1. Записанное таким образом уравнение даст сопряженную фигуру:
2. То есть с теми же асимптотами, но расположенную по-другому, с поворотом на 90°. 
3. Пример на рисунке.

Свойства гиперболы

Их должен знать каждый школьник:

Касательная в произвольной точке H окажется биссектрисой угла F1HF2.

Кривая симметрична относительно осей и своего центра.

Отсеченный асимптотами отрезок касательной делится точкой соприкосновения пополам. Площадь же выделенного треугольника не меняется от изменения точки.

Использование

Где применяются знания о гиперболе:

• для создания эллиптических и других координат;
• в солнечных часах (сечение конуса света);
• для анализа движения космических объектов.

Заключение

Непростая кривая с неожиданными в некоторых случаях применением. Что удивительно, задача о сечениях конуса была поставлена древнегреческими учеными во II-м веке до нашей эры. Это говорит о высочайшем уровне тогдашних инженеров.

Нет, солнечные часы понятно были, а мелких искусственных спутников не было точно. И астероиды не исследовали, но вопросы возникали. И были ответы без ссылок на многочисленных богов. Удивительные люди.

ПредыдущаяСледующая

Источник: https://sprint-olympic.ru/uroki/algebra/78240-giperbola-opredelenie-svoistva-i-vidy-kanonicheskoe-yravnenie-formyla-nahojdeniia-fokysa-algoritmy-i-primery-postroeniia-grafika-fynkcii.html?doing_wp_cron=1585049828.5070910453796386718750