Первообразная и неопределенный интеграл

• План урока:
• Понятие первообразной
• Бесконечное количество первообразных
• Неопределенный интеграл
• Таблица первообразных
• Правила вычисления интегралов
• Физический смысл неопределенного интеграла

Понятие первообразной

Ранее мы познакомились с важнейшим понятием математического анализа – производной. Она имеет большое практическое значение, в частности, с ее помощью можно определить скорость тела, если известен закон его передвижения. Например, если путь, пройденный автомобилем, можно вычислить с помощью функции S = t2, то его скорость в любой момент времени может быть рассчитана по формуле

Однако на практике значительно чаще встречается прямо противоположная задача. Известно, как меняется скорость тела, и найти требуется путь, пройденный им. В таком случае необходимо по производной определить ту функцию, которая «подверглась» дифференцированию.

Задание. Известна производная функции у(х):

В этом примере мы выполнили операцию, обратную дифференцированию. В математическом анализе он называется интегрированием. Если интегрируют некоторую произвольную функцию f(х), то в итоге получают новую функцию, которую чаще всего обозначают как F(x). Её называют первообразной функции f(x).

Приведем несколько примеров первообразной:

Последний пример показывает, что иногда первообразная может и совпадать с исходной функцией.

Задание. Докажите, что функция

Первообразные встречаются и в ряде практических задач, особенно в тех, где рассматривается движение тел.

Задание. Автомобиль Buggati Veyron разгоняется от 0 до 40 м/с за 4 секунды. Какое расстояние проедет эта машина за эти 4 секунды, если разгон осуществляется равномерно?

Решение: Если за 4 секунды машина разгоняется до 30 м/с, то за одну секунду она увеличивает скорость на

Примечание – в будущем мы научимся более строго решать такие задачи, и «угадывать» подходящую первообразную не придётся.

Бесконечное количество первообразных

Рассмотрим функцию

Оказывается, что g1 также является первообразной для у. То есть у одной функции у = 4х3 есть сразу две первообразных:g = x4и g = x4 + 1! Более того, можно доказать, что у любой функции есть бесконечное количество первообразных!

Действительно, рассмотрим сразу все функции

где С – некоторая константа, то есть параметр. В данном случае можно сказать, что мы рассматриваем не одну функцию, а семейство функций. Продифференцируем g:

Мы видим, что у всех функций из этого семейства, независимо от значения параметра С, производная одинакова. Здесь С может принимать любое действительное значение. Так как действительных чисел бесконечно много, то и количество функций, образующих семейство, также бесконечно. И все они являются первообразными для у = 4х3.

Данная особенность операции интегрирования может быть сформулирована в виде следующей теоремы:

Можно дать и графическую иллюстрацию этого правила. Построим произвольный график g = F(x). Далее построим ещё один график

1. Очевидно, что он может быть получен параллельным переносом первого графика на С единиц вверх:
2. Теперь в какой-нибудь точке х0 проведем касательные к обоим графикам первообразных. Очевидно, что они будут иметь одинаковый угол наклона, так как по сути тоже могут быть получены параллельным переносом:
3. Если же углы наклона касательных совпадают, то и производные в этих точках также равны.
4. В связи с наличием у каждой функции бесконечного количества первообразных их часто записывают в общем виде. Например, пусть надо записать первообразную для
5. Однако 2х2 – это лишь одна из бесконечного множества первообразных. Все вместе они образуют семейство, которое записывается так:

Неопределенный интеграл

Каждая математическая операция имеет какое-то особое обозначение. Например, чтобы показать, что мы дифференцируем некоторую функцию, мы ставим после неё штрих (и при необходимости берем в скобки):

Напомним, что операция нахождения первообразной называется интегрированием. Для ее обозначения используется особый знак – интеграл. Например, мы знаем, что первообразная для у = х2 – это семейство функций вида

• Рассмотрим элементы записанного нами равенства:

Исходная функция – это та самая функция, для которой необходимо найти первообразную, то есть интегрируемая функция. Справа от знака «равно» как раз записывается первообразная. Сразу после первообразной надо писать «+ С». Тем самым мы показываем, что у интегрируемой функции есть бесконечное количество первообразных.

После интегрируемой функции стоит так называемый дифференциал dх (читается как «дэ икс»). В данном случае он указывает, что именно буквой х мы обозначаем переменную в интегрируемой функции. Его значение мы разберем несколько позже. Пока что надо запомнить, что после интегрируемой функции необходимо писать «dx». В целом вся запись

читается так: «интеграл от два икс по дэ икс равен икс в квадрате плюс цэ».

В чем разница между первообразной и интегралом? Первообразная – это функция, при дифференцировании которой получается исходная функция. Интеграл же – это не функция, а целое семейство функций (или их множество), которое включает в себя сразу все первообразные интегрируемой функции.

Получили подынтегральное выражение. Значит, мы всё сделали правильно.

Здесь важно заметить, что в математике существует сразу несколько видов интегралов, каждый из которых имеет разное определение. Здесь описан так называемый «неопределенный интеграл». Несложно догадаться, что существует ещё и «определенный интеграл», который мы рассмотрим на следующих уроках. Теперь можно дать следующее определение:

1. Задание. Найдите неопределенный интеграл

Решение. Вспомним таблицу производных элементарных функций. Производная синуса равна косинусу:

• Заметим, что непосредственно из определения следует важное свойство неопределенного интеграла – производная интеграла равна его подынтегральному выражению:
• Грубо говоря, операции интегрирования дифференцирования «сокращают» друг друга.
• Задание. Вычислите производную:

Таблица первообразных

Как же вычислять интегралы? Проще всего начать с тех функций, которые уже есть в таблице производных. Напомним, как она выглядит:

1. Из определения первообразной следует, что для тех функций, которые указаны во втором столбце таблицы, одной из первообразных является соответствующая функция из первого столбца. То есть можно составить такую таблицу первообразных:

Обратите внимание на третью строку снизу. Здесь произошло небольшое изменение – вместо первообразной lnx мы записали ln |x|, то есть использовали модуль числа. Дело в том, что функция

• определена при любом значении аргумента, кроме нуля. В то же время функция

не определена при отрицательных значениях х, так как под знаком логарифма не может стоять отрицательное число. Однако области определения интегрируемой функции и ее первообразной должны совпадать. Использование модуля обеспечивает выполнение этого условия.

1. Полученная нами таблица интегралов не совсем удобна. Предположим, нам надо проинтегрировать функцию
2. отличающуюся от интересующей нас функции лишь множителем перед х5.
3. Однако можно догадаться, что в качестве подходящей первообразной можно взять функцию
4. В связи с этим есть смысл немного подкорректировать таблицу первообразных таким образом, чтобы в первом столбце стояли стандартные функции без неудобных множителей. В результате таблица примет следующий вид:
5. Можно доказать, что каждое равенство в третьем столбце является справедливым. Возьмем, например, равенство

Получили подынтегральное выражение, а это значит, что равенство справедливо. Таким же образом можно доказать и все остальные равенства в таблице.

• Задание. Вычислите неопределенный интеграл:
• Решение. Этот интеграл присутствует в таблице (7-ая строка), а потому мы просто переписываем равенство из неё:
• Задание. Найдите первообразную функции

Правила вычисления интегралов

Что делать в том случае, если надо вычислить интеграл, которого нет в таблице? Существует три несложных правила интегрирования, которые могут помочь в такой ситуации.

1. Докажем это правило. Для этого просто продифференцируем правую часть равенства:

Получили именно то выражение, которое стоит под знаком интеграла в левой части равенства. Это значит, что формула справедлива.

• Рассмотрим пример использования этого правила. Пусть надо найти первообразную функции
• Здесь мы представили исходный интеграл как сумму двух более простых интегралов, которые являются табличными

Обратите внимание, что мы не стали складывать константы интегрирования С как подобные слагаемые и писать 2С. Дело в том, что С – это некоторое произвольное число. Но если сложить два произвольных числа, то в итоге получится третье произвольное число, которое также будет обозначаться как С! Поэтому обычно константу С просто дописывают в самом конце решаемого примера.

1. Естественно, что правило сложения интегралов работает и в случае суммы не двух, а большего количества слагаемых.
2. Задание. Вычислите неопределенный интеграл

Возможна ситуация, когда мы не уверены в правильности полученного решения. В таком случае можно легко проверить себя, просто продифференцировав получившийся интеграл. В итоге мы должны получить исходную функцию (подынтегральное выражение):

• Следующее правило позволяет выносить множитель из-под знака интеграла.
• Для доказательства тождества снова продифференцируем его левую часть:

Получили как раз то выражение, которое стоит под интегралом справа. Следовательно, формула верна.

1. Рассмотрим несколько простейших примеров использования этого метода интегрирования неопределенных интегралов:
2. Естественно, что правила 1 и 2 можно комбинировать друг с другом, решая более сложные примеры.
3. Задание. Вычислите неопределенный интеграл от квадратичной функции

Первые два правила достаточно просты и напоминают аналогичные правила дифференцирования. А вот третий метод вычисления неопределенного интеграла более сложный.

• Проиллюстрируем его на примере. Пусть надо найти первообразную для функции

Но в нашем случае под знаком косинуса стоит не х, а выражение 5х + 7, являющееся линейной функцией. Поэтому, согласно правилу, мы должны написать впервообразной не sinx, а sin (5x + 7), то есть изменить аргумент. Также надо добавить перед синусом «поправочный множитель», равный 1/k, то есть в нашем случае 1/5:

Проверим себя. Продифференцируем получившуюся первообразную. При этом мы используем правило дифференцирования сложной функции:

1. Получили ту самую функцию, которую и надо было проинтегрировать.
2. Приведем ещё несколько примеров использования правила 3:

Напомним, что при изучении производной мы познакомились также с правилами дифференцирования произведения, дроби и сложной функции. Используя их, мы могли найти производную для почти любой функции, которую только могли записать. С решением неопределенных интегралов ситуация значительно сложнее. С помощью приведенных трех правил не получится вычислить такие интегралы, как

• Более того, в записанной нами таблице интегралов отсутствует ряд элементарных функций, поэтому мы не сможем даже проинтегрировать такую простую функцию, как

Дело в том, что задача интегрирования является значительно более сложной, чем задача дифференцирования. Отметим три момента. Во-первых, в нашей школьной таблице интегралов, содержащей всего 11 формул, указаны лишь самые простые элементарные функции. Существуют справочники, где в качестве табличных указаны интегралы десятков, а то и сотен функций.

Во-вторых, есть и более сложные правила интегрирования, которые изучаются уже в институте. В-третьих, существуют такие элементарные функции, первообразную которых в принципе невозможно записать, используя элементарные функции (синус, косинус, логарифм и т.п.).

В связи с этим приходится вводить в рассмотрение новые специальные функции, а также использовать приближенные методы вычислений.

Физический смысл неопределенного интеграла

Напомним физический смысл производной – если известен закон движения материальной точки, то есть некоторая функция S(t), то производная этого закона будет выражать скорость тела в момент времени t:

Отсюда прямо вытекает физический смысл первообразной. Если известен закон изменения скорости v(t), то его первообразная будет являться законом движения S(t). Точнее говоря, законом движения будет являться только одна из первообразных, так как их существует бесконечно много.

Задача. Скорость тела в произвольный момент времени t может быть вычислена по закону

Найдите закон движения материальной точки S(t). Известно, что в начальный момент времени тело находилось в точке с координатой 1,5, то есть S(0) = 1,5.

Решение. Нам надо просто проинтегрировать функцию v(t):

Интеграл вычислен, но это ещё не закон движения, ведь в нем присутствует константа интегрирования. Как от неё избавиться? Надо использовать условие, согласно которому S(0) = 1,5. В общем виде закон движения имеет вид

1. Мы нашли конкретное значение константы интегрирования. С учетом этого закон движения (1) примет вид:

Источник: https://100urokov.ru/predmety/urok-6-integral-i-pervoobraznaya

Урок на тему; Первообразная функции. Неопределенный интеграл

• Государственное бюджетное профессиональное общеобразовательное учреждение
• «Невинномысский энергетический техникум»
• Методическая разработка открытого занятия по дисциплине «Математика»
• Тема занятия:

Первообразная функции. Неопределенный интеграл.

1. Преподаватель математики:
2. Скрыльникова Валентина Евгеньевна
3. Невинномысск 2016 год.
4. Цели занятия:

Образовательная: Сформировать представления об интегральном исчислении, уяснить его суть. Выработать навыки нахождения неопределенного интеграла и первообразных, умения пользоваться свойствами и методами интегрирования.

• Развивающая: Развивать математически грамотную речь, внимание, сознательное восприятие учебного материала.
• Воспитательная: Воспитывать познавательную активность, сообразительность и мышление, благодарность к достижению великих математиков в области интегрирования.
• Вид занятия: урок
• Тип занятия: сообщения новых знаний
• Метод проведения: словесный, наглядный, самостоятельная работа.
• Квалификационные требования:
• Ученики должны:

В ходе изучения темы «Первообразная функции. Неопределенный интеграл» студентам предстоит усвоить основные понятия и утверждения, иметь представления о возможностях применения средств интегрального исчисления в геометрических, физических и др. прикладных задачах.

1. Знать:
2. определение первообразной функции и неопределенного интеграла;
3. свойства и методы нахождения интегралов
4. формулы простейших интегралов.
5. Уметь:
6. вычислять первообразные и неопределенный интеграл, используя основные свойства и методы нахождения.
7. Междисциплинарные связи: физика, история математики.
8. Внутридисциплинарные связи: «Нахождение производной», «Вычисление объемов тел», «Вычисление определенного интеграла».
9. Обеспечение занятия:
10. -Наглядные пособия: портреты великих математиков, имеющих представление к интегральному исчислению
11. -Раздаточный материал: конспект со схемами, карточки с заданиями (на этапе закрепления).
12. -Оборудование: чертежные принадлежности, линейка.
13. Структура занятия.

1. Организационный момент (1 мин.)

1. Мотивация учебной деятельности. (3 мин.)

2. Изложение нового материала. (50-51 мин.)

3. Самостоятельная работа (10 мин)

4. Закрепление изученного материала. (5 мин.)

5. Подведение итогов занятия. (2-3 мин.)

6. Сообщение домашнего задания. (1мин.)

Ход занятия.

1. Организационный момент. (1 мин.)

Преподаватель приветствует студентов, проверяет присутствующих в аудитории.

Учащиеся готовятся к работе. Староста заполняет рапортичку. Дежурные раздают раздаточный материал.

1. Мотивация учебной деятельности.(3 мин.)

Тема сегодняшнего занятия «Первообразная функции. Неопределенный интеграл.». Знания по данной теме нами будет использоваться на следующих уроках при нахождении определенных интегралов, площадей плоских фигур. Большое внимание уделяется интегральному исчислению в разделах высшей математики в высших учебных заведениях при решении прикладных задач.

• Наше сегодняшнее занятие является занятием изучения нового материала, по этому будет носить теоретический характер.
• Цель занятия: сформировать представления об интегральном исчислении, понять его сущность, развивать навыки при нахождении первообразных и неопределенного интеграла.
• Студенты записывают дату и тему занятия.
• 3.Изложение нового материала (50-51 мин)

Тема: «Первообразная функции. Неопределенный интеграл.»

1. Из истории интегрального исчисления. О происхождении терминов и обозначений.

2. Определение первообразной, её основное свойство, правила нахождения первообразных.

3. Понятие неопределенного интеграла, его свойства.

4. Таблица простейших интегралов.

1. История понятия интеграла тесно связана с задачами нахождения квадратур. Задачами о квадратуре той или иной плоской фигуры математики Древней Греции и Рима называли задачами, которые мы сейчас относим к задачам на вычисление площадей.

Многие значительные достижения математиков Древней Греции в решении таких задач связаны с применением метода исчерпывания, предложенным Евдоксом Книдским. С помощью этого метода Евдокс доказал:

1. Площади двух кругов относятся как квадраты их диаметров.

2. Объём конуса равен 1/3 объёма цилиндра, имеющего такие же высоту и основание.

Метод Евдокса был усовершенствован Архимедом и были доказаны такие вещи:

1. Вывод формулы площади круга.

2. Объем шара равен 2/3 объема цилиндра.

Все достижения были доказаны великими математиками с применением интегралов.

Символ введен Лейбницем в 1675 г. Этот знак является изменением латинской буквы S. Само слово «интеграл» придумано Бернулли в 1690 г. Оно происходит от латинского integro, которое переводится, как приводить в прежнее состояние, восстанавливать. Действительно, операция интегрирования обратная операции дифференцирования т.е.

для того, чтобы проверить правильность нахождения интеграла необходимо продифференцировать ответ и получить подынтегральную функцию. Другими словами интегральное исчисление решает задачу: по заданной производной или дифференциалу неизвестной функции требуется определить эту функцию.

Отсюда можно сделать вывод, который мы запишем в виде определения.

2. Определение 1: Функция F(x) называется первообразной для функции f(x) на данном промежутке, если для любого x из этого промежутка F’(x) = f(x).

1. Пример:Первообразной для функции f(x)=x3 на всей числовой оси является F(x)=x4/4, поскольку (x4/4)’=x.
2. Основное свойство первообразных
3. Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C – произвольная постоянная, также является первообразной функции f(x).
4. Геометрическая интерпретация
5. графики всех первообразных данной функции f(x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси y.
6. Три правила нахождения первообразных
7. Правило №1: Если F есть первообразная для функции f, а G – первообразная для g, то F+G – есть первообразная для f+g.
8. (F(x) + G(x))’ = F’(x) + G’(x) = f + g
9. Правило №2: Если F – первообразная для f, а k – постоянная, то функцияkF – первообразная для kf.
10. (kF)’ = kF’ = kf
11. Правило №3: Если F – первообразная для f, а k и b– постоянные (), то функция
12. — первообразная для f(kx+b).

3. Вернемся к теореме 1 и выведем новое определение.

• Определение 2: Выражение F(x) + C, где C — произвольная постоянная, называют неопределенным интегралом и обозначают символом
• Из определения имеем:
• (1)
• Неопределенный интеграл функцииf(x), таким образом, представляет собой множество всех первообразных функций дляf(x).
• В равенстве (1) функциюf(x) называется подынтегральной функцией, а выражение f(x)dx– подынтегральным выражением, переменную x –переменной интегрирования, слагаемое C — постоянной интегрирования.

Интегрирование представляет собой операцию, обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.

1. Неопределенный интеграл
2. Совокупность всех первообразных данной функции f(x) называется ее неопределенным интегралом и обозначается :
3. где C – произвольная постоянная.
4. Свойства неопределенного интеграла.
5. Опираясь на определение первообразной, легко доказать следующие свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции, то есть если  = f(x), то

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению

1. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

1. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов

1. Постоянный множитель можно выносить за знак интеграла, то есть если a=const, то

Таблица простейших интегралов.

Учащиеся записывают фамилии великих математиков и их достижения в области интегрального исчисления.

Учащиеся записывают информацию об истории возникновения интеграла.

Учащиеся записывают лекцию, используя раздаточный материал и объяснения преподавателя. При доказательствах свойств первообразных и интегралов, используют знания по теме дифференцирования.

• Решение примеров на нахождение неопределенного интеграла.
• Самостоятельная работа
• Вариант 1

4.Закрепление изученного материала.(12 мин)

На этапе закрепления изученного материала предлагается игра «Найди свою половинку». Всем присутствующим предлагается разбиться на восемь подгрупп. Каждой подгруппе раздается карточка, на которой написано либо «функция» либо «первообразная» и соответствующее задание, т.е.

1. Если на вашей карточке написано слово «функция», то вы должны используя таблицу простейших интегралов найти интеграл от этой функции.

2. Если написано «первообразная», то вы должны найти саму функцию, используя операцию дифференцирования.

Свою «половинку» найти на доске. После чего прикрепить магнитом свой ответ. После полного набора, убедимся, что все совпадения правильные. Каким образом? Перевернуть ответы обратной стороной, где образуется ключевое слово «Интеграл» — тема занятия.

Придерживаться инструктажа по правилам игры.

Функция

Первообразная

1. Функция
2. Первообразная
3. Функция
4. Первообразная
5. Функция
6. Первообразная
7. Функция
8. Первообразная
9. Функция
10. Первообразная
11. Функция
12. Первообразная
13. Функция
14. Первообразная

5.Подведение итогов занятия.(2 мин.)

Итак, получилось слово «интеграл», т.е. тема нашего сегодняшнего занятия. Применяя знания по новому материалу, вы справились с данной задачей. Преподаватель сообщает оценки за урок.

Участвуют в беседе по подведению итогов.

6.Домашнее задание (1 мин.)

Преподаватель сообщает домашнее задание:

1) Прочитать стр. 179 -182 в учебнике «Алгебра и начала анализа».

• 2) Выучить конспект.
• 3) Назвать фамилии великих математиков, имеющих отношение к теме «Интегральное исчисление».
• 4) Решить задачи № 332 (б, в), №333 (а, в) Колмогоров «Алгебра и начала анализа».
• Записывают домашнее задание
• Литература

1. «Алгебра и начала анализа» — учебник, Колмогоров А.Н., М. 1991 г., стр. 179-182.

2. «Математика» — учебное пособие, Дахневич Т.Ф., Клюева И.А., Волгоград 2002 г., стр. 82 – 85.

3. «Неопределенный интеграл» — задание для внеаудиторной работы, Маринина Н.С., 2006

Источник: https://infourok.ru/urok-na-temu-pervoobraznaya-funkcii-neopredelenniy-integral-1182661.html

Первообразная и интеграл

1. Первообразная

Сам термин «производная можно обосновать «по-житейски»: функция y = f(x) «производит на свет» новую функцию y' = f '(x). Функция y = f(x) выступает как бы в качестве «родителя», но математики, естественно, не называют ее «родителем» или «производителем», они говорят, что это, по отношению к функции y' = f '(x), первичный образ, или первообразная.

   Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для x є X выполняется равенство F '(x) = f(x).

•     Примеры: 
•     1) Функция y = x2 является первообразной для функции y = 2x, поскольку для любого x справедливо равенство (x2)' = 2x.
•     2) Функция y = sin x  является первообразной для функции y = cos x, поскольку для любого x справедливо равенство (sin x)' = cos x.
• Таблица формул для нахождения первообразных:

    При нахождении первообразных используются не только формулы, но и некоторые правила.

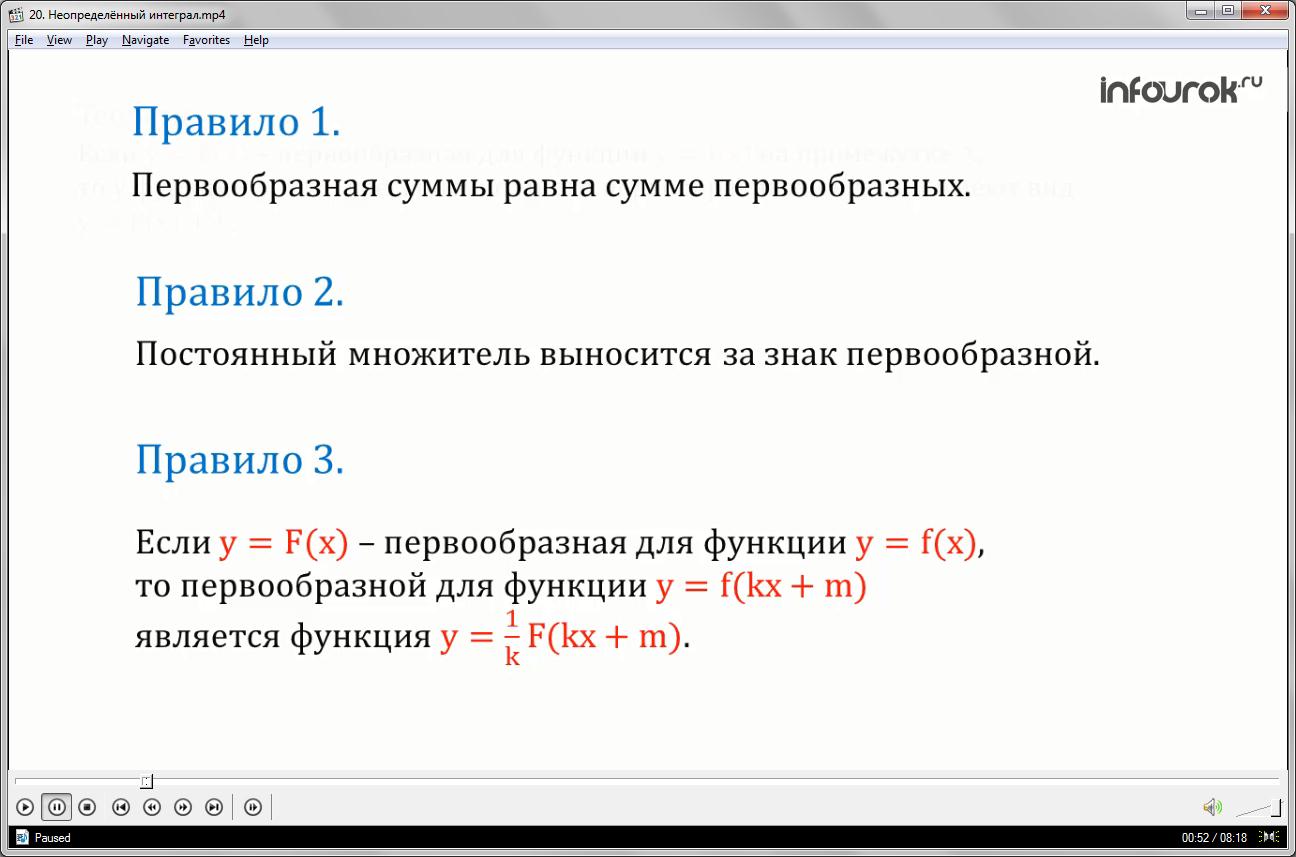
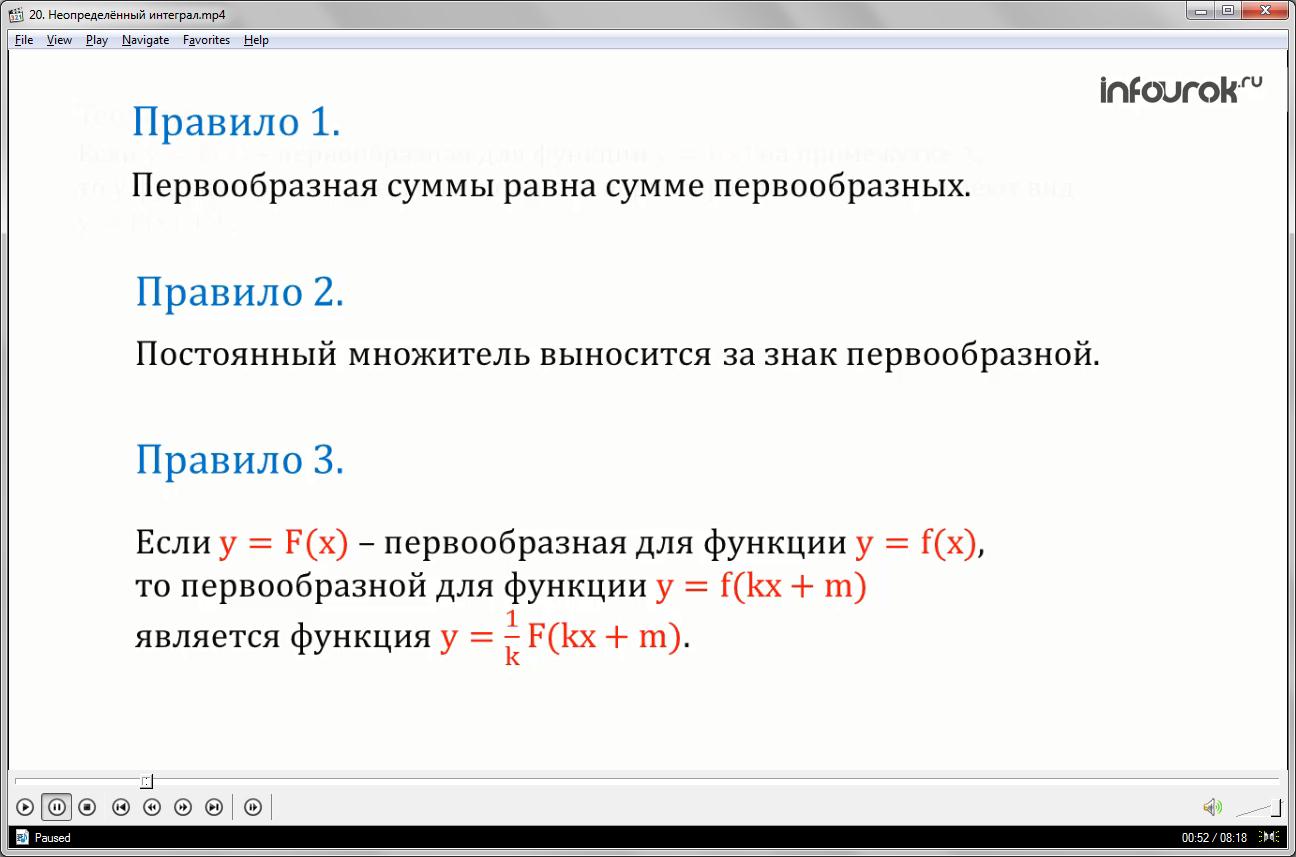
    Правило 1. Первообразная суммы равна сумме первообразных. 

    Если функции у — f(x) и у — g(х) имеют на промежутке X первообразные соответственно у — F(x) и у = G(x), то и сумма функций у = f(x) + g(x) имеет на промежутке X первообразную, причем одной из этих первообразных является функция у = F(x) + G(х).

  Пример 1. Найти первообразную для функции у = 2х + cos х.

   Решение: Первообразной для 2х служит х2; первообразной для cos х служит sin х. Значит, первообразной для функции у = 2х + cos х будет служить функция у = х2 + sin х (и вообще любая функция вида у = х2 + sin х + С).

   Правило 2. Если F(x) — первообразная для f(x), то kF(x) — первообразная для kf(x).    Пример 2. Найти первообразные для функции y = 5 sin x.

    Решение: Первообразной для sin х служит -cos х; значит, для функции у = 5 sin х первообразной будет функция у = -5 cos х.

    Теорема 1. Если у = F(x) — первообразная для функции у = f(x), то первообразной для функции у = f(kx + m) служит функция у = (1/k) F(kx + m).

   Теорема 2. Если у = F(x) — первообразная для функции у = f(x) на промежутке X, то у функции у = f(x) бесконечно много первообразных, и все они имеют вид у = F(x) + С.

1. 2. Определенный интеграл
2. Существуют задачи, приводящие к понятию определенного интеграла. 
3.     В задаче 1 (о вычислении площади криволинейной трапеции) приходят к выводу, что искомая площадь криволинейной трапеции равна пределу последовательности (Sn):
4. S = lim Sn (при n -> ∞);
5. в задаче 2 (о вычислении массы стержня) — физическая масса равна пределу последовательности (Sn):  
6. m = lim Sn (при n -> ∞); 
7. в задаче 3 (о перемещении точки) — искомое перемещение равно пределу последовательности (Sn):  
8. s = lim Sn (при n -> ∞).
9.     Подробное изучение данных задач рассматривается на сайте.

    Дадим математическое описание той модели, которая была построена в трех рассмотренных задачах для функции у = f(x), непрерывной (но необязательно неотрицательной, как это предполагалось в рассмотренных задачах) на отрезке [а; b]:    1) разбиваем отрезок [а; b] на п равных частей;    2) составляем сумму

Sn = f(x0)∆x0 + f(x1)∆x1+ f(x2)∆x2 + … + f(xk)∆xk+ … + f(xn-1)∆xn-1;

    3) вычисляем lim Sn (при n -> ∞).

    В курсе математического анализа доказано, что этот предел в случае непрерывной (или кусочно-непрерывной) функции существует. Его называют определенным интегралом от функции у = f(x) по отрезку [а; b] и обозначают так: 

(читают: интеграл от а до бэ эф от икс дэ икс). Числа а и b называют пределами интегрирования (соответственно нижним и верхним).

    Теорема. Если функция у = f(x) непрерывна на отрезке [а; b], то справедлива формула

 ,где F(x) — первообразная для f(x).    Приведенную формулу обычно называют формулой Ньютона — Лейбница в честь английского физика Исаака Ньютона (1643—1727) и немецкого философа Готфрида Лейбница (1646— 1716), получивших ее независимо друг от друга и практически одновременно.Примеры вычисления интегралов с помощью формулы Ньютона-Лейбница    С помощью интеграла можно вычислять площади не только криволинейных трапеций, но и плоских фигур более сложного вида.

    Площадь S фигуры, ограниченной прямыми х = а, х = b и графиками функций у = f(x), у = g(x), непрерывных на отрезке [а; b] и таких, что для любого х из отрезка [а; b] выполняется неравенство g(x) ≤ f(x) , вычисляется по формуле:

•     Пример:
•     Найти площадь фигуры, ограниченную графиками функций y = 2x — x2 и x + y = 0.

1.     Решение:
2. Найдем координаты точек пересечения кривых:
3.                     2x — x2 = -x,
4.                     x2 — 3x = 0,
5.                     x(x — 3) = 0,
6.                     x1 = 0, x2 = 3.

    Данная область ограничивается сверху параболой  

• y = 2x — x2, а снизу —  прямой линией y = -x.
•     Следовательно, площадь этой области равна

Источник: https://www.sites.google.com/site/pervoobraznaaiintegral/

Первообразная и неопределенный интеграл

В теории дифференцирования рассматривается задача нахождения производной функции, т.е. функции для которой $f(x)=F'(x)$.

В теории интегрирования рассматривается обратная задача, т.е. нахождение функции $F(x)$ для которой $F'(x)=f(x)$.

Определение 1

Первообразная $F(x)$ для функции $y=f(x)$ на отрезке $[a;b]$ — это функция, которая является дифференцируемой в каждой точке этого отрезка и для ее производной выполняется следующее равенство:

[F'(x)=f(x).]

Примечание 1

• Равенство из определения 1 можно записать с помощью дифференциалов следующим образом:
• $frac{dF}{dx} =f(x)$ или $dF=f(x)dx$.
• Для нахождения первообразной некоторой функции можно пользоваться таблицей производных.

Пример 1

1. Вычислить первообразную $F(x)$ заданных функций:
2. 1) $f(x)=x^{2} $; 2) $f(x)=cos x$.
3. Решение:
4. 1) Первообразной функции $f(x)=x^{2} $ является функция $F(x)=frac{x^{3} }{3} $, так как
5. 2) Первообразной функции $f(x)=cos x$ является функция $F(x)=sin x$, так как

[F'(x)=left(frac{x^{3} }{3}
ight)'=frac{3x^{2} }{3} =x^{2} =f(x).]
[F'(x)=left(sin x
ight)'=cos x=f(x).]

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

Примечание 2

Первообразная $F(x)$ функции $f(x)$ имеет конечную производную, что означает, что первообразная $F(x)$ является функцией непрерывной.

Теорема 1

Если функция $F(x)$ — это первообразная для функции $y=f(x)$ на некотором отрезке $[a;b]$, то и функция вида $Phi (x)=F(x)+C$ также является первообразной для исходной функции, при этом $C=const$.

Примечание 3

Теорема 1 показывает, что множество полученных первообразных функций для заданной функции является бесконечным.

Пример 2

• Определить множество первообразных $F(x)$ для заданных функций:
• 1) $f(x)=frac{1}{x} $; 2) $f(x)=sin x$.
• Решение:
• 1) Первообразными функции $f(x)=frac{1}{x} $ является множество функций $F(x)=ln |x|+C$, так как
• 2) Первообразными функции $f(x)=sin x$ является множество функций $F(x)=-cos x+C$, так как

[F'(x)=left(ln |x|+C
ight)'=frac{1}{x} =f(x).]
[F'(x)=left(-cos x+C
ight)'=sin x=f(x).]

Теорема 2

Если $F_{1} (x)$ и $F_{2} (x)$ — две первообразные от одной заданной функции $y=f(x)$ на отрезке $[a;b]$, то разность между ними равна некоторому постоянному числу, т.е.

[F_{1} (x)-F_{2} (x)=C=const.]

Примечание 4

Теорему 2 можно перефразировать следующим образом: каждая функция, являющаяся первообразной для заданной функции $f(x)$, может быть записана в виде $F(x)+C$.

Пример 3

1. Вычислить несколько первообразных $F(x)$ для заданной функции: $f(x)=x$.
2. Решение:
3. Первообразными функции $f(x)=x$ является множество функций $F(x)=frac{x^{2} }{2} +C$, так как
4. Выпишем две первообразные:
5. 1) $F(x)=frac{x^{2} }{2} +2$; 2) $F(x)=frac{x^{2} }{2} +10$.

[F'(x)=left(frac{x^{2} }{2} +C
ight)'=frac{2x}{2} =x=f(x).]

Теорема 3

Каждая функция $y=f(x)$, непрерывная на отрезке $[a;b]$, имеет на данном отрезке первообразную $F(x)$.

Определение 2

Совокупность всех первообразных заданной функции $y=f(x)$, определенной на некотором отрезке, называется неопределенным интегралом от заданной функции $y=f(x)$. Неопределенный интеграл обозначается символом $int f(x)dx $.

Примечание 5

Определение 2 можно записать следующим образом:

[int f(x)dx =F(x)+C.]

Обозначения:

• $int $ — знак интеграла;
• $f (x) $ — подынтегральная функция;
• $f(x)dx$ — подынтегральное выражение;
• $x$ — переменная интегрирования.

Определение 3

Интегрирование функции $y=f(x)$ — это операция нахождения первообразной заданной функции $y=f(x)$ или неопределенного интеграла от заданной функции $y=f(x)$.

Примечание 6

Операция интегрирования является обратной для операции дифференцирования.

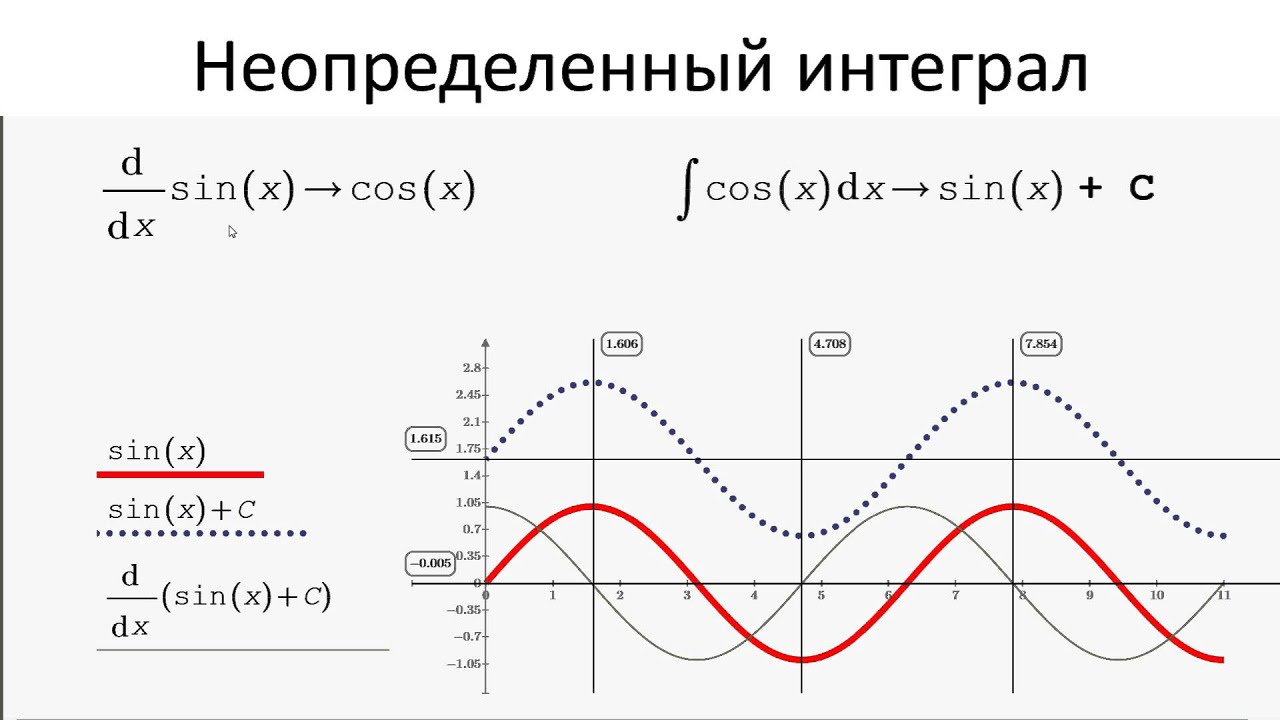
Геометрический смысл: неопределенный интеграл представляет собой семейство параллельно расположенных кривых $F(x)+C$, где каждому конкретному числовому значению постоянной $C$ соответствует определенная кривая из указанного семейства (рис.1).

Рис. 1

Определение 4

График каждой кривой из семейства первообразных называется интегральной кривой.

Пример 4

• Найти неопределенный интеграл от заданной функции $f(x)=2$ и изобразить некоторые кривые на координатной плоскости.
• Решение:
• Для функции $f(x)=2$ неопределенный интеграл имеет вид:
• Выпишем интегралы для разных значений константы:
• 1) $int 2dx =2x$; 2) $int 2dx =2x+1$; 3) $int 2dx =2x+2$.

[int 2dx =2x+C.]

Изобразим полученные кривые на координатной плоскости (рис.2).

Пример 5

1. Найти неопределенный интеграл от заданных функций:
2. 1) $f(x)=x$; 2) $f(x)=sin x$.
3. Решение:
4. 1) Для функции $f(x)=x$ неопределенный интеграл имеет вид:
5. 2) Для функции $f(x)=sin x$ неопределенный интеграл имеет вид:

[int xdx =frac{x^{2} }{2} +C.]
[int sin xdx =-cos x+C.]

Источник: https://spravochnick.ru/matematika/pervoobraznaya_i_neopredelennyy_integral/

Первообразная и неопределенный интеграл, их свойства

Для начала, дадим определение понятиям, которые будут использоваться в данном разделе. В первую очередь это первообразная функции. Для этого введем константу C.

Определение 1

Первообразная функции f(x) на промежутке (a; b) это такая функция F(x), при которое формула F'(x)=f(x) превращается в равенство для любого x из заданного промежутка.

Получается, что функция f(x) имеет множество первообразных F(x)+C, для произвольной константы C. Эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла

Все множество первообразных функции f(x) можно назвать неопределенным интегралом этой функции. С учетом этого формула будет иметь вид ∫f(x)dx=F(x)+C. При этом, выражение f(x)dx является подынтегральным выражением, а f(x) – это подынтегральная функция. Подынтегральное выражение представляет собой дифференциал функции f(x).

Имея заданный дифференциал функции, мы можем найти неизвестную функцию.

Результатом неопределенного интегрирования будет не одна функция F(x), а множество ее первообразных F(x)+C.

• Зная свойства производной, мы можем сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

∫f(x)dx'=F(x)+C'=f(x)

• Производная результата интегрирования равна подынтегральной функции.

∫d(F(x))=∫F'(x)dx=∫f(x)dx=F(x)+C

• Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

∫k·f(x)dx=k·∫f(x)dx, где k – произвольная константа. Коэффициент можно выносить за знак неопределенного интеграла.

• Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

• ∫f(x)±g(x))dx=∫f(x)dx±∫g(x)dx
• Промежуточные равенства первого и второго свойств неопределенного интеграла мы привели в качестве пояснения.
• Для того, чтобы доказать третье и четвертое свойства, необходимо найти производные от правых частей равенств:
• k·∫f(x)dx'=k·∫d(x)dx'=k·f(x)∫f(x)dx±∫g(x)dx'=∫f(x)dx'±∫g(x)dx'=f(x)±g(x)

Производные правых частей равенств равны подынтегральным функциям, что является доказательством первого свойства. Его же мы используем в последних переходах.

Как видите, задача интегрирования представляет собой обратный процесс по отношению к задаче дифференцирования. Обе эти задачи тесно связаны между собой.

Первое свойство может быть использовано для проведения проверки интегрирования. Для проверки нам достаточно вычислить производную полученного результата. Если полученная функция будет равна подынтегральной функции, то интегрирование проведено верно.

Благодаря второму свойству по известному дифференциалу функции мы можем найти ее первообразную и использовать ее для вычисления неопределенного интеграла.

Рассмотрим пример.

Пример 1

1. Найдем первообразную функции f(x)=1x, значение которой равно единице при х=1.
2. Решение
3. Используя таблицу производных основных элементарных функций получаем
4. d(ln x)=(ln x)'dx=dxx=f(x)dx∫f(x)dx=∫dxx=∫d(ln(x))

Используя второе свойство ∫d(ln(x))=ln(x)+C, мы получаем множество первообразных ln(x)+C. При х=1 получим значение ln(1)+C=0+C=C. Согласно условию задачи, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид  ln(x)+1.

Ответ: f(x)=1x=ln(x)+1

Пример 2

• Необходимо найти неопределенный интеграл ∫2sinx2cosx2dx и проверить результат вычисления дифференцированием.
• Решение
• Используем для проведения вычислений формулу синуса двойного угла из курса тригонометрии 2sinx2cosx2=sin x, получим ∫2sinx2cosx2dx=∫sin xdx.
• Используем таблицу производных для тригонометрических функций, получим:
• d(cos x)=cos x'dx=-sin xdx⇒sin xdx=-d(cos x)
• То есть, ∫sin xdx=∫(-d(cos x))
• Используя третье свойство неопределенного интеграла, мы можем записать ∫-d(cos x)=-∫d(cos x).
• По второму свойству получаем -∫d(cos x)=-(cos x+C)
• Следовательно, ∫2sin x2cosx2dx=-cos x-C.
• Проверим полученный результат дифференцированием.
• Продифференцируем полученное выражение:
  -cos x-C'=-(cos x)'-(C)'=-(-sin x)=sin x=2sinx2cosx2

В результате проверки мы получили подынтегральную функцию. Это значит, что интегрирование было проведено нами верно. Для осуществления последнего перехода мы использовали формулу синуса двойного угла.

Ответ: ∫2sin x2cosx2dx=-cos x-C

Если таблицу производных основных элементарных функций переписать в виде дифференциалов, то из нее по второму свойству неопределенного интеграла можно составить таблицу первообразных.

Подробнее эту тему мы рассмотрим в следующем разделе  «Таблица первообразных (таблица неопределенных интегралов)».

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Источник: https://Zaochnik.com/spravochnik/matematika/integraly-integrirovanie/pervoobraznaja-i-neopredelennyj-integral-ih-svojst/

20. Первообразная и неопределенный интеграл, их свойства

Определение
первообразной.

Первообразной
функции f(x) на
промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство для
любого х из
заданного промежутка.

Если
принять во внимание тот факт, что
производная от константы С равна
нулю, то справедливо равенство .
Таким образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.

Определение
неопределенного интеграла.

Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается .

Действие
нахождения неизвестной функции по
заданному ее дифференциалу
называетсянеопределенным интегрированием,
потому что результатом интегрирования
является не одна функция F(x),
а множество ее первообразных F(x)+C.

На
основании свойств производной можно
сформулировать и доказать свойства
неопределенного интеграла (свойства
первообразной).

,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.

Промежуточные
равенства первого и второго свойств
неопределенного интеграла приведены
для пояснения.

Эти
производные равны подынтегральным
функциям, что и является доказательством
в силу первого свойства. Оно же используется
в последних переходах.

Таким
образом, задача интегрирования является
обратной задаче дифференцирования,
причем между этими задачами очень тесная
связь:

-первое
свойство позволяет проводить проверку
интегрирования. Чтобы проверить
правильность выполненного интегрирования
достаточно вычислить производную
полученного результата. Если полученная
в результате дифференцирования функция
окажется равной подынтегральной функции,
то это будет означать, что интегрирование
проведено верно;

-второе
свойство неопределенного интеграла
позволяет по известному дифференциалу
функции найти ее первообразную. На этом
свойстве основано непосредственное
вычисление неопределенных интегралов.

21. Таблица интегралов

22.

Для
вычисления данного интеграла мы должны,
если это возможно, пользуясь теми или
другими способами, привести его к
табличному интегралу и таким образом
найти искомый результат.

В нашем курсе
мы рассмотрим лишь некоторые, наиболее
часто встречающиеся приемы интегрирования
и укажем их применение к простейшим
примерам.

Наиболее
важными методами интегрирования
являются: 
1) метод непосредственного
интегрирования (метод разложения), 
2)
метод подстановки (метод введения новой
переменной), 
3) метод интегрирования
по частям.

I. Метод непосредственного интегрирования

• Задача
  нахождения неопределенных интегралов
  от многих функций решается методом
  сведения их к одному из табличных
  интегралов.
• Пример
  1.
• ∫(1-√x)2dx=∫(1-2√x+x)dx=∫dx-∫2√xdx+∫xdx=∫dx-2∫xdx+∫xdx=

Источник: https://studfile.net/preview/6014081/page:4/