Энергия падающего фотона расходуется на совершение электроном работы выхода из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии:
 или
или  или
или 
- h = 6,62·10–34 Дж·с — постоянная Планка.
- ν — частота электромагнитного излучения (света)
- λ — длина световой волны
- Авых — работа выхода (это минимальное значение энергии, необходимой для
- выхода электрона из металла);
- кинетическая энергия вылетевшего фотоэлектрона;
- m и v — масса и скорость фотоэлектрона
- Законы фотоэффекта.
I. (Закон Столетова):при фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода в единицу времени, пропорционально интенсивности света (сила фототока насыщения пропорциональна энергетической освещенности Ее катода).
где п — число электронов, испускаемых катодом в 1 с.
II. Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой n.
 →
→ 
III. Для каждого вещества существует красная границафотоэффекта, т. е. минимальная νmin частота света (или максимальная длина волны λmax ), при которой фотоэффект еще возможен.
- или .
- Вольт-амперная зарактеристика (ВАХ) фотоэффекта
- ВАХ – это зависимость фототока I, образуемого потоком электронов, испускаемых катодом под действием света, от напряжения U между электродами.
- Такая зависимость, соответствующая трем различным интенсивностям освещения (частота света для всех кривых одинакова), приведена ниже на рис.
- Из вольт-амперных характеристик видно, что:
· а).При U = 0 фототок не равен нулю. Это означает, что фотоэлектроны при вылете обладают кинетической энергией, и даже в отсутствии электрического поля, способны самостоятельно достигать анода, создавая фототок.
· б).При некотором, не очень большом напряжении фототок перестает зависеть от напряжения и достигает насыщения. Это означает, что все электроны, испущенные катодом, попадают на анод.
Сила тока насыщения определяется количеством электронов, испускаемых катодом в единицу времени: ивозрастает с увеличением интенсивности света.
· в). Чтобы фототок стал равным нулю, к аноду нужно приложить отрицательное напряжение, которое называется задерживающим напряжением (Uз ).
Величина U3не зависит от интенсивности падающего света, при U=U3 ни один из электронов, даже обладающий при вылете из катода максимальной скоростью vmax , не может преодолеть задерживающего поля и достигнуть анода, т.е.
- ,
- где е=1,6··10-19 Кл – заряд электрона;
- те =9,1 10-31 кг – масса электрона;
- — кинетическая энергия фотоэлектронов;
- — работа электрического поля по торможению фотоэлектронов.
- · г).Измеряя U3 , можно определить максимальную скорость фотоэлектронов, вылетающих из катода:
- Применение фотоэффекта
- На явлении фотоэффекта основано действие фотоэлектронных приборов, получивших разнообразное применение в различных областях науки и техники
- · Вакуумные фотоэлементы—преобразуют энергию излучения в электрическую применяются для создания солнечных батарей
- · Фотоэлектронные умножители – для усиления фотот ока.
- · Фоторезисторы – (фотосопротивления)
· Разные виды фотоэффекта используются также в производстве для контроля, управления и автоматизации различных процессов, в военной технике для сигнализации и локации невидимым излучением, в технике звукового кино, в различных системах связи и т. д.
§ 5. Масса и импульс фотона. Давление света
- Согласно гипотезе световых квантов Эйнштейна, свет испускается, поглощается и распространяется дискретными порциями (квантами), названнымифотонами.
- Фотон, как и любая другая частица, характеризуется энергией, массой и импульсом
- (1)
- (2)
- (3)
- Выражения (1), (2) и (3) связывают корпускулярные характеристики фотона — массу, импульс и энергию — с волновой характеристикой света — его частотой n.
Если фотоны обладают импульсом, то свет, падающий на тело, должен оказывать на него давление. Согласно квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.
Рассчитаем с точки зрения квантовой теории световое давление, оказываемое на поверхность тела потоком монохроматического излучения (частота n), падающего перпендикулярно поверхности.
Если в единицу времени на единицу площади поверхности тела падает N фотонов, то при коэффициенте отражения r света от поверхности тела rN фотонов отразится, а (1–r )N — поглотится.
Каждый поглощенный фотон передаст поверхности импульс pg=hn / c, а каждый отраженный — 2pg = 2hn / c (при отражении импульс фотона изменяется на –pg ). Давление света на поверхность равно импульсу, который передают поверхности в 1 с N фотонов:
Nhn = Ee есть энергия всех фотонов, падающих на единицу поверхности в единицу времени, т. е. энергетическая освещенность поверхности, a Ee / c = w — объемная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность,
(4)
Формула (4), выведенная на основе квантовых представлений, совпадает с выражением, получаемым из электромагнитной (волновой) теории Максвелла. Таким образом, давление света одинаково успешно объясняется и волновой, и квантовой теорией.
Экспериментальное доказательство существования светового давления на твердые тела и газы дано в опытах П. И. Лебедева. Лебедев использовал легкий подвес на тонкой нити, по краям которого прикреплены легкие крылышки, одни из которых зачернены, а поверхности других зеркальные.
Для исключения конвекции и радиометрического эффекта использовалась подвижная система зеркал, позволяющая направлять свет на обе поверхности крылышек, подвес помещался в откачанный баллон, крылышки подбиралась очень тонкими (чтобы температура обеих поверхностей была одинакова).
Световое давление на крылышки определялось по углу закручивания нити подвеса и совпадало с теоретически рассчитанным. В частности оказалось, что давление света на зеркальную поверхность вдвое больше, чем на зачерненную (см. (4)).
Эффект Комптона
Это явлениеупругого рассеяния коротковолнового электромагнитного излучения (рентгеновского и g-излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны.
Эффект Комптона — это результат упругого столкновения рентгеновских фотонов со свободными электронами вещества (для легких атомов электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными). В процессе этого столкновения фотон передает электрону часть своих энергии и импульса в соответствии с законами их сохранения.
Рассмотрим упругое столкновение двух частиц— налетающего фотона, обладающего импульсом pg = hn/c и энергией eg = hn, с покоящимся свободным электроном (энергия покоя W0 = mc2; т—масса покоя электрона).
Фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения.
При каждом столкновении выполняются законы сохранения энергии и импульса.
- Согласно закону сохранения энергии,
- (1)
- а согласно закону сохранения импульса,
- (2)
- где W0 = mc2 — энергия электрона до столкновения,
- eg = hn — энергия налетающего фотона,
- W= — энергия электрона после столкновения,
- — энергия рассеянного фотона.
- Подставив значения этих величин в (1) и представив (2) в соответствии с рис., получим
- Решая эти уравнения совместно, получим
- Поскольку n = c/l, n ' = c/l' и Dl = l' – l, получим
- Формула Комптона
- где
- Комптоновская длина волны
- Разность Dl = l' – l, не зависит от длины волны падающего излучения и природы рассеивающего вещества, а определяется только величиной угла рассеивания(θ).
Источник: https://cyberpedia.su/8xd4fc.html
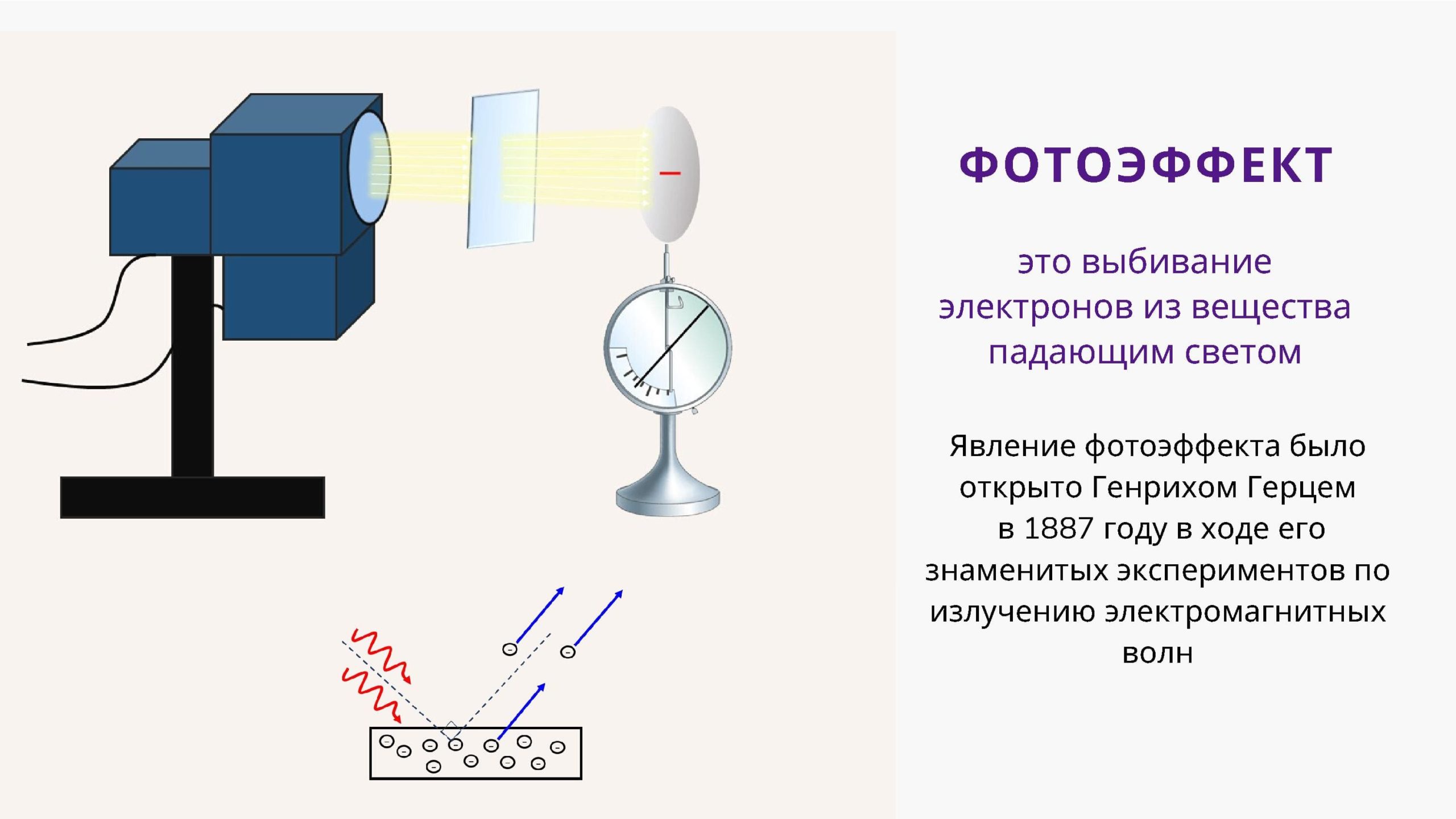
Фотоэффект
Одним из интереснейших квантовых эффектов, рассматриваемых в курсе школьной физики, является фотоэлектрический эффект или фотоэффект. Фотоэффект — явление взаимодействия света с веществом, в результате которого энергия фотонов передаётся электронам вещества.
Рис. 1. Фотоэффект
h u
С точки зрения зрения закона сохранения энергии, можно получить уравнение Эйнштейна:
h u =A+frac{{{m}_{e}}{{upsilon }^{2}}}{2}
- где
- h u — энергия фотона,
- Дж/с — постоянная Планка (константа),
- u — частота фотона,
- — работа выхода (энергия, необходимая электрону, чтобы стать свободным),
- — оставшаяся кинетическая энергия электрона,
- кг — масса электрона,
- — скорость вылетевшего электрона.
- h u — энергия фотона,
Работа выхода электрона () — минимальная энергия, которую необходимо передать электрону, чтобы он «выбрался» на поверхность. Если энергия фотона равна точно энергии выхода, то электрон, «выйдя» на поверхность, там и останавливается, т.е. после выхода электрона, его кинетическая энергия численно равна нулю. Тогда уравнение Эйнштейна примет вид:
(2)
- где
- — энергия фотона,
- Дж/с — постоянная Планка (константа),
- — частота фотона, называемая красной границей фотоэффекта,
- — работа выхода (энергия, необходимая электрону, чтобы стать свободным).
- — энергия фотона,
- Красная граница фотоэффекта () — частота излучения (фотона), ниже которой фотоэффект не происходит.
- Аналогично можно ввести:
- (3)
- где
- — максимальная длина волны, при которой возможен фотоэффект,
- м/с — скорость света (константа),
- — частота фотона, называемая красной границей фотоэффекта.
Вывод: задачи на фотоэффект вводятся именно этим словом. Единственное, что мы можем использовать при этом, — уравнение Эйнштейна (1).
Источник: https://www.abitur.by/fizika/teoreticheskie-osnovy-fiziki/elementy-kvantovoj-fiziki/fotoeffekt/
Уравнение Эйнштейна для фотоэффекта
Гипотеза М. Планка о квантах
В конце XIX века для объяснения экспериментально полученных законов излучения М. Планк выдвинул гипотезу дискретности процессов излучения и поглощения света.
- Гипотеза Планка: излучение и поглощение света происходит не непрерывно, а определёнными конечными порциями энергии – квантами, при этом значение порции энергии прямо пропорционально частоте излучения.
- E = hν,
- где h = 6,63∙10–34 Дж∙с – постоянная Планка.
Квантом можно называть конечную порцию энергии любого электромагнитного излучения. Квант света ещё называют фотоном.
Фотоэффект
Фотоэффект – явление, связанное с освобождением электрона, связанного с ядром атома, под действием электромагнитного излучения. Различают два вида фотоэффекта.
 Внешний фотоэффект (фотоэлектронная эмиссия) – вырывание электрона из вещества под действием электромагнитного излучения. Например: первоначально незаряженное тело заряжается положительно (либо первоначально отрицательно заряженное тело разряжается) под действием света.
Внешний фотоэффект (фотоэлектронная эмиссия) – вырывание электрона из вещества под действием электромагнитного излучения. Например: первоначально незаряженное тело заряжается положительно (либо первоначально отрицательно заряженное тело разряжается) под действием света.
Внутренний фотоэффект – увеличение концентрации свободных электронов в веществе под действием электромагнитного излучения. Например: уменьшение удельного сопротивления полупроводника под действием света.
Опыты А. Г. Столетова
Законы внешнего фотоэффекта
1. Ток насыщения (количество фотоэлектронов) прямо пропорционален интенсивности излучения.
2. Запирающее напряжение (максимальная кинетическая энергия фотоэлектронов) линейно возрастает с увеличением частоты излучения и не зависит от его интенсивности.
3. Для каждого вещества существует красная граница фотоэффекта – минимальная частота (максимальная длина волны), при которой ещё возможен фотоэффект.
Иногда выделяют и четвёртый закон: фотоэффект не обладает инертностью, то есть он немедленно возникает при попадании излучения на поверхность вещества. Второй и третий законы внешнего фотоэффекта показаны графически на следующем рисунке.
 |
Уравнение Эйнштейна для фотоэффекта
Теоретическое обоснование всех законов внешнего фотоэффекта дал в начале XX века А. Эйнштейн. Связанный электрон вещества способен поглотить энергию одного кванта излучения, одна часть которой тратится на совершение работы по выходу из вещества, а другая остаётся у электрона в виде его кинетической энергии:

Уравнение Эйнштейна – это форма записи закона сохранения энергии для фотоэффекта. Уравнение позволяет установить связь между работой выхода из вещества и красной границей фотоэффекта:

Фотон
Фотон – квант света – элементарная частица, обладающая следующими свойствами.
1. Фотон нейтрален, то есть не имеет электрического заряда.
2. Фотон не имеет массы покоя, то есть всегда движется со скоростью света.
c = λν.
3. Фотон обладает энергией и импульсом, как и любой квант электромагнитного излучения.
E = hν;
4. Фотон обладает релятивистской массой, которую можно найти и через энергию, и через импульс фотона.
E = mc2;
p = mc.
Источник: https://megaobuchalka.ru/2/22738.html
Урок 22. фотоэффект — Физика — 11 класс — Российская электронная школа
- Физика, 11 класс
- Урок 22. Фотоэффект
- Перечень вопросов, рассматриваемых на уроке:
- предмет и задачи квантовой физики;
- гипотеза М. Планка о квантах;
- опыты А.Г. Столетова;
- определение фотоэффекта, кванта, тока насыщения, задерживающего напряжения, работы выхода, красной границы фотоэффекта;
- уравнение Эйнштейна для фотоэффекта;
- законы фотоэффекта.
- Глоссарий по теме:
- Квантовая физика — раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
- Фотоэффект – это вырывание электронов из вещества под действием света.
Квант — (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике.
Ток насыщения — некоторое предельное значение силы фототока.
Задерживающее напряжение — минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.
Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.
Основная и дополнительная литература по теме урока:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.
3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г. С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.
4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.
Теоретический материал для самостоятельного изучения
В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.
Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.
- Коэффициент пропорциональности получил название постоянной Планка, и она равна:
- h = 6,63 ∙ 10-34 Дж∙с.
- После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.
- Квантовая физика — раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.
- В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.
- Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.
- Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.
Схема установки для изучения законов фотоэффекта
Первый закон фотоэффекта: фототок насыщения — максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, — прямо пропорционален интенсивности падающего излучения.
- Зависимость силы тока от приложенного напряжения
- Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.
- Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.
hνmin = Aв
- где Ав – работа выхода электронов;
- h – постоянная Планка;
- νmin — частота излучения, соответствующая красной границе фотоэффекта;
- с – скорость света;
- λкр – длина волны, соответствующая красной границе.
- Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.
- Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, «затрудняющее» вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.
Задерживающее напряжение — минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Задерживающее напряжение
Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:
Е – заряд электрона;
Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект.
Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела.
При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:
![]()
В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».
Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны — фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.
Примеры и разбор решения заданий
1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?
- Для каждой величины определите соответствующий характер изменения:
- 1) увеличится
- 2) уменьшится
- 3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Работа выхода | Запирающее напряжение |
- Решение:
- Работа выхода — это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.
- Запирающее напряжение — это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:
- Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.
- Ответ:
| Работа выхода | Запирающее напряжение |
| не изменится | увеличится |
2. Красная граница фотоэффекта для вещества фотокатода λ0 = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.
- Решение.
- Запишем уравнение для фотоэффекта через длину волны:
- Условие связи красной границы фотоэффекта и работы выхода:
- Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:
- Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:
- Подставляя численные значения, получаем: λ ≈ 215 нм.
- Ответ: λ ≈ 215 нм.
Источник: https://resh.edu.ru/subject/lesson/4917/conspect/
Теория фотоэффекта — Класс!ная физика
«Физика — 11 класс»
Все попытки объяснить явление фотоэффекта на основе законов электродинамики Максвелла, согласно которым свет — это электромагнитная волна, непрерывно распределенная в пространстве, оказались безрезультатными. Нельзя было понять, почему энергия фотоэлектронов определяется только частотой света и почему лишь при достаточно малой длине волны свет вырывает электроны.
Объяснение фотоэффекта было дано в 1905 г. Эйнштейном, развившим идеи Планка о прерывистом испускании света. В экспериментальных законах фотоэффекта Эйнштейн увидел убедительное доказательство того, что
- свет имеет прерывистую структуру и поглощается отдельными порциями.
- Энергия Е каждой порции излучения в полном соответствии с гипотезой Планка пропорциональна частоте:
- Е = hν
- где h — постоянная Планка.
- Из того, что свет излучается порциями, еще не вытекает вывода о прерывистости структуры самого света.
Явление фотоэффекта показало: свет имеет прерывистую структуру: излученная порция световой энергии Е = hν сохраняет свою индивидуальность и в дальнейшем. Поглотиться может только вся порция целиком.
- Кинетическую энергию фотоэлектрона можно найти, применив закон сохранения энергии.
- Уравнение Эйнштейна:
- Энергия порции света hν идет на совершение работы выхода (А) и на сообщение электрону кинетической энергии.

Работа выхода (A) — это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Уравнение объясняет основные факты, касающиеся фотоэффекта.
Интенсивность света, по Эйнштейну, пропорциональна числу квантов (порций) энергии hν в световом пучке и поэтому определяет число электронов, вырванных из металла.
Скорость же электронов υ определяется только частотой света ν и работой выхода А, зависящей от типа металла и состояния его поверхности. От интенсивности света скорость не зависит.
Для каждого вещества фотоэффект наблюдается лишь в том случае, если частота v света больше некоторого минимального значения vmin. Ведь, чтобы вырвать электрон из металла даже без сообщения ему кинетической энергии, нужно совершить работу выхода А. Следовательно, энергия кванта должна быть больше этой работы:
- hν > А
- Красная границца фотоэффекта
- Предельную частоту νmin и предельную длину волны λmах называют красной границей фотоэффекта. Они выражаются так:

где λmах(λкр) — максимальная длина волны, при которой фотоэффект еще наблюдается. Это название появилось по аналогии со световыми волнами, так как максимальная длина волны видимого света соответствует красному цвету.
Работа выхода А зависит от рода вещества. Поэтому и предельная частота vmin фотоэффекта (красная граница) для разных веществ различна.
Третий закон фотоэффекта
Для каждого вещества существует максимальная длина волны, при которой фотоэффект еще наблюдается. При больших длинах волн фотоэффекта нет.
Для цинка красной границе соответствует длина волны λmах = 3,7 • 10-7 м (ультрафиолетовое излучение).
Именно этим объясняется опыт по прекращению фотоэффекта с помощью стеклянной пластинки, задерживающей ультрафиолетовые лучи. Работа выхода у алюминия или железа больше, чем у цинка.
У щелочных металлов работа выхода, напротив, меньше, а длина волны λmахтах, соответствующая красной границе, больше.
Так, для натрия λmах = 6,8 • 10-7 м.
Пользуясь уравнением Эйнштейна, можно найти постоянную Планка h. Для этого нужно экспериментально определить частоту света ν, работу выхода А и измерить кинетическую энергию фотоэлектронов. Подобные измерения и расчеты дают h = 6,63 • 10-34 Дж • с.
Точно такое же значение было найдено и самим Планком при теоретическом изучении совершенно другого явления — теплового излучения.
Совпадение значений постоянной Планка, полученных различными методами, дополнительно подтверждает правильность предположения о прерывистом характере излучения и поглощения света веществом
Уравнение Эйнштейна, несмотря на его кажущуюся простоту, объясняет основные закономерности фотоэффекта. Эйнштейн был удостоен Нобелевской премии за работы по теории фотоэффекта.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Следующая страница «Фотоны» Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»
Световые кванты. Физика, учебник для 11 класса — Класс!ная физика
Фотоэффект — Теория фотоэффекта — Фотоны — Применение фотоэффекта — Давление света. Химическое действие света — Краткие итоги главы
Источник: http://class-fizika.ru/11_63.html
5.1.4 Уравнение Эйнштейна для фотоэффекта
- Видеоурок 1: Теория фотоэффекта
- Видеоурок 2: Фотоэффект теория. Уравнение Эйнштейна
- Лекция: Уравнение Эйнштейна для фотоэффекта
Макс Планк был уверен, что свет не только поглощается и излучается определенными конечными порциями, но и распространение его в пространстве происходит благодаря квантам, имеющим единичную энергию h????. До некоторого времени данная гипотеза только позволяла математически рассчитывать энергию, однако только Эйнштейн позволил воплотить её в жизнь. Частицы, которые несли единичную энергию, получили название фотоны. Фотоны света способны передвигаться в пространстве и взаимодействовать с другими частицами. Примером такого взаимодействия является фотоэффект, в результате которого фотоны налетают на электроны, передавая им энергию и импульс, а те в свою очередь начинают направленное движение.
В результате столкновения фотона и частицы, фотон полностью поглощается, в результате чего происходит моментальное изменение кинетической энергии. Как известно, при любых процессах, взаимодействиях и любых других физических законах справедлив закон сохранения энергии. Выведением закона сохранения энергии занимался Эйнштейн, и вот что получилось:

Это формула означает, что для получения фототока, фотоны должны передать такую энергию, которую хватило бы на работу выхода электрона с поверхности вещества под действием тока, а также для придания ему нужной скорости. В данном случае второе слагаемое показывает, какую максимальную кинетическую энергию получит электрон при поглощении фотона.
Данная формула указывает на достаточно простой случай — когда электрон находится на поверхности металла в свободном состоянии. То есть для его вырывания не нужно проникать вглубь вещества, а так же разрушать связи его с атомом.
Законы фотоэффекта говорят, что для выбивания некоторого количества электронов, необходимо какое-то количество фотонов.
Так же можно заметить, что энергия, которую получит электрон для собственного ускорения, зависит от частоты излучения и вовсе не зависит от интенсивности света.
Фотоэффект может получиться и без дополнительной энергии, идущей на кинетическую энергию. Однако в таком случае необходима разность потенциалов.
Однако, в любом случае, разность потенциалов не может вырвать электрон, для этого нужна работа выхода. Поэтому формула фотоэффекта приобретает следующий вид:
![]()
С помощью фотоэффекта можно расчетным путем вычислить величину постоянной Планка.
| Предыдущий урок | Следующий урок |
Источник: https://cknow.ru/knowbase/333-514-uravnenie-eynshteyna-dlya-fotoeffekta.html
Законы внешнего фотоэффекта. Уравнение Эйнштейна для фотоэффекта
Законы внешнего фотоэффекта. Уравнение Эйнштейна для фотоэффекта
В недалеком прошлом русский физик Столетов Александр Григорьевич столкнулся с загадочным явлением — внешним фотоэффектом.
Проводя многократные эксперименты, он установил, что металлическая пластинка, а точнее ее поверхность испускает электроны под действием электромагнитного ультрафиолетового излучения или излучения какого-либо другого диапазона.
Объяснить этого Александр Григорьевич не смог, но все же, эта работа принесла ему мировую известность.
Эксперимент был проведен в 1888 г. Затем фундаментальные исследования были сделаны многими учеными, такими как Планк, Эйнштейн и др. фотоэффект закономерность уравнение квантовый физика
Схема эксперимента была такова: электрометр, с присоединенной к нему цинковой пластинкой, заряженной положительно, при освещении пластины, например электрической дугой, не влияет на быстроту разрядки электрометра. Но если пластину зарядить отрицательно, то световой пучок от дуги разряжает электрометр очень быстро.
Объяснить это можно единственным образом. Свет вырывает электроны с поверхности пластины. Если она заряжена отрицательно, электроны отталкиваются от нее и электрометр разряжается. При положительном заряде пластины вырванные светом электроны притягиваются к пластине и снова оседают на ней. Поэтому заряд электрометра не изменяется.
Однако, когда на пути света поставлено обыкновенное стекло, отрицательно заряженная пластина уже не теряет электроны, какова бы ни было интенсивность излучения. Так как известно, что стекло поглощает ультрафиолетовые лучи, то из этого можно заключить, что именно ультрафиолетовый участок спектра вызывает фотоэффект.
Этот сам по себе не сложный факт нельзя объяснить на основе классической электромагнитной теории света.
Согласно этой теории вырывание электронов является результатом «раскачивание» их в электромагнитном поле световой волны, которое должно усиливаться при увеличении интенсивности света и пропорциональной ей энергетической освещенности фотокатода.
Планк, рассматривая излучения абсолютно черного тела, пришел к выводу, что излучение формулу, сопоставив свои работы с формулой Вина. Кстати, Планк получил нобелевскую премию за эту формулу.
Развивая идеи Планка, Эйнштейн ввел гипотезу световых квантов, согласно которой электромагнитное излучение само состоит из таких квантов, и на ее основе объяснил, и сформулировал ряд закономерностей фотоэффекта, люминисценсии и фотохимических реакций.
За проделанную по настоящему гениальную работу, Эйнштейн в 1921 году был удостоен нобелевской премии. Работы его были удостоены и многих других почетных наград.
Первый закон гласит, что количество электронов, вырываемых с поверхности металла за одну секунду, прямо пропорционально поглощаемой за это время энергии световой волны. В этом ничего неожиданного нет: чем больше энергия светового пучка, тем эффективнее его действие.
Теперь рассмотрим кинетическую энергию световой волны или скорость электронов. Из опыта видно, что при отсутствии напряжения фотоэлектроны достигают правого электрода.
Если изменить полярность батарейки, то образуется некоторое поле, которое будет тормозить электроны и возвращать их на место, то есть при определенном задерживающим напряжением фототок равен нулю.
Дальнейшие эксперименты доказали, что при изменении интенсивности света, задерживающее напряжение не меняется. Из этого можно найти значение кинетической энергии электронов.
Второй закон — максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности. Если частота света меньше определенной для данного вещества минимальной частоты, то фотоэффект не происходит. Эта минимальная частота названа красной границей.
Почему именно красная, а не зеленая? Дело в том, что если рассматривать спектр видимых электромагнитных излучений, то красный свет имеет самую низкую частоту.
По формуле hv, он обладает самой малой энергией, то есть самая маленькая энергия, которая необходима для преодоления сил удерживающих междоузельный электрон на поверхности, названа красной.
Именно Эйнштейн высказал смелую гипотезу о том, что свет имеет двойственную структуру, он ведет себя как поток частиц и как волна одновременно. Также он высказал гипотезу о том, что свет не только излучается в виде отдельных дискретных квантов, но и распространяется в пространстве и поглощается веществом. В данном случае, междоузельный электрон получает энергию фотона.
При очень больших интенсивностях света, достижимых с помощью лазеров, наблюдается многофотонный или нелинейный, фотоэффект. При многофотонном фотоэффекте электрон может одновременно получать энергию не одного, а N фотонов.
По теории Эйнштейна фотоэффект имеет следующее объяснение: поглощая квант света, электрон приобретает энергию Е=hн.
При вылете из металла энергия каждого электрона уменьшается на определенную величину, которую называют работой выхода А. Работа выхода это работа, которую необходимо затратить, чтобы удалить электрон из металла.
Поэтому максимальная кинетическая энергия электронов после вылета (если нет других потерь) равна:
- mv2/2 = hн — A вых.
- Следовательно,
- hн = А вых + mv2/2 .
- Это уравнение носит название уравнения Эйнштейна.
Все результаты работы внесли и даже открыли новую дверь в физику, а точнее квантовую физику. И в большей мере заслуга за этим лежит на Эйнштейне.
Макс Борн сказал: «идеи Эйнштейна дали физической науке импульс, который освободил ее от устаревших философских доктрин, и превратил в одну из решающих сил современного мира людей»
Открытие фотоэффекта имело очень большое значение для более глубокого понимания природы света. Но ценность науки состоит не только в том, что она дает нам в руки средства, используя которые можно совершенствовать производство, улучшать условия материальной и культурной жизни общества.
С помощью фотоэффекта «заговорило» кино и стало возможной передача движущихся изображений (телевидение).
Применение фотоэлектронных приборов позволило создать станки, которые без всякого участия человека изготавливают детали по заданным чертежам.
Основанные на фотоэффекте приборы контролируют размеры изделий лучше любого человека, вовремя включают маяки и уличное освещение. Все это оказалось возможным благодаря изобретению особых устройств — фотоэлементов.
Современный вакуумный фотоэлемент представляет собой стеклянную колбу, часть внутренней поверхности которой покрыта тонким слоем металла с малой работой выхода (красной границей). Это катод на который через прозрачное окошко падает свет.
В центре расположен анод, который служит для улавливания фотоэлектронов. Анод присоединяют к положительному полюсу батареи. Фотоэлементы реагируют на видимые излучения и даже не инфракрасные лучи. На их основе сделаны автоматы, которые могут предотвращать аварии.
На заводе фотоэлементы почти мгновенно останавливает мощный пресс, если рука человека оказывается в опасной зоне.
Что касается фотохимических реакций, то на этой основе сделана фотография.
Объяснение фотоэффекта не единственная заслуга Эйнштейна. Еще он знаменит своей теорией относительности. Специальная теория относительности (частная теория относительности) представляет собой современную физическую теорию пространства и времени.
Специальная теория относительности и квантовая механика служит теоретической базой современной физики и техники (например: ядерной физики, техники).
Специальную теорию относительности часто называют релятивистской теорией, а специфические явления, описываемые этой теорией, — релятивистскими эффектами.
Как правило, релятивистские эффекты проявляются при скоростях движения тел близкой к величине скорости света в вакууме с=10 м/с и называемых релятивистскими скоростями. Релятивистской механикой называется механика движений с релятивистскими скоростями, основанная на специальной теории относительности.
В специальной теории относительности, так же как и в классической ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно.
Первый постулат является обобщением механического принципа относительности Галилея на любые физические процессы. Этот постулат — релятивистский принцип относительности Эйнштейна, гласит: в любых инерциальных системах отсчета все физические явления при одних и тех же условиях протекают одинаково.
Иначе говоря, физические законы не зависимы по отношению к выбору инерциальной системы отсчета. Второй постулат выражает принцип инвариантности скорости света. Она одинакова во всех направлениях и во всех инерциальных системах отсчета, являясь одной из важнейших физических постоянных.
Опыты показывают, что скорость света в вакууме — предельная скорость в природе.
Альберт Эйнштейн был в жизни очень разносторонним человеком (как и все гениальные люди).
Его предки — евреи эмигранты, переселились в Вьюртенберг в XVI веке.
Отец физика, Герман Эйнштейн, выделялся своими математическими способностями, но его родители не обладали средствами, чтобы дать ему высшее образование. Мать, Паулина Эйнштейн — Кох, была музыкально одаренной женщиной, дочерью богатого торговца зерном, музыкальность матери и математические отца не только передались сыну, но и проявились у него гораздо более ярко.
С детских лет у мальчика развивалась глубокая любовь к природе, Алберт Эйнштейн в последствие всегда любил жить в сельской местности или в провинциальных городках.
Еще будучи школьником, в Мюнихе, Эйнштейн занимался музыкой. С шестилетнего возраста его начали учить игре на скрипке.
В начале мальчик воспринимал эти уроки как скучную обязанность, но вскоре музыка увлекла его, а с течением времени она стала его вторым призванием.
Отправляясь в любые поездки, Эйнштейн брал с собой скрипку, даже в первое время появлялся на заседании Берлинской академии наук со скрипичным футляром.
«Альбертель», так его называли родители, держался обычно в стороне от своих школьных сверстников. Больше всего он любил заниматься в одиночестве своими кубиками или выпиливать лобзиком. Иногда он писал стихи, в которых он с насмешкой отзывался о несмелых, робких людях ( сам он к таким не относился).
Еще до того как Эйнштейн поступил в школу, отец однажды подарил ему компас. Этот простой предмет с неожиданной силой возбудил любознательность мальчика, внешность вещей таил в себе что-то глубоко скрытое в пространстве, которое обычно считается пустым.
Хотя знакомство с компасом относилось к тому периоду жизни великого исследователя, когда он был еще далек от занятий наукой, оно оказало сильное влияние на последующую деятельность. Альберт Эйнштейн был человеком прагматичным и даже жадным.
Об этом свидетельствует и тот факт, что люди приходившие в гости, открывая калитку, приводили в действие определенный механизм, который поливал огород изобретателя.
Научное творчество Альберта Эйнштейна поразительным образом сочеталось с активной деятельностью во имя гуманизма и защиты мира. Эйнштейн был буквально основателем государства Израиля, его даже приглашали стать правителем этого государства, но он отказался.
Размещено на Allbest.ru
Источник: https://studwood.ru/1108718/matematika_himiya_fizika/zakony_vneshnego_fotoeffekta_uravnenie_eynshteyna_dlya_fotoeffekta




