Свойства пирамиды, с примерами

Пирамида – многогранник,  основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.

По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.

• Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
• Основание — многоугольник, которому не принадлежит вершина пирамиды.
• Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
• 
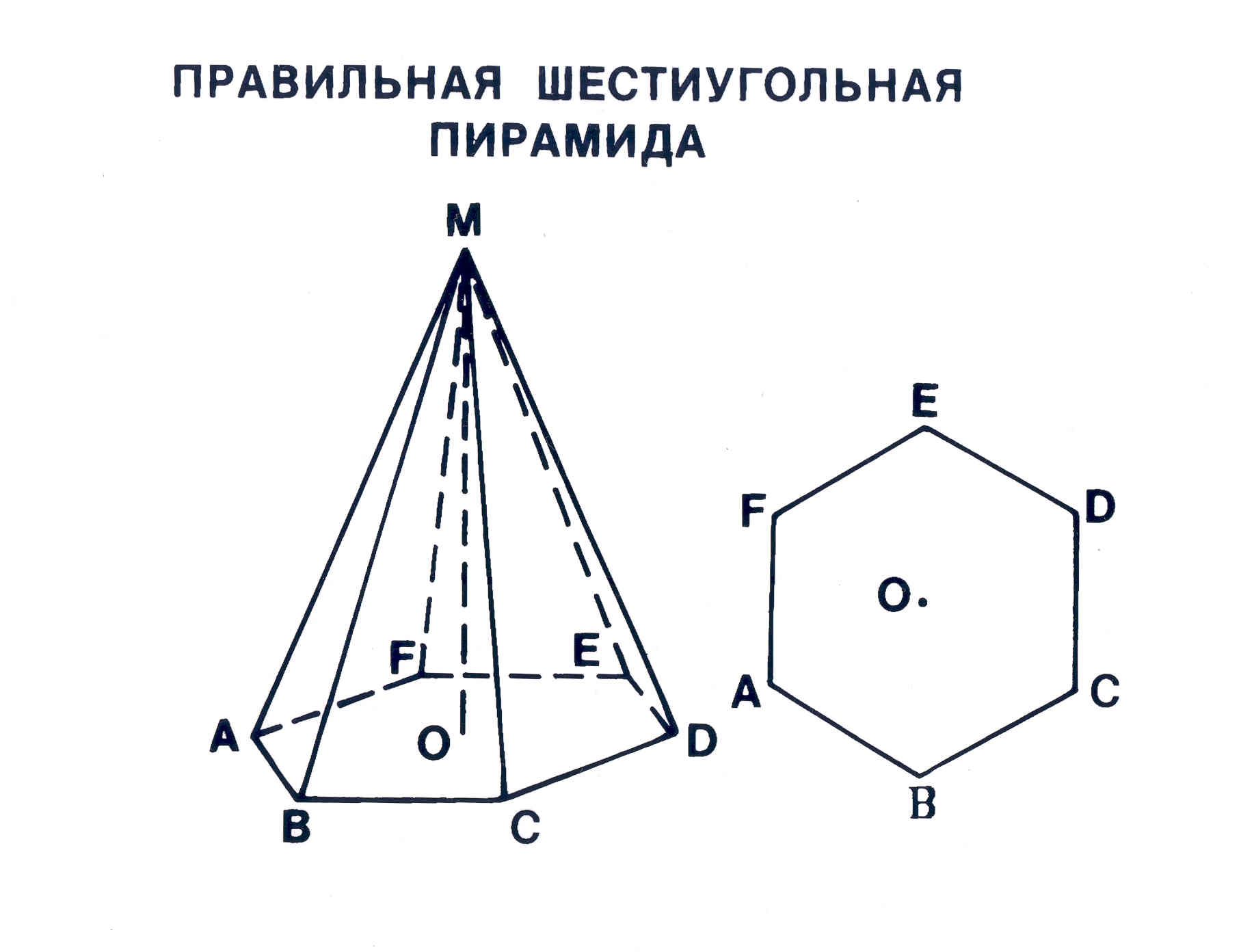
• Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
• 
• Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
• 

Некоторые свойства пирамиды 

1. 1) Если все боковые ребра равны, то 
2. – около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
3. 
4. – боковые ребра образуют с плоскостью основания равные углы
5. 
6. Верно и обратное.
7. Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
8. Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
9. 2) Если все грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
10. 
11. Верно и обратное.

Виды пирамид

• Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
• 
• Для правильной пирамиды справедливо:
• – боковые ребра правильной пирамиды равны;
• – в правильной пирамиде все боковые грани — равные  равнобедренные треугольники;
• – в любую правильную пирамиду можно  вписать сферу;
• – около любой правильной пирамиды можно описать сферу;
• – площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Видео

Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда  это ребро и есть высота пирамиды.

1. 
2. Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
3. 

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

Смотрите также таблицу «Объемы пирамиды и призмы. Площадь поверхности пирамиды и призмы».

Источник: https://egemaximum.ru/piramida/

Свойства пирамид: от магии к науке

Известно, что пирамиды не просто входят в знаменитый перечень семи чудес света, но и открывают этот список. Сегодня они обнаружены не только в Египте и Центральной Америке, но и по всему миру, в том числе, в России. Глядя на эти величественные сооружения, невольно задаешься целым букетом вопросов: кто в седой древности смог воздвигнуть такие гигантские строения? А самое главное – зачем? Это не дворцы, не жилища, даже не фараоновы гробницы, как ошибочно полагают многие. Ведь ни в одной из них так и не нашли усыпальницы фараонов, исследователям удалось обнаружить лишь пустые саркофаги. Настоящие захоронения находятся на западном побережье Нила в Долине Царей, неподалеку от древнего города Фивы, там, в скалистом некрополе на тридцатиметровой высоте скрываются 64 усыпальницы великих фараонов Египта.

Но тогда для чего же строились пирамиды? Ведь возведение таких огромных построек занятие хлопотное и, надо полагать, не дешевое.

Одним из ответов послужил случай, произошедший в 30-тых годах прошлого века.

Французский исследователь Антуан Бови обратил внимание, что внутри пирамиды в мусорных баках находится некоторое количество погибших мелких животных. Оказалось, что все они были мумифицированы.

Но как это произошло? И Бови пришла в голову мысль, что сама форма пирамиды и особенности ее размещения на местности могут давать подобный эффект.

Антуан Бови

Ученый создал уменьшенный макет пирамиды, сориентировал ее к сторонам горизонта (по аналогии с большими пирамидами) и начал эксперимент с мумификацией. И у него получилось! Также оказалось, что внутри этого макета гораздо дольше обычного хранятся скоропортящиеся продукты.

С этого момента начинается настоящий научный бум. Исследователи экспериментируют с пирамидами и обнаруживают все новые и новые уникальные свойства. Так, ученые Институт воды и почвоведения Аризоны обнаружили, что вода, побывавшая в пирамидальной конструкции, может использоваться для лечения ряда болезней, это подтвердили медики.

Инженер из Чехии Карел Дрбал исследует энергопотенциал внутри пирамид, оказалось, что он может как ускорять, так и замедлять важные жизненные процессы.

Он же обнаружил еще одну интересную особенность: внутри пирамид самопроизвольно затачиваются лезвия, их острота повышается в разы! За это исследование Карел получил научный патент, результаты его экспериментов неоднократно подтвердили другие ученые.

Воздействие пирамидальных конструкций на организм человека занимало многие умы. Быстрое заживление ран, обезболивающий эффект, ускоренное срастание переломов – это лишь исходный перечень свойств, заинтересовавших ученых из разных стран.

В России также проводились подобные исследования. Возможно, даже раньше, чем где- либо еще. Так, в имении известного архитектора Николая Львова были возведены пирамиды-хранилища, значит, их хозяину были известны их свойства. О пирамидах Львова мы расскажем в нашей другой статье, а пока познакомимся с тем, что удалось обнаружить отечественным ученым.

пирамида графа Н.А.Львова

А обнаружено было немало. Так, во Всероссийском электротехническом институте им.В.И.Ленина проводили исследования электрического поля. Оказалось, что контур, выстроенный из кусочков гранита, побывавших в пирамиде, обладает мощными защитными свойствами от поражения электрическим разрядом – в 5 раз выше по сравнению с контрольными образцами.

Или еще одни пример: на Ишимбайском месторождении нефти в Башкирии был установлен комплекс пирамид. Вот как он выглядел:

Через неделю после их установки изменилась ситуация в пластах. Уменьшилась вязкость нефти, изменилось количество смол, парафина и других компонентов. Результаты экспериментов подтвердили ученые Московской академии нефти и газа им.Губкина.

Что еще? Противовирусная активность иммуноглобулина, прошедшего обработку внутри пирамидальной формы, увеличилась в 100 раз (!) Это открытие сделали в НИИ вирусологии Ивановского РАМН.

• Ученые из Санкт-Петербурга (научно-исследовательская лаборатория «РАДИАНТ») впервые в мире доказали, что в теле пирамиды существует несколько зон, обладающих разными свойствами.
• Вот что им удалось обнаружить:
• 1. Вода и другие жидкости, размешенные на высоте 2/3 пирамиды, приобретают лечебные свойства;
• 2. На высоте 1/2 заряжают лечебными энергиями алюминиевую фольгу и металлы;
• 3. На высоте 1/3 размещают семена для увеличения всхожести, затачивают лезвия;
• 4. В нижней части пирамиды образуется «мертвая вода», она подавляет рост тканей и микроорганизмов, это хороший антисептик и противоопухолевое средство;
• 5. Ближе к вершине образуется «живая вода», улучшающая деление клеток, она заживляет раны и даже восстанавливает цвет седых волос;

Доктор физико-математических наук НИИ «Графит» А.С.Котосонов говорит следующее:

«…Я с большим недоверием относился к воздействию пирамиды на физические и химические свойства неорганических материалов. Поэтому мы попытались решить этот вопрос комплексно.

Мы использовали целый арсенал имеющихся у нашей лаборатории методов для того, чтобы оценить истинное воздействие или отсутствие такого на физические свойства углеродных материалов в пирамиде (…) Мы были страшно удивлены, но это факт — эксперименты по электропроводности, проведенные в нашей лаборатории Сергеем Владимировичем Кувшинниковым, показали, что электропроводность меняется в разы. Более того, влияние пирамиды зависит от времени суток, когда образцы вкладывались в пирамиду и когда вынимались из нее…» 

Академик Академии естественных наук В.И.Костиков дает такое далеко идущее заключение:

«…Хотелось бы подчеркнуть такую мысль, что раньше во всех видах технологий мы имели 4 варьируемых параметра. А именно: температура, давление, время и концентрация.

Сейчас, возможно, я делаю слишком смелые выводы, но мы можем к этим … параметрам в технологии добавить пятый параметр — ПИРАМИДА — со всеми вытекающими отсюда последствиями.

Наличие пятого параметра в технологии дает нам возможность практически во всех видах химической, металлургической и прочих технологий, используя эти подходы, получить новые результаты. Сейчас можно смело сказать, что это технология XXI века. (…

) Пожалуй, впервые с использованием пирамид мы получили возможность целенаправленно влиять на конечный результат. Вот это принципиальнейшая разница. Раньше мы это знали, чувствовали чисто эмпирически, а сегодня мы получаем возможность, введя этот фактор, варьировать конечный результат. Это я считаю будущей технологической революцией, которой не было равной в истории человечества».

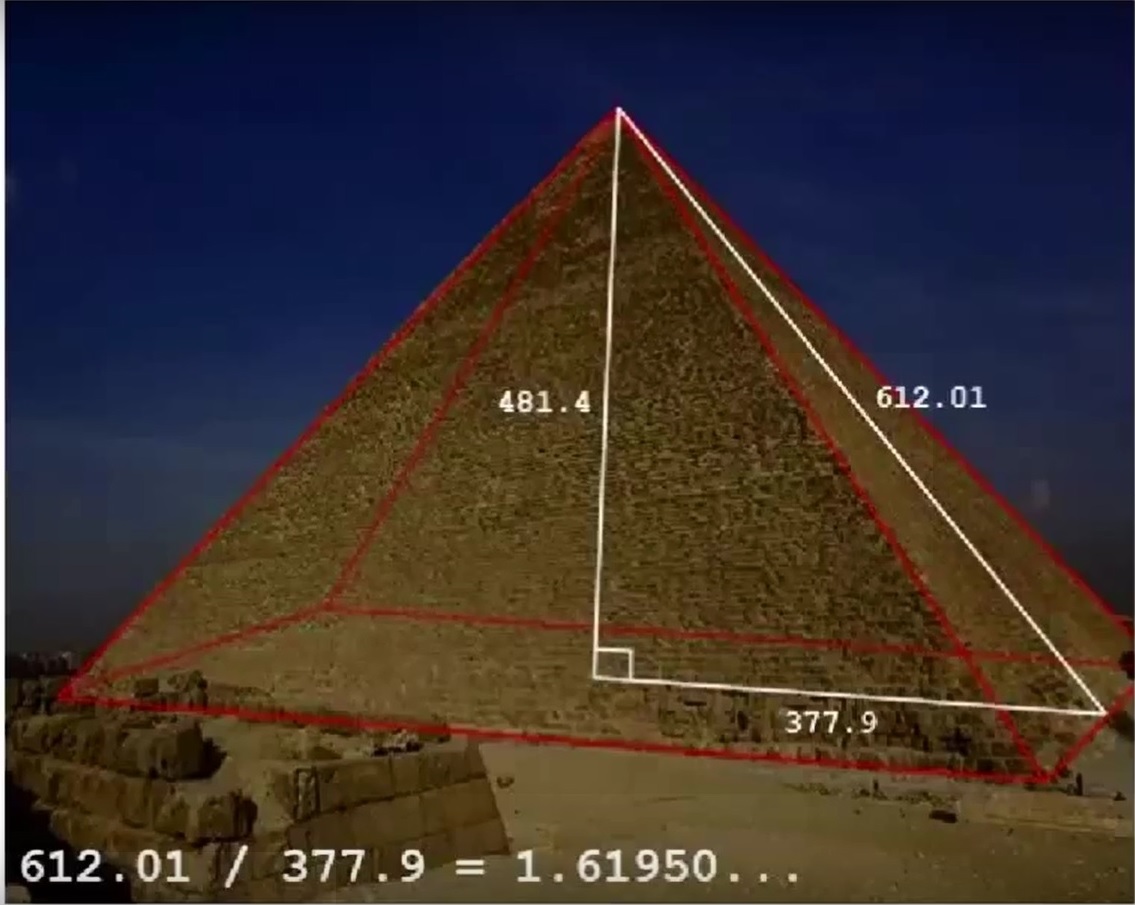
Неподалеку от озера Селигер, 22 км от Осташкова (у деревни Хитино) построена одна из современных пирамид. Ее высота достигает 22 метров. При помощи радиолокации был обнаружен энергетический столб высотой до 1200 м и шириной 500 м по вертикальной оси пирамиды. Причем, это энергетическое образование периодически меняло свою высоту в диапазоне 800 -1200 м.

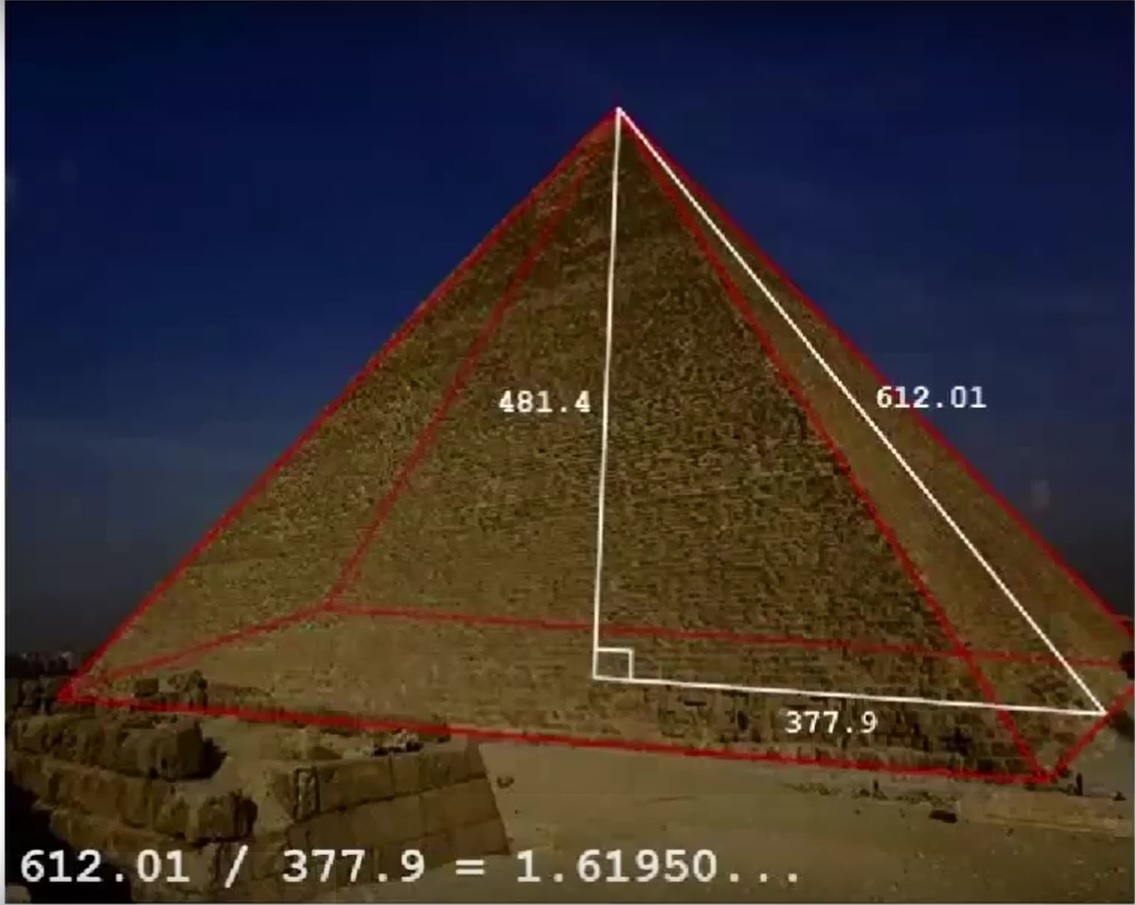
1. Сегодня экспериментально доказано, что энергии внутри пирамидальной формы изменяют структуру помещенных туда объектов. Обнаружены следующие явления:
2. — мумифицирование;
3. — регенерация тканей;
4. — структуризация воды (не замерзает даже при -30 градусах);
5. — улучшение вкусовых качеств и сроков хранения продуктов;
6. — улучшение всхожести семян;
7. — затачивания лезвий (если их разместить на уровне 1/3 от основания на 24 часа);
8. — срезанные цветы в пирамиде не вянут более 3 недель;
9. — если в большой пирамиде установить генератор, она будет давать электричество;
10. Помимо этого, было выявлено, что эти же энергии благотворно воздействуют и на человека:
11. — стабилизируют пульс и давление;
12. — снимают физическое и психическое напряжение;
13. — улучшают показатели крови;
14. — улучшают работоспособность и сон;
15. — уменьшают болевой синдром и восприимчивость к стрессам;
16. Мало того, установлено, что вокруг самой пирамиды:
17. — уменьшается уровень радиации;
18. — нейтрализуются патогенные зоны и электромагнитные излучения;
19. — улучшается экология (очищаются водоемы и воздух);

Оказалось, что пирамиды можно делать даже из картона – и тогда они будут проявлять свои свойства. Мало того, конструкция из одних только ребер пирамидальной формы тоже «работает». Этот принцип сегодня используют, сооружая пирамидальные теплицы, а в Италии выпускают специальные пирамидальные кровати для лечебниц.

В России этот эффект исследовал А.Вейник

 

Но для чего же тогда в древности возводили такие гигантские пирамиды? Оказалось, чем больше строение, тем сильнее его воздействие.

Эксперименты русского ученого А.Е.Голода показали, что с удвоением высоты пирамиды ее воздействие значительно возрастает.

Кстати, в своих пирамидальных конструкциях Голод использует принцип «золотого сечения», при соблюдении этих пропорций энергетические проявления максимальны. И еще одно важный момент – конструкция должна быть строго ориентирована по сторонам света.

Чем дольше находится объект внутри пирамиды, тем сильнее проявляются ее свойства, они со временем накапливаются, правда, если пирамида будет полностью неподвижна.

Мы лишь прикоснулись к магическим свойствам пирамид, многое еще неизвестно и ожидает своих исследователей. Ясно одно: мы все еще имеем приблизительные представления о знаниях людей, живших в глубокой древности.

Возраст некоторых пирамид оценивается десятками тысяч лет, это касается, прежде всего, мегалитических построек, найденных на необъятных просторах России.

Нам почти ничего не известно о технологиях наших Предков, а они были очень обширны, и многое из того, что сохранилось до наших дней, и сегодня поражает воображение.

Поделиться

Источник: https://slavmir.tv/stati/slavyanskoe-nasledie/svoystva-piramid-ot-magii-k-nauke/

Пирамида. Правильная пирамида. Видеоурок. Геометрия 10 Класс

Данный видеоурок поможет пользователям получить представление о теме Пирамида. Правильная пирамида. На этом занятии мы познакомимся с понятием пирамиды, дадим ей определение. Рассмотрим, что такое правильная пирамида и какими свойствами она обладает. Затем докажем теорему о боковой поверхности правильной пирамиды.

На этом занятии мы познакомимся с понятием пирамиды, дадим ей определение.

Рассмотрим многоугольник А1А2…Аn, который лежит в плоскости α, и точку P, которая не лежит в плоскости α (рис. 1). Соединим точку P с вершинами А1, А2, А3, … Аn. Получим n треугольников: А1А2Р, А2А3Р и так далее.

Определение. Многогранник РА1А2…Аn, составленный из n-угольника А1А2…Аn и n треугольников РА1А2, РА2А3 …РАnАn-1, называется n-угольной пирамидой. Рис. 1.

Рис. 1

Рассмотрим четырехугольную пирамиду PABCD (рис. 2).

• Р – вершина пирамиды.
• ABCD – основание пирамиды.
• РА – боковое ребро.
• АВ – ребро основания.

Из точки Р опустим перпендикуляр РН на плоскость основания АВСD. Проведенный перпендикуляр является высотой пирамиды.

1. Рис. 2
2. Полная поверхность пирамиды состоит из поверхности боковой, то есть площади всех боковых граней, и площади основания:
3. Sполн = Sбок + Sосн
4. Пирамида называется правильной, если:

• ее основание – правильный многоугольник;
• отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.

Пояснение на примере правильной четырехугольной пирамиды

Рассмотрим правильную четырехугольную пирамиду PABCD (рис. 3).

Р – вершина пирамиды. Основание пирамиды АВСD – правильный четырехугольник, то есть квадрат. Точка О, точка пересечения диагоналей, является центром квадрата. Значит, РО – это высота пирамиды.

Рис. 3

Пояснение: в правильном n-угольнике центр вписанной и центр описанной окружности совпадает. Этот центр и называется центром многоугольника. Иногда говорят, что вершина проектируется в центр.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой и обозначается hа.

1. все боковые ребра правильной пирамиды равны;

2. боковые грани являются равными равнобедренными треугольниками.

• Доказательство этих свойств приведем на примере правильной четырехугольной пирамиды.
• Дано: РАВСD – правильная четырехугольная пирамида,
• АВСD – квадрат,
• РО – высота пирамиды.
• Доказать:
• 1. РА = РВ = РС = РD

2. ∆АВР = ∆ВCР =∆СDР =∆DAP См. Рис. 4.

Рис. 4

Доказательство.

РО – высота пирамиды. То есть, прямая РО перпендикулярна плоскости АВС, а значит, и прямым АО, ВО, СО и DО, лежащим в ней. Значит, треугольники РОА, РОВ, РОС, РОD – прямоугольные.

Рассмотрим квадрат АВСD. Из свойств квадрата следует, что АО = ВО = СО = DО.

Тогда у прямоугольных треугольников РОА, РОВ, РОС, РОD катет РО – общий и катеты АО, ВО, СО и DО равны, значит, эти треугольники равны по двум катетам. Из равенства треугольников вытекает равенство отрезков, РА = РВ = РС = РD. Пункт 1 доказан.

Отрезки АВ и ВС равны, так как являются сторонами одного квадрата, РА = РВ = РС.  Значит, треугольники АВР и ВCР – равнобедренные и равны по трем сторонам.

Аналогичным образом получаем, что треугольники АВР, ВCР, СDР, DAP равнобедренны и равны, что и требовалось доказать в пункте 2.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему:

1. Для доказательства выберем правильную треугольную пирамиду.
2. Дано: РАВС – правильная треугольная пирамида.
3. АВ = ВС = АС.
4. РО – высота.

Доказать: . См. Рис. 5.

Рис. 5

Доказательство.

РАВС – правильная треугольная пирамида. То есть АВ = АС = ВС. Пусть О – центр треугольника АВС, тогда РО – это высота пирамиды. В основании пирамиды лежит равносторонний треугольник АВС. Заметим, что .

Треугольники РАВ, РВC, РСА – равные равнобедренные треугольники (по свойству). У треугольной пирамиды три боковые грани: РАВ, РВC, РСА. Значит, площадь боковой поверхности пирамиды равна:

Sбок = 3SРАВ

Теорема доказана.

Радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м, высота пирамиды равна 4 м. Найдите площадь боковой поверхности пирамиды.

• Дано: правильная четырехугольная пирамида АВСD,
• АВСD – квадрат,
• r = 3 м,
• РО – высота пирамиды,
• РО = 4 м.

Найти:  Sбок . См. Рис. 6.

1. Рис. 6
2. Решение.
3. По доказанной теореме, .

Найдем сначала сторону основания АВ. Нам известно, что радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м.

• Тогда,  м.
• Найдем периметр квадрата АВСD со стороной 6 м:

 Рассмотрим треугольник BCD. Пусть М – середина стороны DC. Так как О – середина BD, то  (м).

Треугольник DPC – равнобедренный. М – середина DC. То есть, РМ – медиана, а значит, и высота в треугольнике DPC. Тогда РМ – апофема пирамиды.

РО – высота пирамиды. Тогда, прямая РО перпендикулярна плоскости АВС, а значит, и прямой ОМ, лежащей в ней. Найдем апофему РМ из прямоугольного треугольника РОМ.

1.  (м).
2. Теперь можем найти боковую поверхность пирамиды:
3. Ответ: 60 м2.

Радиус окружности, описанной около основания правильной треугольной пирамиды, равен  м. Площадь боковой поверхности равна 18 м2. Найдите длину апофемы.

• Дано: АВСP – правильная треугольная пирамиды,
• АВ = ВС = СА,
• R =  м,
• Sбок = 18 м2.

Найти: . См. Рис. 7.

1. Рис. 7
2. Решение.

В правильном треугольнике АВС дан радиус описанной окружности. Найдем сторону АВ этого треугольника с помощью теоремы синусов.

•  м.
• Зная сторону правильного треугольника ( м), найдем его периметр.
•  м.
• По теореме о площади боковой поверхности правильной пирамиды , где hа – апофема пирамиды. Тогда:
• Ответ: 4 м.

Итак, мы рассмотрели, что такое пирамида, что такое правильная пирамида, доказали теорему о боковой поверхности правильной пирамиды. На следующем уроке мы познакомимся с усечённой пирамидой.

Список литературы

1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
2. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
3. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 008. – 233 с.: ил.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет портал «Якласс» (Источник)
2. Интернет портал «Фестиваль педагогических идей «Первое сентября» (Источник)
3. Интернет портал «Slideshare.net» (Источник)

Домашнее задание

1. Может ли правильный многоугольник быть основанием неправильной пирамиды?
2. Докажите, что непересекающиеся ребра правильной пирамиды перпендикулярны.
3. Найдите величину двугранного угла при стороне основания правильной четырехугольной пирамиды, если апофема пирамиды равна стороне ее основания.
4. РАВС – правильная треугольная пирамида. Постройте линейный угол двугранного угла при основании пирамиды.

Источник: https://interneturok.ru/lesson/geometry/10-klass/mnogogranniki/piramida-pravilnaya-piramida

Пирамида — свойства, признаки и формулы

Пирамида — объёмная фигура, обладающая характеристиками, которые позволяют легко рассчитать основные параметры: площадь поверхности граней и занимаемый ей объём пространства. 

Пирамида является одной из основных фигур в геометрии. О её особенностях рассказано в статье.

Определение пирамиды в геометрии

Эта стереометрическая фигура включает в себя часть пространства, отделённую плоскими многоугольниками: произвольным в основании и гранями — треугольниками, содержащими общую вершину и отрезок в виде общей стороны с ним.

Элементы пирамиды

Элементами этой геометрической фигуры являются:

1. Место, куда сходятся все боковые грани фигуры, является вершиной.

2. Многоугольник, от каждой стороны которого отходят треугольные грани, носит название основания. Например, оно может быть шестиугольным.

3. Треугольники, соединяющиеся у вершины, с общей стороной с основанием, носят название боковых граней. У них противоположная вершина совпадает с точкой вершины пирамиды.

4. Высота фигуры представляет собой вертикальный отрезок, ограниченный многоугольником основания и вершиной.

5. На каждом треугольнике боковой стороны можно указать апофему. Она опускается от вершины по грани до ребра основания, будучи к нему перпендикулярной.

6. Боковыми ребрами называют те отрезки, которые соединяют соседние боковые грани.

7. У пирамиды может быть несколько диагональных сечений. Они включают в себя диагональ многоугольника вместе с вершиной пирамиды.

Виды пирамид

Такие фигуры могут относиться к различным видам, в зависимости от типа основания и расположения вершины.

Можно указать следующие разновидности пирамид:

1. Правильной она будет в том случае, если в основании лежит правильный многоугольник. Проекция вершины на многоугольник основания должна приходиться на центр. Тетраэдр рассматривается как одна из разновидностей правильной пирамиды.

2. У прямоугольной фигуры одна из граней находится в плоскости, перпендикулярной многоугольнику, лежащему в основании.

3. Усеченная — это часть фигуры, находящаяся между пересекающей плоскостью и многоугольником основания. Причём эта плоскость должна располагаться горизонтально.

Свойства пирамиды

У этой объёмной геометрической фигуры имеются следующие свойства при условии равенства боковых рёбер:

• круг возможно описать вокруг многоугольника основания;
• угол, под которым наклонены боковые грани, будет таким же.

В том случае, когда треугольные грани имеют одни и те же углы с основанием, возможно сделать вывод о том, что их рёбра одинаковы.

Свойства правильной пирамиды

У такой фигуры можно отметить особые свойства. 

Вот их список:

1. У правильной пирамиды все боковые треугольники одинаковы.

2. Каждая из них является равнобедренным треугольником.

3. Внутрь любой такого типа пирамиды можно вписать сферу. При этом она будет касаться основания и всех граней, имея с каждой из этих сторон по одной общей точке.

4. Снаружи возможна сфера, касающаяся всех вершин.

5. Нетрудно вычислить площадь поверхности такой фигуры. Для этого надо умножить длину периметра многоугольника, находящегося в её основании, на половину длины апофемы.

6. Особым случаем является ситуация, когда у вписанной и описанной сфер центры совпадают. В этом случае можно утверждать, что если сложить все плоские углы у боковых граней, то их сумма будет равна числу «Пи». При этом, для того чтобы узнать величину каждого из них, достаточно эту величину разделить на количество граней.

Формулы объема и площади поверхности пирамиды с примерами расчета

• Вычислить объём можно с использованием следующей формулы.
• V = (S * h) / 3,
• где используются такие обозначения:

• V – объём;
• S – площадь основания;
• h – высота фигуры.

Полную площадь поверхности можно вычислить как сумму площадей основания и всех боковых треугольников.

Пример решения задачи

Если стороны основания составляют 3 см, а боковые рёбра — 4 см, то по теореме Пифагора можно определить высоту фигуры. 

Сначала по теореме Пифагора находят длину половины диагонали. Она будет равна корню квадратному из 18 (4,25 см), так как является диагональю квадрата. 

Здесь рассматривается четырехугольная пирамида.

По теореме Пифагора находим высоту. Она будет равна примерно 4,5 см.

Площадь основания составляет 3 * 3 = 9 кв. см. Нужно учесть, что это квадрат со стороной 3 см. Подставив значения в формулу для объёма, получим следующее.

V = (1 / 3) * 9 * 4,5 = 13,5 куб. см.

Для расчёта площади поверхности надо узнать площадь квадратного основания и треугольных боковых сторон. Для этого сначала по теореме Пифагора находят длину апофемы. Она будет равна 4,27 см. 

Каждая боковая сторона имеет площадь 12,81 кв. см, а основание — 9 кв. см. Сложив площади всех граней, получим 60,24 кв. см. Посчитать площадь поверхности можно, рассмотрев развертку фигуры.

Источник: https://nauka.club/matematika/geometriya/piramida.html

Пирамида и ее элементы

Здесь собраны основные сведения о пирамидах и связанных с ней формулах и понятиях. Все они изучаются с репетитором по математике при подготовке к ЕГЭ.

Рассмотрим плоскость , многоугольник , лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки называются боковыми ребрами. Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды – тетраэдр. Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.

Комментарий репетитора:
Не путайте понятие «правильная пирамида» и «правильный тетраэдр». У правильной пирамиды боковые ребра совсем не обязательно равны ребрам основания, а в правильном тетраэдре все 6 ребер ребра равные. Это его определение. Легко доказать, что из равенства следует совпадение центра P многоугольника с основанием высоты, поэтому правильный тетраэдр является правильной пирамидой.

Что такое апофема?
Апофемой пирамиды называется высота ее боковой грани. Если пирамида правильная, то все ее апофемы равны. Обратное неверно.

Репетитор по математике о своей терминологии: работа с пирамидами на 80% строится через два вида треугольников:
1) Содержащий апофему SK и высоту SP
2) Содержащий боковое ребро SA и его проекцию PA
Чтобы упростить ссылки на эти треугольники репетитору по математике удобнее называть первый из них апофемным, а второй реберным. К сожалению, этой терминологии вы не встретите ни в одном из учебников, и преподавателю приходится вводить ее в одностороннем порядке.

Формула объема пирамиды:
1) , где – площадь основания пирамиды, а -высота пирамиды
2) , где – радиус вписанного шара, а – площадь полной поверхности пирамиды.
3) , где MN – расстояние любыми двумя скрещивающимися ребрами, а – площадь параллелограмма, образованного серединами четырех оставшихся ребер.

Свойство основания высоты пирамиды:

• Точка P (смотри рисунок) совпадает с центром вписанной окружности в основание пирамиды, если выполняется одно из следующих условий:
  1) Все апофемы равны
  2) Все боковые грани одинаково наклонены к основанию
  3) Все апофемы одинаково наклонены к высоте пирамиды
• 4) Высота пирамиды одинаково наклонена ко всем боковым граням

Комментарий репетитора по математике: обратите внимание, что все пункты объединяет одно общее свойство: так или иначе везде участвуют боковые грани (апофемы — это их элементы). Поэтому репетитор может предложить менее точную, но более удобную для заучивания формулировку: точка P совпадает с центром вписанной окружности основание пирамиды, если имеется любая равная информация о ее боковых гранях. Для доказательства достаточно показать, что все апофемные треугольники равны.

1. Точка P совпадает с центром описанной около основания пирамиды окружностью, если верно одно их трех условий:
   1) Все боковые ребра равны
   2) Все боковые ребра одинаково наклонены к основанию
2. 3) Все боковые ребра одинаково наклонены к высоте

Комментарий репетитора. Аналогично предыдущему пункту текст можно упростить и вместо этих условий произнести : «если имеется любая равная информация о боковых ребрах». При этом все апофемные треугольники будут равны все проекции боковых ребер будет равны P будет равноудалена от всех вершин основания и поэтому окажется центром описанной окружности.

Площадь полной поверхности пирамиды:
Полощадью поверности пирамиды называется сумма площадей всех ее граней .
Площадь боковой поверхностии — сумма площадей всех боковых граней .
Если все апофемы равны (например в правильной пирамиде), то площадь ее боковой поверхности вычисляется по формуле , где p — полупериметр основания, а SK-апофема.

Правильная треугольная пирамида однозначно определяется двумя параметрами: один плоский, а другой пространственный: к плоскому я отношу любой элемент правильного треугольника (кроме угла), а к пространственному любой связующий параметр между основанием и точкой S: апофема, высота, углы наклона ребер, граней, объем, площадь поверхности и др. При наличие в условии задачи этих двух начальных данных репетитор с учеником может найти у такой пирамиды все что угодно.

Пирамида — обязательный пункт подготовки к ЕГЭ по математике. Програмный минимум по стереометрии включает в себя все вышеуказанные сведения, кроме третьей формулы вычисления объема пирамиды.

Колпаков Александр,
репетитор по математике в Москве. Строгино

Источник: https://ankolpakov.ru/piramida-i-ee-elementy/

Свойства пирамид Среднее время прочтения:

Одним из уникальных лечебных средств является пирамида. Своей (пока наукой не объясненной) энергией она достаточно активно стимулирует жизненные силы больного организма, а тот, в свою очередь, уже легче справляется с недугом.

С помощью пирамиды достаточно быстро улучшается состав крови, нормализуется давление, стихают боли, ускоренно заживают переломы костей, раны, а также повреждения, связанные с операциями, радиотерапией и опухолями. Исцеляет пирамида и инфекционные (микробно-паразитарные) заболевания.

— Salik.biz

Иными словами, терапия с помощью пирамиды – уникальное средство при многих заболеваниях, и даже, если человек, будучи в полном здравии, иногда принимает (в малых дозах) воду или съедает небольшие порции пищи, выдержанные в пирамиде, или отдыхает иногда в большой или над малыми пирамидами, то шансы заболеть у него минимальны.

Изготовление пирамид

Пирамида – это многогранник, основанием которого служит многоугольник, а боковыми гранями являются треугольники, имеющие общую величину.

Высота пирамиды равна длине перпендикуляра, опущенного из вершины в центр основания (центром правильного многоугольника, лежащего в основании пирамиды служит точка пересечения его диагоналей).

Кроме высоты характеристиками пирамиды служат длина основания и высота боковой грани (апофема) пирамиды.

Рекламное видео:

Изготавливается пирамида из любого плотного гладкого однородного материала (плотного картона, оргстекла, металлических листов и т.п.), без единого гвоздя и без применения прочих металлов, которые своим полем вносят искажения в поле пирамидального пространства. Лучше всего материал склеивать, и если это металл — заваривать швы.

Домашняя пирамида может иметь любые размеры, но самые эффективные пирамиды имеют в основании равносторонний треугольник, и ее основание соотносится с высотой как 1:7, и изготавливаются из гладких металлических листов.

Следует помнить, что с удвоением высоты пирамиды активность ее действия возрастает во много (50-100 и более) раз. Следовательно, если позволяет возможность, устанавливайте пирамиды с максимальной высотой.

Если пирамида имеет в основании квадрат и высоту более метра, то одно из ребер пирамиды должно быть сориентировано с помощью компаса строго на север, так пирамида будет более эффективно работать с энергией планеты.

Максимальными энергетическими возможностями всех правильно изготовленных и установленных пирамид (больших и малых) обладает их внутреннее пространство на уровне от 1/3 до 2/3 высоты пирамиды. Все остальное пространство пирамид энергетически минимально, соответственно, и отдача минимальна.

Примеры использования пирамид

При тяжелых и множественных заболеваниях больному следует пользоваться большими пирамидами для отдыха – возможности исцеления в них практически не ограничены. Время пребывания в больших пирамидах сугубо индивидуально, для особо чувствительных пациентов – не более 15 минут. При переутомлении достаточно 30 минут пребывания в пирамиде для восстановления сил и избавления от дискомфорта.

Для исцеления организма пустые пирамидки хороши, но в сочетании с приемом пирамидальной воды или травяных настоев, выдержанных в течение 24 часов внутри пирамиды, лечение оказывается гораздо эффективнее. Даже малая толика такой воды приносит больному пользу.

Пирамидный настой делается примерно так: в емкость (стакан или банку) кладут указанное в рекомендации лекарственное сырье, заливают нужным количеством кипятка, закрывают капроновой крышкой и настаивают нужное время в пирамиде.

Вода может храниться в пирамиде длительное время.

При всех внутренних болях, при болях в мышцах и суставах наружно в виде компресса можно использовать алюминиевую фольгу, которую перед этим заряжают в пирамиде 1 неделю. Заряженную таким образом фольгу обворачивают слоем льняного полотна и прикладывают на больное место или сустав.

Сверху этот компресс закрывают, закрепив льняным полотном или бинтом и оставляют на всю ночь. Такие компрессы ставят и при болях головы, живота, груди, конечностей.

С помощью таких компрессов боли, как правило, проходят достаточно быстро – проходят совсем! Фольгу следует располагать так: той стороной, которая была к вершине, нужно прикладывать от тела!

Кроме целительных свойств, пирамиды полезны и для многих других целей

Можно выдерживать семена перед посадкой в пирамиде в течение 10-15 дней, при этом повышается всхожесть и урожайность примерно в 2 раза.

Аквариум можно залить пирамидальной водой, можно накрыть пирамидой, ориентированной по сторонам света на 24 и более часа.

В пирамидах, особенно больших, можно хранить на полках долгое время скоропортящиеся продукты питания без риска, что они испортятся. При этом даже улучшаются их вкусовые качества.

В малых пирамидках кладут затупленные лезвия бритвы для заточки.

Если в большой пирамиде на высоте от 1/3 до 1/ 2 поставить самодельный генератор, то пирамида будет способна вырабатывать электрическую энергию. Генератор делается из листов алюминия, меди или фольгированного пластика.

Собранный генератор нужно подключить к аккумулятору, желательно щелочному, запараллелив его и с нагрузкой.

При изготовлении такого генератора следует иметь в виду, что чем больше в нем будет пластин, тем большее напряжение он сможет дать, и чем больше будет поверхность пластин, тем больший ток сможет вырабатывать генератор.

Рис 3. Примерный вид генератора в горизонтальном (нерабочем) положении.

Рабочее положение – вертикальное.1 – токосъемные металлические пластины; 2 – изоляционные планки (с помощью клея удерживают пластины); 3 – аккумулятор; 4 – нагрузка (лампа).

Размещение генератора в пирамиде.

В засушливых районах можно сделать конденсатор (накопитель) воды и сбора ее из воздуха, размещая пирамиду на фундаменте с уклоном к центру пирамиды с отверстием трубы в центре основания. Труба выводится под уклоном для самостоятельного стока воды за пределы фундамента.

Сверху бетонированную площадку засыпают горкой гравием на возможно большую высоту. Насыпь укрепляют с помощью пирамидального каркаса (можно металлического), обтянутого сеткой (желательно оцинкованной). Такое крепление не мешает свободному притоку и оттоку воздуха.

Пирамида высотой 250 см способна наполнить водой емкость 100-200 л за сутки.

В настоящее время в мире накоплен большой статистический материал раскрывающий различные свойства пирамид:

• энергия пирамид благотворно влияет на окружающую среду,
• уменьшается уровень радиации,
• меняется уровень ионизации с положительного на отрицательный,
• отражается поток электромагнитных излучений технического и естественного происхождения,
• падает вязкость нефти в месторождениях около построенных пирамид,
• пирамиды благотворно влияют на психоэмоциональное состояние людей, снижают уровень озлобления общества.

Достаточно напомнить о таком известном факте: грязная вода озера Селигер стала чистой и прозрачной после постройки на её берегах пирамиды Голода. Вскрылись новые родники, появились цветы, занесённые в Красную книгу. Учёные зарегистрировали столб неизвестной энергии высотой несколько километров над пирамидой.

Энергии внутри пирамиды изменяют внутреннюю структуру объектов находящихся в ней.

Отмечены следующие явления:

• мумифицирование ( обезвоживание и стерилизация )
• регенерация повреждённых тканей
• структуризация воды ( не замерзает при отрицательной температуре ).
• продукты питания улучшают свои вкусовые качества и в несколько раз увеличивается сроки их хранения ( в Болгарии много лет используются овощехранилища пирамидальной формы )
• улучшается всхожесть семян.

Целительные свойства пирамид только начинают систематически изучаться, хотя в древности они использовались повседневно.

Так недавние исследования в этой области показали, что одной из функций пирамид в Египте, в частности пирамиды Хеопса была диагностика и терапия органических заболеваний, а применение небольших обелисков – своеобразных пирамид, было повсеместным ( для домашнего пользования ).

Согласно теории ученых, физический вакуум и материальные объекты, имеющие пространственно-геометрическую структуру искажают линейную структуру физического вакуума. Который является материальной но не вещественной средой с полевой структурой.

Человек также является сложным комплексом торсионных генераторов, начиная с клеточного уровня и кончая чакровыми системами.

Кроме воздействия генерируемыми ими торсионными полями, пирамидальные структуры являются связывающим звеном, воспринимающим космические торсионные потоки и потоки, генерируемые человеком, окружающей средой и Землёй. Можно сказать, что выстраивается цепь: Вселенная, Земля, пирамида, человек. Также существует и обратная связь: человек, пирамида, Земля, Вселенная.

• Теория физического вакуума, торсионных полей в настоящее время продолжает развиваться, причём начинают получать практическое применение разработки с использованием торсионных генераторов и других приборов.
• Но когда начинает внедряться что-то новое, то как часто бывает, опыт идёт впереди научного обоснования и теории идёт набор статистических данных, проводятся исследования, параллельно идёт научная работа и изучение опыта предыдущих цивилизаций.
• подтвержденными целительными свойствами пирамид являются:

• Снимаются напряжения на уровне физическом и психическом.
• Оказывается заметное влияние на парасимпатическую нервную систему ( уменьшаются, стабилизируются показатели пульса и давления ).
• Даёт общий оздоравливающий эффект.
• Улучшаются показатели крови ( повышение гемоглобина, снижение СОЭ, уменьшение лейкоцитов ).
• Уменьшается болевой синдром
• Увеличивается работоспособность, улучшается сон.
• Уменьшается восприимчивость к стрессам.

Биоприборы Ба-Гуа, которые мы распространяем через наш сайт, имеют те же принципы функционирования, что и пирамида. Но они более эффективны, и созданы специально для работы с человеческой биоэнергией.

Источник: https://salik.biz/articles/53562-svoistva-pirami.html

Что такое пирамида с точки зрения математики?

Произнося слово «пирамида», первое, что приходит на ум —  это образы знаменитых египетских гробниц фараонов. Они нам знакомы как одно из древнейших чудес света, монументальные сооружения, построенные египетскими зодчими еще тысячи лет назад.

С ними нераздельно связаны множество тайн и загадок, над решением и объяснением которых ученые бьются и по сей день, порождая все новые версии, споры и заявления.

Но, не смотря на разногласия, все сходятся к одному, что пирамида – это одна из важнейших фигур геометрии, обладающая интересными свойствами.

Что же такое пирамида с точки зрения математики?

Пирамида в математике – это особый многогранник, в его составе есть боковые грани и основание. В качестве основания фигуры может выступать многоугольная фигура: квадрат, треугольник, п-угольник. Роль боковых граней играют треугольники, имеющие одно начало – вершину. Количество углов основания определяет название пирамид: треугольные, четырехугольные, n-угольные.

Однако таким определением пользовались не во все времена. Например, Евклид в свое время предложил термином «пирамида» наделять некие телесные фигуры, которые имеют ограничения плоскостями, исходящими от общей плоскости и сходящихся к единой точке. Как и Герон, Евклид не дает точного понятия «основание», благодаря чему и нет точного понимания термина «пирамида».

Четким представлением о пирамиде как о фигуре геометрической в конце 18 века делится ученый Адриен Мари Лежандр, определяя ее фигурой, образованной благодаря треугольникам, заканчивающимся на разных сторонах основания и сходящимся вершинами в одной точке.

Основные свойства правильных пирамид

Правильные пирамиды – наиболее частый случай этих геометрических фигур, они обладают стабильностью и встречаются в современной архитектуре, строительстве, машиностроении и других отраслях.

Правильная – это та пирамида, в которой правильный многоугольник является основанием, а высота проецируется точно в его центр.

Равносторонний треугольник, лежащий, в основании образует тетраэдр, а квадрат — правильную 4-угольную пирамиду, и так далее.

Для решения любых задач с участием правильных пирамид следует помнить, что:

• боковые грани ее — это равнобедренные треугольники, которые равны между собой по площади и всем признакам, основанию и боковым сторонам, одновременно являющихся ребрами;• вокруг и внутри правильного типа пирамиды можно описать и вписать сферу;

• площадь боковой поверхности правильной пирамиды равна ½ произведения высоты грани (апофемы) и периметра основания фигуры. Не забывайте, что в правильной пирамиде апофемы равны между собой, что значительно упрощает нахождение ответа к множеству задач;

• боковые грани с плоскостью основания образуют углы равной градусной меры, поэтому, зная один из них, легко производить нужные расчеты.

• правильная треугольная пирамида и правильный тетраэдр имеют существенные различия. В первом случае, грани – равнобедренные треугольнике, во втором – равносторонние, что следует учитывать при решении ряда задач.

© #spacefacts 2018

Источник: https://zen.yandex.ru/media/id/5bdd677f9fb30d00aa65bec6/5bdd6d8d1d2f9400abd82c9e