Сохрани ссылку в одной из сетей:
Рассмотрим далее основополагающие
в линейной алгебре понятие о линейной
зависимости и независимости векторов,
а также определение базиса системы
векторов.
Любую конечную последовательность
векторов  будем
будем
называть системой векторов, а любую
ее подпоследовательность – подсистемой
векторов. Линейной комбинацией
векторов 
назовем вектор ,
равный сумме произведений произвольных
чисел 
на векторы системы, т.е.  .
.
Система векторов 
называется линейно независимой,
если их линейная комбинация равна
нулевому вектору только в том случае,
когда все числа 
равны нулю. В обратном случае система
векторов называется линейно зависимой.
Отсюда, система векторов является
линейно зависимой в том случае, когда линейная комбинация векторов равна
нулевому вектору, а хотя бы один числовой
коэффициент отличен от нуля.
Линейная зависимость и независимость
есть свойства системы векторов. Однако
часто соответствующие прилагательные
относят и к самим векторам. Поэтому
вместо «линейно независимая система
векторов» допустимо говорить «линейно
независимые векторы».
Например, двумерные
арифметические векторы и
линейно
независимы. Их линейная комбинация 
равна вектору ,
который обращается в нулевой вектор
только
тогда, когда
и .
- Если взять векторы и
,
то они являются линейно зависимыми, так
как их линейная комбинация равна нулевому
вектору при и
,
не равных нулю. - Из определения линейной зависимости
(независимости) системы векторов вытекают
следующие утверждения. - 1) Если некоторая система
векторов содержит нулевой вектор, то
она является линейно зависимой.
Пусть для определенности первый
вектор системы является нулевым, т.е.

2) Если среди векторов системы
есть такие, которые сами образуют линейно
зависимую подсистему, то вся система
также линейно зависима.
Так как исходная подсистема
линейно зависима, то среди коэффициентов
линейной комбинации векторов подсистемы
имеется хотя бы один отличный от нуля.
Добавим к этой линейной комбинацию
линейную комбинацию векторов, не вошедших
в исходную подсистему, с числовыми
коэффициентами, равными нулю.
Мы получим
линейную комбинацию из векторов полной
системы, которая равна нулевому вектору,
причем имеется хотя бы один коэффициент
отличный от нуля. Таким образом, наше
утверждение доказано.
3) Если система векторов линейно
независима, то и любая ее подсистема
также линейно независима.
Если предположить обратное, т.е.
существование некоторой линейно
зависимой подсистемы, то по предыдущему
утверждению отсюда следует зависимость
исходной системы, что противоречит
условию доказываемой теоремы. Полученное
противоречие доказывает сформулированное
утверждение.
4) Для того чтобы система из
ненулевых
векторов была линейно зависима необходимо
и достаточно, чтобы хотя бы один из
векторов системы мог быть представлен
как линейная комбинация предшествующих
векторов.
Необходимость. Пусть система
векторов 
линейно зависима. Тогда равенство 
выполняется при том условии, что хотя
бы одно из чисел в левой части равенства
отлично от нуля. Будем перебирать эти
числа, начиная с большего номера, и
остановимся на некотором номере
таком, что соответствующий коэффициент
отличен от нуля, т.е. .
Номер
не может быть равен единице, так как
иначе из условий и
теоремы о нулевом произведении следовало
бы равенство ,
что противоречит правилу выбора номера
и условию теоремы. Таким образом ,
и справедливо равенство.
Отсюда находим вектор таким
образом, чтобы он является линейной
комбинацией предшествующих ему векторов,
а именно .
Достаточность. Пусть имеется
некоторый вектор ,
который представлен в виде линейной
комбинации предшествующих ему векторов
.
Тогда выполняется условие ,
что по определению означает линейную
независимость исходной системы векторов.
- По аналогичной схеме доказывается
следующее утверждение. - 5) Система векторов линейно
зависима тогда и только тогда, когда
хотя бы один из векторов системы может
быть представлен в виде линейной
комбинации остальных векторов. - Базис множества векторов и
всего линейного пространства. - Система векторов
называется базисом множества ,
если:
-
все векторы системы принадлежат множеству ;
-
система векторов является линейно независимой системой;
-
любой вектор из множества представим в виде линейной комбинации векторов этой системы, т.е. .
- Если множество совпадает
со всем пространством ,
то базис
является базисом всего линейного
пространства. - Числа называются
координатами вектора в базисе ,
а выражение — разложением вектора по базису . - Теорема (о единственности
разложения по данному базису). - Разложение любого вектора
по базису
является единственным.
Доказательство. Предположим,
что для вектора наряду с разложением
имеется другое разложение .
Вычитая одно разложение из другого,
получим равенство .
Поскольку базисные векторы
линейно независимы, то из полученного
равенства следуют равенства ,
что и доказывает теорему.
Следствие. Любые два вектора
равны тогда и только тогда, когда равны
их координаты в каком – либо базисе.
- Таким образом, при фиксированном
базисе линейного пространства каждый
вектор однозначно определяется своими
координатами в этом базисе. - Теорема (о линейных свойствах
координат векторов). - При сложении любых двух векторов
их координаты в данном базисе складываются,
а при умножении любого вектора на любое
число координаты умножаются на это
число.
Доказательство. Пусть любые
два вектора имеют
в базисе
разложения
,
.
Из аксиом линейного пространства
следует, что сумма векторов и
произведение вектора
на число
представимы в виде , .
- Отсюда и теоремы о единственности
разложения векторов по данному базису
следует истинность доказываемой теоремы. - Теорема о базисном миноре.
- Базисные строки (столбцы)
линейно независимы и образуют базис в
системе всех строк (столбцов) произвольной
матрицы
размера .
- Доказательство.
По определению базиса это
означает, что любая строка или столбец
матрицы могут быть представлены в виде
линейной комбинации базисных строк или
базисных столбцов, причем единственным
образом. Все рассуждения достаточно
провести для строк, так как, транспонировав
исходную матрицу, мы получим доказательство
для столбцов матрицы .
Линейную независимость базисных
строк будем доказывать методом от
обратного.
Пусть некоторые базисные строки
линейно зависимы. Тогда одна из этих
строк является линейной комбинацией
остальных строк. Но тогда из свойств
определителей следует, что базисный
минор равен нулю. Базисный минор по
определению не должен быть равен нулю.
Таким образом, исходное предположение
ложно и базисные строки линейно
независимы.
Докажем теперь, что любая строка
произвольной матрицы
размера
является линейной комбинацией базисных
строк. Для удобства в обозначениях будем
считать, что базисный минор стоит на
пересечении первых
строк и первых
столбцов.
Это предположение не ограничивает
общности доказательства теоремы, так
как всегда можно переставить базисные
строки и столбцы таким образом, чтобы
базисный минор находился в левом верхнем
углу матрицы .
При таких перестановках может измениться
знак определителя, но он не может стать
равным нулю, что изменило бы ранг матрицы.
Пусть
– любое число от 1 до ,
а
– любое число от 1 до .
Убедимся в том, что любой определитель
порядка :
равен нулю. Если
или ,
то указанный определитель будет равен
нулю в силу того, что у него будет два
одинаковых столбца или две одинаковые
строки.
Если оба числа
и строго
больше ,
то любой указанный определитель будет
иметь порядок ,
и равен нулю по определению базисного
минора. Таким образом, при любых значенияхи
наш определитель всегда нулю.
Разложим этот определитель по последнему столбцу:
.
Алгебраические дополнения к
элементам последнего столбца с номером
,очевидно,
не зависят от элементов с номерами,
содержащими .
Поэтому в крайней правой части нашего
разложения они обозначены буквами ,
не включающими индекс .
Значение
всегда не равно нулю, так как оно с
точностью до знака совпадает со значением
базисного минора. Разделив последнее
равенство на число ,
мы получим, что
.
Эти равенства справедливы для
любых чисел
и ,
и означают, что любая строка с номером является
линейной комбинацией первых
базисных строк. Таким образом, теорема
полностью доказана.
Из теоремы о базисном миноре
вытекают два важных следствия.
1. Для любой матрицы число
линейно независимых строк равно числу
линейно независимых столбцов и равно
рангу матрицы.
2. Определитель любого порядка
равен нулю тогда и только тогда, когда
его строки или его столбцы линейно
зависимы.
Отметим, что по закону контрпозиции
равносильное свойству 2 утверждение
формулируется следующим образом:
определитель отличен от нуля тогда и
только тогда, когда его строки или его
столбцы линейно независимы.
Доказательство.
Покажем достаточность условия
второго следствия. Если строки матрицы
линейно зависимы, то по свойству системы
зависимых векторов одна из строк является
линейной комбинацией остальных строк.
Вычитая из этой строки указанную линейную
комбинацию, мы, не изменяя величины
определителя, получим матрицу, содержащую
нулевую строку.
Определитель такой
матрицы всегда равен нулю, что и
требовалось доказать.
Покажем, что условие линейной
зависимости столбцов квадратной матрицы
является необходимым для равенства
нулю определителя матрицы. Если
определитель порядка
равен нулю, то его базисный минор имеет
порядок, заведомо меньший .
Но тогда хотя бы одна из строк является
не базисной. По теореме о базисном миноре
эта строка может быть представлена в
виде линейной комбинации базисных
строк, что и означает линейную зависимость
всех строк исходной матрицы.
Следствие
полностью доказано.
Если размеры
матрицы большие, то ранг матрицы вычисляют,
пользуясь методом элементарных
преобразований. Этот метод является
универсальным и используется также для
исследования и решения систем уравнений,
вычисления определителей и обращения
матриц.
Элементарными преобразованиями
матрицы называют следующие:
-
перестановка строк (столбцов) матрицы;
-
умножение строки (столбца) на число отличное от нуля;
-
прибавление к элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.
Целью элементарных преобразований
является приведение исходной матрицы
к ступенчатой форме. Матрица называется
ступенчатой, если для нее выполняются
следующие условия:
-
если какая – либо строка матрицы состоит из нулей, то и все последующие строки также состоят из нулей;
-
если первый, отличный от нуля, элемент какой – либо строки расположен в одном из столбцов данной матрицы, то все элементы этого столбца, расположенные ниже, являются нулевыми.
- Матрица из одной строки считается
ступенчатой по определению. - Например, матрица является ступенчатой.
- Теорема (о приведении к
ступенчатой матрице). - Любую матрицу можно привести
к ступенчатой матрице, выполнив конечное
число элементарных преобразований. - Теорема доказывается конструктивно
путем перебора конечного числа возможных
матриц с нулевыми элементами.
Пример. Приведем к ступенчатому
виду следующую матрицу: .
На первом шаге выполним следующие
элементарные преобразования над матрицей
:
к элементам второй строки прибавим
элементы первой строки и результат
запишем во вторую строку; из элементов
третьей строки вычтем элементы первой
строки, а результат запишем в третью
строку. В итоге матрица преобразуется
к виду .
На последнем шаге из третьей строки
полученной матрицы вычтем вторую строку,
умноженную на 3, и запишем в третью
строку, в результате чего получим
ступенчатую матрицу:
- .
- Теорема (о ранге ступенчатой
матрицы). - Ранг ступенчатой матрицы равен
числу ее ненулевых строк.
Доказательство. Ненулевые,
ступенчатые строки линейно независимы,
что можно показать, составив линейную
комбинацию этих строк и приравняв ее
нулевой строке. Покомпонентный анализ
этой линейной комбинации показывает,
что все числовые коэффициенты при
строках, начиная с первой, последовательно
обращаются в нули.
По определению это
означает линейную независимость
ненулевых строк. Остальные строки
ступенчатой матрицы нулевые, а добавление
нулевой строки в систему ненулевых
строк превращает новую систему в
зависимую систему. Поэтому только
ненулевые строки линейно независимы.
По следствию 1 теоремы о базисном миноре
это означает, что ранг ступенчатой
матрицы равен числу ее ненулевых строк,
что и требовалось доказать.
Теорема (об инвариантности
ранга при элементарных преобразованиях).
Ранг матрицы не изменяется при
ее элементарных преобразованиях.
Доказательство. При любых
элементарных преобразованиях отличный
от нуля определитель остается таковым.
Поэтому любой найденный базисный минор
останется базисным. Миноры более высокого
порядка равны нулю и останутся таковыми
при любых элементарных преобразованиях.
Таким образом, теорема доказана.
На основе трех, приведенных выше
теорем, формулируется метод элементарных
преобразований: сначала исходная
матрица приводится к ступенчатому виду,
затем ранг исходной матрицы полагается
равным числу ненулевых строк ступенчатой
матрицы.
В рассмотренном выше примере
матрица
была приведена элементарными
преобразованиями к ступенчатой матрице,
имеющей три ненулевые строки. Это
означает, что ранг исходной матрицы
равен трем.
Исследуя систему уравнений
общего вида, необходимо либо доказать,
что она не имеет решений, либо, если она
совместна, найти все возможные решения
и представить их в компактной и наглядной
форме.
Для этого систему уравнений с
помощью элементарных преобразований
приводят к более простому виду,
позволяющему непосредственно увидеть
решения или показать несовместность
системы. При этом центральным понятием
является равносильность двух систем.
Две системы уравнений с одними теми же
неизвестными называются равносильными,
если они имеют одно и то же множество
решений.
- Например, системы и
являются равносильными, так как каждая
из них имеет одно и то же единственное
решение . - Системы и
также являются равносильными, поскольку
каждая из них не имеет решений (множество
решений пусто). - Элементарными преобразованиями системы линейных алгебраических
уравнений называют следующие
преобразования:
-
перестановка местами любых двух уравнений;
-
умножение любого уравнения системы на одно и то же число, отличное от нуля;
-
сложение любых двух уравнений.
- Теорема (о равносильных
переходах). - Любое конечное число элементарных
преобразований системы переводят ее в
систему, равносильную исходной системе. - Доказательство теоремы
следует непосредственно из определения
элементарных преобразований системы
линейных уравнений общего вида. - Как видно из приведенных
определений, элементарным преобразованиям
системы полностью соответствуют
элементарные преобразования строк так
называемой - расширенной матрицы системы
,
которая получается из матрицы коэффициентов
системы добавлением
— го столбца, состоящего из правых частей
уравнений системы. - На приведении расширенной матрицы
системы к ступенчатым матрицам
специального вида основан метод решения
систем линейных уравнений, называемый
методом Гаусса или методом
последовательного исключения неизвестных.
Источник: https://gigabaza.ru/doc/42622-p3.html
Ранг матриц. Теорема о базисном миноре
- Сначала введем понятие линейной зависимости и независимость строк (столбцов) матрицы.
- Определение 6.Строки
 называются линейно зависимыми, если существуют числа
называются линейно зависимыми, если существуют числа  не равные нулю одновременно, такие, что имеет место равенство
не равные нулю одновременно, такие, что имеет место равенство 
Если же равенство (2) (где числа) имеет место тогда и только тогда, когда все числа одновременно равны нулю (  ), то строки
), то строки 
 называются линейно независимыми. Аналогичные понятия вводятся и для столбцов.
называются линейно независимыми. Аналогичные понятия вводятся и для столбцов.

- (здесь ), а столбцы линейно независимы, так как
- Введем теперь следующее важное понятие.
Определение 7.Рангом произвольной матрицы (размера ) называется максимальное число линейно независимых столбцов этой матрицы. Обозначение:
Например, ранг матрицы равен 1, так как только один столбец этой матрицы (любой) линейно независим, а два столбца линейно зависимы.
Пусть дана произвольная матрица . Будем последовательно рассматривать в ней миноры первого, второго, третьего и т.д. порядков.
Определение 8.Базисным минором матрицы называется такой отличный от нуля минор го порядка, что все миноры матрицы порядка выше го равны нулю.
Нетрудно доказать следующее утверждение.
Теорема о базисном миноре.Ранг матрицы равен порядку базисного минора этой матрицы.
Отсюда, в частности, следует, что при транспонировании матрицы ее ранг не изменяется, поэтому ранг матрицы равен также максимальному числу ее линейно независимых строк. Из теоремы о базисном миноре также вытекает, что ранг матрицы ступенчатого вида равен числу её опорных элементов.
Лекция 4. Элементарные преобразования и приведение матрицы к ступенчатому виду. Линейные системы алгебраических уравнений. Линейное пространство, размерность, базис. Теорема Кронекера-Капелли. Структура общего решения однородной и неоднородной систем уравнений. Метод Гаусса решения алгебраических систем уравнений
В основе решения систем линейных уравнений лежат два метода – метод Крамера и метод Гаусса, к изложению которых мы переходим.
Дата добавления: 2016-06-05; просмотров: 1320;
Источник: https://poznayka.org/s8574t1.html
Теорема о базисном миноре


- Теорема о базисном миноре
- Примеры решения, формулы и задачи
- Основная второстепенная теорема. Любой (не Обязательно квадратная матрица A = K-й минор матрицы A является определяющим степень k-ro с элементами на пересечении k рядов 25) где O = @, 0, …, 0) нулевая линия. K столбцов матрицы A (конечно, k не превышает минимального значения (Из чисел m и n).
- Предположим, что хотя бы один элемент ac матрицы A отличается С нуля до Чена. И есть положительное целое число r, как это: Следующие два условия выполняются: 1) Матрица А является младший r-го порядка, кроме 0, 2) все младшие (r + 1) -й, и Высокий (если есть) равен нулю.
Числовое значение r, которое удовлетворяет требованиям 1) и 2), называется рангом. Людмила Фирмаль
Матрица А 26). Ненулевой г следующий минор Позвоните в базу майнеров (конечно же Матрица А Ненулевой кр минор). Ряды и столбцы Назовите каждого, где пересечение является основным несовершеннолетним Базовый ряд и базовый столбец. Докажем следующую основную теорему.
Теорема 1.6 (основная второстепенная теорема). Базовый ряд (ба- Жирные столбцы линейно независимы. Любая строка (любая таблица Matrix A betz) — линейная комбинация базовых рядов (Базовый столбец). Доказательство. Выполняет все аргументы в строке. Теорема 1.5, если базовый ряд линейно зависим.
Одна из этих линий представляет собой линейную комбинацию другой базы Без изменения строки и основных второстепенных значений Вычитает и извлекает указанную линейную комбинацию из этой строки Строка, состоящая полностью из нулей. Это противоречит Базовый несовершеннолетний ненулевой. Таким образом, базовая линия является линейной Самостоятельно он имеет.
Предмет линейная алгебра
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Здесь мы докажем, что любая строка матрицы A линейна Сочетание базовых показателей. Потому что есть какие-то изменения Определитель строки (или столбца) сохраняет свойства уравнения Ли, тогда вы можете принять основы, не теряя общности Несовершеннолетний находится в верхнем левом углу матрицы А.47).
Это значит Жена первого г строки и первого г столбца. Пусть j произвольное число От 1 до p, k — любое число от 1 до t.
(R + 1) BC 0-12 ••• CL r CL j A.48) Арр Ардж & W ••• & кг 0> кДж 26) Ранг матрицы A, где все элементы равны нулю, по определению равен нулю.
Равно нулю Для j ^ r или k ^ r указанный определитель равен. Людмила Фирмаль
Иметь две одинаковые колонки или Две одинаковые линии. А.48) является второстепенным, если оба числа j и k превышают r Матрица А порядка (r + 1), и все такие миноры равны нулю (в Основное второстепенное определение). Следовательно, определитель A.48) равен нулю Для всех j от 1 до n и всех k от 1 до t.
Но затем разверните этот определитель в последнем столбце, показать алгебраические дополнения, не зависящие от числа j Элементы этого столбца с символами A j = ci, A ^ j-ci-, …, Arj = cr, Akj = CR + I, получить его C2OL2J + … + Crarj + Cr + iOLkj = 0 (Все j = 1,2, …, n).
При последнем равенстве гебраическое дополнение кр +1 = акж явно лучше Каждый из них может быть отделен от основного минорного нуля качество cr _ | _ 1.
Но тогда введем обозначение -Cl — ° 2 -Cr Л1-, Л2-, ••.
, Лг-, Sg _ | _ 1 Sg _ | _ 1 Sg _ | _ 1 akj = Xiclij + ^ 2 & 2j + … + Xrarj (все j = = 1, 2, …, n), это означает, что k-я строка является линейной Первая (основная) строка комбинации. Теорема доказана.
Источник: https://9219603113.com/teorema-o-bazisnom-minore/
Ранг матрицы
Минор матрицы. Ранг матрицы. Базисный минор. Линейная зависимость и линейная независимость строк и столбцов матрицы. Критерий линейной зависимости. Теорема о базисном миноре и ее следствия. Инвариантность ранга матрицы относительно ее элементарных преобразований. Способы вычисления ранга матрицы.
Определение 12.1. Минором порядка к матрицы A типа m×n называют определитель, который составлен из элементов этой матрицы, стоящих на пересечении произвольно выбранных к строк и к столбцов с сохранением порядка этих строк и столбцов.
Если выбранные строки имеют номера i1, i2, … , ik, а столбцы — j1, j2, …, jk, то соответствующий минор будем обозначать Мj1, j2, …, jki1, i2, … , ik.
О миноре Мj1, j2, …, jki1, i2, … , ik говорят, что:
— строки i1, i2, …, ik и столбцы j1, j2, … , jk матрицы входят в него;
- — он образован этими строками и столбцами;
- — он располагается на пересечении этих строк и столбцов;
- — он располагается в этих строках и столбцах матрицы.
Строки, входящие в минор, попарно различны, и в обозначении минора естественно упорядочить их по возрастанию номеров. Это же относится и к столбцам.
Правило возрастания номеров означает, что, например, М3,5,61,3,4 является минором некоторой матрицы, расположенным на пересечении 1-й, 3-й и 4-й строк с 3-м, 5-м и 6-м столбцами, в то время как M3,5,61,3,4 минором не является, потому что нарушен порядок столбцов (5-й столбец указан в верхних индексах перед 3-м).
Это просто определитель третьего порядка, который получается из минора М3,5,61,3,4 матрицы при перестановке в нем первых двух столбцов. Поэтому, согласно свойствам определителей, М3,5,61,3,4 = -M3,5,61,3,4.
Итак, мы следуем соглашению, что обозначение Мj1,j2. …jki1,i2. …ik соответствует минору матрицы, если верхние и нижние индексы в нем строго возрастают. В противном случае, если индексы расположены в ином порядке, это обозначение соответствует определителю, который получается из соответствующего минора перестановкой строк и столбцов.
Пример 12.1 У квадратной матрицы третьегь порядка  девять миноров первого порядка, девять миноров второго порядка и один минор третьего порядка.
девять миноров первого порядка, девять миноров второго порядка и один минор третьего порядка.
Определение 12.2. Рангом матрицы называют число, которое равно максимальному порядку среди ее ненулевых миноров.
Для ранга матрицы A используют обозначение Rg A.
Если квадратная матрица порядка n невырождена, то ее ранг равен ее порядку n: ненулевым является единственный минор максимального порядка n, совпадающий с определителем матрицы. В частности, ранг единичной матрицы E порядка n равен n.
Если квадратная матрица вырождена, то ее ранг меньше ее порядка: единственный минор максимального порядка, равного порядку матрицы, является нулевым, и в этом случае ненулевые миноры имеют меньший порядок. Ранг нулевой матрицы полагают равным нулю.
Ранг диагональной матрицы равен количеству ее ненулевых диагональных элементов.
Непосредственно из определения ранга матрицы следует, что ранг имеет следующее свойство, полностью его характеризующее.
Свойство 12.1. Если ранг матрицы равен r, то матрица имеет хотя бы один минор порядка r, не равный нулю, а все ее миноры больших порядков равны нулю.
Теорема 12.1. При транспонировании матрицы ее ранг не меняется, т.е. Rg AT = Rg A.
Если мы покажем, что при транспонировании матрицы A ее ранг r не убывает, т.е. Rg AT ≥ r, то сможем прийти к следующему заключению. Поскольку (AT)T = A, то r = Rg A ≤ Rg AT ≤ Rg(AT)T = Rg A = r, и поэтому Rg AT = r.
Итак, докажем, что Rg AT ≥ r. Согласно определению 12.2 ранга матрицы, существует ее минор порядка r, отличный от нуля. Пусть это будет минор M = j1,j2. …jki1,i2. …ik. При транспонировании строки и столбцы меняются местами. Поэтому минору M, образованному строками i1, i2, … , ir и столбцами j1, j2, …
, jr матрицы A, соответствует минор N = Nj1,j2. …jki1,i2. …ik матрицы AT, образованный строками j1, j2, … , jr и столбцами i1, i2, … , ir. Ясно, что эти миноры получаются один из другого операцией транспонирования. Согласно свойствам определителей, они равны.
Таким образом, найден минор r-го порядка в матрице AT, а именно минор N, который не равен нулю. Следовательно, Rg AT ≥ r. ►
Теорема 12.2. Ранг матрицы не меняется при элементарных преобразованиях ее строк и столбцов. #
- Строки и столбцы матриц можно рассматривать как матрицы-строки и, соответственно, матрицы-столбцы. Поэтому над ними, как и над любыми другими матрицами, можно выполнять линейные операции.Подробнее
- Среди миноров матрицы могут быть как равные нулю, так и отличные от нуля.Подробнее
- Для вычисления ранга матрицы применяют два метода: метод окаймляющих миноров и метод элементарных преобразований.Подробнее
Источник: http://angem.ru/analiticheskaya_geometriya/?lesson=12&id=54
Базисный минор и ранг матрицы. Теорема о базисном миноре
Определение 1.5.1. Минором порядка r матрицы ( ) называется определитель порядка r, все элементы которого расположены на пересечении любых r строк и r столбцов этой матрицы.
Лемма 1.5.1.Если в матрице все миноры порядка r равны нулю, то равны нулю и все миноры более высоких порядков.
Доказательство.
Запишем определитель порядка r+1 и разложим его по элементам строки. После разложения, согласно теореме 1.3.1,определитель будет представлять собой сумму произведений элементов этой строки на их алгебраические дополнения, т. е. миноры порядка r с соответствующими знаками. По условию леммы такой определитель равен нулю.
Определение 1.5.2. В матрице А минор порядка r называется базисным, если он отличен от нуля, а все миноры порядка r+1, полученные присоединением к исходному одной строки и одного столбца, равны нулю или не существуют.
Миноры r+1 порядка из определения называются окаймляющими по отношению к исходному и содержат его целиком внутри себя. Столбцы и строки, на пересечении которых расположен базисный минор, будем называть базисными столбцами и строками.
Замечание 1.5.1.Базисный минор определяется неоднозначно, однако, все базисные миноры имеют одинаковый порядок.
Определение 1.5.3. Рангом матрицы называется порядок ее базисного минора. Обозначается: rang A.
Замечание 1.5.2.Из определения ранга матрицы следует
а) для произвольной матрицы выполняется: ![]() ;
;
b) тогда и только тогда, когда все элементы матрицы равны нулю, т.е. матрица А – нулевая;
c) дляквадратной матрицы А n-го порядка rangА = n тогда и только тогда, когда .
В общем случае для вычисления ранга матрицы будем использовать следующее правило: при вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор r-го порядка , отличный от нуля, то требуется вычислить все миноры r+1 порядка, окаймляющие минор . Если они все равны нулю или не существуют, то ранг матрицы равен r. Если хотя бы один из , то с ним следует поступить также как с минором .
Пример 1.5.1. Вычислить ранги следующих матриц:
- a) b)
- Решение:
- a)
Базисным минором является минор ,и тогда, согласно определению 1.5.3, rangA=2.
b)
Базисным минором матрицы В является минор . Следовательно, rang B =3.
Как мы видим из примеров, поиск ранга матрицы приводит к вычислению некоторого, быть может, очень большого, числа миноров этой матрицы. Существует еще один способ нахождения ранга матрицы, не связанный с вычислениями миноров. Этот метод основан на предварительном упрощении матрицы при помощи элементарных преобразований.
Определение 1.5.4.
Элементарными преобразованиями над матрицей называются следующие преобразования строк (столбцов) матрицы: 1) перестановка двух строк (столбцов) местами; 2) умножение строки (столбца) на любое отличное от нуля число; 3) прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число; 4) вычеркивание нулевой строки (столбца).
Определение 1.5.5. Матрицы А и В называются эквивалентными, если В можно получить из А с помощью конечного числа элементарных преобразований.
Эквивалентные матрицы будем обозначать следующим символом: А~В.
Теорема 1.5.1. Элементарные преобразования не изменяют ранга матрицы.
Действительно, если к матрице применить элементарные преобразования 1–3, то эти же преобразования или часть из них будут совершены и над ее базисным минором.
Из свойств определителя 2, 9 и следствия к свойству 5 следует, что базисный минор, хотя численно и может поменяться, но в нуль в результате данных преобразований не обратится, т.е. ранг матрицы не изменится.
Вычеркивание нулевой строки (столбца) так же не может изменить порядка базисного минора, т.е. ранг матрицы остается прежним.
Определение 1.5.6. Говорят, что прямоугольная матрица порядка имеет диагональную форму, если элементы ( ), а все остальные элементы матрицы равны нулю.
Метод нахождения ранга матрицы при помощи элементарных преобразований состоит в следующем: для нахождения ранга матрицы нужно элементарными преобразованиями привести эту матрицу к диагональной форме и сосчитать количество единиц, стоящих в последней на главной диагонали.
Замечание 1.5.3. На практике для вычисления ранга матрицы удобно сочетать оба метода. А именно, приводя прямоугольную матрицу порядка к трапециевидной форме, вычислять миноры, используя пример 1.3.4.
Пример 1.5.2. Вычислить ранги матриц
- а) b)
- Решение:
- а)
- В результате элементарных преобразований над матрицей А получили эквивалентную ей верхнюю треугольную матрицу. Легко видеть, что
- .
- Следовательно, rang A =3.
- b)
В матрице В минор , а миноров нет. Следовательно, rangВ=2.
Пример 1.5.3. Найти ранг матрицы в зависимости от действительных значений параметра а:
- Решение.
- Элементарными преобразованиями приведем матрицу к трапециевидной (или, если получится, к треугольной) форме:
- После вычеркивания нулевой строки получается прямоугольная матрица размера , эквивалентная данной.
- Если , то имеем матрицу
- Ранг этой матрицы равен двум, так как она содержит, например, минор .
- Если , то имеем матрицу, ранг которой равен трем, так как она содержит минор .
- Таким образом, , если , и , если .
Замечание 1.5.4. Матрица в примере 1.5.3 элементарными преобразованиями приведена к ступенчатому виду
Ранг в этом случае можно также считать по количеству ненулевых строк. То есть, если , то имеем две ненулевых строки и ; если , то имеем три ненулевых строки и .
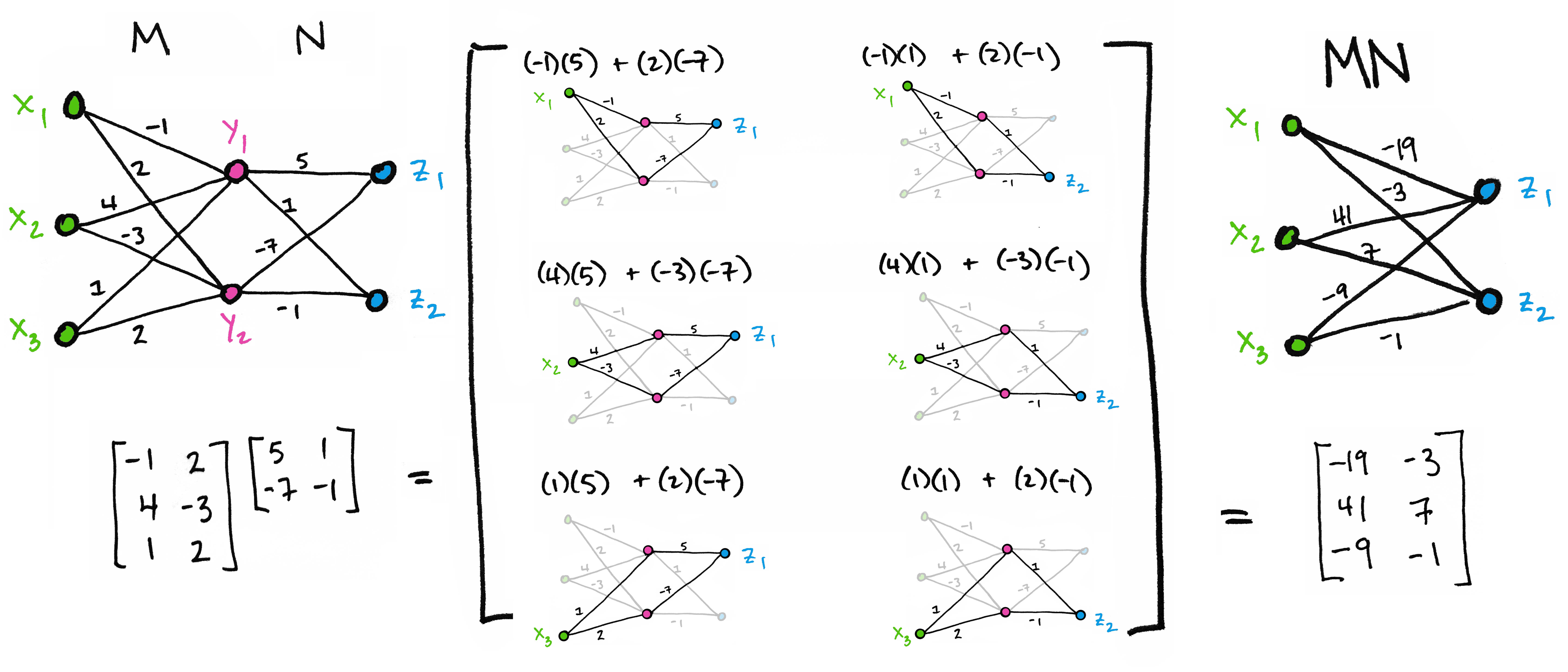
Теорема 1.5.2 (о базисном миноре). Всякая строка (столбец) матрицы А есть линейная комбинация базисных строк (столбцов) этой матрицы.
Доказательство.
Пусть ранг матрицы А равен r. Можно считать, что базисный минор расположен в левом верхнем углу матрицы. Если это не так, то заменой строк (столбцов) можно поместить этот минор в левый верхний угол. Окаймим матрицу базисного минора фрагментами i-й строки и j-го столбца матрицы A, где . Рассмотрим определитель построенной матрицы
Определитель как минор r+1 порядка в матрице с базисным миноромпорядка r. С другой стороны, раскладывая определитель по последнему столбцу (см. (1.3. )), получим:
. (1.5.1)
Здесь элемент стоит в (r+1)-й строке и (r+1)-м столбце определителя , поэтому . Так как , то разделив обе части равенства (1.5.1) на , получим: , где . А это и означает, что i-я строка является линейной комбинацией первых r базисных строк.
Источник: https://cyberpedia.su/10xec7f.html
Определение ранга матрицы
Ниже калькулятор, вычисляющий ранг матрицы. Под ним, как водится, немного теории.
3 2 -1
2 -1 5
1 7 -1
Update: Меня тут попросили сформулировать попроще, что такое ранг матрицы. Если попроще, то это максимальное число линейно-независимых строк/столбцов матрицы (число строк и число столбцов совпадает), то есть таких строк/столбцов, которые нельзя получить друг из друга элементарными преобразованиями.
- Например, у этой матрицы
3 -1 1
6 -2 2 - ранг равен 1, потому что вторая строка есть первая, умноженная на 2.
- Итак, несколько определений.
Пусть дана матрица А размеров n x m и число k, не превосходящее наименьшего из чисел m и n. Выберем произвольно k строк матрицы и k столбцов (номера строк могут отличаться от номеров столбцов).
Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных k строк и k столбцов, называется минором порядка k матрицы A .
(Что такое определитель матрицы можно посмотреть здесь Определитель (детерминант) матрицы).
Рангом матрицы А называется наибольший из порядков миноров матрицы А, отличных от нуля. Ранг нулевой матрицы считается равным нулю.
Ненулевой минор наибольшего порядка называется базисным минором. Или, что тоже самое, минор матрицы А является ее базисным минором, если он не равен нулю, и его порядок равен рангу матрицы А.
Теорема о базисном миноре
Столбцы матрицы А, входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из базисного минора.
Минор Mок матрицы А называют окаймляющим минором для минора М, если он получается из последнего добавлением одной новой строки и одного нового столбца матрицы А. Порядок окаймляющего минора Мок на единицу больше порядка минора М
Понятно, что ранг матрицы можно вычислить, перебирая все миноры, но в данном калькуляторе для вычисления ранга матрицы применяется метод окаймляющих миноров, основанный на следующей теореме.
Теорема: Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным. (А порядок, его, соответственно, равен рангу матрицы).
Метод окаймляющих миноров заключается в нахождении одного из базисных миноров матрицы и состоит в следующем:
Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы). К очередному ненулевому минору последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого сделать нельзя, то последний ненулевой минор является базисным.
Источник: https://planetcalc.ru/1952/
Линейная алгебра и аналитическая геометрия Определители Миноры Обратная матрица Ранг матрицы Теорема о базисном миноре Системы линейных уравнений Матричный. — презентация
1 Линейная алгебра и аналитическая геометрия Определители Миноры Обратная матрица Ранг матрицы Теорема о базисном миноре Системы линейных уравнений Матричный метод Метод Крамера Метод Гаусса Системы линейных однородных уравнений
2 Определение. Матрицей размера называется таблица, образованная из элементов некоторого множества и имеющая m строк и n столбцов. Элементы, из которых составлена матрица, называют элементами матрицы. Если, то матрицу называют прямоугольной, а если – квадратной порядка n. Пример: – элемент первой строки и третьего столбца a 24 – элемент второй строки и четвертого столбца a 13
3 прямоугольная, квадратная порядка n Две матрицы A и B считаются равными, если они одинакового размера, и элементы, стоящие в A и B на одинаковых местах, равны между собой, т.е. a ij =b ij.
4 1. размера матрица – столбец длины m 2. размера матрица – строка длины n 3. нулевая матрица
5 4.Условную линию в квадратной матрице порядка n, на которой расположены элементы a 11, a 22, …, a nn, называют главной диагональю этой матрицы. Условную линию в квадратной матрице порядка n, на которой расположены элементы a 1n, a 2n-1, …, a n1, называют побочной диагональю. диагональная матрица E = единичная матрица
6 5. треугольные матрицы 6. трапециевидная матрица
7 7. Прямоугольную матрицу размера будем называть ступенчатой, если первый ненулевой элемент каждой строки находится правее первого ненулевого элемента предыдущей строки. – ступенчатая – не ступенчатая
8 Определение. Произведением матрицы A=(a ij ) на число называется такая матрица B=(b ij ), элементы которой равны произведениям соответствующих элементов матрицы A на число, т.е.. Определение.
Суммой двух матриц A=(a ij ) и B=(b ij ) одинакового размера называется такая матрица C=(c ij ), элементы которой равны суммам соответ- ствующих элементов матриц A и B, т.е.
(-1)A– противоположная матрице A-A-A
9
10 . Определение. Пусть A и B – матрица-строка и матрица-столбец одинаковой длины. Произведением матрицы-строки A на матрицу-столбец B называется число с, (т.е. матрица ), равное сумме произведений их соответствующих элементов: Определение.
Пусть A – матрица размера, B – матрица размера (т.е. количество столбцов в матрице A совпадает с количеством строк в матрице B).
Произведением матрицы A на матрицу B называется матрица С размера такая, что каждый её элемент c ij является произведением i-той строки матрицы A на j-тый столбец матрицы B:
11 Матрицы A и B, для которых AB=BA, называют перестановочными AE= EA=A AO=OA= O
12 Определение. Пусть A – матрица размера. Матрица размера, полученная из A заменой каждой ее строки столбцом с тем же номером, называется транспонированной к A. Операция нахождения матрицы A T называется транспонированием матрицы A (AT)T=(AT)T= A (A+B)T=(A+B)T=AT+BTAT+BT
13 Факториал натурального числа n: n!n! 0!=1 Расположение n чисел 1, 2, 3, …, n в любом порядке называется перестановкой этих чисел.
Пусть дана некоторая перестановка чисел 1, 2, 3, …, n: Количество пар, образующих инверсию в переста- новке, называется числом инверсий в перестановке.
Говорят, что два числа и образуют инверсию в перестановке, если большее число стоит левее меньшего, т.е. если.
14 Определение. Пусть A – квадратная матрица порядка n.
Определителем матрицы A (определителем порядка n) называется сумма n! членов, составлен- ных следующим образом: членами определителя служат всевозможные произведения n элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы, причём произведение берется со знаком «плюс», если число инверсий в перестановке первых индексов сомножителей и число инверсий в перестановке вторых индексов сомножителей в сумме дают четное число, в противном случае – со знаком «минус».
15
16 Определение. Пусть A – квадратная матрица порядка n.
Определителем матрицы A (определителем порядка n) называется сумма n! членов, составленных следующим образом: членами опреде- лителя служат всевозможные произведения n элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы, причём произведение берется со знаком «плюс», если число инверсий в перестановке первых индексов сомножителей и число инверсий в перестановке вторых индексов сомножителей в сумме дают четное число, в противном случае – со знаком «минус».
17 Правило треугольников:
18 Если все элементы k-той строки определителя |A| являются суммами двух элементов, то определи- тель равен сумме двух определителей |A 1 | и |A 2 |, у которых все строки кроме k-той совпадают со стро- ками |A|, а k-тая строка в определителе |A 1 | состоит из первых слагаемых, а в определителе |A 2 | – из вторых слагаемых. 1.При транспонировании матрицы ее определитель не меняется. 2.При перестановке любых двух строк (столбцов) определитель меняет знак. 3. Общий множитель элементов любой строки (столбца) можно выносить за знак определителя. 4.
19 5.Определитель равен нулю если: а) он имеет строку (столбец), состоящую из нулей; б) он имеет хотя бы две одинаковые строки (столбца); в) он имеет хотя бы две пропорциональные (т.е.
отличающиеся множителем) строки (столбца); г) хотя бы одна строка (столбец) является линейной комбинацией нескольких других строк (столбцов). Определение.
Если некоторая строка (столбец) может быть представлена в виде суммы других k строк, умноженных соответственно на числа, то будем говорить, что данная строка (столбец) является линейной комбинацией указанных строк (столбцов).
20 6. Определитель не изменится, если к каждому элементу i-й строки (столбца) прибавить соответ- ствующий элемент k-й строки (столбца), умножен- ный на число Если A и B – квадратные матрицы порядка n, то
21 Пусть A – матрица размера k – некоторое число, Определение. Выберем в матрице A произвольно k строк и k столбцов. Из элементов, стоящих на пересечении выбранных строк и столбцов, составим определитель M k. Этот определитель называют минором k-го порядка матрицы A (ее определителя).
22 Определение. Пусть A – квадратная матрица порядка n. Выберем в A минор k-го порядка M k (выберем строки с номерами i 1,i 2,…,i k и столбцы с номерами j 1, j 2,…, j k ).
Вычеркнем из матрицы A строки и столбцы, из элементов которых состоит минор M k. Определитель M k *, составленный из оставшихся элементов, называется дополнитель- ным минором к минору M k. Число называют алгебраическим дополнением минора M k.
a ij M ij – дополнительный минор(порядок n-1) A ij – алгебраическое дополнение:
23 Теорема (Лапласа). Пусть в определителе порядка n выбрано k строк (столбцов) (где ).
Тогда определитель равен сумме произведений всех мино- ров k-го порядка, содержащихся в выбранных стро- ках (столбцах), на их алгебраические дополнения. Следствие (теоремы Лапласа).
Определитель равен сумме произведений всех элементов любой строки (столбца) на их алгебраические дополнения, т.е. |A||A| |A||A| (разложение определителя по i-той строке и j-тому столбцу соответственно)
24 = –102
25 Определение. Обратной к матрице А называется матрица, обозначаемая А -1, такая, что Если А имеет обратную, то 1. А – квадратная. 2. Обратная матрица единственная. 3. Определитель матрицы А отличен от нуля.
26 Теорема. Пусть А – квадратная матрица порядка n. Матрица A имеет обратную тогда и только тогда, когда ее определитель |A| отличен от нуля. Причем обратная матрица A -1 может быть найдена по формуле: где S – матрица из алгебраических дополнений элементов матрицы A, т.е.
27 Определение. Рангом матрицы называют макси- мальный порядок ее миноров, отличных от нуля. Базисным минором матрицы называют её отлич- ный от нуля минор, порядок которого равен рангу матрицы. Строки и столбцы, на пересечении которых стоят элементы базисного минора, называются базис- ными.
28 Определение. Элементарными преобразованиями матрицы называются преобразования следующего вида: 1. умножение некоторой строки (столбца) на ненулевое число; 2. прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произволь- ное число; 3.перестановка двух строк (столбцов); 4. вычеркивание нулевой строки (столбца).
29 Определение. Матрица В называется эквивалентной матрице А, если она может быть получена из А эле- ментарными преобразованиями. Теорема (об инвариантности ранга матрицы отно- сительно элементарных преобразований).
Ранг мат- рицы инвариантен относительно элементарных пре- образований (эквивалентные матрицы имеют равные ранги).
1) с помощью элементарных преобразований строк получаем для матрицы А эквивалентную матрицу В, имеющую ступенчатый вид; 2) находим в матрице В базисный минор и определя- ем ранг матрицы В и, следовательно, матрицы А.
30 r(A) = 2 – базисный минор Пример
31 Определение. Строки (столбцы ) S 1, S 2, …, S k называют линейно зависимыми, если существуют числа α 1, α 2, …, α k, не все равные нулю одновременно, такие, что линейная комбинация α 1 S 1 + α 2 S 2 + … + α k S k = 0 (нулевой матрице).
Если же равенство α 1 S 1 + α 2 S 2 + … + α k S k = 0 возможно только при условии α 1 = α 2 = … = α k = 0, то строки (столбцы) S 1, S 2, …, S k называют линейно независимыми.
S 1, S 2, …, S k – строки (столбцы) матрицы А α 1, α 2, …, α k – некоторые числа α 1 S 1 + α 2 S 2 + … + α k S k – линейная комбинация S1S1 S2S2 S3S3 S4S4 = = ( 000)0 = O S 1, S 2, S 4 – линейно зависимы
32 Лемма (о линейной зависимости). Строки (столбцы) S 1, S 2, …, S k линейно зависимы тогда и только тогда, когда хотя бы одна из них является линейной комбинацией других. Теорема (о базисном миноре). 1.
Базисные строки (столбцы) матрицы линейно независимы. 2. Любая строка (столбец) матрицы является линейной комбинацией базисных строк (столбцов). Следствие (критерий равенства нулю определи- теля).
Определитель матрицы A равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.
33 Линейное уравнение – числа. – коэффициенты уравнения b – свободный член Если, то уравнение называют однородным. Если, то уравнение называют неоднородным.
34 Система m линейных уравнений с n неизвестными, т.е. система вида Тогда система принимает вид: AX = B (*)
35 Упорядоченный набор чисел c 1, c 2, …, c n называется решением системы (*), если он обращает в тож- дество каждое уравнение системы. – решение системы
36 Теорема (Кронекера – Капелли). Система линейных уравнений (*) совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы, т.е.
Теорема (критерий единственности решения).
Система линейных уравнений (*) имеет единствен- ное решение тогда и только тогда, когда ранг матри- цы системы равен рангу ее расширенной матрицы и равен числу переменных, т.е.
37 1) Матричный метод Пусть m = n и. Системы такого вида называются невырожденными. 1. решение единственно. 2.по теореме об обратной матрице А имеет обратную.
38 2) Метод Крамера Теорема (Крамера). Если в системе линейных урав- нений число уравнений m и число неизвестных n совпадает и, то система совместна и имеет единственное решение, которое может быть найдено по формулам где, а – определитель, получаемый из определителя заменой его i-го столбца на столбец свободных членов.
39 Пример
40 Определение. Элементарными преобразованиями системы линейных уравнений называются преобра- зования следующего вида: 1. умножение обеих частей уравнения на ненулевое число; 2.
прибавление к одному уравнению другого, умноженного на произвольное число; 3.перестановка двух уравнений; 4. вычеркивание одного из двух пропорциональ- ных или одинаковых уравнений. Определение.
Две системы называются эквивалент- ными (равносильными), если их решения совпадают.
41 Схема метода Гаусса. Прямой ход 1. Элементарными преобразованиями приводим систему к эквивалентной системе, имеющей расширенную матрицу ступенчатого вида. 2.
Выясняем, будет ли система совместна, сравнивая ранги основной и расширенной матриц полученной системы. 3. Выбираем в основной матрице полученной системы базисный минор треугольного вида. 4.
Переносим в правую часть системы слагаемые с неизвестными, коэффициенты которых не вошли в базисный минор.
42 Обратный ход 5. Начиная с последнего уравнения (в обратном порядке) выражаем все зависимые переменные через свободные.
Система, в которой зависимые пере- менные выражены через свободные, называется общим решением системы. 6.
Придавая свободным переменным конкретные числовые значения, получаем бесконечно много решений исходной системы. Каждое из этих решений называют частным решением системы.
43 1. 2. система совместна – общее решение
44 (**), т.е. система совместна– решение. Другие решения называют нетривиальными. Это решение называют нулевым или тривиальным. Теорема (критерий существования нетривиальных решений). Система линейных однородных уравнений обладает нетривиальным решением тогда и только тогда, когда ранг её основной матрицы меньше числа неизвестных, то есть.
45 С 1, С 2, …, С k – матрицы-столбцы, являющиеся решениями системы (**) α 1, α 2, …, α k – некоторые числа α 1 С 1 + α 2 С 2 + … + α k С k – линейная комбинация Теорема (свойство решений системы линейных однородных уравнений). Любая линейная комби- нация конечного числа решений системы (**) является решением этой системы.
46 Теорема (существования фундаментальной системы решений). Пусть r – ранг матрицы системы (**). Если система имеет нетривиальные решения, то найдутся n – r линейно независимых решений таких, что любое другое её решение будет их линейной комбинацией.
Эти решения называются фундаментальной системой решений системы (**). 1.Находим общее решение системы. 2. Записываем любой отличный от нуля определитель порядка n – r. 3.
Записываем n – r решений системы, беря в качестве значений для свободных неизвестных элементы строк поочередно.
47 – общее решение 1) 3) 2) (1, 0, 1, 0, 0), (– 1, 1, 0, 1, 0), (2, 0, 0, 0, 1) – фундаментальная система решений
48 Пусть система АХ = В совместна и r(A) < n. Установим связь между решениями системы АХ = В и соответствующей ей системы АХ = 0. Теорема 1. Сумма любого решения линейной неодно- родной системы и любого решения соответствующей ей однородной системы является решением неодно- родной системы.
Теорема 2. Разность двух произвольных решений ли- нейной неоднородной системы является решением соответствующей однородной системы. Теорема 3. Общее решение линейной неоднородной системы равно сумме любого частного решения этой системы и общего решения соответствующей одно- родной системы.
Источник: http://www.myshared.ru/slide/102262/