Уравнение пропорции и его решение

Чтобы узнать название темы урока, обратите внимание на картинку.

Попробуйте отгадать ребус.

На этом уроке вы узнаете, что называют пропорцией, выведете основное свойство пропорции и с помощью него научитесь решать задачи и уравнения.

Слово «пропорция» (proportio) в переводе с латинского — соразмерность, отношение частей (соотношение).

В IV веке до н.э. древнегреческий математик Евдокс Книдский дал определение пропорции, состоящей из величин любой природы, а не только из натуральных величин.

• Пропорции применяли с древности при решении различных задач.
• Древние греки использовали пропорцию и ее свойство для строительства сооружений, при создании произведений искусства (скульптуры, статуи), в ремесленническом деле и др.
• Соблюдение пропорций, определенных соотношений, активно используется и в настоящее время в архитектуре, искусстве, музыке, при решении физических задач.
• В географии и моделировании пропорциональные зависимости применяют при создании уменьшенной копии реального объекта.
• В швейных технологиях — для изменения размеров выкройки изделия до нужного размера.
• В химии для проведения успешной реакции рассчитывают пропорциональное отношение химических веществ.
• В медицине и фармацевтике используют пропорции при изготовлении лекарственных препаратов.
• В кулинарии, например, с помощью пропорции можно рассчитать рецепт одного и того же блюда для разного количества гостей.

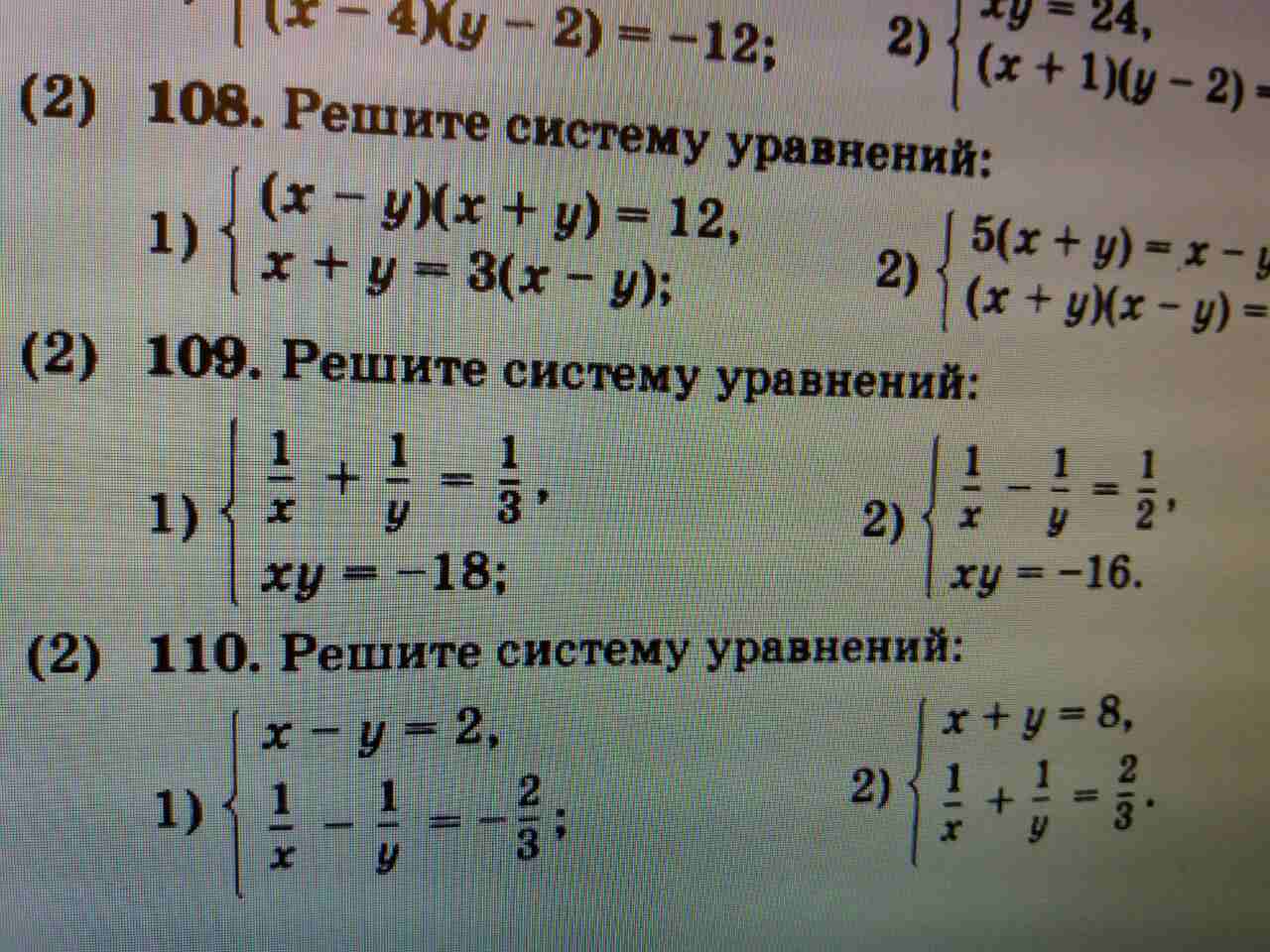
1. Разберем, что же такое пропорция в математическом понимании.
2. Возьмем два отношения: (mathbf{frac{36}{9}}) и (mathbf{frac{12}{3}}) и эти отношения равны, так как (mathbf{36div9=4}) и (mathbf{12div3=4}), значит (mathbf{frac{36}{9}= frac{12}{3}})
3. Равенство двух отношений называют пропорцией.

• С помощью букв запишем пропорцию из двух отношений так: (mathbf{adiv b= cdiv d }) или (mathbf{frac{a}{b}= frac{c}{d}}).
• Эту математическую запись читают так: «Отношение a к b равно отношению c к d» или «a так относится к b, как c относится к d».
• Все члены пропорции не равны нулю: (mathbf{a
  eq 0, b
  eq 0, c
  eq 0, d
  eq 0}).
• Если внимательно посмотреть на пропорцию (mathbf{{a}div{b}= {c}div{d}}), то можно заметить будто величины a и d стоят по краям равенства, а величины b и c в середине пропорции, в связи с этим легко запомнить, что:
• Числа a и d называют крайними членами пропорции.
• Числа b и c называют средними членами пропорции.

У меня есть дополнительная информация к этой части урока!

Закрыть

В мире существует «золотая пропорция», которую называют «золотым сечением». Это пропорциональное деление отрезка на различные по размеру части, но в таком соотношении к друг другу, что меньший отрезок так относится к большему, как больший ко всей величине.

1. Приблизительное значение «золотого сечения» равно 1,618… Число это продолжается бесконечно после запятой, и оно не периодично.
2. В процентном выражении целая часть относится к большей, как большая к меньшей, примерно так: 62% и 38% соответственно.
3. Обозначают число «золотого сечения» математической буквой (mathbf{varphi}) (фи).

Мир живой и неживой природы, мир творений человека полон красоты, симметрии и гармонии. Этот мир описывается законом «золотого сечения».

• Рассмотрим только несколько примеров, где присутствует и используется правило «золотого сечения».
• Считается, что длина фаланг пальцев и длина кисти руки, средний палец и мизинец, или высота лица и расстояние от кончика подбородка до центральной точки соединения губ у пропорционального человека находятся в определенных отношениях, соответствуя правилу «золотого сечения».
• Форма тела ящериц, стрекоз, бабочек соответствует закону «золотого сечения»: отношение грудной и брюшной части тела приближенно равны значению «золотого сечения».
• Спиралевидная форма ракушек тоже описывается числом (mathbf{varphi}) (фи).

«Золотая пропорция» была обнаружена в египетских пирамидах, произведениях искусства, архитектуре и применяется до сих пор в разных областях жизни человека

Теория отношений и пропорции изложена в «Началах» древнегреческого математика Эвклида (3 век до н.э.), в этом же труде было подробно описано и доказано основное свойство пропорции.

1. Давайте рассмотрим, какими же свойствами обладает пропорция и каким правилам подчиняется.
2. Пропорция, в которой произведение крайних членов равно произведению средних членов, является верной пропорцией.
3. Обратное утверждение так же является истинным.
4. Если произведение крайних членов равно произведению средних членов, то пропорция верна.
5. Данное свойство пропорции — это основное свойство пропорции.
6. Найдем произведение крайних членов пропорции (mathbf{adiv b= cdiv d }) и произведение средних членов этой пропорции, получим: (mathbf{acdot d= ccdot b }).

• Пример
• Дана пропорция (mathbf{frac{3}{5}= frac{6}{10}}), где числа 3, 10 — это крайние члены этой пропорции, 5, 6 — это средние члены пропорции.
• По основному свойству пропорции
• (mathbf{3cdot 10= 5cdot 6 = 30 }), значит пропорция (mathbf{frac{3}{5}= frac{6}{10}}) верная.
• Если в верной пропорции поменять местами средние члены или крайние члены, то получатся новые верные пропорции.
• Дополнительный материал
• Пропорция обладает рядом других интересных свойств.
• Так как члены пропорции отличны от нуля, то справедливо следующее: если в пропорции перевернуть отношения, то в результате получится тоже верная пропорция.
• (mathbf{frac{a}{b}= frac{c}{d}})перевернем отношения и получим (mathbf{frac{b}{a}= frac{d}{c}})
• Пример
• (mathbf{frac{12}{2}= frac{6}{1}})  перевернем отношения и получим (mathbf{frac{2}{12}= frac{1}{6}})  , проверим полученное равенство.
• По основному свойству пропорции (mathbf{2cdot 6= 12cdot 1 = 12 })
• Новая пропорция (mathbf{frac{2}{12}= frac{1}{6}}) является верной.
• При решении задач иногда используют правило увеличения и уменьшения пропорции.
• Если есть пропорция (mathbf{frac{a}{b}= frac{c}{d}}), то равенство сохранится в следующих случаях:
• Увеличение пропорции: (mathbf{frac{a + b}{b}= frac{c + d}{d}}),
• Уменьшение пропорции: (mathbf{frac{a — b}{b}= frac{c — d}{d}}).
• Пропорция обладает еще одним свойством: нахождение пропорции сложением или вычитанием членов пропорции.
• Если есть пропорция (mathbf{frac{a}{b}= frac{c}{d}}), то справедливо
• составление пропорции сложением (mathbf{frac{a + c}{b + d}= frac{a}{b} = frac{c}{d}})
• составление пропорции вычитанием (mathbf{frac{a — c}{b — d}= frac{a}{b} = frac{c}{d}})

1. Применяя основное свойство пропорции, можно найти неизвестный член этой пропорции.
2. Решить пропорцию — это значит найти средний или крайний член пропорции.
3. Для решения пропорции с неизвестным крайним членом, при условии, что все остальные члены пропорции определены, необходимо умножить средние члены пропорции и полученный результат разделить на известный крайний член пропорции.
4. Пример 1
5. (mathbf{frac{a}{2}= frac{6}{1}})
6. решите пропорцию, найдя значение крайнего члена пропорции (a).
7. (mathbf{a = frac{2 cdot 6}{1}= 12})
8. Подставьте значение крайнего члена (а) в пропорцию
9. (mathbf{frac{12}{2} = frac{6}{1}= 6}) получили верную пропорцию.
10. Для решения пропорции с неизвестным средним членом, при условии, что все остальные члены пропорции определены, необходимо умножить крайние члены пропорции и полученный результат разделить на известный средний член пропорции.
11. Пример 2
12. (mathbf{frac{12}{b}= frac{6}{1}}) решим пропорцию, найдем значение среднего члена пропорции (b)
13. (mathbf{b = frac{12 cdot 1}{6}= 2})
14. Подставим значение среднего члена (b) в пропорцию
15. (mathbf{frac{12}{2} = frac{6}{1}= 6})  получили верную пропорцию.

Часто для решения пропорции используют способ «крест-накрест».

Чтобы вычислить неизвестный член пропорции, нужно перемножить известные члены пропорции, находящиеся на диагональной линии, а затем разделить результат на оставшееся известное число, находящееся на диагональной линии с неизвестным членом пропорции.

• Пример 3
• (mathbf{frac{8}{2}= frac{x}{8}}) , где x— неизвестный член пропорции,
• (mathbf{8 cdot 8 = 64}) перемножили известные значения членов пропорции, находящиеся по диагонали в этой пропорции.
• Полученный результат делим на известный член, находящийся по диагонали с неизвестным.
• (mathbf{x = 64 div 2 = 32})
• Получили пропорцию (mathbf{frac{8}{2} = frac{32}{8}= 4}), пропорция верна

1. К решению пропорции сводятся многие математические задачи и уравнения.
2. Рассмотрим некоторые из них.
3. Задача 1
4. Решите уравнение (mathbf{frac{y}{1,5}= frac{4}{3}})
5. Решение:
6. Найдем неизвестный член пропорции y, применив основное свойство пропорции.
7. Составим уравнение и решим его
8. (mathbf{3 cdot y = 1,5 cdot 4})
9. (mathbf{y = frac{1,5 cdot 4}{3}})
10. (mathbf{y = frac{6}{3}})
11. (mathbf{y = 2})
12. Ответ: (mathbf{y = 2})
13. Задача 2
14. На товар была сделана скидка 150 рублей, что составляет 15% от первоначальной цены товара.
15. Чему равна первоначальная цена товара?
16. Решение:
17. В задачах на проценты целое принимают за 100% или 1.
18. Неизвестную величину обозначают буквой (чаще всего x или y).
19. Величины в задаче должны быть приведены в одинаковые единицы измерения.
20. Модель решения задач с процентами при помощи пропорции можно представить в виде таблицы:

Или с помощью логической схемы

В результате пропорция получается такого вида:

• Исходя из вышеизложенного, решение задачи будет выглядеть так:
• Пусть x (рублей) — первоначальная цена товара, она составляет 100%.
• Часть от целого (первоначальной цены) = 15%
• Составим условную запись задачи:
• x (руб.) — 100%
• 150 (руб.) — 15%
• Составим пропорцию:(mathbf{frac{x}{150}= frac{100}{15}})
• По основному свойству пропорции решим уравнение.
• (mathbf{x = frac{150 cdot 100}{15}})

(mathbf{x = 1000 (руб.)}) первоначальная цена товара.

Ответ: (mathbf{x = 1000 (руб.)})

Задача 3

За 5 кг Муки заплатили 195 рублей. Какова стоимость 3 кг этой муки?

1. Решение:
2. Пусть x (рублей)- стоимость 3 кг муки.
3. Составим условную запись задачи.
4. 5 (кг)- 195 (руб)
5. 3 (кг)- x (руб)
6. Составим пропорцию: (mathbf{frac{5}{3}= frac{195}{x}})
7. По основному свойству пропорции решим уравнение:
8. (mathbf{x = frac{3 cdot 195}{5}})

(mathbf{x = 117 (руб.)})  стоят 3 кг муки.

Ответ: (mathbf{x = 117 (руб)})

Пройти тест

Пройти тест и получить оценку можно после входа или регистрации

Источник: https://ladle.ru/education/matematika/6class/proporcii

Решение уравнений с пропорцией

Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию. Например, рассмотрим такое уравнение.

Для решения уравнения с пропорцией используют правило пропорции или, как его называют по-другому, правило креста.

Подробно понятие пропорции мы рассматривали в уроке «Пропорции». В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.

Правило пропорции или правило креста

Запомните!

Произведение крайних членов пропорции равно произведению средних.

По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции, то произведения членов пропорции, которые лежат на концах креста, равны .

Вернемся к нашему уравнению. Решим его, использую правило пропорции. Нарисуем поверх пропорции крест.

Теперь по правилу пропорции (правило креста) запишем пропорцию в виде равенства произведений крайних и средних членов пропорции.

Вспомним правило деления и решим уравнение до конца. В ответе не забудем выделить целую часть у дроби.

Рассмотрим другой пример уравнения с пропорцией.

Такое уравнение также решается с помощью правила пропорции.

Важно!

Если в члене пропорции присутствуют знаки «+» или «−», обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.

Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда будете использовать правило пропорции.

После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции для дальнейшего решения.

Теперь раскроем скобки с помощью правила раскрытия скобок.

Из урока «Решение линейных уравнений» используем правило переноса и правило деления для уравнений.

Не забудем при делении на отрицательное число, использовать правило знаков.

Иногда уравнения с пропорцией могут быть представлены следующим образом:

Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение, в общем для пропорции виде.

Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.

• = 18 · x = 6 · 3x 18x = 18x 18x − 18x = 0 0 = 0 Ответ: x — любое число
• = 3x · 6,8 = 0,21 · 1,7
  • 20,4 x=
  • 20
  • x =
  • x =
  • x =
  • x =
  • x =

  · x = = 204x · 1000 = 21 · 17 · 10         |:(204 · 1000) Ответ: x =

Источник: http://math-prosto.ru/?page=pages/linear_equations/solving_equations_with_proportions.php

Решение уравнения с использованием свойства пропорции — «Шпаргалка ЕГЭ»

Решите уравнение:

Данный урок показывает, как применив свойство пропорции: при перемножении крест-накрест двух дробей или если числитель одной дроби умножить на знаменатель другой дроби, а знаменатель первой дроби на числитель второй, то получим верное равенство: 

Указывается необходимость при таком решении определения области допустимых решений уравнения: знаменатели обеих дробей не должны равняться нулю. Для получения окончательного ответа используется раскрытие скобок и приведения подобных слагаемых.

Решение данной задачи рекомендовано для учащихся 7-х классов при изучении тем «Разложение многочленов на множители» («Алгебраические дроби. Сокращение алгебраических дробей», «Тождества») и «Одночлены.

При подготовке к ОГЭ урок рекомендован при повторении тем «Одночлены. Арифметические операции над одночленами», «Квадратичная функция. Функция y=k/x».

• Светлана Иванова К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
  Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
• Влад Долгорукий Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
• Александр Шпик Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.

Источник: http://ShpargalkaEGE.ru/tasks-gia/diagnosticheskaya-rabota-po-matematike-v-formate-gia-9-klass-4/

Задачи и задания на пропорции

• Решение заданий на пропорции
• Задачи на пропорции с решением

Если один из членов пропорции неизвестен и надо его найти, то говорят, что надо решить пропорцию. Решение пропорций всегда выполняется с помощью свойства пропорции.

Задание 1. Найдите неизвестный член пропорции:

a)	x	=	3	;     б)	1	=	5
2	1	3	x

Решение: Так как неизвестны крайние члены пропорции, то для их нахождения надо умножить средние члены и разделить полученный результат на известный крайний член:

a) x =	2 · 3	,   x = 6.	б) x =	3 · 5	,   x = 15.
1	1

Ответ: а) x = 6, б) x = 15.

Задание 2. Решите пропорции:

a)	30	=	5	;     б)	7	=	x
x	8	5	10

Решение: Так как неизвестны средние члены пропорции, то для их нахождения надо умножить крайние члены и разделить полученный результат на известный средний член:

a) x =	30 · 8	,   x = 48.	б) x =	7 · 10	,   x = 14.
5	5

Ответ: а) x = 48, б) x = 14.

Задание 3. Известно, что 21x = 14y. Найдите отношение x к y.

• Решение: сначала сократим обе части равенства на общий множитель 7:
• получим:
• 3x = 2y
• Теперь разделим обе части на 3y, чтобы в левой части у x убрать множитель 3, а в правой части избавиться от y:
• После сокращения отношений у нас остаётся:
• Ответ: 2 к 3.

Задача 1. Из 300 читателей библиотеки 108 человек – студенты. Какой процент всех читателей составляют студенты?

1. Решение: Примем всех читателей библиотеки за 100% и запишем условие задачи кратко:
2. 300 – 100% 108 – ?%
3. Составим пропорцию:
4. Найдём x:
5. Ответ: 36% всех читателей составляют студенты.

Задача 2. При варке варенья используют ягоды и сахар в отношении 5:2. Сколько надо ягод, если взяли 450 грамм сахара?

• Решение: составим пропорцию:
• Найдём x:
• Ответ: На 450 гр сахара надо взять 1125 гр ягод.

Источник: https://naobumium.info/arifmetika/zadachi_na_proportsii.php

Урок математики "Пропорция. Решение уравнений"

• МБОУ «Большеатнинская СОШ»
• Атнинского муниципального района Республики Татарстан
• Разработка урока математики
• по теме «Пропорция. Решение
• уравнений» (6 класс)
• 2014 год
• План конспект урока математики в 6 классе

Тема: «Пропорция. Решение уравнений.»

1. Цель: формировать навык нахождения неизвестных членов пропорции, решения уравнений, имеющих вид пропорции;
2. закрепить основное свойство пропорции на практике: при решении задач и при решении уравнений;
3. воспитывать умение оценивать объективно труд своих товарищей.

Тип урока: урок повторения изученного материала..

• Вид урока: комбинированный.
• Оборудование: учебник, интерактивная доска.
• Ход урока:

1.Организационный момент.

1. Посмотрите, всё ль в порядке:
2. Книжка, ручки и тетрадки.
3. Прозвенел сейчас звонок.
4. Начинается урок.

2. Устный счет.

Тейк офф – тач даун (встает тот, кто знает ответ на заданный вопрос)

1. У стола квадратной формы отпилили 1 угол. Сколько углов осталось? (5)

2. Сколько концов у трех с половиной палок? (8)

3. Врач прописал 5 уколов. Через полчаса — по уколу. Через сколько часов после первого укола будет сделан последний укол? (2ч.)

4. На столе горят 7 свечей, 3 свечи потушили. Сколько свечей останется на столе через 5-6 часов? (3)

5. Назовите взаимно обратные числа.(3/5 и 5/3; 2,5 и 2,5)

6. Найдите 10% от 500; 40% от 300; 50% от 600; 100% от 520.

3. Актуализация знаний.

• 1) Найдите отношения:
• А) 12кг к 400г; (30)
• Б) 40м к 2 км; (0,02)

Какой вывод можно сделать? (Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения).

2) Как называется равенство двух отношений? (пропорция)

4. Сообщение темы урока.

Континиус Раунд Робин (учитель задает вопрос и дает время подумать; четыре ученика в команде по очереди отвечают по кругу до того момента, пока учитель не остановит процесс).

Подумайте, что вы знаете про пропорции? (анализ ответов учащихся)

Сегодня на уроке продолжим работу над темой «Пропорция». Ребята, как вы думаете изученная нами тема «Пропорция» понадобится вам в жизни? Почему и где?

16 : 2 =8; 12 : 1,5 = 8;

Что вы можете сказать про эти записи? (Равенство двух отношении называется пропорцией).

Как называются 16 и 1,5? (крайние члены пропорции).

Как называются 2 и 12? (средние члены пропорции).

Как определить пропорция верна или неверна? (основное свойство пропорции).

Как найти неизвестный крайний член пропорции?

Как найти неизвестный средний член пропорции?

Что произойдет, если поменять местами крайние или средние члены пропорции? (получившиеся новые пропорции тоже верны).

5. Закрепление. Работа в тетрадях.

Задача: Настоящие охотники за приведениями получили новое оборудование – ультрасовременные ловушки. Две такие ловушки захватывают за один раз 18 приведений. Сколько ловушек надо взять на операцию, чтобы отловить одновременно 27 приведений?

2л – 18приведении

Хл — 27приведении

Составляем пропорцию и решаем её. Ответ: 3 ловушки.

Задача 2. Решение уравнений.

№777 (решить уравнения) используя структуру Финк — Райт – Раунд Робин (учитель задает вопрос и дает время подумать; ученики думают и записывают ответы на свой листочек; ученики по очереди зачитывают свой ответ с листочка).

Пришло время ответить на вопрос, заданный в начале урока.

Ребята, как вы думаете изученная нами тема «Пропорция» понадобится вам в жизни? Почему и где? Для ответов мы используем структуру Таймд Пэа Шэа (учитель задает вопрос и дает время подумать; учитель озвучивает, кто начинает первым и сколько времени дается каждому из учеников для ответа; два ученика отвечают на вопрос по очереди в течение данного времени).

6.Домашнее задание №798(составить пропорцию), №799 (при каком значении х верна пропорция) на стр.131.

7. Самостоятельная работа. Выполнение теста по теме «Пропорция» (ваши тесты будут служит билетиками на выход).

8. Подведение итогов урока.

1. Как связаны между собой понятия «отношение» и «пропорция»?
2. Что называют отношение двух чисел?
3. Как называется равенство двух отношений?
4. Что называется пропорцией?
5. Каким свойством обладает пропорция?

Источник: https://videouroki.net/razrabotki/urok-matematiki-proportsiya-reshenie-uravneniy.html

Решение уравнений с использованием основного свойства пропорции

Урок №44

Тема: Решение уравнений с использованием основного свойства пропорции.

Цель: Сформировать понимание правил нахождения неизвестного среднего и крайнего членов пропорции путём составления логической цепочки решения уравнений; отработать умение практического использования составленных алгоритмов решения уравнений на основе свойств пропорции. Развивать логическое мышление, вычислительные навычки, внимание, познавательный интерес к теме. Формировать информационную, социальную, коммуникативную компетентность. Воспитывать трудолюбие, активность, наблюдательность, любознательность, творческое отношение к учебному труду.
Тип урока: Применение знаний и умений.
Оборудование и наглядность: презентация, мультимедийный проектор,

компьютер, экран, карточки, оценочный лист.

Ход урока

І. Организационный момент.

• Сегодня мы ребята совершим путешествие в мир пропорций, гармонии и красоты.
• Что вы ожидаете от сегодняшнего урока?
• Эпиграфом к нашему уроку я хочу взять слова русского математика Софии Ковалевской: (СЛАЙД 1) «Среди всех наук, которые открывают путь к познанию законов природы, самой великой является математика».
• — Какие вопросы у вас возникли при выполнении домашнего задания?

ІІ. Мотивация учебной деятельности.

На прошлом уроке мы изучили содержание понятия «пропорция» и «основное свойство пропорции», а сегодня на уроке мы научимся решать уравнения применяя основное свойство пропорции.

ІІІ. Актуализация опорных знаний.

— Говорят «Математика» — гимнастика для ума», а что такое гимнастика? Это система упражнений для физического развития человека. Гимнаст — человек ловкий, сильный, стройный. Математика развивает ум, закаляет характер. Наш урок мы начнём с разминки.

1. У каждого есть оценочный лист, где вы будете себе выставлять балы за каждый правильный ответ.
2. (СЛАЙД 2)
3. Станция «Теоретическая»

1. Какое действие скрывается за словом «отношение»?.
2. Верно ли, что обыкновенная дробь – это отношение его числителя к знаменателю?
3. Сформулируйте основное свойство отношения.
4. Что такое пропорция?
5. Как называются элементы x и y в пропорции х : а = b : y?
6. Как называются элементы b и c в пропорции a : b = c : d ?
7. Сформулируйте основное свойство пропорции.

(СЛАЙД 3)

Станция «Практическая»

а) 20 к 4; б) 15 к 30; в) 1,2 к 4; г) 0,9 к 0,3; д) к а) 10 : 2 и 15 : 3; б) 30 : 3 и 45 : 5; в) 1 : 3 = 0,5 : 1,5

1. Является ли верной пропорцией равенство:

а) 3 : 4 = 9 :12; б) = ; в) 60 : 3 = 40 : 2;

• г) 0,5 : 10 = 1 : 20
• ІV. Изучение нового материала

• Запишите дату, классная робота
• Дать определение уравнения.

Цель нашего урока: научиться решать уравнения имеющие вид пропорции.

• Основное свойство пропорции используют при решении уравнений, имеющих вид пропорции. Любой член пропорции можно определить, если известны три других её числа.

а) =

1. Какой член пропорции неизвестен?
2. А как бы вы нашли неизвестный крайний член пропорции?
3. 7 • х = 21• 5
4. А можно ли это записать по-другому, чтобы упростить вычисления?
5. х =
6. х = 3 • 5
7. х = 15
8. Ответ: 15

• Давайте попробуем составить правило нахождения крайнего члена пропорции.

(СЛАЙД 4)

Определение 1. Чтобы найти неизвестный крайний член пропорции, нужно произведение её средних членов разделить на известный крайний член.

х =
б) =

• Какой член пропорции неизвестен?
• А как бы вы нашли неизвестный средний член пропорции?
  х =
• х = 3 • 3
• х = 9
• Ответ : 9
• (СЛАЙД 5)
• Определение 2. Чтобы найти неизвестный средний член пропорции, нужно произведение её крайних членов разделить на известный средний член пропорции

— Давайте попробуем составить правило нахождения неизвестного среднего члена пропорции.

= ; х =

• давайте найдём в учебнике эти правила. Работа с учеником над правилом стр. 128 . Учащиеся два раза читают каждое правило и повторяют хором.

V. Применение знаний, умений. Решение уравнений. Работа с учебником, стр.131.
№672 (б,в)
б) = в) =
№674 (а,г)
а) = 7 г) 8 =
(СЛАЙД 6)

1. Физминутка
2. Дружно встал 6-Б класс – это «раз»
3. Повернулась голова – это «два»
4. И глазами покрути – это «три»
5. Свои плечи развернули на «четыре»
6. Пальцы надо нам размять – это «пять»
7. Всем ребятам надо сесть- это «шесть».
   №677 (а,б)
   б) =
8. №678 (в)
9. в) =
   Найти неизвестный член пропорции:
10. а) 12 : х = 0,4 : 1,8 б) 7 : 1 = 3,6 : х г) : = : х

(СЛАЙД 7)

• Станция «Историческая»
• Мир пропорций огромен и разнообразен.

1. Пропорции начали изучать ещё в древности. Слово «пропорция» ввёл в употребление Цицерон (древнеримский политик и философ) в І веке до н.э. Само слово «пропорция» означает «соразмерность», определённое соотношение частей между собой.
2. В IV веке до н.э. древнегреческий математик Евдокс дал определение пропорции.

Очень интересная история записи пропорции.

1. В 1631 году Вильям Оутред, английский математик предложил следующую запись пропорции.

а • b : : c • d

1. Рене Декарт, французский математик, философ, физик, физиолог в XVII веке записал пропорцию так:

1. В 1693 году Лейбниц, немецкий философ, логик, математик, физик, юрист, историк, дипломат, изобретатель, языковед предложил современную запись пропорции.

a : b = c : d VІ. Закрепление знаний. Выполнение самостоятельной работы.
а) 7 : 8 = х : 96; б) = ; в) = ;

(СЛАЙД 8)

Ответы: а) 84; б) 2; в) 3 .

(СЛАЙД 9)

VІІ. Применение пропорции.

— А на каких уроках вы встречались с пропорциями?

В истории и географии вы сталкиваетесь с масштабом карты. Когда начнёте изучать черчение вы увидите, что при выполнении чертежей тоже нужно соблюдать масштаб, значит, и здесь присутствует пропорция. Химия изучает вещества, и вы будете сталкиваться с пропорциями при решении задач на концентрации растворов, тоесть процентное содержание вещества в растворе.

(СЛАЙД 1)

Станция «Познавательная»

1. Учение о пропорциях особенно успешно развивалось в ІV веке до н.э. в древней Греции, славившейся произведениями искусства, архитектуры. С пропорциями связывались представление о красоте, порядке и гармонии, о созвучных аккордах в музыке. Пропорциональность в природе, искусстве, архитектуре означает соблюдение, определённых соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.
2. Первым ввёл термин «золотое сечение» итальянский художник, великий учёный и гений Леонардо до Винчи.

(СЛАЙД 11, 12, пентаграмма)

1. «Золотым сечением» и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина отрезка так относится к длине его большей части, как длина большей части к меньшей и это отношение равно 8 : 5

(СЛАЙД 13,14,15)

— «Золотое сечение чаще всего применяется в произведениях искусства, архитектуры, законах природы.

(СЛАЙД 16)

1. Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев третья расположена в месте «золотого сечения».

(СЛАЙД 17)

— «Золотое сечение» в элементах одежды».

IX. Домашнее задание.

1. (СЛАЙД 18)
2. Выучить § 19 (определения).
3. Выполнить: №673 (б,г); №674 (б,в) – средний уровень.
4. №677 (в,г); №682 – достаточный уровень.
5. №678 (б,г); №683 – высокий уровень.

Творческое задание. Привести примеры применения пропорции на кухне.

X. Подведение итогов урока.

• Используя приём «Рефлексия» учитель задаёт вопросы учащимся.
• — Что нового мы выучили на уроке?
• — Для чего мы это делали?
• — Достигли вы ожидаемых результатов?
• — Что было для вас интересным?
• — Что для вас было трудным?

— Понравилась ли вам форма проведения урока?

Источник: http://mognovse.ru/edn-reshenie-uravnenij-s-ispolezovaniem-osnovnogo-svojstva-pro.html