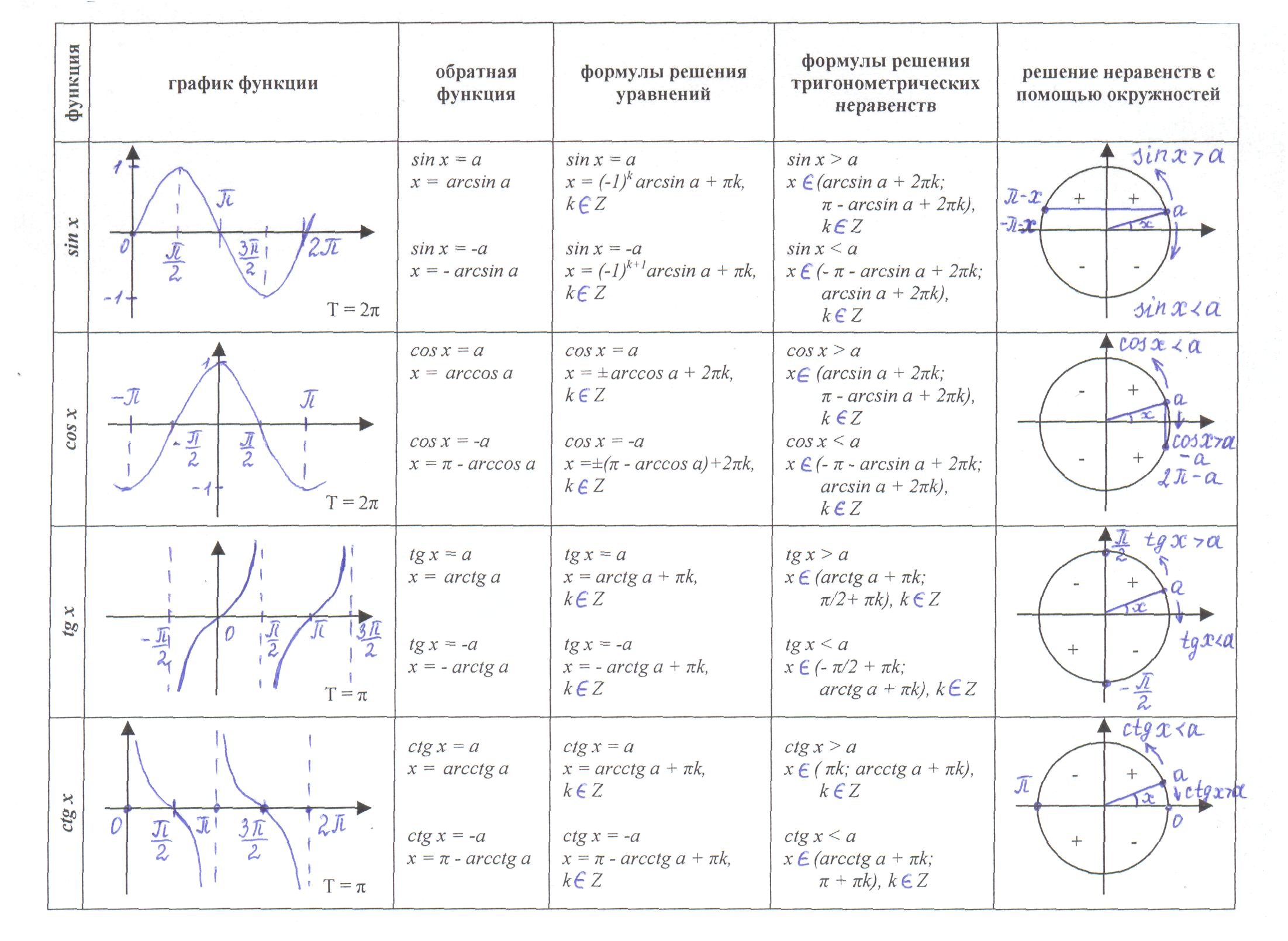
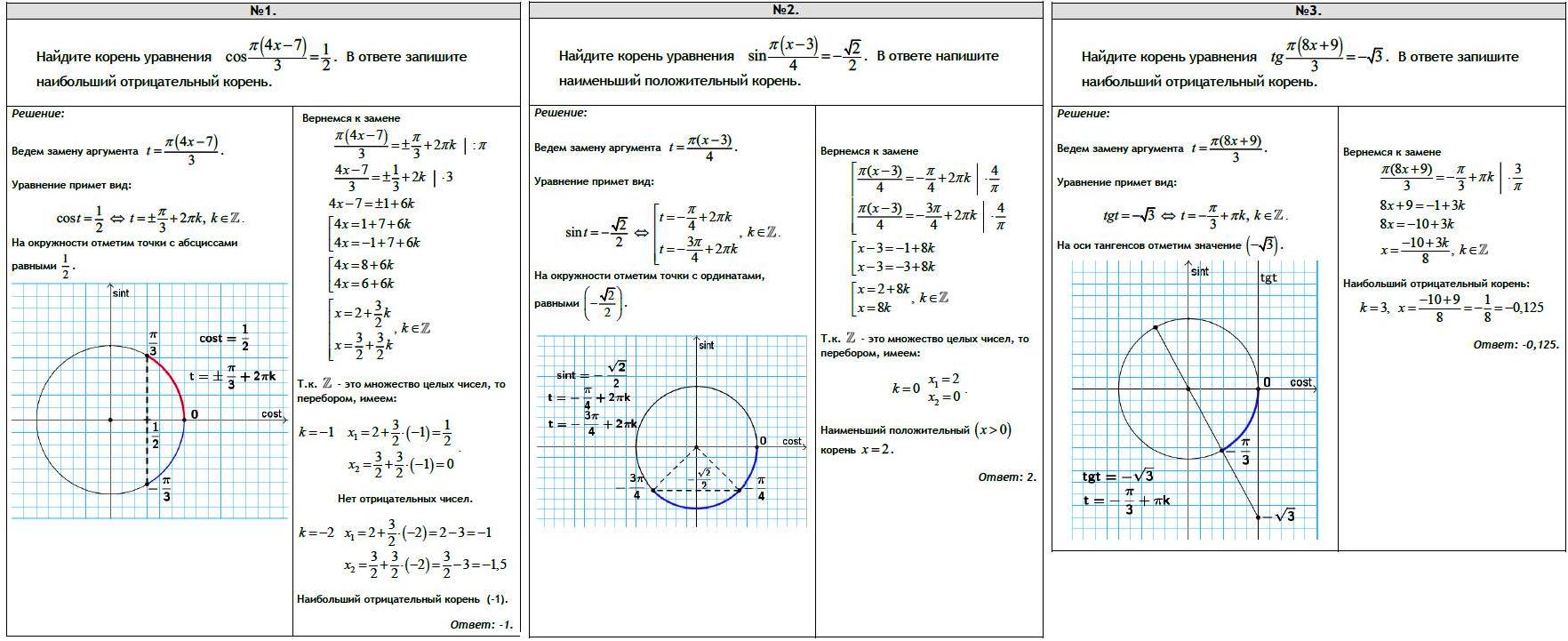
Тригонометрические уравнения, примеры решений

Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим. 

Простейшие тригонометрические уравнения.

 

Методы решения тригонометрических уравнений

Решение тригонометрического уравнения состоит из двух этапов:  преобразование уравнения для получения его простейшего вида ( см. выше ) и  решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения  тригонометрических уравнений.

1. Алгебраический метод. 

Этот метод нам хорошо известен из алгебры

( метод замены переменной и подстановки ).

2. Разложение на множители. 

Этот метод рассмотрим на примерах.

    П р и м е р  1.  Решить уравнение:  sin x + cos x = 1 .

•     Р е ш е н и е .   Перенесём все члены уравнения влево:
•                                                                sin x + cos x – 1 = 0 ,
•                                преобразуем и разложим на множители выражение в
•                                левой части уравнения:

    П р и м е р   2.   Решить уравнение:  cos 2 x + sin x · cos x = 1.

1.     Р е ш е н и е .     cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,
2.                                             sin x · cos x – sin 2 x = 0 ,
3.                                             sin x · ( cos x – sin x ) = 0 ,

    П р и м е р   3.   Решить уравнение:  cos 2x – cos 8x + cos 6x = 1. 

•      Р е ш е н и е .    cos 2x + cos 6x = 1 + cos 8x ,
•                                2 cos 4x cos 2x = 2 cos ² 4x ,
•                                cos 4x · ( cos 2x –  cos 4x ) = 0 ,
•                                cos 4x · 2 sin 3x · sin x = 0 ,

                              1).  cos 4x = 0 ,               2).  sin 3x = 0 ,          3). sin x = 0 ,

Уравнение называется однородным относительно  sin  и  cos, если все его члены одной и той же степени относительно sin  и cos  одного и того же угла. Чтобы решить однородное уравнение, надо:    а)  перенести все его члены в левую часть;    б)  вынести все общие множители за скобки;    в)  приравнять все множители и скобки нулю;    г)  скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на          cos ( или sin ) в старшей степени;     д)  решить полученное алгебраическое уравнение относительно tan .      П р и м е р .   Решить уравнение:  3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.     Р е ш е н и е .  3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,                              sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,                              tan 2 x + 4 tan x + 3 = 0 ,  отсюда  y 2 + 4y +3 = 0 ,                              корни этого уравнения:  y1 = -1,  y2 = -3,  отсюда                              1)   tan x = –1,                  2)   tan x = –3,

4. Переход к половинному углу.

Рассмотрим этот метод на примере:

    П р и м е р .  Решить уравнение:  3 sin x – 5 cos x = 7. 

1.     Р е ш е н и е .  6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
2.                                                                          = 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
3.                              2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
4.                              tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

                                     .   .   .   .   .   .   .   .   .   .

5. Введение вспомогательного угла.

• Рассмотрим уравнение вида:
•                                            a sin x + b cos x = c ,
•     где  a, b, c – коэффициенты;  x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение принимает вид:

 

6. Преобразование произведения в сумму

Здесь используются соответствующие формулы.

    П р и м е р .  Решить уравнение:  2 sin x · sin 3x = cos 4x.

1.     Р е ш е н и е .  Преобразуем левую часть в сумму:
2.                                         cos 4x – cos 8x = cos 4x ,
3.                                                  cos 8x = 0 ,
4.                                                  8x = p / 2 + pk ,
5.                                                  x = p / 16 + pk / 8 .

7. Универсальная подстановка.

Рассмотрим этот метод на примере.

      П р и м е р .   Решить уравнение:  3 sin x – 4 cos x = 3 .

•                              Таким образом, решение даёт только первый случай.

Источник: https://www.sites.google.com/site/trigonometriavneskoly/metody-resenia-trigonometriceskih-uravnenij

Алгебра – 10 класс. Тригонометрические уравнения

Что будем изучать:

1. Что такое тригонометрические уравнения?
2. Простейшие тригонометрические уравнения.
3. Два основных метода решения тригонометрических уравнений.
4. Однородные тригонометрические уравнения.
5. Примеры.

Что такое тригонометрические уравнения?

Ребята, мы с вами изучили уже арксинуса, арккосинус, арктангенс и арккотангенс. Теперь давайте посмотрим на тригонометрические уравнения в общем.

Тригонометрические уравнения – уравнения в котором переменная содержится под знаком тригонометрической функции. Повторим вид решения простейших тригонометрических уравнений: 1)Если |а|≤ 1, то уравнение cos(x) = a имеет решение: x= ± arccos(a) + 2πk 2) Если |а|≤ 1, то уравнение sin(x) = a имеет решение:

3) Если |а| > 1, то уравнение sin(x) = a и cos(x) = a не имеют решений
4) Уравнение tg(x)=a имеет решение: x=arctg(a)+ πk 5) Уравнение ctg(x)=a имеет решение: x=arcctg(a)+ πk Для всех формул k- целое число

Простейшие тригонометрические уравнения имеют вид: Т(kx+m)=a, T- какая либо тригонометрическая функция

Пример. Решить уравнения: а) sin(3x)= √3/2 Решение: а) Обозначим 3x=t, тогда наше уравнение перепишем в виде: sin(t)=1/2. Решение этого уравнения будет: t=((-1)^n)arcsin(√3 /2)+ πn.

Из таблицы значений получаем: t=((-1)^n)×π/3+ πn. Вернемся к нашей переменной: 3x =((-1)^n)×π/3+ πn, тогда x= ((-1)^n)×π/9+ πn/3 Ответ: x= ((-1)^n)×π/9+ πn/3, где n-целое число.

(-1)^n – минус один в степени n.

Ещё примеры тригонометрических уравнений

Решить уравнения: а) cos(x/5)=1 б)tg(3x- π/3)= √3 Решение: а) В этот раз перейдем непосредственно к вычислению корней уравнения сразу:
x/5= ± arccos(1) + 2πk. Тогда x/5= πk => x=5πk Ответ: x=5πk, где k – целое число. б) Запишем в виде: 3x- π/3=arctg(√3)+ πk.

Мы знаем что: arctg(√3)= π/3 3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3 Ответ: x=2π/9 + πk/3, где k – целое число. Решить уравнения: cos(4x)= √2/2. И найти все корни на отрезке [0; π].

Решение: Решим в общем виде наше уравнение: 4x= ± arccos(√2/2) + 2πk 4x= ± π/4 + 2πk; x= ± π/16+ πk/2;

Теперь давайте посмотрим какие корни попадут на наш отрезок. При k
При k=0, x= π/16, мы попали в заданный отрезок [0; π].
При к=1, x= π/16+ π/2=9π/16, опять попали.

При k=2, x= π/16+ π=17π/16, а тут вот уже не попали, а значит при больших k тоже заведомо не будем попадать. Ответ: x= π/16, x= 9π/16

Два основных метода решения

Мы рассмотрели простейшие тригонометрические уравнения, но существуют и более сложные. Для их решения применяют метод ввода новой переменной и метод разложения на множители. Давайте рассмотрим примеры. Решим уравнение:

Решение:
Для решения нашего уравнения воспользуемся методом ввода новой переменной, обозначим: t=tg(x).

В результате замены получим: t2 + 2t -1 = 0

Найдем корни квадратного уравнения: t=-1 и t=1/3 Тогда tg(x)=-1 и tg(x)=1/3, получили простейшее тригонометрическое уравнение, найдем его корни. x=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk. Ответ: x= -π/4+πk; x=arctg(1/3) + πk.

Пример решения уравнения

• Решить уравнений: 2sin2(x) + 3 cos(x) = 0
• Воспользуемся тождеством: sin2(x) + cos2(x)=1
• Наше уравнение примет вид:2-2cos2(x) + 3 cos (x) = 0
• 2 cos2(x) — 3 cos(x) -2 = 0
• введем замену t=cos(x): 2t2 -3t — 2 = 0

Решение:

Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2 Тогда cos(x)=2 и cos(x)=-1/2. Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней. Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk Ответ: x= ±2π/3 + 2πk

Однородные тригонометрические уравнения

Определение: Уравнение вида a sin(x)+b cos(x) называются однородными тригонометрическими уравнениями первой степени. Уравнения вида
однородными тригонометрическими уравнениями второй степени.

Пусть cos(x)=0, тогда asin(x)+0=0 => sin(x)=0, но синус и косинус одновременно не равны нулю, получили противоречие, поэтому можно смело делить на ноль.

Решить уравнение:

Пример: cos2(x) + sin(x) cos(x) = 0 Решение: Вынесем общий множитель: cos(x)(c0s(x) + sin (x)) = 0 Тогда нам надо решить два уравнения: cos(x)=0 и cos(x)+sin(x)=0 cos(x)=0 при x= π/2 + πk; Рассмотрим уравнение cos(x)+sin(x)=0 Разделим наше уравнение на cos(x): 1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk Ответ: x= π/2 + πk и x= -π/4+πk

Однородные тригонометрические уравнения второй степени

Как решать однородные тригонометрические уравнения второй степени?
Ребята, придерживайтесь этих правил всегда! 1. Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде 2. Если a≠0, то нужно поделить обе части уравнения на косинус в квадрате, получим:

Делаем замену переменной t=tg(x) получаем уравнение:

Решить пример №:3

Решить уравнение: Разделим обе части уравнения на косинус квадрат:
Делаем замену переменной t=tg(x): t2 + 2 t — 3 = 0 Найдем корни квадратного уравнения: t=-3 и t=1 Тогда: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk tg(x)=1 => x= π/4+ πk Ответ: x=-arctg(3) + πk и x= π/4+ πk

Решить пример №:4

Решить уравнение:

Решение:
Преобразуем наше выражение:

Решать такие уравнение мы умеем: x= — π/4 + 2πk и x=5π/4 + 2πk

Ответ: x= — π/4 + 2πk и x=5π/4 + 2πk

Решить пример №:5

Решить уравнение:

Решение:
Преобразуем наше выражение:

Введем замену tg(2x)=t:22 — 5t + 2 = 0 Решением нашего квадратного уравнения будут корни: t=-2 и t=1/2 Тогда получаем: tg(2x)=-2 и tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2 2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2 Ответ: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2

Задачи для самостоятельного решения

1) Решить уравнение а) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 д) ctg(0.5x) = -1.7 2) Решить уравнения: sin(3x)= √3/2. И найти все корни на отрезке [π/2; π ].

1. 3) Решить уравнение: ctg2(x) + 2ctg(x) + 1 =0
2. 4) Решить уравнение: 3 sin 2(x) + √3sin (x) cos(x) = 0
3. 5) Решить уравнение:3sin2(3x) + 10 sin(3x)cos(3x) + 3 cos2(3x) =0
4. 6)Решить уравнение:cos2(2x) -1 — cos(x) =√3/2 -sin2(2x)

Источник: https://mathematics-tests.com/10-klass-urok-na-temu-trigonometricheskie-uravneniya

Методы решения сложных тригонометрических уравнений

Методы решения сложных

тригонометрических уравнений

І тип. Двучленные уравнения. Уравнения, содержащие две тригонометрические функции с коэффициентами 1.

Пример 1.

Решение

или

• Ответ: ;
• Пример 2.
• Решение

1. Ответ: ; .

ІІ тип. Многочленные тригонометрические уравнения. Все функции содержащиеся в этом уравнении, переносят в левую часть и полученный тригонометрический многочлен раскладываю на множители.

• Если многочлен уравнения содержит четную степень, то формулам понижают степень и превращают в произведение.
• Если тригонометрический многочлен содержит функции таким образом, что этот многочлен будет стандартного вида, то применяют метод подстановки.
• 1)
• 2)

ІІІ тип. Однородные тригонометрические уравнения.

1. 1) (уравнение І степени)
2. 2) (уравнение ІІ степени)
3. 3) ( уравнение ІІІ степени)
4. Эти уравнения решаются делением этого уравнения на старшую степень
5. или .
6. 1) /: ,
7. 2)
8. 3)
9. Пример 1.
10. Решение
11. Пусть тогда
12. Ответ:
13. Пример 2.
14. Решение
15. Это уравнение можно свести к однородному третьего порядка относительно или если заменить
16. Получим
17. Разделили обе части уравнения на получим
18. Пусть
19. Легко проверить, что является корнем этого уравнения.
20. Поэтому
21. или
22. корней нет.
23. Ответ:

ІV тип. Линейные неоднородные тригонометрические уравнения.

• 1) если то делим на
• 2) если тогда применяем метод универсальной подстановки
• и так далее.
• 3) если то неоднородное уравнение приводим к однородному второй степени с помощью тригонометрической единицы.

V тип. Уравнения, содержащие тригонометрические дроби.

Находим ОДЗ ( т.к. знаменатель 0). Либо приводим к общему знаменателю, либо применяем метод подстановки.

1. Пример 1.
2. Решение
3. ОДЗ:
4. Пусть , тогда
5. Это уравнение упростим, обозначив тогда
6. Тогда
7. корней нет
8. Ответ:

VІ тип. Иррациональные тригонометрические уравнения.

• Содержание тригонометрические функции под знаком радикала.
• Указать ОДЗ.
• Пример 1. Решить уравнение
• Решение
• при любых
• Сделав замену получим иррациональное уравнение
• которое равносильно системе
• Поэтому неравенству системы удовлетворяет только
• Значит .
• Ответ:

VІІ тип. Функциональные.

1. В качестве аргументов используются другие функции.
2. Пример 1.
3. или
4. при при
5. Ответ: где при
6. где при
7. Пример 2.
8. Решение
9. Так как то
10. Пусть
11. или

т.к. то не удовлетворяет

• условию
• Подставив вместо t его значение
• Ответ:

VІІІ тип. Уравнения, в которых в качестве коэффициента число перед или, то делают числовую подстановку или .

1. Пример.1 Решить уравнение
2. Решение
3. или
4. Ответ:
5. ІX тип. Уравнения вида
6. решаются с помощью замены или
7. 1) 2)
8. Пример 1. Решить уравнение
9. Решение
10. Пусть
11. Тогда,
12. корней нет.
13. Ответ:
14. Метод оценок при решении тригонометрических уравнений
15. Некоторые тригонометрические уравнения удается решить, используя неравенства: верны для всех
16. Пример 1. Решить уравнение
17. Решение
18. Поскольку и то причем
19. равенство здесь имеет место тогда и только тога, корда одновременно выполняются равенства и Значит исходное уравнение равносильно системе:
20. Изобразим эти решения соответствующими точками единичной окружности
21. ( решения первого уравнения , решение второго уравнения – точки помеченные крестиком *).
22. *
23. Число х будет решением системы тогда и только тогда, когда оно является решением обоих уравнений системы. Из рисунка видно, что такими числами являются числа
24. Ответ:
25. Пример 2. Решить уравнение
26. Решение
27. Воспользуемся формулой
28. и , значит
29. Равенство возможно при и Значит данное неравенство равно системе:
30. Решениями системы являются те и только те значения для которых при некоторых и выполняются равенства Найдем целые и , для которых Сократив на получим, что но это равенство возможно только при и Таким образом система, а значит , и исходное уравнение имеют единственное решение
31. Ответ:
32. Пример 3. Решить уравнение
33. Решение
34. или
35. , данное уравнение равносильно
36. Решения первого уравнения , решение второго уравнения – точки помеченные крестиком *.
37. Ответ:
38. Использование области определения функции при решении уравнений.
39. К «функциональным» методам решения тригонометрических уравнений и неравенств относится применение основных свойств тригонометрических функций.

Иногда знание областей определения функций, входящих в уравнение или неравенство, дает возможность показать, что уравнение или неравенство не имеет решений. Иногда знание ОДЗ позволяет найти решения уравнения или неравенства непосредственной подстановкой чисел из ОДЗ.

• Решить уравнение:
• Решение
• ОДЗ этого уравнения состоит из всех , удовлетворяющих условиям:
• ОДЗ:
• Подставляя эти значения в уравнение, получаем, что его правая и левая части равны нулю, а это означает, что все являются его решением.
• Ответ:
• Тригонометрические уравнение типа
• Решение таких уравнений сводится к группировке, последующему разложению правой части уравнения на множители и переходу к решению эквивалентной совокупности простейших уравнений.
• Пример 1.
• Решение
• ОДЗ:
• или или
• В общем случае предположим, что серия решений содержит параметр
• а серия решений — параметр Чтобы выяснить, содержится ли одна из этих серий в другой, нужно приравнять эти решения и найти зависимость от
• Если эта зависимость линейна и то серия решений содержится в серии решения Если хотя бы один из коэффициентов ( или ) не целый, то нужно найти зависимость от Если эта зависимость имеет вид где то серия решений содержится в серии решений При условии, что либо либо не целое, серии решений и не содержат одно другое.
• Выясним, не содержатся ли какие – либо из полученных серий решений в других:
• 1) следовательно решение содержится в
• решении поэтому исключают из решения.
• 2) что невозможно
• при
• Ответ:
• Пример 2.
• Решение
• или
• или
• Сравним полученные решения
• Следовательно серия решения содержится в серии решений
• что невозможно при
• Ответ:
• Пример 3.
• Решение
• или
• Сравним решения
• Серия не содержится в серии
• Значит и серия не содержится в серии
• Ответ:

Источник: https://vseosvita.ua/library/metody-resenia-sloznyh-trigonometriceskih-uravnenij-75991.html

Тригонометрические уравнения 1

В этой статье будут рассмотрены тригонометрические уравнения с корнями. Прежде чем приступить к решению, вспомним, когда появляется опасность потерять корни или приобрести посторонние. Итак:

• При решении тригонометрических уравнений могут появиться посторонние корни, если:
• 1)      Уравнение содержит тангенс или котангенс;
• 2)      Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;
• 3)      Обе части уравнения возводятся в квадрат.
• При решении тригонометрических уравнений могут быть потеряны корни, если:
• 1)      Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;
• 2)      Используются тригонометрические формулы, которые справедливы не при всех значениях неизвестного;
• 3)      При решении системы тригонометрических уравнений для обозначения целого числа в найденных значениях x и y используется только одна буква.
• Теперь можно начать решение.
• Задача 1. Решить уравнение:
• Возводим обе части уравнения в квадрат:

Сгруппируем слагаемые:

Видим, что в первой скобке – квадрат суммы:

Приравниваем к нулю каждый множитель и решаем два получившихся уравнения:

1. При возведении в квадрат:

Заметим, что по решению синус и косинус равны по модулю, но разные по знаку. В этом варианте решения в исходном уравнении слева под корнем окажется величина отрицательная, значит, это – посторонние корни, поэтому мы даже не будем их записывать. Приобрели мы посторонние корни в результате возведения уравнения  квадрат.

• Второе:
• Возводим в квадрат:
• Снова уравнение распалось на два:
• – это посторонний корень, который приведет к появлению в исходном уравнении корня из отрицательного числа в правой части.

или  – данный корень тоже содержит посторонние корни, которые также приобретены в результате возведения уравнения в квадрат. При синусе, равном нулю, косинус может быть равен как 1, так и (-1). Второе – недопустимо: в этом случае в правой части исходного уравнения – отрицательное число под корнем. Поэтому решение у уравнения всего одно: .

1. Задача 2. Решить уравнение:
2. Возводим обе части уравнения в квадрат:
3. Косинус двойного аргумента заменяем, также от синуса переходим к косинусу с помощью основного тригонометрического тождества:
4. Вводим замену:
5. Корни:
6. Обратная замена:
7. или
8. Решения:
9. Проверка показывает, что все корни удовлетворяют исходному уравнению.
10. Задача 3. Решить уравнение:
11. Чтобы избавиться от корня, возведем в квадрат:
12. Домножим на 2 для удобства:
13. Произведем перегруппировку:
14. или
15. Первое:
16. При возведении в квадрат:
17. Так как правая часть уравнения должна быть неотрицательной, и, кроме того, синус и косинус – разных знаков, то решение одно:
18. Второе:
19. Так как решения уравнения не являются решениями исходного уравнения, то деление на не приведет к потере корней, тогда разделим на :

Решением этого уравнения является угол, синус и косинус которого имеют разные знаки. При этом угол в четвертом квадранте нам не подойдет: у такого угла отрицательный синус и положительный косинус, а это противоречит исходному уравнению: приведет к отрицательному значению операции извлечения корня. Угол во втором квадранте нас устроит.

• Ответ: ,
• Задача 4. Решить уравнение:
• Сразу делаем вывод, что полученный нами далее в ходе решения должен быть неположительным , иначе результат извлечения корня не будет положительным.
• Возводим все уравнение в квадрат, чтобы избавиться от корня:
• Раскрываем формулу двойного аргумента и заменяем синусы на косинусы:
• Получили квадратное уравнение относительно косинусов:
• или   – очевидно, что решение второго – пустое множество.
• С учетом того, что синус должен быть отрицателен (или равен нулю), решение единственное:
• Ответ: .
• Задача 5. Решить уравнение:
• Полученный в ходе решения косинус может быть или отрицательным числом, или нулем.
• Возводим уравнение в квадрат:
• Формулу тройного аргумента раскроем:
• или – сумма коэффициентов уравнения равна 0, поэтому первый корень – 1, а второй – с/a – (-1/2)
• Итак, имеем: , или , или
• Решения первого уравнения:
• Решения второго уравнения:
• – не являются решениями исходного уравнения, так как косинус должен быть отрицателен.
• Решения третьего:
• Ответ: ,
• Задача 6. Решить уравнение:
• Замечаем, что синус должен быть неотрицательным числом, так как слева – корень.
• Возводим в квадрат:
• Раскроем формулу тройного аргумента:
• Домножим на 3 для удобства:
• Приравняем к нулю оба множителя:
• или 
• Решаем теперь второе, квадратное, уравнение:
• Корни получаются такие: 2/3 и (-3/4) – последний корень не подходит по ОДЗ, так как результат извлечения корня не может быть отрицательным.
• Второму корню будет соответствовать решение:
• и , эти два решения можно объединить в одно и записать:
• Ответ: , .

Источник: https://easy-physic.ru/trigonometricheskie-uravneniya-1/

Решение однородных тригонометрических уравнений

Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-02-29

Главная » СТАТЬИ » ТРИГОНОМЕТРИЯ » Решение однородных тригонометрических уравнений

В этой статье мы рассмотрим способ решения однородных тригонометрических уравнений.

Однородные тригонометрические уравнения имеют ту же структуру, что и однородные уравнения любого другого вида. Напомню способ решения однородных уравнений второй степени:

• Отличительные признаки однородных уравнений:
• а) все одночлены имеют одинаковую степень,
• б) свободный член равен нулю,
• в) в уравнении присутствуют степени с двумя различными основаниями.
• Однородные уравнения решаются по сходному алгоритму.
• Чтобы решить уравнение такого типа, разделим обе части уравнения на  (можно разделить на  или на )

Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.

Если является, то мы выписываем этот корень, чтобы потом про него не забыть, а затем делим на это выражение.

Вообще, первым делом, при решении любого уравнения, в правой части которого стоит ноль, нужно попытаться разложить левую часть уравнения на множители любым доступным способом. А затем каждый множитель приравнять к нулю. В этом случае мы точно не потеряем корни.

1. Сократим числитель и знаменатель второй и третьей дроби:
2. Введем замену:
3. ,
4. Получим квадратное уравнение:
5. Решим квадратное уравнение, найдем значения ,  а затем вернемся к исходному неизвестному.
6. При решении  однородных тригонометрических уравнений, нужно помнить несколько важных вещей:
7. 1. Свободный член можно преобразовать к квадрату синуса и косинуса с помощью основного тригонометрического тождества:
8. 2. Синус и косинус двойного аргумента являются одночленами второй степени —  синус двойного аргумента легко преобразовать к произведению синуса и косинуса, а косинус двойного аргумента — к квадрату синуса или косинуса:

• Рассмотрим несколько примеров решения однородных тригонометрических уравнений.
• 1. Решим уравнение:
• Это классический пример однородного тригонометрического уравнения первой степени: степень каждого одночлена равна единице, свободный член равен нулю.

Прежде чем делить  обе части уравнения на , необходимо проверить, что корни уравнения  не являются корнями исходного уравнения. Проверяем: если , то , следовательно их сумма не равна нулю.

1. Разделим обе части уравнения на .
2. Получим: 
3. , где 
4. , где 
5. Ответ: , где 
6. 2. Решим уравнение:

Это пример однородного тригонометрического уравнения второй степени. Мы помним, что если мы можем разложить левую часть уравнения на множители, то желательно это сделать. В этом уравнении мы можем вынести за скобки . Сделаем это:

• Приравняем каждый множитель к нулю:
• Решение первого уравнения: , где 

Второе уравнение — однородное тригонометрическое уравнение первой степени. Чтобы его решить, разделим обе части уравнения на . Получим:

1. , где 
2. Ответ:  , где ,
3. , где 
4. 3. Решим уравнение:
5. Чтобы это уравнение «стало» однородным, преобразуем  в произведение, и представим число 3 в виде суммы квадратов синуса и косинуса:
6. Перенесем все слагаемые влево, раскроем скобки и приведем подобные члены. Получим:
7. Разложим левую часть на множители и приравняем каждый множитель к нулю:
8. Отсюда:
9. , где ,
10. , где 
11. Ответ: , где ,
12. , где 
13. 4. Решим уравнение:
14. Мы видим, что можем вынести за скобки . Сделаем это:
15. Приравняем каждый множитель к нулю:
16. Решение первого уравнения:
17. , где 
18. Второе уравнение совокупности представляет собой классическое однородное уравнение второй степени. Корни уравнения  не являются корнями исходного уравнения, поэтому разделим обе части уравнения на  :
19. Отсюда:
20. Решение первого уравнения:
21. , где 
22. Решение второго уравнения:
23. , где 
24. Ответ: , где ,
25. , где ,
26. , где .

И.В. Фельдман, репетитор по математике.

Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и С1»

Источник: https://ege-ok.ru/2012/02/29/reshenie-odnorodnyih-trigonometricheskih-uravneniy

Как научить решать тригонометрические уравнения и неравенства: методика преподавания

Пример задания. Найти приближенно углы, косинусы которых равны 0,8.

Решение. Косинус — это абсцисса соответствующей точки единичной окружности. Все точки с абсциссами, равными 0,8, принадлежат прямой, параллельной оси ординат и проходящей через точку C(0,8; 0). Эта прямая пересекает единичную окружность в двух точках: Pα° и Pβ°, симметричных относительно оси абсцисс.

• С помощью транспортира находим, что угол α° приближенно равен 37°. Значит, общий вид углов поворота с конечной точкой Pα°:
• α° ≈ 37° + 360°n, где n — любое целое число.
• В силу симметрии относительно оси абсцисс точка Pβ° — конечная точка поворота на угол –37°. Значит, для нее общий вид углов поворота:
• β° ≈ –37° + 360°n, где n — любое целое число.
• Ответ: 37° + 360°n, –37° + 360°n, где n— любое целое число.

Пример задания. Найти углы, синусы которых равны 0,5.

Решение. Синус — это ордината соответствующей точки единичной окружности. Все точки с ординатами, равными 0,5, принадлежат прямой, параллельной оси абсцисс и проходящей через точку D(0; 0,5).

Эта прямая пересекает единичную окружность в двух точках: Pφ и Pπ–φ, симметричных относительно оси ординат. В прямоугольном треугольнике OKPφ катет KPφ равен половине гипотенузы OPφ, значит, 

Общий вид углов поворота с конечной точкой Pφ:

где n — любое целое число. Общий вид углов поворота с конечной точкой Pπ–φ:

где n — любое целое число.

Ответ:  где n — любое целое число.

2. Тангенс и котангенс любого угла (пропедевтика к изучению тригонометрических уравнений)

Пример 2. Найти общий вид углов, тангенс которых равен –1,2.

Пример задания. Найти общий вид углов, тангенс которых равен –1,2.

Решение. Отметим на оси тангенсов точку C с ординатой, равной –1,2, и проведем прямую OC. Прямая OC пересекает единичную окружность в точках Pα° и Pβ° — концах одного и того же диаметра.

Углы, соответствующие этим точкам, отличаются друг от друга на целое число полуоборотов, т.е. на 180°n (n — целое число). С помощью транспортира находим, что угол Pα° OP0 равен –50°.

Значит, общий вид углов, тангенс которых равен –1,2, следующий: –50° + 180°n (n — целое число)

1. Ответ: –50° + 180°n, n ∈ Z.
2. По синусу и косинусу углов 30°, 45° и 60° легко найти их тангенсы и котангенсы. Например,
3. Перечисленные углы довольно часто встречаются в разных задачах, поэтому полезно запомнить значения тангенса и котангенса этих углов.

α°	30°	45°	60°
φ рад
tg φ	1
ctg φ	1

3. Простейшие тригонометрические уравнения

Вводятся обозначения: arcsin α, arccos α, arctg α, arcctg α. Не рекомендуется торопиться с введением объединенной формулы. Две серии корней значительно удобнее записывать, особенно, когда нужно отбирать корни на интервале.

tg φ = α, φ = arctg α + πn, n ∊ Z, т.е. arctg α — угол из промежутка  тангенс которого равен α, tg (arctg α) = α.

ctg φ = α, φ = arcctg α + πn, n ∊ Z, 0 < arcctg α < π, т.е. arcctg α — угол из промежутка (0; π), котангенс которого равен α, ctg (arcctg α) = α.

При изучении темы «простейшие тригонометрические уравнения», уравнения чаще всего сводятся к квадратам.

4. Формулы приведения

Формулы приведения являются тождествами, т. е. они верны для любых допустимых значений φ. Анализируя полученную таблицу, можно заметить, что:

1) знак в правой части формулы совпадает со знаком приводимой функции в соответствующей четверти, если считать φ острым углом;

2) название меняют только функции углов  и 

α	φ + 2πn	– φ	π – φ	π + φ
sin α	sin φ	– sin φ	sin φ	– sin φ
cos α	cos φ	cos φ	– cos φ	– cos φ
tg α	tg φ	– tg φ	– tg φ	tg φ
ctg α	ctg φ	– ctg φ	– ctg φ	ctg φ
α
sin α	cos φ	cos φ	– cos φ	– cos φ
cos α	sin φ	– sin φ	– sin φ	sin φ
tg α	ctg φ	– ctg φ	ctg φ	– ctg φ
ctg α	tg φ	— tg φ	tg φ	– tg φ

5. Свойства и график функции y = sin x

Простейшие тригонометрические неравенства решаются либо по графику, либо на окружности. При решении тригонометрического неравенства на окружности важно не перепутать, какую точку указывать первой.

6. Свойства и график функции y = cos x

Задачу построения графика функции y = cos x можно свести к построению графика функции y = sin x. Действительно, поскольку  график функции y = cos x можно получить из графика функции y = sin x сдвигом последнего вдоль оси абсцисс влево на

7. Свойства и графики функций y = tg x и y = ctg x

Область определения функции y = tg x включает в себя все числа, кроме чисел вида  где n ∈ Z. Как и при построении синусоиды, сначала постараемся получить график функции y = tg x на промежутке

В левом конце этого промежутка тангенс равен нулю, а при приближении к правому концу значения тангенса неограниченно увеличиваются. Графически это выглядит так, как будто график функции y = tg x прижимается к прямой  уходя вместе с ней неограниченно вверх.

8. Зависимости между тригонометрическими функциями одного и того же аргумента

Равенства  и  выражают соотношения между тригонометрическими функциями одного и того же аргумента φ. С их помощью, зная синус и косинус некоторого угла, можно найти его тангенс и котангенс. Из этих равенств легко получить, что тангенс и котангенс связаны между собой следующим равенством.

• tg φ · ctg φ = 1
• Есть и другие зависимости между тригонометрическими функциями.
• Уравнение единичной окружности с центром в начале координат x2 + y2 = 1 связывает абсциссу и ординату любой точки этой окружности.
• Основное тригонометрическое тождество
• cos2 φ + sin2 φ = 1

9. Синус и косинус суммы и разности двух углов

Формула косинуса суммы

cos (α + β) = cos α cos β – sin α sin β

Формула косинуса разности

cos (α – β) = cos α cos β + sin α sin β

Формула синуса разности

sin (α – β) = sin α cos β – cos α sin β

Формула синуса суммы

sin (α + β) = sin α cos β + cos α sin β

10. Тангенс суммы и тангенс разности двух углов

Формула тангенса суммы

Формула тангенса разности

11. Тригонометрические функции двойного угла

Формула тангенса двойного угла

1. cos2α = 1 – 2sin2α cos2α = 2cos2α – 1
2. Пример задания. Решить уравнение
3. Решение.
4. Понизим степень еще раз:
5. Ответ:

12. Преобразование произведения тригонометрических функций в сумму. Обратное преобразование

Основные формулы

Переход от суммы к произведению

Переход от произведения к сумме

13. Решение тригонометрических уравнений

В большинстве случаев исходное уравнение в процессе решения сводится к простейшим тригонометрическим уравнениям. Однако для тригонометрических уравнений не существует единого метода решения. В каждом конкретном случае успех зависит от знания тригонометрических формул и от умения выбрать из них нужные. При этом обилие различных формул иногда делает этот выбор довольно трудным.

Уравнения, сводящиеся к квадратам

• Пример задания. Решить уравнение 2 cos2x + 3 sinx = 0
• Решение. С помощью основного тригонометрического тождества это уравнение можно свести к квадратному относительно sinx:
• 2cos2x + 3sinx = 0, 2(1 – sin2x) + 3sinx = 0,
• 2 – 2sin2x + 3sinx = 0, 2sin2x – 3sinx – 2 = 0
• Введем новую переменную y = sin x, тогда уравнение примет вид: 2y2 – 3y – 2 = 0.
• Корни этого уравнения y1 = 2, y2 = –0,5.
• Возвращаемся к переменной x и получаем простейшие тригонометрические уравнения:
• 1) sin x = 2 – это уравнение не имеет корней, так как sin x < 2 при любом значении x;
• 2) sin x = –0,5, 
• Ответ:

Однородные тригонометрические уравнения

Пример задания. Решить уравнение 2sin2x – 3sinxcosx – 5cos2x = 0.

Решение. Рассмотрим два случая:

1) cosx = 0 и 2) cosx ≠ 0.

Случай 1. Если cos x = 0, то уравнение принимает вид 2sin2x = 0, откуда sinx = 0. Но это равенство не удовлетворяет условию cosx = 0, так как ни при каком x косинус и синус одновременно в нуль не обращаются.

Случай 2. Если cos x ≠ 0, то можно разделить уравнение на cos2x и получить 2tg2x – 3tgx – 5 = 0. Вводя новую переменную y = tg x, получаем квадратное уравнение 2y2 – 3y — 5 = 0.

1. Корни этого уравнения y1 = –1, y2 = 2,5.
2. Возвращаемся к переменной x.
3. tg x = 2,5,
4. x = arctg 2,5 + πn, n ∈ Z.
5. Ответ:
6. Уравнение, левая часть которого — многочлен, каждый член которого имеет вторую степень, а правая — нуль, называют однородным уравнением второй степени относительно переменных u и v.
7. Обозначив в исходном уравнении sin x буквой u, а cos x буквой v, получим уравнение вида au2 + buv + cv2 = 0.
8. Делением на v2 такое уравнение сводится к квадратному относительно

Напоминаем, что апробировать учебник «Алгебра и начало математического анализа. 10 класс», как и многие другие издания, можно на платформе LECTA. Для этого воспользуйтесь предложением «5 учеников бесплатно».

#ADVERTISING_INSERT#

Источник: https://rosuchebnik.ru/material/kak-nauchit-reshat-trigonometricheskie-uravneniya-i-neravenstva-metodi/

Решение тригонометрических уравнений. Как решить тригонометрическое уравнение

Решение тригонометрических уравнений требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие.

Для тех, кто их забыл или не знает рекомендуем прочитать статью «Основные тригонометрические формулы».
Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике.

Решение тригонометрических уравнений при правильном подходе – довольно увлекательное занятие, как, например, собрать кубик Рубика.

Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.

Рассмотрим, как решить такие тригонометрические уравнения, для наглядности будем использовать уже знакомый тригонометрический круг.

sinх = а

cos x = a

tg x = a

cot x = a

Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение. Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.

• Пример.
• Решить уравнение 2cos2 (x + /6) – 3sin( /3 – x) +1 = 0
• Используя формулы приведения получим:
• 2cos2 (x + /6) – 3cos(x + /6) +1 = 0
1. 2y2 – 3y + 1 + 0
2. Корни которого y1 = 1, y2 = 1/2
3. Теперь идем в обратном порядке

Подставляем найденные значения y и получаем два варианта ответа:

1. cos(x + /6) = 1

   x + /6 = 2 k

   x1 = — /6 + 2 k

2. cos(x + /6) = ?

   x + /6 = ±arccos 1/2 + 2 k

   x2 = ± /3 — /6+ 2 k

• Пример.
• Как решить уравнение sin x + cos x = 1 ?
• Перенесем все влево, чтобы справа остался 0:
• sin x + cos x – 1 = 0
• Воспользуемся вышерассмотренными тождествами для упрощения уравнения:
• sin x — 2 sin2 (x/2) = 0
• Делаем разложение на множители:
• 2sin(x/2) * cos(x/2) — 2 sin2 (x/2) = 0
• 2sin(x/2) * [cos(x/2) — sin(x/2)] = 0
• Получаем два уравнения
1. 2sin(x/2) = 0
   1. Это простейшее тригонометрическое уравнение, решение которого
   2. х/2 = k
   3. x1 = 2 k
2. cos(x/2) — sin(x/2) = 0
   • Это уравнение является однородным и решается третьим методом, который мы рассмотрим ниже.
   • Делим уравнение на cos(x/2) и получаем опять же простейшее тригонометрическое уравнение:
   • 1 — tg(x/2) = 0
   • tg(x/2) = 1
   • x/2 = arctg 1 + k
   • x/2 = /4+ k
   • x2 = /2+ 2 k
1. Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла. Для решения однородного уравнения, поступают следующим образом:
2. а) переносят все его члены в левую часть;
3. б) выносят все общие множители за скобки;
4. в) приравнивают все множители и скобки к 0;
5. г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;
6. д) решают полученное уравнение относительно tg.
7. Пример.
8. Решить уравнение 3sin2x + 4 sin x • cos x + 5 cos2x = 2
9. Воспользуемся формулой sin2 x + cos2 x = 1 и избавимся от открытой двойки справа:
10. 3sin2x + 4 sin x • cos x + 5 cos x = 2sin2x + 2cos2x
11. sin2x + 4 sin x • cos x + 3 cos2x = 0
12. Делим на cos x:
13. tg2x + 4 tg x + 3 = 0
14. Заменяем tg x на y и получаем квадратное уравнение:
15. y2 + 4y +3 = 0, корни которого y1=1, y2 = 3
16. Отсюда находим два решения исходного уравнения:
17. 1) tg x = –1
18. x1 = /4+ k
19. 2) tg x = –3
20. x2 = arctg 3 + k
• Пример.
• Решить уравнение 3sin x – 5cos x = 7
• Переходим к x/2:
• 6sin(x/2) * cos(x/2) – 5cos2 (x/2) + 5sin2 (x/2) = 7sin2 (x/2) + 7cos2 (x/2)
• Пререносим все влево:
• 2sin2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos2 (x/2) = 0
• Делим на cos(x/2):
• tg2 (x/2) – 3tg(x/2) + 6 = 0
• Ну а дальше уже по отработанной схеме …
1. Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,
2. где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.
3. Обе части уравнения разделим на :

Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:

• cos * sin x + sin * cos x = С
• или sin(x + ) = C
• Решением этого простейшего тригонометрического уравнения будет
• х = (-1) k * arcsin С — + k, где
• Следует отметить, что обозначения cos и sin взаимозаменяемые.
• Пример.
• Решить уравнение sin 3x – cos 3x = 1
• В этом уравнении коэффициенты:
• а = , b = -1, поэтому делим обе части на = 2
• (/2) * sin 3x – (1/2)cos 3x = 1/2
• cos( /6) * sin 3x – sin( /6) * cos 3x =1/2
• sin(3x – /6) = 1/2
• Получаем ответ
• x = (-1) k * /18 + /18 + k/3
1. Здесь мы будем просто использовать тригонометрические формулы
2. Пример.
3. Решить уравнение 2 sin x * sin 3x = cos 4x
4. Левую часть преобразуем в сумму:
5. cos 4x – cos 8x = cos 4x
6. Получаем простейшее уравнение:
7. cos 8x = 0
8. 8x = /2 + k
9. x = /16 + k/8
• Пример.
• Решить тригонометрическое уравнение 3sin x – 4cos x = 3
• Здесь возможны 2 случая:
1. x (2k + 1) ,
   тогда, воспользовавшись тригонометрическими формулами, получим:
   1. 3[(2tg(x/2))/(1 + tg2 (x/2)] — 4[(1 – tg2 (x/2))/(1 + tg2 (x/2)] = 3
   2. 6tg(x/2) – 4 + 4tg2 (x/2) = 3 + 3tg2 (x/2)
   3. tg2 (x/2) + 6tg(x/2) – 7 = 0
   4. Делаем замену tg(x/2) на y и получаем квадратное уравнение:
   5. y2 + 6y -7 = 0
   6. корни которого y1 = -7, y2 = 1
   7. Идем обратно и получаем два простейших уравнения:
   8. 1) tg(x/2) = -7
   9. х1 = -2arctg 7 + 2 k
   10. 2) tg(x/2) = 1
   11. x2 = /2 + 2k
2. x = (2k + 1) ,

   тогда 3sin[(2k +1) ] – 4cos[(2k + 1) ] = 4 3

   Получаем – решение имеет только первое условие.

Основные методы решения тригонометрических уравнений, мы рассмотрели. Если у вас остались какие либо вопросы о том, как решать тригонометрические уравнения, задавайте их в х ниже.

Будем рады любым ваших вопросам.

Заметка: собираетесь выступать http://prezentacii.com портал готовых презентаций.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Источник: https://reshit.ru/Reshenie-trigonometricheskih-uravneniy