Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Первый вопрос, который может возникнуть: описанная – вокруг чего?
Ну, вообще-то иногда бывает и вокруг чего угодно, а мы будем рассуждать об окружности, описанной вокруг (иногда ещё говорят «около») треугольника. Что же это такое?
| Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана. |
Вот так:

И вот, представь себе, имеет место удивительный факт:
| Вокруг всякого треугольника можно описать окружность. |
Почему этот факт удивительный?
Но ведь треугольники – то бывают разные!

И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта можешь найти в следующих уровнях теории, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины. Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!

А есть только для прямоугольника:

Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
| Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника. |
Знаешь ли ты, что такое серединный перпендикуляр?
 |
Это прямая, проходящая через середину отрезка и перпендикулярная ему.Прямая – это серединный перпендикуляр к отрезку . |
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке .
 |
Это и есть центр описанной около (вокруг) треугольника окружности. |
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
Вот так:

А вот если остроугольный, то – внутри:

Что же делать с прямоугольным треугольником?
| В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы. |
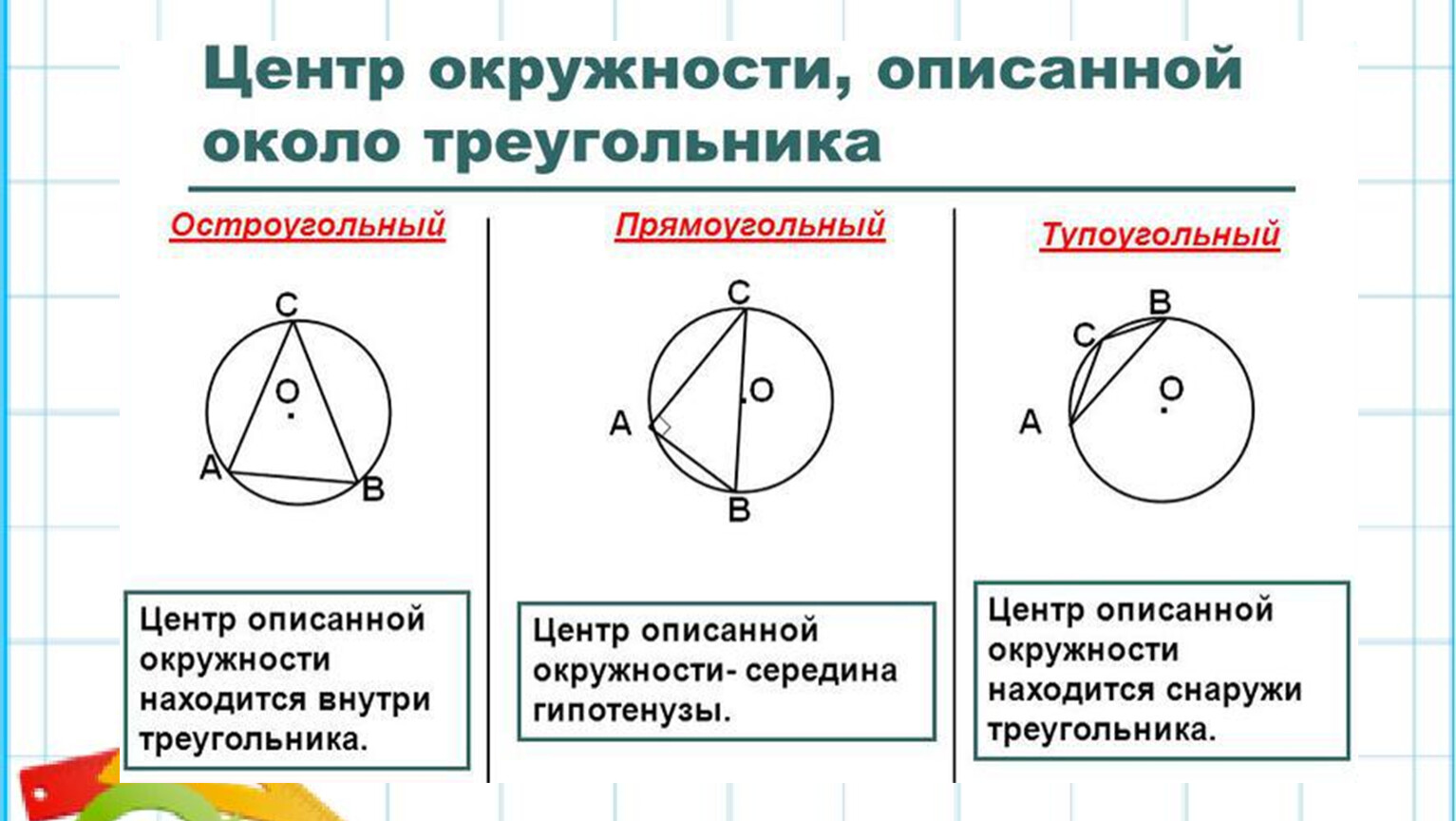 |
Правда, здорово?Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов! |
Да ещё с дополнительным бонусом:
| в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы |
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
А именно:

| В произвольном треугольнике: |
Ну и, конечно,
Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол. Хорошая формула? По-моему, просто отличная!
Описанная окружность. средний уровень
В этой части мы обсудим окружность, описанную вокруг (часто говорят «около») треугольника. Прежде всего дадим определение.
| Окружность, описанная около треугольника – такая окружность, что происходит через все три вершины этого треугольника. |
1. Существование и центр описанной окружности
Тут возникает вопрос: а для всякого ли треугольника существует такая окружность? Вот оказывается, что да, для всякого. И более того, мы сейчас сформулируем теорему, которая ещё и отвечает на вопрос, где же находится центр описанной окружности.
| Теорема.Вокруг всякого треугольника можно описать окружность, при том единственным образом. Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника. |
Смотри, вот так:
Давай наберёмся мужества и докажем эту теорему. Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
| Геометрическое место точек, обладающих свойством « » — такое множество точек, что все они обладают свойством « » и никакие другие точки этим свойством не обладают. |
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.
А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.
В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
| Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка. |
Тут множество – это серединный перпендикуляр, а свойство « » — это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
- Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
- Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему.
| Проверим 1. Пусть точка лежит на серединном перпендикуляре к отрезку . |
Соединим с и с .Тогда линия является медианой и высотой в . Значит, – равнобедренный, – убедились, что любая точка , лежащая на серединном перпендикуляре, одинаково удалена от точек и .
| Теперь 2. Почти точно так же, но в другую сторону. Пусть точка равноудалена от точек и , то есть . |
Возьмём – середину и соединим и . Получилась медиана . Но – равнобедренный по условию не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка — точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
Рассмотрим треугольник . Проведём два серединных перпендикуляра и , скажем, к отрезкам и . Они пересекутся в какой-то точке, которую мы назовем .
А теперь, внимание!
Точка лежит на серединном перпендикуляре ; точка лежит на серединном перпендикуляре . И значит, и .
- Отсюда следует сразу несколько вещей:
- Во – первых, точка обязана лежать на третьем серединном перпендикуляре, к отрезку .
- То есть серединный перпендикуляр тоже обязан пройти через точку , и все три серединных перпендикуляра пересеклись в одной точке.
Во – вторых: если мы проведём окружность с центром в точке и радиусом , то эта окружность также пройдёт и через точку , и через точку , то есть будет описанной окружностью . Значит, уже есть, что пересечение трёх серединных перпендикуляров – центр описанной окружности для любого треугольника.
И последнее: о единственности. Ясно (почти), что точку можно получить единственным образом, поэтому и окружность – единственная. Ну, а «почти» — оставим на твоё размышление. Вот и доказали теорему. Можно кричать «Ура!».
2. Радиус описанной окружности
А если в задаче стоит вопрос «найдите радиус описанной окружности»? Или наоборот, радиус дан, а требуется найти что – то другое? Есть ли формула, связывающая радиус описанной окружность с другими элементами треугольника?
| Есть, конечно! И эта формула называется «Теорема синусов» (доказательство смотри именно в этой теме). |
То есть:
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, тебе нужна одна сторона (любая!) и противолежащий ей угол. И всё!
3. Центр окружности – внутри или снаружи
А теперь вопрос: может ли центр описанной окружности лежать снаружи треугольника. Ответ: ещё как может. Более того, так всегда бывает в тупоугольном треугольнике.
И вообще:
| В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника. |
| В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника |
| В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы. |
Описанная окружность. коротко о главном
1. Окружность, описанная около треугольника
– это окружность, которая проходит через все три вершины этого треугольника.
|
2. Существование и центр описанной окружности
|
3. Радиус описанной окружности
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, нужна одна сторона (любая!) и противолежащий ей угол.
4. Центр окружности – внутри или снаружи
|
|
|
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
- Стать учеником YouClever,
- Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
- А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
Источник: https://youclever.org/book/opisannaya-okruzhnost-1
Ортоцентр треугольника: полезные факты
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим.
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 

 2016-01-09
2016-01-09
Главная » СТАТЬИ » 16 Задание (2016) (C4) » Ортоцентр треугольника: полезные факты
- Ортоцентр треугольника: полезные факты
- В этой статье доказываются некоторые факты, касающиеся точки пересечения высот треугольника (ортоцентра треугольника), которые могут быть весьма полезны при решении задач.
- Пусть — точка пересечения высот треугольника , — центр описанной окружности.
- Тогда:
- 1) радиусы окружностей, описанных около треугольников , , и равны;
- 2) расстояние от вершины до точки вдвое больше расстояния от центра описанной окружности до стороны ;
- 3) расстояние между серединами отрезков и равно радиусу описанной окружности треугольника ;
- 4)
 ;
; - 5) точки, симметричные точке относительно прямой и относительно середины стороны , лежат на описанной окружности треугольника .
- Доказательство.
- 1) Радиусы окружностей, описанных около треугольников , , и равны.

- Радиус окружности, описанной около треугольника можно найти по формуле:
-

- , где — произвольная сторона треугольника, а — величина противолежащего угла.
- Для треугольника радиус описанной окружности
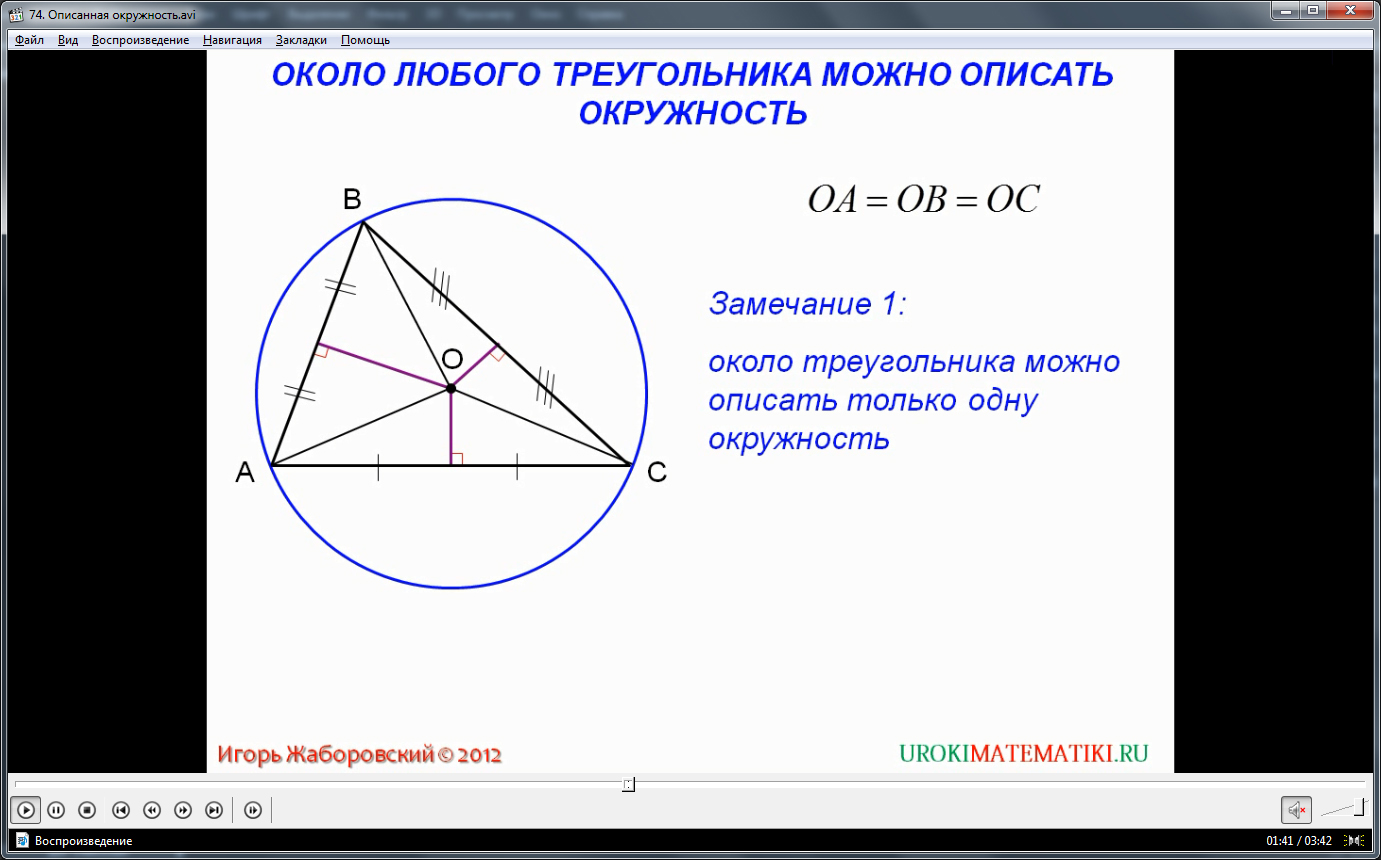
- Рассмотрим четырехугольник :
 по свойству вертикальных углов.
по свойству вертикальных углов. 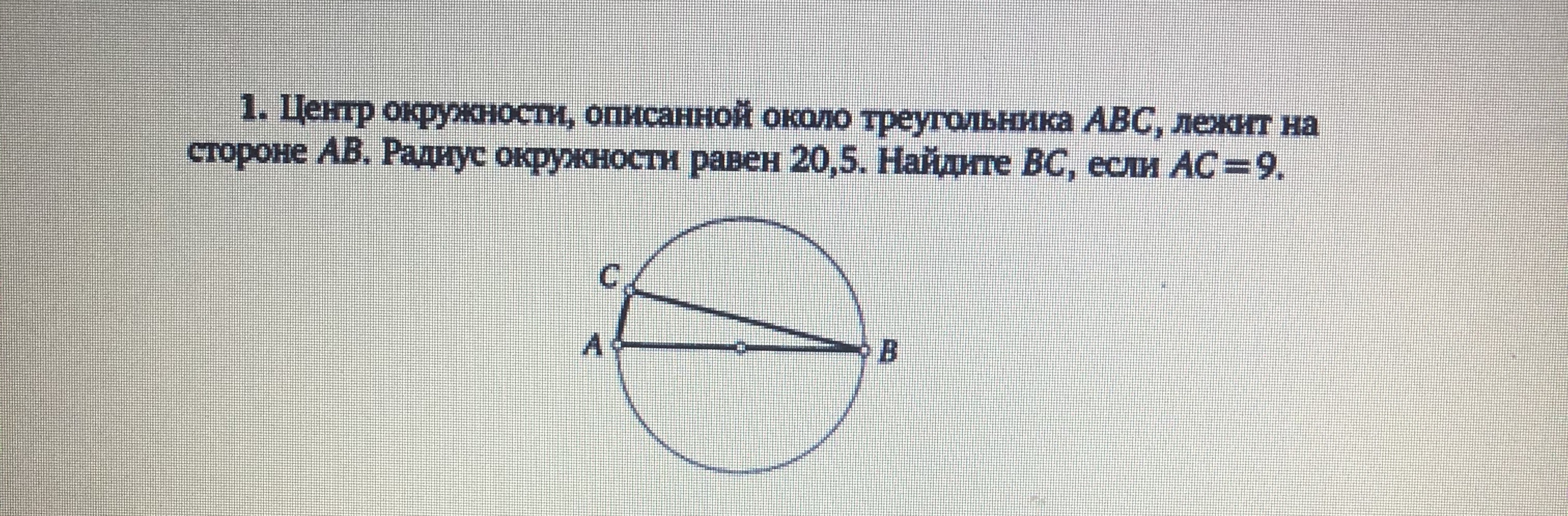
- Тогда для треугольника радиус описанной окружности , то есть равен радиусу описанной окружности треугольника .
- 2) Расстояние от вершины до точки вдвое больше расстояния от центра описанной окружности до стороны .
Докажем, что , где — центр описанной окружности, а — основание серединного перпендикуляра, опущенного из точки на сторону . (Вспомним, что центр описанной окружности лежит в точке пересечения серединных перпендикуляров.)
- Пусть точка симметрична точке относительно отрезка .
- Рассмотрим треугольник .
- Из соображений симметрии , следовательно, .
- Так как расстояние от точки до точек и равно радиусу окружности, описанной около треугольника , и мы только что доказали, что радиус окружности, описанной около треугольника также равен , следовательно, точка — центр окружности, описанной около треугольника , и .
- Проведем окружность с центром в точке , описанную около треугольника :
Мы видим, что при параллельном переносе на вектор окружность с центром в точке переходит в окружность c центром в точке , и точка переходит в точку , следовательно, . Но так как , получили, что .
- Что и требовалось доказать.
- 3) Расстояние между серединами отрезков и равно радиусу описанной окружности треугольника .
- Рассмотрим четырехугольник .
Мы доказали, что . Кроме того, по доказанному выше, . Следовательно, этот четырехугольник — параллелограмм. Точка — середина отрезка , является также серединой отрезка . Следовательно, отрезок, соединяющий точку с точкой — серединой отрезка , параллелен отрезкам и и равен им:
- .
- Что и требовалось доказать.
- 4)
- Используем доказанные выше факты.
- Четырехугольник — ромб, следовательно, по правилу параллелограмма для сложения векторов получаем :
- Далее, четырехугольник -параллелограмм, следовательно, .
- Утверждение доказано.
- 5) Точки, симметричные точке относительно прямой и относительно середины стороны , лежат на описанной окружности треугольника .
- Пусть точка симметрична точке относительно прямой :
Точка симметрична точке относительно прямой . Следовательно, окружность с центром в точке симметрична окуржности с центром в точке . Точка лежит на окружности с центром в точке (см. п. 2), следовательно, симметричная ей относительно прямой точка симметричной окружности с центром в точке , то есть описанной около треугольника .
- Пусть точка симметрична точке относительно относительно середины стороны :
- Треугольники равны по двум сторонам и углу между ними, следовательно, , и точка лежит на окружности, описанной около треугольника .
- Утверждение доказано.
И. В. Фельдман, репетитор по математике.
Источник: https://ege-ok.ru/2016/01/09/ortocentr-treugolnika-poleznye-fakty
Окружность, описанная около треугольника.Треугольник, вписанный в окружность. Теорема синусов
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
![]()
Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Рис.1
Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство. Рассмотрим произвольную точку D, лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Рис.2
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB. Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку.
Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3).
В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D.

Рис.3
Докажем, что отрезок AE длиннее отрезка EB. Действительно,
![]()

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Рис.4
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE. Действительно,
![]()
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2. Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.
Рис.5
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
| Серединные перпендикулярык сторонам треугольника | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.Посмотреть доказательство | |
| Окружность, описанная около треугольника | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.Посмотреть доказательство | |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.Посмотреть доказательство | |
| Центр описанной около тупоугольного треугольника окружности | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. | |
| Теорема синусов |
|
|
| Площадь треугольника |
|
|
| Радиус описанной окружности |
|
| Серединные перпендикуляры к сторонам треугольника |
| Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.Посмотреть доказательство |
| Окружность, описанная около треугольника |
| Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности |
| Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. |
| Центр описанной около прямоугольного треугольника окружности |
| Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |
| Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |
|
| Площадь треугольника |
|
| Радиус описанной окружности |
|
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC, и обозначим точку их пересечения буквой O (рис. 6).
- Рис.6
- Поскольку точка O лежит на серединном перпендикуляре к отрезку AC, то в силу теоремы 1 справедливо равенство:
- CO = AO .
- Поскольку точка O лежит на серединном перпендикуляре к отрезку AB, то в силу теоремы 1 справедливо равенство:
- AO = BO .
- Следовательно, справедливо равенство:
- CO = BO ,
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство. Рассмотрим точку O, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
- При доказательстве теоремы 3 было получено равенство:
- AO = OB = OC ,
- из которого вытекает, что окружность с центром в точке O и радиусами OA, OB, OC проходит через все три вершины треугольника ABC, что и требовалось доказать.
Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)
- Рис.7
- справедливы равенства:
- .
- Доказательство. Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R, на которую опирается вписанный угол величины φ , вычисляется по формуле:
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
- Рис.8
- Угол MPN, как угол,опирающийся на диаметр, является прямым угломугол,опирающийся на диаметр, является прямым углом, и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.
- Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
- Формула (1) доказана.
- Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Теорема синусов доказана.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник: https://www.resolventa.ru/spr/planimetry/otcircle.htm
Описанная окружность
Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника.
Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности.
На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.
Теорема
| Около любого треугольника можно описать окружность. |
Доказательство
- Дано: произвольный АВС.
- Доказать: около АВС можно описать окружность.
- Доказательство:
1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.
Замечание 1
| Около треугольника можно описать только одну окружность. |
Доказательство
Предположим, что около треугольника можно описать две окружности.
Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника.
Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.
Замечание 2
| Около четырехугольника не всегда можно описать окружность. |
Доказательство
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис.
3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е.
нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
| В любом вписанном четырехугольнике сумма противоположных углов равна 1800. |
Доказательство
Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 3600, т.е. АDС + АВС = 3600, тогда В + D = 3600 = 1800. Что и требовалось доказать.
Верно и обратное утверждение:
| Если сумма противоположных углов четырехугольника равна 1800, то около него можно описать окружность. |
Доказательство
- Дано: четырехугольник АВСD, BАD + BСD = 1800.
- Доказать: около АВСD можно описать окружность.
- Доказательство:
Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е.
является описанной около четырехугольника АВСD.
Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.
Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).
ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)
Углы ВFD и FDE — вписанные.
По теореме о вписанном угле ВFD = ВАD и FDE= ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.
BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).
Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 3600, т.е. ВЕD + ВАD = 3600, тогда BАD + BСD3600 = 1800.
Итак, мы получили, что BАD + BСD1800. Но это противоречит условию BАD + BСD =1800, и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.
Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).
- По теореме о сумме углов треугольника в ВСF: С + В + F = 1800, откуда С = 1800 — ( В + F). (2)
- В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)
- F и ВFD — смежные, поэтому F + ВFD = 1800, откуда F = 1800 — ВFD = 1800 — ВАD. (4)
- Подставим (3) и (4) в (2), получим:
- С = 1800 — (ЕF + 1800 — ВАD) = 1800 — ЕF — 1800 + ВАD = (ВАD — ЕF), следовательно, СВАD.
А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD).
Но это противоречит условию А + С =1800, и, значит, наше предположение ошибочно, т.е.
точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.
Примечание:
Окружность всегда можно описать:
Источник: https://budu5.com/manual/chapter/3523
6.3. Окружности, описанные около треугольника и вписанные в него
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром или медиатриссой.
Свойство 6.4.
Серединный перпендикуляр является ГМТ, равноудаленных от концов отрезка.
Теорема 6.4.
Серединные перпендикуляры к двум сторонам треугольника пересекаются.
Пусть ABC – треугольник, а a и b – серединные перпендикуляры к его сторонам AC и BC. Допустим, прямые a и b не пересекаются, то есть – параллельны. Прямая AC a, BC b и, следовательно, (BC) a, так как a || b. Таким образом, (AC) a и (BC) a, и, значит, (AC) || (BC). Но это неверно. Прямые AC и BC пересекаются в точке C. Полученное противоречие доказывает теорему.
|
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Теорема 6.5.
Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.
| Пусть a и b – серединные перпендикуляры к сторонам AC и BC треугольника ABC, а точка O – точка их пересечения. Из свойств серединного перпендикуляра AO = OC = OB. Следовательно, точка O лежит на серединном перпендикуляре к стороне AB. Таким образом, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Кроме того, точка пересечения серединных перпендикуляров равноудалена от вершин треугольника. Отсюда, по определению, центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам треугольника. Теорема доказана. |
- Окружность называется вписанной в треугольник, если она касается всех его сторон.
- Для определения центра вписанной в треугольник окружности пользуются свойством биссектрисы угла.
Свойство 6.5.
Биссектриса угла является ГМТ, равноудаленных от его сторон.
Пусть луч c с началом в точке O является биссектрисой угла, образованного лучами a и b. Пусть C – произвольная точка биссектрисы. Опустим перпендикуляры к сторонам a и b угла из точки C, и пусть A и B соответственно основания этих перпендикуляров. Треугольники OBC и OAC равны. Действительно BOC = AOC, так как [OC) – биссектриса, углы при вершинах A и B прямые по построению, сторона OC общая. Следовательно, CB = CA.
Теперь пусть точка D одинаково удалена от сторон угла O, т. е. DM = DN. Прямоугольные треугольники ODM и ODN равны, так как у них общая гипотенуза OD и равные катеты DM и DN. Значит, Δ DOM = Δ DON, и точка D лежит на биссектрисе угла O. |
Теорема 6.6.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Пусть окружность ω (O; P) вписана в угол (ab) с вершиной A. Пусть B и C – точки касания окружности прямыми b и a соответственно. Соединим точки B и C с центром O окружности. По свойству 6.1 (OB) b и (OC) a и OB = OC = R. Таким образом, точка O равноудалена от сторон угла на расстояние, равное радиусу окружности и по свойству 6.5 принадлежит биссектрисе и только ей. Пусть теперь AMN – данный треугольник, а O – центр вписанной в него окружности. По определению окружность одновременно вписана в каждый угол треугольника и по следствию 6.4 его центр лежит на биссектрисах его углов. Следовательно, точка O лежит на пересечении всех трех биссектрис углов треугольника. Теорема доказана.
|
Теорема 6.7.
Градусная мера угла, образованного хордой и касательной к окружности, проведенной через конец хорды, равна половине градусной меры дуги, лежащей в данном плоском угле.
Пусть AB – некоторая хорда окружности ω (O; R), через конец A которой проведена касательная l к окружности . Соединим точки A и B с центром O окружности и проведем в треугольнике AOB высоту OD на сторону AB. Треугольник AOB – равнобедренный, так как стороны AO и OB равны радиусу окружности. Поэтому высота, проведенная к основанию, является одновременно и медианой и биссектрисой. В частности, Кроме того, AOD + OAD = 90°. С другой стороны, (OA) l по свойству касательной и, следовательно, (l , (AD)) – OAD = 90°. Сравнивая эти равенства, получаем Теорема доказана.
|
Следствие 6.3.
Если один из лучей с вершиной в точке P касается окружности в точке C, а другой пересекает окружность в точках A и B, то AP · BP = PC2. Более коротко: квадрат отрезка касательной к окружности равен произведению отрезка секущей, проведенной из той же точки, на внешнюю ее часть.
Рассмотрим треугольники CAP и BCP. Угол CBP равен углу ACP. Действительно угол CBP – вписанный в окружность и его величина равна половине угловой величины угла CA. С другой стороны угол ACP образован хордой AC и касательной к окружности, проведенной через конец C хорды AC. По теореме 6.7 градусная мера угла ACP так же равна половине градусной меры дуги CA. Так как сумма углов любого треугольника – 180°, то углы BCP и CAP данных треугольников так же равны. Следовательно, по следствию 5.1 имеем Из последнего равенства получаем что и доказывает утверждение.
|
Теорема 6.8.
Градусная мера угла между хордами равна полусумме градусных мер дуг, принадлежащих данному плоскому углу, и соответствующему вертикальному углу.
Пусть точка A лежит в круге, [AC) и [AE) – стороны угла, а точки D и B – точки пересечения с окружностью лучей, дополнительных к [AC) и [AE) соответственно. Угол CAE является внешним углом треугольника ABC и, следовательно, его величина равна сумме величин несмежных с ним углов треугольника, т.е. CAE = BCA + ABC. Но углы BCA и ABC – вписанные в окружность и равны половине величины дуги CmE и BnD, соответственно. Поэтому Теорема доказана.
|
Теорема 6.9.
Градусная мера угла между секущими равна полуразности дуг, лежащих в данном плоском угле.
Пусть A – точка, лежащая вне круга, [AB) и [AD) – стороны угла с вершиной в точке A и луч AB пересекает окружность в точках B и E, а луч AD – в точках C и D. Соединим точки B и C отрезком. В полученном треугольнике ABC угол BCD – внешний и равен сумме углов BAD и ABC. Но а Отсюда имеем Следовательно, Теорема доказана.
|
Источник: https://mathematics.ru/courses/planimetry/content/chapter6/section/paragraph3/theory.html