Свойства высоты для всех фигур, с примерами

Как мы уже знаем, фигурой в геометрии называется множество точек на плоскости. Прямая, отрезок, луч, треугольник, окружность, квадрат и так далее – всё это примеры геометрических фигур.

В повседневной жизни нас с вами окружают множество различных предметов. Часть из них имеют одинаковые размеры и одинаковую форму. Например, две одинаковые ручки или две одинаковых монеты и т.д. В геометрии фигуры, имеющие одинаковые размеры и форму, называются равными фигурами.

Из этого определения следует, например, что если прямоугольник и квадрат имеют равные площади, то это не значит, что они являются равными фигурами, так как это разные по форме фигуры.

Равными фигурами являются, например, два отрезка одинаковой длины, два круга с одинаковым радиусом, два прямоугольника с попарно равными сторонами.

Следует отметить, что не все фигуры можно сравнивать. Нельзя определить равенство прямых, т. к. любая прямая бесконечна и, следовательно, все прямые, можно сказать, равны между собой. То же самое касается лучей. Хотя у них есть начало, но нет конца.

Если же мы имеем дело с произвольными фигурами, то иногда даже сложно определить, имеют ли они одинаковую форму. Таким образом, нужно иметь надежный метод сравнения фигур. Он заключается в следующем: две геометрические фигуры называются равными, если их можно совместить наложением.

Но как быть в том случае, когда, скажем, длина стороны треугольника равна  км? В данном случае можно воспользоваться признаками равенства треугольников, которые мы рассматривали на предыдущих уроках.

Смысл этих признаков в следующем: равенство трех элементов треугольников гарантирует равенство самих треугольников, а значит, и равенство остальных элементов, которые совместятся при наложении (биссектрис, высот, медиан).

• А что если форму оставить без изменений, а все размеры пропорционально изменить (увеличить или уменьшить в одинаковое количество раз)?
• Рассмотрим данную ситуацию на примере треугольника.
• Пример 1

Пусть дан правильный треугольник  со стороной  (см. рис. 1).

Рис. 1. Правильный треугольник

Уменьшив стороны треугольника  в  раза, получим правильный треугольник  со стороной  (см. рис. 2). То есть форма треугольника осталась прежней, а все размеры изменились (уменьшились) в  раза. Докажем это.

Рис. 2. Правильный треугольник  с уменьшенными сторонами

Доказательство:

Такой треугольник мы уже встречали на предыдущих уроках. Это треугольник, вершины которого лежат на серединах сторон исходного треугольника (см. рис. 3).

Рис. 3. Иллюстрация к доказательству

1. То есть из исходного правильного треугольника мы получили другой правильный треугольник, длина стороны которого уменьшилась в  раза.
2. Такие треугольники в геометрии называются подобными.
3. Обозначение:.

Коэффициент подобия – это число, равное отношению сходственных сторон в подобных фигурах. В нашем случае коэффициент подобия равен .

Обозначение:.

Пример 2

Дом на большом расстоянии имеет форму прямоугольника. Если постепенно приближаться к нему можно заметить, что его форма не меняется, но его размеры увеличиваются. Из этого можно сделать вывод, что его размеры изменяются в одинаковое число раз. Это ещё один пример подобных фигур.

Пример 3

Подобие фигур также используется при нанесении местности на карту. Возьмем, например, Крым и его изображение на карте с масштабом . Понятно, что форма Крыма на карте аналогична реальной форме, но размеры изменены в  раз.

Таковы при­ме­ры подобных фигур – фигур, ко­то­рые имеют оди­на­ко­вую форму, но раз­ные раз­ме­ры. При­чем раз­ме­ры из­ме­ня­ют­ся в одно и то же число раз.

Можно сформулировать признаки подобия треугольников. Эти признаки позволяют по некоторой информации об исходных треугольниках получить более подробную (дополнительную) информацию о них.

Пример 4

Пусть есть  подобных треугольника  с коэффициентом подобия . Тогда можно утверждать, что соотношение длин соответствующих сторон треугольников пропорционально . То есть: . Как и в случае признаков равенства, гарантируется пропорциональность соответствующих элементов треугольников (медиан, биссектрис, высот и т.д.).

Рассмотрим еще один подобный пример.

Пример 5

Предположим, что коэффициент подобия треугольников  и  равен . Тогда для них можно записать следующее соотношение: . Из этого следует, что . Как мы уже знаем, по третьему признаку эти треугольники будут равными (Второй и третий признаки равенства треугольников). Отсюда можно сделать вывод, что равенство фигур является частным случаем подобия фигур с коэффициентом .

Признаки подобия фигур, в частности признаки подобия треугольников, являются полезными приемами в математике, они применяются для упрощения и решения множества задач. Однако для изучения этих признаков необходимо перевести некоторые понятия на строгий математический язык. 

Пропорциональные отрезки

Понятия «отношение» и «пропорциональность» играют важную роль в изучении признаков подобия фигур.

Для начала рассмотрим понятие отношения отрезков на примере отрезков  и  (см. рис. 4).

Рис. 4. Отрезки  и

• Определение
• Отношение длин отрезков  и  называется отношением отрезков  и .
• Рассмотрим задачу на данное определение.
• Задача 1
• Дано
• Два отрезка  и
• Найти
• Отношение отрезков  и
• Решение
• Поскольку отношение отрезков – это отношение длин соответствующих отрезков, то имеем:
• Ответ:.
• Отметим, что отношение отрезков – это безразмерная величина.
• Теперь предположим, что отношение пары отрезков   и   равно отношению пары других отрезков  и . Это записывается следующим образом:

В таком случае говорят о пропорциональности отрезков. А именно: отрезки  и   пропорциональны отрезкам  и  соответственно.

По свойству пропорции  и  можно поменять местами: . От этого смысл выражения не поменяется.

Пропорциональные отрезки встречаются в формулировке обобщенной теоремы Фалеса (Задачи на параллелограмм).

Стороны угла рассекаются параллельными прямыми на пропорциональные части (см. рис.5). То есть:

1. Аналогичное соотношение можно записать и для суммы длин отрезков:

Рис. 5. Иллюстрация к теореме Фалеса

Рассмотрим два треугольника  и , у которых соответствующие углы равны (см. рис. 6):

Рис. 6. Треугольники с равными углами

• Стороны, которые лежат против равных углов треугольников, называются сходственными.
• Перечислим сходственные стороны:  и  (лежат против равных углов  ),  и  (лежат против равных углов  ),  и  (лежат против равных углов  ).
• Определение
• Два треугольника  и  называются подобными, если соответствующие углы равны, а сходственные стороны – пропорциональны:
• Причем  , где  – это коэффициент подобия треугольников.

Оказывается, можно ограничиться лишь некоторыми из этих равенств чтобы гарантировать факт подобия. В этом заключается суть признаков подобия треугольников, которые подробно будут рассмотрены на следующих уроках.

Можно заметить, что пропорциональные отрезки играют важную роль в определении подобных треугольников. Рассмотрим задачу на пропорциональность отрезков.

1. Задача на пропорциональность отрезков
2. Теорема
3. Биссектриса угла треугольника рассекает противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
4. Докажем эту теорему.
5. Дано
6. Произвольный треугольник ,  – биссектриса угла .
7. Доказать
8. Доказательство

Запишем выражения для площадей образовавшихся треугольников   и . Для этого опустим высоту из вершины .Выполним рисунок к задаче (см. рис. 1).

• Рис. Иллюстрация к доказательству теоремы
• Поскольку площадь треугольника равна половине произведения основания на высоту получаем: , . Теперь найдем отношение этих площадей:

С другой стороны, биссектриса – это геометрическое место точек, равноудаленных от сторон угла. Этим свойством обладают все точки, принадлежащие биссектрисе, в том числе точка . Поэтому расстояние от точки  до сторон одинаковое, обозначим его . Тогда высоты треугольников   и , опущенные к соответствующим основаниям  и , равны . Можно переписать отношение площадей этих треугольников:

1. Левые части этих двух равенств равна, значит и правые часть также равны:
2. Теорема доказана.

На данном уроке мы рас­смот­ре­ли по­до­бие фигур, вспомнили признаки равенства треугольников, дали опре­де­ле­ние по­доб­ным тре­уголь­ни­кам. Вспом­ни­ли о про­пор­ци­о­наль­но­сти от­рез­ков, тео­ре­му Фа­ле­са и их роль в ре­ше­нии дан­ных задач.

Спи­сок ре­ко­мен­до­ван­ной ли­те­ра­ту­ры

1. Алек­сан­дров А.Д. и др. Гео­мет­рия, 8 класс. – М.: Про­све­ще­ние, 2006.
2. Бу­ту­зов В.Ф., Ка­дом­цев С.Б., Пра­со­лов В.В. Гео­мет­рия, 8 класс. – М.: Про­све­ще­ние, 2011.
3. Мерз­ляк А.Г., По­лон­ский В.Б., Якир С.М. Гео­мет­рия, 8 класс. – М.: ВЕН­ТА­НА-ГРАФ, 2009.

Ре­ко­мен­до­ван­ные ссыл­ки на ре­сур­сы сети Ин­тер­нет:

1. Интернет-портал «egemaximum.ru» (Источник)
2. Интернет-портал «ru.solverbook.com» (Источник)
3. Интернет-портал «math10.com» (Источник)

До­маш­нее за­да­ние

1. Могут ли быть по­доб­ны­ми: а) пря­мо­уголь­ный и рав­но­сто­рон­ний тре­уголь­ни­ки; б) рав­но­бед­рен­ный и рав­но­сто­рон­ний тре­уголь­ни­ки; в) тре­уголь­ник с углом  и тре­уголь­ник с углом ?
2. Из от­рез­ков дли­ной , , , ,  и  см со­ста­ви­ли два по­доб­ных между собой тре­уголь­ни­ка. Най­ди­те ко­эф­фи­ци­ент по­до­бия этих тре­уголь­ни­ков.

Источник: https://interneturok.ru/lesson/geometry/8-klass/podobnye-treugolniki/podobie-obschih-figur?trainers

4. Объем фигур — Фигуры В Пространстве

   Объем — это величина фигуры в дину, высоту и ширину, измеряемая в кубических единицах.

    Свойства объемов:

• Равные тела имеют равные объемы.
• Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.

   1. Объем куба равен кубу длины его граней.

    Формула объема куба:  

    где V— объем куба,

          a — длина грани куба. 

    2. Объем призмы равен произведению основания призмы на ее высоту.

    Формула объема призмы: 

    3. Объем параллелепипеда равен произведению площади снования на высоту.    Формула объема параллелепипеда: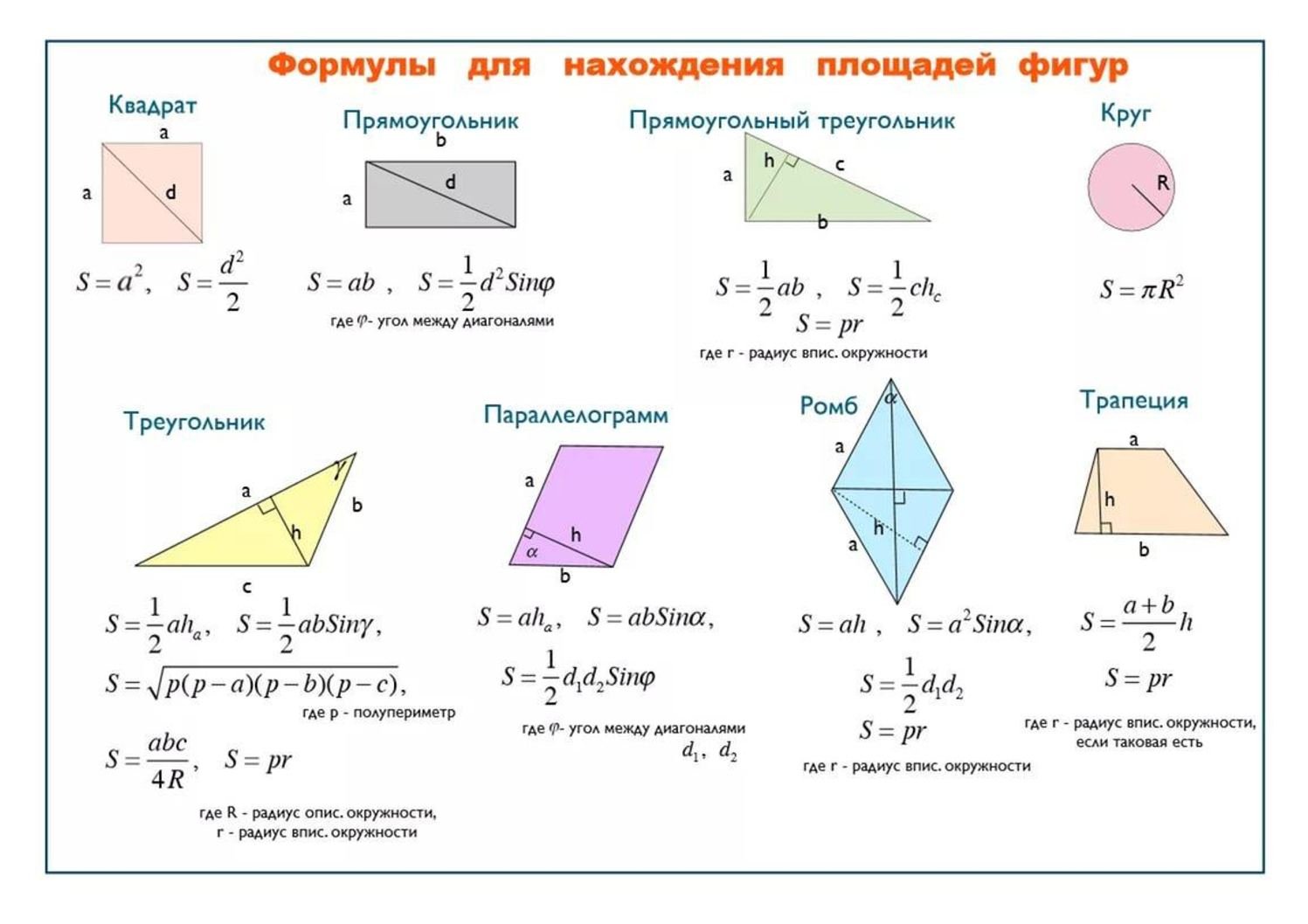 

    где  — объем параллелепипеда,  — площадь основания, — длина высоты.

  Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты. Формула объема прямоугольного параллелепипеда: 

    где  — объем прямоугольного параллелепипеда, 

           a

 — длина, 

            b

— ширина, 

            h

 — высота.

    4. Объем пирамиды равен трети от произведения площади ее основания на высоту.

    Формула объема пирамиды:

    где — объем пирамиды,  — площадь основания пирамиды,  — длина высоты пирамиды.

   5. Объем цилиндра равен произведению площади его основания на высоту.

    Формулы объема цилиндра:

    где  — объем цилиндра,  — площадь основания цилиндра,  — радиус цилиндра,  — высота цилиндра, .

   6. Объем конуса равен трети от произведения площади его основания на высоту.

    Формулы объема конуса: 

    где  — объем конуса,  — площадь основания конуса,  — радиус основания конуса,  — высота конуса, .

    7. Объем шара равен четырем третьим от его радиуса в кубе помноженного на число.

    Фор

    где  — объем шара,  — радиус шара, .

Источник: https://www.sites.google.com/site/figuryvprostranstve/4-obem-figur

Формулы площади геометрических фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

1. Формула площади треугольника по стороне и высоте Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
2. Формула площади треугольника по трем сторонам

   S = √p(p — a)(p — b)(p — c)

3. Формула площади треугольника по двум сторонам и углу между ними Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
4. Формула площади треугольника по трем сторонам и радиусу описанной окружности
5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника, a, b, c — длины сторон треугольника, h — высота треугольника, γ — угол между сторонами a и b, r — радиус вписанной окружности, R — радиус описанной окружности,
   
   

   p =	a + b + c	— полупериметр треугольника.
   2

1. Формула площади параллелограмма по длине стороны и высоте Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

   S = a · h

2. Формула площади параллелограмма по двум сторонам и углу между ними Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

   S = a · b · sin α

3. Формула площади параллелограмма по двум диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними. где S — Площадь параллелограмма, a, b — длины сторон параллелограмма, h — длина высоты параллелограмма, d1, d2 — длины диагоналей параллелограмма, α — угол между сторонами параллелограмма, γ — угол между диагоналями параллелограмма.

1. Формула площади ромба по длине стороны и высоте Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

   S = a · h

2. Формула площади ромба по длине стороны и углу Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

   S = a2 · sin α

3. Формула площади ромба по длинам его диагоналей Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба, a — длина стороны ромба, h — длина высоты ромба, α — угол между сторонами ромба, d1, d2 — длины диагоналей.

1. Формула Герона для трапеции
   
   

   S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
   |a — b|

2. Формула площади трапеции по длине основ и высоте Площадь трапеции равна произведению полусуммы ее оснований на высоту где S — площадь трапеции, a, b — длины основ трапеции, c, d — длины боковых сторон трапеции,
   
   

   p =	a + b + c + d	— полупериметр трапеции.
   2

1. Формула площади четырехугольника по длине диагоналей и углу между ними Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними: где S — площадь четырехугольника, d1, d2 — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника.
2. Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности) Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

   S = p · r

3. Формула площади четырехугольника по длине сторон и значению противоположных углов

   S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ

   где S — площадь четырехугольника,

   • a, b, c, d — длины сторон четырехугольника,
   • p = a + b + c + d2  — полупериметр четырехугольника,
   • θ = α + β2  — полусумма двух противоположных углов четырехугольника.
4. Формула площади четырехугольника, вокруг которого можно описать окружность

   S = √(p — a)(p — b)(p — c)(p — d)

1. Формула площади круга через радиус Площадь круга равна произведению квадрата радиуса на число пи.

   S = π r2

2. Формула площади круга через диаметр Площадь круга равна четверти произведения квадрата диаметра на число пи. где S — Площадь круга, r — длина радиуса круга, d — длина диаметра круга.

© 2011-2020 Довжик МихаилКопирование материалов запрещено.

Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com

Источник: https://ru.onlinemschool.com/math/formula/area/

Высоты треугольника, точка их пересечения и теоремы

Решение задач по геометрии часто сводится к самой простой фигуре, называемой треугольником, точка пересечения высот которого обладает важными свойствами, помогающими найти неизвестные величины: стороны, углы, периметр и площадь. В интернете можно найти немало информации по этой теме, но, как правило, она не систематизирована. В результате тратится много времени на поиск формул и важных утверждений.

Общие сведения

Перед переходом к основным соотношениям высот с другими параметрами треугольника нужно ознакомиться с теоретическими сведениями об этой фигуре.

Треугольник — фигура, состоящая из трех вершин, не лежащих на одной прямой, и отрезков, соединяющих их. Упрощенная форма записи в математике — символ «тильда», т. е. Δ. После последнего идут названия трех вершин, например, ΔPTS.

Угол обозначается символом ∠, а после него указывается полная запись (∠РТS) или сокращенная (∠a).

Специалисты рекомендуют не называть вершины русскими буквами, поскольку эта запись не является верной. Треугольники бывают нескольких типов, на основании которых можно применить некоторые свойства, утверждения (теоремы) и формулы.

Типы треугольников

Математики классифицируют треугольные фигуры по определенным правилам или критериям. Они отличаются между собой по сторонам и углам. В первом случае фигуры бывают:

• произвольными;
• равнобедренными;
• равносторонними.

К первым принадлежат все фигуры с различными сторонами, ко вторым — с двумя равными, а к третьим — с тремя. Если классифицировать Δ по углам, то фигуры можно разделить на три типа. К ним принадлежат:

• прямоугольные;
• тупоугольные;
• остроугольные.

В прямоугольном Δ один из углов является прямым, т. е. равным 90 градусам. Тогда, используя свойство суммы его ∠, можно сделать вывод, что при сложении последних получается величина, равная 90°. Если Δ тупоугольный, то один из его ∠ эквивалентен величине, которая больше 90°. В остроугольном Δ все ∠ имеют градусную меру меньше 90°.

Следует отметить, что произвольные и равнобедренные Δ бывают прямоугольными и тупоугольными. Однако равносторонние (правильные) могут быть только остроугольными, поскольку все их углы эквивалентны значению 60°. Это можно определить по формуле: ∠K = ∠L = ∠M = 180 / 3 = 60. Кроме того, только вокруг этого типа фигуры можно описать окружность.

Основные и дополнительные параметры

У каждой фигуры, а треугольник не является исключением, существуют основные и дополнительные параметры. К первым относятся стороны и углы, ко вторым — периметр, площадь, высота, медиана и биссектриса.

Периметр — совокупность или алгебраическая сумма значений длин всех его сторон. Площадью является размерность фигуры, которая рассчитывается по некоторому соотношению. Она может быть только у плоских элементов геометрии, кроме точки, прямой, угла, луча и отрезка.

Следует отметить, что при решении задач в фигуре проводятся дополнительные элементы: высота, биссектриса и медиана. Первой называется отрезок, который проводится из вершины треугольника на противоположную сторону под углом 90 градусов. Высота образует подобный Δ относительного того, где она проведена. Это утверждение следует из равенства двух углов и пропорциональности сторон.

Все высоты в остроугольном треугольнике расположены внутри него. Если Δ является прямоугольным, то высоты, которые проводятся из вершин его острых углов, совпадают с катетами. В тупоугольном Δ высота, проведенная из вершины любого острого ∠, всегда находится вне фигуры.

Следующим вспомогательным отрезком является медиана. Она проводится из вершины, как и высота, но не под прямым углом, а соединяет среднюю точку противоположной стороны, посредством которой и будет делиться на две равные части. Биссектриса делит угол на две равные части. Она проводится из вершины Δ.

В произвольном Δ количество высот, медиан и биссектрис эквивалентно числу его вершин, то есть можно провести по три элемента. Однако бывают исключения из этого правила: если фигура равнобедренная или равносторонняя, то ее высота является медианой и биссектрисой.

Информация об ортоцентре

Теорема об ортоцентре позволяет вывести важные свойства высот треугольника, пересекающихся в одной точке. Ее формулировка следующая: высоты, проведенные в произвольном Δ, пересекаются в одной точке. Для доказательства требуется начертить произвольный ΔKLM. Он не должен содержать прямой или тупой угол. Далее нужно действовать по такому алгоритму:

1. Из двух вершин следует провести высоты, которые пересекают противоположную сторону под прямым углом, то есть из вершины L опустить LN на сторону КМ. Аналогичную операцию нужно выполнить для вершины К (KU к LM).
2. Высоты пересекутся в некоторой точке — будущем ортоцентре треугольника. Ее следует обозначить W.
3. Предположим, что высоты не пересекаются. Следовательно, они параллельны. Это записывается таким образом: LN || KU. Сторона KL является секущей по определению.
4. Исходя из третьего пункта, алгебраическая сумма значений углов (∠К/2 и ∠L/2) эквивалентна 180. Из равенства получается, что ∠К + ∠L = 360. Если ∠К и ∠L — внутренние углы ΔKLM, то их сумма не может составлять 360 градусов. Следовательно, предположение ошибочно.
5. На основании доказанного в четвертом пункте утверждения можно сделать вывод, что высоты пересекаются в точке W.
6. Аналогичным образом доказывается, что высота MV, опущенная из вершины M, проходит через ортоцентр. Для этого нужно повторить 1—5 пункты алгоритма, но вместо KU провести MV.
7. Утверждение доказано.

Однако теоремы о высотах недостаточно для решения задач по геометрии. Для этого случая математики вывели полезные свойства и соотношения, облегчающие нахождение неизвестной величины или доказательства нового утверждения.

Полезные свойства и формулы

При решении задач могут потребоваться некоторые свойства ортоцентра, которые были доказаны математиками. К ним относятся следующие:

1. Расположение ортоцентра: остроугольный — в центре, прямоугольный — совпадает с образующей прямой угол вершиной, тупоугольный — внешний (находится за пределами треугольника).
2. Ортоцентр остроугольного Δ — центр окружности, вписанной в него.
3. Алгебраическая сумма квадратов расстояний от вершин до ортоцентра (KW, LW и MW) с учетом квадратов сторон (KL, LM и KM) эквивалентна двенадцати квадратам радиуса окружности R, которая описана вокруг треугольника: KW2 + LW2 + MW2 + KL2 + LM2 + KM2 = 12 * R2.
4. Расстояние (К{kl}) от ортоцентра до середины стороны KL: К{kl} = KL / (2 * tg (∠K)). Для других величин (К{lm} и К{mk}): К{lm} = LM / (2 * tg (∠L)) и К{mk} = MK / (2 * tg (∠M)) соответственно.
5. Величина расстояний от W до вершин (KW, LW и MW): KW = KL / tg (∠K), LW = LM / tg (∠L) и MW = KM / tg (∠M).
6. Площадь S: S = KL2 * sin (∠K) / 2 = LM2 * sin (∠L) / 2 = KM2 * sin (∠M) / 2.

Существует определенный класс задач, в которых требуется найти координаты ортоцентра. В этом случае нужно начертить декартовую систему координат и отметить на ней вершины, а затем соединить их отрезками. Далее необходимо провести высоты и найти ортоцентр треугольника, а затем начертить из искомой точки проекции на координатные прямые.

Таким образом, расположение ортоцентра треугольника зависит от его вида и является важным параметром для построения вписанных и описанных окружностей.

Источник: https://1001student.ru/geometriya-2/vysoty-treugolnika-tochka-ih-peresecheniya-i-teoremy.html

Высоты треугольника

Высота треугольника — это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. На Рис.1 АН — высота треугольника АВС (точку Н называют основанием высоты АН).

Любой треугольник имеет три высоты. На Рис.2 (), АН, ВМ, СК  — высоты треугольника АВС (АНВС, ВМАС, СКАВ).  

Замечательное свойство высот треугольника: в любом треугольнике высоты или их продолжения пересекаются в одной точке. На Рис.

2 ( ,б ) в точке О пересекаются высоты треугольника АВС, а на Рис.3 в точке О пересекаются продолжения высот треугольника АВС.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

• Треугольник
• Равенство треугольников
• Первый признак равенства треугольников
• Перпендикуляр к прямой
• Медианы треугольника
• Биссектрисы треугольника
• Равнобедренный треугольник
• Свойства равнобедренного треугольника
• Второй признак равенства треугольников
• Третий признак равенства треугольников
• Окружность
• Построения циркулем и линейкой
• Треугольники

Правило встречается в следующих упражнениях:

1. 7 класс
2. Задание 133, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
3. Задание 307, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
4. Задание 490, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
5. Задание 578, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
6. Задание 587, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
7. Задание 689, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8. Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
9. Задание 861, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
10. Задание 910, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
11. Задание 955, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

• © budu5.com, 2020
• Пользовательское соглашение
• Copyright
• Нашли ошибку?
• Связаться с нами

Источник: https://budu5.com/manual/chapter/3318

Точка пересечения высот треугольника — свойства, координаты и расположение ортоцентра — Помощник для школьников Спринт-Олимпиады

Точка пересечения высот треугольника называется ортоцентром и традиционно обозначается латинской буквой H. «Ортос» в переводе с греческого означает «прямой», «правильный». Ортоцентр может находиться внутри фигуры и вне ее. Местоположение зависит только от самой фигуры и не зависит от порядка расположения сторон и вершин.

Что такое высота

Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.

У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе.

Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр.

В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.

Свойства ортоцентра

Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.

Ортоцентр по отношению к фигуре может быть расположен:

• внутри;
• снаружи;
• в вершине (у прямоугольных треугольников)

Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.

Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:

• биссектрис,
• высот,
• медиан.

Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.

Полезные факты

Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.

Пусть:

• H — ортоцентр в ABC;
• О — центр описанной окружности.

Тогда:

• окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
• отрезок BH вдвое длиннее отрезка АС;
• середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.

Задача Фаньяно

Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.

• Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.
• Площадь ортотреугольника рассчитывается по формуле:
• Здесь S — площадь, а, b, c — стороны.

Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.

История изучения

Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.

В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.

Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.

ПредыдущаяСледующая

Источник: https://Sprint-Olympic.ru/uroki/geometrija/85610-tochka-peresecheniia-vysot-treygolnika-svoistva-koordinaty-i-raspolojenie-ortocentra.html

Высота треугольника

Урок содержит описание свойств и формулы нахождения высоты треугольника, а также примеры решения задач. Если Вы не нашли решение подходящей задачи — пишите про это на форуме. Наверняка, курс будет дополнен. 

Высота треугольника – опущенный из вершины треугольника перпендикуляр, проведенный на противолежащую вершине сторону или на ее продолжение. Свойства высоты треугольника: Если в треугольнике две высоты равны, то такой треугольник — равнобедренный В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащих на двух сторонах, непараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины этой стороны всегда можно провести окружность В остроугольном треугольнике две его высоты отсекают от него подобные треугольники Минимальная высота в треугольнике всегда проходит внутри этого треугольника Ортоцентр треугольника Все три высоты треугольника (проведенные из трех вершин) пересекаются в одной точке, которая называется ортоцентром. Для того, чтобы найти точку пересечения высот, достаточно провести две высоты (две прямые пересекаются только в одной точке). Расположение ортоцентра (точка О) определяется видом треугольника. У остроугольного треугольника точка пересечения высот находится в плоскости треугольника. (Рис.1). У прямоугольного треугольника точка пересечения высот совпадает с вершиной прямого угла (Рис.2). У тупоугольного треугольника точка пересечения высот находится за плоскостью треугольника (Рис.3). У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают. У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.

ВИСОТА ТРИКУТНИКА Висота трикутника — опущений з вершини трикутника перпендикуляр, проведений на протилежну вершині бік або на її продовження. Всі три висоти трикутника (проведені з трьох вершин) перетинаються в одній точці, яка називається ортоцентром. Для того, щоб знайти точку перетину висот, досить провести дві висоти (дві прямі перетинаються тільки в одній точці). Розміщення ортоцентра (точка О) визначається видом трикутника. У гострокутного трикутника точка перетину висот знаходиться в площині трикутника. (Мал.1). У прямокутного трикутника точка перетину висот збігається з вершиною прямого кута (Мал.2). У тупоугольного трикутника точка перетину висот знаходиться за площиною трикутника (Мал.3). У рівнобедреного трикутника медіана, бісектриса і висота, проведені до основи трикутника, збігаються. У рівностороннього трикутника всі три «помітні» лінії (висота, бісектриса і медіана) збігаються і три «помітні» точки (точки ортоцентра, центру ваги і центру вписаного і описаного кіл) знаходяться в одній точці перетину «помітних» ліній, тобто теж збігаються.

Формулы нахождения высоты треугольника

• Высота в формулах обозначается буквой h, нижний индекс которой соответствует стороне, на которую она опущена.
• Другие обозначения: a,b,c — длины сторон треугольника ha — высота треугольника, проведенная к стороне a из противолежащего угла hb — высота, проведенная к стороне b hc — высота, проведенная к стороне c R — радиус описанной окружности r — радиус вписанной окружности

Пояснения к формулам. Высота треугольника равна произведению длины стороны, прилежащей к углу, из которой опущена эта высота на синус угла между этой стороной и стороной, на которую такая высота опущена (Формула 1) Высота треугольника равна частному от деления удвоенной величины площади треугольника на длину стороны, к которой опущена эта высота (Формула 2) Высота треугольника равна частному от деления произведения сторон, прилежащих к углу, из которого опущена эта высота, на удвоенный радиус описанной вокруг него окружности (Формула 4). Высоты сторон в треугольнике соотносятся между собой в той же самой пропорции, как соотносятся между собой обратные пропорции длин сторон этого же треугольника, а также в той же самой пропорции между собой относятся произведения пар сторон треугольника, которые имеют общий угол (Формула 5).  Сумма обратных значений высот треугольника равна обратному значению радиуса вписанной в такой треугольник окружности (Формула 6) Площадь треугольника можно найти через длины высот этого треугольника (Формула 7)

Длину стороны треугольника, на которую опущена высота, можно найти через применение формул 7 и 2.

Задача на подобие треугольников

В прямоугольном треугольнике ABC (угол C = 900) проведена высота CD. Определите CD, если AD = 9 см, BD = 16 см

Решение.

Треугольники ABC, ACD и CBD подобны между собой . Это непосредственно следует из второго признака подобия (равенство углов в этих треугольниках очевидно).

Прямоугольные треугольники — единственный вид треугольников, которые можно разрезать на два треугольника, подобных между собой и исходному треугольнику.

Обозначения этих трех треугольников в таком порядке следования вершин: ABC, ACD, CBD. Тем самым мы одновременно показываем и соответствие вершин. (Вершине A треугольника ABC соответствует также вершина A треугольника ACD и вершина C треугольника CBD и т. д.)

1. Треугольники ABC и CBD подобны. Значит:
2. AD/DC = DC/BD, то есть
3. DC2=AD*BD
4. DC2=9*16
5. DC=12 см

Задача на применение теоремы Пифагора. 

Треугольник ABC является прямоугольным. При этом C-прямой угол. Из него проведена высота CD=6см.  Разность отрезков BD-AD=5 см. 

• Найти: Стороны треугольника ABC. 
• Решение. 
• 1.Составим систему уравнений согласно теореме Пифагора
• CD2+BD2=BC2
• CD2+AD2=AC2
• поскольку CD=6
• 36+BD2=BC2
• 36+AD2=AC2
• Поскольку BD-AD=5, то
• BD = AD+5, тогда система уравнений принимает вид
• 36+(AD+5)2=BC2
• 36+AD2=AC2

Сложим первое и второе уравнение. Поскольку левая часть прибавляется к левой, а правая часть к правой — равенство не будет нарушено. Получим: 

1. 36+36+(AD+5)2+AD2=AC2+BC2
2. 72+(AD+5)2+AD2=AC2+BC2
3. 2. Теперь, взглянув на первоначальный чертеж треугольника, по той же самой теореме Пифагора, должно выполняться равенство:
4. AC2+BC2=AB2
5. Поскольку AB=BD+AD, уравнение примет вид: 
6. AC2+BC2=(AD+BD)2
7. Поскольку BD-AD=5, то BD = AD+5, тогда
8. AC2+BC2=(AD+AD+5)2 

3. Теперь взглянем на результаты, полученные нами при решении в первой и второй части решения. А именно:

72+(AD+5)2+AD2=AC2+BC2

AC2+BC2=(AD+AD+5)2

Они имеют общую часть AC2+BC2 . Таким образом, приравняем их друг к другу.

• 72+(AD+5)2+AD2=(AD+AD+5)2
• 72+AD2+10AD+25+AD2=4AD2+20AD+25
• -2AD2-10AD+72=0 
• В полученном квадратном уравнении дискриминант равен D=676, соответственно, корни уравнения равны:
• х1=-3,5
• x2=4 
• Поскольку длина отрезка не может быть отрицательной, отбрасываем первый корень.
• AD=4
• Соответственно
• BD = AD + 5 = 9
• AB = BD + AD = 4 + 9 = 13
• По теореме Пифагора находим остальные стороны треугольника:
• AC = корень из (52)
• BC = корень из (117).
• 0  

 Треугольник (Трикутник) | Описание курса | Сумма углов треугольника 

Источник: https://profmeter.com.ua/communication/learning/course/course7/lesson47/