Числовые неравенства и их решение

Содержание

Данный урок посвящён теме «Свойства числовых неравенств». В ходе этого занятия вы вспомните определение неравенства. Сможете получить представление об основных свойствах числовых неравенств, которые впоследствии пригодятся для решения задач.

Что такое числовое неравенство.
Вспомним, что означают неравенства: и :
означает, что и означает, что

Вывод: число считается большим числа b, если разность является положительным числом. Число считается меньше числа b, если разность является отрицательным числом.

Геометрическая интерпретация.

Свойства числовых неравенств.

Если , то

Доказательство: Поскольку по условию , то разницы и являются положительными числами. Тогда положительной будет и их сумма Имеем: .Таким образом, разница – положительное число, и отсюда следует, что .

Если и с – любое число, то .

Доказательство:

Рассмотрим разность Имеем: . Поскольку по условию , то разность – положительное число и . Что и требовалось доказать.

Если и c – положительное число, то . И если и c – отрицательное число, то .

Доказательство:

Если , то произведение – отрицательное число, и разность отрицательная, т. е.

Пример: , умножим обе части неравенства на 2 и получим , но если обе части неравенства умножить на -2, то знак неравенства поменяется на противоположный: .

Свойство 4.

Свойство 5.
Рассмотрим перемножение неравенств.

Если все числа положительные, то их можно перемножить, и получим . Если умножать на отрицательное число, то знак неравенства меняется на противоположный.

Свойство 6.
Рассмотрим возведение в степень неравенств.
и тогда .

Даны два положительных числа и .И . Доказать, что их обратные величины связаны противоположным неравенством:

Так как даны положительные числа и то нужно убедиться, что . Чтобы дробь была отрицательным числом, надо, чтобы числитель был отрицательным числом. Умножаем на -1 и получаем .

Дано:

а) Оценить число

Решение: Обе части неравенства умножаем на 2. Тогда . Задача решена.

б) Оценить число -3

Решение: будет меняться в пределах . Умножаем неравенство на 3. Получаем ;

в) Oценить разность

Решение: . Неравенства одного знака можно складывать. Получаем:

Ответ:
Дано:

Решение: Переносим все в одну сторону.. Приводим к общему знаменателю: Знаменатель по условию , значит и числитель должен быть положительным числом, т. е. . Квадрат числа всегда равен положительному числу, кроме, если а=1. Что и требовалось доказать.

Подведение итога урока.

На данном уроке была рассмотрена тема: «Свойства числовых неравенств». В ходе этого занятия вы вспомнили определение неравенства. Получили представление об основных свойствах числовых неравенств, которые впоследствии пригодятся для решения задач.

Список литературы

Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

ЕГЭ по математике (Источник).
Интернет-портал Frezzii.narod.ru (Источник).
Фестиваль педагогических идей «Открытый урок» (Источник).

Домашнее задание

Сравните числа а и b, если: а) ; б) в)
Какое из чисел больше х или у, если известно, что: а) ; б)
№530, 532. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

Источник: https://interneturok.ru/lesson/algebra/8-klass/neravenstva/svoystva-chislovyh-neravenstv?chapter_id=17

Задачи ЕГЭ по математике

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Показать ответ

Ответ:

Показать решение

Решение:
Ответ:

Источник: https://matematushka.ru/Zadachi_Ege/8

Линейные неравенства. Подробная теория с примерами

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Раз уж ты оказался на этой теме, то ты наверняка уже знаком с темой «Линейные уравнения».
Если нет, то лучше скорей отправляйся исправлять это недоразумение.
Без усвоенной темы «Линейные уравнения» спокойное плавание в «Линейных неравенствах» не гарантировано.
Итак, надеюсь, ты уже знаком с линейными уравнениями, поэтому можно смело покорять неравенства!

Что такое «линейные неравенства»?

Если ты ознакомился с линейными уравнениями, то уже знаком с Васей, который раздавал яблоки своим друзьям. Давай вернемся к примеру с Васей (может, и нам что-то перепадет?).

Так вот, предположим, что у Васи больше, чем яблок. Все свои яблоки он хочет раздать поровну троим друзьям. По сколько яблок получит каждый друг?

Если обозначить через количество яблок, которое достанется каждому из трех друзей, то получим следующее линейное неравенство:
Дальше мы делим обе части составленного неравенства на и получаем:
Таким образом, каждый друг щедрого Васи получит больше, чем яблока.
Ну вот и справились с неравенством!
Сейчас я введу формализованное определение линейного неравенства и будем разбираться с ним дальше.

Линейные неравенства — это неравенства вида: где и – любые числа, причем ; — неизвестная переменная.

Например:

Все приведенные выше неравенства являются линейными.

Во всех них «сидит» очень важная особенность: в таких неравенствах нет иксов в квадрате, в кубе и т.д., кроме того в этих неравенствах нет деления на икс и икс не находится под знаком корня.

Чтобы лучше распознавать линейные неравенства, настоятельно рекомендую тебе еще раз заглянуть в раздел «Скрытые» линейные уравнения или…» темы «Линейные уравнения. Начальный уровень.».

Линейные неравенства обладают не меньшим талантом «скрываться».

Чтобы не попасть впросак и с легкостью преобразовывать любые неравенства надо знать и успешно применять 3 очень важных правила. Эти знания здорово упростят тебе жизнь на пути в решении неравенств.

Правила преобразования неравенств

Два неравенства равносильны, если они имеют одинаковые решения.
Решить неравенство – значит найти все значения переменной, при которых неравенство обращается в верное числовое неравенство.
Для упрощения процесса нахождения всех корней неравенства проводятся равносильные преобразования, то есть проводится замена данного неравенства более простым, при этом не должны потеряться никакие решения и не должно возникнуть никаких посторонних корней.

В общем, это все пока только слова. Давай разбираться прямо на правилах.

ПРАВИЛО 1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные).

Например,
Таким образом, можно с уверенностью сказать, что равносильно .
Или вот такой пример:
В теме «Линейные уравнения» говорилось, что для удобства принято переносить слагаемые с переменной в левую часть, а остальные в правую – так и поступим:
Здесь все должно быть понятно, перейдем к следующему правилу.

ПРАВИЛО 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.

Вернемся к нашим двум предыдущим примерам.

В первом примере мы остановились на . Применим правило 2, разделив обе части неравенства на положительное число :

Заметил, знак неравенства как был «больше», так и сохранился? Все это потому, что мы делили на положительное число.

Давай закрепим на втором примере, где мы остановились на . Разделим обе части неравенства на :

Делили на положительное число , поэтому знак неравенства сохранился.

Почему так акцентируется внимание на том, что знак неравенства сохраняется? А вот потому, что в отличие от преобразований линейных уравнений, преобразования линейных неравенств имеют свою особенность, можно даже сказать «подводный камень». Что это за «камень» должно прояснить правило 3.

ПРАВИЛО 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак на знак , и наоборот; знак на знак , и наоборот).

Заметил важное отличие от правила 2? Все верно:

При умножении/делении на положительное число знак неравенства сохраняется
При умножении/делении на отрицательное число знак неравенства меняется на противоположный

Например:
Делим на отрицательное число , тогда знак неравенства меняется на противоположный:
Заметил, знак (меньше) заменили на знак (больше)?
Или вот такой пример:
Делим обе части на отрицательное число , меняя при этом знак неравенства на противоположный:
Усвоил? Тогда давай закреплять на примерах

Не пугайся, что примеры, на первый взгляд, сложней, чем мы с тобой разбирали. Мы ведь знаем все необходимые правила преобразования линейных неравенств, а значит, не пропадем.

Ну что, приступим? Как-никак, это не Эверест покорять.

1.
Раскроем для начала скобки и приведем подобные слагаемые:
А теперь можем применять наши правила преобразования линейных неравенств:

Ну вот, мы почти решили наше неравенство – осталось записать ответ в виде промежутка. Неравенство у нас нестрогое, поэтому число включается в наш промежуток. Для наглядности изображу решения на оси:

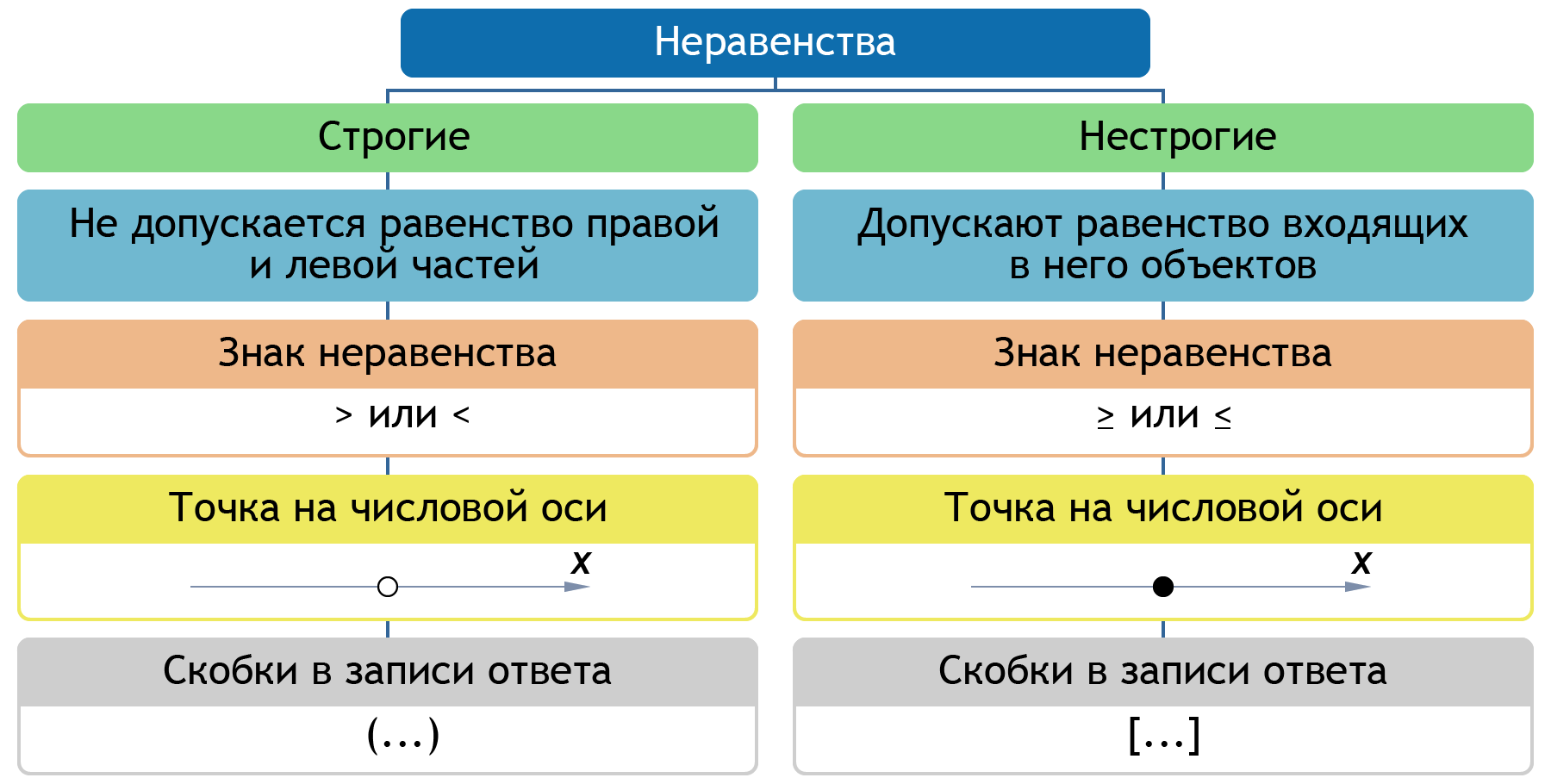
Запишем ответ: .
2.
Все, как в первом примере: раскрываем скобки, приводим подобные слагаемые, осуществляем необходимые преобразования:
Неравенство у нас нестрогое, поэтому число включается в наш промежуток:

Ответ:

Думаешь это не линейное неравенство? А что мы говорили в теме Линейные уравнений об их «скрытности»?

Поспешных выводов делать не стоит, давай лучше проведем все возможные преобразования и убедимся, что это линейное неравенство, либо докажем обратное.

Сейчас будем делить обе части неравенства на отрицательное число . Что же тогда произойдет со знаком неравенства? Все верно – он поменяется на противоположный!

Неравенство нестрогое, значит, включается в наш промежуток.
Ответ:
4.
Проводим соответствующие преобразования:
Делим обе части на отрицательное число , не забывая поменять знак неравенства на противоположный:
Неравенство нестрогое, поэтому — не включается в промежуток:

Ответ:
5.
Этот пример проще, поэтому сразу запишу ход решения без комментариев:
Ответ:

Линейные неравенства с двумя переменными

В теме Линейные уравнения достаточно подробно разобрано понятие линейного уравнения с двумя переменными. Линейное неравенство представляет собой практически то же самое, только знак равенства меняется на знак неравенства .

Линейные неравенства с двумя переменными имеют вид: где , и – любые числа, .

А вся разница с линейным неравенством с одной переменной только в том, что в неравенство добавляется еще одна переменная .

Решением неравенства с двумя переменными называется множество пар чисел , которые удовлетворяют этому неравенству (т.е. при подстановке этих точек неравенство верно).

Для решения линейных неравенств с двумя переменными, используется графический способ.
Давай разберем вот такой пример:
Решение:
Как уже упоминалось, решается такое неравенство графически.

Построим график уравнения . Как ты уже должен был знать из темы «Линейные уравнения», графиком будет прямая.

Строим график по двум точкам, через которые проходит прямая, к примеру, и . Вот, что у меня получилось:

Так как неравенство в этом примере у нас строгое, то координаты точек самого графика прямой не будут являться решением исходного неравенства. Поэтому обозначим линию пунктиром на графике:

Как можно заметить, прямая разбила плоскость на две полуплоскости. Все точки одной из полуплоскостей будут являться решением исходного неравенства.

Так как в исходном неравенстве у нас стоит знак , то мы должны выбрать те точки, которые лежат выше графика прямой. Изобразим все решения неравенства на графике:

Все решения «затушеваны» голубым цветом. Вот и все, неравенство с двумя переменными решено. Это значит, что координаты и любой точки из закрашенной области – решения неравенства.

Линейные неравенства. коротко о главном

Линейными неравенствами называются неравенства вида:
где и – любые числа, причем ; — неизвестная переменная.
Правила преобразования неравенств:

Правило 1.

Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные).

Правило 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.

Правило 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак на знак , и наоборот; знак на знак , и наоборот).

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.

можно кликнув по этой ссылке.

Источник: https://youclever.org/book/linejnye-neravenstva-1

Решение линейных неравенств

Решение линейных неравенств Как записать ответ неравенства

Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.

Символ Название Тип знака

>	больше	строгий знак (число на границе не включается)
<	меньше	строгий знак (число на границе не включается)
≥	больше или равно	нестрогий знак (число на границе включается)
≤	меньше или равно	нестрогий знак(число на границе включается)

Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.

В отличии от уравнения в неравенстве вместо знака равно «=» используют любой знак сравнения: «>», « 0

Используем правило переноса и перенесём все числа без неизвестного, в правую часть.

2x − 16 > 0 2x > 16

Теперь нам нужно сделать так, чтобы при неизвестном «x» стоял коэффициент «1». Для этого достаточно разделить и левую, и правую часть на число «2».

Запомните!

При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.

Если неравенство умножается (делится) на положительное число, то знак самого неравенства остаётся прежним.
Если неравенство умножается (делится) на отрицательное число, то знак самого неравенства меняется на противоположный.

Разделим «2x > 16» на «2». Так как «2» — положительное число, знак неравенства останется прежним.

2x > 16 | (:2) 2x (:2) > 16 (:2) x > 8 Ответ: x > 8

Рассмотрим другое неравенство.
9 − 3x > 0
Используем правило переноса.
9 − 3x > 0 −3x > −9

Разделим неравенство на «−3». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.

−3x ≥ −9 −3x ≥ −9 | :(−3) −3x : (−3) ≤ −9 :(−3) x ≤ 3 Ответ: x ≤ 3

Примеры решения линейных неравенств

4(x − 1) ≥ 5 + x 4x − 4 ≥ 5 + x 4x − x ≥ 5 + 4 3x ≥ 9 | (:3) 3x (:3) ≥ 9 (:3) x ≥ 3 Ответ: x ≥ 3
x + 2 < 3(x + 2) − 4 x + 2 < 3x + 6 − 4 x − 3x < 6 − 4 − 2 −2x < 6 − 6−2x 0 : (−2) x > 0 Ответ: x > 0

Источник: http://math-prosto.ru/?page=pages/inequalities/solution_linear_inequality.php

Решение неравенств. Доступно о том, как решать неравенства

В статье рассмотрим решение неравенств. Расскажем доступно о том, как строиться решение неравенств, на понятных примерах!

Перед тем, как рассмотреть решение неравенств на примерах, разберемся с базовыми понятиями.

Общи сведения о неравенствах

Неравенством называется выражение, в котором функции соединяются знаками отношения >, , . Неравенства бывают как числовые, так и буквенные.
Неравенства с двумя знаками отношения, называются двойными, с тремя — тройными и т.д. Например:
a(x) > b(x),
a(x) < b(x),

a(x) b(x).
a(x) < c(x) < b(x) — двойное неравенство. Неравенства, содержащие знак > или < , называются строгими, а неравенства, содержащие

или — нестрогими.

Решением неравенства является любое значение переменой, при котором это неравенство будет верно.
«Решить неравенство» означает, что надо найти множество всех его решений. Существуют различные методы решения неравенств. Для решения неравенства пользуются числовой прямой, которая бесконечна. Например, решением неравенства x > 3 есть промежуток от 3 до +, причем число 3 не входит в этот промежуток, поэтому точка на прямой обозначается пустым кружком, т.к. неравенство строгое.
+
Ответ будет следующим: x (3; +).
Значение х=3 не входит в множество решений, поэтому скобка круглая. Знак бесконечности всегда выделяется круглой скобкой. Знак означает «принадлежание».
Рассмотрим как решать неравенства на другом примере со знаком :
x 2
— +
Значение х=2 входит в множество решений, поэтому скобка квадратная и точка на прямой обозначается закрашенным кружком.

Ответ будет следующим: x [2; +).

Свойства неравенств

Выделяют три основных свойства неравенств:

Можно перенести любой член неравенства из одной части неравенства в другую с противоположным знаком, при этом знак неравенства не меняется.

Пример: Зх + 5 > х2 равносильно Зх — х2 + 5 > 0, при этом x2 был перенесен с противоположным знаком.

Можно умножать или делить обе части неравенства на одно и то же положительное число, при этом знака неравенства не меняется.

Пример:
9х — 3 > 12х2 равносильно 3х — 1 > 4х2, при этом обе части первого неравенства были разделены на положительное число 3.

Можно умножить или разделить обе части неравенства на одно и то же отрицательное число, при этом знак неравенства меняется на противоположный.

Пример: -2х2 — Зх + 1 < 0 равносильно 2х2 + Зх — 1 > 0, при этом обе части первого неравенства умножили на отрицательное число -1, и знак неравенства изменился на противоположный.

Решение систем неравенств

Системой называется запись нескольких неравенств, обозначенная фигурной скобкой, при этом количество и вид неравенств, входящих в систему, может быть любым. Решением системы неравенств является пересечение решений всех неравенств, входящих в эту систему. Например, двойное неравенство f(x) < g(x) < h(x) записывается следующим образом: Пример.

Требуется решить следующую систему неравенств
Решение:
Система аналогична неравенству х > 1, поэтому ответ: x (1; +).

Решение линейных неравенств

Линейным называется неравенство вида ax>b, при этом знак неравенства может быть любым.
Допустим a>0, тогда ax>b равносильно , таким образом множество решений неравенства является промежуток .

Допустим a>0, тогда ax>b равносильно , таким образом множество решений неравенства является промежуток .
Если же a=0, тогда 0*x>b, т.е.

неравенство не имеет решений при b0, и верно при любых х при b 0, в котром a, b, c – некоторые действительные числа и a0
Простейшими квадратными неравенствами являются неравенства x2 < m и x2 > m
Множество решений неравенства x2 < m:

при m< 0 нет чисел, которые в квадрате дают отрицательное число (т.е. нет решений)

при m>0 x (-; ), т.е. — < x < или m:

при mR (т.е. x — любое действительное число);
при m>0 x (-; — ) (; +), т.е. — < x < — и < x < + или > .

Решение более сложных квадратных неравенств сводиться к простому переводу выражения вида
ax2 + bx + c > 0
в неравенство
(x-x1)(x-x2) > 0 , где x1 и х2 — корни квадратного уравнения ax2 + bx + c = 0.

Полученное неравенство мы раскладываем таким же образом на систему простых неравенств и легко находим решение.

Решение неравенств методом интервалов

Методом интервалов можно Формулу Неравества вида h(x) > 0 (,) свести к решению уравнения h(x) = 0.
Данный метод заключается в следующем:

Находится ОДЗ неравенства.
Неравенство приводится к виду h(x) > 0(

Источник: https://reshit.ru/Reshenie-neravenstv

Неравенства

Неравенство – это запись, в которой числа, переменные или выражения соединены знаком , ⩽ или ⩾. То есть неравенством можно назвать сравнение чисел, переменных или выражений. Знаки , ⩽ и ⩾ называются знаками неравенства.

Виды неравенств и как они читаются:

a < b	— a меньше b;
a > b	— a больше b;
a ⩽ b	— a меньше или равно b (a не больше b);
a ⩾ b	— a больше или равно b (a не меньше b).

Как видно из примеров, все неравенства состоят из двух частей: левой и правой, соединённых одним из знаков неравенства. В зависимости от знака, соединяющего части неравенств, их делят на строгие и нестрогие.

Строгие неравенства – неравенства, у которых части соединены знаком < или >. Нестрогие неравенства – неравенства, у которых части соединены знаком ⩽ или ⩾.

Рассмотрим основные правила сравнения в алгебре:

Любое положительное число больше нуля.
Любое отрицательное число меньше нуля.
Из двух отрицательных чисел больше то, у которого абсолютное значение меньше. Например, -1 > -7.
Если разность двух неравных чисел a и b положительна: a — b > 0, то a больше b (a > b).
Если разность двух неравных чисел a и b отрицательна: a — b < 0, то a меньше b (a < b).
Если число больше нуля, то оно положительное: a > 0, значит a – положительное число.
Если число меньше нуля, то оно отрицательное: a < 0, значит a – отрицательное число.

Равносильные неравенства – неравенства, являющиеся следствием другого неравенства. Например, если a меньше b, то b больше a:

a < b и b > a – равносильные неравенства

Если к обеим частям неравенства прибавить одно и то же число или вычесть из обеих частей одно и то же число, то получится равносильное неравенство, то есть,
если a > b, то a + c > b + c и a — c > b — c

Из этого следует, что можно переносить члены неравенства из одной части в другую с противоположным знаком. Например, прибавив к обеим частям неравенства a — b > c — d по d, получим:
- a — b > c — d
- a — b + d > c — d + d
- a — b + d > c
Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное неравенство, то есть,

если a > b, то ac > bc и a > b

c c

Если обе части неравенства умножить или разделить на одно и то же отрицательное число, то получится неравенство противоположное данному, то есть

если a > b умножить на -c, то -ac < -bc и —

-c

(-a + b) · -1 < (-c) · -1

a — b < c

Неравенство -a + b > -c равносильно неравенству a — b < c

Источник: https://naobumium.info/algebra/neravenstva.php

Числовые неравенства

1) Основное понятие неравенства

2) Основные свойства числовых неравенств. Неравенства содержащие переменную.

3) Графическое решение неравенств второй степени

4) Системы неравенств. Неравенства и системы неравенств с двумя переменными.

5) Решение рациональных неравенств методом интервалов
6) Решение неравенств, содержащих переменную под знаком модуля
1. Основное понятие неравенства

Неравенство [inequality] — соотношение между числами (или любыми математическими выражениями, способными принимать численное значение), указывающее, какое из них больше или меньше другого.

Над этими выражениями можно по определенным правилам производить следующие действия: сложение, вычитание, умножение и деление (причем при умножении или делении Н. на отрицательное число смысл его меняется на противоположный).

Одно из основных понятий линейного программирования — линейные неравенства вида

a1x1+ a2x2 +… + anxn * b,

где a1,…, an, b — постоянные и знак * — один из знаков неравенства, напр. ≥,

В матричной алгебре знак ≥ означает что все элементы матрицы, расположенной слева, не меньше (а хотя бы часть из них больше) соответствующих элементов матрицы, расположенной справа.

В отличие от этого знак ≤ означает, что все элементы левой матрицы не меньше соответствующих элементов правой матрицы; в частности, все соответствующие элементы могут быть попарно равны.

(Иногда применяются и другие обозначения.)

Классификация неравенств

Неравенства, содержащие неизвестные величины, подразделяются на:[1]
· алгебраические
· трансцендентные

Алгебраические неравенства подразделяются на неравенства первой, второй, и т. д. степени.

Пример:

Неравенство — трансцендентное.

2. Основные свойства числовых неравенств. Неравенства содержащие переменную

1) Если a>b , bc a>c;
3) Если a>b a+c>b+c;
4) Если a+b>c a> c-b;
5) Если обе части верного неравенства умножить на одно и то же положительное число, то получится верное неравенство;
6) Если обе части верного неравенства умножить на одно и то же число и изменить знак на противоположный, то получится верное неравенство;
7) Множество всех х, при которых имеют смысл выражения f(x) и g(x), называется областью определения неравенства f(x) >g(x);
8) Два неравенства, содержащие одну и ту же переменную, называются равносильными, если они имеют общее множество решений (множество решений этих неравенств совпадают);
9) Если к обеим частям неравенства прибавить(или вычесть) любую функцию J(x). область определения которой содержит область определения неравенств, то получится новое неравенств, равносильное данному;
10) Если обе части неравенства f(x) >g(x) умножить (или разделить) на любую функцию J(x), определенную для всех значений переменной х из области определения данного неравенства, сохраняющую постоянный знак и отличную от нуля, то при J(x)>0 получится неравенство, равносильное данном, а при J(x)

Неравенства с одной переменной. Пусть дано неравенство f(x) >g(x). Всякое значение переменной, при котором данное неравенство с одной переменной обращается в верное числовое неравенство, называется решением неравенства с одной переменной. Решить неравенство с переменной — значит найти все его решения или доказать, что их нет.

Два неравенства с одной переменной называются равносильными, если решения этих неравенств совпадают.
3. Графическое решение неравенств второй степени
1) Графиком квадратичной функции y = ах2 +bх + с является парабола с ветвями, направленными вверх, если а > 0, и вниз, если а < 0 (иногда говорят, что парабола направлена выпуклостью вниз, если а > 0 и выпуклостью вверх, если а < 0). При этом возможны три случая:

2) Парабола пересекает ось 0х (т. е. уравнение ах2 + bх + с = 0 имеет два различных корня). То есть, если а

y = ах2 +bх + с a>0 D>0 y = ах2 +bх + с aD>0,

Парабола имеет вершину на оси 0х (т. е. уравнение ах2 + х + с = 0 имеет один корень, так называемый двукратный корень) То есть, если d=0, то при a>0 решением неравенства служит вся числовая прямая, а при aах2 + х + с

y = ах2 +bх + с a>0 D= y = ах2 +bх + с aD=0,

3) Если d2 +bх + с не пересекает ось Ох и лежит выше этой оси при a>0 и ниже ее при a
4)
y = ах2 +bх + с a>0 D

Пусть требуется решить неравенство (x-α1)(x-α2)…(x-αn)>0, где α1, α2…αn-1, αn — фиксированные числа, среди которых нет равных, причем такие, что α1 < α2 0 методом интервалов поступают следующим образом: на числовую ось наносят числа α1, α2…αn-1, αn; в промежутке справа от наибольшего из них, т.е.

числа αn, ставят знак «плюс», в следующем за ним справа налево интервале ставят знак «минус», затем — знак «плюс», затем знак «минус» и т.д. Тогда множество всех решений неравенства (x-α1)(x‑α2)…

(x-αn)>0 будет объединение всех промежутков, в которых поставлен знак «плюс», а множество решений неравенства (x-α1)(x-α2)…(x‑αn)

1) Решение рациональных неравенств (т.е неравенств вида P(x) Q(x) где – многочлены) основано на следующем свойстве непрерывной функции: если непрерывная функция обращается в нуль в точках х1 и х2 (х1;х2) и между этими точками не имеет других корней, то в промежутках(х1;х2) функция сохраняет свой знак.

Поэтому для нахождения промежутков знакопостоянства функции y=f(x) на числовой прямой отмечают все точки, в которых функция f(x) обращается в нуль или терпит разрыв.

Эти точки разбивают числовую прямую на несколько промежутков, внутри каждого из которых функция f(x) непрерывна и не обращается в нуль, т.е. сохраняет знак.

Чтобы определить этот знак, достаточно найти знак функции в какой либо точке рассматриваемого промежутка числовой прямой.

2) Для определения интервалов знакопостоянства рациональной функции, т.е. Для решения рационального неравенства, отмечаем на числовой прямой корни числителя и корни знаменателя, которые как и являются корнями и точками разрыва рациональной функции.

Решение неравенств методом интервалов

3. < 20.

Решение. Область допустимых значений определяется системой неравенств:

.

Для функции f(x) = – 20. Находим f(x):

откуда x = 29 и x = 13.

f(30) = – 20 = 0,3 > 0,

f(5) = – 1 – 20 = – 10 < 0.

Ответ: [4; 29).

х2+х-2

Пусть f(x)=х2+х-2 тогда найдем такие х при которых f(x)

Источник: http://znakka4estva.ru/dokumenty/matematika/chislovye-neravenstva/