У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:

Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
![]()
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
![]()
Подставляем значения и вычисляем:

Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:

Теперь можно рассчитать КПД:

Или, умножая на 100, получаем значение КПД в процентах:

Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
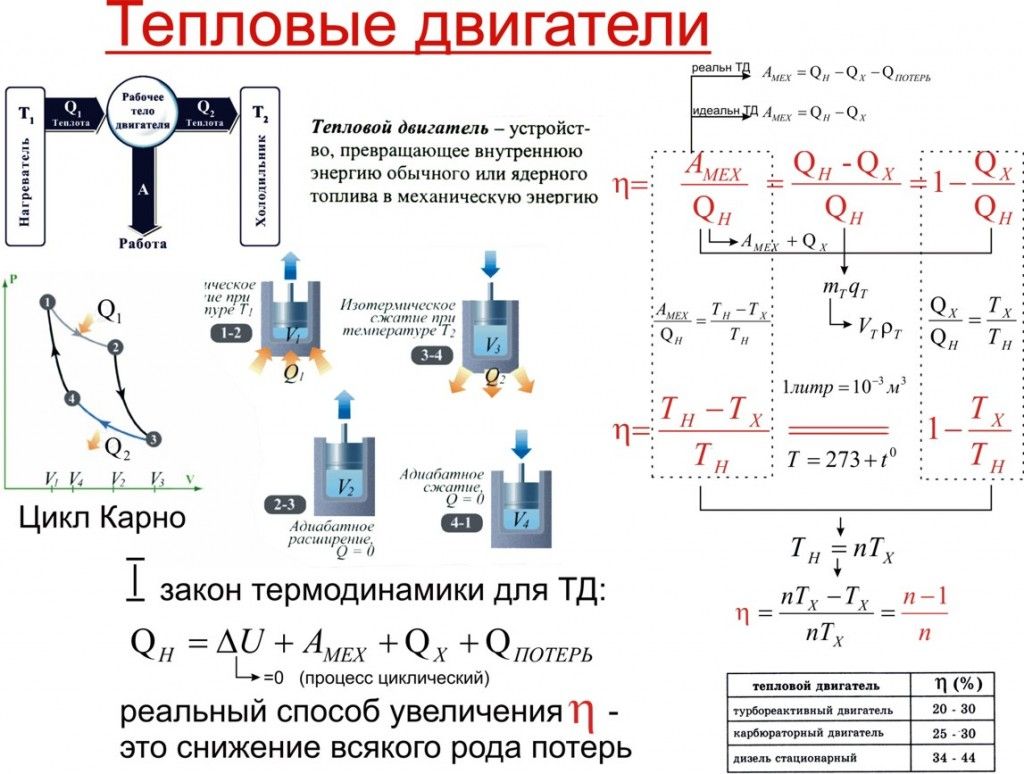
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:

По условию:
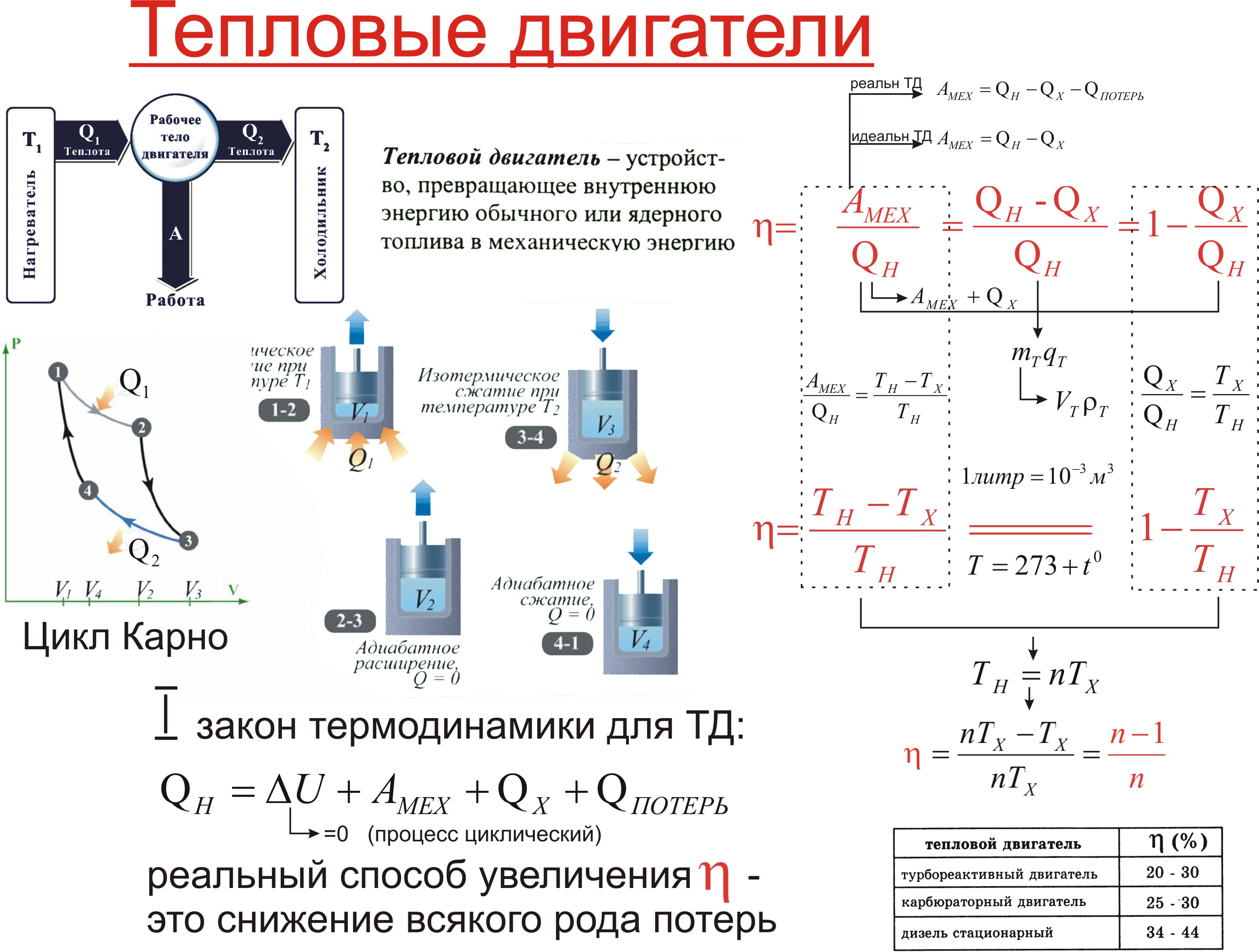
Вычислим сначала работу, а затем КПД:
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
- Аналогично:
- Получим результат:
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
- Решение
- Запишем формулу для КПД:
- Отсюда:
- Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
- Решение
- Рассчитаем КПД цикла:
- С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
- Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
- Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
- Решение
- Формула для КПД цикла Карно:
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
Ответ: 17%.
Задача на цикл Карно №3
- Условие
- Изобразите цикл Карно на диаграмме и опишите его
- Решение
- Цикл Карно на диаграмме PV выглядит следующим образом:
- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в х. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
Источник: https://Zaochnik-com.ru/blog/zadachi-na-kpd-teplovogo-dvigatelja-primery-reshenija/
По какой формуле находится работа. Коэффициент полезного действия. Формула, определение
Коэффициент полезного действия показывает отношение полезной работы, которая выполняется механизмом или устройством, к затраченной. Часто за затраченную работу принимают количество энергии, которое потребляет устройство для того, чтобы выполнить работу.
- Вам понадобится
- Автомобиль;
— термометр; - — калькулятор.
- Спонсор размещения P&G
Статьи по теме «Как найти коэффициент полезного действия»
Как вычислить КПД
Как посчитать КПД
Как найти силу трения - Инструкция
- Другие новости по теме:
- Полезная работа, выполняемая любой тепловой машиной, равна отношению разности теплоты полученной нагревателем и холодильником к теплоте, полученной нагревателем. В идеальной тепловой машине с максимальным КПД (цикл Карно), он равен отношению разности температур нагревателя и холодильника к
Для того чтобы рассчитать коэффициент полезного действия (КПД) поделите полезную работу Ап на работу затраченную Аз, а результат умножьте на 100% (КПД=Ап/Аз 100%). Результат получите в процентах.
При расчете КПД теплового двигателя, полезной работой считайте механическую работу, выполненную механизмом. За затраченную работу берите количество теплоты, выделяемое сгоревшим топливом, которое является источником энергии для двигателя.
Пример. Средняя сила тяги двигателя автомобиля составляет 882 Н. На 100 км пути он потребляет 7 кг бензина. Определите КПД его двигателя. Сначала найдите полезную работу. Она равна произведению силы F на расстояние S, преодолеваемое телом под ее воздействием Ап=F S. Определите количество теплоты, которое выделится при сжигании 7 кг бензина, это и будет затраченная работа Аз=Q=q m, где q – удельная теплота сгорания топлива, для бензина она равна 42 10^6 Дж/кг, а m – масса этого топлива. КПД двигателя будет равен КПД=(F S)/(q m) 100%= (882 100000)/(42 10^6 7) 100%=30%.
В общем случае чтобы найти КПД, любой тепловой машины (двигателя внутреннего сгорания, парового двигателя, турбины и т.д.), где работа выполняется газом, имеет коэффициент полезного действия равный разности теплоты отданной нагревателем Q1 и полученной холодильником Q2, найдите разность теплоты нагревателя и холодильника, и поделите на теплоту нагревателя КПД= (Q1-Q2)/Q1. Здесь КПД измеряется в дольных единицах от 0 до 1, чтобы перевести результат в проценты, умножьте его на 100.
Чтобы получить КПД идеальной тепловой машины (машины Карно), найдите отношение разности температур нагревателя Т1 и холодильника Т2 к температуре нагревателя КПД=(Т1-Т2)/Т1. Это предельно возможный КПД для конкретного типа тепловой машины с заданными температурами нагревателя и холодильника.
Для электродвигателя найдите затраченную работу как произведение мощности на время ее выполнения. Например, если электродвигатель крана мощностью 3,2 кВт поднимает груз массой 800 кг на высоту 3,6 м за 10 с, то его КПД равен отношению полезной работы Ап=m g h, где m – масса груза, g?10 м/с? ускорение свободного падения, h – высота на которую подняли груз, и затраченной работы Аз=Р t, где Р – мощность двигателя, t – время его работы. Получите формулу для определения КПД=Ап/Аз 100%=(m g h)/(Р t) 100%=%=(800 10 3,6)/(3200 10) 100%=90%. Как просто
Мощность электродвигателя, как правило, указывается в технической документации к нему или в специальной табличке на корпусе. Если так ее найти невозможно, рассчитайте ее самостоятельно. Это можно сделать, измерив ток в обмотках и напряжение на источнике. Также можно определить его мощность по
Коэффициент полезного действия (КПД) — это показатель эффективности какой либо системы, будь то двигатель автомобиля, машина или иной механизм. Он показывает, как эффективно данная система использует получаемую энергию. Вычислить КПД очень легко. Спонсор размещения P&G Статьи по теме «Как вычислить
Чтобы найти коэффициент полезного действия любого двигателя, нужно полезную работу поделить на затраченную и умножить на 100 процентов. Для теплового двигателя найдите данную величину по отношению мощности, умноженной на длительность работы, к теплу, выделившемуся при сгорании топлива. Теоретически
КПД (коэффициент полезного действия) – безразмерная величина, характеризующая эффективность работы. Работа есть сила, влияющая на процесс в течение некоторого времени. На действие силы затрачивается энергия. Энергия вкладывается в силу, сила вкладывается в работу, работа характеризуется
Для того чтобы найти номинальный ток для определенного проводника, воспользуйтесь специальной таблицей. В ней указывается, при каких значениях силы тока проводник может разрушиться. Для нахождения номинального тока для электрических двигателей различных конструкций, воспользуйтесь специальными
Коэффициент полезного действия (КПД)
— это характеристика результативности системы в отношении преобразования или передачи энергии, который определяется отношением полезно использованной энергии к суммарной энергии, полученной системой.
КПД
— величина безразмерная, обычно ее выражают в процентах: ![]()
Коэффициент полезного действия (КПД) теплового двигателя определяется по формуле: , где A = Q1Q2. КПД теплового двигателя всегда меньше 1.

Круговой цикл, включающий в себя две изотермы и две адиа- баты, соответствует максимальному КПД.
Французский инженер Сади Карно в 1824 г.
вывел формулу максимального КПД идеального теплового двигателя, где рабочее тело — это идеальный газ, цикл которого состоял из двух изотерм и двух адиабат, т. е. цикл Карно.
Цикл Карно — реальный рабочий цикл теплового двигателя, свершающего работу за счет теплоты, подводимой рабочему телу в изотермическом процессе.
![]()
Тепловые двигатели
— это конструкции, в которых тепловая энергия превращается в механическую.
Тепловые двигатели многообразны как по конструкции, так и по назначению. К ним относятся паровые машины, паровые турбины, двигатели внутреннего сгорания, реактивные двигатели.
Однако, несмотря на многообразие, в принципе действия различных тепловых двигателей есть общие черты. Основные компоненты каждого теплового двигателя:
- нагреватель;
- рабочее тело;
- холодильник.
Нагреватель выделяет тепловую энергию, при этом нагревает рабочее тело, которое находится в рабочей камере двигателя. Рабочим телом может быть пар или газ. Приняв количество теплоты, газ расширяется, т.к. его давление больше внешнего давления, и двигает поршень, производя положительную работу.
При этом его давление падает, а объем увеличивается. Если сжимать газ, проходя те же состояния, но в обратном направлении, то совершим ту же по абсолютному значению, но отрицательную работу. В итоге вся работа за цикл будет равна нулю.
Для того чтобы работа теплового двигателя была отлична от нуля, работа сжатия газа должна быть меньше работы расширения.
Чтобы работа сжатия стала меньше работы расширения, необходимо, чтобы процесс сжатия проходил при меньшей температуре, для этого рабочее тело нужно охладить, поэтому в конструкцию теплового двигателя входит холодильник. Холодильнику рабочее тело отдает при соприкосновении с ним количество теплоты.
Источник: https://les74.ru/by-what-formula-is-the-work-efficiency.html
Кпд определение и формула в физике
Физика — это наука, которая изучает процессы, происходящие в природе.
Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено.
Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.
Но в то же время физика — наука далеко непростая, как, собственно, и сама природа, но разобраться в ней было бы очень интересно. Сегодня мы будем говорить о коэффициенте полезного действия. Мы узнаем, что такое КПД и зачем он нужен. Рассмотрим все наглядно и интересно.
Определение и расшифровка КПД
Расшифровка аббревиатуры — коэффициент полезного действия. Однако и такое толкование с первого раза может оказаться не особо понятным. Этим коэффициентом характеризуется эффективность системы или какого-либо отдельного тела, а чаще — механизма. Эффективность характеризуется отдачей или преобразованием энергии.
Этот коэффициент применим практически ко всему, что нас окружает, и даже к нам самим, причём в большей степени. Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».
Важно учесть, что этот коэффициент — величина неограниченная, она, как правило, представляет собой либо математические значения, к примеру, 0 и 1, либо же, как это чаще бывает — в процентах.
В физике этот коэффициент обозначается буквой Ƞ, или, как её привыкли называть, Эта.
Полезная работа
При использовании каких-либо механизмов или устройств мы обязательно совершаем работу. Она, как правило, всегда больше той, что необходима нам для выполнения поставленной задачи.
Исходя из этих фактов различается два типа работы: это затраченная, которая обозначается большой буквой, А с маленькой з (Аз), и полезная — А с буквой п (Ап). Для примера, возьмем такой случай: у нас есть задача поднять булыжник определенной массой на определенную высоту.
В этом случае работа характеризует только преодоление силы тяжести, которая, в свою очередь, действует на груз.
В случае когда для подъема применяется какое-либо устройство, кроме силы тяжести булыжника, важно учесть еще и силу тяжести частей этого устройства. И кроме всего этого, важно помнить, что, выигрывая в силе, мы всегда будем проигрывать в пути.
Все эти факты приводят к одному выводу, что затрачиваемая работа в любом варианте окажется больше полезной, Аз > Ап, вопрос как раз заключается в том, насколько её больше, ведь можно максимально сократить эту разницу и тем самым увеличить КПД, наш или нашего устройства.
Полезная работа — это часть затрачиваемой, которую мы совершаем, используя механизм. А КПД — это как раз та физическая величина, которая показывает, какую часть составляет полезная работа от всей затраченной.
Итог:
- Затрачиваемая работа Aз всегда больше полезной Ап.
- Чем больше отношение полезной к затрачиваемой, тем выше коэффициент, и наоборот.
- Ап находится произведением массы на ускорение свободного падения и на высоту подъема.

Физическая формула КПД
Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.
Кран шаровый маркировка таблица
Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.
В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.
Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
Итак, формула КПД:
Ƞ=А/Q, где
- A — полезная работа, которую выполняет система.
- Q — энергия, которую потребляет система.
Применение в разных сферах физики
Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.
Рассмотрим несколько из примеров процессов с наличием КПД.
К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую.
В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1.
Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.

Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.
Видео
Это видео поможет вам понять, что такое КПД.
Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта») [1] . КПД является безразмерной величиной и часто измеряется в процентах.
Содержание
Определение [ править | править код ]
- Математически КПД определяется как
- η = A Q ,
- где А — полезная работа (энергия), а Q — затраченная энергия.
- Если КПД выражается в процентах, эту формулу иногда записывают в виде
- η = A Q × 100 % .
Здесь умножение на 100 % не несёт содержательного смысла, поскольку 100 % = 1 . В связи с этим второй вариант записи формулы менее предпочтителен (одна и та же физическая величина может быть выражена в различных единицах независимо от формул, где она участвует).
В силу закона сохранения энергии и в результате неустранимых потерь энергии КПД реальных систем всегда меньше единицы, то есть невозможно получить полезной работы больше или столько, сколько затрачено энергии.
КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле
Меры безопасности при работе под напряжением
где Q 1 — количество теплоты, полученное от нагревателя, Q 2 — количество теплоты, отданное холодильнику. Наибольшим КПД среди циклических машин, оперирующих при заданных температурах нагревателя T1 и холодильника T2, обладают тепловые двигатели, работающие по циклу Карно; этот предельный КПД равен
η k = T 1 − T 2 T 1
Другие похожие показатели [ править | править код ]
Не все показатели, характеризующие эффективность энергетических процессов, соответствуют вышеприведённому описанию. Даже если они традиционно или ошибочно называются «коэффициент полезного действия», они могут иметь другие свойства, в частности, превышать 100 %.
КПД котлов [ править | править код ]
КПД котлов на органическом топливе традиционно рассчитывается по низшей теплоте сгорания; при этом предполагается, что влага продуктов сгорания покидает котёл в виде перегретого пара. В конденсационных котлах эта влага конденсируется, теплота конденсации полезно используется.
При расчёте КПД по низшей теплоте сгорания он в итоге может получиться больше единицы. В данном случае корректнее было бы считать его по высшей теплоте сгорания, учитывающей теплоту конденсации пара; однако при этом показатели такого котла трудно сравнивать с данными о других установках.
Тепловые насосы и холодильные машины [ править | править код ]
Достоинством тепловых насосов как нагревательной техники является возможность получать больше теплоты, чем расходуется энергии на их работу. Холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается энергии на организацию процесса.
- Эффективность машин характеризует холодильный коэффициент (англоязычный аналог COP)
- ε X = Q X / A ,
- где Q X — тепло, отбираемое от холодного конца (в холодильных машинах холодопроизводительность); A — затрачиваемая на этот процесс работа (или электроэнергия).
- Для тепловых насосов используют термин коэффициент трансформации
- ε Γ = Q Γ / A ,
- где Q Γ — тепло конденсации, передаваемое теплоносителю; A — затрачиваемая на этот процесс работа (или электроэнергия).
- В идеальной машине Q Γ = Q X + A , отсюда для идеальной машины ε Γ = ε X + 1
- Наилучшими показателями производительности для холодильных машин обладает обратный цикл Карно: в нём холодильный коэффициент
- ε = T X T Γ − T X over -T_ >>> ,
где T Γ , T X — температуры горячего и холодного концов, K [2] .
Данная величина, очевидно, может быть сколь угодно велика; хотя практически к ней трудно приблизиться, холодильный коэффициент может превосходить единицу.
Это не противоречит первому началу термодинамики, поскольку, кроме принимаемой в расчёт энергии A (напр., электрической), в тепло Q идёт и энергия, отбираемая от холодного источника.
Полезное действие
Рассмотрим устройство, которое поднимает груз массы m на высоту H. В идеальном случае работа совершается только против силы тяжести. Таким образом, энергия, которую необходимо затратить для подъема груза, равна mgH. Но в реальности в любом устройстве наличествует сила трения; а также сила тяжести действует и на само устройство.
Рис. 1. Подъем груза через блок.
Таким образом, та энергия, которую необходимо затратить в идеальном случае, называется полезной работой, а вся энергия, необходимая для выполнения задачи – затраченной работой.
Что такое коэффициент полезного действия
Отношение полезной работы к затраченной – это коэффициент полезного действия. Для двигателя внутреннего сгорания, на котором работает большая часть автомобилей, КПД колеблется в пределах 20-25%.
Часть энергии тратится на нагрев деталей, часть – на преодоление трения, вдобавок к этому не всё топливо сгорает, а еще большая доля тепла выходит с выхлопными газами.
Для сравнения КПД электромобиля составляет примерно 94%.
Рис. 2. Потери ДВС.
Формула коэффициента полезного действия в общем виде выглядит так:
Красивая крыша для гаража
- где А – полезная работа, а Q – вся энергия, затраченная на выполнения задачи
- КПД теплового двигателя циклической машины определяется по формуле:
- где $Q_1 – Q_2$ – разность полученного тепла и тепла, отданного холодильнику.
- Максимальный КПД теплового двигателя, работающего по циклу Карно, равен:
- где $T_1$ – температура нагревателя, а $T_2$ – холодильника.
Рис. 3. Цикл Карно.
В случае электродвигателя КПД можно найти по формуле:
где P_2 – полезная мощность, затраченная на преобразование электрической энергии в механическую, а P_1 – общая мощность двигателя.
Задачи
- В чайник налили 1,5 л холодной воды, ее температура – 283˚ К. Чтобы довести ее до кипения, понадобилось 6 минут. Сила тока, потребляемая чайником – 11 А. Напряжение в электрической сети – 228 В. Рассчитать КПД чайника.
Решение
Полезной работой в этом случае будет энергия, которая необходима для разогрева воды от 283˚ К до 373˚ К. Затраченной работой будет мощность чайника, умноженная на время закипания. Поэтому формулу КПД чайника запишем так:
Так как $m =
ho V$, а $P = UI$, то окончательная формула КПД чайника будет выглядеть так:
Подставив в нее данные из условия, получим, что $eta = 0,63$. Или в процентах – 63%.
- С помощью механического устройства груз массой 9 кг подняли на 20 м. КПД устройства – 70%. Найти силу, которую необходимо приложить к устройству, чтобы поднять груз.
Решение
И $F = = 130 Н$ – сила, которую необходимо приложить к устройству.
Что мы узнали?
В ходе урока были разобраны два важнейших понятия – полезная работа и затраченная работа, было дано определение коэффициента полезного действия, приведена его общая формула, а также ее частные вариации для различных устройств. В заключении урока разобраны две задачи.
Тест по теме
Оценка доклада
Средняя оценка: 4.7 . Всего получено оценок: 141.
Не понравилось? — Напиши в х, чего не хватает.
Содержание
- Полезное действие
- Что такое коэффициент полезного действия
- Задачи
- Что мы узнали?
Бонус
- Потенциальная энергия
- Броуновское движение
- Золотое правило механики Коэффициент полезного действия
- Превращение энергии
- Центр тяжести тела
- Условия равновесия тел
- Единицы мощности
- Закон сохранения энергии
- Кинетическая и потенциальная энергия
- Кинетическая энергия покоя
- Кинетическая энергия вещества
- Закон сохранения механической энергии
- показать все
- По многочисленным просьбам теперь можно: сохранять все свои результаты, получать баллы и участвовать в общем рейтинге.
- 1. Данил Лысогорский 356
- 2. анастасия паранина 228
- 3. Parlefiano Fuello 169
- 4. Ксю Пашнина 143
- 5. Антон Огурцов 106
- 6. Валерий Рубцов 104
- 7. No-Name No-Famili 100
- 8. Алина Сайбель 84
- 9. Михаил Беляев 77
- 10. Мария Корнеева 77
- 1. Мария Николаевна 13,550
- 2. Лариса Самодурова 12,795
- 3. Liza 12,355
- 4. Кристина Волосочева 11,595
- 5. TorkMen 11,476
- 6. Ekaterina 11,361
- 7. Юлия Бронникова 11,235
- 8. Влад Лубенков 11,125
- 9. Лиса 11,070
- 10. Вячеслав 10,865
Самые активные участники недели:
- 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
- 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
- 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.
Три счастливчика, которые прошли хотя бы 1 тест:
- 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
- 2. Николай З — подарочная карта книжного магазина на 500 рублей.
- 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.
Источник: https://englishpromo.ru/stroitelstvo/kpd-opredelenie-i-formula-v-fizike
Коэффициент полезного действия механизмов (КПД)
Известно, что вечный двигатель невозможен. Это связано с тем, что для любого механизма справедливо утверждение: совершённая с помощью этого механизма полная работа (в том числе на нагревание механизма и окружающей среды, на преодоление силы трения) всегда больше полезной работы.
Например, больше половины работы двигателя внутреннего сгорания совершается впустую тратится на нагревание составных частей двигателя; некоторое количество теплоты уносят выхлопные газы.
Часто необходимо оценивать эффективность механизма, целесообразность его использования. Поэтому, чтобы рассчитывать, какая часть от совершённой работы тратится впустую и какая часть с пользой, вводится специальная физическая величина, которая показывает эффективность механизма.
Эта величина называется коэффициентом полезного действия механизма
Коэффициент полезного действия механизма равен отношению полезной работы к полной работе. Очевидно, коэффициент полезного действия всегда меньше единицы. Эту величину часто выражают в процентах. Обычно её обозначают греческой буквой η (читается «эта»). Сокращённо коэффициент полезного действия записывают КПД.
η = (А_полн /А_полезн) * 100 %,
где η КПД, А_полн полная работа, А_полезн полезная работа.
Среди двигателей наибольший коэффициент полезного действия имеет электрический двигатель (до 98 %). Коэффициент полезного действия двигателей внутреннего сгорания 20 % — 40 %, паровой турбины примерно 30 %.
Отметим, что для увеличения коэффициента полезного действия механизма часто стараются уменьшить силу трения. Это можно сделать, используя различные смазки или шарикоподшипники, в которых трение скольжения заменяется трением качения.
Примеры расчета КПД
Рассмотрим пример. Велосипедист массой 55 кг поднялся на велосипеде массой 5 кг на холм, высота которого 10 м, совершив при этом работу 8 кДж. Найдите коэффициент полезного действия велосипеда. Трение качения колёс о дорогу не учитывайте.
- Решение. Найдём общую массу велосипеда и велосипедиста:
- m = 55 кг + 5 кг = 60 кг
- Найдем их общий вес:
- P = mg = 60 кг * 10 Н/кг = 600 Н
- Найдём работу, совершённую на подъём велосипеда и велосипедиста:
- Aполезн = РS = 600 Н * 10 м = 6 кДж
- Найдём КПД велосипеда:
- = А_полн /А_полезн * 100 % = 6 кДж / 8 кДж * 100 % = 75 %
- Ответ: КПД велосипеда равен 75 %.
Рассмотрим ещё один пример. На конец плеча рычага подвешено тело массой m. К другому плечу прилагают силу F, направленную вниз, и его конец опускается на h. Найдите, насколько поднялось тело, если коэффициент полезного действия рычага равен η %.
Решение. Найдём работу, совершённую силой F:
A = Fh
η % от этой работы совершено на то, чтобы поднять тело массой m. Следовательно, на поднятие тела затрачено Fhη / 100. Так как вес тела равен mg, тело поднялось на высоту Fhη / 100 / mg.
Ответ: тело поднялось на высоту Fhη / 100 / mg.
Нужна помощь в учебе?
 Предыдущая тема: Приложение закона равновесия рычага к блоку: золотое правило механики
Предыдущая тема: Приложение закона равновесия рычага к блоку: золотое правило механики
Следующая тема: Энергия: потенциальная и кинетическая энергия
Источник: http://www.nado5.ru/e-book/koehfficient-poleznogo-deistviya-mekhanizmov
Коэффициент полезной работы
Определение
Коэффициентом полезного действия (КПД) называют отношение полезной работы к полной. Обозначим КПД буквой $eta $, тогда:
[eta =frac{A_p}{A_{poln}} left(2right).]
[eta =frac{A_p}{A_{poln}}cdot 100% left(2right).]
При создании механизмов пытаются увеличить их КПД, но механизмов с коэффициентом полезного действия равным единице (а тем более больше единицы) не существует.
https://www.youtube.com/watch?v=ytadvertiseru
И так, коэффициент полезного действия – это физическая величина, которая показывает долю, которую полезная работа составляет от всей произведенной работы. При помощи КПД оценивают эффективность устройства (механизма, системы), преобразующей или передающей энергию, совершающего работу.
[A_papprox A_{poln}left(3right).]
Понятие мощности
Единицей измерения мощности в системе СИ является ватт.
Мощность характеризует быстроту совершения работы. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина или механизм.
где — сила, совершающая работу, — скорость движения тела.
Золотое правило механики
Необходимо помнить, что выигрыша в работе, используя простой механизм добиться нельзя.
[F_1s_1approx F_2s_2left(4right).]
Выражение (4) показывает, что используя простой механизм, мы выигрываем в силе столько же, сколько проигрываем в пути. Данный закон называют «золотым правилом» механики. Это правило сформулировал в древней Греции Герон Александрийский.
Это правило не учитывает работу по преодолению сил трения, поэтому является приближенным.
Примеры задач на коэффициент полезного действия
Пример 1
Задание. Двигатель подъемного крана имеет мощность $N$. За отрезок времени равный $Delta t$ он поднял груз массой $m$ на высоту $h$. Каким является КПД крана?textit{}
Решение. Полезная работа в рассматриваемой задаче равна работе по подъему тела на высоту $h$ груза массы $m$, это работа по преодолению силы тяжести. Она равна:
[A_p=mgh left(1.1right).]
Полную работу, которая выполняется при поднятии груза, найдем, используя определение мощности:
[N=frac{A_{poln}}{Delta t}to A_{poln}=NDelta tleft(1.2right).]
Воспользуемся определением коэффициента полезного действия для его нахождения:
[eta =frac{A_p}{A_{poln}}cdot 100%left(1.3right).]
Формулу (1.3) преобразуем, используя выражения (1.1) и (1.2):
[eta =frac{mgh}{NDelta t}cdot 100%.]
Ответ. $eta =frac{mgh}{NDelta t}cdot 100%$
Пример 2
Задание. Идеальный газ выполняет цикл Карно, при этом КПД цикла равно $eta $. Какова работа в цикле сжатия газа при постоянной температуре? Работа газа при расширении равна $A_0$
Решение. Коэффициент полезного действия цикла определим как:
[eta =frac{A_p}{Q}left(2.1right).]
Рассмотрим цикл Карно, определим, в каких процессах тепло подводят (это будет $Q$).

Так как цикл Карно состоит из двух изотерм и двух адиабат, можно сразу сказать, что в адиабатных процессах (процессы 2-3 и 4-1) теплообмена нет. В изотермическом процессе 1-2 тепло подводят (рис.
1 $Q_1$), в изотермическом процессе 3-4 тепло отводят ($Q_2$). Получается, что в выражении (2.1) $Q=Q_1$.
Мы знаем, что количество теплоты (первое начало термодинамики), подводимое системе при изотермическом процессе идет полностью на выполнение газом работы, значит:
[Q=Q_1=A_{12}left(2.2right).]
Газ совершает полезную работу, которую равна:
[A_p=Q_1-Q_2left(2.3right).]
Количество теплоты, которое отводят в изотермическом процессе 3-4 равно работе сжатия (работа отрицательна) (так как T=const, то $Q_2=-A_{34}$). В результате имеем:
[A_p=A_{12} A_{34}left(2.4right).]
Преобразуем формулу (2.1) учитывая результаты (2.2) – (2.4):
[eta =frac{A_{12} A_{34}}{A_{12}}to A_{12}eta =A_{12} A_{34}to A_{34}=(eta -1)A_{12}left(2.4right).]
- Так как по условию $A_{12}=A_0, $окончательно получаем:
- [A_{34}=left(eta -1right)A_0.]
- Ответ. $A_{34}=left(eta -1right)A_0$
Все механизмы или двигатели предназначены для выполнения определенной механической работы, которую называют полезной работой. Однако любой машине приходится совершать большую по величине работу, так как вследствие действия сил трения некоторая часть подводимой к машине энергии не преобразовывается в механическую работу.
Эффективность работы машины или механизма характеризуют коэффициентом полезного действия.
где и полезная и затраченная мощности соответственно.
Кпд при передаче энергии
- [eta =frac{A_p}{Q}cdot 100% left(5right).]
- [eta =frac{Q_n-Q_{ch}}{Q_n}left(6right),]
- где $Q_n$ – количество теплоты, полученное от нагревателя; $Q_{ch}$ – количество теплоты переданное холодильнику.
- [eta =frac{T_n-T_{ch}}{T_n}left(7right),]
Источник: https://kz-nn.ru/koeffitsient-poleznoy-raboty/
Мощность и коэффициент полезного действия — урок. Физика, 8 класс
Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.
Среднее значение мощности — это работа, выполненная за единицу времени.
- Величина мощности прямо пропорциональна величине совершённой работы (A) и обратно пропорциональна времени (t), за которое работа была совершена.
- Мощность (N) определяют по формуле:
- N=At.
- Единицей измерения мощности в системе (СИ) является (Ватт) (русское обозначение — (Вт), международное — (W)).
Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт.
Пример:
Мощность двигателя автомобиля равна примерно (90 л.с. = 66240 Вт).
- Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля (F) и скорость его движения (v).
- N=F⋅v
- Эту формулу получают, преобразуя основную формулу определения мощности.
Ни одно устройство не способно использовать (100) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.
Пример:
Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс).
При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах (40 — 45) %.
Таким образом, получается, что только около (40) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.
Если мы заправим в бак автомобиля (20) литров бензина, тогда только (8) литров будут расходоваться на перемещение автомобиля, а (12) литров сгорят без совершения полезной работы.
Коэффициент полезного действия обозначается буквой греческого алфавита («эта») η, он является отношением полезной мощности (N) к полной или общей мощности Nполная.
Для его определения используют формулу: η=NNполная. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.
Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η=NNполная⋅100%.
Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы (A) к общей или полной проделанной работе Aполная. В этом случае формула для определения коэффициента полезного действия будет выглядеть так:
η=AAполная⋅100%.
Коэффициент полезного действия всегда меньше (1), или (100) % (η < 1, или η < (100) %).
Источники:
E. Šilters, V. Regusts, A. Cābelis. «Fizika 10. klasei», Lielvārds, 2004, 256 lpp.
(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)
Источник: https://www.yaklass.ru/p/fizika/8-klass/teplovye-iavleniia-12324/vnutrenniaia-energiia-dva-sposoba-izmeneniia-vnutrennei-energii-rabota-i-_-12579/re-49e67d7d-4fef-4f21-89cb-1c63e11559ac
Формула КПД
Для оценки эффективности расхода энергии на выполнение работы необходимо выяснить, как найти КПД. Полученные сведения пригодятся для оптимизации параметров электрических компонентов цепи, рычагов и других передаточных механизмов. С помощью предварительных вычислений можно увеличить длительность действия автономного источника питания, решить другие практические задачи.
Формула КПД поясняет основные определения
Что такое КПД источника тока
Неподвижный заряд не выполняет работу. Уменьшение энергетического запаса в аккумуляторе происходит за счет химических реакций. Фактически это свидетельство несовершенства конструкции.
После подключения источника к проводникам с подключенной нагрузкой заряды перемещаются по цепи, выполняя определенную работу. Полезная составляющая мощности (Pпол) определяется параметрами внешнего контура. Полная (Pп) – содержит совокупные затраты. Если электротехник пользуется привычными терминами, он быстро установит для коэффициента полезного действия формулу:
КПД = Рпол/Рп = (U*I)/(Е*I) = U/E.
Для чего нужен расчет КПД
Как рассчитать потребление электрической энергии
Наглядный пример недостаточно эффективного устройства – классическая лампа накаливания. Пропускание тока через вольфрамовую спираль повышает температуру проводника.
В рабочем режиме значительное количество потребляемой мощности расходуется на генерацию излучения. Однако к видимой части диапазона относится только небольшая часть спектра.
Так как вырабатываемая теплота не выполняет полезного действия, соответствующие энергетические затраты следует узнавать по излишним.
Если выразить КПД через мощность в этом случае, следует одновременно учесть долговечность. Эта методика повышает точность оценки, так как подразумевает необходимость периодической замены испорченного излучателя.
В типовом рабочем режиме лампа накаливания нагревает нить до 2600-2800К. При таком значении срок службы составляет 900-1200 часов, КПД – от 5 до 7%. Увеличить эффективность в 2-5 раз можно повышением температуры до 3400-3600К. Однако в этом варианте долговечность уменьшается до 5-6 часов. Подобные практические характеристики нельзя признать удовлетворительными.
Сравнение эффективности и других параметров разных типов ламп
Эта таблица демонстрирует превосходство экономичных источников света. Срок службы современных светодиодов измеряется десятками тысяч часов. Даже на завершающих этапах рабочих циклов обеспечиваются высокая яркость и качественное распределение спектральных составляющих.
Нахождение тока в полной цепи
Для изучения эффективности потребления энергии в электротехнике можно использовать базовые формулы. В полной цепи по базовому определению рассматривают источник тока (I) с внутренним сопротивлением (r). Подключенная нагрузка потребляет определенную мощность. Она характеризуется электрическим сопротивлением R.
Прохождение тока по такой цепи обеспечивает энергия источника, которая определена значением электродвижущей силы (ЭДС – E).
Ее можно выразить как отношение выполненной сторонними силами работы (A) по передвижению заряда (q) с положительным знаком по соответствующему контуру.
С учетом известной формулы I= q/t несложно определить зависимость между рассматриваемыми величинами:
А = E * I * t,
где t – контрольный временной интервал.
Отдельно можно рассмотреть участки с внутренним и внешним сопротивлением. Каждый из них выделяет определенное законом Джоуля-Ленца количество теплоты Q = I2 * R * t. Так как энергия не пропадает бесследно, можно сделать правильный вывод о равенстве Q = A. Подставив значения в исходное выражение, получают:
- E = I*R + I*r.
- ЭДС полной цепи вычисляется сложением двух падений напряжений на внутреннем и внешнем участке. Элементарное преобразование позволяет узнать силу тока в соответствующем проводнике:
- I = E/ (R+r).
Расчет КПД электрической цепи
Частота вращения: формула
После определения основных параметров можно перейти к изучению эффективности системы. Для вычисления КПД обозначение потребления электроэнергии удобно сделать по стандартным формулам.
Определить мощность можно по следующим соотношениям силы тока, напряжения, электрического сопротивления
Выполняемая работа в цепи определяется количеством перемещенных зарядов, а также скоростью данного процесса. Для объективной оценки последнего параметра измерения выполняют с учетом определенных временных интервалов (Δt). Работу и мощность можно определить следующими формулами:
Как и в классической механике, работу можно измерить в джоулях (Дж). Мощность, по стандартам СИ, указывают в ваттах (Вт). Зависимость между отмеченными единицами:
- Вт = Дж/ с (для электрических цепей вольт * ампер).
- Для обозначения КПД символ «η» применяют в типовых формулах. Базовое определение с учетом приведенных замечаний можно преобразовать следующим образом:
- η = A / Q * 100%,
- где:
- A – выполненная работа;
- Q – энергия, полученная из источника.
Как найти КПД, формула для полной цепи
Любое подключенное устройство характеризуется определенными потерями. Резистор выделяет тепло. Трансформатор тратит часть энергии на преобразование электромагнитных волн.
На примере лампы накаливания показана низкая эффективность изделия. С применением КПД увеличивают объективность оценки разных систем, подключаемых потребителей, генераторов.
В следующем пункте представлена технология проверки силовых агрегатов.
Методика и порядок измерений
Идеальные условия можно рассматривать только в теории. Для корректной оценки замкнутой системы необходимо учитывать энергетические потери на выполнение необходимой работы. Ниже показано, как определить КПД механических силовых агрегатов с применением разных исходных данных.
Движению поршня в блоке цилиндров двигателя внутреннего сгорания препятствует сила трения. Поступательно-возвратные движения в ходе стандартного цикла преобразуются во вращение вала с дополнительными потерями.
Высокая температура не выполняет в данном случае полезные функции. Чтобы не допустить разрушения агрегата, необходимо поддерживать определенный тепловой режим.
Приходится обеспечить циркуляцию охлаждающей жидкости с помощью помпы.
Понятно, что в подобном случае сделать общий КПД расчет с учетом каждого компонента конструкции непросто. Однако можно узнать в ходе эксперимента с высокой точностью, какое количество топлива (масса – m) придется затратить на 100 км пробега машины за соответствующее время (t). Далее нужно взять из сопроводительной документации (справочников) следующие данные:
- мощность мотора – Рм;
- удельную теплоту бензина – У.
- В этом варианте для расчета КПД двигателя формула преобразуется следующим образом:
- η = (Pм * t) / (У * m).
- Для отображения результата в % итоговое значение умножают на 100.
Если мощность силового агрегата не известна, определять эффективность можно по массе авто (Mа). Измерять ее несложно с помощью промышленных весов (на станции техосмотра, элеваторе). В ходе эксперимента разгоняются с места до контрольной скорости (v). Массу топлива вычисляют по объему (переведенному из литров в м кв.), который умножают на плотность (справочная величина в кг на куб. м).
- В этом случае КПД расчет находят по формуле:
- η = (Mа * v2)/(2 * У * m).
- Следует перевести предварительно скорость из км/час в м/с.
Проще измеряется эффективность электродвигателя с паспортной мощностью (P). Его подключают к источнику питания с известным напряжением (U). После выхода на стабильную частоту вращения фиксируют значение тока (I) в цепи. Далее применяют классическую формулу:
η = P/ (U * I).
Если сопроводительная документация отсутствует, технические параметры берут с официального сайта производителя. Однако и в этом случае следует понимать ограниченную точность подобных данных.
В процессе эксплуатации характеристики могут ухудшиться за счет естественного износа.
Погрешность увеличивается после длительной интенсивной эксплуатации, при подключении редуктора или другого переходного устройства.
Значительно улучшить точность можно с применением простой методики:
- устанавливают на вал шкив с закрепленным тросом;
- поднимают на контрольную высоту (h) груз c массой m;
- секундомером фиксируют время (t) на выполнение этой работы;
- мультиметром измеряют напряжение (U) и силу тока (I) на клеммах источника питания и в разрыве цепи, соответственно.
- Для нахождения КПД в физике формула выглядит следующим образом:
- η = (m * h * g)/(I * U * t),
- где g – это гравитационная постоянная (9,80665).
Эффективность любого силового агрегата определяют по соотношению полезной работы к расходованной энергии. Чтобы корректно определять класс техники, пользуются переводом в проценты. Следует подчеркнуть, что значение больше 100% обозначает ошибку в расчетах. Создатель подобного агрегата станет «властелином мира», так как изобретет вечный двигатель.
Видео
Источник: https://amperof.ru/teoriya/formula-kpd.html
Коэффициент полезного действия (КПД) — формулы и расчеты — Помощник для школьников Спринт-Олимпиады
Эффективность и продолжительность работы силового агрегата зависит от коэффициента полезного действия (КПД). При эксплуатации двигатель превращает тепловую энергию, которая образуется в результате сгорания топлива в механическую. Чтобы найти коэффициент, учитываются характеристики мотора. Формула КПД в физике представлена в виде процентного отношения полезной работы к общей.
Трактовка понятия
Электродвигатель и другие механизмы выполняют определённую работу, которая называется полезной. Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:
- А1 — полезная работу, которую выполняет машина либо мотор;
- А2 — общий цикл работы;
- η – обозначение КПД.
Показатель измеряется в процентах. Для нахождения коэффициента в математике используется следующая формула: η= А/Q, где А — энергия либо полезная работа, а Q — затраченная энергия. Чтобы выразить значение в процентах, КПД умножается на 100%. Действие не несёт содержательного смысла, так как 100% = 1. Для источника тока КПД меньше единицы.
В старших классах ученики решают задачи, в которых нужно найти КПД тепловых двигателей. Понятие трактуется следующим образом: отношение выполненной работы силового агрегата к энергии, полученной от нагревателя. Расчет производится по следующей формуле: η= (Q1-Q2)/Q1, где:
- Q1 — теплота, полученная от нагревательного элемента;
- Q2 — теплота, отданная холодильной установке.
Максимальное значение показателя характерно для циклической машины. Она оперирует при заданных температурах нагревательного элемента (Т1) и холодильника (Т2). Измерение осуществляется по формуле: η= (Т1-Т2)/Т1. Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.
Плюс теплового насоса как нагревательного прибора заключается в возможности получать больше энергии, чем он может затратить на функционирование. Показатель трансформации вычисляется путём деления тепла конденсации на работу, затрачиваемую на выполнение данного процесса.
Мощность разных устройств
По статистике, во время работы прибора теряется до 25% энергии. При функционировании двигателя внутреннего сгорания топливо сгорает частично. Небольшой процент вылетает в выхлопную трубу. При запуске бензиновый мотор греет себя и составные элементы. На потерю уходит до 35% от общей мощности.
При движении механизмов происходит трение. Для его ослабления используется смазка. Но она неспособна полностью устранить явление, поэтому затрачивается до 20% энергии. Пример на автомобиле: если расход составляет 10 литров топлива на 100 км, на движение потребуется 2 л, а остаток, равный 8 л — потеря.
Если сравнивать КПД бензинового и дизельного моторов, полезная мощность первого механизма равна 25%, а второго — 40%. Агрегаты схожи между собой, но у них разные виды смесеобразования:
Асинхронные механизмы
Расшифровка термина «асинхронность» — несовпадение по времени. Понятие используется во многих современных машинах, которые являются электрическими и способны преобразовывать соответствующую энергию в механическую. Плюсы устройств:
- простое изготовление;
- низкая цена;
- надёжность;
- незначительные эксплуатационные затраты.
Чтобы рассчитать КПД, используется уравнение η = P2 / P1. Для расчёта Р1 и Р2 применяются общие данные потери энергии в обмотках мотора. У большинства агрегатов показатель находится в пределах 80−90%.
Для быстрого расчёта используется онлайн-ресурс либо личный калькулятор. Для проверки возможного КПД у мотора внешнего сгорания, который функционирует от разных источников тепла, используется силовой агрегат Стирлинга.
Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.
Принцип его функционирования основан на постепенном нагреве и охлаждении объекта за счёт извлечения энергии из давления. Подобный механизм применяется на косметическом аппарате и современной подводной лодке. Его работоспособность наблюдается при любой температуре. Он не нуждается в дополнительной системе для запуска. Его КПД возможно расширить до 70%, в отличие от стандартного мотора.
Значения показателя
В 1824 году инженер Карно дал определение КПД идеального двигателя, когда коэффициент равен 100%. Для трактовки понятия была создана специальная машина со следующей формулой: η=(T1 — Т2)/ T1. Для расчёта максимального показателя применяется уравнение КПД макс = (T1-T2)/T1x100%. В двух примерах T1 указывает на температуру нагревателя, а T2 — температуру холодильника.
На практике для достижения 100% коэффициента потребуется приравнять температуру охладителя к нулю. Подобное явление невозможно, так как T1 выше температуры воздуха.
Процедура повышения КПД источника тока либо силового агрегата считается важной технической задачей. Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери.
В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.
Мощность стандартного двигателя увеличивается следующими способами:
- подключение к системе многоцилиндрового агрегата;
- применение специального топлива;
- замена некоторых деталей;
- перенос места сжигания бензина.
КПД зависит от типа и конструкции мотора. Современные учёные утверждают, что будущее за электродвигателями. На практике работа, которую совершает любое устройство, превышает полезную, так как определённая её часть выполняется против трения. Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.
Решение примеров
Задача 1. Поезд на скорости 54 км/ч развивает мощность 720 кВт. Нужно вычислить силу тяги силовых агрегатов. Решение: чтобы найти мощность, используется формула N=F x v. Если перевести скорость в единицу СИ, получится 15 м/с. Подставив данные в уравнение, определяется, что F равно 48 kН.
Задача 2. Масса транспортного средства соответствует 2200 кг. Машина, поднимаясь в гору под уклоном в 0,018, проходит расстояние 100 м. Скорость развивается до 32,4 км/ч, а коэффициент трения соответствует 0,04.
Нужно определить среднюю мощность авто при движении. Решение: вычисляется средняя скорость — v/2.
Чтобы определить силу тяги мотора, выполняется рисунок, на котором отображаются силы, воздействующие на машину:
- тяжесть — mg;
- реакция опоры — N;
- трение — Ftr;
- тяга — F.
Первая величина вычисляется по второму закону Ньютона: mg+N+Ftr+F=ma. Для ускорения используется уравнение a=v2/2S. Если подставить последние значение и воспользоваться cos, получится средняя мощность. Так как ускорение считается постоянной величиной и равно 9,8 м/с2, поэтому v= 9 м/с. Подставив данные в первую формулу, получится: N= 9,5 kBt.
При решении сложных задач по физике рекомендуется проверить соответствие предоставленных в условиях единиц измерения с международными стандартами. Если они отличаются, необходимости перевести данные с учётом СИ.
ПредыдущаяСледующая
Источник: https://Sprint-Olympic.ru/uroki/fizika/96851-koefficient-poleznogo-deistviia-kpd-formyly-i-raschety.html




