Формулы неподвижного блока

Инфоурок › Физика ›Презентации›Презентация по физике «Блоки. «Золотое правило» механики.

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Простые механизмы –

2 слайд Описание слайда:

Разминка 1. В каком из перечисленных явлений под действием силы совершается работа: А) на стол действует вес гири; Б)поршень выталкивается из цилиндра под действием силы давления газа. 2.

В каком из перечисленных ниже явлений сила тяжести совершает работу: А) шар катится по горизонтальной поверхности; Б) самолет снижается на посадку. 3.

Поставьте пропущенные буквы в формулы: А) А=F В) N=A/ Д) А= S Б) N= /t Г) =FS Е) = A/t

3 слайд Описание слайда:

РАЗМИНКА 4. Поставьте пропущенные единицы физических величин: А) Нм= Б) Вт= /с В) Дж=Н Г) Вт=Дж/ Д) Дж= с Е) Дж= м 5. Рычаг –это 6. Плечо силы-это 7. Сформулируйте правило равновесия рычага 8. Сформулируйте правило моментов сил

4 слайд
5 слайд Описание слайда:

Блоки. «Золотое правило» механики.

6 слайд Описание слайда:

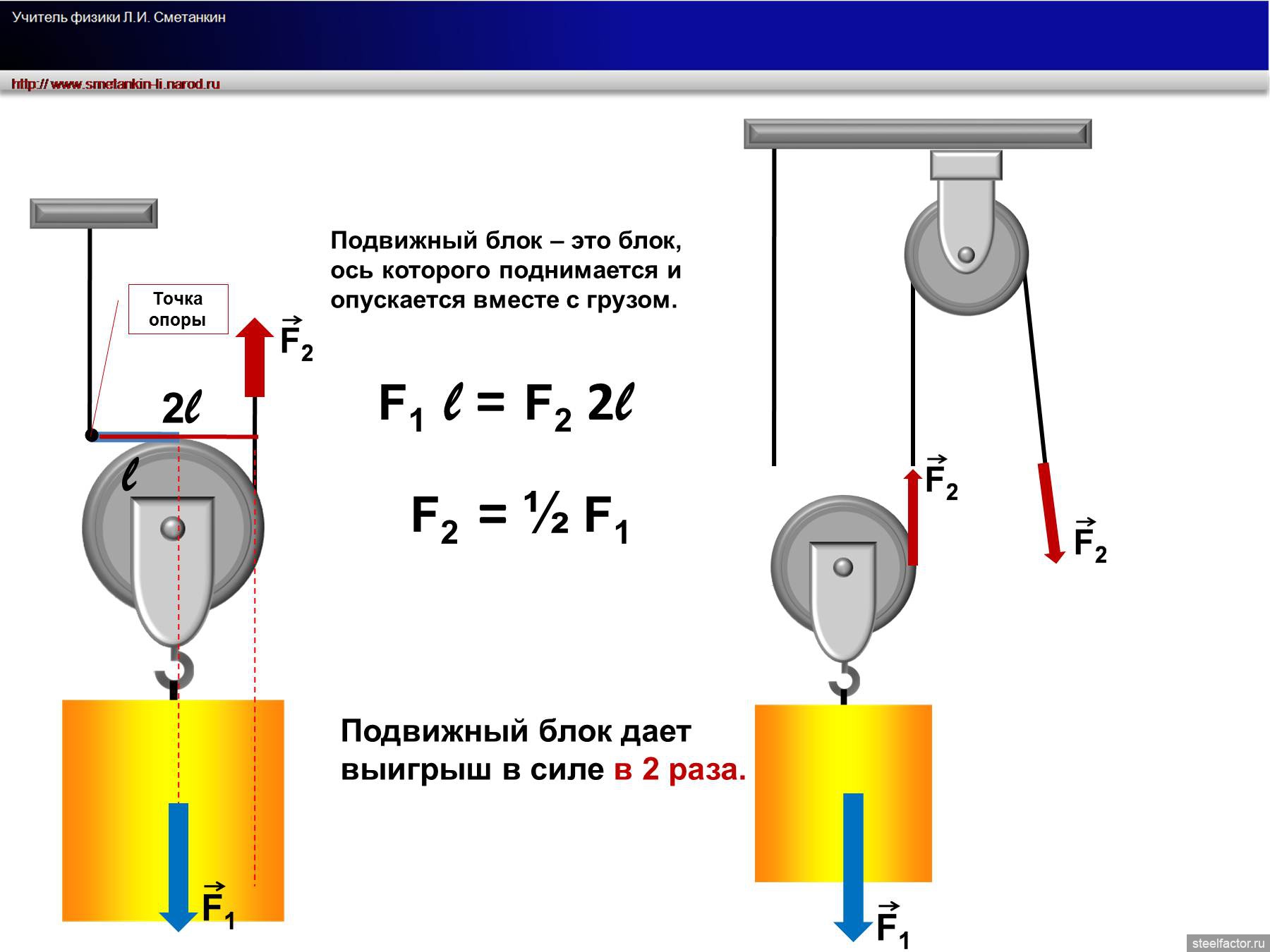
блок неподвижный подвижный Это блок, ось которого закреплена и не поднимается и не опускается вместе с грузом Это блок, ось которого поднимается и опускается вместе с грузом

7 слайд Описание слайда:

Неподвижный блок Условие равновесия: Вывод: Неподвижный блок не даёт выигрыш в силе. Меняет направление действия силы.

8 слайд Описание слайда:

Подвижный блок Вывод. Подвижный блок даёт выигрыш в силе в 2 раза.

9 слайд Описание слайда:

Комбинация подвижного и неподвижного блоков

10 слайд Описание слайда:

11 слайд Описание слайда:

ЗАКРЕПИМ Что такое неподвижный блок? Что такое подвижный блок? Какой выигрыш в силе дает неподвижный блок? Какой выигрыш в силе дает подвижный блок?

12 слайд Описание слайда:

Задание 1. Груз какого веса можно поднять при помощи подвижного блока, прилагая силу 500 Н? 2. Прилагая силу 240 Н к одному концу рычага, поднят груз 1200 Н на высоту 5 см. Чему равен выигрыш в силе? Какова работа по перемещению? Получен ли выигрыш в работе? Во сколько раз проиграно в расстоянии?

13 слайд Описание слайда:

Задание Какую силу нужно приложить к блоку, чтобы поднять груз? Дано Р=600Н Найти F-?

14 слайд Описание слайда:

Подвижный блок A = F ∙ S A = F ∙ S P ∙ h = F ∙ 2h S1 S2 F2 F1 = 2h h = P F A1 = A2 Не даёт выигрыш в работе. Получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути S1 S2 S1 S2 = = = F2 F1 F2 F1 h h P F P ∙ h = F ∙ h A1 = A2 A1 = A2 F1 ∙ S1 = F2 ∙ S2 Не даёт выигрыш в работе. Получая выигрыш в силе, проигрывают в пути Не даёт выигрыш в работе. Пути одинаковы, силы одинаковы

15 слайд
16 слайд
17 слайд Описание слайда:

Лебёдка состоит из 2-х блоков разного диаметра

18 слайд Описание слайда:

Во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии

19 слайд Описание слайда:

АРХИМЕД (около 287-212 г. до н.э.) — величайший математик, физик и инженер древности. «Дайте мне точку опоры, и я переверну Землю» Архимед писал сиракузскому царю Гиерону: «Если бы была другая Земля, я перешел бы на нее и сдвинул бы нашу Землю»-

20 слайд
21 слайд Описание слайда:

Д/З: прочитать § 58,59. Записать в тетрадь простые механизмы, которыми пользуетесь дома или встречаетесь в природе.

22 слайд Описание слайда:

Спасибо всем!

Скрыть

Важно! Узнайте, чем закончилась проверка учебного центра «Инфоурок»?

Курс повышения квалификации

ЕГЭ по физике: методика решения задач

Общая информация

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Источник: https://infourok.ru/prezentaciya-po-fizike-bloki-zolotoe-pravilo-mehaniki-533018.html

Презентация на тему: Виды блоков (Неподвижный блок. Подвижный блок)

Презентация на тему: Виды блоков (Неподвижный блок. Подвижный блок)

Скачать эту презентацию

Получить код Наши баннеры

Скачать эту презентацию

№ слайда 1

Описание слайда:

Виды блоков:Неподвижный блок.Подвижный блок

№ слайда 2

Описание слайда:

Неподвижным блоком называют такой блок, ось которого закреплена и при подъеме грузов не поднимается и не опускается. Такой блок не дает выигрыша в силе, но позволяет менять направление действия силы.

№ слайда 3

Описание слайда:

Подвижным блоком называют такой блок, ось которого поднимается и опускается вместе с грузом. Подвижный блок дает выигрыш в силе.

№ слайда 4

Описание слайда:

Применение правила равновесия рычага к блоку

№ слайда 5

Описание слайда:

Макеты блоков

№ слайда 6

Описание слайда:

Результаты работы:

№ слайда 7

Описание слайда:

Вывод: Для поднятия груза на определенную высоту используют подвижный блок. Он дает выигрыш в силе. А неподвижный блок используют для изменения направления действия силы.

№ слайда 8

Описание слайда:

Применение простых механизмов. Лифт Примерно такой лифт установил в "золотом доме" римский император Нерон (64 г. до н.э.)

№ слайда 9

Описание слайда:

Подъемник мостаТак поднимали мосты в средневековых замках.

№ слайда 10

Описание слайда:

Башенный кранНа любой строительной площадке работают башенные подъемные краны — это сочетание рычагов, блоков, воротов. В зависимости от "специальности" краны имеют различные конструкции и характеристики.

№ слайда 11

Описание слайда:

Портальный кранПортальные поворотные краны. Грузоподъемность — 300 кН. Скорость подъема груза — 0,17 м/с.

№ слайда 12

Описание слайда:

№ слайда 13

Описание слайда:

Трубоукладчик Рычаги, блоки, вороты, лебедки — непременные составные части путе- и трубоукладчиков.

№ слайда 14

Описание слайда:

Экскаватор Простые механизмы используются и в устройстве шагающих экскаваторов. В его большом ковше может поместиться экскаватор для городских строек

№ слайда 15

Описание слайда:

Электролебедка Простые механизмы помогут передвинуть дом, чтобы расширить улицу. Под дом подводят рамы, опускают на катки, уложенные на рельсы, и включают электролебедки

Скачать эту презентацию

Скачивание материала начнется через 60 сек. А пока Вы ожидаете, предлагаем ознакомиться с курсами видеолекций для учителей от центра дополнительного образования «Профессионал-Р» (Лицензия на осуществление образовательной деятельности

№3715 от 13.11.2013).

Получить доступ

Источник: https://ppt4web.ru/fizika/vidy-blokov.html

Простые механизмы. Блок — Класс!ная физика

В современной технике для переноса грузов на стройках и предприятиях широко используются грузоподъемные механизмы, незаменимыми составными частями которых можно назвать простые механизмы.

Среди них древнейшие изобретения человечества: блок и рычаг.

Древнегреческий ученый Архимед облегчил труд человека, дав ему при использовании своего изобретения выигрыш в силе, и научил менять направление действия силы.

Блок — это колесо с желобом по окружности для каната или цепи, ось которого жестко прикреплена к стене или потолочной балке.

Грузоподъемные устройства обычно используют не один, а несколько блоков. Система блоков и тросов, предназначенная для повышения грузоподъемности, называется полиспаст.

Подвижный и неподвижный блок — такие же древнейшие простые механизмы, как и рычаг. Уже в 212 г.до н.эры с помощью крюков и захватов, соединенных с блоками, сиракузцы захватывали у римлян средства осады. Сооружением военных машин и обороной города руководил Архимед.

Неподвижный блок Архимед рассматривал как равноплечий рычаг. Момент силы, действующей с одной стороны блока, равен моменту силы, приложенной с другой стороны блока. Одинаковы и силы, создающие эти моменты.

Выигрыш в силе при этом отсутствует, но такой блок позволяет изменить направление действия силы, что иногда необходимо.

Подвижный блок Архимед принимал за неравноплечий рычаг, дающий выигрыш в силе в 2 раза. Относительно центра вращения действуют моменты сил, которые при равновесии должны быть равны.

Архимед изучил механические свойства подвижного блока и применил его на практике.

По свидетельству Афинея, «для спуска на воду исполинского корабля, построенного сиракузским тираном Гиероном, придумывали много способов, но механик Архимед, применив простые механизмы, один сумел сдвинуть корабль с помощью немногих людей. Архимед придумал блок и посредством него спустил на воду громадный корабль».

Блок не дает выигрыша в работе, подтверждая золотое правило механики. В этом легко убедиться, обратив внимание на расстояния, пройденные рукой и гирей.

Спортивные парусные суда, как и парусники прошлого, не могут обойтись без блоков при постановке парусов и управлении ими. Современным судам нужны блоки для подъема сигналов, шлюпок.

Эта комбинация подвижных и неподвижных блоков на линии электрофицированной железной дороги для регулировки натяжения проводов.

Такой системой блоков могут пользоваться планеристы для подъема в воздух своих аппаратов.

СМОЖЕШЬ ЛИ СООБРАЗИТЬ?

1. Через неподвижный блок перекинута веревка. Один конец ее прикреплен к поясу монтажника, а второй он тянет вниз с некоторой силой. Какова эта сила, если вес рабочего 700 Н? Трением в блоке и массой веревки пренебречь.

2. При проверке динамометром оказывается, что сила, удерживающая груз на неподвижном блоке, немного меньше силы тяжести груза, а при равномерном подъеме больше ее. Чем это объясняется?

3.Почему у подъемных строительных кранов крюк, который переносит груз, закреплен не на конце троса, а на обойме подвижного блока?

Ответы./ Но сначала подумай сам!/

Источник: http://class-fizika.ru/7_blok.html

Чем отличается подвижный блок от неподвижного?

Под термином «блок» понимается некоторое механическое устройство, представляющее из себя ролик, который закреплен на перпендикулярной оси.

Этот ролик или может свободно перемещаться, или напротив – закреплен жестко. Упростим определение — если ось вращения ролика перемещается в пространстве, то блок подвижный.

На ролике есть желобок, в который вставляется веревка или трос. Картинка ниже демонстрирует внешний вид блока.

Смысл использования подвижного блока – выигрыш в силе при подъеме или перемещении грузов и физических тел. Неподвижный же блок выигрыша не даёт, однако часто сильно упрощает перемещение тела и используется в системах совместно с подвижным блоком.

Система блоков встречается повсеместно. Это и подъемные краны, и различные устройства для перемещения грузов в гараже, и даже приводные ремни в современном автомобиле. Часто блок используется даже без четкого понимания того, что это тот самый механизм.

Наверняка на строительных площадках вам встречались подвижные колесики, закрепленные на верхних этажах строящегося дома.

Через такое колесо перекинута веревка или цепь и рабочий, закрепляя ведро на первом этаже, поднимает его на верхний этаж, перемещая веревку. Это простой пример использования неподвижного блока.

Если же к ведру добавить ещё одно колесико, то получится система блоков — подвижный и неподвижный.

Примеров использования этих простых механизмов вокруг нас очень много.

Самое известное устройство, которое работает на принципе блоков — это полиспаст. Оно активно применяется в подъемных механизмах. Система блоков уменьшает силу и общая работа сокращается в 4-8 раз.

В задачах по физике часто необходимо определить, какой суммарный выигрыш в силе будет получен при использовании блоков. Ученику предлагается сложная схема, где соединены подряд несколько блоков разного типа.

Ключ к решению подобных задач лежит в умении разобраться во взаимодействии этих устройств. Каждый блок рассчитывается отдельно, а затем добавляется в общую формулу. Расчётная формула для всей задачи составляется согласно схеме, которую нарисовал ученик, читая условие.

Для лучшего понимания подобных задач следует помнить, что блок – это своеобразный рычаг. Выигранная сила даёт потерю в расстоянии (в случае подвижного блока).

Расчётная формула очень простая.

Для неподвижного блока F=fmg, где F – это сила, f – коэффициент сопротивления блока, m – масса груза, g – гравитационная постоянная. Иными словами, F – это та сила, которую нужно приложить, чтобы поднять, например, ящик с земли с использованием неподвижного блока. Как видите, зависимость прямая и коэффициента нет.

Для подвижного блока мы имеем двукратный выигрыш в силе. Расчётная формулаF=0,5fmg, где буквенные обозначения аналогичны формуле чуть выше. Соответственно, при использовании подвижного блока, такой ящик с массой m будет поднять в два раза легче с блоком, чем с использованием одной лишь только собственной спины.

Обратите внимание, что коэффициент сопротивления – это то противодействие, которое возникает в блоке при перемещении по нему веревки. Обычно эти величины заданы в условии задачи или являются табличной величиной. Иногда в школьных задачах эти коэффициенты вовсе опускаются и не учитываются.

Кроме того, не нужно забывать, что если сила прилагается под углом, то нужно использовать стандартную методику расчёта треугольника сил. Если в задаче сказано, что человек тянет груз за веревку, которая находится под 30 градусами к линии горизонта, то это безусловно должно быть учтено и обозначено на расчётной схеме.

Источник: https://www.kakprosto.ru/kak-953740-chem-otlichaetsya-podvizhnyy-blok-ot-nepodvizhnogo

IT News

Дата Категория: Физика

Блок состоит из одного или нескольких колес (роликов), огибаемых цепью, ремнем или тросом. Так же, как и рычаг, блок уменьшает усилие, необходимое для подъема груза, но плюс к этому может изменять направление прикладываемой силы.

За выигрыш в силе приходится расплачиваться расстоянием: чем меньшее усилие требуется для подъема груза, тем больше путь, который должна пройти точка приложения этого усилия.

Система блоков увеличивает выигрыш в силе за счет использования большего количества грузонесущих цепей.

Подобные силосберегающие устройства имеют очень широкий диапазон применения — от перемещения на высоту массивных стальных балок на строительных площадках до подъема флагов.

Как и в случае других простых механизмов, изобретатели блока неизвестны. Хотя, возможно, блоки существовали и раньше, первое упоминание о них в литературе относится к пятому веку до нашей эры и связано с использованием блоков древними греками на кораблях и в театрах.

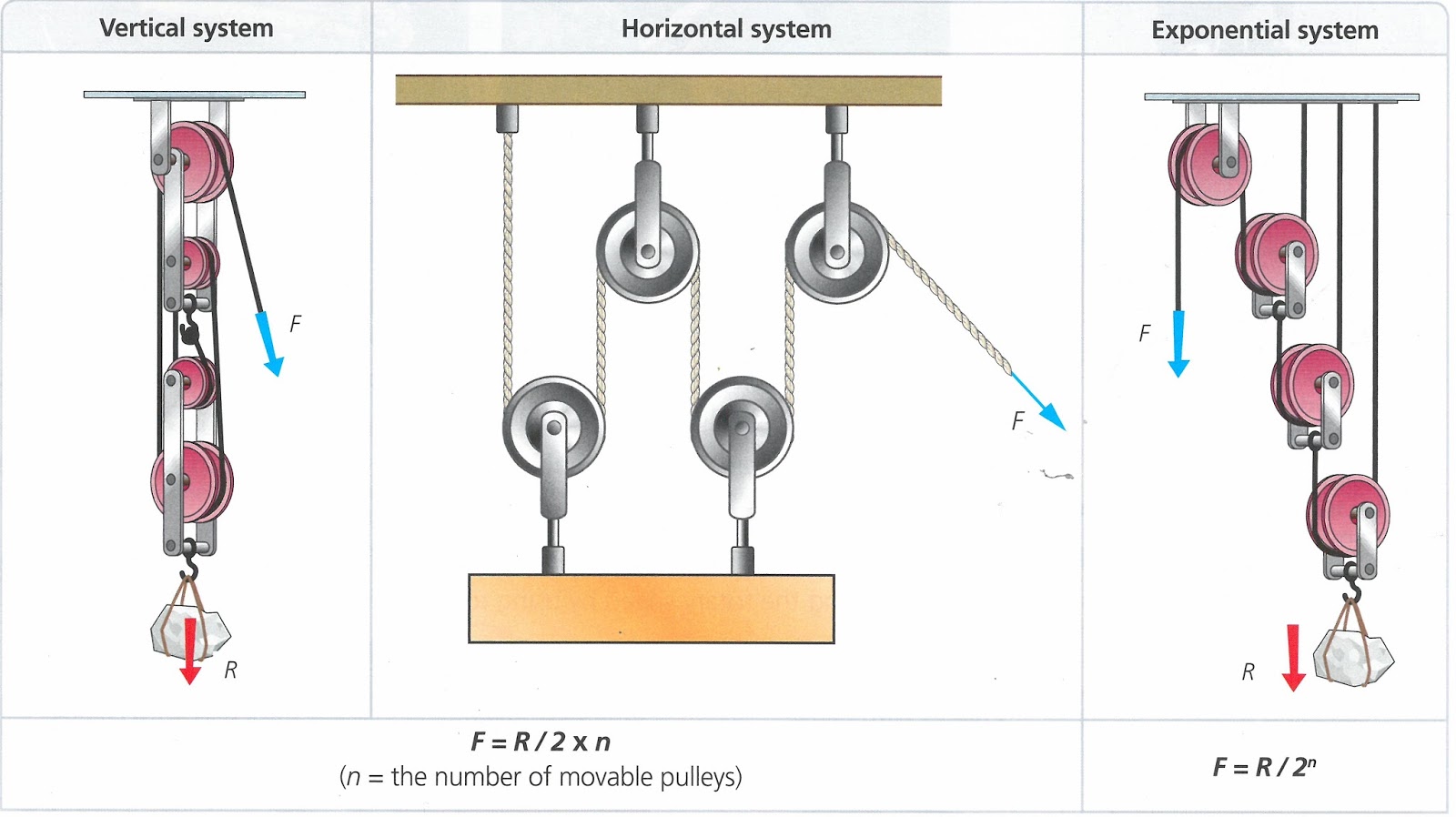
Установленные на подвесном рельсе подвижные системы блоков (рисунок сверху) широко распространены на сборочных линиях, поскольку существенно облегчают перемещение тяжелых деталей. Прикладываемая сила (F) равна частному от деления веса груза (W) на используемое количество поддерживающих его цепей (n).

Одинарные неподвижные блоки

Этот простейший тип блока не уменьшает усилие, необходимое для подъема груза, но зато изменяет направление прикладываемой силы, как это показано на рисунках сверху и справа вверху. Неподвижный блок на верхней части флагштока облегчает подъем флага, позволяя тянуть шнур, к которому привязан флаг, вниз.

Одинарные подвижные блоки

Одинарный блок, имеющий возможность перемещения, уменьшает наполовину усилие, требующееся для подъема груза. Однако уменьшение вдвое прикладываемой силы означает, что точка ее приложения должна пройти в два раза больший путь. В данном случае сила равна половине веса (F=1/2W).

Системы блоков

При использовании комбинации неподвижного блока с подвижным прикладываемая сила кратна общему количеству грузонесущих цепей. В данном случае сила равна половине веса (F=1/2W).

Груз, подвешенный через блок вертикально, позволяет туго натягивать горизонтальные электрические провода.

Подвесной подъемник (рисунок сверху) состоит из цепи, обвитой вокруг одного подвижного и двух неподвижных блоков. Подъем груза требует прикладывания силы, составляющей всего лишь половину от его веса.

Полиспаст, обычно используемый в больших подъемных кранах (рисунок справа), состоит из комплекта подвижных блоков, к которому подвешивается груз, и комплекта неподвижных, прикрепленного к стреле крана.

Получая выигрыш в силе от столь большого количества блоков, кран может поднимать очень тяжелые грузы, например, стальные балки.

В данном случае сила (F) равна частному от деления веса груза (W) на количество поддерживающих тросов (n).

Источник: http://Information-Technology.ru/sci-pop-articles/23-physics/211-kak-rabotayut-bloki

Простые механизмы. Подвижный и неподвижный блоки

Описание устройства

Блок — простой механизм, представляющий собой колесо с желобом по окружности для каната или цепи, способное свободно вращаться вокруг своей оси. Тем не менее, верёвка, переброшенная через древесную ветку тоже в какой-то степени является блоком. 

Зачем же нужны блоки?

В зависимости от своей конструкции блоки могут позволить изменять направление приложенной силы (например, для того, чтобы поднять некий груз, подвешенный на верёвке, переброшенной через древесную ветку, необходимо тянуть другой конец верёвки вниз… или в сторону). При этом, данный блок не даст выигрыша в силе.

Такие блоки называются неподвижными, так как ось вращения блока жёстко закреплена (конечно, если ветка не сломается). Такие блоки применяются для удобства.

Например, при поднятии груза на высоту гораздо легче тянуть веревку с грузом перекинутую через блок вниз, прикладывая к ней вес своего тела, чем стоять наверху и подтягивать к себе груз с веревкой. 

Кроме этого, существуют блоки, которые позволяют не только изменять направление приложенной силы, но и дают выигрыш в силе. Такой блок называется подвижным и он работает с точностью до наоборот нежели подвижный блок.

Для того, чтобы получить выигрыш в силе необходимо жёстко закрепить один конец верёвки (например привязать её к ветке).

Далее на верёвку устанавливается колесо с желобом к которому и подвешивается груз (это необходимо сделать таким образом, чтобы колесо с грузом могло свободно ездить по нашей верёвке).

Теперь, потянув за свободный конец верёвки вверх, мы увидим, что блок с грузом также начали подниматься.

Усилия, которые нам необходимо будет затратить для подъёма груза таким образом будут примерно в 2 раза меньше нежели вес груза вместе с блоком. К сожалений данный вид блока не позволяет изменять направление силы в широких пределах, поэтому его часто используют в паре с неподвижным (жёстко закреплённым) блоком.

Описание опыта

Вначале на видео происходит демонстрация принципа работы неподвижного блока: к жёстко закреплённому блоку подвешиваются грузы одинаковой массы, при этом блок находится в равновесии. Но стоит лишь подвесить один лишний грузик, как сразу же начинается перевес в большую сторону.

Таким образом можно сделать вывод, что подвижный блок даёт двукратный выигрыш в силе.

Это интересно

А вы знаете, что подвижные и неподвижные блоки широко используются в передаточных механизмах автомобилей? Кроме этого, блоки используются строителями для подъёма больших и малых грузов (ну или самих себя.

Например, при ремонте внешних фасадов зданий, строители часто работают в люльке, которая может перемещаться между этажами. По завершении работы на этаже, рабочие достаточно быстро могут передвинуть люльку на этаж выше, используя при этом лишь собственную силу).

Блоки получили такое широкое распространение из-за простоты их сборки и удобства работы с ними.  

Источник: http://virtuallab.by/publ/video_opyty/video_opyty/prostye_mekhanizmy_podvizhnyj_i_nepodvizhnyj_bloki/1-1-0-28

Блок — урок. Физика, 7 класс

Блок является простым механизмом, который используют для подъёма тяжёлых грузов.

Блок состоит из закреплённого на оси диска, по окружности которого имеется жёлоб для скольжения в нём, к примеру, верёвки.

Блоки подразделяют на два вида:

2. подвижный блок.

У неподвижногоблока ось диска закреплена, в связи с чем во время подъёма груза диск только крутится вокруг своей оси. Выигрыш в силе (экономия силы) при таком виде блока отсутствует, но такой блок позволяет изменить направление действия силы, что часто необходимо для удобства.

Неподвижный блок (на рисунке мы видим направление действующих сил)

У подвижного блока диск перемещается вместе с грузом, в связи с чем достигается двукратная экономия силы.

Подвижный блок (на рисунке мы видим только направление действующих сил)

Если груз весит (100) Н, то для его подъёма при помощи неподвижного блока потребуется сила в (100) Н, в свою же очередь, при помощи подвижного блока потребуется сила всего в (50) Н.

Обрати внимание!

Несмотря на то, что подвижный блок даёт экономию силы, которая необходима для подъёма груза, в целом для подъёма груза необходимо совершить такую же работу, как и в случае неподвижного блока!

Если объединить неподвижный и подвижный блоки, можно достичь не только изменения направления прилагаемой силы, но и экономии силы.

Примеры применения блоков:

Механизм блока используется в лодочных лебёдках.

При подъёме грузов подъёмными кранами используют блоки.

Работу различных подъёмников обеспечивает механизм блока.

Источник: https://www.yaklass.ru/p/fizika/7-klass/rabota-i-moshchnost-energiia-11875/blok-11879/re-3e051b45-d5dc-4ae6-b6ed-aec331f6f861

Задачи на системы блоков с решениями

Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость.

Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).

Неподвижный блок

Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.

Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:

Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны:

так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу.

Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:

при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:

Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.

Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.

Комбинация неподвижных блоков

Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось.

К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в таком случае будут неравными. Двойной блок действует как рычаг с плечами разной длины. На рис.

2 изображена схема двойного блока.

Условие равновесия для рычага на рис.2 станет формула:

Двойной блок может преобразовывать силу. Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.

Подвижный блок

Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Рассмотрим рис. 3. Плечо силы в два раза больше, чем плечо силы , следовательно, для равновесия необходимо, чтобы величина силы F была в два раза меньше, чем модуль силы P:

• Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как:
• Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:

Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия.

Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка.

В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.

Золотое правило механики

Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.

  Как в аутлуке сделать автоматический ответ

1. В виде формулы «золотое правило№ можно записать так:
2. где – путь, который проходит точка приложения силы – путь проходимый точкой приложения силы .

Золотое правило является самой простой формулировкой закона сохранения энергии. Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( и ) как:

• Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:
• Если силы и уравновешены, то блок покоится или движется равномерно.

Примеры решения задач

Задание	Используя систему из двух подвижных и двух неподвижных блоков, рабочие поднимают строительные балки, при этом прикладывают силу равную 200 Н. Чему равна масса (m) балок? Трение в блоках не учитывайте.
Решение	Сделаем рисунок.

1. Вес груза, приложенный к системе грузов, будет равен силе тяжести, которая приложена к поднимаемому телу (балке):

Неподвижные блоки выигрыша в силе не дают. Каждый подвижный блок дает выигрыш в силе в два раза, следовательно, при наших условиях мы получим выигрыш в силе в четыре раза.

Это значит, что можно записать:

• Получаем, что масса балки равна:
• Вычислим массу балки, примем :

Ответ
m=80 кг

Задание	Пусть высота, на которую поднимают балки рабочие, в первом примере равна м. Чему равна работа, которую совершают рабочие? Какова работа груза по перемещению на заданную высоту?
Решение	В соответствии с «золотым правилом» механики, если мы, используя имеющуюся систему блоков, получили выигрыш в силе в четыре раза, то проигрыш в перемещении составит тоже четыре. В нашем примере это означает, что длина веревки (l) которую рабочим следует выбрать составит длину в четыре раза большую, чем расстояние, которое пройдет груз, то есть:

1. Работа, которую совершат строители, равна:
2. Вычислим :
3. Работа груза (): массы кг (получено в примере 1) равна:
4. Вычислим , получим:

Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?

• Со­глас­но за­ко­ну со­хра­не­ния ме­ха­ни­че­ской энер­гии, имеем два ра­вен­ства:
• где и — ско­ро­сти ле­тя­щей пули со­от­вет­ствен­но на вы­со­те и не­по­сред­ствен­но перед ми­ше­нью. Вся энер­гия под­ле­тев­шей к ми­ше­ни пули по­тра­че­на на ме­ха­ни­че­скую ра­бо­ту, так что
• Решая по­лу­чен­ную си­сте­му урав­не­ний, на­хо­дим массу пули:

Здравствуйте! Не учтена работа силы тяжести во время движения пули внутри ствола (2 сантиметра), ведь сказано, что пистолет направлен вертикально вниз. Следовательно, пока разжимается пружина, разгоняя пулю, на эту пулю уже действует сила тяжести, совершающая работу по разгону пули.

Потенциальная энергия пули отсюда эм*же*(аш1+дельта икс). Я неправ?

— этим смещением можно пренебречь.

Если бы это было существенно, тогда в условии должна была быть информация, от какой точки пистолета отсчитывается расстояние до мишени: от конца пружины в сжатом состоянии, от конца пружины в несжатом состоянии, от конца дула?

Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему.

Коэффициент трения скольжения между бруском и столом На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 30 %?

1. Пусть m — масса куска пла­сти­ли­на, M — масса брус­ка, — на­чаль­ная ско­рость брус­ка с пла­сти­ли­ном после вза­и­мо­дей­ствия. Со­глас­но за­ко­ну со­хра­не­ния им­пуль­са имеем:
2. Так как то
3. По усло­вию ко­неч­ная ско­рость брус­ка с пла­сти­ли­ном По за­ко­ну из­ме­не­ния ме­ха­ни­че­ской энер­гии имеем:
4. Ответ:
5. Объясните пожалуйста формулу (после слов: «По закону изменения механической энергии имеем: . «)

Там просто записан закон сохранения энергии. Его можно мыслить следующим образом: кинетическая энергия системы переходит в тепло за счет работы силы трения и в новую кинетическую энергию .

• Можно всю эту строчку переписать следующим образом:
• Эту запись мы трактуем следующим образом: изменение кинетической энергии равно работе силы трения (работа этой силы отрицательна в данном случае).
• Как записывать — это вопрос привычки и удобства.

  Игры для интернет друзей

Очень некорректное задание. мы, почему-то, до момента столкновения не учитываем коэффициент трения бруска, ведь он по мере приближение с пластилином замедляется.

И совершенно не понятно, как пластилин перестал касаться поверхности. Запрыгнул на брусок что ли? да же если и так, то мы так же как и с бруском должны были учесть его коэффициент трения до столкновения.

Тогда было бы хорошо указать, что пластилин с поверхностью не создает трения.

В условиях задачи даны скорости пластилина и бруска перед самим моментом удара. Если авторы ничего не говорят про коэффициент трения пластилина о поверхность, то можно считать, что пластилин с поверхностью не создает трения либо оно пренебрежимо мало.

Доброго времени суток!

Можно узнать, считается ли ошибкой, если решать задачу иным способом? Т.е. после закона сохранение импульса расписать все силы, действующие на брусок и пластилин, оттуда найти, что ma=Fтр, а отсюда a=mюg. Далее же просто поставить все под формулу

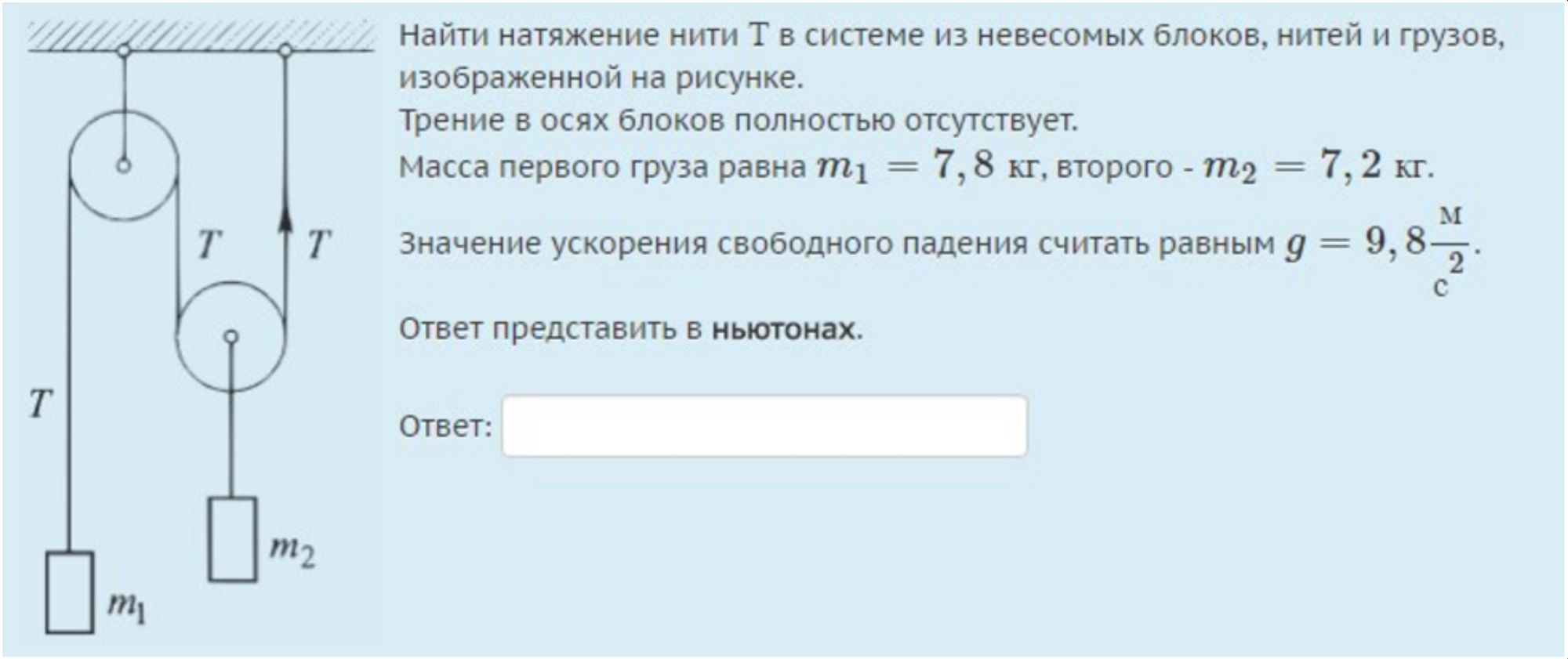
Два одинаковых груза массой каждый подвешены на концах невесомой и нерастяжимой нити, перекинутой через невесомый блок с неподвижной осью. На один из них кладут перегрузок массой после чего система приходит в движение. Найдите модуль силы действующей на ось блока во время движения грузов. Трением пренебречь.

Запишем, на основании второго закона Ньютона, уравнения движения для обоих грузов в проекции на вертикальную ось, направленную вниз (см. рис.):

1. Здесь через и обозначены проекции ускорений грузов и на вертикальную ось, а через и — проекции сил натяжения нити на ту же ось.
2. В силу условия задачи из-за нерастяжимости нити а из-за невесомости блока и нити и отсутствия трения Кроме того, в силу третьего закона Ньютона (здесь — сила, действующая на блок со стороны его оси).
3. Из написанных уравнений получаем:
4. Подставляя числовые данные и проверяя размерность, имеем:
5. Ответ:

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На уроке мы рассмотрим решение задач на движение связанных тел. Это довольно часто встречающийся вид движения, примером могут быть как железнодорожный состав, проходящий мимо, автомобиль с прицепом, так и чисто лабораторные примеры, когда несколько тележек, движутся под действием какой-то силы.

Общий случай решения

Рассмотрим общий случай. Имеется неподвижный блок, через который перекинута нить, к концам которой подвешены два грузика массой

Рис. 1. Схема блока

На первый грузик действует сила притяжения к земле и сила натяжения нити, которая направлена вверх. Соответственно, на второй грузик будут действовать те же силы. Величины сил натяжения их будут одинаковы по модулю при условии, что трение в оси блока отсутствует и сам блок невесом, то есть его не нужно раскручивать какой-то парой сил.

Сила натяжения – это внутренняя сила, возникающая в системе связанных тел, друг на друга они действуют посредством нити. Ускорение у этих грузиков будет иметь разное направление, так как первый грузик тяжелее, то он будет двигаться вниз, а второй вверх, но величины ускорений будут одинаковы и равны а, при условии, что нить нерастяжима.

При разборе таких задач оси рисовать не обязательно, потому что подразумевается, что для каждого тела можно выбрать свое направление оси. Так как первое тело движется вниз, то ось Задача 1

Одинаковые бруски, связанные нитью, движутся под действием внешней силы

Рис. 2. Иллюстрация к задаче 1 (Источник)

В этой задаче необходимо найти отношение силы натяжения

Рис. 3. Решение задачи 1 (Источник)

Растянутая нить в этой системе действует на брусок 2, заставляя его двигаться вперед, но она также действует и на брусок 1, пытаясь препятствовать его движению. Эти две силы натяжения равны по величине, и нам как раз необходимо найти эту силу натяжения. В таких задачах необходимо упростить решение следующим образом: считаем, что сила

  Заработок на играх steam

Рис. 4. Иллюстрация к задаче 2 (Источник)

На столе лежит брусок массой 1 кг, к которому привязана нить, перекинутая через неподвижный блок. Ко второму концу нити подвешен груз массой 0,5 кг (Рис. 6). Определить ускорение, с которым движется брусок, если коэффициент трения бруска о стол составляет 0,35.

Рис. 6. Иллюстрация к задаче 3 (Источник)

Рис. 7. Решение задачи 3 (Источник)

Необходимо помнить, что силы натяжения Задача 4

В вершине двух наклонных плоскостей, составляющих с горизонтом углы

Рис. 8. Иллюстрация к задаче 4 (Источник)

Рис. 9. Решение задачи 4 (Источник)

Мы помним, что если одна плоскость составляет угол в 60 0 с горизонтом, а вторая плоскость – 30 0 с горизонтом, то угол при вершине будет 90 0 , это обычный прямоугольный треугольник.

Через блок перекинута нить, к которой подвешены бруски, они тянут вниз с одной и той же силой, и действие сил натяжения Fн1 и Fн2 приводит к тому, что на блок действует их результирующая сила.

Но между собой эти силы натяжения будут равны, составляют они между собой прямой угол, поэтому при сложении этих сил получается квадрат вместо обычного параллелограмма. Искомая сила Fд является диагональю квадрата. Мы видим, что для результата нам необходимо найти силу натяжения нити.

Проведем анализ: в какую сторону движется система из двух связанных брусков? Более массивный брусок, естественно, перетянет более легкий, брусок 1 будет соскальзывать вниз, а брусок 2 будет двигаться наверх по склону, тогда уравнение второго закона Ньютона для каждого из брусков будет выглядеть:

1. Решение системы уравнений для связанных тел выполняется методом сложения, далее преобразовываем и находим ускорение:
2. Это значение ускорения необходимо подставить в формулу для силы натяжения и найти силу давления на ось блока:
3. Мы выяснили, что сила давления на ось блока приблизительно равна 16 Н.
4. Мы рассмотрели различные способы решения задач, которые многим из вас пригодятся в дальнейшем, чтобы понять принципы устройства и работы тех машин и механизмов, с которыми придется иметь дело на производстве, в армии, в быту.
5. Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Источник: https://galaxys6blog.ru/zadachi-na-sistemy-blokov-s-reshenijami/

Блоки как простые механизмы

☰

Чаще всего простые механизмы используют, чтобы получить выигрыш в силе. То есть меньшей силой переместить больший по-сравнению с ней вес. При этом выигрыш в силе достигается не «бесплатно».

Расплатой за него является потеря в расстоянии, то есть требуется сделать большее перемещение, чем без использования простого механизма.

Однако когда силы ограничены, то «обмен» расстояния на силу выгоден.

Подвижный и неподвижный блоки являются одними из видов простых механизмов. Кроме того, они являются видоизмененным рычагом, который также является простым механизмом.

Неподвижный блок не дает выигрыш в силе, он просто изменяет направление ее приложения. Представьте, что вам надо поднять за веревку тяжелый груз вверх. Вам придется тянуть его вверх.

Без использования неподвижного блока надо было бы прикладывать такую же силу, но она достигалась бы исключительно за счет силы мышц.

Неподвижный блок представляет собой колесо с желобом для веревки. Колесо закреплено, оно может вращаться вокруг своей оси, но не может перемещаться. Концы веревки (троса) свисают вниз, к одному прикреплен груз, а к другом прикладывается сила. Если тянуть за трос вниз, то груз поднимается вверх.

Так как здесь нет выигрыша в силе, то нет и проигрыша в расстоянии. На какое расстояние поднимется груз, на такое же расстояние надо опустить веревку.

Использование подвижного блока дает выигрыш в силе в два раза (в идеале). Это значит, что если вес груза равен F, то чтобы его поднять, надо приложить силу F/2. Подвижный блок состоит всё из того же колеса с желобом для троса. Однако здесь закреплен один конец троса, а колесо подвижно. Колесо движется вместе с грузом.

Вес груза — это сила, направленная вниз. Его уравновешивают две силы, направленные вверх. Одну создает опора, к которой прикреплен трос, а другую тянущий за трос. Сила натяжения троса одинакова с обоих сторон, значит, между ними поровну распределяется вес груза. Поэтому каждая из сил в 2 раза меньше веса груза.

В реальных ситуациях выигрыш в силе меньше, чем в 2 раза, так как поднимающая сила частично «тратится» на вес веревки и блока, а также трение.

Подвижный блок, давая почти двойной выигрыш в силе, дает двойной проигрыш в расстоянии. Чтобы поднять груз на определенную высоту h, надо чтобы веревки с каждой стороны блока уменьшились на эту высоту, то есть в сумме получается 2h.

plustilino © 2019. All Rights Reserved

Источник: https://scienceland.info/physics7/pulley