На этом практическом занятии мы рассмотрим примеры, демонстрирующие методы построения графиков основных типов простейших функций, решим задания на исследование функции по изображенному графику и задачи на преобразования графиков функций.
Данный урок поможет Вам подготовиться к одному из типов заданий С5.
Подготовка к ЕГЭ по математике
Эксперимент
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций
- Практика
- Конспект урока
- Сначала разберем примеры на построение графиков основных функций.
Задача №1. Построить графики функций: а) ; б) ; в) ; г) .
Решение. Воспользуемся методом построения линейных функций «по точкам».
а)

Как видим, и угол наклона к оси острый, смещение по оси .
б)

и можно сделать аналогичные выводы, как и в первом пункте.
в)

угол наклона к оси острый, график проходит через начало координат.
г)

константная функция, прямая проходит через точку и параллельно оси .
Задача №2. Построить графики функций: а) ; б) ![]() ; в)
; в) ![]() .
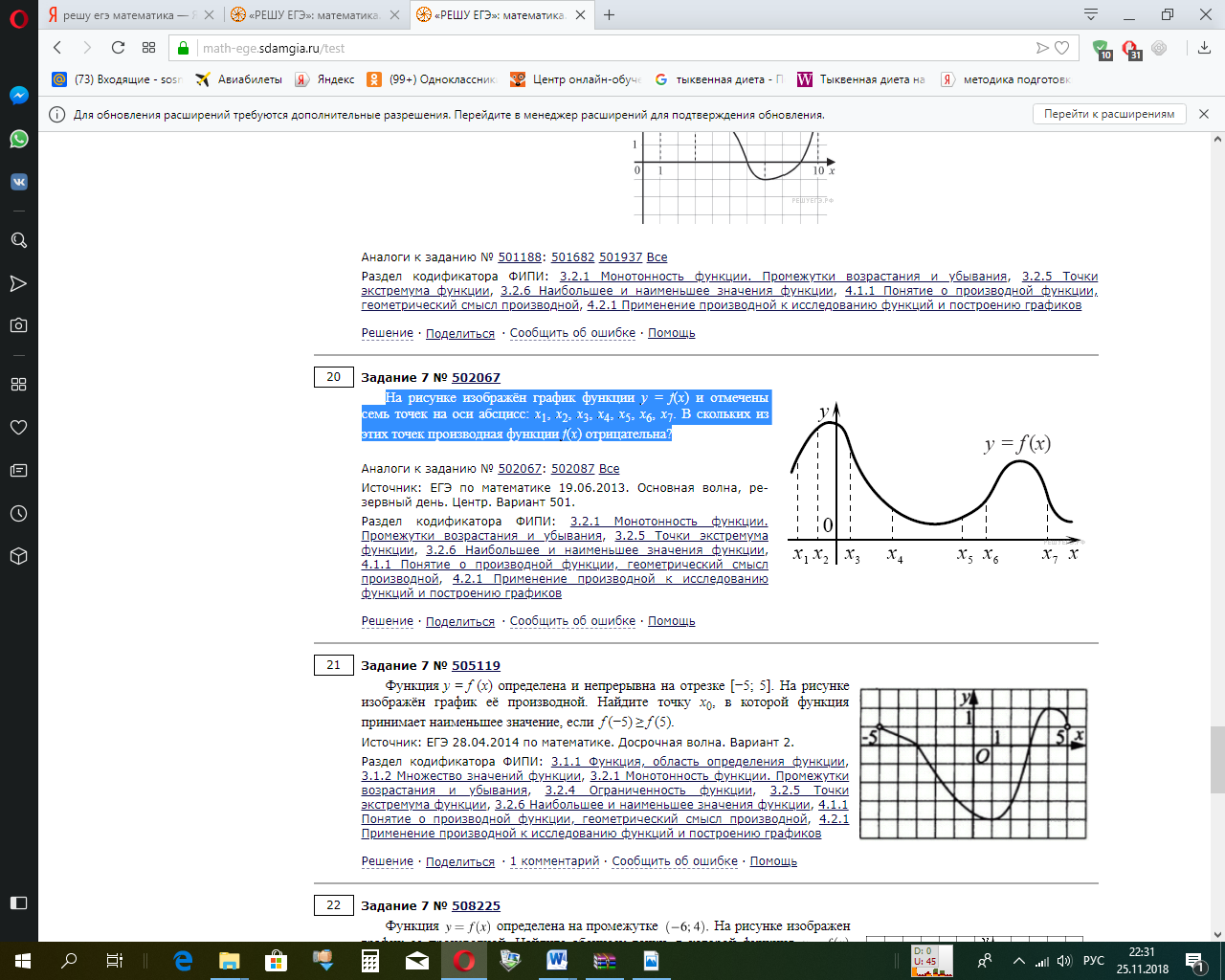
.
Решение. Воспользуемся методом построения квадратичных функций «по вершине».
- а)
- ветки параболы направлены вверх, .


Если возникает вопрос, как точно строится парабола, т.е. с какой именно скоростью растут и убывают ее ветки, то можно запомнить следующий факт: если старший коэффициент или , как это часто бывает, то при смещении от иксовой координаты вершины на единицу влево или вправо значение функции сначала изменяется на 1, потом на 3, затем на 5 и т.д., т.е. на нечетные числа.
Например, в нашем графике:

Для функций, у которых старший коэффициент , значения изменений функции умножаются на это «». Например, построение функции выглядит так:

- Но, как правило такая точность построения не важна, а нужен только эскиз графика, поэтому в дальнейшем мы не будем это учитывать.
- б)
- ветки параболы направлены вверх, .
- в)
- ветки параболы направлены вниз, .
- Кстати, график проходит через ноль, что легко проверить подстановкой в функцию точки или обратив внимание на то, что .
Задача №3. Построить графики функций: а) ; б) ; в) .
Решение. Воспользуемся нашим методом построения дробно-рациональных функций «по асимптотам».
а)
Вертикальная асимптота определяется решением уравнения, которое показывает, что знаменатель дроби равен нулю: .
Горизонтальную асимптоту определим по тому быстрому способу, который мы указали в лекции. Она определяется отношением коэффициентов при иксах в числителе и знаменателе: .
Для определения расположения веток гиперболы подставим в функцию любую точку из области определения, т.е. кроме, например, : , т.е. координаты этой точки через нее и проведем одну ветку гиперболы, вторая будет располагаться наискось.
- Теперь строим гиперболу, прижимая ее к асимптотам:
- Остальные пункты строим аналогично.
- б)
- Вертикальная асимптота: .
Горизонтальная асимптота: , т.е. асимптотами являются оси координат.
- Проверочная точка: .
- в)
- Вертикальная асимптота: .
- Горизонтальная асимптота: .
- Проверочная точка: .
Задача №4. Построить графики функций: а) , б) , в) .
Решение. По сути дела, указаны функции, которые не имеют особых методов построения их графиков. Поэтому если необходимо изобразить их эскиз, то просто вспоминаем теорию, а если необходимо построить графики более точно, то следует подставить несколько контрольных точек, так и поступим.
- а)
- Подставим полные квадраты, чтобы вычислить из них целые значения корня.
- б)
- Подставим несколько значений и учтем общий вид графика.
Т.к. основание степени , то функция растет.
в)
Подставим такие значения аргумента, при которых значения логарифма будут целыми. При построении учтем общий вид графика.
Т.к. основание логарифма , то функция убывает.
- Теперь давайте попробуем научиться решать обратную задачу – по изображенному графику исследовать функцию.
- Задача №5. По виду графика определить знаки коэффициентов общего вида функции :
- а)
- б)
- в)
- г)
Решение. Для определения знаков коэффициентов и вспомним, как от них зависят формы графиков.
а) Острый угол наклона прямой к оси (функция возрастает) – это . Точка пересечения с осью — это .
- Далее аналогичные рассуждения.
- б)
- в)
г) Константная функция, т.к. график параллелен оси , т.е. , а .
- Задача №6. По виду графика определить знаки коэффициентов общего вида функции :
- а)
- б)
- в)
Решение. Вспомним, как параметры и определяют положение параболы.
- а) Ветви вниз, следовательно, .
- Точка пересечения с осью .
- Иксовая координата вершины .
- б) Ветви вверх, следовательно, .
- Точка пересечения с осью .
Иксовая координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, .
в) Ветви вниз, следовательно, .
Точка пересечения с осью .
Иксовая координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, .
И теперь переходим к рассмотрению примеров на преобразование графиков функций.
Задача №7. Построить графики функций: а) ; б) ; в) ; г) ; д) .
Решение. Когда сложная функция получена из простейшей путем нескольких преобразований, то преобразования графиков выполняются в порядке арифметических действий с аргументом, например, умножение идет до сложения и т.п.
- а)
- Преобразование в одно действие типа .
- Сдвигаем график вверх на 1:
- б)
- Преобразование в одно действие типа .
- Сдвигаем график вправо на 1:
- в)
- В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках , затем сложение .
- Сдвигаем график вправо на 1:
- Сдвигаем график вверх на 2:
Конечно же, можно построить эту функцию как квадратичную после раскрывания скобок. Проверьте это самостоятельно.
- г)
- Преобразование в одно действие типа .
- Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
- д)
- Мы видим три преобразования вида , и .
Для выполнения преобразований в порядке действий обратим внимание, что сначала будет выполняться умножение, затем сложение, а затем смена знака. Чтобы умножение применялось ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
- Сжимаем график в два раза вдоль оси абсцисс:
- Сдвигаем график влево на вдоль оси абсцисс:
- Отражаем график симметрично относительно оси абсцисс:
- В этом практическом уроке мы привели множество примеров на работу с графиками функций.
Источник: https://interneturok.ru/lesson/algebra/11-klass/bzadachi-iz-egeb/urok-13-postroenie-i-preobrazovanie-grafikov-funktsiy-obzor-grafikov-osnovnyh-funktsiy-praktika
Исследование функции и построение графика функции
 |
Приведем примерный алгоритм получения необходимых данных.
1.Нахождение области определения функции
Определение интервалов, на которых функция существует.
!!! Очень подробно об области определения функций и примеры нахождения области определения тут.
2.Нули функции
Для вычисления нулей функции, необходимо приравнять заданную функцию к нулю и решить полученное уравнение. На графике это точки пересечения с осью ОХ.
3.Четность, нечетность функции
Функция четная, если y(-x) = y(x). Функция нечетная, если y(-x) = -y(x). Если функция четная – график функции симметричен относительно оси ординат (OY). Если функция нечетная – график функции симметричен относительно начала координат.
4.Промежутки знакопостоянства
Расстановка знаков на каждом из интервалов области определения. Функция положительна на интервале — график расположен выше оси абсцисс. Функция отрицательна — график ниже оси абсцисс.
5. Промежутки возрастания и убывания функции
Для определения вычисляем первую производную, приравниваем ее к нулю. Полученные нули и точки области определения выносим на числовую прямую. Для каждого интервала определяем знак производной. Производная положительна — график функции возрастает, отрицательна — убывает.
6. Выпуклость, вогнутость
Вычисляем вторую производную. Находим значения, в которых вторая производная равна нулю или не существует. Вторая производная положительна — график функции выпукл вверх. Отрицательна — график функции выпукл вниз.
7. Наклонные асимптоты
Пример исследования функции и построения графика №1
Исследовать функцию средствами дифференциального исчисления и построить ее график.
![]()


Пример исследования функции и построения графика №2
Исследовать функцию средствами дифференциального исчисления и построить ее график.
![]()


Пример исследования функции и построения графика №3
Исследовать функцию средствами дифференциального исчисления и построить ее график.


Пример исследования функции и построения графика №4
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №5
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №6
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №7
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №8
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №9
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №10
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №11
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №12
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №13
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №14
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №15
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №16
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №17
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №18
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №19
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №20
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №21
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №22
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №23
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №24
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №25
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пример исследования функции и построения графика №26
- Исследовать функцию средствами дифференциального исчисления и построить ее график.
Источник: http://matecos.ru/mat/matematika/issledovanie-funktsii-i-postroenie-grafika-funktsii.html
Решение задачи исследования функций и построения графиков
При исследовании заданной функции y=f(x) и построении ее графика необходимо руководствоваться следующим алгоритмом:
Исследование функции y=f(x) по ее внешнему виду.
- Найти область определения функции.
- Исследовать функцию на четность/нечетность.
- Найти точки пересечения графика функции с осями координат (так называемые нули функции).
- Найти точки разрыва функции и определить их характер.
- Найти асимптоты графика функции.
5*. Если функция содержит тригонометрические компоненты, необходимо исследовать ее периодичность.
Исследование функции y=f(x) по первой производной.
- Определить интервалы возрастания, убывания и экстремумы функции.
Исследование функции y=f(x) по второй производной.
- Определить интервалы выпуклости, вогнутости и точки перегиба графика функции, найти значения функции в точках перегиба.
Построение графика функции y=f(x).
- Нанести на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построить ее график. Если внешний вид графика после исследования трудно определить, то необходимо взять несколько контрольных точек.
Замечание. Область определения функции необходимо искать, используя известные свойства элементарных функций, например следующие:
- Функция не определена при значениях аргумента x, при которых g(x)=0.
- Корни четной степени (
 и т.д.) определены только при неотрицательных значениях подкоренного выражения ().
и т.д.) определены только при неотрицательных значениях подкоренного выражения (). - Логарифмическая функция определена только при положительных значениях x (x>0).
- Функции y=arcsin x и y=arcos x определены только при .
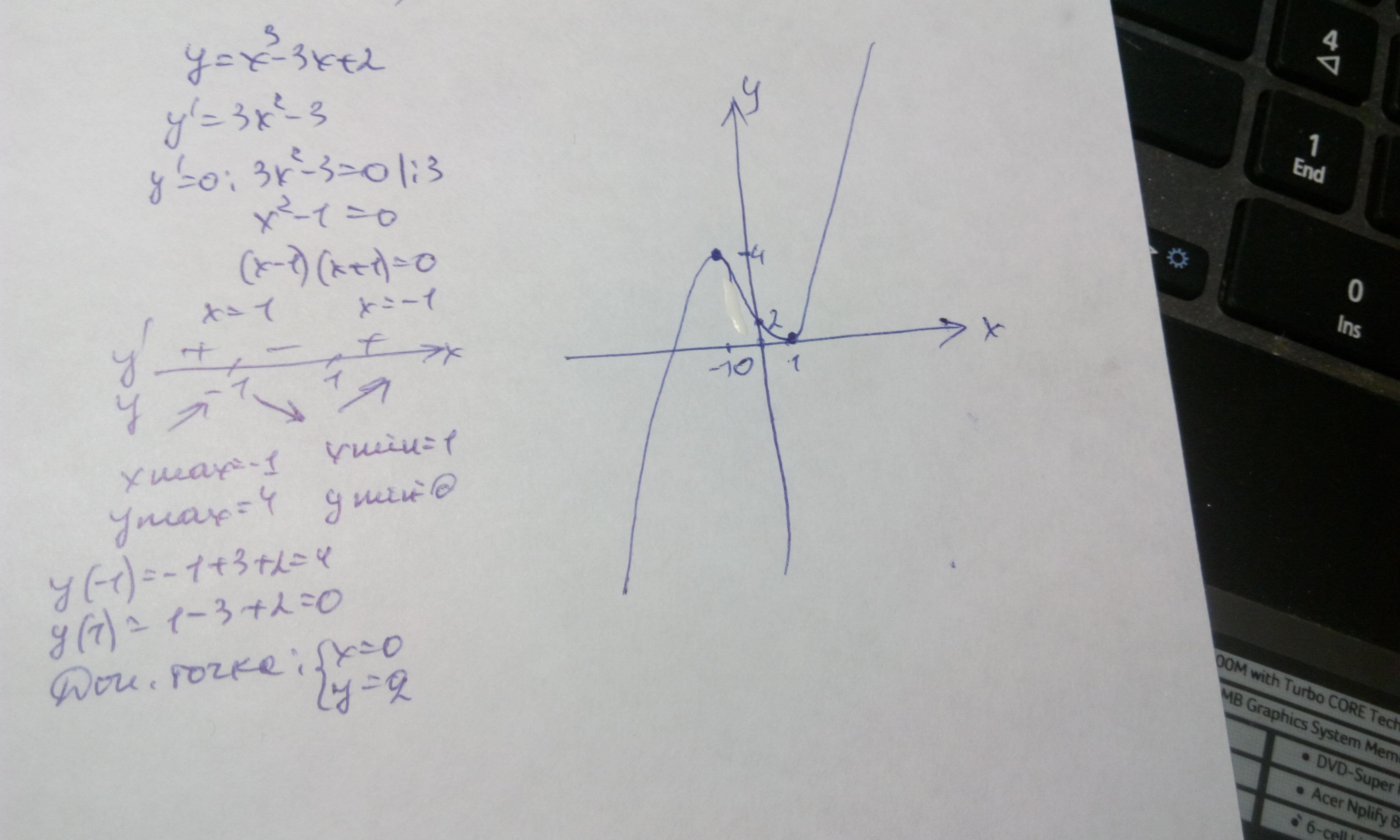
Пример 1: Исследовать функцию и построить ее график.
- Функция определена для всех
 . (см. замечания к алгоритму исследования).
. (см. замечания к алгоритму исследования). - Найдем y(-x):
 данная функция не является ни четной, ни нечетной.
данная функция не является ни четной, ни нечетной. - Найдем точки пересечения графика функции с осями координат:
Если , то , то есть график функции пересекает ось Оy в точке А(0,-4).
Если , тогда из уравнения найдем ![]() . То есть график функции пересекает ось Ох в точках В(1,0), С(-2,0).
. То есть график функции пересекает ось Ох в точках В(1,0), С(-2,0).
- Заданная функция непрерывна во всех точках числовой оси как многочлен третьей степени.
- График функции не имеет вертикальных асимптот, так как заданная функция непрерывна на всей числовой оси.
- График функции не имеет горизонтальных асимптот, так как:

- Определим, имеет ли график функции наклонные асимптоты:

- Следовательно, угловой коэффициент наклонной асимптоты не является конечным и график функции таковой асимптоты не имеет.
- Исследуем заданную функцию на возрастание, убывание и экстремумы.
- Найдем первую производную:

- Приравняем производную к нулю и решим полученное уравнение:
- Найдем промежутки знакопостоянства первой производной:
- Таким образом, функция :
- — возрастает на интервалах
- — убывает на интервале
- — в точке имеет максимум ();
- — в точке имеет минимум ().
- Определим интервалы выпуклости, вогнутости и точки перегиба графика функции.
- Найдем вторую производную:
- Приравняем производную к нулю и решим полученное уравнение:
- Найдем промежутки знакопостоянства второй производной:
- Таким образом кривая:
- — выпукла на интервале
- — вогнута на интервале
- Точка — точка перегиба ().
- Нанесем на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построим ее график.
Замечание. Для удобства построения можно объединить полученные результаты в таблицу:
| -2 | -1 | |||||
| + | 0 | — | — | 0 | + | |
| — | — | 0 | + | + | ||
| max 0 |
прг -2 |
min -4 |
Рис.1: График функции .
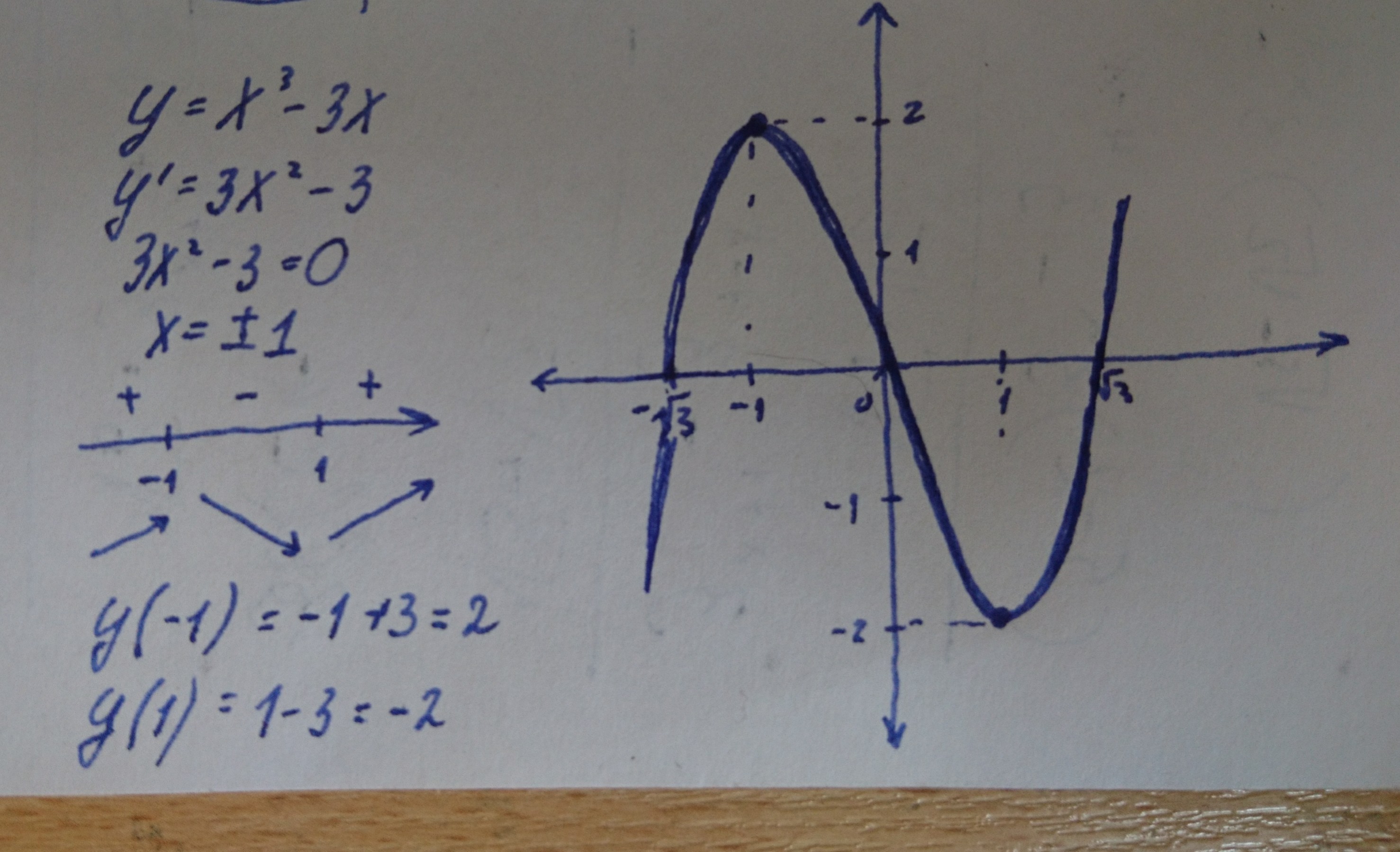
Пример 2: Исследовать функцию и построить ее график.
- Функция определена при всех значениях, то есть . (см. замечания к алгоритму исследования).
- Найдем y(-x): данная функция является нечетной и график функции будет симметричен относительно начала координат.
- Найдем точки пересечения графика функции с осями координат:
Если , то ,если , то . Следовательно, график функции проходит через начало координат O(0,0).
- Найдем точки разрыва и определим их характер.
- Функция не определена при . Исследуем поведение функции вблизи точек разрыва :
- Следовательно, — точки разрыва второго рода.
- Прямые — двусторонние вертикальные асимптоты. (см. п. 4 данного исследования).
- График функции не имеет горизонтальных асимптот, так как:
- Определим, имеет ли график функции наклонные асимптоты:
- Следовательно, k=1, b=0 и прямая y = x (y = kx+b) является наклонной асимптотой графика функции.
- Исследуем заданную функцию на возрастание, убывание и экстремумы.
- Найдем первую производную:
- Приравняем производную к нулю и решим полученное уравнение:
- Найдем промежутки знакопостоянства первой производной:
-
- Таким образом, функция :
- — возрастает на интервалах
- — убывает на интервалах
- — в точке имеет максимум ();
- — в точке имеет минимум ().
- Определим интервалы выпуклости, вогнутости и точки перегиба графика функции.
- Найдем вторую производную:
- Приравняем производную к нулю и решим полученное уравнение:
- Найдем промежутки знакопостоянства второй производной:
- Таким образом кривая:
- — выпукла на интервалах
- — вогнута на интервалах
- Точка — точка перегиба ().
- Нанесем на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построим ее график.
Объединим полученные результаты в таблицу:
| —2 | 2 | |||||||
| + | 0 | — | — | — | — | 0 | + | |
| — | — | + | — | + | + | |||
| max | рзр II рода |
прг 0 |
рзр II рода |
min |
Рис.2: График функции .
Пример 3: Исследовать функцию и построить ее график.
- Функция определена при положительных значениях, то есть . (см. замечания к алгоритму исследования).
- —
- Найдем точки пересечения графика функции с осью Ох, т.к. не входит в область определения функции и точек пересечения с осью Оy не будет:
Если , тогда из уравнения найдем . То есть график функции пересекает ось Ох в точке В(1,0).
- В области определения функция является непрерывной, как произведение непрерывных функций.
- Так как заданная функция является непрерывной, то вертикальных асимптот нет.
- Исследуем поведение функции вблизи граничной точки :
- При исследовании применялось правило Лопиталя.
- График функции не имеет горизонтальных асимптот, так как:
- Определим, имеет ли график функции наклонные асимптоты:
- Следовательно, угловой коэффициент наклонной асимптоты не является конечным и график функции таковой асимптоты не имеет.
- Исследуем заданную функцию на возрастание, убывание и экстремумы.
- Найдем первую производную:
- Приравняем производную к нулю и решим полученное уравнение:
- Найдем промежутки знакопостоянства первой производной:
- Таким образом, функция :
- — возрастает на интервале
- — убывает на интервале
- — в точке имеет минимум
- Определим интервалы выпуклости, вогнутости и точки перегиба графика функции.
- Найдем вторую производную:
- Приравняем производную к нулю и решим полученное уравнение:
- Найдем промежутки знакопостоянства второй производной:
- Таким образом кривая:
- — выпукла на интервале
- — вогнута на интервале
- Точка — точка перегиба .
- Нанесем на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построим ее график.
Объединим полученные результаты в таблицу:
| — | — | + | |
| — | + | + | |
| прг | min |
Стрелка на графике показывает, что точка не входит в область определения функции и имеет конечный предел
Рис.3: График функции.
Пример 4: Исследовать функцию и построить ее график.
- Функция определена для всех . (см. замечания к алгоритму исследования).
- Найдем y(-x): данная функция является четной и график функции будет симметричен относительно оси Оу.
- Найдем точки пересечения графика функции с осями координат:
- Если , то , то есть график функции пересекает ось Оy в точке А(0,3).
- Если , тогда из уравнения найдем . То есть график функции пересекает ось Ох в точках
- .
- Заданная функция непрерывна во всех точках числовой оси как многочлен четвертой степени.
- График функции не имеет вертикальных асимптот, так как заданная функция непрерывна на всей числовой оси.
- График функции не имеет горизонтальных асимптот, так как:
- Определим, имеет ли график функции наклонные асимптоты:
- Следовательно, угловой коэффициент наклонной асимптоты не является конечным и график функции таковой асимптоты не имеет.
- Исследуем заданную функцию на возрастание, убывание и экстремумы.
- Найдем первую производную:
- Приравняем производную к нулю и решим полученное уравнение:
- Найдем промежутки знакопостоянства первой производной:
- Таким образом, функция :
- — возрастает на интервалах
- — убывает на интервалах
- — в точке имеет максимум ();
- — в точках имеет минимум .
- Определим интервалы выпуклости, вогнутости и точки перегиба графика функции.
- Найдем вторую производную:
- Приравняем производную к нулю и решим полученное уравнение:
- Найдем промежутки знакопостоянства второй производной:
- Таким образом кривая:
- — выпукла на интервале
- — вогнута на интервалах
- Точки — точки перегиба .
- Нанесем на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построим ее график.
| 0 | |||||||||
| — | 0 | + | + | 0 | — | — | 0 | + | |
| + | + | 0 | — | — | 0 | + | + | ||
| min | Прг | max 3 |
Прг | min |
Рис.4: График функции.
Источник: http://KtoReshit.ru/kak-reshit/nachala-analiza/reshenie-zadachi-issledovaniya-funktsii-i-postroeniya-grafikov
Полное исследование функции и построение графика
Если в задаче необходимо произвести полное исследование функции f(x)=x24x2-1 с построением его графика, тогда рассмотрим этот принцип подробно.
Для решения задачи данного типа следует использовать свойства и графики основных элементарных функций. Алгоритм исследования включает в себя шаги:
Нахождение области определения
Так как исследования проводятся на области определения функции, необходимо начинать с этого шага.
Пример 1
Заданный пример предполагает нахождение нулей знаменателя для того, чтобы исключить их из ОДЗ.
4×2-1=0x=±12⇒x∈-∞; -12∪-12; 12∪12; +∞
В результате можно получить корни, логарифмы, и так далее. Тогда ОДЗ можно искать для корня четной степени типа g(x)4 по неравенству g(x)≥0, для логарифма logag(x) по неравенству g(x)>0.
Исследование границ ОДЗ и нахождение вертикальных асимптот
На границах функции имеются вертикальные асимптоты, когда односторонние пределы в таких точках бесконечны.
Пример 2
- Для примера рассмотрим приграничные точки, равные x=±12.
- Тогда необходимо проводить исследование функции для нахождения одностороннего предела. Тогда получаем, что: limx→-12-0f(x)=limx→-12-0x24x2-1==limx→-12-0x2(2x-1)(2x+1)=14(-2)·-0=+∞limx→-12+0f(x)=limx→-12+0x24x-1==limx→-12+0x2(2x-1)(2x+1)=14(-2)·(+0)=-∞limx→12-0f(x)=limx→12-0x24x2-1==limx→12-0x2(2x-1)(2x+1)=14(-0)·2=-∞limx→12-0f(x)=limx→12-0x24x2-1==limx→12-0x2(2x-1)(2x+1)=14(+0)·2=+∞
- Отсюда видно, что односторонние пределы являются бесконечными, значит прямые x=±12 — вертикальные асимптоты графика.
Исследование функции и на четность или нечетность
Когда выполняется условие y(-x)=y(x), функция считается четной. Это говорит о том, что график располагается симметрично относительно Оу. Когда выполняется условие y(-x)=-y(x), функция считается нечетной. Значит, что симметрия идет относительно начала координат. При невыполнении хотя бы одного неравенства, получаем функцию общего вида.
Выполнение равенства y(-x)=y(x) говорит о том, что функция четная. При построении необходимо учесть, что будет симметричность относительно Оу.
Нахождение возрастания и убывания, точек экстремума
Для решениянеравенства применяются промежутки возрастания и убывания с условиями f'(x)≥0 и f'(x)≤0 соответственно.
Определение 1
Стационарные точки – это такие точки, которые обращают производную в ноль.
Критические точки — это внутренние точки из области определения, где производная функции равняется нулю или не существует.
При решении необходимо учитывать следующие замечания:
- при имеющихся промежутках возрастания и убывания неравенства вида f'(x)>0 критические точки в решение не включаются;
- точки, в которых функция определена без конечной производной , необходимо включать в промежутки возрастания и убывания (к примеру, y=x3, где точка х=0 делает функцию определенной, производная имеет значение бесконечности в этой точке, y'=13·x23, y'(0)=10=∞, х=0 включается в промежуток возрастания);
- во избежание разногласий рекомендовано пользоваться математической литературой, которая рекомендована министерством образования.
Включение критических точек в промежутки возрастания и убывания в том случае, если они удовлетворяют области определения функции.
Определение 2
Для определения промежутков возрастания и убывания функции необходимо найти:
- производную;
- критические точки;
- разбить область определения при помощи критических точек на интервалы;
- определить знак производной на каждом из промежутков, где + является возрастанием, а — является убыванием.
Пример 3
- Найти производную на области определения f'(x)=x2'(4×2-1)-x24x2-1'(4×2-1)2=-2x(4×2-1)2.
- Решение
- Для решения нужно:
- найти стационарные точки, данный пример располагает х=0;
- найти нули знаменателя, пример принимает значение ноль при x=±12.
Выставляем точки на числовой оси для определения производной на каждом промежутке. Для этого достаточно взять любую точку из промежутка и произвести вычисление. При положительном результате на графике изображаем +, что означает возрастание функции, а — означает ее убывание.
Например, f'(-1)=-2·(-1)4-12-12=29>0, значит, первый интервал слева имеет знак +. Рассмотрим на числовой прямой.

Ответ:
- происходит возрастание функции на промежутке -∞; -12 и (-12; 0];
- происходит убывание на промежутке [0; 12) и 12; +∞.
На схеме при помощи + и — изображается положительность и отрицательность функции, а стрелочки – убывание и возрастание.
Точки экстремума функции – точки, где функция определена и через которые производная меняет знак.
Пример 4
Если рассмотреть пример, где х=0, тогда значение функции в ней равняется f(0)=024·02-1=0. При перемене знака производной с + на — и прохождении через точку х=0, тогда точка с координатами (0; 0) считается точкой максимума. При перемене знака с — на + получаем точку минимума.
Нахождение промежутков выпуклости и вогнутости функции и точек перегиба
Выпуклость и вогнутость определяется при решении неравенств вида f''(x)≥0 и f''(x)≤0. Реже используют название выпуклость вниз вместо вогнутости, а выпуклость вверх вместо выпуклости.
Определение 3
Для определения промежутков вогнутости и выпуклости необходимо:
- найти вторую производную;
- найти нули функции второй производной;
- разбить область определения появившимися точками на интервалы;
- определить знак промежутка.
Пример 5
- Найти вторую производную из области определения.
- Решение
- f''(x)=-2x(4×2-1)2'==(-2x)'(4×2-1)2—2x4x2-12'(4×2-1)4=24×2+2(4×2-1)3
- Находим нули числителя и знаменателя, где на примере нашего примера имеем, что нули знаменателя x=±12
- Теперь необходимо нанести точки на числовую ось и определить знак второй производной из каждого промежутка. Получим, что
Ответ:
- функция является выпуклой из промежутка -12; 12;
- функция является вогнутой из промежутков -∞; -12 и 12; +∞.
Определение 4
Точка перегиба – это точка вида x0; f(x0). Когда в ней имеется касательная к графику функции, то при ее прохождении через x0 функция изменяет знак на противоположный.
Иначе говоря, это такая точка, через которую проходит вторая производная и меняет знак, а в самих точках равняется нулю или не существует. Все точки считаются областью определения функции.
В примере было видно, что точки перегиба отсутствуют, так как вторая производная изменяет знак во время прохождения через точки x=±12. Они , в свою очередь, в область определения не входят.
Нахождение горизонтальных и наклонных асимптот
При определении функции на бесконечности нужно искать горизонтальные и наклонные асимптоты.
Определение 5
Наклонные асимптоты изображаются при помощи прямых, заданных уравнением y=kx+b, где k=limx→∞f(x)x и b=limx→∞f(x)-kx.
При k=0 и b, не равному бесконечности, получаем, что наклонная асимптота становится горизонтальной.
Иначе говоря, асимптотами считают линии, к которым приближается график функции на бесконечности. Это способствует быстрому построению графика функции.
Если асимптоты отсутствуют, но функция определяется на обеих бесконечностях, необходимо посчитать предел функции на этих бесконечностях, чтобы понять, как себя будет вести график функции.
Пример 6
На примере рассмотрим, что
k=limx→∞f(x)x=limx→∞x24x2-1x=0b=limx→∞(f(x)-kx)=limx→∞x24x2-1=14⇒y=14
является горизонтальной асимптотой. После исследования функции можно приступать к ее построению.
Вычисление значения функции в промежуточных точках
Чтобы построение графика было наиболее точным, рекомендовано находить несколько значений функции в промежуточных точках.
Пример 7
Из рассмотренного нами примера необходимо найти значения функции в точках х=-2 , х=-1 , х=-34 ,х=-14. Так как функция четная, получим, что значения совпадут со значениями в этих точках, то есть получим х=2 , х=1 , х=34 , х=14.
Запишем и решим:
f(-2)=f(2)=224·22-1=415≈0,27f(-1)-f(1)=124·12-1=13≈0,33f-34=f34=3424342-1=920=0,45f-14=f14=1424·142-1=-112≈-0,08
Построение графика
Для определения максимумов и минимумов функции, точек перегиба, промежуточных точек необходимо строить асимптоты. Для удобного обозначения фиксируются промежутки возрастания, убывания, выпуклость, вогнутость. Рассмотрим на рисунке, изображенном ниже.

Необходимо через отмеченные точки проводить линии графика, что позволит приблизить к асимптотам, следуя стрелочкам.

На этом заканчивается полное исследование функции. Встречаются случаи построения некоторых элементарных функций, для которых применяют геометрические преобразования.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Источник: https://Zaochnik.com/spravochnik/matematika/funktsii/polnoe-issledovanie-funktsii-i-postroenie-grafika/
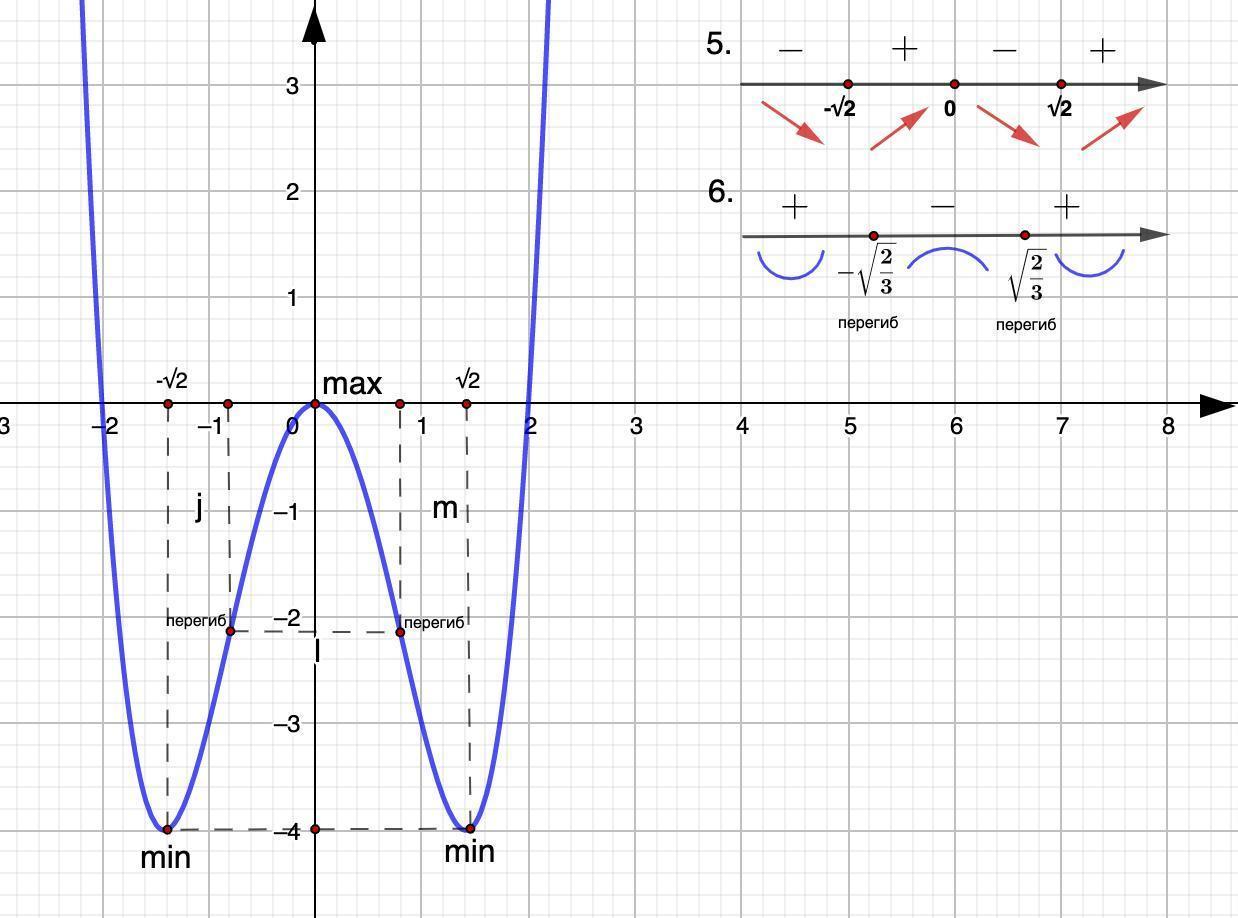
Исследование графика функции
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции
- область значений функции
- нули функции
- промежутки возрастания и убывания
- точки максимума и минимума
- наибольшее и наименьшее значение функции на отрезке.
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
- Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
- Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
- Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Источник: https://ege-study.ru/ru/ege/materialy/matematika/issledovanie-grafika-funkcii/
Открытый урок по теме "Исследование функций и построение графиков" методическая разработка по алгебре (11 класс) по теме
Государственное образовательное учреждение
высшего профессионального образования
«Хакасский государственный университет им. Н.Ф. Катанова»
- Сельскохозяйственный институт
- Сельскохозяйственный колледж
- План занятия №___6___
- ПО ДИСЦИПЛИНЕ Математика
ПРЕПОДАВАТЕЛЬ Петухова И.С.
ГРУППА 2-14
СПЕЦИАЛЬНОСТЬ: Ихтиология и Рыбоводство
ДАТА 27.10.10
- АУДИТОРИЯ: 318
- ВРЕМЯ: 930-1050
- ТЕМА: Дифференциал функции.
- ЦЕЛИ:
- Проверить степень усвоения знаний по теме «Производная функции».
- Дать понятие дифференциала функции и его приложения к приближенным вычислениям.
- Развивать мыслительные способности.
- Воспитывать свободное владение специальной терминологией.
- ВИД ЗАНЯТИЯ: урок
- ТИП УРОКА: комбинированный
- ОБОРУДОВАНИЕ УРОКА: мультимедиа, раздаточный материал
| Ход урока | Методы |
|
БеседаВизуально |
2. Проверка знаний студентов по теме «Производная функции»:Вопросы:
|
Устный фронтальный опросИндивидуальная работа по карточкам с элементами взаимоконтроля |
| 3. Подведение итогов проверки знаний студентов | Анализ, комментарии преподавателя |
| 4. Сообщение темы и целей урока. Начальная мотивация учебной познавательной деятельности. | Беседа |
5. Изложение нового материала по теме«Дифференциал функции»
|
Объяснительно-иллюстративныйс применением мультимедиа |
6. Закрепление изученного материала.
|
Решение задач письменно с ми преподавателя |
| 6. Подведение итогов урока, выставление оценок. | Обобщение с ми преподавателя |
| 7. Задание для самостоятельной работы студентов во внеурочное время:сборник домашних работ, работа №5, конспект | Пояснение |
Изложение нового материала:
Определение дифференциала функции.
Сегодня мы продолжаем изучение раздела Дифференциальное исчисление и знакомимся с таким понятием как Дифференциал функции. Научимся применять это понятие к решению математических и не только задач. Новое понятие дифференциала функции мы рассмотрим на частном примере.
Источник: https://nsportal.ru/shkola/algebra/library/2015/09/12/otkrytyy-urok-po-teme-issledovanie-funktsiy-i-postroenie-grafikov




