Плечо силы. момент силы

Плечо силы — это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!

На камень действуют сила тяжести, сила трения, сила реакции опоры, две дополнительные внешние силы F1 и F2

Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести — это длина перпендикуляра (отрезок d) на рисунке

Плечо силы реакции опоры определяется аналогично

Если перпендикуляр нет возможности построить, то вектор силы продлевается в необходимом направлении, после чего строим перпендикуляр к этой линии. Плечо силы F2

Плечо силы F1

Осталась сила трения! Если точка О и сила лежат на одной линии, то плечо этой силы равно нулю. Плечо силы трения равно нулю.

При решении задач выгодно точку О выбирать в точке пересечения нескольких сил. Тогда плечи всех этих сил будут нулевыми. Например, если точку О в предыдущем примере выбрать иначе, то плечи сил будут иными.

Плечи сил F1, F2 и силы тяжести равны нулю, так как точка О лежит с ними на одной прямой (или на самой силе). Плечо силы реакции опоры — это длина d1. Плечо силы трения — это длина d2.

Момент силы

Это векторная величина, определяется по формуле

Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак «+», если против часовой, тогда знак «-«.

Момент силы реакции опоры отрицательный, так как сила реакции опоры «поворачивает» тело против часовой стрелки

• Момент силы тяжести положительный, так как сила тяжести «поворачивает» тело по часовой стрелки
• Если точка О выбрана на теле
• Момент силы реакции опоры и силы трения положительные, так как силы «поворачивают» тело по часовой стрелки

Источник: http://fizmat.by/kursy/statika/plecho_moment

Статика

Статика — это раздел механики, который занимается изучением равновесия

Плечо силы

Плечо силы — это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!

На камень действуют сила тяжести, сила трения, сила реакции опоры, две дополнительные внешние силы F1 и F2

Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести — это длина перпендикуляра (отрезок d) на рисунке

Плечо силы реакции опоры определяется аналогично

Если перпендикуляр нет возможности построить, то вектор силы продлевается в необходимом направлении, после чего строим перпендикуляр к этой линии. Плечо силы F2

Плечо силы F1

Осталась сила трения! Если точка О и сила лежат на одной линии, то плечо этой силы равно нулю. Плечо силы трения равно нулю.

При решении задач выгодно точку О выбирать в точке пересечения нескольких сил. Тогда плечи всех этих сил будут нулевыми. Например, если точку О в предыдущем примере выбрать иначе, то плечи сил будут иными.

Плечи сил F1, F2 и силы тяжести равны нулю, так как точка О лежит с ними на одной прямой (или на самой силе). Плечо силы реакции опоры — это длина d1. Плечо силы трения — это длина d2.

Момент силы

Это векторная величина, определяется по формуле

Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак «+», если против часовой, тогда знак «-«.

• Момент силы реакции опоры отрицательный, так как сила реакции опоры «поворачивает» тело против часовой стрелки
• Момент силы тяжести положительный, так как сила тяжести «поворачивает» тело по часовой стрелки
• Если точка О выбрана на теле
• Момент силы реакции опоры и силы трения положительные, так как силы «поворачивают» тело по часовой стрелки

Равновесие

Состояние тела, которое не изменяется со временем. Например, тело длительно находится в покое или движется равномерно, или длительно вращается.

Первое условие равновесия

1. Векторная сумма всех действующих на тело сил равна нулю.
2. Рассмотрим на примере первое условие равновесия
3. Предмет будет находиться в равновесии, если векторная сумма всех сил (Fтр1, Fтр2, N1, N2, mg) равна нулю. То есть

Второе условие равновесия

Векторная сумма моментов сил равна нулю

Точку О выберем в точке пересечения Fтр2 и N2. Плечи этих сил равны нулю, значит и моменты этих сил равны нулю.

Определяем плечи сил Fтр1, N1 и mg и направление моментов сил (положительное или отрицательное).

Виды равновесия. Опрокидывание

Равновесие бывает устойчивым (тело возвращается в свое первоначальное положение), неустойчивым (тело не возвращается в свое первоначальное состояние), безразличное (тело остается в равновесии, несмотря на то, что на него подействовали (например переложили книгу из одного места на столе в другое). Тело стремится занять такое состояние, при котором его потенциальная энергия будет минимальной, центр масс стремиться быть ниже.

1 — безразличное равновесие, 2 — неустойчивое равновесие, 3 — устойчивое равновесие

На рисунке изображено условие опрокидывания тела.

Тело слева возвращается в исходное состояние. Тело справа опрокидывается.

Тело, имеющее площадь опоры, находится в состоянии устойчивого равновесия, если вертикаль, проведенная через центр масс этого тела, не выходит за рамки контура, ограниченного точками соприкосновения тела с опорой. Если же эта вертикаль проходит вне указанного контура, тело опрокидывается.

Центр тяжести

• Центр тяжести тела — точка приложения силы тяжести (равнодействующей гравитационных сил).
• Пусть тело состоит из двух шаров массами m1 и m2, насаженных на стержень, массой стержня можно пренебречь.
• Система будет в равновесии, если опору разместить в центре тяжести, точке С. В этом случае векторная сумма моментов сил относительно точки С равна нулю, получим
• Центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс.

Центр масс

Центр масс — точка пересечения прямых, вдоль которых действуют внешние силы, вызывающие поступательное движение тела. Это более общее понятие, чем понятие центра тяжести. Центр тяжести и центр масс часто совпадают. Центр масс симметричных тел находится в их геометрическом центре.

Определение центра масс

Определение центра масс. Если тело можно разбить на n элементов, массы которых m1, m2, … , mn и если известны координаты центров масс этих элементов x1, x2, …, xn, то координата масс тела вычисляется по формуле:

Такое же соотношение можно записать для yC и zC.

Источник: http://msk.edu.ua/ivk/Fizika/Konspekt/statika.php

Формула плеча силы

Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${overline{F}}_1$ и ${overline{F}}_2$, действующие на рычаг направлены в одну сторону.

Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.

Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $left|OA
ight|=d_1$- плечо силы $F_1$; $left|OA
ight|=d_2$- плечо силы $F_2$.

Рычаг находится в состоянии равновесия, если выполняется равенство:

[frac{F_1}{F_2}=frac{d_2}{d_1}left(1
ight).]

Предположим, что материальная точка движется по окружности (рис.2) под действием силы $overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($varepsilon $) точки определяется тангенциальной составляющей ($F_{ au }$) силы $overline{F}$:

[mRvarepsilon =F_{ au }left(2
ight),]

где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_{ au }$ — проекция силы на направление скорости движения точки.

Если угол $alpha $ — это угол между вектором силы $overline{F}$ и радиус — вектором $overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:

[F_{ au }=F{sin alpha left(3
ight). }]

Расстояние $d$ между центром O и линией действия силы $overline{F}$ называют плечом силы. Из рис.2 следует, что:

[d=R{sin alpha left(4
ight). }]

Если на точку будет действовать сила ($overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $alpha $ станет равен $frac{pi }{2}$.

Момент силы и плечо

Понятие плечо силы иногда используют, для записи величины момента силы ($overline{M}$), который равен:

[overline{M}=left[overline{r}overline{F}
ight]left(5
ight),]

где $overline{r}$ — радиус — вектор проведенный к точке продолжения силы$ overline{F}$. Модуль вектора момента силы равен:

[M=F{rsin alpha = }Fd left(6
ight).]

Построение плеча силы

И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз).

При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.

Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).

Примеры задач с решением

Пример 1

Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={
m 2 }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?

• Решение. Основой решения задачи является правило равновесия рычага:
• где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:
• Из выражения (1.2) получим искомую массу $m_1$:
• Вычислим искомую массу:
• Ответ. $m_1=0,5 кг$

[frac{F_1}{F_2}=frac{d_2}{d_1}left(1.1
ight),] [frac{m_1g}{m_2g}=frac{d_2}{d_1} o frac{m_1}{m_2}=frac{d_2}{d_1}left(1.2
ight).] [m_1=frac{m_2d_2}{d_1}.] [m_1=2cdot frac{1}{4}=0,5 (кг).]

Пример 2

Задание. Однородный стержень длинной $l $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $alpha $. На стержне на расстоянии $b $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?

Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $Moverline{g}$, вес груза, расположенного на нем $overline{P}=m_1overline{g}$, сила реакции наклонной плоскости: $overline{N}$; сила реакции опоры в точке A: $overline{N}'$.

1. Плечи сил будем искать относительно точки A. Плечо силы $overline{N'}$ будет равно нулю, так как сила приложена к стержню в точке А:
2. Плечо другой силы реакции опоры ($overline{N}$) равно длине перпендикуляра AC:
3. Плечо силы $Moverline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:
4. Плечо силы $m_1overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:
5. Ответ. $d_{N'}=0;; d_N=l{sin (90-alpha ) }=l{cos alpha left(м
   ight), }d_{Mg}=frac{l}{2}, d_{m_1g}=b$

[d_{N'}=0 left(2.1
ight).] [d_N=l{sin (90-alpha ) }=l{cos alpha left(2.2
ight). }] [d_{Mg}=frac{l}{2}left(2.3
ight).] [d_{m_1g}=b.]

Читать дальше: формула полезной мощности.

Источник: https://www.webmath.ru/poleznoe/fizika/fizika_137_formula_plecha_sily.php

Определение и свойства момента силы

Определения момента силы относительно точки и оси. Определение плеча силы относительно точки. Формулировки и доказательства свойств момента силы. Выражение абсолютного значения момента в виде произведения плеча силы на модуль силы.

Момент силы относительно точки O – это векторное произведение вектора , проведенного из точки O в точку приложения силы A, на вектор силы : (1)   .

Если выбрать прямоугольную систему координат Oxyz с центром в точке O, то момент силы будет иметь следующие компоненты: (1.1)   ; (1.2)   ; (1.3)   . Здесь – координаты точки A в выбранной системе координат: . Компоненты представляют собой значения момента силы относительно осей , соответственно.

Определение плеча силы

Плечо силы относительно точки – это расстояние между линией действия силы и точкой, относительно которой определяется плечо. То есть плечо силы – это длина перпендикуляра, опущенного из точки на линию действия силы.

Свойства

• Если точку приложения силы переместить вдоль линии ее действия, то момент, при таком перемещении, не изменится. Доказательство ⇓
• Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки. Доказательство ⇓
• Момент относительно точки O, от силы, линия действия которой проходит через эту точку, равен нулю. Доказательство ⇓
• Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке: . Доказательство ⇓

Тоже самое относится и к силам, чьи линии продолжения пересекаются в одной точке. При этом в качестве точки приложения суммы сил берется точка пересечения линий их действия.

Если векторная сумма сил равна нулю: , то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:

.

Доказательство ⇓

Момент силы является псевдовектором или, что то же самое, аксиальным вектором.

Это свойство следует из свойства векторного произведения. Поскольку векторы и являются истинными (или полярными) векторами, то их векторное произведение является псевдовектором. Это означает то, что мы можем определить только абсолютное значение и ось, вдоль которой направлено векторное произведение.

Это направление мы и берем за направление векторного произведения.

Но если бы мы определили направление по правилу левого винта, то векторное произведение было бы направлено в противоположную сторону. При этом никакого противоречия не возникает.

То есть фактически, аксиальные векторы могут иметь два взаимно противоположных направления. Чтобы не усложнять математические формулы, мы выбираем одно из них, применяя правило правого винта.

По этой причине, псевдовекторы нельзя геометрически складывать с истинными векторами. Но их можно перемножать, используя скалярное или векторное произведение.

Момент силы относительно оси

Определение

Часто встречаются случаи, когда нам не нужно знать все компоненты момента силы относительно выбранной точки, а нужно знать только момент силы относительно выбранной оси.

Момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси.

Пусть – единичный вектор, направленный вдоль оси. И пусть O – произвольная точка, принадлежащая ей. Тогда момент силы относительно оси является скалярным произведением: . Такое определение возможно, поскольку для любых двух точек O и O′, принадлежащих оси, проекции моментов относительно этих точек на ось равны. Покажем это.

Воспользуемся векторным уравнением : ; . Умножим это уравнение скалярно на единичный вектор , направленный вдоль оси: . Поскольку вектор параллелен оси, то . Отсюда . То есть проекции моментов на ось, относительно точек O и O′, принадлежащих этой оси, равны.

Свойства

Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю. Доказательство ⇓

Момент относительно оси от силы, параллельной этой оси равен нулю. Доказательство ⇓

Доказательство свойств

Перемещение точки приложения силы вдоль линии ее действия

Все свойства ⇑ Если точку приложения силы переместить вдоль линии действия силы, то момент, при таком перемещении, не изменится.

Доказательство

Пусть сила приложена в точке A. Через точку A проведем прямую, параллельную вектору силы. Эта прямая является линией ее действия. Переместим точку A приложения силы в точку A′, принадлежащую линии действия. Тогда .

Вектор проведен через две точки линии действия. Поэтому его направление совпадает или противоположно направлению вектора силы . Тогда , где λ – параметр; .   , если точка A′ смещена относительно A в направлении вектора .

В противном случае .

Таким образом, вектор, проведенный из O в A′, имеет вид: . Найдем момент силы, приложенной в точке A′, применяя свойства векторного произведения: . Мы видим, что момент не изменился:

1. .
2. Свойство доказано.

Абсолютная величина момента силы

Все свойства ⇑ Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.

Доказательство

Абсолютное значение момента M относительно точки O равно произведению силы F на ее плечо d = |OD|.

Пусть мы имеем силу , приложенную в точке A. Рассмотрим момент этой силы относительно некоторой точки O. Заметим, что точки O, A и вектор лежат в одной плоскости. Изобразим ее на рисунке. Через точку A, в направлении вектора проводим прямую AB. Эта прямая называется линией действия силы . Через точку O опустим перпендикуляр OD к линии действия.

И пусть D является точкой пересечения линии действия и перпендикуляра. Тогда – плечо силы относительно центра O. Обозначим его буквой . Воспользуемся предыдущим свойством ⇑, согласно которому точку приложения силы можно перемещать вдоль ее линии действия. Переместим ее в точку D. Момент силы: .

Поскольку векторы и перпендикулярны, то по свойству векторного произведения, абсолютное значение момента: , где – абсолютное значение силы.

Заметим, что вектор момента перпендикулярен плоскости рисунка. Его направление определяется по правилу правого винта. Если мы будем вращать винт, проходящий через точку O перпендикулярно плоскости рисунка, в направлении силы F, то он будет перемещаться на нас. Поэтому вектор момента перпендикулярен плоскости рисунка и направлен на нас.

Свойство доказано.

Момент относительно точки от силы, проходящей через эту точку

Все свойства ⇑ Момент относительно точки O, от силы, линия действия которой проходит через эту точку, равен нулю.

Доказательство

Пусть линия действия силы проходит через точку O. Тогда плечо этой силы относительно O равно нулю: . Согласно предыдущему свойству ⇑, абсолютное значение момента силы относительно выбранной точки равно нулю: .

Свойство доказано.

Момент суммы сил, приложенных в одной точке

Все свойства ⇑ Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке: .

Доказательство

Пусть силы приложены в одной точке A. Пусть – векторная сумма этих сил. Находим момент относительно некоторой точки O от векторной суммы , приложенной в точке A. Для этого применяем свойства векторного произведения: .

Свойство доказано.

Момент системы сил, векторная сумма которых равна нулю

• Все свойства ⇑ Если векторная сумма сил равна нулю: , то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
• .

Доказательство

Пусть силы приложены в точках , соответственно. И пусть точки O и C обозначают два центра, относительно которых мы будем вычислять моменты. Тогда имеют место следующие векторные уравнения: . Используем их при вычислении суммы моментов относительно точки O: . Здесь мы воспользовались тем, что по условию,

1. .
2. Свойство доказано.

Момент относительно оси от силы, проходящей через эту ось

Все свойства ⇑ Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.

Доказательство

В определении ⇑ указано, что момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси. В качестве такой точки возьмем точку пересечения линии действия силы с осью. Но, согласно доказанному выше ⇑, момент относительно этой точки равен нулю. Поэтому равна нулю и его проекция на эту ось.

Свойство доказано.

Момент относительно оси от силы, параллельной этой оси

Все свойства ⇑ Момент относительно оси от силы, параллельной этой оси равен нулю.

Доказательство

Пусть O – произвольная точка на оси. Рассмотрим момент силы относительно этой точки. Согласно определению: . Согласно свойству векторного произведения, вектор момента перпендикулярен вектору силы . Поскольку вектор силы параллелен оси, то вектор момента ей перпендикулярен. Поэтому проекция момента относительно точки O на ось равна нулю.

Свойство доказано.

Источник: https://1cov-edu.ru/mehanika/statika/moment-sily-opredelenie-i-svojstva/

Е

§ 4.1.Теоретическое введение.

Комнатная дверь может поворачиваться вокруг вертикальной оси. Надавив на дверь недалеко от оси вращения, мы заметим, что, для того чтобы таким образом открыть ее, надо приложить значительное усилие. Наоборот, дверь открывается легко, если действовать на нее на большом расстоянии от оси.

Пример с дверью показывает, что вращающее действие силы зависит не только от величины самой силы, но и от расстояния между вектором силы и осью вращения.

Длина перпендикуляра, проведенная от оси вращения до прямой, совпадающей с направлением действия силы, называется плечом силы.

Вращающее действие прямо пропорционально величине силы длине плеча этой силы. Поэтому вращающее действие силы принято характеризовать особой величиной, измеряемой произведением силы на плечо.

• Величина, равная произведению силы на ее плечо, называется вращающим моментом силы или просто моментом силы.
• Если обозначить момент силы через , то данное определение можно выразить формулой:
•                                        .

Для указания направления вращения тела его сопоставляют с движение часовой стрелки. Момент, вращающий тело по часовой стрелке, принято считать положительным, против часовой стрелки – отрицательным.

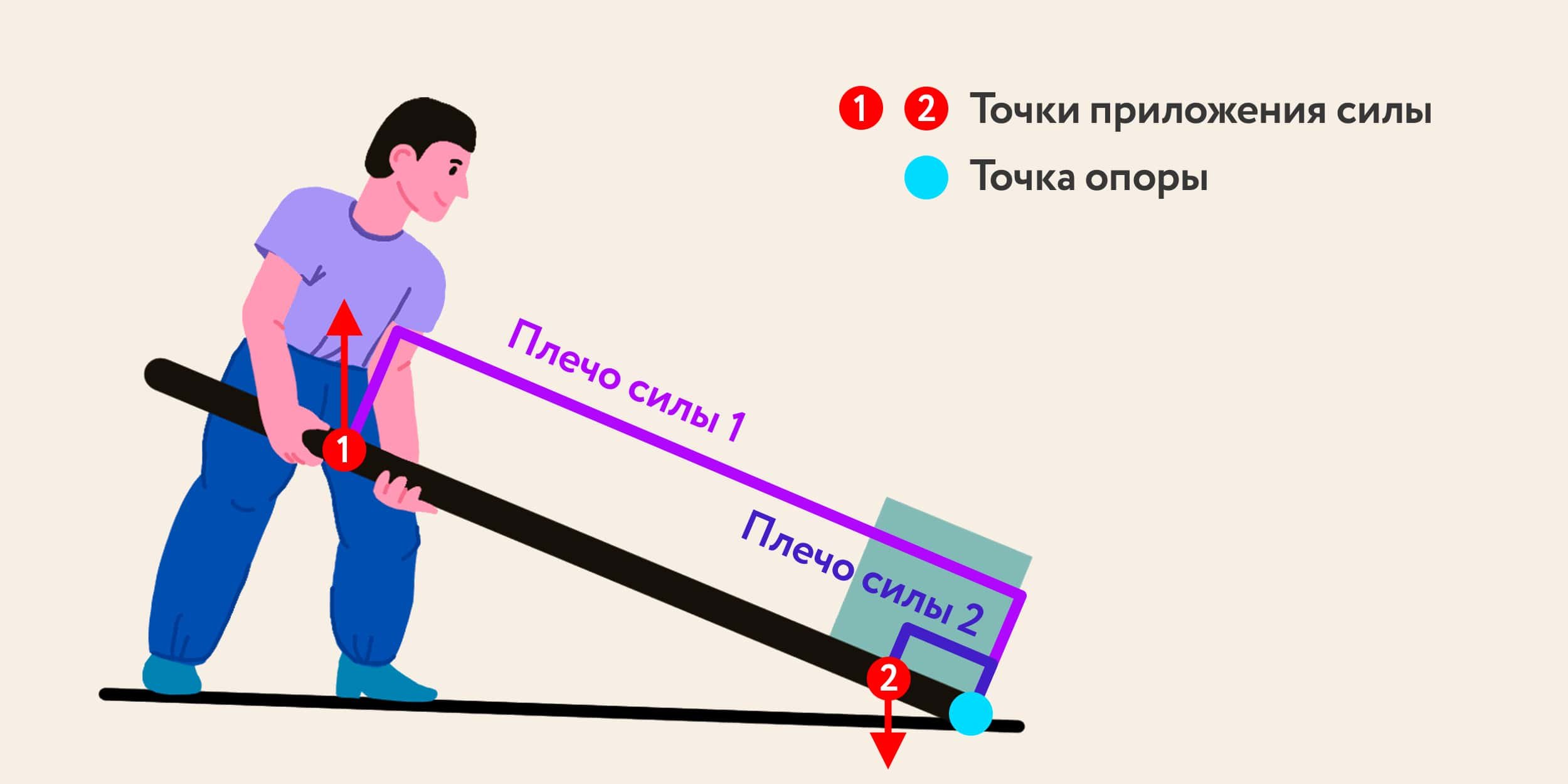
Может ли человек удержать на весу 100 тонн груза? Можно ли рукой расплющить кусок железа? Может ли ребенок оказать противодействие силачу? Да, могут.

Если предложить силачу повернуть колесо, ухватившись за спицу у самой оси. Момент силы в данном случае будет невелик: сила большая, да плечо маленькое. Если ребенок будет тянуть колесо в обратную сторону, ухватившись за спицу у самого обода колеса, то момент силы может оказаться и большим: сила мала да плечо большое, и он вполне может противостоять силачу. Условием равновесия будет: 

  или  .

«Механизмы» здесь – это любое приспособление, позволяющее силе, приложенной к одной точке, уравновесить или преодолеть другую силу в другой точке.

Приложенная сила называется усилием, а сила, которую «механизм» должен преодолеть, будем называть нагрузкой. Наиболее ярким примером служит действие рычагов.

Рычаги подразделяются на три вида, смотря по тому, где

Рис42

помещена точка опоры по отношению к точкам приложения сил. Как видно из рисунка, точка опоры не всегда находится между усилием и нагрузкой.

Рычаги 1-го рода имеют точку опоры между силами. Примеры: качели в виде доски с опорой посередине, ножницы, лом.

Лом, положенный на опору, — весьма распространенный вид рычага. Выигрыш в силе с помощью лома бывает примерно в 10 – 20 раз. Длина лома около 1,5 м, а точку опоры обычно трудно установить ближе, чем на 10 см от конца. Поэтому плечо одной силы будет больше другого в 15 – 20 раз, а значит, таким же будет и выигрыш в силе.

Рычаги 2-го рода. Нагрузка прикладывается между усилием и точкой опоры. Примеры: щипцы для орехов, тачка.

Рычаги 3-го рода. Усилие прикладывается между нагрузкой и точкой опоры. Примеры: предплечье человека, пинцет.

Преодолевая при помощи рычажного инструмента какую-либо силу  на пути , мы можем проделать это силой  много меньшей . Но перемещение руки  должно быть во столько же раз больше , во сколько раз мускульная сила  меньше .

Часто этот закон выражается короткой фразой: выигрыш в силе равен проигрышу в расстоянии.

Правило рычага было открыто величайшим ученым древности – Архимедом. Увлеченный силой доказательств, этот замечательный ученый написал сиракузскому царю Герону: «Если бы была другая Земля, я перешел бы на нее, и сдвинул бы нашу Землю». Очень длинный рычаг, точка опоры, которого была бы расположена близко к земному шару, кажется, дал бы возможность решить такую задачу.

Оценим, прав ли был Архимед. Пофантазируем: пусть у нас будет прочный рычаг, который мы установим на опоре, и к одному из его концов его подвесим наш «маленький» земной шарик весом в … Н.

А к противоположному концу рычага приложим мускульную силу, развиваемую в среднем человеком – 600Н. Тогда для смещения земного «шарика» на 1 см руке Архимеда пришлось бы проделать путь в  раз больше. 1023 см это 1018 км, что в три миллиарда раз больше диаметра земной орбиты.

Этот пример показывает масштабы «проигрыша в пути» при работе рычага.

Проигрыш в пути, как оплата за выигрыш в силе есть общий закон не только рычажных инструментов, но и любых других приспособлений и механизмов, используемых человеком.

Еще одним примером распространенного механизма является блок. Это — колесо с желобом, свободно вращающееся на оси. Если ось блока при работе не опускается и не поднимается, то блок называют неподвижным.

Этот блок не дает выигрыша в силе, но позволяет изменить направление действия силы.

Подвижный блок (ось которого поднимается и опускается вместе с грузом) позволяет получить выигрыш в силе в два раза.

 следующая страница >>

Используются технологии uCoz

Источник: http://sgpu-fmf.narod.ru/FMSh/1/4_1.htm

Момент силы: правило и применение

Почти две тысячи лет просуществовало правило рычага,  открытое Архимедом еще в третьем веке до нашей эры, пока в семнадцатом веке с легкой руки французского ученого Вариньона не получило более общую форму.

• Было введено понятие момента сил. Момент силы – это физическая величина, равная произведению силы на ее плечо:
• M=Fl,
• где M – момент силы,F – сила,
• l – плечо силы.
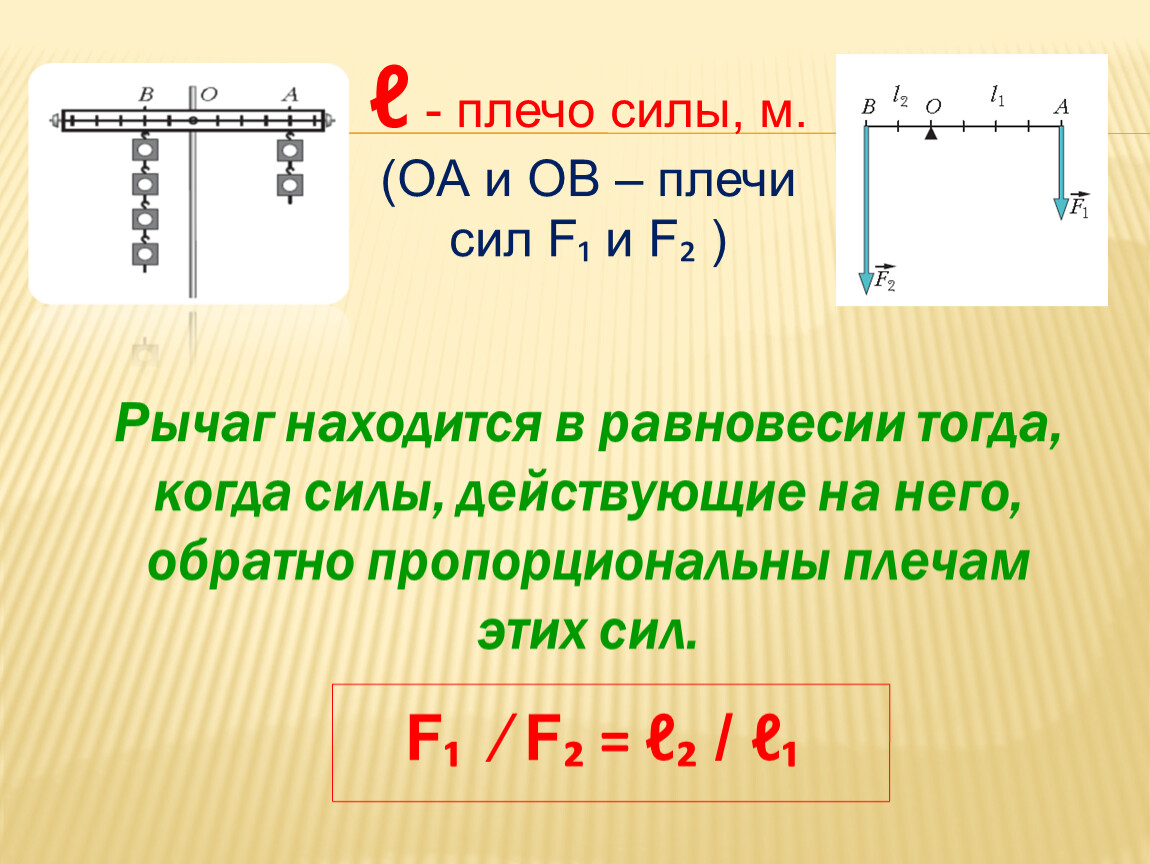
• Из правила равновесия рычага напрямую вытекает правило моментов сил:
• F1 / F2 = l2 / l1 или, по свойству пропорции F1 * l1= F2 * l2, то есть M1 = M2

В словесном выражении правило моментов сил звучит следующим образом: рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.

Правило моментов сил справедливо для любого тела, закрепленного вокруг неподвижной оси. На практике момент силы находят следующим образом: по направлению действия силы проводят линию действия силы.

Потом из точки, в которой находится ось вращения, проводят перпендикуляр до линии действия силы.  Длина этого перпендикуляра будет равняться плечу силы. Умножив значение модуля силы на ее плечо, получаем значение момента силы относительно оси вращения.

То есть, мы видим, что момент силы характеризует вращающее действие силы. Действие силы зависит и от самой силы и от ее плеча.

Применение правила моментов сил в различных ситуациях

Отсюда вытекает применение правила моментов сил в различных ситуациях. Например, если мы открываем дверь, то толкать ее мы будем в районе ручки, то есть, подальше от петель. Можно проделать элементарный опыт и убедиться, что толкать дверь тем легче, чем дальше мы прилагаем силу от оси вращения. Практический эксперимент в данном случае прямо подтверждается формулой.

Так как, дабы моменты сил при разных плечах были равны, надо, чтобы большему плечу соответствовала меньшая сила и наоборот, меньшему плечу соответствовала большая. Чем ближе к оси вращения мы прилагаем силу, тем она должна быть больше. Чем дальше от оси мы воздействуем рычагом, вращая тело, тем меньшую силу нам необходимо будет приложить.

Числовые значения легко находятся из формулы для правила моментов.

За единицу момента силы принят ньютон на метр (1 Н/м). это момент силы 1 ньютон, имеющей плечо в 1 метр.

Нужна помощь в учебе?

Предыдущая тема: Простые механизмы и их применение: рычаг, равновесие сил на рычаге
Следующая тема:   Рычаги в природе, быту и технике

Источник: http://www.nado5.ru/e-book/moment-sily

Момент силы. Пара сил и ее свойства (стр. 1 из 2)

• 1. Плоская система сходящихся сил
• Система сходящихся сил находится в равновесии, когда алгебраические суммы проекций ее слагаемых на каждую из двух координатных осей равны нулю.
• Проекция силы на ось.

Осью называют прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной.

Проекция вектора считается положительной (+), если направление от начала к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (-), если направление от начала проекции к ее концу противоположно положительному направлению оси.

Если сила совпадает с положительным направлением оси, но угол будет тупой – тогда проекция силы на ось будет отрицательною.

Итак, проекция силы на ось координат равна произведению модуля силы на косинус или синус угла между вектором силы и положительным направлением оси.

Силу, расположенную на плоскости хОу, можно спроецировать на две координатные оси Ох и Оу:

; ; .

Проекция векторной суммы на ось.

Геометрическая сумма, или равнодействующая, этих сил

определяется замыкающей стороной силового многоугольника: ,

1. где п – число слагаемых векторов.
2. Итак, проекция векторной суммы или равнодействующей на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
3. 2. Пара сил

Сумма проекций пары сил на ось х и на ось у равна нулю, поэтому пара сил не имеет равнодействующей. Несмотря на это тело под действием пары сил находится в равновесии.

Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние между линиями действия сил. Обозначим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютное значение момента:

• Кратчайшее расстояние между линиями действия сил называется – плечом пары, поэтому можно сказать, что момент пары сил по абсолютному значению равен произведению одной из сил на ее плечо.
• Момент пары сил можно показывать дугообразной стрелкой, указывающей направление вращения.
• Момент пары сил будем считать положительным, если пара стремится повернуть тело по направлению хода часовой стрелки, и отрицательным, если – против часовой стрелки.

Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой механическое состояние тела не изменяется, т.е. не изменяется движение тела или не нарушается его равновесие.

Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение.

Еще одно свойство пары сил, которое является основой для сложения пар:

− не нарушая состояния тела, можно как угодно изменять модули сил и плечо пары, только бы момент пары оставался неизменным.

По определению пары сил эквивалентны, т.е. производят одинаковое действие, если их моменты равны.

Если, изменив значения сил и плечо новой пары, мы сохраним равенство их моментов М 1 = М 2 или F1 a = F 2 b, то состояние тела от такой замены не нарушится.

Момент результирующей пары определится по формуле:

М= М 1 + М 2 +... + М п.=

М і,

Где моменты пар, вращающие по часовой стрелке, принимаются положительными, а против часовой стрелки – отрицательными.

На основании приведенного правила сложения пар устанавливается условие равновесия системы пар лежащих в одной плоскости, а именно: для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары равнялся нулю или чтобы алгебраическая сумма моментов пар равнялась нулю:

1. Момент силы относительно точки и оси.
2. Момент силы относительно точки определяется произведением модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы.
3. При закреплении тела в точке О сила

стремится поворачивать его вокруг этой точки. Точка О, относительно которой берется момент, называется центром момента, а длина перпендикуляра а – плечом относительно центра момента.

Момент силы

относительно О определяется произведением силы на плечо: .

Момент принято считать положительным, если сила стремится вращать тело по часовой стрелке, а отрицательным — против часовой стрелки. Между моментом пары и моментом силы есть одно существенное различие.

Численное значение и направление момента пары сил не зависит от положения этой пары в плоскости.

Значение и направление (знак) момента силы зависит от положения точки, относительно которой определяется момент.

• Если сила расположена в плоскости, перпендикулярной к оси, момент этой силы определяется произведением ее величины на плечо
• Следовательно, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы относительно точки пересечения оси с этой плоскостью.
• 3. Метод кинетостатики
• Представим себе материальную точку массой т, движущуюся с ускорением а под действием какой-то системы активных и реактивных сил, равнодействующая которых равна F.
• Воспользуемся одной из известных нам формул (основным уравнением динамики) для того, чтобы уравнения движения записать в форме уравнений равновесия (метод кинетостатики):
• F = ma.
• Перепишем это уравнение в следующем виде:
• F + (-/ma) = 0.
• Выражение обозначается Кин и называется силой инерции:
• Kин= -mа.
• Сила инерции есть вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению.

относительно точки пересечения оси и плоскости:

Это равенство, являющееся математическим выражением принципа, который носит имя французского ученого Даламбера (1717—1783), можно рассматривать как уравнение равновесия материальной точки. Следует подчеркнуть, что полученное равенство, хотя и названо уравнением равновесия, в действительности является видоизмененным уравнением движения материальной точки.

Принцип Даламбера формулируется гак: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия.

Следует помнить, что сила инерции приложена к рассматриваемой материальной точке условно, но для связи, вызывающей ускорение, она в определенном смысле является реальной.

Обладая свойством инерции, всякое тело стремится сохранять свою скорость по модулю и направлению неизменной, в результате чего оно будет действовать на связь, вызывающую ускорение, с силой, равной силе инерции.

В качестве примера действия сил инерции можно привести случаи разрушения маховиков при достижении ими критической угловой скорости. Во всяком вращающемся теле действуют силы инерции, так как каждая частица этого тела имеет ускорение, а соседние частицы являются для нее связями.

Отметим, что весом тела называется сила, с которой тело вследствие притяжения Земли действует на опору (или подвес), удерживающую его от свободного падения. Если тело и опора неподвижны, то вес тела равен его силе тяжести.

4. Момент силы относительно точки

Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие. Если взять гаечный ключ в несколько раз длиннее, то прилагая то же усилие, гайку можно затянуть значительно сильнее. Из этого следует, что одна и та же сила может оказывать различное вращательное действие. Вращательное действие силы характеризуется моментом силы.

1. Понятие момента силы относительно точки ввел в механику итальянский ученый и художник эпохи Возрождения Леонардо да Винчи (1452—1519).
2. Моментом силы относительно точки называется произведение модуля силы на ее плечо:
3. М0(¥) = РИ.

Точка, относительно которой берется момент, называется центром момента. Плечом силы относительно точки называется кратчайшее расстояние от центра момента до линии действия силы.

Источник: https://mirznanii.com/a/322317/moment-sily-para-sil-i-ee-svoystva