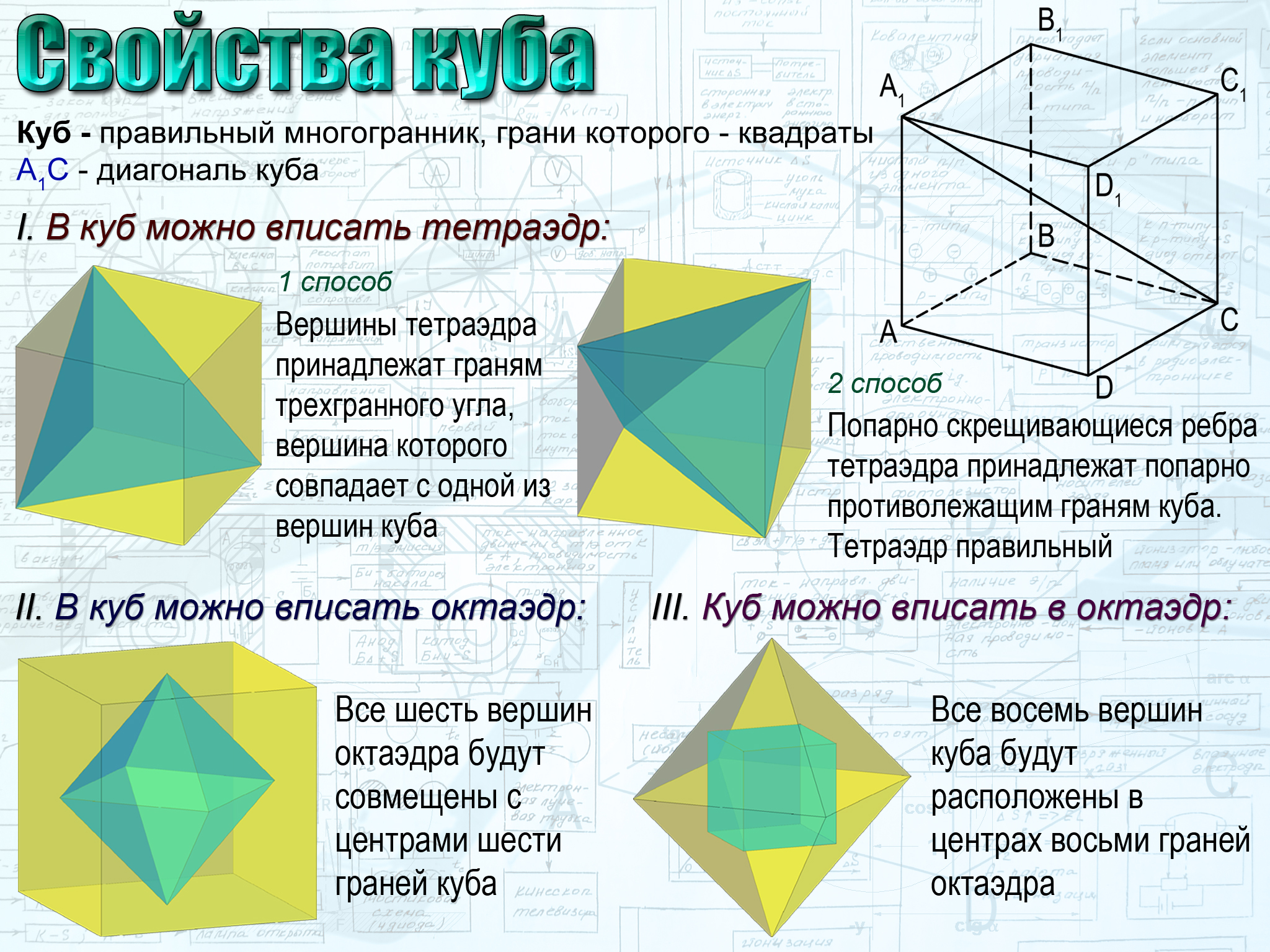
Параллелепипед – это геометрическая фигура, все 6 граней которой представляют собой параллелограммы.
В зависимости от вида этих параллелограммов различают следующие виды параллелепипеда:
- прямой;
- наклонный;
- прямоугольный.
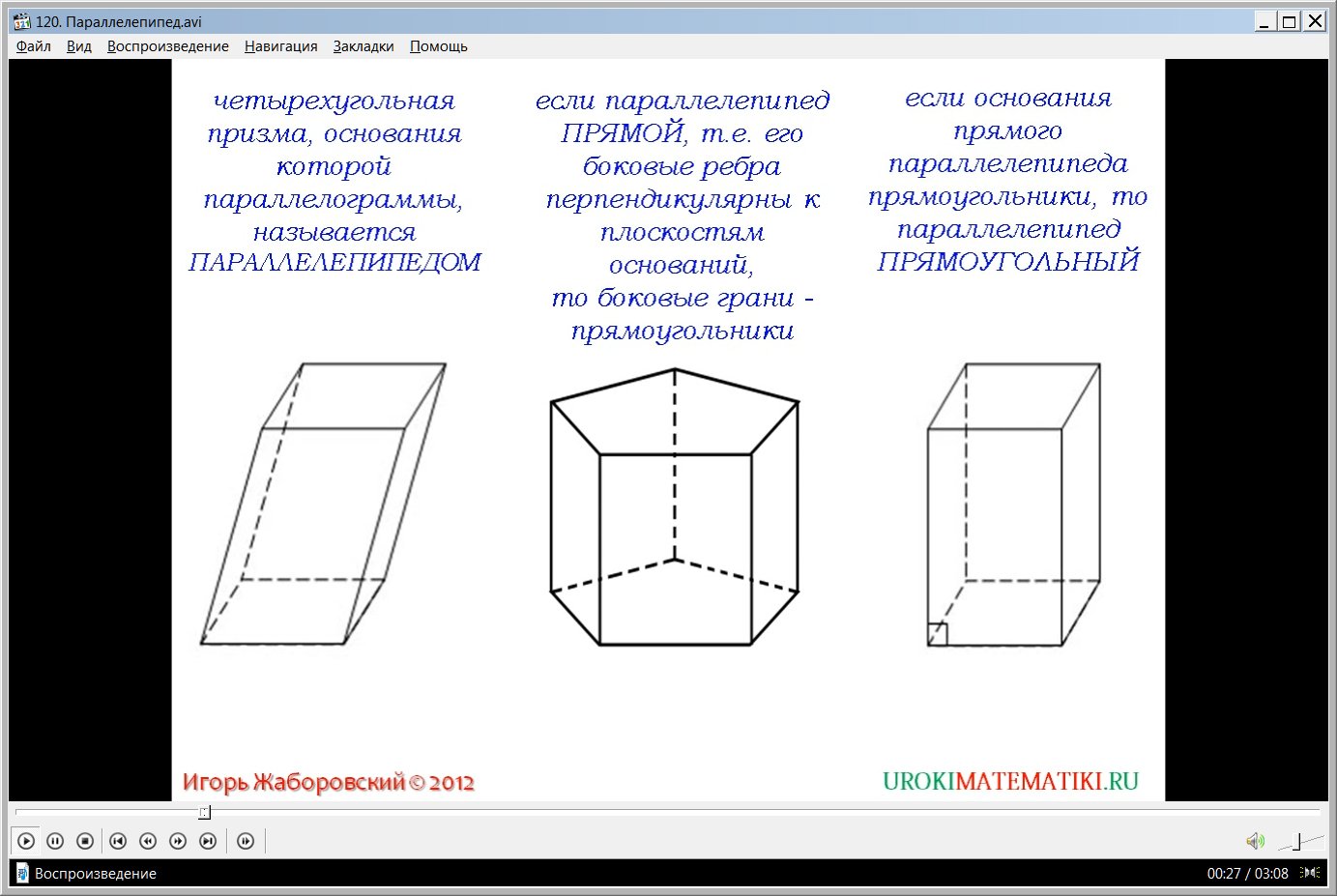
Прямым параллелепипедом называют четырехугольную призму, ребра которой составляют с плоскостью основания угол 90 °.
Прямоугольным параллелепипедом называют четырехугольную призму, все грани которой являются прямоугольниками. Куб есть разновидность четырехугольной призмы, у которой все грани и ребра равны между собой.
Свойства параллелепипеда
Особенности фигуры предопределяют ее свойства. К ним относят 4 следующих утверждений:
- Противолежащие ребра и грани фигуры параллельны и равны между собой.
- Углы сонаправленных сторон равны между собой. На фотографии ниже представлено графическое изображение сонапрвленных лучей OA и O1А1. Прямая рассекает пространство на две плоскости. Если лучи расположены в одной полуплоскости и параллельны друг другу, то их называют сонаправленными.
- 4 главные диагонали параллелепипеда пересекаются в одной точке внутри фигуры. Любой отрезок, проведенный между двумя плоскостями граней, через данную точку будет поделен ею пополам. Следствием данного свойства можно сформулировать следующим образом: плоскости, в которых лежат главные диагонали параллелепипеда, симметрично делят геометрическое тело.
- Согласно теореме Пифагора, квадрат диагонали параллелепипеда равен сумме квадратов ее измерений.
Запомнить все приведенные свойства просто, они легки для понимания и выводятся логически исходя из вида и особенностей геометрического тела. Однако, незамысловатые утверждения могут быть невероятно полезны при решении типовых заданий ЕГЭ и позволят сэкономить время необходимое для прохождения теста.
Формулы параллелепипеда
Для поиска ответов на поставленную задачу недостаточно знать только свойства фигуры. Также могут понадобиться и некоторые формулы для нахождения площади и объема геометрического тела.
Площадь оснований находится также как и соответствующий показатель параллелограмма или прямоугольника. Выбирать основание параллелограмма можно самостоятельно. Как правило, при решении задач проще работать с призмой, в основании которой лежит прямоугольник.
Формула нахождения боковой поверхности параллелепипеда, также может понадобиться в тестовых заданиях.
Примеры решения типовых заданий ЕГЭ
Задание 1
Дано: прямоугольный параллелепипед с измерениями 3, 4 и 12 см.
Необходимо найти длину одной из главных диагоналей фигуры.
Решение: Любое решение геометрической задачи должно начинаться с построения правильного и четкого чертежа, на котором будет обозначено «дано» и искомая величина.
На рисунке ниже приведен пример правильного оформления условий задания.
Рассмотрев сделанный рисунок и вспомнив все свойства геометрического тела, приходим к единственно верному способу решения. Применив 4 свойство параллелепипеда, получим следующее выражение:
После несложных вычислений получим выражение b2=169, следовательно, b=13. Ответ задания найден, на его поиск и чертеж необходимо потратить не более 5 минут.
Задание 2
Дано: наклонный параллелепипед с боковым ребром 10 см, прямоугольник KLNM с измерениями 5 и 7 см, являющийся сечением фигуры параллельным указанному ребру.
Необходимо найти площадь боковой поверхности четырехугольной призмы.
Решение: Сначала необходимо зарисовать дано.
Для решения данного задания необходимо применить смекалку. Из рисунка видно, что стороны KL и AD – неравны, как и пара ML и DC. Однако, периметры данных параллелограммов очевидно равны.
Следовательно, боковая площадь фигуры будет равна площади сечения помноженной на ребро AA1, так как по условию ребро перпендикулярно сечению. Ответ: 240 см2.
Источник: https://karate-ege.ru/matematika/parallelepiped-osnovnye-svojstva-i-formuly.html
Лекция по математике на тему "Параллелепипед"
Рассмотрим эти предметы:
- Строительный кирпич
- Игральный кубик
- Микроволновая печь
- Эти предметы объединяет форма.
- Поверхность, состоящая из двух равных параллелограммов АВСD и А1В1С1D1
- и четырех параллелограммов АА1В1В и ВВ1С1С, СС1D1D, АА1D1D называется параллелепипедом.
Параллелограммы, из которых составлен параллелепипед, называются гранями. Грань А1В1С1D1. Грань ВВ1С1С. Грань АВСD.
При этом грани АВСD и А1В1С1D1 чаще называют основаниями, а остальные грани боковыми.
Стороны параллелограммов называются ребрами параллелепипеда. Ребро А1В1. Ребро СС1. Ребро АD.
Ребро СС1, не принадлежит основаниям, оно называются боковое ребро.
Вершины параллелограммов называют вершинами параллелепипеда.
Вершина D1. Вершина В. Вершина С.
- Вершины D1 и В
- не принадлежат одной грани и называются противоположными.
- Параллелепипед можно изображать разными способами
- Параллелепипед в основании, которого лежит ромб, При этом изображениями граней являются параллелограммы.
Параллелепипед в основании, которого лежит квадрат. Невидимые рёбра АА1, АВ, АD изображаются штриховыми линиями.
Параллелепипед в основании, которого лежит квадрат
Параллелепипед в основании, которого лежит прямоугольник или параллелограмм
Параллелепипед, у которого все грани квадраты. Чаще его называют кубом.
На экране появляется фото:
На экране изображение добавляется
- Строительный кирпич
- Игральный кубик
- На экране добавляется изображение
Микроволновая
печь
На рисунке с анимацией появляется формы
На экране изображение
На экране обновляется изображение:
На экране изображение с анимацией элементов.
Грани:
- АВСD–нижнее основание
- А1В1С1D1-верхнее основание
- АА1В1В
- ВВ1С1С
- СС1D1D
- АА1D1D
- На экране изображение с анимаций элементов:
Рёбра:
- АВ, ВС,CD,
- AD, А1В1,В1С1,
- C1D1, A1D1,
- АА1, ВВ1, СС1, DD1–боковые рёбра
- На экране изображение с анимацией появления элементов
- Вершины:
- А, В, С, D,
- А1,В1,С1,D1
D1 и В
- А1 и С
- D и В1
- А и C1
- противоположные
- вершины
- На экране изображение и текст:
- Способы изображения параллелепипеда
- На экране изображение и текст:
- Способы изображения параллелепипеда
На экране изображение и текст:
- Способы изображения параллелепипеда
- На экране изображение и текст:
- Способы изображения параллелепипеда
| Все рассмотренные параллелепипеды обладают свойствами. Сформулируем и докажем их. | |
Свойство 1. Противоположные грани параллелепипеда параллельны и равны.
|
На экране изображение и текст: Свойство 1. Противоположные грани параллелепипеда параллельны и равны. Доказательство: |
- К рисунку добавляется пункт 1)
- 1)АВСD– параллелепипед
- К рисунку добавляется пункт 2)
- 2)АВВ1А1–параллелепипед ВВ1
- К рисунку добавляется пункт 3)
- 3)
- К рисунку добавляется пункт 4)
- 4) ВС=АD, ВВ1 =АА1 (по свойству паралл-мма),
- К рисунку добавляется пункт 5)
- 5) В1ВС=А1АD (как углы с сонаправленами сторонами)
- К рисунку добавляется пункт 6)
- 6)
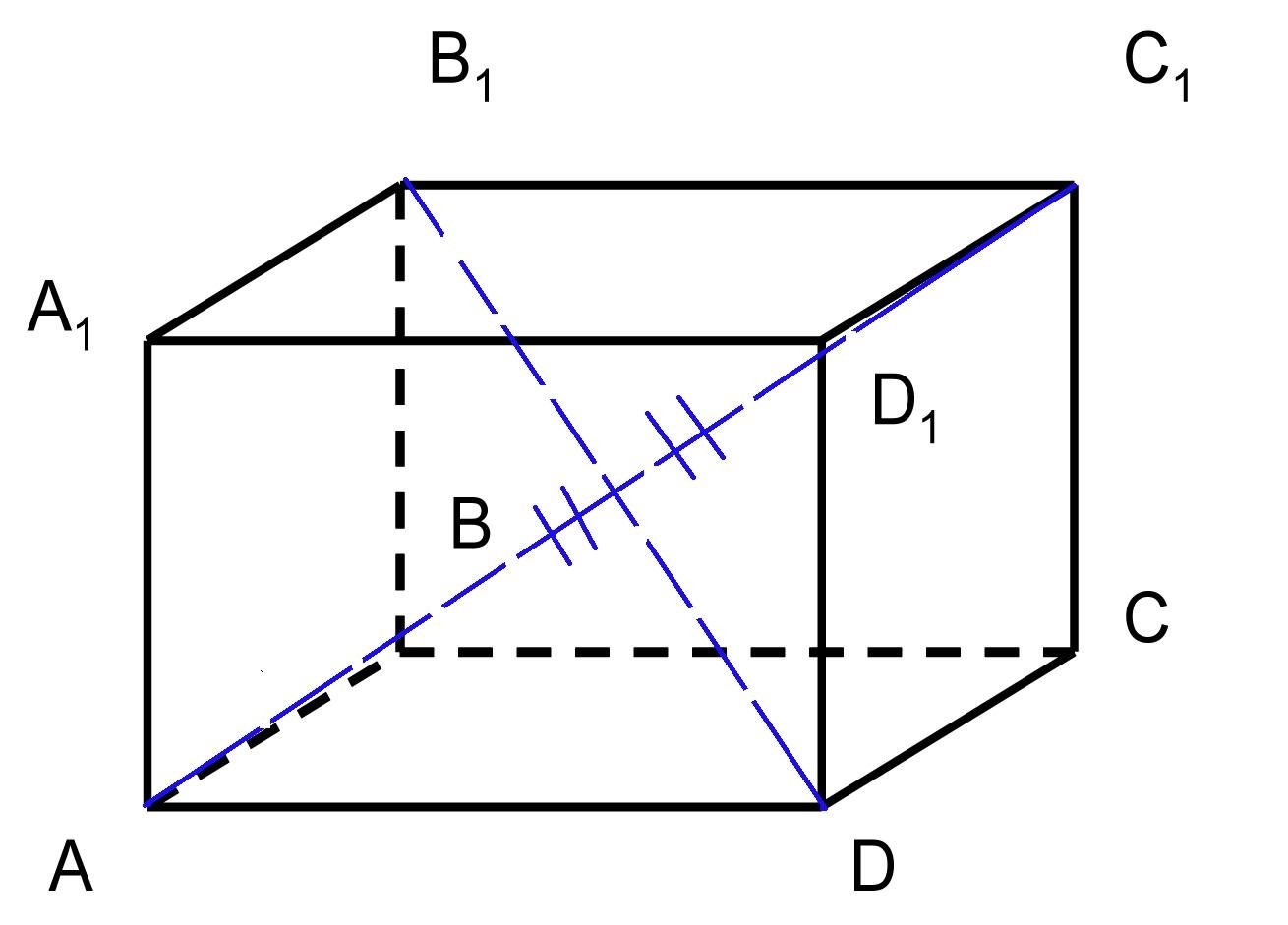
Параллелепипед обладает ещё свойством о диагоналях . Диагональю параллелепипеда называется отрезок соединяющий не соседние вершины. На чертеж пунктирной линией показаны диагонали В1D, BD1, А1С.
Итак, свойство 2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Для доказательства свойства рассмотрим четырехугольник ВВ1D1D. Его диагонали В1D, BD1 являются диагоналями параллелепипеда АВСDА1В1С1D1.
В первом свойстве мы уже выяснили, что ребро ВВ1 параллельно и равно ребру АА1, но ребро АА1 параллельно и равно ребру DD1. Следовательно рёбра ВВ1 и DD1 параллельны и равны, что доказывает четырехугольник ВВ1D1D– параллелограмм. А в параллелограмме по свойству диагонали В1D, BD1 пересекаются в некоторой точке О и этой точкой делятся пополам.
Четырехугольник ВС1D1А также является параллелограммом и его диагонали С1А, пересекаются в одной точке и делятся этой точкой пополам. Диагонали параллелограмма С1А, ВD1 являются диагоналями параллелепипеда, а значит сформулированное свойство доказано.
На экране чертёж и текст
Определение. Диагональю параллелепипеда -это отрезок соединяющий противоположные вершины.
На экране текст и чертеж:
Свойство 2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
- К рисунку добавляется пункт 1)
- 1)ВВ1=АА1, (из свойства грани)
- АА1=DD1, АА1DD1 (по свойству грани)
- К рисунку добавляется пункт 2)3)
- 2) ВВ1=АА1, АА1=DD1;
- , АА1DD1 .
- 3)
-параллелограмм, значит В1DBD1=О, причём В1О=ОD, BO=OD1. - К рисунку добавляется пункт 4)
- 4) ВС1D1А–параллелограмм, значит С1А, С1А, .
- Для закрепления теоретических знаний о параллелепипеде рассмотрим задачу на доказательство.
На рёбрах параллелепипеда отмечены точки L,M,N,P так, что BL=CM=A1N=D1P. Доказать, что ALMDNB1C1P параллелепипед.
- Грань ВВ1А1А параллелограмм, значит ребро ВВ1 равно и параллельно ребру АА1, но по условию отрезки BL и A1N, значит равны и параллельны отрезки LB1 и NA.
- 3)Следовательно, четырехугольник LB1NA по признаку параллелограмм.
- 4) Так как СС1D1D–параллелограмм, значит ребро СС1 равно и параллельно ребру D1D, а СМ равно D1P по условию, значит равны и параллельны отрезки МС1и DP
- Следовательно, что четырехугольник MC1PD тоже параллелограмм.
- 5) Углы LB1N и MC1P равны как углы с соответственно параллельными и одинаково направленными сторонами.
- 6) Мы получили, что у параллелограммов и MC1PD соответствующие стороны равны и углы между ними равны, значит параллелограммы равны.
- 7) Отрезки равны по условию, значит BLMC- параллелограмм и сторона BC параллельна стороне LM параллельна стороне В1С1.
- 8) Аналогично из параллелограмма NA1D1P следует, что сторона A1D1 параллельна стороне NP и параллельна стороне AD.
- 9)Противоположные грани ABB1A1 и DCC1D1 параллелепипеда по свойству параллельны, а отрезки параллельных прямых заключенных между параллельными плоскостями равны, значит отрезки В1С1, LM, AD,NP равны.
Получено, что в четырехугольниках ANPD, NB1C1P, LB1C1M, ALMD две стороны параллельны и равны , значит они параллелограммы. Тогда наша поверхность ALMDNB1C1P состоит из шести параллелограммов , два из которых равны, а по определению это параллелепипед.
На экране текст задачи:
На рёбрах параллелепипеда отмечены точки L,M,N,P так, что BL=CM=A1N=D1P. Доказать, что ALMDNB1C1P параллелепипед.
На экране анимация чертежа и текст доказательства:
Доказательство:
-
ВВ1А1А– параллелограмм, значит ВВ1 =АА1, ВВ1||АА1.
-
LB1 = NA, LB1||NA
На экране появляется пункт доказательства 3)
На экране анимация чертежа и добавляется пункт 4)
Доказательство:
- СС1D1D–параллелограмм, значит СС1||D1D, СС1=D1D.
- MC1=DP, MC1 || DP
- MC1PD – параллелограмм.
- На экране анимация чертежа и добавляется пункт 5)
Доказательство:
-
∠LB1N=∠MC1P (как углы с сонаправленными сторонами)
На экране добавляется пункт 6)
-
LB1NA= MC1PD
Добавляется пункт доказательства 7)
-
||В1С1
Добавляется пункт доказательства 8)
-
A1N=D1P NA1D1P–параллелограмм||AD.
На экране анимация рисунка и добавляется пункт 9)
Доказательство:
-
По свойству (ABB1A1)||(DCC1D1)
В1С1= LM=AD=NP
На экране добавляется пункт 10) 11
-
ANPD, NB1C1P, LB1C1M, ALMD –параллелограммы по признаку.
-
Так как ANPD, NB1C1P, LB1C1M, ALMD –параллелограммы, а параллелограммы равны , то по определению ALMDNB1C1P параллелепипед.
Источник: https://infourok.ru/lekciya-po-matematike-na-temu-parallelepiped-1447706.html
Параллелепипед — определение, свойства и измерение фигуры
Общая характеристика
В мире имеется множество предметов с формой параллелепипеда. Люди обычно не задумываются об этом, но архитектура и различные массивные строения состоят из нескольких граней. Выглядеть параллелепипед может по-разному в зависимости от типа.
Основные понятия и классификация
Определение параллелепипеда, пирамиды, куба и других многогранников было известно с древнейших времен. Основными характеристиками являются простота и значимость.
Выведенные формулы V и S значимы для решения различных задач с практическим содержанием и доказательства теорем (по чертежам). Виды параллелепипеда:
- Прямой. Четыре боковые грани имеют углы по 90 градусов.
- Прямоугольный. Каждая сторона фигуры является прямоугольной.
- Наклонный.
- Двугранный, трехгранный. Состоит из нескольких граней под углом 90 градусов.
- Наклонный, диагональный. Боковые грани не перпендикулярны основаниям.
- Ромбоэдр. Стороны являются одинаковыми ромбами.
- Куб. Параллелепипед с равными (квадратными) сторонами.
В 6 классе на уроке геометрии изучают планиметрию (плоские фигуры). Здесь представлена развертка плоскостей.
Две стороны параллелепипеда, не имеющие общего ребра, называются противоположными, а содержащие единую линию — смежными. С точки зрения плоскостей, расположенных параллельно, внутри пересекаются три их пары. Эти вершины соединяет отрезок — диагональ. Длина трех ребер правильного многогранника называется измерением. Главным условием является общая вершина.
При решении задач важно понятие высоты — перпендикуляра, опущенного из любой вершины на обратную сторону. Грань, на которую опускается высота, считается основанием. Свойства параллелепипеда:
- любые стороны являются параллелограммами (с симметрией);
- стороны, расположенные друг против друга, будут параллельными и равными.
Кирпич — отличный пример прямоугольного параллелепипеда (ПП). Также его форму имеют девятиэтажные панельные дома, шифоньеры, шкафы-купе, контейнеры для хранения продуктов и прочие предметы быта.
Диагонали поверхности пересекаются и этой центральной точкой делятся на несколько частей. Они равны d2=a2+b2+c2
Грани параллелепипеда спереди и сзади равнозначны, также как верхняя и нижняя стороны, но не равны, поскольку не противоположные, а смежные.
Формулы и анализ
Для ПП верно мнение, что его объем равен величине тройного произведения векторов трех сторон, исходящих из единой вершины. Формулы для ПП:
- V=a*b*c.
- S б =2*c*(a+b).
- S п =2*(a*b+b*c+a*c).
Расшифровка обозначений: V — объем фигуры, S — площадь поверхности, a — длина, b — ширина, c — высота.
Особым случаем параллелепипеда, в котором все стороны квадраты, является куб. Если любую из сторон обозначить буквой a, то для поверхности и объема используются формулы: S=6*a*2, V=3*а. В них V — объем фигуры, a — длина грани.
Последняя разновидность параллелепипеда — прямой тип. Его основанием будет параллелограмм, а основанием ПП — прямоугольник. Формулы, используемые в математике и геометрии: Sб=Ро*h, Sп=Sб+2Sо, V=Sо*h.
Для нахождения ответов недостаточно знать только свойства геометрической фигуры. Могут пригодиться формулы для вычисления S и V.
Диагональ ПП равна сложению квадратов его измерений: d2 = a2 + b2 + c2. Эта формула получается из теоремы Пифагора.
∆BAD — прямоугольный, поэтому BD2 = AB2 + AD2 = b2 + c2.
∆BDD1 является прямоугольным, значит, BD12 = BD2 + DD12. Нужно подставить значение: d2 = a2 + b2 + c2.
Стандартная формула: V= Sосн*h. Расшифровка обозначений: V — объем параллелепипеда, Sосн — площадь основания, h — высота.
S находится так же, как показатель параллелограмма или прямоугольника. При решении тестов и экзаменационных задач легче вычислять показатели призмы, в основе которой находится прямой угол. Также может пригодиться формула расчета стороны параллелепипеда Sбок = P*h, где:
- Sбок — площадь параллелепипеда;
- Р — периметр;
- h — высота, перпендикулярная основанию.
Объем фигуры равен величине смешанного произведения нескольких векторов, выпущенных из единой точки.
Практическое применение
Для вычисления объема, высоты и прочих характеристик фигуры нужно знать теоретические основы и формулы. Решение задач входит в программу сдачи ЕГЭ и билеты при поступлении в вуз.
Доказательство теорем
Теоретически S боковой поверхности ПП равна S б. п. = 2 (a+b)c. S полной поверхности равна Sполн. поверхности ПП=2 (ab+ac+bc).
Объем ПП равен произведению трех его боковых частей, выходящих из единой вершины (три измерения ПП): abc.
Доказательство: так как у ПП боковые ребра перпендикулярны основанию, то они являются и его высотами — h=AA1=c. Если в основании лежит прямоугольник, то Sосн=AB ⋅ AD=ab. Диагональ d ПП можно найти по формуле d2=a2+b2+c2, где a, b, c — измерения ПП.
Если в основании расположен прямоугольник, то △ ABD прямоугольный, значит, по теореме Пифагора BD2=AB2+AD2=a2+b2. Если все боковые грани перпендикулярны основной линии, то BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD.
Когда △ BB1D прямоугольный, то по теореме Пифагора B1D=BB12+BD2.
Решение задач
Задача 1: известны ПП: 3, 4, 12 см, необходимо найти длину главной диагонали фигуры.
Поиск ответа на вопрос начинается с выстраивания схематического изображения, на котором означаются величины. Используется формула B1D2 = AB2 + AD2 + AA12. После вычислений получается выражение b2=169, b=13.
Задача 2: ребра ПП, выходящие из общей точки, равны 3 и 4, общая S — 94. Нужно найти третье ребро, выходящее из той же вершины.
Ребра обозначаются а1 и а2, а неизвестное — а3. Площадь поверхности выражается S = 2 (a1a2 + a1a3 + a2a3).
Далее получаем a3 (a1 + a2) = S/2 — a1a2. Неизвестное ребро: a3 = S/2 — a1a2/a1 + a2 = 47−12/7 = 5.
Задача 3: два ребра прямоугольного параллелепипеда, выходящие из общей точки, составляют 72 и 18, диагональ равна 78. Нужно определить объем фигуры.
Для решения требуется найти диагональ по формуле вычисления квадратного корня из суммы (a2 + b2 + c2), где a, b, c — ребра фигуры. 78 — корень из суммы 722 + 182 + c2. Решение:
- 78 = корень из суммы 5508+с2
- 782 = 5508 + с2
- с2 = 6084 — 5508.
- С2 = 576.
Ответ: объем составляет 576.
Задача 4: ребро наклонного параллелепипеда составляет 10 см, прямоугольник KLNM с измерениями 5 и 7 см является сечением фигуры, параллельным ребру. Нужно определить площадь боковой поверхности призмы.
KL и AD не являются равными, как пара ML и DC. Боковая S фигуры эквивалентна S сечения, умноженной на AA1, так как ребро перпендикулярно сечению. Ответ: 240 см².
Задача 5: ABCDA1B1C1D1 = 3, 4 см, боковое ребро — 12 см. Нужно определить диагональ ПП.
В основании лежит прямоугольник со сторонами АВ 3 см и AD 4 см. Боковое ребро составляет 3 см. BB1 является высотой ПП и равняется 12 см. Диагональ B1D2 = AB2 + BB1 2 += 9+16+144 = 169. B1D= 13 см.
Задача 6: основанием ПП служит квадрат, одна из вершин его верхнего основания одинаково удалена от всех вершин нижней части. Нужно найти высоту фигуры, если диагональ основания равна 8 см, а боковое ребро — 5 см.
Одна из вершин основания (F) равнозначно удалена от всех вершин нижнего основания параллелепипеда. Вместе с диагональю нижней части (AC) она образует равнобедренный ∆AFC. AF = AC по условию. AF является ребром фигуры.
В равнобедренном ∆AFC стороны одинаковы: AF=FC=5 см, AC=8 см. Высота ∆AFC будет являться высотой параллелепипеда.
Высота треугольника делит его основание пополам. По теореме Пифагора она равна:
- FK2 + (AC/2)2 = FC2;
- FK2 + 16 = 25;
- FK2 =25−16 = 9;
- FK = 3 см.
Высота фигуры составляет 3 см.
Установленные теоремы, доказательства, а также выведенные формулы помогают вычислить различные значения для фигуры.
Источник: https://nauka.club/matematika/geometriya/parallelepiped.html
Наклонный параллелепипед: свойства, формулы и задачи репетитора по математике
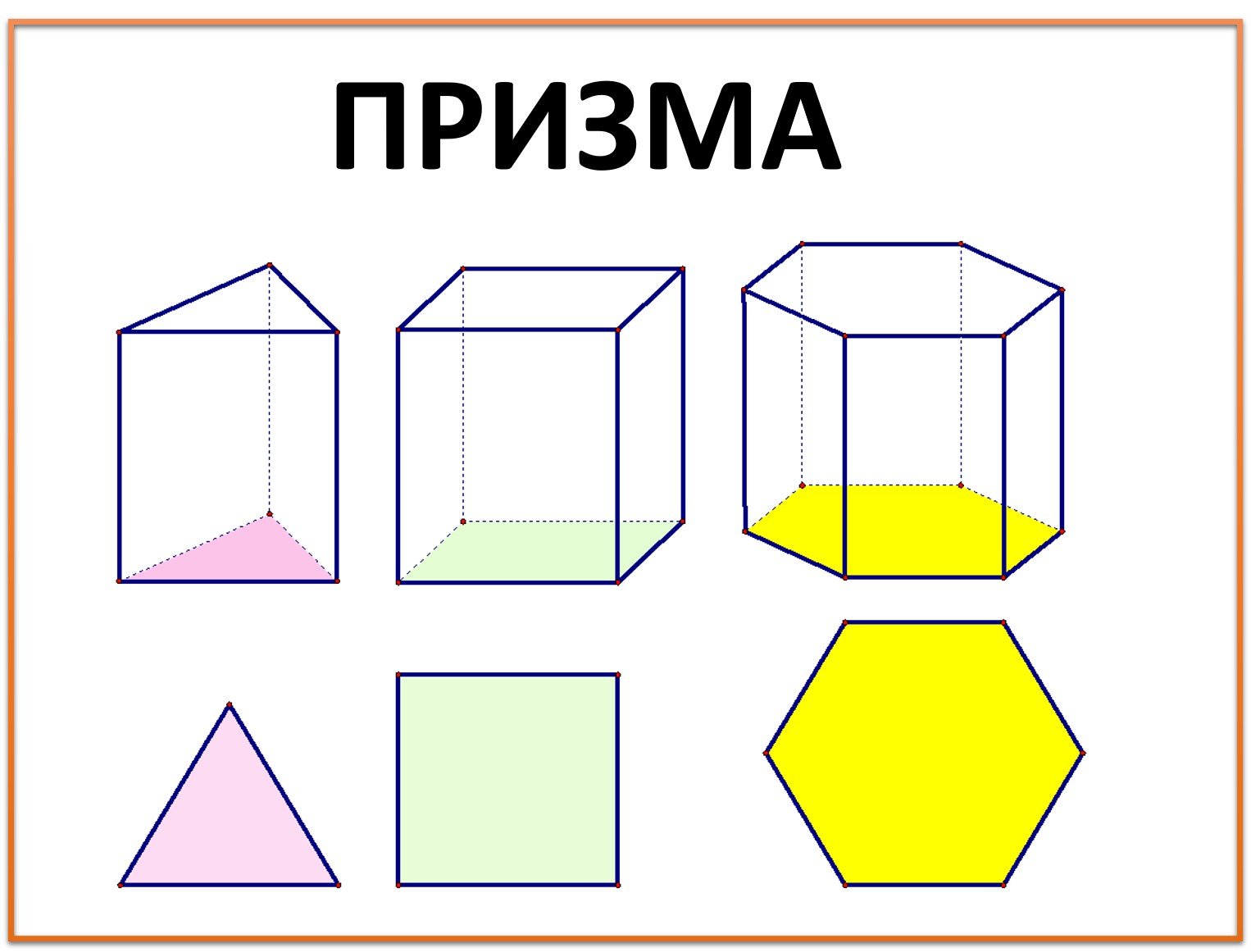
Параллелепипедом называется четырехугольная призма, в основаниях которой лежат параллелограммы. Высотой параллелепипеда называют расстояние между плоскостями его основаниями. На рисунке высота показана отрезком . Различают два вида параллелепипедов: прямой и наклонный. Как правило, репетитор по математике сначала дает соответствующие определения для призмы, а затем переносит их на параллелепипед. Мы сделаем также.
Напомню, что призма называется прямой, если ее боковые ребра перпендикулярны основаниям, если перпендикулярности нет – призму называют наклонной. Эту терминологию наследует и параллелепипед. 
Прямой параллелепипед – ни что иное, как разновидность прямой призмы, боковое ребро которой совпадает с высотой. Сохраняются определения таких понятий, как грань, ребро и вершина, являющиеся общими для всего семейства многогранников. Появляются понятие противоположные грани. У параллелепипеда 3 пары противоположных граней, 8 вершин ти 12 ребер.
Свойства наклонного параллелепипеда:
1) Все его грани – параллелограммы, а противоположные грани — равные параллелограммы.
3)
Каждый параллелепипед состоит из шести равных по объему треугольных пирамид. Чтобы показать их ученику репетитор по математике должен отрезать от параллелепепеда половинку его диагональным сечением и разбить ее отдельно на 3 пирамиды. Их основания должны лежать в разных гранях исходного паралеллепипеда. Репетитор математики найдет применение этого свойства в аналитической геометрии. Оно используется для вывода объема пирамиды через смешанное произведение векторов.
Формулы объема параллелепипеда:
1) , где — площадь основания, h – высота.
2) Объем параллелепипеда равен произведению площади поперечного сечения на боковое ребро .
Репетитору по математике: Как известно, формула является общей для всех призм и если репетитор уже доказал ее, нет смысла повторять тоже самое для параллелепипеда. Однако в работе со учеником среднего уровня (слабому формула не пригодиться) преподавателю желательно действовать с точностью до наоборот. Призму оставить в покое, а для параллелепипеда провести аккуратное доказательство.
3) , где –объем одной из шести треугольных пирамиды из которых состоит параллелепипед.
4) Если , то
Площадью боковой поверхности параллелепипеда называется сумма площадей всех его граней:
Полная поверхность параллелепипеда – это сумма площадей всех его граней, то есть площадь + две площади основания: .
О работе репетитора с наклонным параллелепипедом:
Задачами на наклонный параллелепипед репетитор по математике занимается не часто. Вероятность их появления на ЕГЭ достаточно мала, а дидактика неприлично бедная.
Более-менее приличная задача на объем наклонного параллелепипеда вызывает серьезные проблемы, связанные с пределением расположения точки Н — основания его высоты.
В этом случае репетитору по математике можно посоветовать обрезать параллелепипед до одной из шести его пирамид (о которых идет речь в свойстве №3), попробовать найти ее объем и умножить его на 6.
Если боковое ребро параллелепипеда имеет равные углы со сторонами основания, то Н лежит на биссектрисе угла A основания ABCD. И если, например, ABCD — ромб, то
Задачи репетитора по математике:
1) Грани параллелепипеда равные роибы со стороной 2см и острым углом . Найти объем параллелепипеда.
2) В наклонном параллелепипеде боковое ребро равно 5см. Сечение, перпендикулярное ему, является четырехугольником со взаимно перпендикулярными диагоналями, имеющими длины 6см и 8 см. Вычислить объем паралеллепипеда.
3) В наклонном параллелепипеде известно, что , а в онованием ABCD является ромб со стороной 2см и уголом . Определите объем параллелепипеда.
Репетитор по математике, Александр Колпаков
Источник: https://ankolpakov.ru/naklonnyj-parallelepiped-svojstva-formuly-i-zadachi-repetitora-po-matematike/
Свойства прямоугольного параллелепипеда
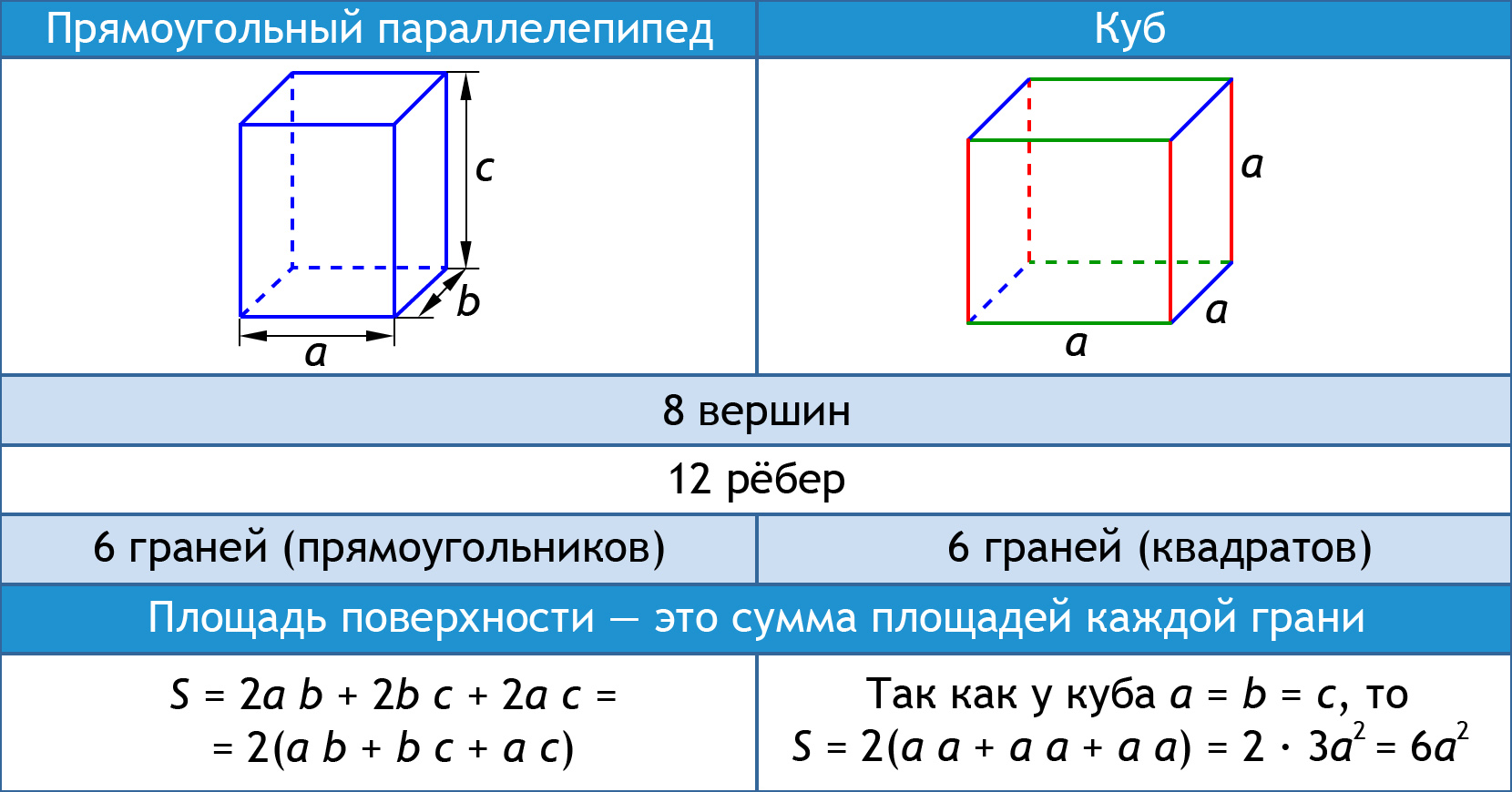
Измерениями прямоугольного параллелепипеда называются длины трёх рёбер с общей вершиной. Например, в качестве измерений у прямоугольного параллелепипеда ABCDA1B1C1D1 можно взять длины рёбер D1D, D1C1 и D1A1, которые имеют общую вершину D1.
У прямоугольника два измерения — длина и ширина.При этом квадрат диагонали прямоугольника равен сумме квадратов двух его измерений (данное утверждение основывается на теореме Пифагора).
Свойство
| Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. |
- Доказательство
- Дано: ABCDA1B1C1D1 — прямоугольный параллелепипед, В1В, В1С1, В1А1 — измерения
- Доказать: BD12 = В1В2 + В1С12 + В1А12
- Доказательство:
ВВ1 A1B1C1D1, т.е. данное ребро перпендикулярно любой прямой, которая принадлежит плоскости этой грани и проходит через точку В1. Следовательно, D1B1B = 900. По теореме Пифагора для D1B1B запишем: BD12 = В1В2 + В1D12 . ABCDA1B1C1D1 — прямоугольный параллелепипед, то есть основание A1B1C1D1 является прямоугольником, значит, В1D1 есть диагональ прямоугольника и В1D12 = В1С12 + В1А12. Следовательно, BD12 = В1В2 + В1С12 + В1А12, что и требовалось доказать.
Мы знаем, что площадь прямоугольника равна произведению его измерений. По аналогии для прямоугольного параллелепипеда справедливо:
| Объём прямоугольного параллелепипеда равен произведению трёх его измерений. |
Чтобы доказать данное утверждение воспользуемся принципом Кавальери:
Рассмотрим сначала прямоугольный параллелепипед с измерениями , и 1 и куб с ребром 1, которые «стоят» на плоскости .
Нам известно, что данный куб будет являться единицей измерения объёмов, т.е. его объём равен 1. Любая секущая плоскость, параллельная плоскости , даёт в качестве сечения данного параллелепипеда прямоугольник, площадь которого равна , а куба — квадрат, площадь которого равна 1. То есть площадь сечения параллелепипеда в раз больше площади сечения куба, а, значит, согласно принципу Кавальери, объём рассматриваемого параллелепипеда больше объёма куба в раз, то есть равен .
Далее рассмотрим два прямоугольных параллелепипеда с измерениями , , и , , 1, которые «стоят» на плоскости так, чтобы основания принадлежащие этой плоскости имели измерения , и , 1.
Объём второго параллелепипеда равен (см. доказано выше). Любая секущая плоскость, параллельная плоскости , даёт в качестве сечения первого параллелепипеда прямоугольник, площадь которого равна , а второго — прямоугольник, площадь которого равна .
То есть площадь сечения первого параллелепипеда в раз больше площади сечения второго параллелепипеда, а, значит, согласно принципу Кавальери, объём первого параллелепипеда больше объёма второго параллелепипеда в раз, то есть равен V = , что и требовалось доказать.
В прямоугольном параллелепипеде с измерениями , , , который изображен выше, площадь основания S равна , а высота равна боковому ребру: = . Значит, формулу V = можно записать в виде: V = S.
Объём прямоугольного параллелепипеда
| Объём прямоугольного параллелепипеда равен произведению площади основания на высоту. |
Объём призмы
| Объём призмы равен произведению площади основания на высоту. |
Источник: https://budu5.com/manual/chapter/3592
Параллелепипед — это… Что такое Параллелепипед?
Параллелепи́пед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.
Типы параллелепипеда
Различается несколько типов параллелепипедов:
- Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники;
- Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники;
- Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основания
- Куб — это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.
Основные элементы
Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.
Свойства
- Параллелепипед симметричен относительно середины его диагонали.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Противолежащие грани параллелепипеда параллельны и равны.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Основные формулы
Прямой параллелепипед
- Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота
- Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания
- Объём V=Sо*h
Прямоугольный параллелепипед
- Основная статья: Прямоугольный параллелепипед
- Площадь боковой поверхности Sб=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда
- Площадь полной поверхности Sп=2(ab+bc+ac)
- Объём V=abc, где a, b, c — измерения прямоугольного параллелепипеда.
Куб
- Площадь боковой поверхности Sб=4a², где а — ребро куба
- Площадь полной поверхности Sп=6a²
- Объём V=a³
Произвольный параллелепипед
Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры.
Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины.
Соотношение между длинами сторон параллалепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения[1]:215.
В математическом анализе
В математическом анализе под n-мерным прямоугольным параллелепипедом понимают множество точек вида
Примечания
Прямоугольный параллелепипед
Источник: https://dic.academic.ru/dic.nsf/ruwiki/79270
