Уравнение состояния идеального газа в физике

Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона).
Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние. В 1834 г. французский физик Б.  Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеаль­ного газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул.
В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m. Мы знаем, что . Следовательно, . Учитывая, что , получим: .
Таким образом, имеем:  — уравнение состояния (уравнение Менделеева – Клапейрона).
Другие формы записи уравнения состояния идеального газа.
1.Уравнение для 1 моля вещества. Если n=1 моль, то, обозначив объем одного моля Vм, получим: .
2. Запись уравнения через плотность: — плотность зависит от температуры и давления!
3.  Уравнение Клапейрона.
Эта запись означает, что  для данной массы данного газа справедливо равенство:
Для постоянной массы идеального газа отношение произве­дения давления на объем к абсолютной  температуре в данном состоянии есть величина постоянная: .
Газовые законы.
1.      Закон Авогадро. В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов). Условие: V1=V2=…=Vn;  p1=p2=…=pn; T1=T2=…=Tn
Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.
2.      Закон Дальтона. Давление смеси газов равно сумме парциальных (частных) давлений каждого газа. Доказать: p=p1+p2+…+pn
3.      Закон Паскаля. Давление, производимое на жидкость или газ, передается во все стороны без изменения.

Источник: https://www.eduspb.com/node/1742

Уравнение состояния идеального газа. Изопроцессы

Соотношение

связывающее давление газа с его температурой и концентрацией молекул, получено в 3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений.

Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν.

Для этого нужно использовать равенства

Здесь N – число молекул в сосуде, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:

Соотношение

(*)

• называется уравнением состояния идеального газа.
• Для одного моля любого газа это соотношение принимает вид:
• Если температура газа равна Tн = 273,15 К (0 °С), а давление pн = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V0, равный

V0 = 0,0224 м3/моль = 22,4 дм3/моль.

Это утверждение называется законом Авогадро.

Для смеси невзаимодействующих газов уравнение состояния принимает вид

pV = (ν1 + ν2 + ν3 + …)RT,

где ν1, ν2, ν3 и т. д. – количество вещества каждого из газов в смеси.

Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Бенуа Клайпероном, в форме (*) оно было впервые записано Дмитрием Ивановичем Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.

Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение (*) можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории.

Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими.

В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс.

Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах p, V) в виде некоторой траектории, каждая точка которой представляет равновесное состояние.

Изотермический процесс (T = const)

Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. Из уравнения (*) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:

Модель. Изотермический процесс.

На плоскости (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гипербол p ~ 1 / V, которые называются изотермами.

Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры, изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис. 3.3.1).

Уравнение изотермического процесса было получено из эксперимента английским физиком Робертом Бойлем (1662 г.) и независимо французским физиком Эдмом Мариоттом (1676 г.). Поэтому это уравнение называют законом Бойля–Мариотта.

Рисунок 3.3.1.Семейство изотерм на плоскости (p, V). T3 > T2 > T1

1. Изохорный процесс (V = const)
2. Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.
3. Как следует из уравнения (*) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p ~ T или

Модель. Изохорный процесс.

На плоскости (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 3.3.2).

Рисунок 3.3.2.Семейство изохор на плоскости (p, T). V3 > V2 > V1

Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля.

Уравнение изохорного процесса может быть записано в виде:

где p0 – давление газа при T = T0 = 273,15 К (т. е. при температуре 0 °С). Коэффициент α, равный (1/273,15) К–1, называют температурным коэффициентом давления.

• Изобарный процесс (p = const)
• Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p.
• Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:

где V0 – объем газа при температуре 0 °С. Коэффициент α равен (1/273,15) К–1. Его называют температурным коэффициентом объемного расширения газов.

Модель. Изобарный процесс.

На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3.3.3), которые называются изобарами.

Рисунок 3.3.3.Семейство изобар на плоскости (V, T). p3 > p2 > p1

Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Жозефом Гей-Люссаком (1862 г.). Поэтому уравнение изобарного процесса называют законом Гей-Люссака.

Экспериментально установленные законы Бойля–Мариотта, Шарля и Гей-Люссака находят объяснение в молекулярно-кинетической теории газов. Они являются следствием уравнения состояния идеального газа.

Источник: https://questions-physics.ru/molekulyarnaya-fizika-i-termodinamika/uravnenie_sostoyaniya_idealnogo_gaza_izoprotsessi.html

Инфофиз — мой мир..

   Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.

   Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:

• все вещества состоят из мельчайших частиц (молекул, атомов, элементарных частиц), между которыми есть промежутки;
• частицы находятся в непрерывном тепловом движении;
• между частицами вещества существуют силы взаимодействия (притяжения и отталкивания); природа этих сил электромагнитная.

   Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.

   Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.

   Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.

   Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.

   Существует еще одно состояние вещества – плазма. Плазма — частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы.

При достаточно сильном нагревании любое вещество испаряется, превращаясь в газ. Если увеличивать температуру и дальше, резко усилится процесс термической ионизации, т. е.

молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.

Модель идеального газа. Связь между давлением и средней кинетической энергией.

   Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)

   Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.

   Свойства идеального газа:

1. расстояние между молекулами много больше размеров молекул;
2. молекулы газа очень малы и представляют собой упругие шары;
3. силы притяжения стремятся к нулю;
4. взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими;
5. молекулы этого газа двигаются беспорядочно;
6. движение молекул по законам Ньютона.

   Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.

   Объем газа обозначается V. Объем газа всегда совпадает с объемом того сосуда, который он занимает. Единица объема в СИ м3.

•    Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.
•    p = F/S       Единица давления в СИ паскаль [Па]
•    До настоящего времени употребляются внесистемные единицы давления:
•    техническая атмосфера 1 ат = 9,81-104 Па;
•    физическая атмосфера 1 атм = 1,013-105 Па;

   миллиметры ртутного столба 1 мм рт. ст.= 133 Па;

   1 атм = = 760 мм рт. ст. = 1013 гПа.

   Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени дей­ствует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.

   Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.

   Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.

   В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной.

   Приборы, измеряющие давление, называют манометрами. Манометры фиксиру­ют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.

   Жидкостные манометры:

1. открытый – для измерения небольших давлений выше атмосферного 
2. закрытый — для измерения небольших давлений ниже атмосферного, т.е. небольшого вакуума

        

    Металлический манометр – для измерения больших давлений.

   Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.

1.  
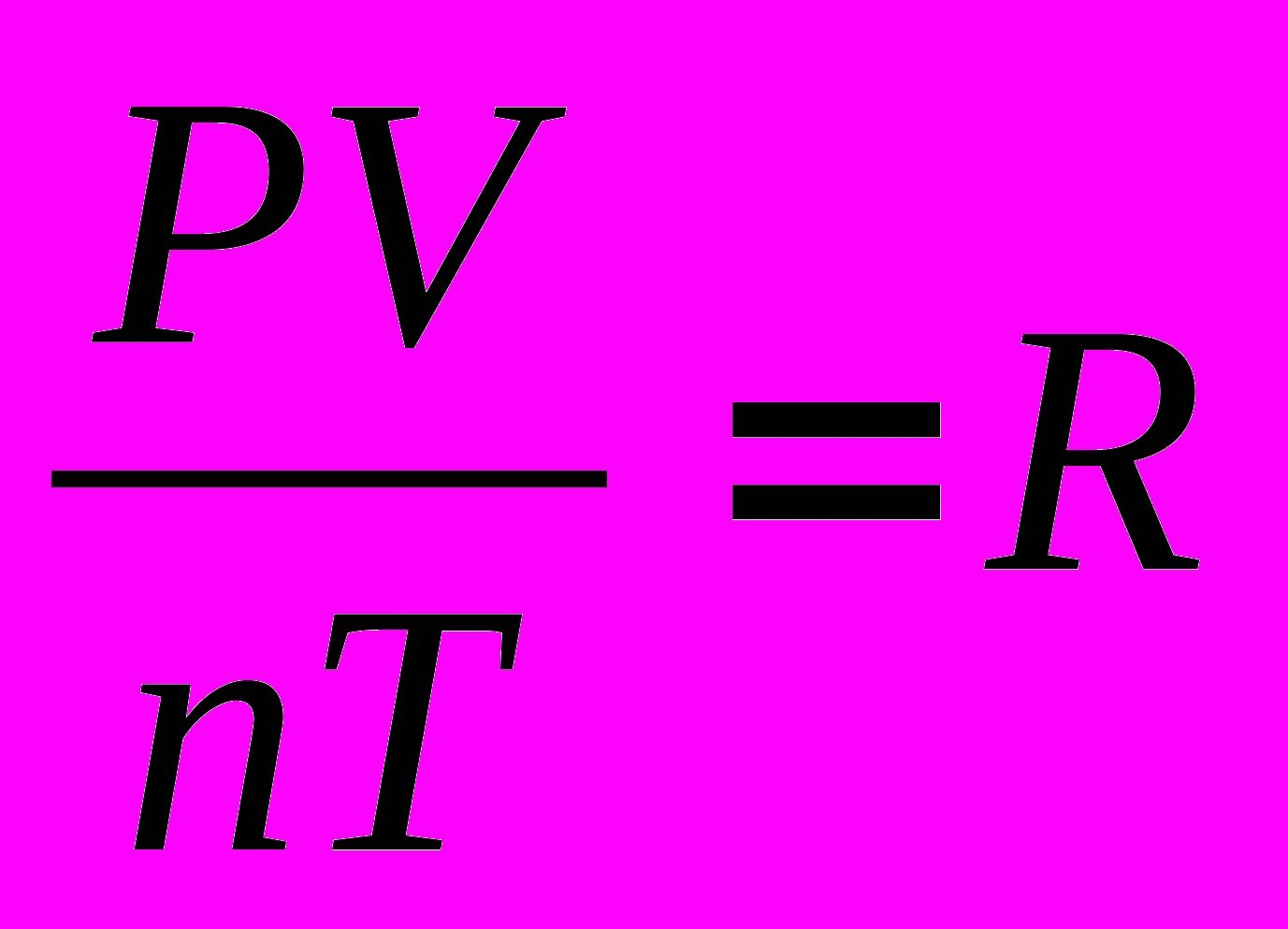
2. Основное уравнение молекулярно-кинетической теории идеального газа.
3.    Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул
4.    p = 1/3·m0·n·v2
5.    m0 — масса одной молекулы газа;
6.    n = N/V – число молекул в единице объема, или концентрация молекул;
7.    v2 — средняя квадратичная скорость движения молекул.
8.    Так как средняя кинетическая энергия поступательного движения молекул E = m0*v2/2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m0· v2)/2 = 2/3·E·n
9.    p = 2/3·E·n
10.    Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.
11.    Так как m0·n = m0·N/V = m/V = ρ,   где ρ – плотность газа, то имеем     p = 1/3· ρ· v2
12. Объединенный газовый закон.
13.    Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.
14.    Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
15.    Всякое изменение состояния газа называется термодинамическим процессом.
16.    В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
17.    Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.
18.    Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.
19. p = nkT 

   Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

•    где n – концентрация молекул, N – общее число молекул, V – объем газа
•    Тогда получим  или      
•    Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
•    При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.

Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.

1.    Уравнение Клайперона можно записать в другой форме.
2. p = nkT,
3.    учитывая, что
4.  
5.    Здесь N – число молекул в сосуде, ν – количество вещества, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

•    Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.
•    Ее численное значение в СИ   R = 8,31 Дж/моль·К
•    Соотношение                                                        

   называется уравнением состояния идеального газа.

   В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`

   Для одного моля любого газа это соотношение принимает вид: pV=RT

Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.

1.    Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)
2.    и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим   pΔV = R
3.    ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
4.    pSΔh = R
5.    pS = F – сила давления.
6.    Получим FΔh = R, а   произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
7.    Таким образом, R = A.
8.    Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.

Источник: http://infofiz.ru/index.php/mirfiziki/lkf/124-lk18

Идеальный газ. Уравнение идеального газа. Изопроцессы

Подробности Категория: Молекулярно-кинетическая теория Опубликовано 05.11.2014 07:28 Просмотров: 15468

Газ — одно из четырёх агрегатных состояний, в которых может находиться вещество.

Частицы, из которых состоит газ, очень подвижны. Они практически свободно и хаотично движутся, периодически сталкиваясь друг с другом подобно биллиардным шарам. Такое столкновение называют упругим столкновением. Во время столкновения они резко изменяют характер своего движения.

Так как в газообразных веществах расстояние между молекулами, атомами и ионами намного превышает их размеры, то между собой эти частицы взаимодействую очень слабо, и их потенциальная энергия взаимодействия очень мала по сравнению с кинетической.

Связи между молекулами в реальном газе сложные. Поэтому также довольно сложно описывать зависимость его температуры, давления, объёма от свойств самих молекул, их количества, скорости их движения. Но задача значительно упрощается, если вместо реального газа рассматривать его математическую модель — идеальный газ.

Предполагается, что в модели идеального газа между молекулами нет сил притяжения и отталкивания. Все они движутся независимо друг от друга. И к каждой из них можно применить законы классической механики Ньютона. А между собой они взаимодействуют только во время упругих столкновений. Время самого столкновения очень мало по сравнению со временем между столкновениями.

Классический идеальный газ

 

Попробуем представить молекулы идеального газа маленькими шариками, находящимися в огромном кубе на большом расстоянии друг от друга. Из-за этого расстояния они не могут друг с другом взаимодействовать. Следовательно, их потенциальная энергия равна нулю.

Но эти шарики двигаются с огромной скоростью. А значит, обладают кинетической энергией. Когда они сталкиваются друг с другом и со стенками куба, они ведут себя как мячики, то есть упруго отскакивают. При этом они меняют направление своего движения, но не меняют скорости.

Примерно так выглядит движение молекул в идеальном газе.

Газ можно считать идеальным, если в нём выполняются следующие допущения:

1. Потенциальная энергия взаимодействия молекул идеального газа настолько мала, что ею пренебрегают по сравнению с кинетической энергией.
2. Молекулы в идеальном газе также имеют настолько маленькие размеры, что их можно считать материальными точками. А это означает, что и их суммарный объём также ничтожно мал по сравнению с объёмом сосуда, в котором находится газ. И этим объёмом также пренебрегают.
3. Среднее время между столкновениями молекул намного превышает время их взаимодействия при соударении. Поэтому временем взаимодействия пренебрегают также.

Газ всегда принимает форму сосуда, в котором находится. Движущиеся частицы сталкиваются друг с другом и со стенками сосуда. Во время удара каждая молекула действует на стенку с некоторой силой в течение очень короткого промежутка времени. Так возникает давление. Суммарное давление газа складывается из давлений всех молекул.

Уравнение состояния идеального газа

•  
• Состояние идеального газа характеризуют три параметра: давление, объём и температура. Зависимость между ними описывается уравнением:
•  
• где р — давление,
• VM — молярный объём,
• R — универсальная газовая постоянная,
• T — абсолютная температура (градусы Кельвина).
• Так как VM = V/n, где V — объём, n — количество вещества, а n = m/M, то
•  

где m — масса газа, М — молярная масса. Это уравнение называется уравнением Менделеева-Клайперона.

1. При постоянной массе уравнение приобретает вид:
2.  
3. Это уравнение называют объединённым газовым законом.
4. Используя закон Менделеева-Клайперона, можно определить один из параметров газа, если известны два других.

Изопроцессы

С помощью уравнения объединённого газового закона можно исследовать процессы, в которых масса газа и один из важнейших параметров — давление, температура или объём — остаются постоянными. В физике такие процессы называются изопроцессами.

Из объединённого газового закона вытекают другие важнейшие газовые законы: закон Бойля-Мариотта, закон Гей-Люссака, закон Шарля, или второй закон Гей-Люссака.

Изотермический процесс

• 
• Процесс, в котором изменяются давление или объём, но температура остаётся постоянной, называется изотермическим процессом.
• При изотермическом процессе T = const, m = const.

Поведение газа в изотермическом процессе описывает закон Бойля-Мариотта. Этот закон открыли экспериментальным путём английский физик Роберт Бойль в 1662 г. и французский физик Эдм Мариотт в 1679 г. Причём сделали они это независимо друг от друга. Закон Бойля-Мариотта формулируется следующим образом: В идеальном газе при постоянной температуре произведение давления газа на его объём также постоянно.

Уравнение Бойля-Мариотта можно вывести из объединённого газового закона. Подставив в формулу Т = const,получаем

p·V = const

Это и есть закон Бойля-Мариотта. Из формулы видно, что давление газа при постоянной температуре обратно пропорционально его объёму. Чем выше давление, тем меньше объём, и наоборот.

Как объяснить это явление? Почему же при увеличении объёма газа его давление становится меньше?

Так как температура газа не меняется, то не меняется и частота ударов молекул о стенки сосуда. Если увеличивается объём, то концентрация молекул становится меньше.

Следовательно, на единицу площади придётся меньшее количество молекул, которые соударяются со стенками в единицу времени. Давление падает. При уменьшении объёма число соударений, наоборот, возрастает.

Соответственно растёт и давление.

Графически изотермический процесс отображают на плоскости кривой, которую называют изотермой. Она имеет форму гиперболы.

Каждому значению температуры соответствует своя изотерма. Чем выше температура, тем выше расположена соответсвующая ей изотерма.

Изобарный процесс

Процессы изменения температуры и объёма газа при постоянном давлении, называются изобарными. Для этого процесса m = const, P = const.

Зависимость объёма газа от его температуры при неизменяющемся давлении также была установлена экспериментальным путём французским химиком и физиком Жозефом Луи Гей-Люссаком, опубликовавшем его в 1802 г.

Поэтому её называют законом Гей-Люссака: «При постоянном давлении отношение объёма постоянной массы газа к его абсолютной температуре является постоянной величиной».

При Р = const уравнение объединённого газового закона превращается в уравнение Гей-Люссака.

Пример изобарного процесса — газ, находящийся внутри цилиндра, в котором перемещается поршень. При повышении температуры растёт частота ударов молекул о стенки. Увеличивается давление, и поршень приподнимается. В итоге увеличивается объём, занимаемый газом в цилиндре.

1. Графически изобарный процесс отображается прямой линией, которая называется изобарой.
2. Чем больше давление в газе, тем ниже расположена на графике соответствующая изобара.

Изохорный процесс

• Изохорным, или изохорическим, называют процесс изменения давления и температуры идеального газа при постоянном объёме.
• Для изохорного процесса m = const, V = const.

Представить такой процесс очень просто. Он происходит в сосуде фиксированного объёма.

Например, в цилиндре, поршень в котором не двигается, а жёстко закреплён.

Изохорный процесс описывается законом Шарля: «Для данной массы газа при постоянном объёме его давление пропорционально температуре». Французский изобретатель и учёный Жак Александр Сезар Шарль установил эту зависимость с помощью экспериментов в 1787 г. В 1802 г. её уточнил Гей-Люссак. Поэтому этот закон иногда называют вторым законом Гей-Люссака.

1. При V = const из уравнения объединённого газового закона получаем уравнение закона Шарля, или второго закона Гей-Люссака.
2. При постоянном объёме давление газа увеличивается, если увеличивается его температура.
3. На графиках изохорный процесс отображается линией, которая называется изохорой.
4. Чем больше объём занимаемый газом, тем ниже расположена изохора, соответствующая этому объёму.

В реальности ни один параметр газа невозможно поддерживать неизменным. Это возможно сделать лишь в лабораторных условиях.

Конечно, в природе идеального газа не существует. Но в реальных разреженных газах при очень низкой температуре и давлении не выше 200 атмосфер расстояние между молекулами намного превышает их размеры. Поэтому их свойства приближаются к свойствам идеального газа.

Источник: http://ency.info/materiya-i-dvigenie/molekulyarno-kineticheskaya-teoriya/354-idealnyj-gaz-ravnenie

Уравнение состояния идеального газа — Класс!ная физика

«Физика — 10 класс»

В этой главе речь пойдёт о следствиях, которые можно извлечь из понятия температуры и других макроскопических параметров. Основное уравнение молекулярнокинетической теории газов вплотную приблизило нас к установлению связей между этими параметрами.

Как можно рассчитать массу воздуха в кабинете физики? Какие параметры воздуха будут необходимы для определения этой массы?

Мы детально рассмотрели поведение идеального газа с точки зрения молекулярно-кинетической теории. Была определена зависимость давления газа от концентрации его молекул и температуры (см. формулу (9.17)).

Формулой (9.17) можно пользоваться только до давления порядка 10 атм.

Уравнение, связывающее три макроскопических параметра р, V и Т, называют уравнением состояния идеального газа.

Подставим в уравнение р = nkT выражение для концентрации молекул газа. Учитывая формулу (8.8), концентрацию газа можно записать так:

где NA — постоянная Авогадро, m — масса газа, М — его молярная масса. После подстановки формулы (10.1) в выражение (9.17) будем иметь

Произведение постоянной Больцмана k и постоянной Авогадро NA называют универсальной (молярной) газовой постоянной и обозначают буквой R:

R = kNA = 1,38 • 10-23 Дж/К • 6,02 • 1023 1/моль = 8,31 Дж/(моль • К). (10.3)

Подставляя в уравнение (10.2) вместо kNA универсальную газовую постоянную R, получаем уравнение состояния идеального газа произвольной массы

• Единственная величина в этом уравнении, зависящая от рода газа, — это его молярная масса.
• Из уравнения состояния вытекает связь между давлением, объёмом и температурой идеального газа, который может находиться в двух любых состояниях.
• Если индексом 1 обозначить параметры, относящиеся к первому состоянию, а индексом 2 — параметры, относящиеся ко второму состоянию, то согласно уравнению (10.4) для газа данной массы

Правые части этих уравнений одинаковы, следовательно, должны быть равны и их левые части:

Известно, что один моль любого газа при нормальных условиях (р0 = 1 атм = 1,013 • 105 Па, t = 0 °С или Т = 273 К) занимает объём 22,4 л. Для одного моля газа, согласно соотношению (10.5), запишем:

Мы получили значение универсальной газовой постоянной R.

Таким образом, для одного моля любого газа

Уравнение состояния в форме (10.4) было впервые получено великим русским учёным Д. И. Менделеевым. Его называют уравнением Менделеева—Клапейрона.

Уравнение состояния в форме (10.5) называется уравнением Клапейрона и представляет собой одну из форм записи уравнения состояния.

Б. Клапейрон в течение 10 лет работал в России профессором в институте путей сообщения. Вернувшись во Францию, участвовал в постройке многих железных дорог и составил множество проектов по постройке мостов и дорог.

1. Его имя внесено в список величайших учёных Франции, помещённый на первом этаже Эйфелевой башни.
2. Уравнение состояния не надо выводить каждый раз, его надо запомнить. Неплохо было бы помнить и значение универсальной газовой постоянной:
3. R = 8,31 Дж/(моль • К).

До сих пор мы говорили о давлении идеального газа. Но в природе и в технике мы очень часто имеем дело со смесью нескольких газов, которые при определённых условиях можно считать идеальными.

Самый важный пример смеси газов — воздух, являющийся смесью азота, кислорода, аргона, углекислого газа и других газов. Чему же равно давление смеси газов?

• Для смеси газов справедлив закон Дальтона.
• Закон Дальтона
• Давление смеси химически невзаимодействующих газов равно сумме (ЦЩй их парциальных давлений

p = p1 + p2 + … + pi + … .

где рi — парциальное давление i-й компоненты смеси.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»

Основные положения МКТ. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика

Почему тепловые явления изучаются в молекулярной физике — Основные положения молекулярно-кинетической теории. Размеры молекул — Примеры решения задач по теме «Основные положения МКТ» — Броуновское движение — Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел — Идеальный газ в МКТ.

Среднее значение квадрата скорости молекул — Основное уравнение молекулярно-кинетической теории газов — Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» — Температура и тепловое равновесие — Определение температуры. Энергия теплового движения молекул — Абсолютная температура.

Температура — мера средней кинетической энергии молекул — Измерение скоростей молекул газа — Примеры решения задач по теме «Энергия теплового движения молекул» — Уравнение состояния идеального газа — Примеры решения задач по теме «Уравнение состояния идеального газа» — Газовые законы — Примеры решения задач по теме «Газовые законы» — Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»

Источник: http://class-fizika.ru/10_a196.html

Уравнение состояния идеального газа — это… Что такое Уравнение состояния идеального газа?

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

Так как , где 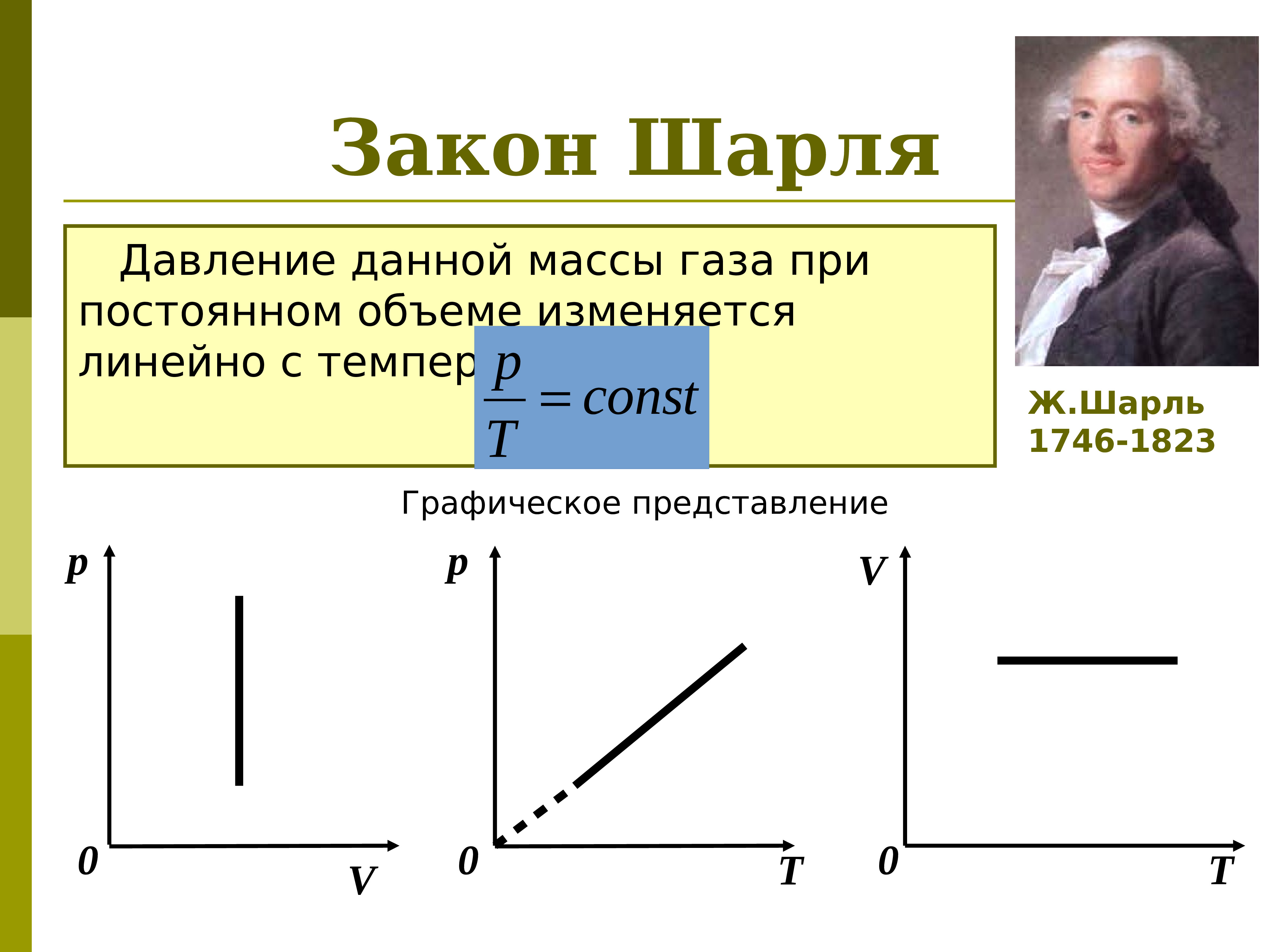 — количество вещества, а , где  — масса,  — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта.
 — Закон Гей-Люссака.
 — закон Шарля (второй закон Гей-Люссака, 1808 г.)

А в форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое.

С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:

1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:

 — закон Бойля — Мариотта.

Закон Бойля — Мариотта назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.

В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

где  — показатель адиабаты,  — внутренняя энергия единицы массы вещества.

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. И это обстоятельство может быть прояснено на основании молекулярных представлений.

С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.

С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе.

Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения.

При не слишком больших давлениях более существенным является второе обстоятельство и произведение немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение увеличивается.

См. также

• Реальный газ
• Уравнение состояния реального газа

Литература

• Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высш. шк., 2009. — 527 с. — ISBN 978-5-06-006161-1

Источник: https://dis.academic.ru/dic.nsf/ruwiki/51238

Термодинамика и молекулярная физика

Автор Чивилев Виктор Иванович 383 статьи

• Связь между давлением, концентрацией и температурой для идеального газа можно получить, исключив  из равенств (1) и (2):
• P1V=ν1RTP=nkT     (4)
• Поскольку n=NVn=frac NV (NN – число молекул в сосуде объёмом VV), то равенство (4) принимает вид:
• PV=NkTPV=NkT   (5)

Пусть mm – масса газа в сосуде, μmu – молярная масса данного газа, тогда ν=mμ
u=frac mmu  есть число молей газа в сосуде. Число молекул NN в сосуде, число молей газа ν
u и постоянная Авогадро NАN_А связаны соотношением N=νNАN=
u N_А. Подставляя это выражение для NN в (5), получаем: PV=vNаkTPV=vN_аkT. Произведение постоянной Авогадро NА=6,02·1023 N_А=6,02cdot10^{23;} моль-1{}^{-1} на постоянную Больцмана kk называют универсальной газовой постоянной: R=NA·k≈8,31R=N_Acdot kapprox8,31  Дж/(моль·cdotК)  Таким образом,

1. PV=νRTPV=
   u RT.   (6)
2. Это уравнение, связывающее давление PP объём  VV температуру TT  (по шкале Кельвина) и число молей идеального газа ν
   u, в записи
3. PV=mμRTPV=frac mmu RT   (7)
4. называется уравнением Менделеева – Клапейрона.
5. Из равенства (7) легко получить зависимость между давлением PP плотностью ρ
   ho (ρ=mV)(
   ho=frac mV)  и температурой TT идеального газа
6. P=ρμRTP=frac
   homu RT.    (8)      

Каждое из уравнений (5), (6) и (7), связывающих три макроскопических параметра газа PP, VV и TT  и  называется уравнением состояния идеального газа. Здесь, конечно, речь идёт только о газе, находящемся в состоянии термодинамического равновесия, которое означает, что все макроскопические параметры не изменяются со временем.

Несколько слов о равновесных процессах. Если процесс с идеальным газом (или любой термодинамической системой) идёт достаточно медленно, то давление и температура газа во всём объёме газа успевают выровняться и принимают в каждый момент времени одинаковые по всему объёму значения.

Это означает, что газ проходит через последовательность равновесных (почти равновесных) состояний. Такой процесс с газом называется равновесным. Другое название равновесного процесса – квазистатический. Все реальные процессы протекают с конечной скоростью и поэтому неравновесны.

Это означает, что равновесный процесс можно изображать в виде графиков этих зависимостей. Неравновесный процесс изобразить графически невозможно.

Напомним ещё раз, что соотношения (4) – (8) справедливы только для идеальных газов. В смеси нескольких идеальных газов уравнения вида (4) – (8) справедливы для каждого газа в отдельности, причём объём VV и температура TT у всех газов одинаковы, а парциальные давления отдельных газов и общее давление в смеси связаны законом Дальтона.

• Покажем, что для смеси идеальных газов общее давление PP, объём VV, температура TT и суммарное число молей  связаны равенством
• PV=νRTPV=
  u RT   (9)
•                                                                                                   которое внешне совпадает с равенством (6) для одного газа.
• Запишем уравнение состояния для каждого сорта газа:
• P1V=ν1RTP_1V=
  u_1RT,
• P2V=ν2RTP_2V=
  u_2RT,
• ………dotsdotsdots
• Сложив все уравнения и учтя, что ν=v1+ν2+⋯
  u=v_1+
  u_2+cdots и P=P1+P2+⋯P=P_1+P_2+cdots (по закону Дальтона), получим (9).
• Для смеси идеальных газов можно записать уравнение
• PV=mμсрRTPV=frac m{mu_{ср}}RT   (10)

аналогичное уравнению (7) для одного газа. Здесь PP – давление в смеси, VV – объём смеси, m=m1+m2+⋯m=m_1+m_2+cdots – масса смеси, TT – температура смеси,   μср=mνmu_{ср}=frac m
uсредняя молярная масса смеси, состоящей из ν=v1+ν2+⋯
u=v_1+
u_2+cdots молей.

Действительно, равенство (9) для смеси идеальных газов можно записать в виде PV=mmνRTPV=frac m{displaystylefrac m
u}RT Учитывая, что mνfrac m
u есть μсрmu_{ср} получим (10). Например, средняя молярная масса атмосферного воздуха, в котором азот (μN2mu_{N_2}= 28 г /моль) преобладает над кислородом (μO2mu_{O_2}= 32 г / моль) равна 29 г/моль

Поведение реальных газов при достаточно низких температурах и больших плотностях газов уже плохо описывается моделью идеального газа.

Источник: https://zftsh.online/course/1179/uravnenie-sostoyaniya-idealnogo-gaza