Формула напряжения электрического поля

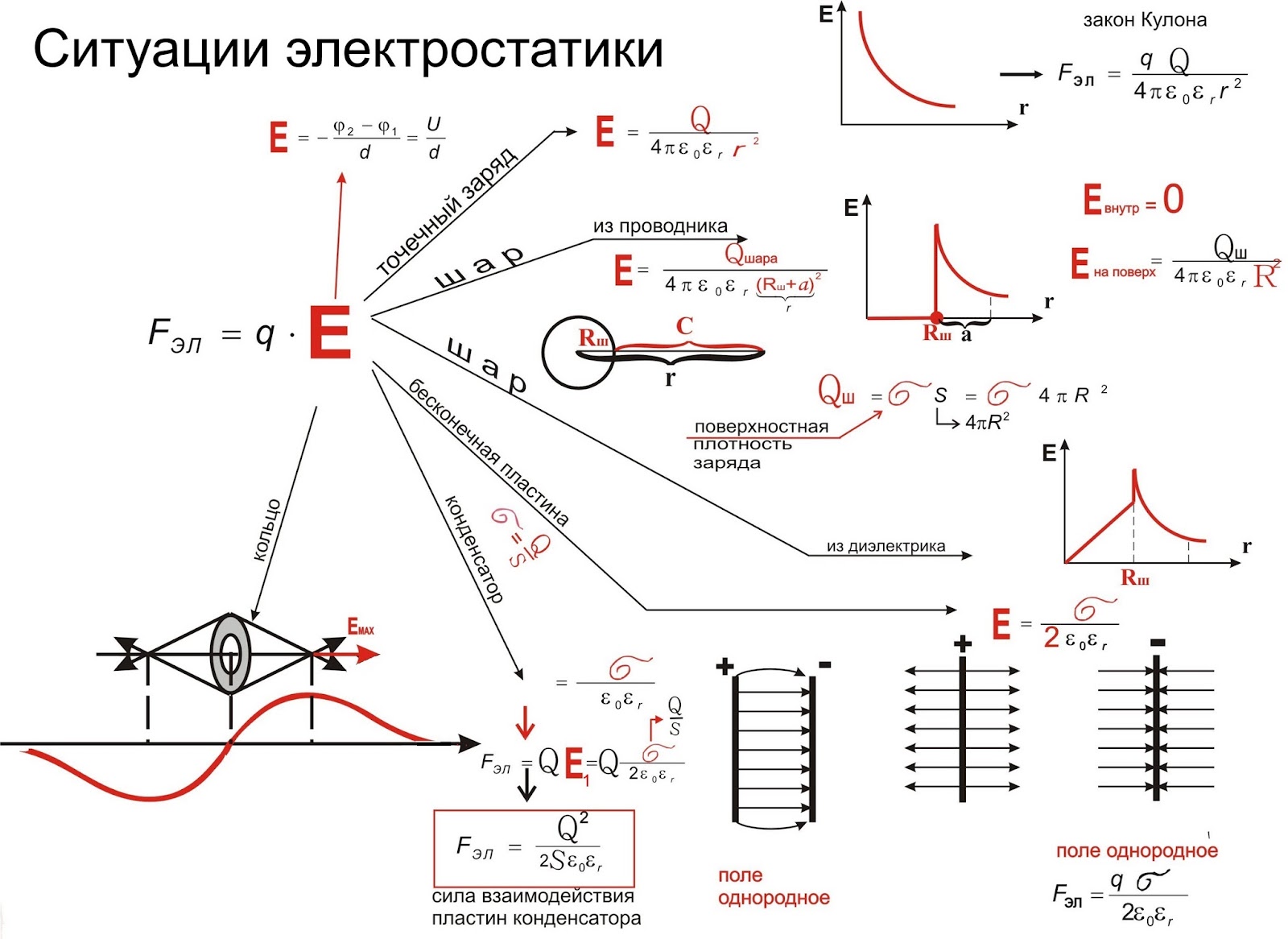
Электрическое поле, которое окружает заряд, это реальность, независящая от нашего желания что-либо изменить и как-то повлиять на это. Отсюда можно сделать вывод, что электрическое поле является одной из форм существования материи, так же как и вещество.

Электрическое поле зарядов, находящихся в состоянии покоя, называют электростатическим.

Чтобы обнаружить электростатическое поле определенного заряда нужно внести в его поле другой заряд, на который будет действовать определенная сила в соответствии с законом Кулона.

Напряженностью Е характеризуют электростатическое поле. Напряженность в некоторой точке электрического поля – физическая величина, которая равна силе, действующей на помещенный в определенную точку поля единичный положительный покоящийся заряд, и направленная в сторону действия силы.

Если в электрическое поле, создаваемое  зарядом q, внести «пробный» положительный точечный заряд qпр, то по закону Кулона на него будет действовать сила:

Если в одну точку поля помещать различные пробные заряды q/пр,  q//пр и так далее, то на каждый из них будут действовать различные силы, пропорциональные величине заряда. Отношение F/qпр для всех зарядов, вносимых в поле, будет идентичным, а также будет зависеть лишь от q и r, определяющих электрическое поле в данной точке. Данную величину можно выразить формулой:

Если предположить, что qпр = 1, то E = F. Отсюда делаем вывод, что напряженность электрического поля является его силовой характеристикой. Из формулы (2) с учетом выражения кулоновской силы (1) следует:

Из формулы (2) видно, что за единицу напряженности принимается напряженность в определенной точке поля, где на единицу заряда будет действовать единица силы. Поэтому в системе СГС единицей напряженности является дин/СГСq, а в системе СИ будет Н/Кл. Соотношение между приведенными единицами называют абсолютной электростатической единицей напряженности (СГСЕ):

• 
• Вектор напряженности направлен от заряда вдоль радиуса при образующем поле положительном заряде q+, а при отрицательном – q – по направлению к заряду вдоль радиуса.
• Если электрическое поле образовано несколькими зарядами, то силы, которые будут действовать на пробный заряд, складываются по правилу сложения векторов. Поэтому напряженность системы, состоящей из нескольких зарядов, в данной точке поля будет равна векторной сумме напряженностей каждого заряда в отдельности:
• 
• Данное явление носит название принцип суперпозиции (наложения) электрических полей.
• Напряженность в любой точке электрического поля двух точечных зарядов – q2 и +q1 можно найти использовав принцип суперпозиции:
• 
• По правилу параллелограмма будет происходить сложение векторов Е1 и Е2. Направление результирующего вектора Е определяется построением, а его абсолютная величина может быть вычислена с использованием формулы ниже:
• 
• Где α – угол между векторами Е1 и Е2.

Давайте рассмотрим электрическое поле, которое создает диполь. Электрический диполь – это система равных по величине (q = q1 = q2), но противоположных по знаку зарядов, расстояние между которыми очень мало, если сравнивать с расстоянием до рассматриваемых точек электрического поля.

Электрический дипольный момент p, являющийся основной характеристикой диполя и определяемый как вектор, направленный от отрицательного заряда к положительному, и равный произведению плеча диполя l на заряд q:

Также вектором является плечо диполя l, направленным от отрицательного заряда к положительному, и определяет расстояние между зарядами. Линия, которая проходит через оба заряда, носит название – ось диполя.

Давайте определим напряженность электрического поля в точке, которая лежит на оси диполя по середине (рисунок ниже а)):

В точке В напряженность Е будет равна векторной сумме напряженностей Е/ и Е//, которые создаются положительными и отрицательными зарядами но отдельности. Между зарядами –q и +q векторы напряженностей Е/ и Е// направлены в одну сторону, поэтому по абсолютной величине результирующая напряженность Е будет равна их сумме.

1. Если же нам необходимо найти Е в точке A, лежащей на продолжении оси диполя, то в разные стороны будут направлены вектора Е/ и Е//, соответственно по абсолютной величине результирующая напряженность будет равна их разности:
2. 
3. Где r – расстояние между точкой, которая лежит на оси диполя и в которой происходит определение напряженности, и средней точкой диполя.
4. В случае r>>l, величиной (l/2) в знаменателе можно пренебречь, тогда получим следующее соотношение:
5. Где p – момент электрический диполя.
6. Данная формула в системе СГС примет вид:
7. Теперь нужно вычислить напряженность электрического поля в точке С (рисунок выше б)), лежащей на перпендикуляре, восстановленном из средней точки диполя.
8. Так как r1 = r2, то будет иметь место равенство:
9. В точке С вектор результирующей напряженности по абсолютной величине будет равен:
10. Так как r>>l, то можно считать r1 ≈ r, тогда представленную выше формулу можно записать в другом виде:
11. Напряженность диполя в произвольной точке можно определить по формуле:
12. Где α – угол между плечом диполя l и радиус-вектором r, r – расстояние от точки, в которой определяется напряженность поля, до центра диполя, р – электрический момент диполя.

Пример

На расстоянии R = 0,06 м друг от друга находятся два одинаковых точечных заряда q1 = q2 = 10-6 Кл (рисунок ниже):

Необходимо определить напряженность электрического поля в точке А, которая расположена на перпендикуляре, восстановленном в центре отрезка, который соединяет заряды, на расстоянии h = 4 см от этого отрезка. Также нужно определить напряженность и в точке В, находящейся на середине отрезка,  который соединяет заряды.

Решение

По принципу суперпозиции (наложением полей) определяется напряженность поля Е. Таким образом, векторной (геометрической) суммой определяется Е, создаваемых каждым зарядом в отдельности: Е = Е1 + Е2.

• Напряженность электрического поля первого точечного заряда равна:
• Где q1 и q2 – заряды, образующие электрическое поле; r – расстояние от точки, в которой вычисляется напряженность, до заряда; ε0 – электрическая постоянная; ε – относительная диэлектрическая проницаемость среды.

Для определения напряженности в точке В сначала нужно построить векторы напряженности электрических полей от каждого заряда. Поскольку заряды положительны, то векторы Е/ и Е// будут направлены от точки В в разные стороны. По условию q1 = q2:

1. Это значит, что в средине отрезка напряженность поля равна нулю.
2. В точке А необходимо произвести геометрическое сложение векторов Е1 и Е2. В точке А напряженность будет равна:

Источник: https://elenergi.ru/elektrostaticheskij-dipol-elektrostaticheskoe-pole-napryazhennost.html

Определение напряженности электрического поля с помощью потенциала

Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.

Формулу можно использовать для определения разности потенциалов между двумя точками электрического поля, если напряженность поля в области между этими точками известна. Обращая эту формулу мы можем выразить напряженность электрического поля через его потенциал, т. е., зная V, мы сможем определить Е. Посмотрим, как это делается.

• Уравнение можно переписать в дифференциальной форме:
• dV = -E·dl = -Eldl,
• где dV — бесконечно малая разность потенциалов между точками на расстоянии dl друг от друга, а El — составляющая напряженности электрического поля в направлении этого бесконечно малого перемещения dl.Тогда:

Таким образом, составляющая напряженности электрического поля по любому направлению равна градиенту потенциала в этом направлении, взятому с обратным знаком. Градиентом величины V называется ее производная по определенному направлению dV/dl.

Если направление не указывается, то градиент соответствует направлению наиболее быстрого изменения V; это соответствует направлению вектора Е в данной точке, поскольку именно в таком направлении составляющая вектора Е совпадает с полной величиной напряженности поля:

Если расписать составляющие вектора Е по координатам х, у, z и в качестве l взять направления вдоль осей х у, z, то уравнение (24.8) можно записать в виде:

Здесь dV/dx — частная производная V по направлению х при условии, что у и z фиксированы.

В последнем примере мы вычислили напряженность электрического поля Е диполя в произвольной точке пространства. Складывая векторы напряженностей, создаваемых каждым зарядом в отдельности, получить этот результат было бы гораздо сложнее.

Вообще говоря, для многих распределений зарядов гораздо проще рассчитать потенциал, а затем по формуле (24.

9) — напряженность электрического поля Е, чем вычислять по закону Кулона по отдельности Е для каждого заряда: скалярные величины складывать намного проще, чем векторы.

Электростатическая потенциальная энергия

Предположим, что точечный заряд q перемещают в пространстве из точки а в точку b, электрические потенциалы в которых, обусловленные другими зарядами, равны соответственно Va и Vb. Изменение электростатической потенциальной энергии заряда q в поле других зарядов составляет:

ΔU = Ub — Ua = q(Vb — Va) = qVba

Пусть теперь имеется система нескольких точечных зарядов. Чему равна электростатическая потенциальная энергия системы? Удобнее всего выбрать за нуль потенциальную энергию зарядов на очень больших (в идеале бесконечно больших) расстояниях друг от друга.

Потенциальная энергия уединенного точечного заряда Q1 равна нулю, поскольку в отсутствие других зарядов на него не действует никакая сила.

Если к нему поднести второй точечный заряд, Q2, потенциал в точке, где находится второй заряд, будет равен:

Здесь r1 2 — расстояние между зарядами. Потенциальная энергия двух зарядов равна:

Она характеризует работу, необходимую для перемещения заряда Q2 из бесконечности (V = 0) на расстояние r1 2 до заряда Qi (или со знаком минус работу, необходимую для разнесения зарядов на бесконечно большое расстояние).

Если система состоит из трех зарядов, то ее полная потенциальная энергия будет равна работе по перемещению всех трех зарядов из бесконечности в место их расположения.

Работа по сближению зарядов Q2 и Q1 определяется выражением (24.

10); чтобы перенести заряд Q3 из бесконечности в точку на расстоянии r1 3 от Q1 и на расстоянии r2 3 от Q2, требуется совершить работу:

В этом случае потенциальная энергия системы трех точечных зарядов будет равна:

Для системы четырех зарядов выражение для потенциальной энергии будет содержать шесть таких членов и т.п. (При составлении подобных сумм необходимо следить за тем, чтобы не учитывать одну и ту же пару дважды). Часто нас интересует не полная электростатическая потенциальная энергия, а лишь часть ее.

Например, может возникнуть необходимость найти потенциальную энергию одного диполя в присутствии другого диполя. Во взаимодействии участвуют четыре заряда: Q1 и -Q1 первого диполя и Q2 и -Q2 второго диполя.

Потенциальная энергия одного диполя и в присутствии другого (иногда ее называют энергией взаимодействия) представляет собой работу по сближению диполей с бесконечно большого расстояния.

В этом случае нас не интересует взаимная потенциальная энергия зарядов Q1 и -Q1 или Q2 и -Q2; выражение для потенциальной энергии двух диполей будет содержать лишь четыре члена, соответствующие энергиям взаимодействия между зарядами: Q1 и Q2 ; Q1 и -Q2 ; -Q1 и Q2 ; -Q1 и -Q2.

Заключение

Электрический потенциал в любой точке пространства определяется как электростатическая потенциальная энергия единицы заряда. Разность потенциалов между двумя точками определяется взятой с обратным знаком работой, которая совершается полем при перемещении единичного электрического заряда между этими точками.

Разность потенциалов измеряется в вольтах (1 В = 1 Дж/Кл) и иногда называется напряжением. Изменение потенциальной энергии заряда q при прохождении им разности потенциалов Vbа равно ΔU = qVba.

Разность потенциалов Vbа между точками b и a в однородном электрическом поле напряженностью Е определяется формулой V = — Ed, где d — расстояние вдоль силовой линии поля между этими точками. В неоднородном электрическом поле Е соответствующее выражение имеет вид . Таким образом, зная Е, всегда можно определить Vbа. Если значение V известно, то составляющие напряженности поля Е можно найти, обращая приведенное соотношение:

Еx = -dV/dх , Еy = -dV/dу , Ez = -dV/dz .

Эквипотенциальные линии или поверхности представляют собой геометрическое место точек одного потенциала; они всюду перпендикулярны силовым линиям поля. Электрический потенциал уединенного точечного заряда Q относительно нулевого потенциала (на бесконечности) равен:

1. Потенциал произвольного распределения зарядов можно определить, суммируя (интегрируя) потенциалы отдельных зарядов.
2. где r — расстояние от элемента заряда dq до точки, в которой определяется V.
3. Продолжение следует. Коротко о следующей публикации:
4. Электрическая емкость, диэлектрики, накопление электрической энергии.

Конденсатор — устройство для накопления электрического заряда, который состоит из двух проводников (обкладок), расположенных близко друг к другу, но не соприкасающихся.

• Альтернативные статьи: Постоянный ток, Переменный ток.
• Замечания и предложения принимаются и приветствуются!

Источник: https://tel-spb.ru/statika/pole-potencial.php

Напряжённости электрического поля: описание, определение единицы измерения, стандартная формула

Краткое описание

Увидеть невооружённым взглядом электрическое поле (ЭП) невозможно: его можно обнаружить в процессе воздействия на заряженные тела. Удивительно, но прямого касания может и не быть, так как должна присутствовать силовая природа.

Ведь всем известно, что наэлектризованные волосы будут притягиваться к другим предметам. Многочисленные исследования смогли доказать, что аналогичный принцип действия имеют гравитационные поля.

Этот феномен был впервые описан в законе Кулона.

Стандартная формула электрического поля выглядит так: F = d₁ d₂ / 4 π q q₀ r ².

Расшифровка:

• d₁ и d₂ — параметры разрядов в кулонах.
• q ₀ — этим символом может обозначаться только электрическая постоянная.
• q — показатель диэлектрической проницаемости.
• F — сила взаимодействия разных зарядов (может измеряться в ньютонах).
• r — расстояние между двумя рассматриваемыми объектами в метрах.

Благодаря формуле напряжённости электростатического поля можно определить тот факт, что чем дальше находиться от центра, тем меньше будет ощущаться его воздействие. Графически его можно изобразить в виде силовых линий. Итоговое их расположение напрямую зависит от геометрических параметров носителя.

• На сегодняшний день специалисты научились выделять несколько разновидностей полей:

1. Специфические неоднородное. Рассматривается поле вокруг шарообразного или же точечного заряда. Все силовые линии расходятся только в том случае, если этот параметр имеет положительное значение.
2. Однородное поле. Все силовые линии располагаются исключительно параллельно друг другу. Эксперты утверждают, что идеальным является тот вариант, когда заряженные пластины бесконечны.

Индуцированные электрическим зарядом силовые линии относятся к замкнутому типу. Иная ситуация наблюдается только у вихревого поля, сформированного вокруг меняющегося магнитного потока.

Ключевые особенности

Так как в промежутке этого расстояния нет плотных тел, можно утверждать о существовании определённого невидимого поля. А так как оно связано со специфическими явлениями, то его начали называть электрическим. Такие поля существуют вокруг всех предметов, только из-за их невидимости и скомпенсированности взаимодействия друг на друга создаётся впечатление, что они проявляются.

Базовые параметры

Изобразить формулу напряжённости можно при помощи как математических закономерностей, так и графических приёмов.

Последние характеристики относятся к векторной категории, имеющей определённое направление.

Все эти нюансы крайне важны, так как во время решения практических задач часто приходится оперировать не стандартным модулем величины, а специфической проекцией вектора на заранее выбранную ось.

К основным свойствам ЭП можно отнести следующие факты:

• Оно может как притягивать, так и отталкивать.
• Невидимость для невооружённого глаза (итоговое определение осуществляется через поведение пробного электрического заряда).
• Всегда присутствует вокруг заряженных частиц, чего нельзя сказать о магнитном поле.
• Имеет векторное направление.
• Взаимодействует исключительно с ЭП.
• Отличается свойствами неоднородности и концентрации (напряжённость).

Электрическое поле можно определить при помощи обычного точного заряда. Если он будет направлен в интересующую точку пространства, то можно выяснить — присутствует ли в этом месте ЭП. Такой метод определения считается наиболее простым и понятным. Интенсивность излучаемого ЭП используется как обозначение напряжённости.

Влияющие на один и тот же заряд силы будут отличаться друг от друга по направлению и размеру в разных измеряемых точках.

Стоит отметить, что закон Кулона не адаптирован под современные требования. Для одной точки поля сила F будет прямо пропорциональна величине точечного заряда.

На фоне этого эксперты провели множество исследований. Теперь принято считать силовой характеристикой единицы измерения напряжённости «Е». Этот параметр является векторной величиной.

Найти напряжённость электрического поля можно в Ньютонах на Кулон.

Отдельно стоит учесть, что если ЭП образуется сразу несколькими зарядами, то общая напряжённость в определённой точке находится как общая геометрическая сумма.

Изучение потенциала

Именно этот параметр считается распространённой характеристикой ЭП. Потенциал выступает в роли накопленной ценной энергии, используемой для перемещения различных зарядов. В итоге потенциал может весь израсходоваться, из-за чего его показатель будет равен нулю.

Процесс накопления происходит в обратном порядке. В качестве яркого примера можно использовать всё тот же заряд, но находящийся вне ЭП. Только когда определённая сила перемещает его внутрь и постепенно двигает там, появляется необходимый потенциал.

Если человек только столкнулся с этой отраслью и хочет в ней разобраться, то ему лучше представить обычную пружину.

В спокойном состоянии у неё отсутствует какой-либо потенциал, из-за чего она может расцениваться только как небольшой металлический предмет. Но как только человек начнёт её постепенно сдавливать, будет образовываться потенциал.

Если быстро отпустить пружину, то она мгновенно выпрямится и при этом сдвинет со своего пути все посторонние предметы.

Этот пример ярко демонстрирует то, что уровень потенциала всегда будет соответствовать приложенным усилиям на перемещение заряда. В современной науке этот показатель можно измерить в вольтах.

Сферы применения

Стандартные характеристики ЭП обязательно включают в себя два свойства, которые активно применяются человечеством.

Они могут образовывать универсальные ионы, а погруженные в определённую жидкость электроды позволяют без каких-либо усилий разделять их по функциям.

Эксперты доказали, что универсальной и доступность электрических полей активно используется в различных отраслях:

• Очистка. В этой отрасли активно используется система качественного разделения разных жидкостей. Эта функция высоко ценится в очистных сооружениях. Ведь та вода, в которой содержится большое количество различного мусора, очень вредна для человека. При этом с такой жидкостью очень сложно что-то сделать, так как далеко не все фильтры могут справиться с проблемой. Именно в такой ситуации на помощь приходят ЭП. Они разделяют воду, за счёт чего отделяются загрязнения. Благодаря этому можно пользоваться быстрым и доступным способом очистки.
• Медицина. Квалифицированные доктора практически ежедневно используют систему воздействия на поражённые ткани пациента направленными ионами. За счёт этого улучшается регенерация органа, убиваются микробы и очищается рана. К тому же уникальные характеристики и свойства ЭП позволяют им работать с большей частотой. Такой эффект широко востребован в медицине, так как за короткий промежуток времени можно повысить температуру некоторых отдельных частей тела, за счет чего восстанавливается кровоток, а также улучшается общее самочувствие пациента.
• Химия. Без электрических полей просто невозможна нормальная работа некоторых отраслей промышленности, где нужно разделять разные жидкости. Такая наука активно используется в стандартных лабораторных условиях, но чаще всего её можно встретить в сфере массовой добычи нефти. Большой спрос спровоцирован тем, что природный материал часто содержит загрязняющие частицы, избавиться от которых традиционным способом весьма проблематично. Более экономичным является применение ЭП. Они позволяют быстро разделить нефть, убрав весь ненужный мусор, облегчив дальнейшую обработку.

Конечно, существует множество других вариантов применения формулы напряжённости электрического поля.

К примеру: эксперты могут применять такое явление в качестве беспроводной системы передачи тока к разным приборам. Но в большинстве случае все такие разработки носят экспериментальный и теоретический характер.

Закон Кулона

Направление вектора напрямую зависит от имеющегося знака заряда. Если он плюсовой, то ЭП будет «передвигаться» по радиусу. В противном случае сам вектор будет направлен в сторону заряда.

Чтобы разобраться в ключевых особенностях закона, можно изучить основные рисунки и диаграммы, где изображены силовые линии. В учебниках основные характеристики ЭП объясняются довольно сложно.

Если же для изучения этой темы использовать специализированную литературу, тогда нужно учесть, что при построении рисунков силовых линий их итоговая густота является пропорциональной модулю вектора напряжённости.

Это своего рода подсказка от экспертов, которая может помочь во время экзамена или просто для контроля знаний.

Принцип воздействия

Свойства ЭП чаще всего постоянны и однообразны. Для планеты свойственен свой защитный фон, который на живые организмы практически никак не влияет. Незначительные проявления становятся заметными для человека только во время сильной грозы. В такой ситуации может даже казаться, что воздух дрожит от напряжения. Но для большинства людей это не представляет никакой угрозы.

Даже если включить сразу все бытовые устройства, максимальный показатель не будет превышен. Взрослый человек может получить небольшой процент негативного воздействия только при длительном нахождении возле высоковольтных проводов.

В такой среде напряжение очень большое, из-за чего долго стоять или же работать на таком участке категорически запрещено.

Специалисты, которые вынуждены по служебным обстоятельствам находиться в окружении таких ЭП, должны успевать выполнить все работы максимум за полтора часа.

Внедрение в технику

Современные масштабы ЭП нашли весьма интересное применение в современном мире. Специалистами был разработан способ беспроводной передачи сигнала от основного источника до потребителя, хотя ещё до недавнего времени всё носило экспериментальный и теоретический характер.

На сегодняшний день уже имеется эффективная реализация технологии зарядки смартфонов без использования гибкого кабеля. Конечно, этот вариант пока не позволяет передавать энергию на дальние расстояния, но все функции находятся в стадии совершенствования.

Стоит отметить, что изучением электрического поля занималось уже много людей. Огромный след в истории оставил известный во всём мире сербский изобретатель Николай Тесла. Благодаря приложенным усилиям ему удалось достичь больших успехов, но не в плане энергетической эффективности.

Источник: https://rusenergetics.ru/praktika/formula-napryazhyonnosti-elektricheskogo-polya

Электрическое поле: определение, классификация, характеристики

Нас окружает материальный мир. Материю мы воспринимаем с помощью зрения и других органов чувств. Отдельным видом материи является электрическое поле, которое можно выявить только через его влияние на заряженные тела или с помощью приборов. Оно порождает магнитные поля и взаимодействует с ними. Эти взаимодействия нашли широкое практическое применение.

Определение

Электрическое поле неразрывно связано с магнитным полем, и возникает в результате его изменения. Эти два вида материи являются компонентами электромагнитных полей, заполняющих пространство вокруг заряженных частиц или заряженных тел.

Таким образом, данный термин означает особый вид материи, обладающий собственной энергией, являющийся составным компонентом векторного электромагнитного поля. У электрического поля нет границ, однако его силовое воздействие стремится к нулю, при удалении от источника – заряженного тела или точечных зарядов [1].

Важным свойством полевой формы материи является способность электрического поля поддерживать упорядоченное перемещение носителей зарядов.

Рис. 1. Определение понятия «электрическое поле»

Энергия электрического поля подчиняется действию закона сохранения. Её можно преобразовать в другие виды или направить на выполнение работы.

Силовой характеристикой полей выступает их напряжённость – векторная величина, численное значение которой определяется как отношение силы, действующей на пробный положительный заряд, к величине этого заряда.

Характерные физические свойства:

• реагирует на присутствие заряженных частиц;
• взаимодействует с магнитными полями;
• является движущей силой по перемещению зарядов – как положительных ионов, таки отрицательных зарядов в металлических проводниках;
• поддаётся определению только по результатам наблюдения за проявлением действия.

Оно всегда окружает неподвижные статичные (не меняющиеся со временем) заряды, поэтому получило название – электростатическое. Опыты подтверждают, что в  электростатическом поле действуют такие же силы, как и в электрическом.

Электростатическое взаимодействие поля на заряженные тела можно наблюдать при поднесении наэлектризованной эбонитовой палочки к мелким предметам. В зависимости от полярности наэлектризованных частиц, они будут либо притягиваться, либо отталкиваться от палочки.

Вследствие распределения зарядов проводник становится заряженным, что является признаком влияния электрического поля.

Классификация

Электрические поля бывают двух видов: однородные и неоднородные.

Однородное
электрическое поле

Состояние поля определяется пространственным расположением линий напряжённости. Если векторы напряжённости идентичны по модулю и они при этом сонаправлены во всех точках пространства, то электрическое поле – однородно. В нём линии напряжённости расположены параллельно.

В качестве примера является электрическое поле, образованное разноимёнными зарядами на участке плоских металлических пластин (см. рис. 2).

Рис. 2. Пример однородности

Неоднородное электрическое поле

Чаще встречаются поля, напряжённости которых в разных точках отличаются. Линии напряжённости у них имеют сложную конфигурацию.

Простейшим примером неоднородности является электрический диполь, то есть система из двух разноимённых зарядов, влияющих друг на друга (см. рис. 3).

Несмотря на то, что векторы напряжённости электрического диполя образуют красивые линии, но поскольку они не равны, то такое поле неоднородно. Более сложную конфигурацию имеют вихревые поля (рис 4).  Их неоднородность очевидна.

Рис. 3. Электрический диполь Рис. 4. Вихревые поля

Характеристики

Основными характеристиками являются:

• потенциал;
• напряжённость;
• напряжение.

Потенциал

Термин означает отношение потенциальной энергии W, которой обладает пробный заряд q′ в данной точке к его величине. Выражение φ =W/q′. называется потенциалом электрического поля в этой точке.

Другими словами: количество накопленной энергии, которая потенциально может быть потрачена на выполнение работы, направленной на перемещение единичного заряда в бесконечность, или в другую точку с условно нулевой энергией,  называется потенциалом рассматриваемого электрического поля в данной точке.

Энергия поля учитывается по отношению к данной точке. Её ещё называют потенциалом в данной точке. Общий потенциал системы равен сумме потенциалов отдельных зарядов. Это одна из важнейших характеристик поля. Потенциал можно сравнить с энергией сжатой пружины, которая при высвобождении способна выполнить определённую работу.

Единица измерения потенциала – 1 вольт. При бесконечном удалении точки от наэлектризованного тела, потенциал в этой точке уменьшается до 0: φ∞=0.

Напряжённость поля

Достоверно известно, что электрическое поле отдельно взятого заряда q действует с определённой силой F на точечный пробный заряд, независимо от того, на каком расстоянии он находится. Сила, действующая на изолированный положительный пробный заряд, называется напряжённостью и обозначается символом E.

Напряжённость – векторная величина. Значение модуля вектора напряжённости: E=F/q′.

Линиями напряжённости электрического поля (известные как силовые линии), называются касательные, которые в точках касания совпадают с ориентацией векторов напряжённости. Плотность силовых линий определяет величину напряжённости.

Рис. 5. Электрическое поле положительного и отрицательного вектора напряжённости

Напряженность вокруг точечного заряда Q на расстоянии r от него, определяется по закону Кулона: E = 14πε0⋅Qr2. Такие поля называют кулоновскими.

Векторы напряженности положительного точечного заряда направлены от него, а отрицательного – до центра (к заряду). Направления векторов кулоновского поля видно на рис. 6.

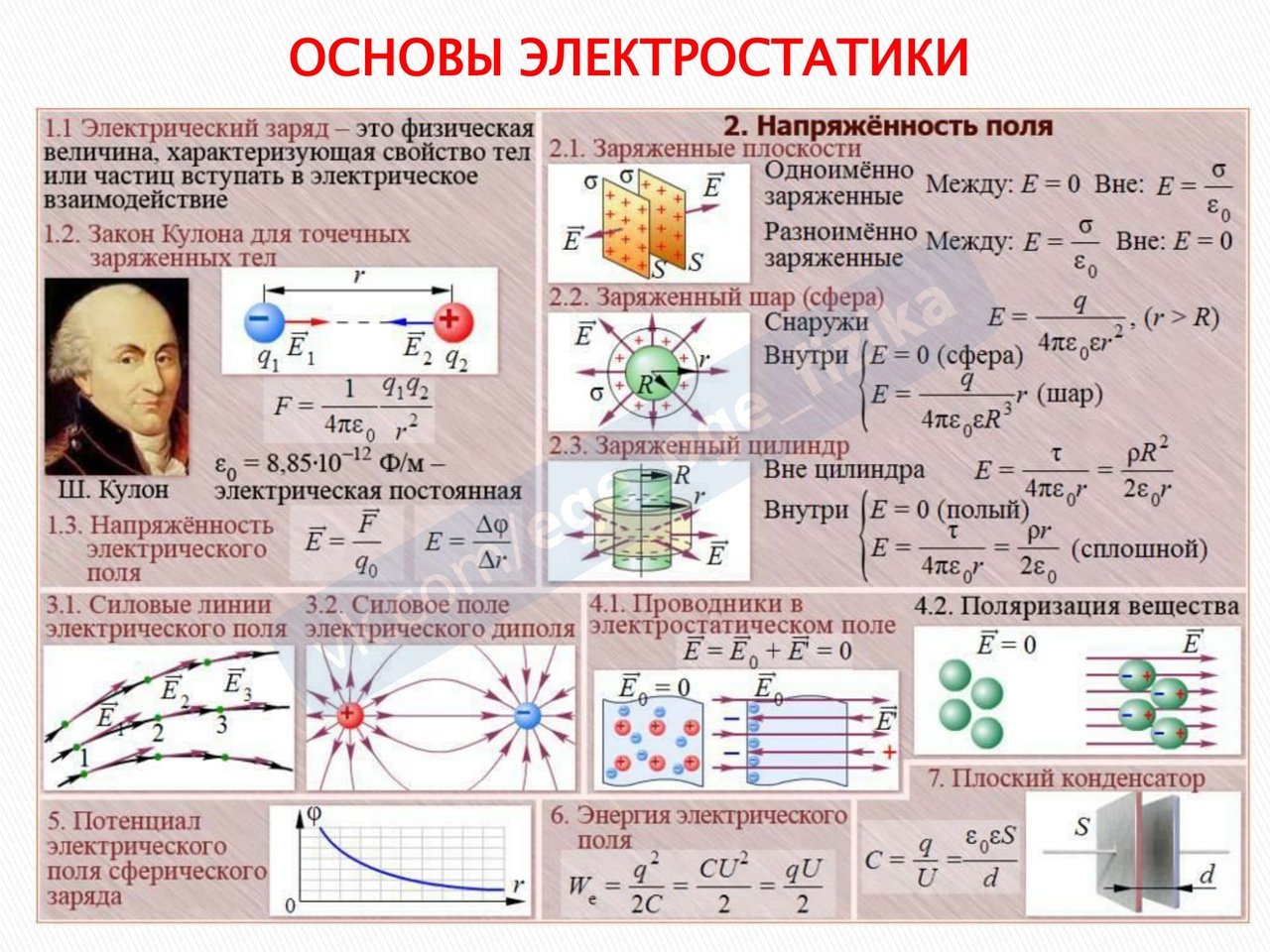Рис. 6. Направление линий напряжённости положительных и отрицательных зарядов

Для кулоновских полей справедлив принцип суперпозиции. Суть принципа в следующем:вектор напряжённости нескольких зарядов может быть представлен в виде геометрической суммы напряжённостей, создаваемых каждым отдельно взятым зарядом, входящих в эту систему.

Для общего случая распределения зарядов имеем:

Линии напряжённости схематически изображены на рисунке 7. На картинке видно линии, характерные для полей:

• электростатического;
• дипольного;
• системы и одноимённых зарядов;
• однородного поля.

Рис. 7. Линии напряжённости различных полей

Напряжение

Поскольку силы электрического поля способны выполнять работу по перемещению носителей элементарных зарядов, то наличие поля является условием для существования электрического тока. Электроны и другие элементарные заряды всегда двигаются от точки, обладающей более высоким потенциалом, к точке с низшим потенциалом. При этом часть энергии расходуется на выполнение работы по перемещению.

Для поддержания постоянного тока (упорядоченного движения носителей элементарных зарядов) необходимо на концах проводника поддерживать разницу потенциалов, которую ещё называют напряжением. Чем больше эта разница, тем активнее выполняется работа, тем мощнее ток на этом участке. Функции по поддержанию разницы потенциалов возложены на источники тока.

Методы обнаружения

Органы чувств человека не воспринимают электрических полей. Поэтому мы не можем их увидеть, попробовать на вкус или определить по запаху. Единственное, что может ощутить человек – это выпрямление волос вдоль линий напряжённости. Наличие слабых воздействий мы просто не замечаем.

Обнаружить их можно через воздействие на мелкие кусочки бумаги, бузиновые шарики и т.п. Электрическое поле воздействует на электроскоп – его лепестки реагируют на такие воздействия.

Очень простой и эффективный метод обнаружения с помощью стрелки компаса. Она всегда располагается вдоль линий напряжённости.

Существуют очень чувствительные электронные приборы, с лёгкостью определяющие наличие электростатических полей.

Методы расчета электрического поля

Для расчётов параметров используются различные аналитические или численные методы:

• метод сеток или конечных разностей;
• метод эквивалентных зарядов;
• вариационные методы;
• расчёты с использованием интегральных уравнений и другие.

Выбор конкретного метода зависит от сложности задачи, но в основном используются численные методы, приведённые в списке.

Использование

Изучение свойств электрического поля открыло перед человечеством огромные возможности. Способность поля перемещать электроны в проводнике позволила создавать источники тока.

На свойствах электрических полей создано различное оборудование, применяемое в медицине, химической промышленности, в электротехнике. Разрабатываются приборы, применяемые в сфере беспроводной передачи энергии к потребителю. Примером могут послужить устройства беспроводной зарядки гаджетов. Это пока только первые шаги на пути к передачи электричества на большие расстояния.

Сегодня, благодаря знаниям о свойствах полевой формы материи, разработаны уникальные фильтры для очистки воды. Этот способ оказался дешевле, чем использование традиционных сменных картриджей.

К сожалению, иногда приходится нейтрализовать силы полей. Обладая способностью электризации предметов, оказавшихся в зоне действия, электрические поля создают серьёзные препятствия для нормальной работы радиоэлектронной аппаратуры. Накопленное статическое электричество часто является причиной выхода из строя интегральных микросхем и полевых транзисторов.

Источник: https://www.asutpp.ru/elektricheskoe-pole.html

Напряженность электрического поля

Напряженность электрического поля является векторной величиной, а значит имеет численную величину и направление. Величина напряженности электрического поля имеет свою размерность, которая зависит от способа ее вычисления.

Электрическая сила взаимодействия зарядов описывается как бесконтактное действие, а иначе говоря имеет место дальнодействие, то есть действие на расстоянии. Для того, чтобы описать такое дальнодействие удобно ввести понятие электрического поля и с его помощью объяснить действие на расстоянии.

Давайте возьмем электрический заряд, который мы обозначим символом Q. Этот электрический заряд создает электрическое поле, то есть он является источником действия силы.

Так как во вселенной всегда имеется хотя бы один положительный и хотя бы один отрицательный заряд, которые действую друг на друга на любом, даже бесконечно далеком расстоянии, то любой заряд является источником силы, а значит уместно описание создаваемого ими электрического поля.

В нашем случае заряд Q является источником электрического поля и мы будем его рассматривать именно как источник поля.

Напряженность электрического поля источника заряда может быть измерена с помощью любого другого заряда, находящегося где-то в его окрестностях.

Заряд, который используется для измерения напряженности электрического поля называют пробным зарядом, так как он используется для проверки напряженности поля.

Пробный заряд имеет некоторое количество заряда и обозначается символом q.

При помещении пробного заряда в электрическое поле источника силы (заряд Q), пробный заряд будет испытывать действие электрической силы — или притяжения, или отталкивания. Силу можно обозначить как это обычно принять в физике символом F. Тогда величину электрического поля можно определить просто как отношение силы к величине пробного заряда.

Если напряженность электрического поля обозначается символом E, то уравнение может быть переписано в символической форме как

Для понимания сути такого предмета как напряженность электрического поля гораздо важнее размерность в метрической системе в Н/Кл, потому как в такой размерность отражается происхождение такой характеристики как напряженность поля. Обозначение в Вольт/Метр делает понятие потенциала поля (Вольт) базовым, что в некоторых областях удобно, но не во всех.

В приведенном выше примере участвуют два заряда Q (источник) и q пробный. Оба этих заряда являются источником силы, но какой из них следует применять в вышеприведенной формуле? В формуле присутствует только один заряд и это пробный заряд q (не источник).

Напряженность электрического поля не зависит от количества пробного заряда q. На первый взгляд это может привести вас в замешательство, если, конечно, вы задумаетесь над этим. Беда в том, что не все имеют полезную привычку думать и пребывают в так называемом блаженном невежестве. Если вы не думаете, то и замешательства такого рода у вас и не возникнет.

Так как же напряженность электрического поля не зависит от q, если q присутствует в уравнении? Отличный вопрос! Но если вы подумаете об этом немного, вы сможете ответить на этот вопрос. Увеличение количества пробного заряда q — скажем, в 2 раза — увеличится и знаменатель уравнения в 2 раза.

Но в соответствии с Законом Кулона, увеличение заряда также увеличит пропорционально и порождаемую силу F. Увеличится заряд в 2 раза, тогда и сила F возрастет в то же количество раз. Так как знаменатель в уравнении увеличивается в два раза (или три, или четыре), то и числитель увеличится во столько же раз.

Эти два изменения компенсируют друг друга, так что можно смело сказать, что напряженность электрического поля не зависит от количества пробного заряда.

Таким образом, независимо от того, какого количества пробный заряд q используется в уравнении, напряженность электрического поля E в любой заданной точке вокруг заряда Q (источника) будет одинаковой при измерении или вычислении.

Более подробно о формуле напряженности электрического поля

Выше мы коснулись определения напряженности электрического поля в том, как она измеряется.

Теперь мы попробуем исследовать более развернутое уравнение с переменными, чтобы яснее представить саму суть вычисления и измерения напряженности электрического поля.

Из уравнения мы сможем увидеть, что именно влияет, а что нет. Для этого нам прежде всего потребуется вернутся к уравнению Закона Кулона.

Если внести в уравнение Закона Кулона два наших заряда Q (источник) и q (пробный заряд), тогда мы получим следующую запись:

Если выражение для электрической силы F, как она определяется Законом Кулона подставить в уравнение для напряженности электрического поля E, которое приведено выше, тогда мы получим следующее уравнение:

Обратите внимание, что пробный заряд q был сокращен, то есть убран как в числителе так и в знаменателе. Новая формула для напряженности электрического поля E выражает напряженность поля в терминах двух переменных, которые влияют на нее.

Напряженность электрического поля зависит от количества исходного заряда Q и от расстоянии от этого заряда d до точки пространства, то есть геометрического места, в котором и определяется значение напряженности.

Таким образом у нас появилась возможность характеризовать электрическое поле через его напряженность.

Закон обратных квадратов

Как и все формулы в физике, формулы для напряженности электрического поля могут быть использованы для алгебраического решения задач (проблем) физики.

Точно также, как и любую другую формулу в ее алгебраической записи, можно исследовать и формулу напряженности электрического поля. Такое исследование способствует более глубокому пониманию сути физического явления и характеристик этого явления.

Одна из особенностей формулы напряженности поля является то, что она иллюстрирует обратную квадратичную зависимость между напряженностью электрического поля и расстоянием до точки в пространстве от источника поля.

Сила электрического поля, создаваемого в источнике заряде Q обратно пропорционально квадрату расстояния от источника. Иначе говорят, что искомая величина обратно пропорциональна квадрату.

Напряженность электрического поля зависит от геометрического места в пространстве, и ее величина уменьшается с увеличением расстояния.

Так, например, если расстояние увеличится в 2 раза, то напряженность уменьшится в 4 раза (22), если расстояния между уменьшится в 2 раза, то напряженность электрического поля увеличится в 4 раза (22).

Если же расстояние увеличивается в 3 раза, то напряженность электрического поля уменьшается в 9 раз (32). Если расстояние увеличивается в 4 раза, то напряженность электрического поля уменьшается в 16 (42).

Направление вектора напряженности электрического поля

Как упоминалось ранее, напряженность электрического поля является векторной величиной. В отличие от скалярной величиной, векторная величина является не полностью описанной, если не определено ее направление. Величина вектора электрического поля рассчитывается как величина силы на любой пробный заряд, расположенный в электрическом поле.

Сила, действующая на пробный заряд может быть направлена либо к источнику заряда или непосредственно от него. Точное направление силы зависит от знаков пробного заряд и источника заряда, имеют ли они тот же знак заряда (тогда происходит отталкивание) или же их знаки противоположные (происходит притяжение).

Чтобы решить проблему направления вектора электрического поля, направлен он к источнику или от источника были приняты правила, которые используются всеми учеными мира. Согласно этим правилам направление вектора всегда от заряда с положительным знаком полярности.

Это можно представить в виде силовых линий, которые выходят из зарядов положительных знаков и заходят в заряды отрицательных знаков.

Дата: 29.04.2015

© Valentin Grigoryev (Валентин Григорьев)

Источник: http://electricity-automation.com/page/napryazhennost-elektricheskogo-polya