Формула силы тяжести

Содержание

На начальных этапах знакомства с наукой физикой школьникам рассказывают об основных понятиях и явлениях, которые играют определяющую роль в протекании природных процессов. Одним из таких понятий является сила тяжести, формула которой позволяет численно рассчитать величину воздействия гравитационного поля на различные имеющие массу объекты.

Историческая справка

Движением звезд, планет, комет и других небесных тел человеческие умы интересовались с древних времен. Наибольших успехов в этом вопросе достигли философы античной Греции и Рима.

Так, греческий философ II века нашей эры, Клавдий Птолемей, анализируя большое количество данных наблюдений за перемещением звезд и планет по небесному куполу, смог создать первую геометрическую модель движения тел в космосе.

Она получила название геоцентрической и просуществовала в качестве основной в астрономии до начала XVI столетия, когда Николай Коперник разработал новую теорию Вселенной — гелиоцентрическую.

В XVII столетии благодаря практическим наблюдениям и исследованиям таких философов и ученых, как Галилей, Кеплер и Ньютон начинает формироваться стройная теория описания движения тел в пространстве, которая могла численно предсказать траектории перемещения объектов.

Следует отметить большой вклад Исаака Ньютона, который, используя знания своих предшественников, смог показать и доказать, что небесные тела (планеты, звезды, астероиды и другие) в процессе своего перемещения подчиняются тем же математическим законам, что камень, брошенный вверх вблизи поверхности Земли, или падающий с дерева лист. Феномен, который описывает все эти явления, получил название силы тяжести.

Основной закон

Прежде чем переходить к формуле силы тяжести в физике 7 класса, следует показать, откуда она берется. Исследуя процесс движения летящих и падающих тел, и анализируя большое количество полученных данных, Ньютон пришел к следующим выводам о характере действующей на них силы:

она прямо пропорциональна массам взаимодействующих тел;
убывает достаточно быстро с увеличением расстояния между ними;
ее вектор направлен от центра масс одного тела к этому центру другого тела;
сила всегда имеет характер притягивающий, ни в одном эксперименте не было замечено отталкивания между телами разной природы.

Эти умозаключения позволили английскому ученому вывести формулу, которая в настоящее время носит название Всемирного закона тяготения. Записывается он в следующей форме:
F = G*m1*m2/R2.
Здесь введены следующие обозначения:

m1, m2 — массы взаимодействующих тел, которые в системе СИ выражаются в килограммах;
R — расстояние в метрах между центрами масс притягивающихся объектов;
G — некоторая постоянная величина, получившая наименование универсальной гравитационной.

Постоянная G приблизительно составляет 6,67*10^(-11) Н*м2 /кг2 .

Это значение говорит о том, что два тела, массы которых составляют по 1 кг, находящиеся на расстоянии 1 метр друг от друга, будут испытывать притяжение между собой, сила которого будет равна 6,67*10^(-11) Н.

Это чрезвычайно мизерная величина, которая объясняет, почему в обычной жизни люди не чувствуют притяжения друг к другу и к окружающим их объектам.

Сила притяжения, вес и ускорение

Уже в 7 классе, в первый год изучения физики в школе, ученики знают, что для вычисления силы тяжести следует умножить массу на свободного падения ускорение. Однако, мало кто понимает, откуда берется эта простая формула, и является ли она справедливой не только на нашей планете, но и в других космических системах.

Упрощенная формула

Если применить закон Всемирного тяготения к системе тело — Земля, то можно увидеть, что одна из масс в числителе является постоянной величиной. Это масса нашей голубой планеты.

Кроме того, любой объект на Земле, насколько большим он бы не был, имеет геометрические размеры намного меньшие, чем радиус планеты. Так, высота самой большой горы (Эверест) составляет всего 0,15% от радиуса Земли.

Эти факты позволяют преобразовать записанную Ньютоном формулу в следующем виде:

F = m*g, где g = G*M/R2.

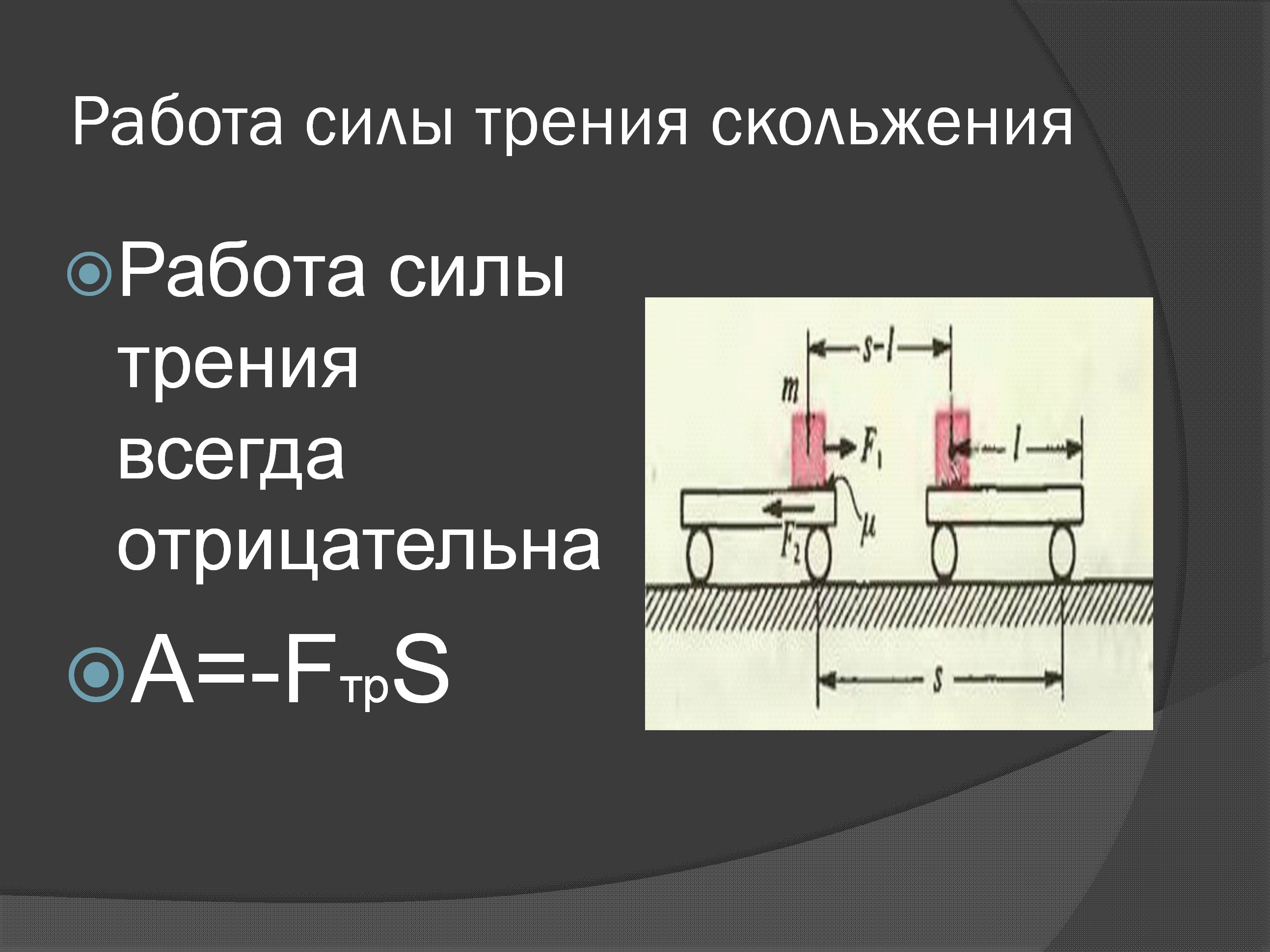
Здесь M — масса Земли, R — ее радиус, буквой F обозначается сила тяжести. Если подставить эти значения в формулу для g, то получается, что g будет приблизительно равно 9,81 м/с2. Чтобы определить силу F, необходимо умножить массу тела на величину g.

Единицей измерения F является ньютон (Н) в системе СИ. Один ньютон — это такая сила, которая сообщает ускорение 1 м/с2 телу, масса которого составляет 1 кг.

Следует сказать о том, что полученная упрощенная формула для F справедлива в следующих случаях:

вблизи поверхности нашей планеты, вплоть до высот в несколько километров;
вблизи любой другой планеты, звезды и произвольного космического тела, только в этих случаях величина g будет собственная для каждого рассматриваемого массивного объекта.

Для всех ситуаций, которые не попадают в число названных, следует применять общую формулу закона Всемирного тяготения.

Понятие о величине P

Латинской буквой P принято обозначать вес тела. Существует два равноправных определения этой величины:

Под ней понимают силу, с которой объект давит на опору.
Это сила, растягивающая любой подвес, к которому прикреплено тело.

В обоих случаях существование веса тела объясняется наличием силового воздействия с его стороны на другой объект (опору, подвес).

Часто величину P путают с силой F. В большинстве случаев наличие у тел веса связано с воздействием F, однако, это не всегда так.

Например, если в невесомости привязать нитку к заряженному телу, и в стороне от него разместить другое электрически заряженное тело противоположного знака, то возникшее притяжение между объектами приведет к натяжению нити (растягивание подвеса), а значит, к появлению веса у привязанного тела, хотя величина F при этом не будет играть никакой роли.

В невесомости тела не воздействуют ни на какие опоры, поэтому вес их равен нулю. Для определения величины P для любых тел в любых системах следует рассмотреть уравнение, основывающееся на втором законе Ньютона:
F1 + F2 + … + Fn = m*a.
Здесь на тело m действует совокупность сил F1, F2, …, Fn, которые все вместе сообщают ему ускорение a.

Свободное падение

Когда на тело действует исключительно сила F, то говорят о его свободном падении или подъеме. Ярким примером этого явления является вертикальное падение камня, отпущенного вниз с высокого холма. За каждую секунду своего падения он будет увеличивать свою скорость на 9,81 м/с. Величина g, которая появляется в формуле для величины F, называется ускорением свободного падения.

Справедливости ради следует отметить, что вблизи поверхности планеты во время свободного полета тел на них помимо силы гравитации действует еще сопротивление воздуха.

При больших плотностях тел и малых скоростях их перемещения сопротивлением воздуха можно пренебречь.

В противном случае его необходимо учитывать, поскольку оно кардинальным образом изменяет кинематические характеристики рассматриваемого объекта.

Хорошим примером свободного падения и падения с влиянием сопротивления воздуха являются опыты Галилея.

Ученый сбрасывал два разных по массе, но сделанных из одного материала (стали), шарика, с высокой башни. Оба достигали поверхности за одно и то же время.

Однако, когда с одинаковой высоты были сброшены шарик и перо, последнее достигло поверхности за гораздо большее время из-за влияния сопротивления воздуха.

Ускорение g является константой лишь вблизи поверхности одной планеты. При перемещении на другую планету его значение становится другим, однако, сам вид формулы для величины F сохраняется:

F = m*g.

Например, на Луне g = 1,62 м/с2, а на самой большой планете Солнечной системе — Юпитере g = 24,79 м/с2. Знание этой величины позволяет определить либо массу планеты, либо оценить значение ее геометрических размеров.

Пример задачи

Для закрепления знаний и более глубокого понимания сути влияния силы F на движение тел, следует решить интересную и простую задачу. Для этого необходимо воспользоваться вторым законом Ньютона, а также некоторыми уравнениями кинематики для пройденного пути, скорости и ускорения.

Пусть человек бросает камень массой 1 кг с некоторой высоты вертикально вниз, придавая ему начальную скорость 10 м/с. Следует вычислить расстояние, на которое переместится камень за время падения между 5 и 6-й секундами своего полета, а также действующую на него силу притяжения.

Эта задача решается несложно, если вспомнить формулу для расчета пути во время равноускоренного движения. Характер постоянного ускорения обеспечивает действующая сила F, которая направлена в процессе падения вертикально вниз. Рабочая формула имеет вид:

s = v0*t + g*t2/2.
Где v0 = 10 м/с, t — время падения. Сначала следует найти пути s, которые пролетит камень за 5 с и за 6 с, соответственно:

s5 = 10*5 + 9,81*52/2 = 172,625 м;
s6 = 10*6 + 9,81*62/2 = 236,58 м.

Взяв разницу между полученными значениями пройденного пути, можно вычислить расстояние, на которое упадет камень за 6-ю секунду своего полета:
s = s6 — s5 = 236,58 — 172,625 = 63,955 м.
В действительности, если поставить описанный эксперимент, то камень пролетит меньшее расстояние из-за влияния сопротивления воздуха.
Для нахождения модуля силы F следует применить упрощенную формулу:
F = m*g = 1*9,81 = 9,81 Н.

Таким образом, гравитация, действующая между любыми телами имеющими массу, является причиной возникновения силы тяжести. Формула для ее расчета предполагает знание двух величин: ускорения свободного падения и массы рассматриваемого объекта.

Источник: https://na5.club/fizika/formula-sily-tyazhesti-i-ee-edinicza-izmereniya.html

Сила тяжести и ускорение свободного падения

Свободное падением — это падение тел в вакууме (без сопротивления воздуха) только под действием силы тяжести без начальной скорости. Независимо от массы, все тела при свободном падении движутся одинаково. Свободное падение тела относится к равноускоренному движению.

Свободное падение тел открыл Галилей в конце XVI, роняя тела разной массы с Пизанской башни и сделал следующий вывод:

брошенные тела достигают поверхности земли практически в один и тот же момент времени, независимо от их массы.

Ускорение свободного падения тела есть величина постоянная и равна g=9,8 м/с2
Ускорение свободного падения на полюсе равно g=9,832 м/с2, а на экваторе g=9,78 м/с2
Ускорение свободного падения определяется по формуле:
$g = frac{{2s}}{{{t^2}}}$
Здесь приведена таблица значений ускорения свободного падения на разных планетах солнечной системы.
Сила тяжести находится по формуле:
Fтяж=m·g

Сила тяжести (сила притяжения, гравитационная сила) — это сила с которой планета Земля притягивает все тела, имеющие массу. Сила тяжести направлена к центру Земли, вертикально вниз.

Центр тяжести тела — это точка приложения силы тяжести см. рисунок ниже.

Формула для определения скорости свободного падения тела в любой момент времени:
v=g·t
Ускорение свободного падения тел на Земле рассчитывается из выражения:
Mз — масса Земли;
Rз — радиус Земли;
G — гравитационная постоянная определяется из закона всемирного тяготения 6,67·10-11 Н м2/кг2
Формула ускорения свободного падения на Земле, если тело поднято на высоту h над поверхностью Земли:

Ускорение свободного падения на Луне — формула:

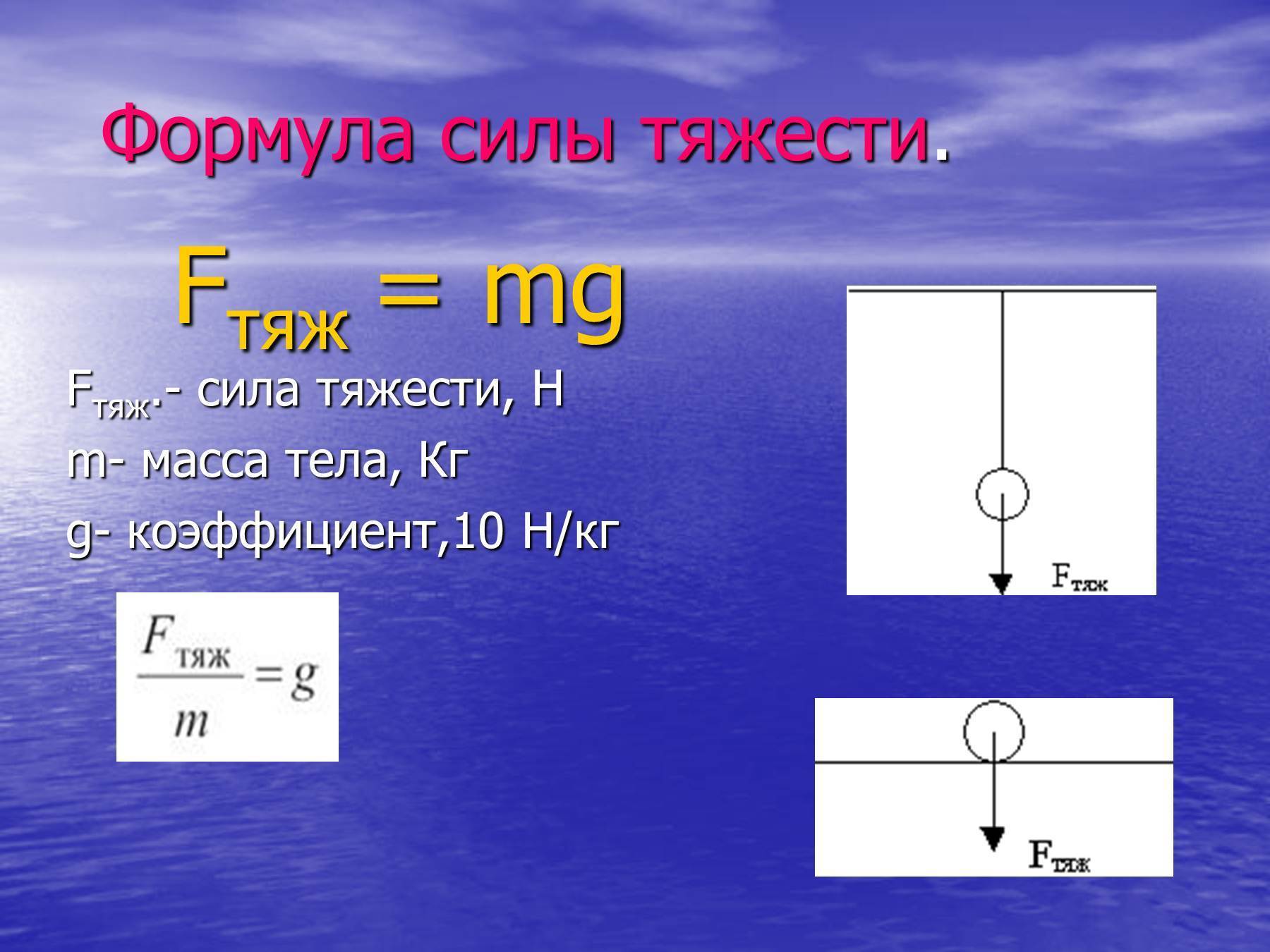
Mл — масса Луны;
Rл — радиус Луны.

Источник: https://www.matematicus.ru/fizika/mehanika/sila-tyazhesti-i-uskorenie-svobodnogo-padeniya

03-г. Сила тяжести и вес тела

§ 03-г. Сила тяжести и вес тела

В § 2-а мы начали знакомство с явлением гравитации вообще и земным тяготением в частности. Теперь настало время более подробного изучения силы тяжести на Земле и других планетах.

На рисунке изображён опыт с двумя гирями и динамометрами. Вы видите, что при массе гири 200 г (то есть 0,2 кг) на неё действует сила тяжести 2 Н, а при массе 500 г (то есть 0,5 кг) – сила тяжести 5 Н. Обратим внимание на закономерность:

Проделав опыты с многими телами, мы обнаружим ту же самую закономерность: отношение силы тяжести, действующей на тело, к массе этого тела является постоянной величиной, не зависящей ни от силы тяжести, ни от массы тела. Эту величину называют коэффициентом силы тяжести:

Формулу для вычисления коэффициента «g» можно преобразовать, поместив слева силу тяжести:

В опыте с двумя гирями мы выяснили, что вблизи поверхности Земли коэффициент «g» имеет значение 10 Н/кг (более точные значения 9,78 Н/кг и 9,83 Н/кг – см. далее в таблице).

Опыты показывают, что по мере удаления от Земли сила тяжести ослабевает. Например, на высоте 300 км значение коэффициента «g» уменьшается приблизительно до 9 Н/кг.

Повторяя опыт с гирями и динамометрами в различных местах Земли, а также на поверхности Луны, Марса и так далее, можно выяснить, что коэффициент «g» зависит от места наблюдения:

Коэффициенты силы тяжести, Н/кг

Табл. 3.14. Значения коэффициентов силы тяжести на поверхности Земли и некоторых небесных тел

Луна	1,7	Земля:	» 10
Марс	3,8	а) полюс	9,83
Юпитер	24	б) экватор	9,78

В обыденной жизни под словом «вес» мы зачастую подразумеваем массу тела, не делая различия между этими терминами. Однако это неверно.

Весом тела называют силу, с которой тело давит на опору или тянет подвес. Например, на рисунке медведь действует на опору – прогнувшуюся доску. Согласно определению, сила давления медведя на доску – вес медведя. На рисунке правее медведь действует на подвес – канат. Эта сила тоже является весом, но уже медведя вместе с доской.

Часто вес тела равен действующей на него силе тяжести. В виде формулы это записывается так:

Однако эта формула верна не всегда. Например, если тело погружено в жидкость или газ. В этом случае возникает выталкивающая сила, обычно приводящая к уменьшению веса.

Многочисленные опыты показывают, что вес тела равен действующей на него силе тяжести, когда тело и его опора (подвес) покоятся или движутся вместе равномерно и прямолинейно, и не действуют другие силы, кроме силы тяжести.

Это – границы применимости формулы W = Fтяж

Забегая вперед, скажем, что когда тело или его опора (подвес) движутся непрямолинейно или неравномерно, вес тела никогда не равен силе тяжести. Он может быть как больше, так и меньше неё, а также направлен в другую сторону.

Силы в природеФормулы Физика Теория 7 класс

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Источник: https://calcsbox.com/post/03-g-sila-tazesti-i-ves-tela.html

Сила тяжести: формула, определение

Абсолютно на все тела во Вселенной действует волшебная сила, каким-то образом притягивающая их к Земле (точнее к ее ядру).

Никуда не сбежать, нигде не укрыться от всеобъемлющего магического тяготения: планеты нашей Солнечной системы притягиваются не только к огромному Солнцу, но и друг к другу, все предметы, молекулы и мельчайшие атомы также взаимно притягиваются.

Исаак Ньютон, известный даже маленьким детям, посвятив жизнь изучению этого явления, установил один из величайших законов — закон всемирного тяготения.

Что такое сила тяжести?

Определение и формула давно и многим известны. Напомним, сила тяжести — это определенная величина, одно из естественных проявлений всемирного тяготения, а именно: сила, с которой всякое тело неизменно притягивается к Земле.

Сила тяжести: формула

Как вычислить силу тяжести, направленную на определенное тело? Какие другие величины необходимо знать для того? Формула расчета силы тяжести довольно проста, ее изучают в 7-м классе общеобразовательной школы, в начале курса физики. Чтобы ее не просто выучить, но и понять, следует исходить из того, что сила тяжести, неизменно действующая на тело, прямо пропорциональна его количественной величине (массе).

Единица силы тяжести названа по имени великого ученого— Ньютон.

Сила тяжести (гравитация) всегда направлена строго вниз, к центру земного ядра, благодаря ее воздействию все тела равноускоренно падают вниз. Явления тяготения в повседневной жизни мы наблюдаем повсеместно и постоянно:

предметы, случайно или специально выпущенные из рук, обязательно падают вниз на Землю (или на любую препятствующую свободному падению поверхность);
запущенный в космос спутник не улетает от нашей планеты на неопределенное расстояние перпендикулярно вверх, а остается вращаться на орбите;
все реки текут с гор и не могут быть обращены вспять;
бывает, человек падает и травмируется;
на все поверхности садятся мельчайшие пылинки;
воздух сосредоточен у поверхности земли;
тяжело носить сумки;
из облаков и туч капает дождь, падает снег, град.

Наряду с понятием «сила тяжести» используется термин «вес тела». Если тело расположить на ровной горизонтальной поверхности, то его вес и сила тяжести численно равны, таким образом, эти два понятия часто подменяют, что совсем не правильно.

Ускорение свободного падения

Понятие «ускорение свободного падения» (иначе говоря, гравитационная постоянная) связано с термином «сила тяжести». Формула показывает: для того чтобы вычислить силу тяжести, нужно массу умножить на g (ускорение св. п.).

«g» = 9,8 Н/кг, это постоянная величина. Однако более точные измерения показывают, что из-за вращения Земли значение ускорения св. п. неодинаково и зависит от широты: на Северном полюсе оно = 9,832 Н/кг, а на знойном экваторе = 9,78 Н/кг.

Читайте также: Формула мощности

Получается, в разных местах планеты на тела, обладающие равной массой, направлена разная сила тяжести (формула же mg все равно остается неизменной).

Для практических расчетов было принято решение не обращать внимания на незначительные погрешности этой величины и пользоваться усредненным значением 9,8 Н/кг.

Пропорциональность такой величины, как сила тяжести (формула доказывает это), позволяет измерять вес предмета динамометром (похож на обычный бытовой бизмен). Обратите внимание, что прибор показывает только силу, так как для определения точной массы тела необходимо знать региональное значение «g».

Действует ли сила тяжести на любом (и близком, и далеком) расстоянии от земного центра? Ньютон выдвинул гипотезу, что она действует на тело даже при значительном удалении от Земли, но ее значение снижается обратно пропорционально квадрату расстояния от предмета до ядра Земли.

Гравитация в Солнечной системе

Есть ли на других планетах сила тяжести? Определение и формула относительно других планет сохраняют свою актуальность. С одной лишь разницей в значении «g»:

на Луне = 1,62 Н/кг (в шесть раз меньше земного);
на Нептуне = 13,5 Н/кг (почти в полтора раза выше, чем на Земле);
на Марсе = 3,73 Н/кг (более чем в два с половиной раза меньше, чем на нашей планете);
на Сатурне = 10,44 Н/кг;
на Меркурии = 3,7 Н/кг;
на Венере = 8,8 Н/кг;
на Уране = 9,8 Н/кг (практически такое же, как у нас);
на Юпитере = 24 Н/кг (почти в два с половиной раза выше).

Источник: https://autogear.ru/article/301/125/sila-tyajesti-formula-opredelenie/

Сила тяжести

Большинство задач классической механики рассматриваются в поле тяготения Земли, поэтому определение силы тяжести, действующей на тело в этом поле – необходимость. И поэтому нужно понимать ее природу и уметь рассчитывать ее как на поверхности планеты, так и на высоте от нее.

Ньютоном было установлено, что любые тела испытывают друг к другу притяжение, и оно тем сильнее, чем ближе тела друг к другу расположены. Часто говорят, что всё началось с истории о яблоке. Отчасти это верно. Цепочка рассуждений привела Ньютона к новому закону, на котором выросла классическая механика неба.

Этот закон установил, что сила притяжения тел друг к другу, или сила тяготения (гравитационная), выражается формулой:

$vec F = gamma {m_1m_2 over r^3} vec r$ – (1),

где m1 и m2 – массы первого и второго тела, r – расстояние между ними, а $gamma$ – некоторая постоянная, которую назвали гравитационной. Причем, согласно третьему закону Ньютона, первое тело действует на второе, и второе на первое. Модуль их сил одинаков, но направлены они против друг друга.

Рис. 1. Закон всемирного тяготения.

Если записать это, используя второй закон Ньютона для одного из тел, то найдем ускорение, с которым первое тело притягивается ко второму:

$vec a = gamma {m_2 over r^3} vec r$ – (2)

Из формулы (2) видно, что ускорение тела не зависит от его массы. Ему дали название – ускорение свободного падения, и ввели специальное обозначение – g.

Величину $varphi = gamma {m over r}$ – называют потенциалом поля тяжести объекта массой m.

Геометрическое место точек, удаленное от объекта на расстояние r – сфера, значение потенциала на любой ее точке одно и тоже. Такую поверхность называют эквипотенциальной.

Потенциал, умноженный на массу тела, помещенного в гравитационное поле объекта, называют потенциальной энергией тела в поле объекта.

Рис. 2. Эквипотенциальная поверхность.

Если в формулу (2) подставить значения массы Земли и ее радиуса, то получим ускорение свободного падения на Земле.

В силу того, что наша планеты приплюснута с боков, то значение g будет наибольшим на полюсах и наименьшим на экваторе. Влияет также и вращение планеты вокруг собственной оси, что создает инерциальные силы.

В целом g принимают равным 9,8 м/с2, что является средним значением на поверхности Земли.

Рис. 3. Форма Земли и значение g.

С подъемом на высоту ускорение свободного падения уменьшается, но незначительно. На 5 км оно все еще приблизительно равно 9,8 м/с2. Поэтому в большинстве задач этим изменением пренебрегают.

Произведение $mg$ называет силой тяжести, действующей на тело массой m в гравитационном поле Земли. Сила тяжести является одной из трех важнейших сил в классической механике.

Масса Юпитера ${1,9 cdot 10^{27}}$, его радиус – 69911 км, масса космического корабля – 20 тонн. Найти ускорение свободного падения на поверхности Юпитера. Найти силу тяжести, которая действует на космический корабль на высоте 120 км от поверхности Юпитера.

Решение первой задачи
$g_1 = gamma {M over R^2} = {6,67 cdot 10^{-11}}{{1,9 cdot 10^{27}} over 69911^2} = 25,9 м/c$ – ускорение свободного падения на поверхности Юпитера.
$g_2 = gamma {M over (R+h)^2} = {6,67 cdot 10^{-11}}{{1,9 cdot 10^{27}} over 70031^2} = 25,8 м/c$ – ускорение свободного падения на высоте 120 км от поверхности Юпитера.
$F = mg_2 = 516 кН$ – сила тяжести, действующая на космический корабль на высоте 120 км от поверхности Юпитера.

Масса космонавта – 70 кг. Масса планеты Земля ${5,97 cdot 10^{24}}$, ее радиус – 6371 км, масса Луны – ${7,35 cdot 10^{22}}$, а ее радиус – 1737 км. Рассчитать силу тяжести, которая действует на космонавта на поверхности Луны и на высоте 500 км от поверхности Земли. Сравнить их величины.

Решение второй задачи
$F_1 = gamma {mM_1 over (R_1+h)^2} = {6,67 cdot 10^{-11}}{{133 cdot 10^{24}} over 6871^2} = 568 Н$ – сила тяжести, действующая на космонавта на высоте 500 км от поверхности Земли.
$F_2 = gamma {mM_2 over (R_2)^2} = {6,67 cdot 10^{-11}}{{515 cdot 10^{22}} over 1737^2} = 15,6 Н$ – сила тяжести, действующая на космонавта на Луне.
$F_1 – F_2 = 552,4 Н$

В ходе урока был разобран закон всемирного тяготения, выведена формула для расчета ускорения свободного падения и введено понятие потенциала гравитационного поля. После чего было рассмотрено ускорение свободного падение на Земле и приведена формула силы тяжести, действующей на тела в гравитационном поле нашей планеты. В завершении урока были разобраны две задачи на пройденную тему.

Средняя оценка: 4.6. Всего получено оценок: 126.

Источник: https://obrazovaka.ru/fizika/sila-tyazhesti-formula.html

Сила тяжести — урок. Физика, 7 класс

Силу гравитации, с которой Земля притягивает тело, находящееся на её поверхности или вблизи неё, называют силой тяжести. Эта сила направлена к центру Земли.

Сила гравитации Земли для нас является самой важной, поэтому ей и дано особое название.
Земля притягивает всё, что находится вокруг неё: твёрдые тела, жидкости, газы.
Из-за того, что есть сила тяжести, возможно существование атмосферы (молекулы газа не улетают в космос), воды морей и океанов удерживаются на своих местах, если какой-либо предмет приподнимают и роняют, этот предмет падает вниз — в направлении Земли.

Силу, с которой Земля притягивает тела, можно рассчитать по формуле F=m⋅g, где (m) — масса тела, а (g) — ускорение свободного падения.

Ускорение свободного падения — это ускорение, которое вблизи Земли приобретает тело, падающее свободно и беспрепятственно. Вблизи поверхности Земли значение (g) равно примерно (9,81) мс2, для приблизительных расчётов можно использовать значение (10) мс2.

Что означает эта единица измерения?

Скорость свободно падающего тела каждую секунду увеличивается на (9,81) метров в секунду (м/с).
Если предмет падает, например, в течение (4) секунд, то скорость его падения в самом начале равна (0) м/с;
за (1)-ю секунду он достигает скорости (9,81) м/с;
за (2)-ю секунду он достигает скорости: (9,81), умноженное на (2) м/с (=) (19,62) м/с;
за (3)-ю секунду он достигает скорости: (9,81), умноженное на (3) м/с (=) (29,43) м/с;

за (4)-ю секунду тело достигает скорости: (9,81), умноженное на (4) м/с (=) (39,24) м/с, что приблизительно составляет (141) км/ч.

Обрати внимание!

Интересно, что кирпич и яблоко падают с одинаковой скоростью. Только падение лёгких предметов сопротивление воздуха замедляет сильнее, например, птичье перо из-за сопротивления воздуха будет падать медленнее.

Ускорение свободного падения на поверхности Луны составляет только (1,62) мс2.

На Юпитере значение (g) приблизительно равно (26,2) мс2, это примерно так же, как если бы человек в дополнение к своим (60) кг веса взвалил бы на плечи ещё примерно (102) кг.

Источник: https://www.yaklass.ru/p/fizika/7-klass/dvizhenie-i-vzaimodeistvie-tel-11864/sila-sila-tiazhesti-11870/re-924aeee5-b7c6-45b4-8a41-3988a18f7166

Ускорение силы тяжести – определение, формулы — Помощник для школьников Спринт-Олимпиады

Процесс изменения скорости при движении физического тела характеризуется ускорением. Ускорение силы тяжести (обозначается буквой g) возникает в результате влияния силы тяжести, которая действует на любое тело у поверхности Земли или другой планеты. Разберемся от чего зависит значение g и как его определяют.

Основные формулы для равноускоренного движения

Равноускоренное движение — самый простой вид неравномерного движения. Равноускоренным называется движение с ускорением, постоянным по модулю и направлению:
$ a = {Δvover Δt} = const $ (1),
где:
Δv — изменение скорости (“дельта v “), м/с;
Δt — промежуток времени, (“дельта t “)за которое произошло изменение скорости, с.
Из формулы (1) следует, что размерность ускорения будет выражаться в метрах на секунду в квадрате:
$ {1 м/сover 1 c} = 1 м/с^2 $ (2).
Второй закон Ньютона гласит:
$ F = m * a $ (3),
где:
F — сила, действующая на тело, Н;
m — масса тела, кг;
a — ускорение, м/с2.

Сила тяжести и ускорение свободного падения

При свободном падении на Землю все тела, независимо от их массы, движутся одинаково. Свободное движение является равноускоренным движением.

Ускорение, с которым падают на Землю тела в пустоте, называется ускорением свободного падения (или ускорением силы тяжести).

Условие пустоты или, что тоже самое, вакуума, требуется для исключения влияния сопротивления атмосферного воздуха. Сила притяжения Fт со стороны Земли на тело массой m, называется силой тяжести:

$ F_т = m * g $ (4),

Определением ускорения силы тяжести впервые систематически занимался Галилео Галилей — итальянский математик, физик, астроном. Будучи профессором университета в городе Пиза, Галилей измерял время падения предметов с высоты местной, слегка наклонной, башни.

Рис. 1. Галилео Галилей измеряет ускорение свободного падения.

В результате этих наблюдений он пришел к следующим выводам:

Время падения не зависит от массы тела. Все тела падают одинаково;
Падение тел представляет собой равноускоренное движение с ускорением $ g = 9,81{ мover c^2} $ .

И хотя это открытие датировано 1589г., современное, общепринятое среднее значение g практически не отличается от этого значения. Когда от расчетов не требуется высокой точности, то принимают, что модуль g равен 10 м/с2.

Последовавшие за Галилеем более точные измерения показали, что значение g не является абсолютной константой, а зависит от местоположения измерений в разных точках Земли. Ответ на этот вопрос нашел английский ученый Исаак Ньютон.

Закон всемирного тяготения

В 1682 г. Ньютон открыл закон всемирного тяготения, из которого следует:

все тела притягиваются друг к другу;
сила тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними;
векторы сил тяготения направлены вдоль прямой, соединяющей тела.

Этот закон универсален, и для случая пары тел, одно из которых является произвольным телом массой m, а второй — Земля, в виде формулы выглядит так:
$ F_т = G * {{m * Mз }over {(R_з + h)^2} } $ (5),
где:
Mз — масса Земли, кг;
Rз — радиус Земли, м;
h — высота, на которой находится тело, относительно поверхности Земли, м;
G — гравитационная постоянная, равная 6,6720 * 10-11 Н*м2 * кг-2.
Из формул (4) и (5) следует, что:
$ g = G * {{ Mз }over {(R_з + h)^2 } }$ (6)
Из (6) следует, что ускорение силы тяжести будет зависеть от высоты h и величины радиуса Земли, который для обычных расчетов принимается равным примерно 6400 км. Но поскольку форма Земли не является идеальным шаром, а сплюснута к полюсам, то точные значения g будут отличаться от среднего значения в 9,81 м/с2:

максимальное значение gмакс = 9,83 м/с2 — на полюсах Земли, где Rз меньше;
минимальное значение gмин = 9,79 м/с2 — на экваторе Земли, где Rз больше.

Рис. 2. Зависимость ускорения свободного падения на полюсах, экваторе и от вращения Земли.

Из формулы (6) также следует, что ускорение силы тяжести на других планетах, имеющих массу, отличающуюся от массы Земли, будет для космонавтов значительно отличаться от привычных земных условий. Так, например:

На Марсе — gМарса = 3,86 м/с2;
На Меркурии — gМеркурия = 3,7 м/с2;
На Луне — gЛуны = 1,62 м/с2;
На Нептуне — gНептуна = 11,0 м/с2.

Как определяют ускорение силы тяжести

Для точного измерения силы тяжести, а значит, и ускорения, используется прибор, называемый гравиметром. Прибор применяется при поиске полезных ископаемых и для сбора информации археологами, палеонтологами, гидрологами и представителями других профессий, изучающих поверхность Земли.

Рис. 3. Гравиметры:.

Следует упомянуть еще два фактора, влияющих на значение ускорения свободного падения:

Известно, что Земля вращается вокруг своей оси, имея при этом так называемое центростремительное ускорение, которое влияет на величину ускорения свободного падения;
Масса Земли распределена неравномерно, например, в местах расположения больших месторождений металлических руд ускорение силы тяжести будет больше, а там, где есть пустоты (газовые месторождения) ускорение будет несколько меньше.

Эти факторы дают очень малые отклонения от средних значений g , но зато их регистрация позволяет, например, геологам находить новые месторождения полезных ископаемых.

Что мы узнали?

Итак, мы узнали, что такое ускорение силы тяжести. Сила тяжести возникает вследствие действия силы гравитации, подчиняющейся закону Ньютона (формула (5)). На Земле среднее значение ускорения силы тяжести gЗемли равно 9,81 м/с2. Для точного определения ускорения силы тяжести требуется использование современных приборов, называемых гравиметрами.

ПредыдущаяСледующая

Источник: https://Sprint-Olympic.ru/uroki/fizika/18216-yskorenie-sily-tiajesti-opredelenie-formyly.html

Как найти силу тяжести

Сила тяжести – величина, на которую тело притягивается к земле под действием ее притяжения. Данный показатель напрямую зависит от веса человека или массы предмета. Чем больше вес, тем он выше. В этой статье мы расскажем, как найти силу тяжести.

Из школьного курса физики: сила притяжения прямо пропорциональна весу тела. Рассчитать величину можно по формуле F=m*g, где g – коэффициент, равный 9,8 м/с2. Соответственно для человека, который весит 100 кг, сила притяжения равна 980. Стоит отметить, что на практике все немного иначе, и на силу тяжести влияет множество факторов.

Факторы, влияющие на силу тяжести:

расстояние от земли;
географическое расположение тела;
время суток.

Запомните, что на северном полюсе постоянная g равна не 9,8, а 9,83. Это возможно из-за наличия в земле залежей полезных ископаемых, которые обладают магнитными свойствами. Незначительно увеличивается коэффициент в местах залежей железной руды. На экваторе коэффициент равен 9,78. Если тело находится не на земле или в движении, то для определения силы притяжения необходимо знать ускорение предмета. Для этого можно воспользоваться специальными приборами – секундомером, спидометром или акселерометром. Для расчета ускорения определите конечную и начальную скорости движения объекта. Отнимите от конечной величины начальную скорость, а полученную разницу разделите на время, за которое предмет прошел расстояние. Можно подсчитать ускорение, подвигав предмет. Для этого необходимо передвинуть тело из состояния покоя. Теперь расстояние умножьте на два. Полученную величину разделите на время, возведенное в квадрат. Этот способ расчета ускорения подходит, если тело вначале находится в состоянии покоя. Если имеется спидометр, то для определения ускорения необходимо возвести в квадрат начальную и конечную скорости тела. Найдите разницу квадратов конечной и начальной скоростей. Полученный результат разделите на время, умноженное на 2. Если тело движется по окружности, то оно имеет свое ускорение, даже при постоянной скорости. Для нахождения ускорения возведите скорость тела в квадрат и разделите на радиус окружности, по которой оно движется. Радиус необходимо указывать в метрах. Для определения мгновенного ускорения используйте акселерометр. Если вы получили отрицательное значение ускорения, это значит, что предмет тормозит, то есть его скорость уменьшается. Соответственно при положительном значении предмет разгоняется, а его скорость увеличивается. Помните, коэффициент 9,8 можно использовать лишь в том случае, если сила тяжести определяется для предмета, который находится на земле. Если тело установлено на опору, следует учесть сопротивление опоры. Эта величина зависит от материала, из которого изготовлена опора.

Если тело волочат не в горизонтальном направлении, то стоит взять во внимание угол, на который отклоняется предмет от горизонта. В итоге формула будет иметь следующий вид: F=m*g – Fтяги*sin. Измеряется сила тяжести в ньютонах. Для проведения расчетов используйте скорость, измеренную в м/с. Для этого поделите скорость в км/час на 3,6.

Источник: https://sovetclub.ru/kak-najti-silu-tyazhesti