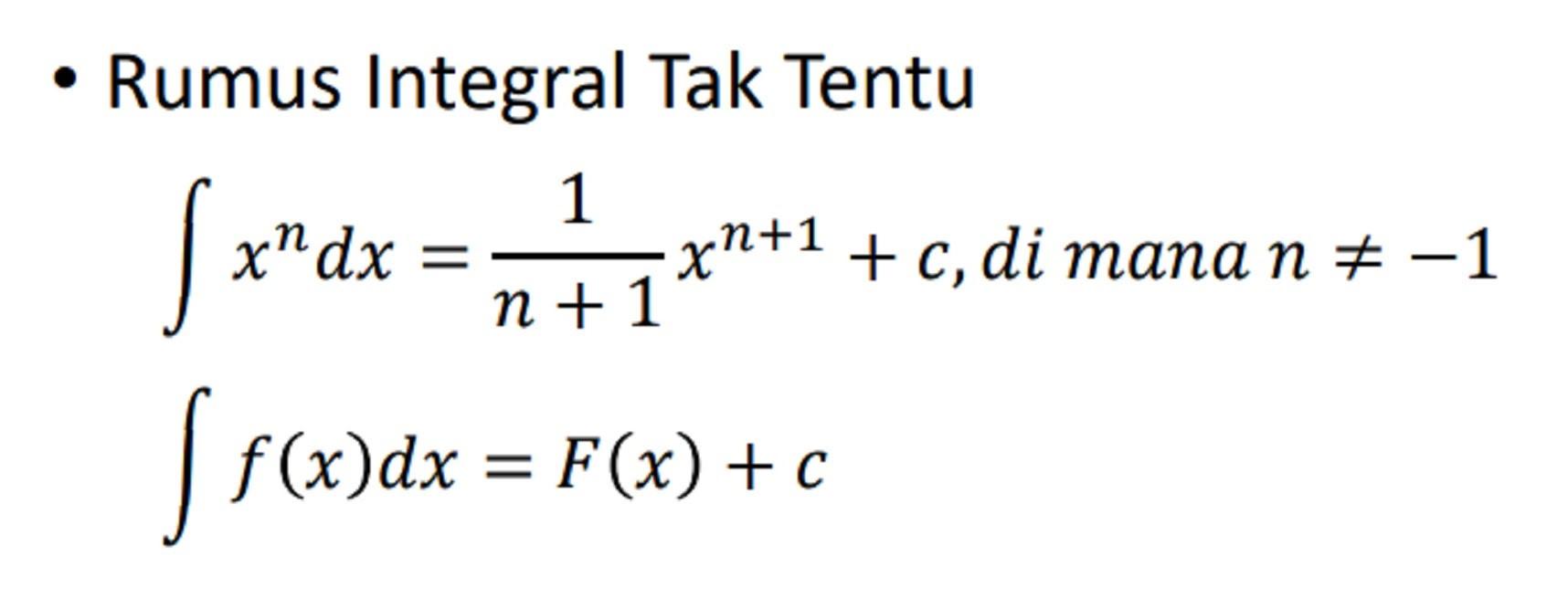 В предыдущих записях мы рассматривали нахождение неопределенных интегралов от синуса во второй и третьей степенях. Продолжая этот процесс решим задачу нахождения неопределенного интеграла от синуса в четвертой степени, т.е.
В предыдущих записях мы рассматривали нахождение неопределенных интегралов от синуса во второй и третьей степенях. Продолжая этот процесс решим задачу нахождения неопределенного интеграла от синуса в четвертой степени, т.е.
Для нахождения этого неопределенного интеграла воспользуемся формулой понижения степени синуса:
![]()
- Интеграл



- Далее воспользуемся свойством линейности неопределенного интеграла:
![]()
и формулой понижения степени косинуса
![]()
При этом, интеграл от синуса в 4-й степени
![]()
![]()
![]()
- где — произвольная действительная постоянная.
- Здесь при нахождении неопределенного интеграла от синуса в четвертой степени также было использовано свойство дифференциала по которому
- Таким образом
- где — произвольная действительная постоянная.
- Также для успешного освоения темы и формирования навыка нахождения интегралов будет полезно посмотреть следующее видео занятие, где подробно и с ми приведено решение примера по нахождению неопределенного интеграла от синуса в 4-й степени.
Источник: http://vmatematika.ru/matematicheskij-analiz/neopredelennyj-integral/neopredelennyj-integral-ot-sinusa-v-chetvertoj-stepeni.html
Обратная тригонометрическая функция: Арксинус (arcsin)
- Определение
- График арксинуса
- Свойства арксинуса
- Таблица арксинусов
- Арксинус (arcsin) – это обратная тригонометрическая функция.
- Арксинус x определяется как функция, обратная к синусу x, при -1≤x≤1.
- Если синус угла у равен х (sin y = x), значит арксинус x равняется y:
- arcsin x = sin-1 x = y
- Примечание: sin-1 x означает обратный синус, а не синус в степени -1.
- Например:
- arcsin 1 = sin-1 1 = 90° (π/2 рад)
График арксинуса
Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):

Свойства арксинуса
Ниже в табличном виде представлены основные свойства арксинуса с формулами.
| Свойство | Формула |
| Синус арксинуса | sin (arcsin x) = x |
| Арксинус синуса | arcsin (sin x) = x + 2kπ,где k∈ℤ (k — целое число) |
| Арксинус отрицательного числа | arcsin (-x) = -arcsin x |
| Дополнительные углы | arcsin x = π/2 — arccos x = 90° — arccos x |
| Сумма арксинусов |  |
| Разность арксинусов |  |
| Косинус арксинуса |  |
| Тангенс арксинуса |  |
| Производная арксинуса |  |
| Неопределенный интеграл арксинуса |  |
microexcel.ru
Таблица арксинусов
| x | arcsin x (рад) | arcsin x (°) |
| -1 | -π/2 | -90° |
| -√3/2 | -π/3 | -60° |
| -√2/2 | -π/4 | -45° |
| -1/2 | -π/6 | -30° |
| 0 | 0 | 0° |
| 1/2 | π/6 | 30° |
| √2/2 | π/4 | 45° |
| √3/2 | π/3 | 60° |
| 1 | π/2 | 90° |
microexcel.ru
(1
Источник: https://MicroExcel.ru/arksinus/
Алгебра – 10 класс. Арксинус, arcsin(x)
Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арксинуса.
6. Примеры.
Что такое арксинус?
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2.
Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения.
Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk, а x2= 2π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение sin(x)= 5/6.
Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk, где x1 – длина дуги AF, x2 – длина дуги AG. Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.

Немного истории арксинуса

История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.

Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и x= π — arcsin(a) + 2πk

Перепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).
Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1. С учётом этого, запишем общую формула решения для уравнения sin(x)=a:

Есть три случая, в которых предпочитают записывать решения более простым способом:
- sin(x)=0, то x= πk,
- sin(x)=1, то x= π/2 + 2πk,
- sin(x)=-1, то x= -π/2 + 2πk.
- Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).
Таблица значений арксинуса
Таблица значений синуса

Таблица значений арксинуса
Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
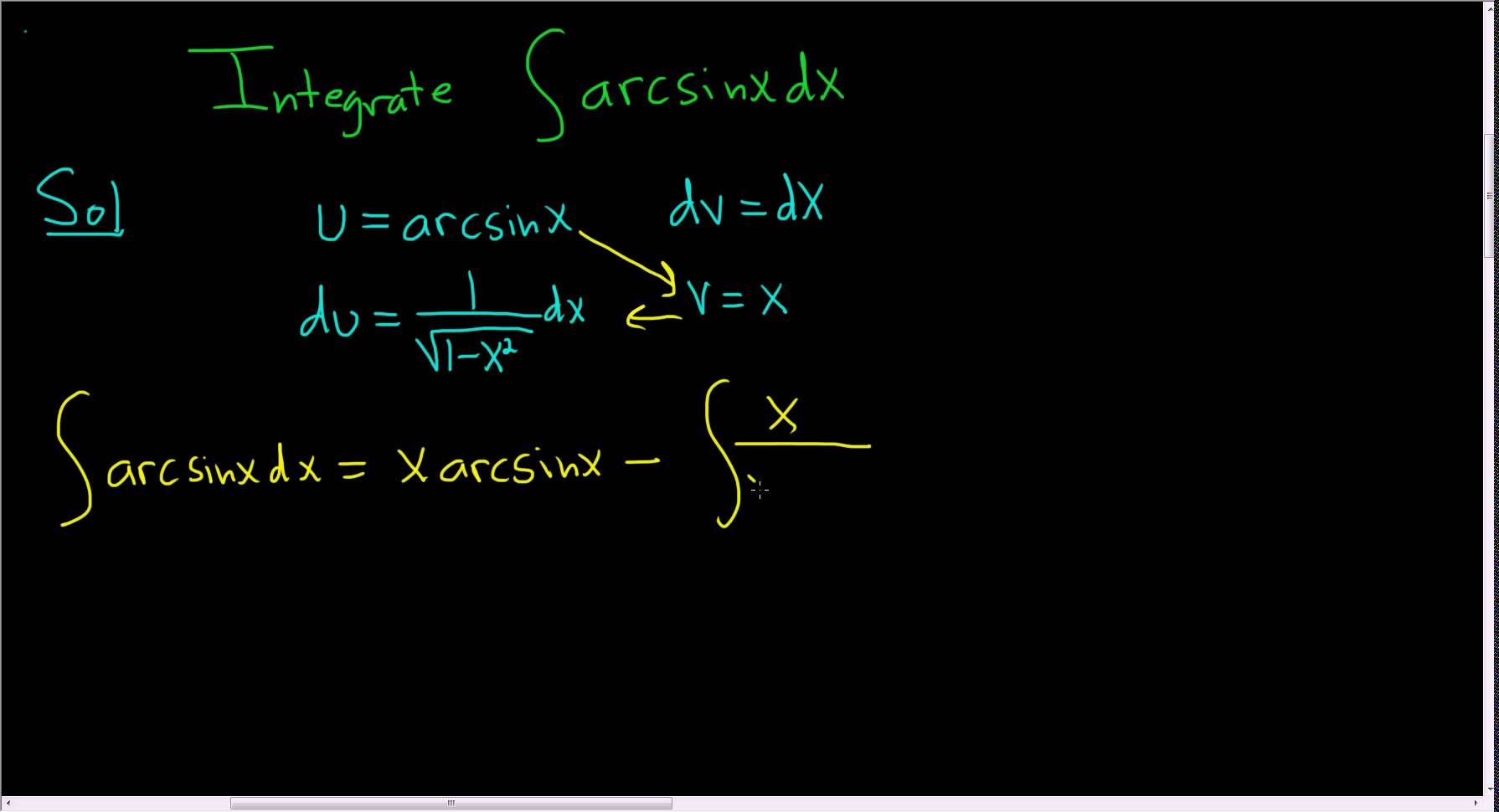
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.
2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
4. Решить уравнение: sin(x) = -√2/2.
Решение: Воспользуемся определением, тогда решение запишется в виде: x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2 ) + 2πk. Посмотрим в таблице значение: arcsin (-√2/2 )= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде: x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk
6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде: x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1)n — arcsin(3/5) + πk.
7. Решить неравенство sin(x)< 0.7. Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Источник: https://mathematics-tests.com/10-klass-urok-na-temu-y-arcsin-x
Интегралы от тригонометрических функций, умноженных на многочлен
- Общее правило: за всегда обозначается многочлен
- Пример 7
- Найти неопределенный интеграл.
![]()
Интегрируем по частям:


Хммм, …и комментировать нечего.
Пример 8
![]()
Это пример для самостоятельного решения
Пример 9


- Если возникли трудности или недопонимание с нахождением интеграла , то рекомендую посетить урок Интегралы от тригонометрических функций.
- Пример 10
- Найти неопределенный интеграл
- Это пример для самостоятельного решения.
Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….
- Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен
- Общее правило: за всегда обозначается обратная тригонометрическая функция.
- Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»
- Пример 11
- Найти неопределенный интеграл.
- Решаем.
- Интегрируем по частям:
Интеграл найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример мы разбирали на уроке Метод замены переменной в неопределенном интеграле.
- Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.
- Пример 12
- Найти неопределенный интеграл.
- Это пример для самостоятельного решения
И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для маньяков желающих лучше разобраться в методе интегрирования по частям. Пример, пожалуй, будет тоже для самостоятельного решения, поскольку меня немного утомил тот логарифм в квадрате.
Пример 13
Найти неопределенный интеграл.
Что касаемо интегрирования по частям, почти всё разобрали. Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.
- А сейчас, как любила говорить моя учительница по математике, пора кончать.
- Желаю успехов!
- Пример 3:Решение:
- Пример 4:Решение:
- Интегрируем по частям:
- Пример 6:Решение:
- Дважды интегрируем по частям:
- Пример 8:Решение:
- Интегрируем по частям:
- Пример 10:Решение:
- Интегрируем по частям:
Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла . Её можно было использовать и сразу: , а потом интегрировать по частям.
Похожим способом также решаются интегралы вроде , – в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул. Более подробно – см. Интегралы от тригонометрических функций.
- Пример 12: Решение:
- Интегрируем по частям:
- Пример 13: Решение:
- Интегрируем по частям:
- Определенный интеграл. Примеры решений
И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.
- Для того чтобы научиться решать определенные интегралы необходимо:
- 1) Уметь находить неопределенные интегралы.
- 2) Уметь вычислить определенный интеграл.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой . Верхний предел интегрирования стандартно обозначается буквой . Отрезок называется отрезком интегрирования.
Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.
Что такое определенный интеграл? Считаю немного преждевременным рассказать про разбиения отрезка и предел интегральных сумм, поэтому пока я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.
Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
- Как решить определенный интеграл?С помощью знакомой со школы формулы Ньютона-Лейбница:
- Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
- Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа в определенном интеграле не добавляется. Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: .
3) Подставляем значение нижнего предела в первообразную функцию: .
4) Рассчитываем (без ошибок!) разность , то есть, находим число.
Готово.
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: .
Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас.
Будет здорово помогать на протяжении всего курса высшей математики.
Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция быланепрерывнойна отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывнана отрезке интегрирования.
По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?».
В упрощенном варианте ситуация выглядит примерно так:
???! Нельзя подставлять отрицательные числа под корень! Что за фигня?! Изначальная невнимательность.
Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде , то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике.
– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
- В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
- Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:
- – в таком виде интегрировать значительно удобнее.
- Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
- – это справедливо не только для двух, но и для любого количества функций.
- В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
- Для определенного интеграла справедлива формула интегрирования по частям:
- Пример 1
- Вычислить определенный интеграл
- Решение:
- (1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?
(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
- Пример 2
- Вычислить определенный интеграл
- Это пример для самостоятельно решения, решение и ответ в конце урока.
- Немного усложняем задачу:
- Пример 3
- Вычислить определенный интеграл
- Решение:
- (1) Используем свойства линейности определенного интеграла.
- (2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница: СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ.
Будьте внимательны! Особое внимание заостряю на третьем слагаемом: – первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут (особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:
Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов: (в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.
Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе. Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.
Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная находится в одной скобке.
Источник: https://cyberpedia.su/1x6f8d.html
Таблица основных неопределенных интегралов
Перечисленные интегралы — это базис, основа основ. Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.
Обратите особое внимание на формулы (5), (7), (9), (12), (13), (17) и (19). Не забывайте при интегрировании добавлять к ответу произвольную постоянную С!
Интеграл от константы
∫ Adx=Ax+C (1)
Интегрирование степенной функции
В действительности, можно было ограничиться только формулами (5) и (7), но остальные интегралы из этой группы встречаются настолько часто, что стоит уделить им немного внимания.
∫ xdx= x 2 2 +C (2) ∫ x 2 dx= x 3 3 +C (3) ∫ 1 x dx=2 x +C (4) ∫ 1 x dx=ln| x |+C (5) ∫ 1 x 2 dx=− 1 x +C (6) ∫ x n dx= x n+1 n+1 +C(n≠−1) (7)
Интегралы от показательной функции и от гиперболических функций
Разумеется, формулу (8) (пожалуй, самую удобную для запоминания) можно рассматривать как частный случай формулы (9). Формулы (10) и (11) для интегралов от гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения.
∫ e x dx= e x +C (8) ∫ a x dx= a x lna +C(a>0,a≠1) (9) ∫ shx dx=chx+C (10) ∫ chx dx=shx+C (11)
Базовые интегралы от тригонометрических функций
Ошибка, которую часто делают студенты: путают знаки в формулах (12) и (13). Запомнив, что производная синуса равна косинусу, многие почему-то считают, что интеграл от функции sinx равен сosx. Это неверно! Интеграл от синуса равен «минус косинусу», а вот интеграл от cosx равен «просто синусу»:
∫ sinxdx=−cosx+C (12) ∫ cosxdx=sinx+C (13) ∫ 1 cos 2 x dx=tgx+C (14) ∫ 1 sin 2 x dx=−ctgx+C (15)
Формула (16), приводящая к арктангенсу, естественно, является частным случаем формулы (17) при a=1. Аналогично, (18) — частный случай (19).
∫ 1 1+ x 2 dx=arctgx+C=−arcctgx+C (16) ∫ 1 x 2 + a 2 = 1 a arctg x a +C(a≠0) (17) ∫ 1 1− x 2 dx=arcsinx+C=−arccosx+C (18) ∫ 1 a 2 − x 2 dx=arcsin x a +C=−arccos x a +C(a>0) (19) Репетитор по математическому анализу
Данные формулы тоже желательно запомнить. Они также используются достаточно часто, а их вывод довольно утомителен.
∫ 1 x 2 + a 2 dx=ln| x+ x 2 + a 2 |+C (20) ∫ 1 x 2 − a 2 dx=ln| x+ x 2 − a 2 |+C (21) ∫ a 2 − x 2 dx= x 2 a 2 − x 2 + a 2 2 arcsin x a +C(a>0) (22) ∫ x 2 + a 2 dx= x 2 x 2 + a 2 + a 2 2 ln| x+ x 2 + a 2 |+C(a>0) (23) ∫ x 2 − a 2 dx= x 2 x 2 − a 2 − a 2 2 ln| x+ x 2 − a 2 |+C(a>0) (24)
- 1) Интеграл от суммы двух функций равен сумме соответствующих интегралов: ∫ (f(x)+g (x))dx= ∫ f(x)dx+ ∫ g(x)dx (25)
- 2) Интеграл от разности двух функций равен разности соответствующих интегралов: ∫ (f(x)−g (x))dx= ∫ f(x)dx− ∫ g(x)dx (26)
- 3) Константу можно выносить за знак интеграла: ∫ Cf(x) dx=C ∫ f(x)dx (27)
- Легко заметить, что свойство (26) — это просто комбинация свойств (25) и (27).
- 4) Интеграл от сложной функции, если внутренняя функция является линейной: ∫ f(Ax+B) dx= 1 A F(Ax+B)+C(A≠0) (28)
Здесь F(x) — первообразная для функции f(x). Обратите внимание: эта формула подходит только для случая, когда внутренняя функция имеет вид Ax + B.
Важно: не существует универсальной формулы для интеграла от произведения двух функций, а также для интеграла от дроби:
∫ f(x)g(x) dx=? ∫ f(x) g(x) dx=? (30)
Это не означает, конечно, что дробь или произведение нельзя проинтегрировать. Просто каждый раз, увидев интеграл типа (30), вам придется изобретать способ «борьбы» с ним. В каких-то случаях вам поможет интегрирование по частям, где-то придется сделать замену переменной, а иногда помощь могут оказать даже «школьные» формулы алгебры или тригонометрии.
Пример 1. Найти интеграл: ∫ (3 x 2 +2sinx−7 e x +12)dx
Воспользуемся формулами (25) и (26) (интеграл от суммы или разности функций равен сумме или разности соответствующих интегралов. Получаем: ∫ 3 x 2 dx + ∫ 2sinxdx− ∫ 7 e x dx+ ∫ 12dx
Вспомним, что константу можно выносить за знак интеграла (формула (27)). Выражение преобразуется к виду
3 ∫ x 2 dx +2 ∫ sinxdx−7 ∫ e x dx+12 ∫ 1dx
А теперь просто воспользуемся таблицей основных интегралов. Нам потребуется применить формулы (3), (12), (8) и (1). Проинтегрируем степенную функцию, синус, экспоненту и константу 1. Не забудем добавить в конце произвольную постоянную С:
3 x 3 3 −2cosx−7 e x +12x+C
После элементарных преобразований получаем окончательный ответ:
x 3 −2cosx−7 e x +12x+C
Проверьте себя дифференцированием: возьмите производную от полученной функции и убедитесь, что она равна исходному подинтегральному выражению.
| ∫ Adx=Ax+C |
| ∫ xdx= x 2 2 +C |
| ∫ x 2 dx= x 3 3 +C |
| ∫ 1 x dx=2 x +C |
| ∫ 1 x dx=ln| x |+C |
| ∫ 1 x 2 dx=− 1 x +C |
| ∫ x n dx= x n+1 n+1 +C(n≠−1) |
| ∫ e x dx= e x +C |
| ∫ a x dx= a x lna +C(a>0,a≠1) |
| ∫ shx dx=chx+C |
| ∫ chx dx=shx+C |
| ∫ sinxdx=−cosx+C |
| ∫ cosxdx=sinx+C |
| ∫ 1 cos 2 x dx=tgx+C |
| ∫ 1 sin 2 x dx=−ctgx+C |
| ∫ 1 1+ x 2 dx=arctgx+C=−arcctgx+C |
| ∫ 1 x 2 + a 2 = 1 a arctg x a +C(a≠0) |
| ∫ 1 1− x 2 dx=arcsinx+C=−arccosx+C |
| ∫ 1 a 2 − x 2 dx=arcsin x a +C=−arccos x a +C(a>0) |
| ∫ 1 x 2 + a 2 dx=ln| x+ x 2 + a 2 |+C |
| ∫ 1 x 2 − a 2 dx=ln| x+ x 2 − a 2 |+C |
| ∫ a 2 − x 2 dx= x 2 a 2 − x 2 + a 2 2 arcsin x a +C(a>0) |
| ∫ x 2 + a 2 dx= x 2 x 2 + a 2 + a 2 2 ln| x+ x 2 + a 2 |+C(a>0) |
| ∫ x 2 − a 2 dx= x 2 x 2 − a 2 − a 2 2 ln| x+ x 2 − a 2 |+C(a>0) |
 Скачайте таблицу интегралов (часть I) по этой ссылке
Скачайте таблицу интегралов (часть I) по этой ссылке Скачайте таблицу интегралов (часть II) по этой ссылке
Скачайте таблицу интегралов (часть II) по этой ссылке
Если Вы учитесь в ВУЗе, если у Вас возникли сложности с высшей математикой (математический анализ, линейная алгебра, теория вероятностей, статистика), если Вам нужны услуги квалифицированного преподавателя, зайдите на страничку репетитора по высшей математике. Будем решать Ваши проблемы вместе!
Возможно, вас заинтересуют также
Источник: http://www.repetitor2000.ru/integrals.html
Решение определенных интегралов
Данный калькулятор позволит найти определенный интеграл онлайн.
Определенный интеграл – это разность значений первообразной для подынтегральной функции. Проще говоря, определенный интеграл численно равен площади части графика функции в определенных пределах, то есть площади криволинейной трапеции. Определенный интеграл можно вычислить по формуле Ньютона-Лейбница.
Для того чтобы найти определенный интеграл, нужно ввести верхнюю и нижнюю границы и подынтегральную функцию. Калькулятор поможет найти решение определенных интегралов онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
Основные функции
модуль x: abs(x)
|
Интегралы Для того, чтобы найти неопределенный интеграл от функции нужно написать в строке: f[x], x. Найти определенный интеграл так же просто: f[x], {x, a, b} либо e f(x), x=a..b. Важно подчеркнуть, что калькулятор выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа. Примеры
|
Источник: https://allcalc.ru/node/670




