‹— Назад При вычислении производной, наличие формул для производной суммы, разности, произведения, частного и композиции — всех тех операций, при помощи которых элементарные функции образуются из минимального набора — приводит к тому, что производная любой элементарной функции снова является элементарной функцией.
При нахождении неопределённых интегралов, однако, формул для первообразной произведения, частного и композиции нет. Это приводит к такому положению, что отнюдь не для любой элементарной подынтегральной функции можно «взять интеграл», то есть выразить некоторую первообразную для подынтегральной функции в виде некоторого выражения, использующего лишь элементарные функции.
Дело не в том, что пока что не придумано способа это сделать, а в принципиальной невозможности: никакая из первообразных в случае «неберущегося» интеграла никаким образом не может быть выражена как комбинация элементарных функций, связанных знаками арифметических действий и знаками композиции.
Не следует думать, что если такое представление невозможно, то и функции такой нет1: можно считать, что для её выражения просто не хватает запаса рассматриваемых операций или запаса рассматриваемых исходных функций, и их надо расширить, то есть выйти за рамки множества функций, называемых элементарными2.
В науке и её приложениях в технике, экономике и других дисциплинах применяются многие неэлементарные функции; часто их называют специальными. К специальным функциям относятся и многие первообразные для элементарных функций, причём часто не столь уж «сложной» структуры.
Интегралы, выражающиеся через такие первообразные, называются (по традиции, берущей начало в 18 веке) неберущимися. Итак, интеграл 
не берётся, если функция не является элементарной. Приведём примеры неберущихся интегралов и названия первообразных — специальных функций, связанных с этими интегралами. Пример 1.8 Неберущимся является интеграл 
Здесь одна из первообразных, которую мы обозначили , выделяется из всего набора первообразных условием . Функция называется функцией Лапласа. Она широко применяется в теории вероятностей, физике, математической и прикладной статистике и других разделах науки и её приложений. Для вычисления значений функции Лапласа составлены таблицы, имеющиеся во многих учебниках, задачниках и справочниках по теории вероятностей и статистике. Возможность вычисления предусмотрена также на многих моделях калькуляторов (не самых дешёвых) и уж, обязательно, на тех, что предназначены для статистической обработки числового материала. Так что, с практической точки зрения, пользоваться функцией Лапласа ничуть не сложнее, чем, скажем, синусом, арктангенсом или натуральным логарифмом, которые мы условно относим к элементарным функциям. Пример 1.9 Не берётся также интеграл 
Доопределим подынтегральную функцию , полагая её равной 1 при . В соответствии с тем, что , доопределённая функция будет непрерывна на всей числовой оси. Среди её первообразных выделим ту, для которой . Эта неэлементарная функция называется интегральным синусом и обозначается . Именно её мы использовали в приведённой выше формуле. Пример 1.10 Ещё один неберущийся интеграл: 
Одна из первообразных — та, что мы использовали в правой части и обозначили — называется интегральным косинусом. Пример 1.11 
— это тоже неберущийся интеграл. Одна из первообразных, которую мы обозначили , — специальная функция, называющаяся интегральной экспонентой. Пример 1.12 Не берётся интеграл 
(при одна из первообразных, , называется интегральным логарифмом.
Используя специальные функции, заданные предыдущими примерами, мы с помощью изученных выше правил интегрирования можем выражать через эти функции и другие интегралы. Приведём такой пример.
Пример 1.13 Выразим через функцию Лапласа следующий интеграл: Для этого сделаем замену переменного :
 |
 |
Заметим, что та первообразная для 
, для которой , обозначается . Функция называется в теории вероятностей и статистике функцией ошибок.
Упражнение 1.3 Выразите функцию ошибок через функцию Лапласа и наоборот, функцию Лапласа через функцию ошибок.
Пример 1.14 К интегралу предыдущего примера можно свести и тем самым выразить через функцию Лапласа, например, такой интеграл:
 |
Для вычисления мы применили формулу интегрирования по частям. Пример 1.15 Вычислим интеграл от интегральной экспоненты . Заметим, что по определению первообразной. Применяя формулу интегрирования по частям, получаем:
Кроме приведённых выше, в приложениях встречаются и многие другие неберущиеся интегралы, например:
Эти четыре интеграла называются интегралами Френеля.
Упражнение 1.4 Сделав соответствующую замену переменного, выразите последние два из интегралов Френеля через функции и , которые стоят в правых частях первых двух интегралов Френеля.
Не берутся также интегралы
и многие другие.
Тем не менее, для многих классов интегралов, наиболее часто встречающихся в приложениях, первообразную всё же удаётся выразить через элементарные функции. В следующей главе мы изучим такие классы интегралов.
Упражнение 1.5 С помощью соответствующих замен переменного, докажите следующие соотношения: (при (при (на самом деле функции и определяются так, что обе постоянные равны 0).
- Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Источник: http://mathserfer.narod.ru/node6-2.html
Как вычислить неберущийся интеграл с помощью Вольфрам Альфа
Эта статья о том, как вычислить неберущийся интеграл онлайн, содержит примеры вычисления неберущихся интегралов с помощью Вольфрам Альфа.
Здесь продолжена тема, которая рассматривалась в статьях Определенный интеграл в Wolfram|Alpha, Как вычислить приближенное значение определенного интеграла в Wolfram|Alpha, используя численные методы решения интегралов, Численное интегрирование в Wolfram|Alpha, и рассмотрены основные способы вычисления неберущихся интегралов в системе Вольфрам Альфа.
Вычислить интеграл — так говорят об определенном интеграле, поскольку определенный интеграл, по его определению, есть число, которое «вычисляется», в отличие от неопределенного интеграла, который есть переменная величина, и поэтому «находится». Что же такое «неберущийся» интеграл? Так называют неопределенные интегралы, которые не выражаются через элементарные функции. То есть, это интегралы, в которых первообразную подынтегральной функции нельзя найти легко и быстро. Найти-то ее в принципе можно, но лень. Или же не хватает времени, знаний… Тогда и говорят, что первообразная не существует, и интеграл неберущийся. Определенные интегралы также называют неберущимися, когда определенный интеграл существует, как предел интегральной суммы, но подынтегральная функция не имеет первообразной, либо когда первообразная подынтегральной функции не выражается через элементарные функции.
Таким образом, различают, когда определенный интеграл, как предел интегральной суммы, в принципе существует, но «не берется», и когда определенный интеграл не существует в принципе. Примеры можно также найти в статье Несобственные интегралы в Wolfram|Alpha.
Вот простой пример неберущегося интеграла:
integrate e^(x^2), x=0..1
Здесь erf(x) — функция ошибок (интеграл вероятностей), неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Другие типичные примеры неберущихся интегралов, которые находят применение в физике, точнее, в оптике:
integrate sin(x^2), x=0..1
integrate cos(pi*t^2/2) dt, t= 0..x — C-интеграл Френеля
 |
К таким же не элементарным функциям относятся Ci(x) — интегральный косинус, Si(x) — интегральный синус, li(x) — интегральный логарифм, соответственно:
integrate -cos(t)/t, t= x..inf — интегральный косинус 
integrate sin(t)/t, t= 0..x — интегральный синус 
integrate 1/ln(t), t= 0..x — интегральный логарифм 
Соответственно, через эти функции выражаются такие интегралы, как
integrate cos(x)/x, x= 1..inf 
integrate sin(x)/x, x= 0..1
Последний интеграл также неберущийся. Он выражается через эллиптический интеграл второго рода E(x).
Однако, из правила всеядности Вольфрам Альфа существуют исключения. Вот почему, когда используете Вольфрам Альфа, все же лучше строго соблюдать правила математической нотации. Например,
integrate sqrt(1-sin(x^2)/4), x=0..pi
Кстати, этот последний интеграл, который, как и предыдущие, тоже является «неберущимся». Но при этом он не выражается даже через неэлементарные функции. В этом легко убедится непосредственно, найдя неопределенный интеграл, который, как видим, представляется в виде степенного ряда:
integrate sqrt(1-sin(x^2)/4)
integrate 1/ln(x), x= -1..3
integrate 1/ln(x), x= -1..0
В последнем примере для вычисления интеграла используется еще одна неэлементарная функция, на этот раз Ei(x). Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Посетите страницу Как поддержать наш сайт?
Источник: http://www.wolframalpha-ru.com/2018/11/kak-vychislit-neberushhijsja-integral-s-pomoshhju-Wolfram-Alpha.html
Этб-11 ТюмГНГУ (ЯФ) — Небурущийся интеграл
При вычислении производной, наличие формул для производной суммы, разности, произведения, частного и композиции — всех тех операций, при помощи которых элементарные функции образуются из минимального набора — приводит к тому, что производная любой элементарной функции снова является элементарной функцией.
При нахождении неопределённых интегралов, однако, формул для первообразной произведения, частного и композиции нет. Это приводит к такому положению, что отнюдь не для любой элементарной подынтегральной функции можно «взять интеграл», то есть выразить некоторую первообразную для подынтегральной функции в виде некоторого выражения, использующего лишь элементарные функции.
Дело не в том, что пока что не придумано способа это сделать, а в принципиальной невозможности: никакая из первообразных в случае «неберущегося» интеграла никаким образом не может быть выражена как комбинация элементарных функций, связанных знаками арифметических действий и знаками композиции.
Не следует думать, что если такое представление невозможно, то и функции такой нет1: можно считать, что для её выражения просто не хватает запаса рассматриваемых операций или запаса рассматриваемых исходных функций, и их надо расширить, то есть выйти за рамки множества функций, называемых элементарными2.
В науке и её приложениях в технике, экономике и других дисциплинах применяются многие неэлементарные функции; часто их называют специальными. К специальным функциям относятся и многие первообразные для элементарных функций, причём часто не столь уж «сложной» структуры.
Интегралы, выражающиеся через такие первообразные, называются (по традиции, берущей начало в 18 веке) неберущимися. Итак, интеграл 
не берётся, если функция не является элементарной. Приведём примеры неберущихся интегралов и названия первообразных — специальных функций, связанных с этими интегралами. Пример Неберущимся является интеграл 
Здесь одна из первообразных, которую мы обозначили , выделяется из всего набора первообразных условием . Функция называется функцией Лапласа. Она широко применяется в теории вероятностей, физике, математической и прикладной статистике и других разделах науки и её приложений. Для вычисления значений функции Лапласа составлены таблицы, имеющиеся во многих учебниках, задачниках и справочниках по теории вероятностей и статистике. Возможность вычисления предусмотрена также на многих моделях калькуляторов (не самых дешёвых) и уж, обязательно, на тех, что предназначены для статистической обработки числового материала. Так что, с практической точки зрения, пользоваться функцией Лапласа ничуть не сложнее, чем, скажем, синусом, арктангенсом или натуральным логарифмом, которые мы условно относим к элементарным функциям. Пример Не берётся также интеграл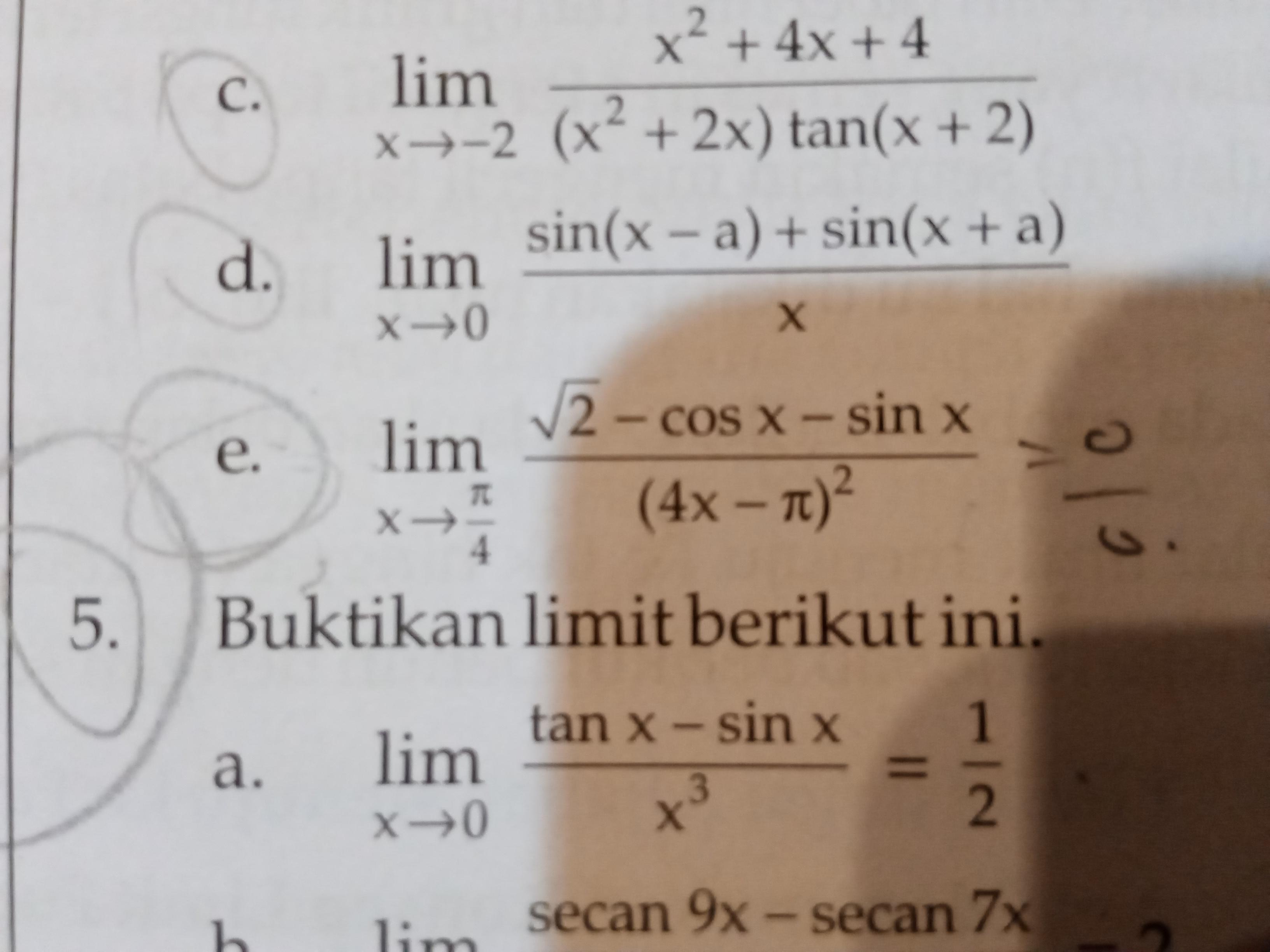 
Доопределим подынтегральную функцию , полагая её равной 1 при . В соответствии с тем, что , доопределённая функция будет непрерывна на всей числовой оси. Среди её первообразных выделим ту, для которой . Эта неэлементарная функция называется интегральным синусом и обозначается . Именно её мы использовали в приведённой выше формуле. Пример Ещё один неберущийся интеграл: 
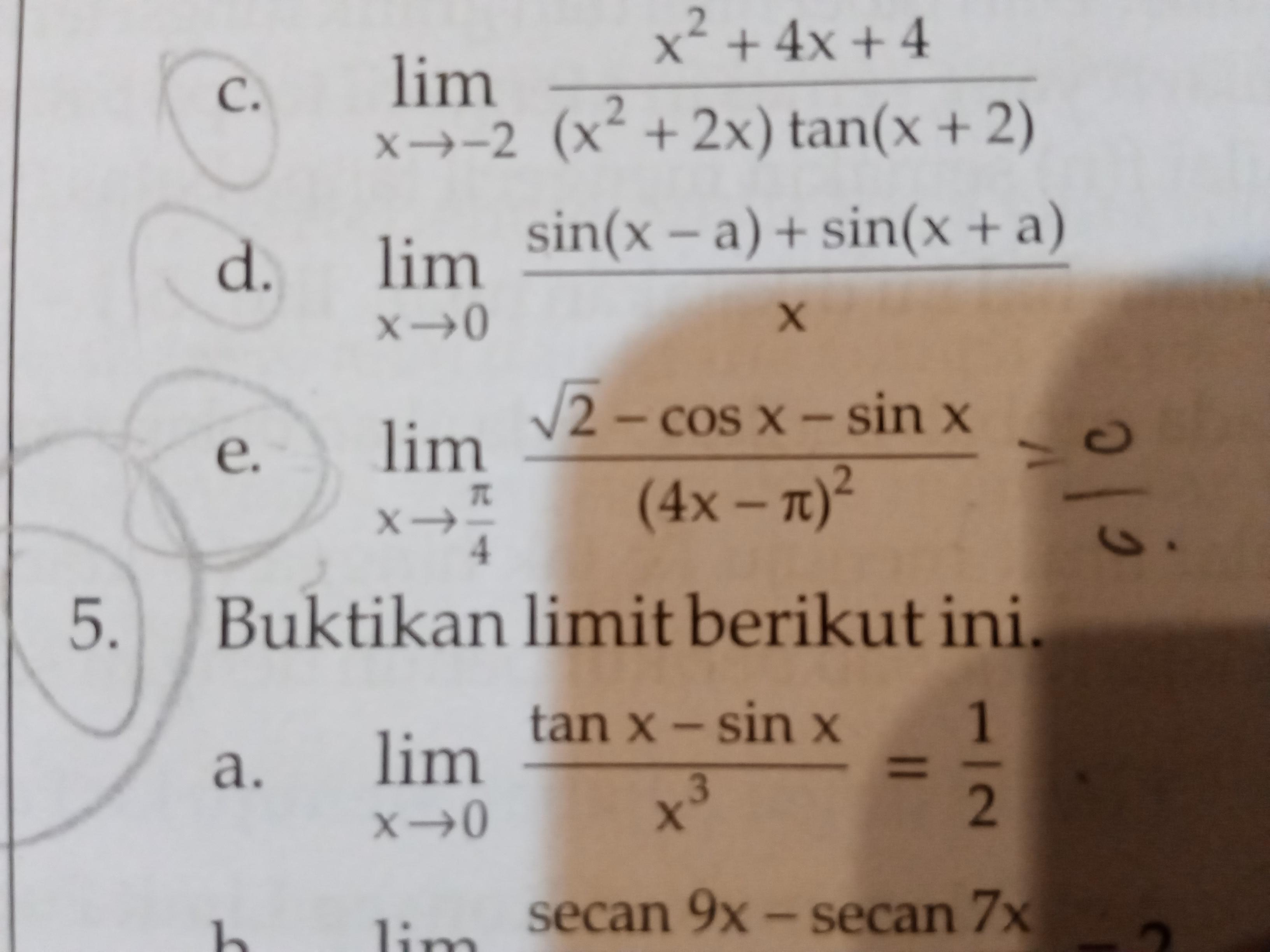Одна из первообразных — та, что мы использовали в правой части и обозначили — называется интегральным косинусом. Пример 
— это тоже неберущийся интеграл. Одна из первообразных, которую мы обозначили , — специальная функция, называющаяся интегральной экспонентой. Пример Не берётся интеграл 
(при одна из первообразных, , называется интегральным логарифмом.
Используя специальные функции, заданные предыдущими примерами, мы с помощью изученных выше правил интегрирования можем выражать через эти функции и другие интегралы. Приведём такой пример.
Пример Выразим через функцию Лапласа следующий интеграл: Для этого сделаем замену переменного :
 |
 |
Заметим, что та первообразная для 
, для которой , обозначается . Функция называется в теории вероятностей и статистике функцией ошибок.
Упражнение 1.3 Выразите функцию ошибок через функцию Лапласа и наоборот, функцию Лапласа через функцию ошибок.
Пример 1.14 К интегралу предыдущего примера можно свести и тем самым выразить через функцию Лапласа, например, такой интеграл:
 |
Для вычисления мы применили формулу интегрирования по частям. Пример Вычислим интеграл от интегральной экспоненты . Заметим, что по определению первообразной. Применяя формулу интегрирования по частям, получаем:
Кроме приведённых выше, в приложениях встречаются и многие другие неберущиеся интегралы, например:
Эти четыре интеграла называются интегралами Френеля.
Упражнение Сделав соответствующую замену переменного, выразите последние два из интегралов Френеля через функции и , которые стоят в правых частях первых двух интегралов Френеля.
Не берутся также интегралы
и многие другие.
Тем не менее, для многих классов интегралов, наиболее часто встречающихся в приложениях, первообразную всё же удаётся выразить через элементарные функции. В следующей главе мы изучим такие классы интегралов.
Упражнение С помощью соответствующих замен переменного, докажите следующие соотношения: (при (при (на самом деле функции и определяются так, что обе постоянные равны 0).
Статистика
- Онлайн всего: 1
- Гостей: 1
- Пользователей:
Радио
Источник: https://ya-economist-11.ucoz.ru/index/neburushhijsja_integral/0-279
29. Понятие о неберущихся интегралов
не
всякая подынтегральная функция имеет
первообразную, которая может быть
выражена в элементарных функциях.
Так,
например, та из первообразных которая
обращается в нуль приx=0, называется
функцией Гаусса и обозначается Ф(x).
Таким образом,,
если .
Эта
функция хорошо изучена. Составлены
подробные таблицы ее значений при
различных значениях. Графически это
можно представить
Здесь одна из первообразных, которую
мы обозначили,
выделяется из всего набора первообразных
условием.
Функцияназывается
функцией Лапласа. Она широко применяется
в теории вероятностей, физике,
математической и прикладной статистике
и других разделах науки и её приложений.
Для вычисления значений функции Лапласа
составлены таблицы, имеющиеся во многих
учебниках, задачниках и справочниках
по теории вероятностей и статистике.
Возможность вычисления предусмотрена
также на многих моделях калькуляторов
(не самых дешёвых) и уж, обязательно, на
тех, что предназначены для статистической
обработки числового материала.
Так что,
с практической точки зрения, пользоваться
функцией Лапласа ничуть не сложнее,
чем, скажем, синусом, арктангенсом или
натуральным логарифмом, которые мы
условно относим к элементарным функциям.
Пример
1.9Не берётся также
интеграл
Доопределим
подынтегральную функцию ,
полагая её равной 1 при.
В соответствии с тем, что
png» width=»63″>,
доопределённая функция будет непрерывна
на всей числовой оси. Среди её первообразныхF(x) выделим
ту, для которой.
Эта неэлементарная функция называется
интегральным синусом и обозначается.
Именно её мы использовали в приведённой
выше формуле.
Пример
1.10Ещё один неберущийся
интеграл:
Пример
1.11—
Пример
1.12Не берётся интеграл(приодна из первообразных,,
называется интегральным логарифмом.
30. Определенный интеграл. Понятия и определения
Вычисление
площади криволинейной трапеции.Пусть
на отрезкезадана непрерывная функция
png» width=»63″>,
принимающая на этом отрезке неотрицательные
значения :при.
Требуется определить площадь
png» width=»18″>трапеции,
ограниченной снизу отрезком,
слева и справа — прямымии
png» width=»40″>,
сверху — функцией.
Для решения этой задачи разделим
произвольным образом основание фигуры точкамина
png» width=»18″>частейсимволомбудем обозначать длину
png» width=»14″>-го
отрезка:.
На каждом из отрезковвыберем произвольную точку
png» width=»20″>,
найдём,
вычислим произведение(это произведение равно площади
прямоугольника
png» width=»23″>с основаниеми высотой)
и просуммируем эти произведения по всем
прямоугольникам. Полученную сумму
обозначим
dHy8/img-ZMilEM.png» width=»39″>:.
равно площади ступенчатой фигуры,
образованной прямоугольниками,;
на левом рисунке эта площадь заштрихована.
не равна искомой площади,
она только даёт некоторое приближение
к.
Для того, чтобы улучшить это приближение,
будем увеличивать количествоотрезков таким образом, чтобы максимальная
длина этих отрезков
png» width=»82″>стремилась к нулю (на рисунке ступенчатые
фигуры изображены при(слева) и при(справа)). При
png» width=»158″>разница междуибудет тоже стремиться к нулю, т.е..
Определение
определённого интеграла. Пусть на
отрезкезадана функция.
Разобьём отрезок
png» width=»46″>произвольным образом наnчастей точками;
длину-го
отрезка обозначим:
png» width=»184″>;
максимальную из длин отрезков обозначим.
На каждом из отрезковвыберем произвольную точкуи составим сумму
dHy8/img-w4Rsgo.png» width=»202″>.
Сумма
называется интегральной суммой. Если
существует (конечный) предел
последовательности интегральных суммпри
png» width=»41″>,
не зависящий ни от способа разбиения
отрезкана части,
ни от выбора точек,
то функция
dHy8/img-ZIwBKC.png» width=»40″>называется интегрируемой по отрезку,
а этот предел называется определённым
интегралом от функциипо отрезку
png» width=»46″>и обозначается.
Функция
,
как и в случае неопределённого интеграла,
называется подынтегральной, числаaиb- соответственно, нижним
и верхним пределами интегрирования.
Кратко определение иногда записывают
так:.
В этом
определении предполагается, что b>a.
Для других случаев примем, тоже по
определению: Еслиb=a,
то;
еслиb
Источник: https://studfile.net/preview/4241718/page:13/
