Центр окружности вписанной в треугольник

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Вписанная окружность

Здесь мы будем говорить об окружностях, связанных с треугольником. Оставим пока в стороне страшное слово «вневписанная» и поговорим об окружности, вписанной в треугольник. Итак, что же это такое?

Окружность называется вписанной в треугольник, если она касается всех (трёх) его сторон.

Для всякого ли треугольника можно подобрать такую окружность? И как найти ее центр?

На эти вопросы отвечает следующая теорема (математически называют очень важные утверждения теоремами)

Во всякий треугольник можно вписать окружность, причём единственным образом. Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

И повторим ещё раз то, что очень нужно запомнить.

Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

• Если тебя заинтересовал вопрос, а почему это все три биссектрисы обязаны пересечься, и какое отношение имеют биссектрисы к тому, что окружность касается сторон треугольника, то добро пожаловать к темам «Биссектриса».
• Но для начала хватит просто запомнить то, что центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
• Теперь немножко о радиусе.

Посмотри, пусть у нас в   вписана окружность с центром  . Тогда отрезки  ,  , и   – радиусы этой окружности.

Поэтому они, конечно же, равны, но ещё – они все перпендикулярны сторонам. Это происходит оттого, что радиус, проведенный в точку касания, перпендикулярен касательной. Итак, запомни и используй:

Радиусы вписанной окружности, проведенные в точки касания, перпендикулярны сторонам треугольника.

Что же ещё? Давай представим, что мы откуда-то узнали все три стороны треугольника.

Можно ли найти как-то отрезочки  ,  ,   и.д. — отрезки, на которые точки касания разбивают стороны треугольника? Представь себе, можно, и даже очень легко. Для этого нужно знать только то, что отрезки касательных, проведённых из одной точки, равны (если ещё не успел это узнать – загляни в тему «Касательные, касающиеся окружности»).

Итак, начнём поиск!

Посмотри внимательно: из точки   проведено две касательных, значит их отрезки   и   равны.

Мы обозначим их « ». Далее, точно так же:   (обозначили).   (обозначили).

Теперь вспомним-ка, что мы знаем длины всех трёх сторон треугольника. Обозначим эти длины « », « », « » — смотри на рисунок. Что же теперь получилось? А вот, например, отрезок « » состоит из двух отрезков « » и « », да и отрезки « » и « » тоже из чего-то состоят. Запишем это всё сразу:

Ух ты! Выход в алгебру! Три уравнения и три неизвестных! Сейчас решим!

1. Сложим первые два уравнения и вычтем третье:
2.  , то есть:
3. А теперь сложим первое и третье уравнение и вычтем второе:
4.  , то есть:
5. И последний шаг: сложим второе и третье, а потом вычтем первое.
6. Ну вот, всё нашли:

Очень много плюсов и минусов – аж в глазах рябит. Как же это запомнить? А оказывается, очень просто. Смотри-ка на картинку и формулу сразу.

Секрет вот в чём: те стороны, на которых есть « » (« » и « ») будут с плюсом, а та сторона, где нет « » (это « »), будет с минусом. Ну, а пополам поделить всё хозяйство. С другими буквами точно так же

На « » и « » есть « » — они с плюсом, на « » нет « » — она с минусом

На « » и « » есть « » — они с плюсом, на « » нет « » — она с минусом.

Вписанная окружность и площадь

• Здесь скажем совсем коротко:
• Есть такая формула:
•  ,
• где   — это полупериметр треугольника, то есть  , а   — радиус вписанной окружности.

Вневписанная окружность

Ну вот, пора приступать к самому непонятному. Что же это за зверь такой: «вневписанная окружность»? Сначала посмотри на картинку:

Видишь, окружность тоже чего-то касается, но «сидит» как-то снаружи, вне треугольника? Вот поэтому и называется вневписанной.

Окружность называется вневписанной для треугольника, если она касается ОДНОЙ стороны треугольника и продолжений двух других сторон.

А как ты думаешь, сколько у одного треугольника может быть вневписанных окружностей? Вот, представь себе, аж три!

Посмотри, вот, так:

Захватывает дух? Насладись впечатлением. Подробное обсуждение этой картинки смотри в следующих уровнях теории. Там ответим на всякие вопросы, типа

1. — A откуда взялся  ?
2. — A что это за точка  ?
3. — И что это вообще за тьма линий на рисунке?
4. А сейчас вернёмся к одной, какой-нибудь, вневписанной окружности и узнаем всего один, но очень важный факт.

•  ,
• или, что то же самое:  , где   — полупериметр.
• Доказывать не будем, но ещё раз посмотри и запомни:

до «дальней» точки касания вневписанной окружности – ровно полупериметр.

Вписанная и вневписанная окружность

Вписанная в треугольник окружность — окружность, которая касается всех (трёх) сторон треугольника.

Теорема: В любой треугольник можно вписать окружность, причём единственным образом.

Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

Радиусы вписанной окружности, проведенные в точки касания, перпендикулярны сторонам треугольника:  ,  ,  .

Отрезки от вершин треугольника до точек касания выражаются по формулам:  .

Площадь треугольника через радиус вписанной окружности:  , где   — полупериметр треугольника, а   — радиус вписанной окружности.

Вневписанная окружность — окружность, которая касается одной стороны треугольника и продолжений двух других сторон.

Центр вневписанной окружности лежит на пересечении биссектрисы внутреннего угла треугольника ( ) и биссектрис двух внешних углов (  и  ).

Площадь треугольника через радиус вневписанной окружности:  , где   — полупериметр треугольника, а   — радиус вневписанной окружности.

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

1. Стать учеником YouClever,
2. Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц», 
3. А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.

можно кликнув по этой ссылке.

 

Источник: https://youclever.org/book/vpisannaya-i-vnevpisannaya-okruzhnost-1

Свойства вписанной в треугольник окружности

В этой статье Вы сможете найти свойства вписанной в треугольник окружности, а также их доказательства.

Вписанная в треугольник окружность — это такая окружность, которая находится внутри треугольника и при этом касается всех его сторон (то есть все стороны треугольника являются касательными к окружности). Стоит отметить, что в этом случае сам треугольник является описанным вокруг данной окружности.

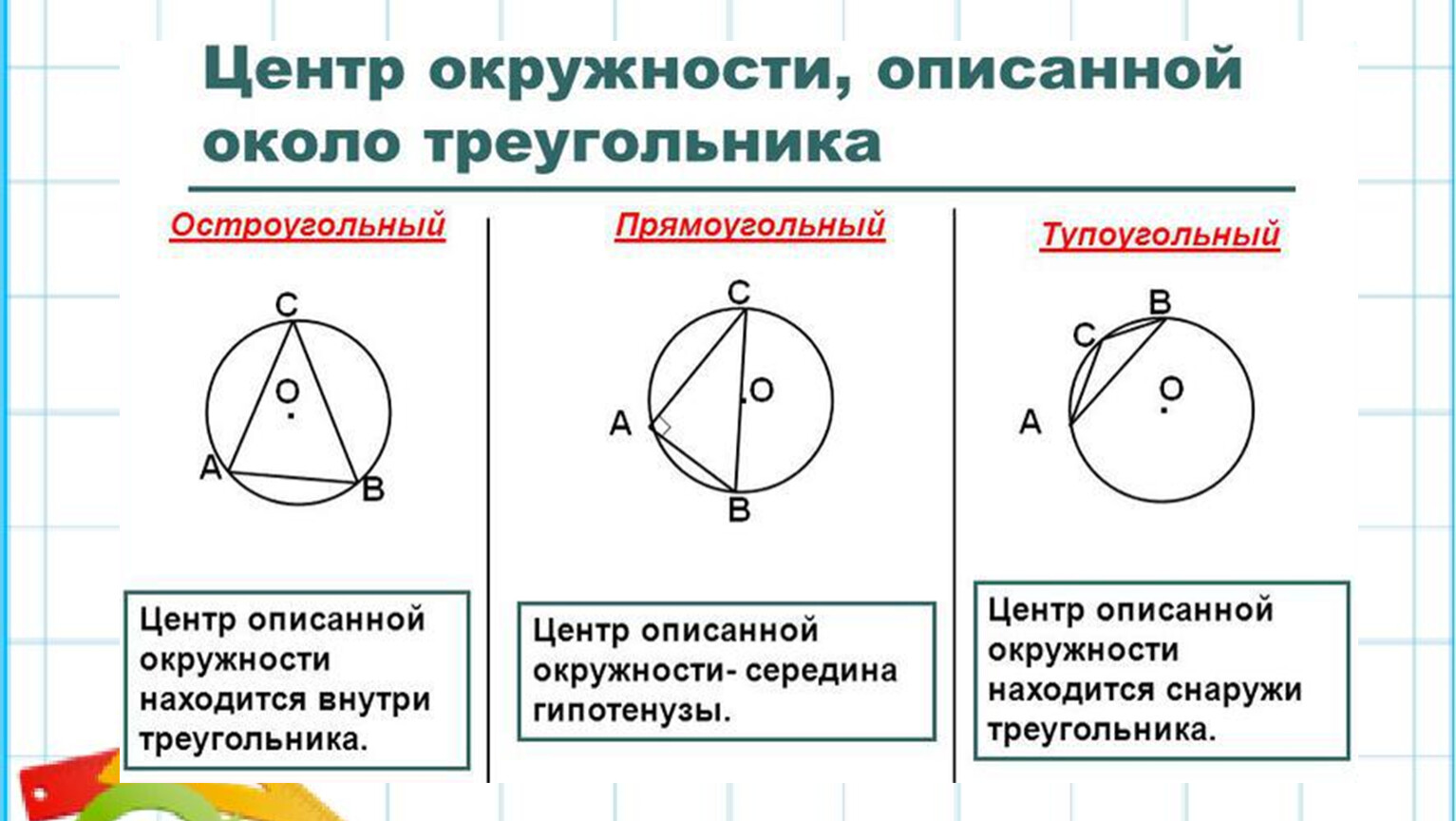
Рисунок 1

1. Центр вписанной в треугольник окружности (на рис. 1 – точка О) лежит на пересечении биссектрис треугольника (на рис.1 – АО, ВО и СО).
2. В любой треугольник вписывается окружность и притом только одна.
3. Радиус вписанной в треугольник окружности равен: Где S – это площадь треугольника, p — полупериметр треугольника, a, b, c — стороны треугольника.

Доказательства свойств

Первое свойство

Доказать, что центр вписанной в треугольник окружности находится на пересечении биссектрис.

Доказательство.

1. Опустим из центра окружности перпендикуляры (OL, OK и OM) к каждой из сторон треугольника ABC (рис. 2). Также из каждого угла проведем прямую к центру окружности (OA, OC и OB).

   Рисунок 2

2. Рассмотрим 2 треугольника AOM и AOK. Они являются прямоугольными, т.к. OM и OK – перпендикуляры к сторонам AC и AB. Гипотенуза OA является общей для обоих треугольников.
3. Поскольку касательная к окружности перпендикулярна радиусу, проведенному в точку касания (свойство касательной к окружности), то катеты OМ и OК являются радиусами окружности и, следовательно, равны.
4. Из вышесказанного следует, что прямоугольные треугольники AOМ и AOК равны по гипотенузе и катету. Т.к. треугольники равны, то углы OAМ и OAК тоже равны, отсюда следует, что OA – биссектриса угла BAC.
5. Аналогичным образом доказывается, что OC – биссектриса угла ACB, а OB – биссектриса угла ABC.
6. То есть биссектрисы треугольника пересекаются в одной точке и этой точкой является центр вписанной окружности.

Что и требовалось доказать.

Второе свойство

Доказать, что в любой треугольник можно вписать окружность и притом только одну.

Доказательство

1. В треугольник можно вписать окружность только в том случае, если найдется точка равноудаленная от его сторон.
2. Проведем 2 биссектрисы OA и OC. Опустим из точки их пресечения перпендикуляры (OK, OL и OM) ко всем трем сторонам треугольника ABC (рис. 3).

   Рисунок 3

3. Рассмотрим треугольники AOK и AOM.
4. У них общая гипотенуза AO. Углы OAK и OAM равны (т.к. OA – биссектриса угла KAM). Углы OKA и OMA прямые (т.е. тоже равны), т.к. OK и OM – перпендикуляры к сторонам AB и AC соответственно.
5. Поскольку 2 пары углов равны, то и 3-я пара (AOM и AOK) также является равной.
6. Из вышенаписанного следует, что треугольники AOK и AOM равны по стороне (AO) и 2-м прилежащим к ней углам (рис. 4).

   Рисунок 4

7. Отсюда следует, что стороны OM и OK равны, т.е. равноудалены от сторон треугольника AC и AB соответственно.
8. Аналогичным образом доказывается, что OM и OL равны, т.е. они равноудалены от сторон треугольника AC и BC соответственно.
9. Из вышенаписанного следует, что точка O равноудалена от сторон треугольника, т.е. является центром вписанной окружности.
10. Аналогичным образом можно найти точку внутри любого треугольника, которая будет равноудалена от его сторон, то есть будет центром вписанной в этот треугольник окружности.
11. Из вышенаписанного следует, что в любой треугольник можно вписать окружность.
12. Следует отметить, что центр данной окружности лежит на пересечении биссектрис треугольника.
13. Допустим, что в треугольник можно вписать две (или более) окружности.
14. Проведя 3 отрезка из вершин треугольника к центру этой окружности и, опустив перпендикуляры из этого центра к каждой из сторон треугольника, мы сможем доказать, что эта окружность лежит на пересечении биссектрис треугольника (см. доказательство первого свойства).
15. То есть центр этой окружности совпадает с центром первой окружности, уже вписанной в треугольник, а ее радиус равен перпендикуляру, опущенному на сторону треугольника (как и в первом случае). Это говорит о том, что данные окружности совпадают.
16. Аналогичным образом можно доказать, что любая новая вписанная окружность совпадает с первой, которую мы впишем.
17. То есть вписать в треугольник можно только одну окружность.

Что и требовалось доказать.

Третье свойство

Доказать, что радиус вписанной окружности r равен отношению площади треугольника S к полупериметру p.

А также равенство:

Доказательство.

Рисунок 5

1. Рассмотрим произвольный треугольник ABC со сторонами a, b и c (рис 5). Полупериметр данного треугольника p рассчитывается по формуле:
2. Центр нашей окружности (точка O на рис. 5) находиться на пересечении биссектрис треугольника. Отрезки OA, OB и OC, соединяющие O с вершинами треугольника АВС, делят треугольник на три: AOC, COB, BOA. Площадь треугольника ABC можно найти как сумму площадей этих трех треугольников.
3. Поскольку площадь любого треугольника равна половине произведения его основания на высоту, а высота треугольников AOC, COB, BOA равна радиусу окружности r, то площади треугольников AOC, COB и BOA можно найти как:
4. Выразим площадь S треугольника ABC через сумму площадей этих трех треугольников:
5. Заметив, что второй множитель – это полупериметр треугольника ABC, можно представить наше равенство в виде: Или
6. Итак, мы доказали, что радиус вписанной окружности равен отношению площади треугольника к полупериметру.
7. Вспомним формулу Герона, которая в нашем случае будет иметь вид:
8. Теперь радиус можно выразить как:

Что и требовалось доказать.

Источник: https://people-ask.ru/nauki/geometriya/svojstva-vpisannoj-v-treugolnik-okruzhnosti

5.1.5 Окружность, вписанная в треугольник, и окружность, описанная около треугольника

• Видеоурок 1: Вписанная окружность
• Видеоурок 2: Окружность, описанная около треугольника
• Лекция: Окружность, вписанная в треугольник, и окружность, описанная около треугольника
• Около некоторых треугольников можно описать окружность, а в некоторые можно окружность вписать.
• Вписанный треугольник

Если все вершины некоторого треугольника лежат на окружности, то такой треугольник называется вписанным.

Обратите внимание, если некоторый треугольник вписан в окружность, то все прямые, которые соединяют центр окружности с вершинами треугольника, равны. Более того, они имеют величину радиуса.

Существуют несложные формулы, позволяющие определить стороны треугольника по известному радиусу окружности, или же наоборот определить радиус по сторонам:

Если в окружность вписан правильный треугольник, то формулы упрощаются. Хотелось бы напомнить, что правильным называется тот треугольник, у которого все стороны равны:

Формула для нахождения площади правильного треугольника, если он вписан в окружность:

Если некоторый треугольник располагается внутри окружности, то существует правило размещения центра окружности.

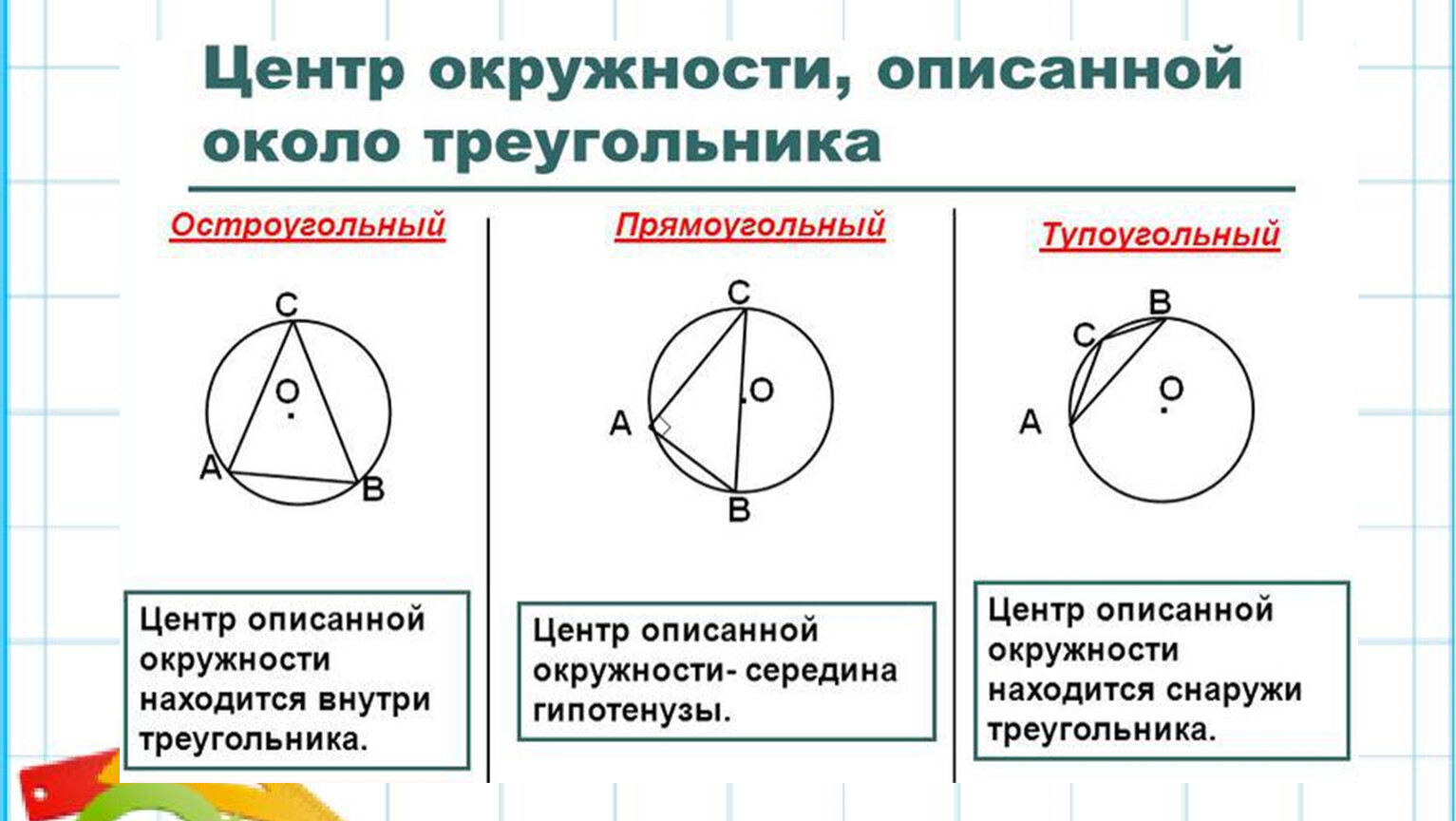
Если в окружность вписали любой остроугольный треугольник, то центр этой окружности будет находится внутри треугольника:

Если в окружность вписан правильный треугольник, то центр окружности будет считаться центром треугольником, а также точкой пересечения его высот.

Если в окружность вписанный прямоугольный треугольник, то центр окружности будет лежать на середине гипотенузы:

Если в окружность вписан тупоугольный треугольник, то центр окружности будет находится за пределами треугольника:

1. Вписанная окружность
2. Окружность можно назвать вписанной в том случае, если она касается всех сторон треугольника в одной точке.
3. Для треугольника, в который вписана окружность, существует некоторое правило:

Своими точками касания окружность отсекает три пары равных отрезков: КВ = BL, AK = AM, MC = CL.

Определить связь радиусов окружностей и длин сторон можно с помощью следующих формул:

Если окружность вписана в правильный треугольник, то формула упрощается:

Предыдущий урок

Следующий урок

Источник: https://cknow.ru/knowbase/713-515-okruzhnost-vpisannaya-v-treugolnik-i-okruzhnost-opisannaya-okolo-treugolnika.html

Вписанная окружность

Геометрия

Вписанная в выпуклый многоугольник окружность-это окружность, которая касается всех сторон данного многоугольника, а центр данной окружности находится внутри данной фигуры. Общие свойства всех фигур,  описанных около окружности:

Центр вписанной окружности находится на точке пересечения биссектрис.

   ∠EBO=∠MBO; ∠EAO=∠OAK; ∠KCO=∠OCM;

Вершина равноудалена от точек касания, находящихся на сторонах, содержащих данную вершину.

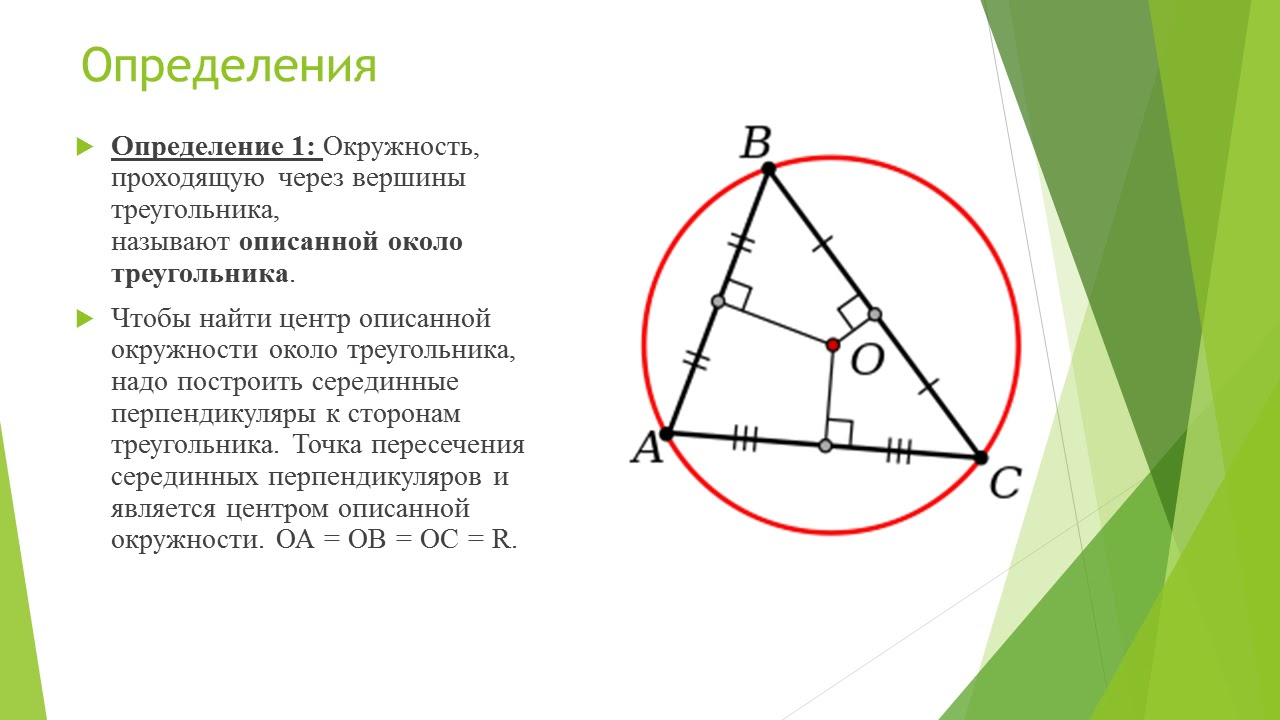  BE=BM; AE=AK; CK=CM;

Радиус, выпущенный в точку касания, перпендикулярен касательной

.  EO⊥AB; OM⊥AC; OK⊥BC;

Свойства четырехугольника, описанного около окружности:

Суммы длин противоположных  сторон четырехугольника, описанного около окружности,  равны.

• AB+CD=AD+BC;
• Формулы для нахождения радиуса:
• Общая формула для нахождения радиуса окружности, вписанной в правильный многоугольник: 

,где a-сторона многоугольника,  N-количество сторон многоугольника.

Формула для нахождения радиуса окружности, вписанной в произвольный треугольник:

1. , где S-площадь треугольника, а p-полупериметр треугольника.
2. Вывод формулы:
3. Дано:
4. EO=MO=KO=r;
5. Доказать:

• Доказательство:
• S∆ABC=S∆AOB+S∆AOC+S∆BOC;
• S∆ABC=1/2 AB×OE+1/2 AC×OM+1/2 BC×OK;
• S∆ABC=1/2 r(AB+AC+BC);

1. Формула для нахождения радиуса окружности, вписанной в произвольный треугольник:
2. , где p-полупериметр треугольника, а a,b,c-стороны треугольника.
3. Вывод формулы:
4. Используя формулу Герона и формулу r=S/P, имеем:
5. Формула, для нахождения радиуса окружности, вписанной в равнобедренный треугольник:
6. , где r-радиус вписанной окружности, a- боковая сторона треугольника, b-основание треугольника.
7. Вывод формулы:
8. Зная, что   и что в равнобедренном треугольнике b=c и 
9. , имеем:
10. Формула для нахождения радиуса окружности, вписанной в равносторонний треугольник: 
11. ,где -радиус вписанной окружности, a-сторона треугольника.
12. Вывод формулы:
13. Зная, что   и что в равностороннем треугольнике a=b=c и 
14. p=(a+b+c)/2, имеем:
15. Формула, для нахождения радиуса окружности, вписанной в прямоугольный треугольник:
16. ,где r-радиус вписанной окружности, a и b- катеты, с- гипотенуза.
17. Вывод формулы:
18. Дано:
19. ABC- прямоугольный треугольник;
20. OE=OK=OM=r;
21. Доказательство:
22. OM⊥AC,по свойству радиуса, выпущенного в точку касания ,=>∠OMC-прямой.
23. OK⊥BC,по свойству радиуса, выпущенного в точку касания,=> ∠OKC-прямой.
24. OK=OM
25. Принимая во внимание 3 предыдущих утверждения, можем сказать, что OMCK-квадрат.
26. AM=AC-r;
27. AM=AE, по свойству касательных, выпущенных из одной точки к окружности.
28. AE=AC-r;
29. BK=BC-r;
30. BK=BE, по свойству касательных, выпущенных из одной точки к окружности.
31. BE=BC-r;                                                                                                                                              
32. AB=AE+BE;
33. AB=AC-r+ BC-r;
34. AB=AC+BC-2r;
35. ,где AC и BC –катеты,а AB-гипотенуза.
36. Формула для нахождения радиуса окружности,  вписанной в квадрат:
37. ,где r-радиус вписанной окружности, a-сторона квадрата.
38. Вывод формулы:
39. ДАНО:
40. ABCD- квадрат;
41. OK=OE=OM=ON=r;
42. Доказательство:
43. OK⊥BC,по свойству радиуса, выпущенного в точку касания, и OK=OE=>OEBK- квадрат.
44. BK=OK=KC=r;
45. BC=BK+KC;
46. BC=2r; 
47. ,где BC- сторона квадрата.
48. Формула для нахождения радиуса окружности, вписанной в равнобедренную трапецию:
49. , где r-радиус вписанной окружности,a и b- основания трапеции. 
50. Вывод формулы:
51. Дано:
52. ABCD- трапеция;
53. EK-средняя линия;
54. YX=2r;
55. Доказательство:
56.  ∆ABM-прямоугольный.
57. AD=AM+MN+ND;
58. AM=ND;
59. MN=BC;
60. AD=2AM+BC;
61. AM=(AD-BC)/2;
62. AB=EK,по свойству средней линии трапеции;
63. EK=(AD+BC)/2;
64. AB=(AD+BC)/2;
65. Формула для нахождения радиуса окружности, вписанной в правильный шестиугольник:
66. , где r-радиус вписанной окружности,a-сторона шестиугольника.
67. Вывод формулы:
68. Для доказательства будем использовать формулу:
69. Автор статьи: Исмаилов Илькин Илхамович
70. Редактор: Гаврилина Анна Викторовна

Источник: http://www.teslalab.ru/articles/geometry/61/

Центр вписанной в треугольник окружности

Где лежит центр вписанной в треугольник окружности? Что можно сказать о центре окружности, вписанной в многоугольник?

Теорема.

Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника.

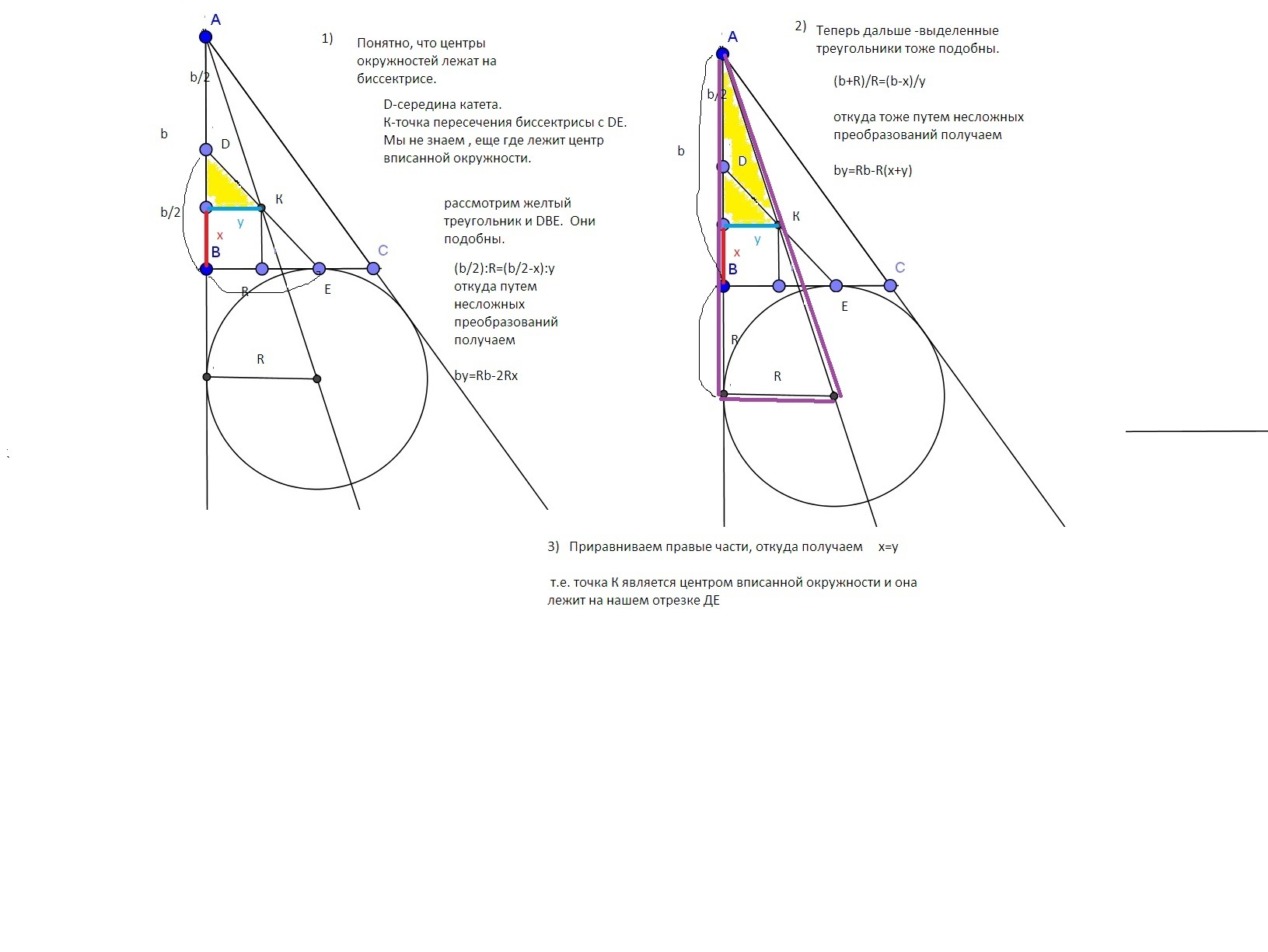
O — точка пересечения биссектрис треугольника ABC.

Дано: ∆ ABC,

окр. (O; r) — вписанная.

• Доказать:
• O — точка пересечения биссектрис ∆ ABC.
• Доказательство:

Обозначим точки касания вписанной в треугольник окружности со сторонами AC, BC и AB соответственно M, K. F.

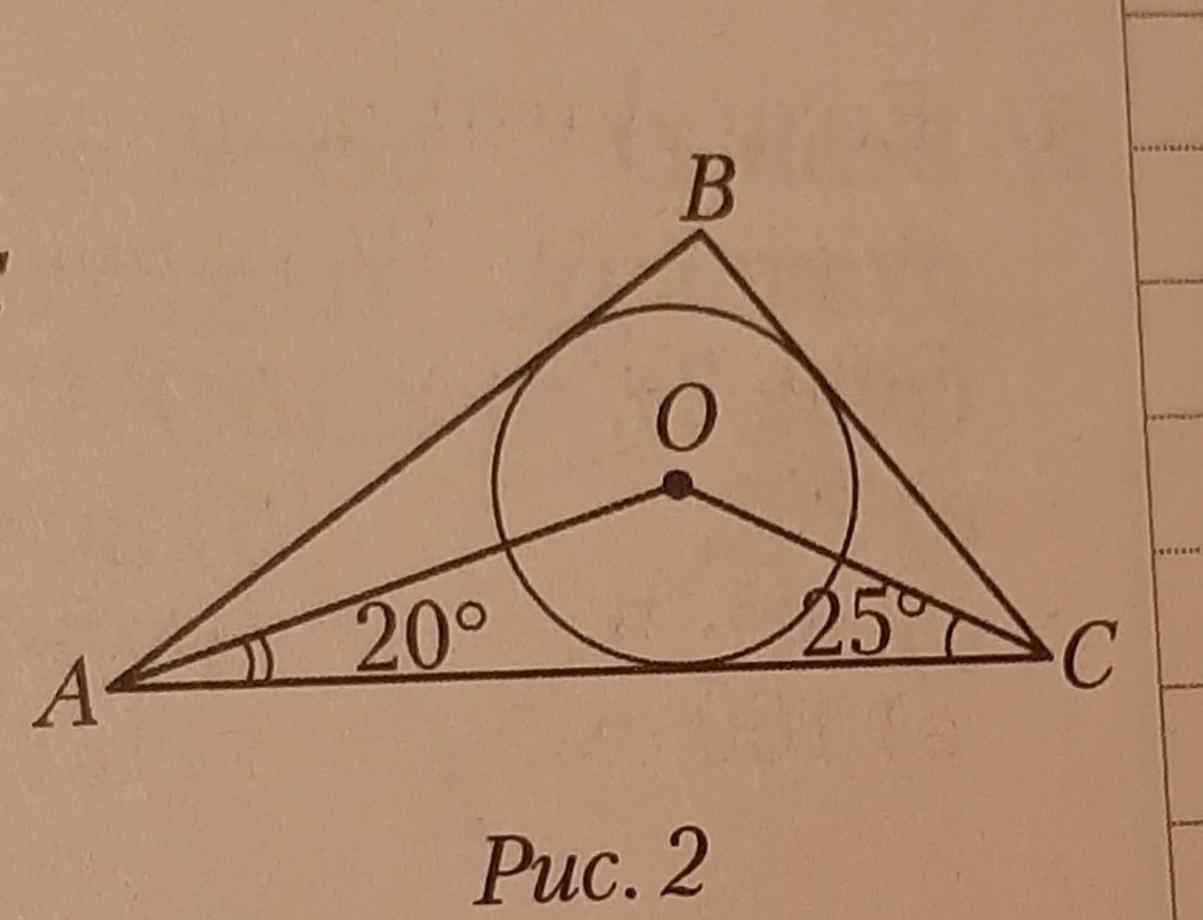
(как радиусы, проведенные в точки касания). Следовательно, треугольники AOF и AOM — прямоугольные.

1. У них общая гипотенуза AO, катеты OF=OM (как радиусы).
2. Следовательно, треугольники AOF и AOM равны (по катету и гипотенузе).
3. Из равенства треугольников следует равенство соответствующих углов: ∠OAF=∠OAM.
4. Значит, точка O лежит на биссектрисе треугольника, проведенной из вершины A.
5. Аналогично из равенства треугольников BOF и BOK, COM и COK доказывается, что точка O лежит на биссектрисах треугольника ABC, проведенных из вершин B и C.
6. Следовательно, центр вписанной в треугольник окружности лежит в точке пересечении биссектрис этого треугольника.
7. Что и требовалось доказать.
8. Замечание.
9. Доказательство теоремы можно основать непосредственно на свойстве биссектрисы угла.
10. 1) OM=OF=OK (как радиусы),
11. 2) OM⊥AC, OM⊥AB, OK⊥BC (как радиусы, проведённые в точку касания).
12. Значит точка O равноудалена от сторон углов BAC, ABC и ACB.
13. Так как любая точка, лежащая внутри неразвёрнутого угла и равноудалённая от сторон этого угла, лежит на его биссектрисе, то AO, BO и CO — биссектрисы треугольника ABC, O — точка их пересечения.
14. Аналогично, центр вписанной в многоугольник окружности (если в него можно вписать окружность) лежит в точке пересечения биссектрис этого многоугольника.

Источник: http://www.treugolniki.ru/centr-vpisannoj-v-treugolnik-okruzhnosti/

Расчет центра вписанной окружности в треугольник

В каждый треугольник можно вписать окружность, притом только одну.
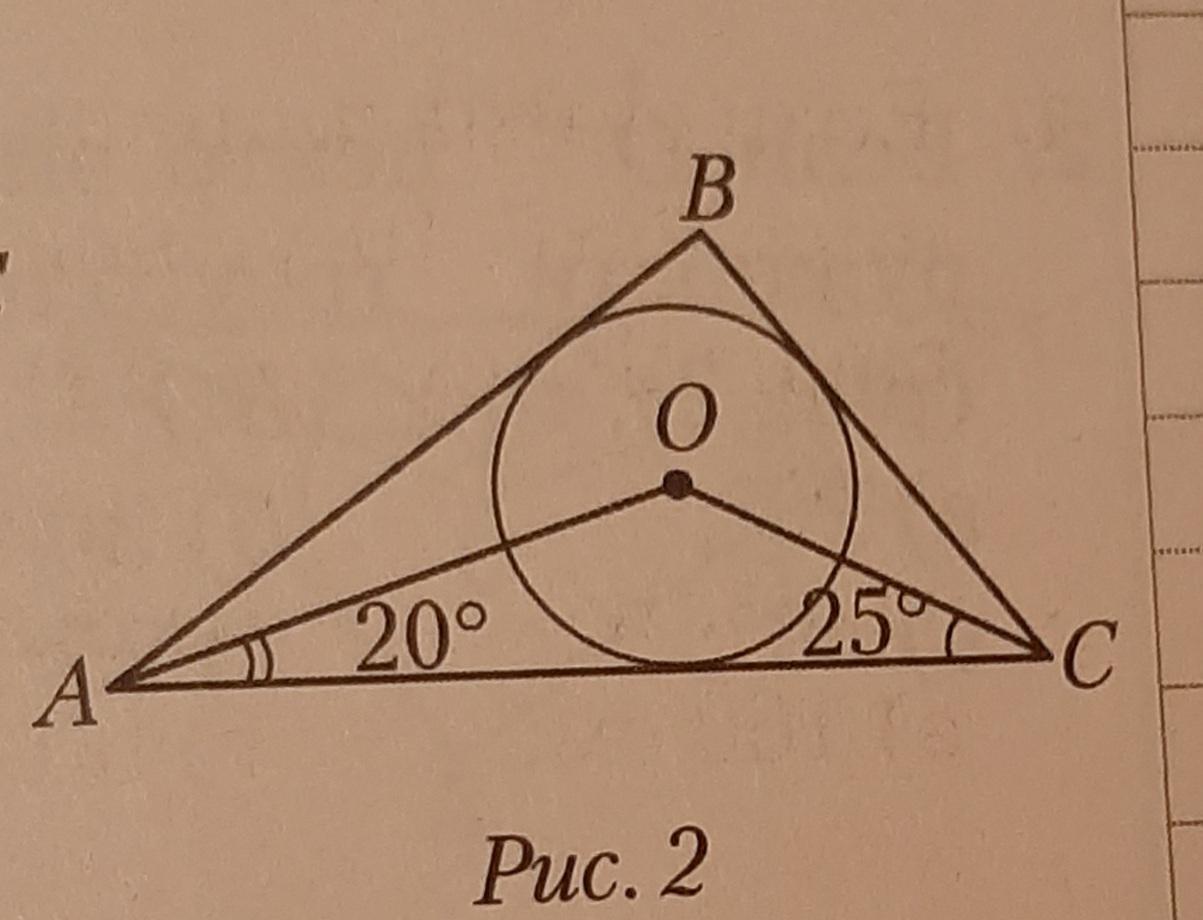
Центр вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.

В приведенном ниже примере, O является центров окружности.

Метод расчета центра окружности вписанного в треугольник

Даны точки вершин треугольника A(5,7), B(6,6) и C(2,-2). Итак, нам известны координаты точек вершин треугольника x1,y1, x2,y2 и x3,y3.
Для нахождения точки центра вписанной окружности необходимо найти уравнение биссектрисы.

Шаг 1 :

Давайте рассчитаем средние точки всех сторон треугольника AB, BC и CA заданных координатами x и y

• Средняя точка стороны = x1+x2/2, y1+y2/2
• Средняя точка AB = 5+6/2, 7+6/2 = (11/2, 13/2)
• Средняя точка BC = 6+2/2, 6-2/2 = (4, 2)
• Средняя точка CA = 2+5/2, -2+7/2 = (7/2, 5/2)

Шаг 2 :

Далее, найдем углы сторон AB, BC и CA используя формулу y2-y1/x2-x1. Пожалуйста, обратите внимание, что угол обозначается буквой ‘m’.

• Угол AB (m) = 6-7/6-5 = -1.
• Угол BC (m) = -2-6/2-6 = 2.
• Угол CA (m) = 7+2/5-2 = 3.

Шаг 3 :

Теперь, давайте вычислить угол биссектрисы сторон AB, BC и CA.

• Угол биссектрисы = -1/угол линии (стороны).
• Угол биссектрисы стороны AB = -1/-1 = 1
• Угол биссектрисы стороны BC = -1/2
• Угол биссектрисы стороны CA = -1/3

Шаг 4 :

После того, как мы находим угол перпендикулярных линий, мы должны найти уравнение перпендикуляра, биссектрис с углом и серединой. Уравнение перпендикуляра АВ с серединами (11/2, 13/2) и углом 1.

• Уравнение центра окружности y-y1 = m(x-x1)
• y-13/2 = 1(x-11/2)
• Упростив, мы получим уравнение -x + y = 1
• Кроме того, мы должны найти уравнение перпендикуляра, биссектрис линий BE и CF.
• Для BC с средней точкой (4,2) и углом -1/2 y-2 = -1/2(x-4)
• Упростив, мы получим уравнение x + 2y = 8
• Для CA с средней точкой (7/2,5/2) и углом -1/3 y-5/2 = -1/3(x-7/2)
• Упростив, мы получим уравнение x + 3y = 11

Шаг 5 :

Найдем значения x и y решив любые 2 из указанных 3 уравнений.

В этом примере, значение x и y равны (2,3) которые являются координатами центра (o) вписанной окружности в треугольник.

Источник: https://wpcalc.com/okruzhnost-v-treugolnike/