Формулы интерференции

1.1. Интерференция от двух источников

1.2. Определим положение m-ого интерференционного максимума. Определим ширину интерференционного максимума

1.3. Интерференция на тонкой плёнке

1.4. Интерференция на клине (полосы равной толщины)

1.5. Кольца Ньютона

• Интерференцией волн называется явление усиления колебаний в одних и ослабление колебаний в других точках пространства в результате наложения двух или нескольких волн, приходящих в эти точки пространства.
• Для наблюдения устойчивой во времени интерференционной картины необходимы условия, при которых частоты, поляризация и разность фаз интерферирующих волн, были бы постоянными в течение всего времени наблюдения.
• Интерферируют когерентные, монохроматические волны.
• Когерентные волны — волны одинаковой частоты, колебания в которых отличаются постоянной разностью фаз, не изменяющейся со временем.

1.1. Интерференция от двух источников

Свет от одного источника с помощью непрозрачного экрана с двумя отверстиями даёт возможность получить два когерентных источника волн (схема Юнга). Расстояние между источниками (В, С) равно l. Длина волны, излучаемая источниками λ, расстояние до экрана, где наблюдается интерференция. О – центр экрана.

Пусть в точке М – экрана происходит наложение когерентных волн. Получим условие усиления и ослабления волнами друг друга. Расстояние от В источника до точки М – d1, от С до точки М – d2. Колебания точки М, вызываемые первым.

источником волн: , а колебания, вызываемые 2-ым источником: , где А – амплитуда колебаний источников, ω – частота колебаний, k=2π/λ – βолновое число.

Результирующее колебание точки М:

1. Амплитуда колебаний точки М:
2. AM=2Acos(k(d2-d1)/2) зависит от положения точки на экране и может быть равной 2А, если волны усиливают друг друга или нулю, если волны ослабляют друг друга.
3. Получим условие усиления или максимум интерференции. Чтобы АМ=2А, необходимо чтобы
4. |cos(k(d2-d1)/2)|=1
5. Это выполняется, если
6. ; .
7. Значит d2-d1=±mλ.
8. Пусть d2-d1=Δd – разность хода интерферирующих лучей, а ΔФ=2π(d2-d1)/λ=2πΔd/λ – разность фаз интерферирующих волн, тогда
9. ΔΤ=2π/λ (d2-d1) =2π/λ Δd – ρоотношение между разность фаз и разность хода волн.

Если d2-d1=Δd=± mλ, γде m=0,1…, то АМ=2А и, следовательно, в этих точках пространства (экрана) наблюдается максимум интерференции. Разность фаз волн при этом будет равна ΔФ=±2πmλ/λ=±2πm.

• Условие ослабления или минимум интерференции
• Ам=0,
• |cos(k(d2-d1)/2)|=0.
• Это выполняется, если (k(d2-d1)/2)=±(2m+1)λ/2; следовательно
• Δd=±(2m+1)λ/2.
• Волны ослабляют друг друга, если разность хода при этом
• ΔΤ=±2πmλ /(2λ)(2m+1)=±(2m+1)π,

m – называется порядком интерференционного максимума или минимума. В центре экрана наблюдается максимум нулевого порядка: d2-d1=Δd=0.

1.2. Определим положение m-ого интерференционного максимума. Определим ширину интерференционного максимума

Рисунок 1. В точке М наблюдается максимум m-ого порядка. Обозначим расстояние от центра экрана до точки М – ym. Воспользуемся геометрией рисунка 1. Отрезок CD=d2-d1. Треугольники BCD и AMO – подобны. Из подобия

Чтобы в точке наблюдался максимум m-ого порядка Δd=d2-d1=±mλ.

Ширина интерференционного максимума – расстояние между двумя соседними максимумами или минимумами.

Если положение m-ого максимума ym=mLλ/l, то положение (m+1)-го максимума ym+1=(m+1)Lλ/l. Тогда Δy= ym+1-ym=Lλ/l, γде Δy – ширина интерференционного максимума.

1.3. Интерференция на тонкой плёнке

На тонкую плёнку толщиной d и показателем преломления n падает монохроматический свет с длиной волны λ. Угол падения α. Среда около плёнки – воздух. Определим условие наблюдения максимума и минимума интерференции на тонкой плёнке.

Интерферирующие лучи показаны на рисунке 2. Часть первого луча проходит через плёнку, преломляясь на границе раздела, отражается от нижней границы плёнки и выходит в точке С. Часть второго луча отражается от верхней поверхности плёнки и в точке С интерферирует с лучом 1.

Обозначим Δ – оптическую разность хода волны.

1. Оптическая разность хода волн 1 и 2:
2. Δ=n(AB+BC)-(DC+λ/2),
3. где n(AB+BC) – путь (оптический) первой волны,

(DC+λ/2) – путь второй волны. При отражении волны от поверхности плёнки, фаза волны меняется на π, т.к. отражение происходит от более плотной среды (nb=1);

• n>nb.
• Изменение фазы на π соответствует дополнительному ходу, равному λ/2.
• Используя геометрию рисунка и законы преломления света, получим, что оптическая разность хода интерферирующихся волн равна:
• или ,

где β – угол преломления. Запишем условие усиления волнами друг друга или максимума интерференции: Δ=+- mλ. Значит:

1. ,
2. .
3. Толщина плёнки, при которой интерферирующие волны будут усиливать друг друга:
4. ,
5. m – порядок интерференции (m=0,1,2…).
6. Если m=0, то
7. – это минимальная толщина плёнки, при которой плёнка будет окрашена цветом соответствующим данной длине волн λ. Условие ослабления при интерференции или минимум интерференции:
8. Δ=(2m+1)λ/2.
9. .
10. .

Толщина плёнки, при которой плёнка будет казаться тёмной, т.к. наблюдается ослабление волнами друг друга, равна:

, m=0,1,2…

1.4. Интерференция на клине (полосы равной толщины)

Две поверхности, расположение под малым углом α, образуют систему получившую название клин.

Клин имеет разную толщину, а поэтому при освещении поверхности клина монохроматическим светом на поверхности клина будут наблюдаться интерференционные максимумы и минимумы (смотри интерференцию на плёнке), т.к.

в одних точках поверхности толщина клина соответствует условию наблюдению максимума, а в других – условию минимума.

Пусть в точке А поверхности клина возникает максимум m-ого порядка. Толщина клина — dm+1. В точке В возникает максимум (m+1)-го порядка. Толщина плёнки в этом месте — dm+1. Условие наблюдения максимума при толщине dm и dm+1:

• 2dmn=(2m+1)λ/2; 2dm+1n=(2m+3) λ/2.
• Вычтем из второго уравнения первое:
• .

dm+1-dm – разность толщины клина в местах наблюдения m-ого и (m+1)-го максимумов. На рисунке 3. Из прямоугольника:

1. AB=Δy=BD/sinα,
2. Δy – ширина интерференционной полосы
3. .
4. Если угол при вершине мал, то ,
5. , α[рад].
6. Ширина интерференционного минимума или расстояния между соседними минимумами равна ширине интерференционного максимума.

1.5. Кольца Ньютона

Частым случаем полос равной толщины являются кольца Ньютона, которые наблюдаются в схеме, изображённой на рисунке 4.

Плосковыпуклая линза с большим радиусом кривизны R выпуклой поверхностью лежит на плоской пластине и соприкасается с ней в точке О.

Параллельный пучок света падает нормально на плоскую поверхность промежутка между линзой и пластиной. При наложении отраженных волн возникают интерференционные полосы равной толщины, имеющие вид колец.

Вид этих колец в случае монохроматического света показан на рисунке 5.

В центре наблюдается минимум нулевого порядка (тёмное пятно). Центральный минимум окружён системой чередующихся окрашенных и тёмных колец, ширина и интенсивность которых постоянно убывает по мере удаления от центрального пятна.

• Расчёт радиусом окрашенных и тёмных колец.
• На рисунке 6 изображены интерферирующие волны, распространяются вдоль лучей 1 и 2.
• Разность хода волн равна:
• ,
• где d – толщина зазора между линзой и пластиной, где наблюдается интерференция, n – показатель преломления прослойки, λ/2 – потеря полволны при отражении 1-ой волны от стеклянной пластинки (при условии n

Источник: https://siblec.ru/estestvennye-nauki/optika/1-interferentsiya-svetovykh-voln

Интерференция света

Интерференция света
Явление интерференции свидетельствует о том, что свет — это волна. Интерференцией световых волн называется сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.
Условия интерференции Волны должны быть когерентны. Когерентность – согласованность. В простейшем случае когерентными являются волны одинаковой длины, между которыми существует постоянная разность фаз.
Все источники света, кроме лазера, некогерентны, однако Т. Юнг впервые пронаблюдал (1802) явление интерференции, разделив волну на две с помощью двойной щели. Свет от точечного монохроматического источника S падал на два небольших отвер­стия на экране. Эти отверстия действуют как два когерентных источника света S1 и S2.  Волны от них интерферируют в области перекрытия, проходя разные пути: ℓ1 и ℓ2.  На экране наблюдается чередование светлых и темных полос.
Условие максимума. Пусть разность хода между двумя точками , тогда условие максимума:   т. е. на разности хода волн укладывается четное число полуволн (k= 1, 2, 3, …).	или
Условие минимума Пусть разность хода между двумя точками , тогда условие минимума: , т. е. на разности хода волн укладывается нечетное число полуволн (k= 1, 2, 3, …).
Интерференция света в тонких пленках Тогда условие максимального усиле­ния интерферирующих лучей в отраженном свете следую­щее: . Если потерю полуволны не учитывать, то   .
Кольца Ньютона Интерференционная карти­на в тонкой прослойке воздуха между стеклянными пластина­ми — кольца Ньютона. Волна 1 — результат отра­жения ее от точки А (граница стекло —воздух). Волна 2 — отражение от плоской пласти­ны (точка В, граница воздух — стекло). Волны когерентны: возникает интерференционная картина в прослойке  воздуха между точками А и В в виде-концентрических колец. Зная радиусы колец, можно вычислить длину волны, используя формулу , где r — радиус кольца, R — радиус кри­визны выпуклой поверхности линзы.
Использование интерференции в технике
Проверка качества обра­ботки поверхности до одной де­сятой длины волны. Несовершенство обра­ботки определяют но искрив­лению интерференционных по­лос, образующихся при отра­жении света от проверяемой поверхности. Интерферометры служат для точного измерения показателя преломления газов и других веществ, длин световых волн.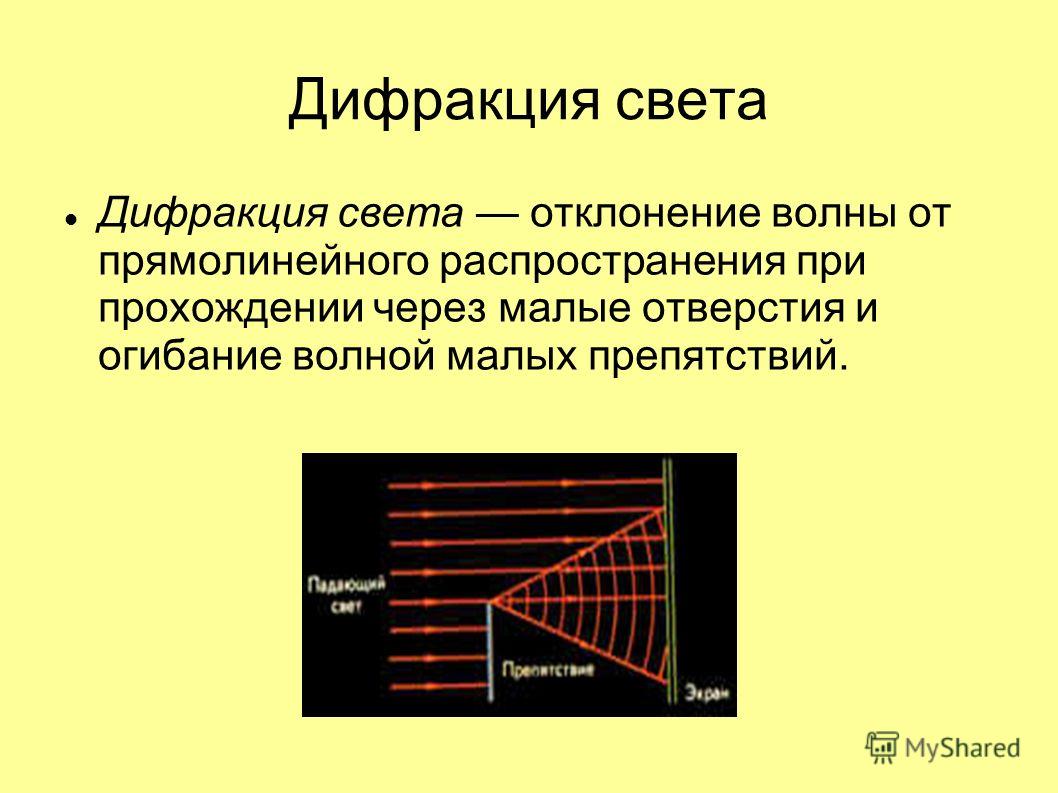
Просветление оптики. Объективы фотоаппаратов и кинопроекторов, перископы под­водных лодок и другие оптические устройства состоят из большого числа оптических стекол, линз, призм. Каждая отполиро­ванная поверхность стекла отражает около 5% падающего на нее света. Чтобы уменьшить долю отражаемой энергии, исполь­зуется явление интерференции света.
На поверхность оптическо­го стекла наносят тонкую пленку. Для того чтобы волны 1 и 2 ослабляли друг друга, должно выполняться условие минимума. В отраженном свете разность хода волн равна:  . Потеря полуволны происходит при отражении как от пленки, так и от стекла (показатель преломления стекла больше, чем пленки), поэтому, эту потерю можно не учитывать. Следо­вательно, , где n — показатель преломления пленки; h — толщина пленки. Минимальная толщина пленки будет при k=0. Поэтому . При равенстве амплитуд гашение света будет полным. Толщину пленки подбирают так, чтобы пол­ное гашение при нормальном падении имело место для длин волн средней части спектра (для зеленого цвета):  . Чтобы рассчитать толщину пленки в этой формуле необходимо взять длину волны и показатель преломления зеленого света. Лучи красного и фиолетового цвета ослабляются незначительно.поэтому объективы оптических приборов в отраженном свете имеют сиреневые оттенки

Источник: https://www.eduspb.com/node/1808

Формулы интерференции

В переводе с французского interferer означает вмешиваться.

Интерференцией света называют явление, устойчивого во времени усиления интенсивности света в одних точках поля и ослабления в других, возникающее в результате наложения когерентных волн света, которые имеют колебания вектора напряженности электромагнитного поля, происходящие в одном направлении. Необходимым условием существования явления интерференции является когерентность источников волн.

Если происходит наложение одного потока бегущих волн, на когерентный поток подобных волн, создающий колебания волны с такой же амплитудой, то интерференция колебаний ведет к неизменному во времени расслоению поля волны на:

1. Области усиления колебаний.
2. Области ослабления колебаний.

• Геометрическое расположение места интерференционного усиления колебаний определяет разность хода волн (). Наибольшее усиление колебаний располагается там, где:
•    
• где n – целое число; – длина волны.
• Максимальное ослабление колебаний происходит, где:
•    
• Если происходит наложение некогерентных волн, то явления интерференции не наблюдают. Для интерференции света условия максимумов записывают как:
•    
•    
•    
• Если выполняется равенство:
•    

длина волны света в вакууме; — оптическая разность хода лучей. Оптической разностью хода () называют разность оптических длин, которые проходят волны: L — это оптической длины пути (геометрическая длина пути (s), умноженная на показатель преломления среды (n)):

то в рассматриваемой точке наблюдается минимум. Выражение (6) называют условием интерференционного минимума.

Картина интерференции в тонких пленках определена толщиной пленки ( у нас b), длиной волны падающего света, показателем преломления вещества пленки и углом падения ().

Для перечисленных параметров каждому наклону лучей () соответствует своя интерференционная полоса. Полосы, возникающие в результате интерференции лучей, падающих на пленку под одинаковыми углами, носят названия полос равного наклона.

Явление интерференции может наблюдаться только, если удвоенная толщина пленки меньше, чем длины когерентности падающей волны.

1. При интерференции в тонких пленках условие наблюдения максимума записывают как (при котором ):
2.    
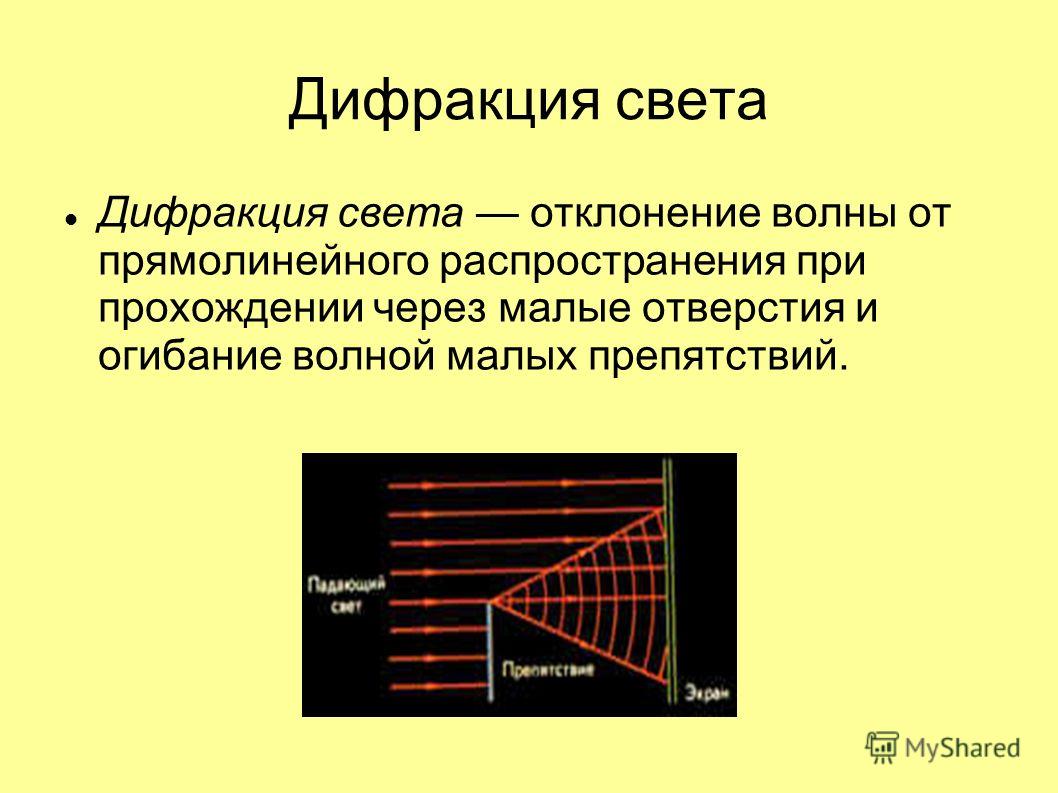
3. По условию для максимумов интерференции, в некоторой точке мы получим максимум интенсивности, если:
4.    

• Минимум интенсивности будет наблюдаться в рассматриваемой точке, если:
•    
• где
• В проходящем свете отражение волны света происходит от среды оптически менее плотной и дополнительной разности хода лучей света не возникает.
• Радиусы светлых колец Ньютона в отраженном свете (темных в проходящем) () вычисляют как:
• где k=1,2,3,… – номер кольца; R – радиус кривизны поверхности линзы, которая соприкасается с плоскопараллельной пластиной.
• Радиусы темных колец Ньютона в отраженном свете ( светлых в проходящем) находят как:

Примеры решения задач по теме «Интерференция»

Понравился сайт? Расскажи друзьям!

Источник: http://ru.solverbook.com/spravochnik/formuly-po-fizike/formuly-interferencii/

3.7. Интерференция световых волн



Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.

Первый эксперимент по наблюдению интерференции света в лабораторных условиях принадлежит И. Ньютону.

Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 3.7.1).

Рисунок 3.7.1.Наблюдение колец Ньютона. Интерференция возникает при сложении волн, отразившихся от двух сторон воздушной прослойки. «Лучи» 1 и 2 – направления распространения волн; h – толщина воздушного зазора

Рисунок 3.7.2.Кольца Ньютона в зеленом и красном свете

Ньютон не смог с точки зрения корпускулярной теории объяснить, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов (см. § 3.6).

Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2 (рис. 3.7.3).

Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались.

В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.

Рисунок 3.7.3.Схема интерференционного опыта Юнга

Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S1 и S2, которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S.

При симметричном расположении щелей вторичные волны, испускаемые источниками S1 и S2, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r1 и r2. Следовательно, фазы колебаний, создаваемых волнами от источников S1 и S2 в точке P, вообще говоря, различны.

Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами.

Утверждение о том, что волны от источников S1 и S2 распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.

Монохроматическая (или синусоидальная) волна, распространяющаяся в направлении радиус-вектора , записывается в виде

где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны.

При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ:

E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ).

Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2.

Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:

(*)

где Δ = r2 – r1 – так называемая разность хода.

Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2, …). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивности Imin = (a1 – a2)2 

Источник: https://physics.ru/courses/op25part2/content/chapter3/section/paragraph7/theory.html

Инфофиз — мой мир..

Интерференция – явление характерное для волн любой природы: механических, электромагнитных.

Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при определенных условиях при наложении двух или нескольких световых пучков. Интенсивность света в области перекрытия пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков.

Интерференция волн – сложение в пространстве двух (или нескольких) волн, при котором в разных его точках получается усиление или ослабление результирующей волны. Для образования устойчивой интерференционной картины необходимы когерентные (согласованные) источники волн.

• Когерентными называются волны, имеющие одинаковую частоту и постоянную разность фаз.
• Интерференцией называется постоянное во времени явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн.
• В результате в пространстве образуется устойчивая картина чередования областей усиленных и ослабленных колебаний.

При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета мыльных пузырей и масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.

Интерференция света – пространственное перераспределение энергии светового излучения при наложении двух или нескольких световых волн. Следовательно, в явлении интерференции света соблюдается закон сохранения энергии. В области интерференции световая энергия только перераспределяется, не превращаясь в другие виды энергии.

Возрастание энергии в некоторых точках интерференционной картины относительно суммарной световой энергии компенсируется уменьшением её в других точках (суммарная световая энергия – это световая энергия двух световых пучков от независимых источников). Светлые полоски соответствуют максимумам энергии, темные – минимумам.

Из естественных проявлений интерференции света наиболее известно радужное окрашивание тонких плёнок (масляные плёнки на воде, мыльные пузыри, окисные плёнки на металлах), возникающее вследствие интерференции света, отражённого двумя поверхностями плёнки.

В тонких плёнках переменной толщины при освещении протяжённым источником локализация интерфереционных колец происходит на поверхности плёнки, при этом данная интерференционная полоса соответствует одной и той же толщине плёнки (полосы равной толщины).

В белом свете полосы окрашены.

Радужная окраска крыльев бабочек, стрекоз, жуков, перьев птиц, перламутровых раковин — все это проявление интерференции в тонких пленках.

Явление интерференции света находит широкое применение в современной технике.

Явление интерференции применяется для улучшения качества оптических приборов (просветление оптики). Отполированная поверхность стекла отражает примерно 4% падающего на нее света. Современные оптические приборы состоят из большого числа деталей, изготовленных из стекла. Проходя через каждую из этих деталей, свет ослабляется на 4%.

Общие потери света в объективе фотоаппарата составляют примерно 25%, в призменном бинокле и микроскопе — 50% и т. д. Для уменьшения световых потерь в оптических приборах все стеклянные детали , через которые проходит свет, покрывают пленкой, показатель преломления которой меньше показателя преломления стекла.

Толщина пленки равна четверти длины волны.

Другим применением явления интерференции является получение хорошо отражающих покрытий, необходимых во многих отраслях оптики. В этом случае используют тонкую пленку толщиной, равной четверти длины волны λ/4 из материала, коэффициент преломления которого n 2 больше коэффициента преломления n3 .

В этом случае отражение от передней границы происходит с потерей полволны, так как n 1 < n 2 , а отражение от задней границы происходит без потери полволны (n 2 > n 3 ). В результате разность хода d =λ/4+λ/4+λ/2=λ и отраженные волны усиливают друг друга.

 Характерной особенностью такой высокоотражательной системы является то, что она действует в очень узкой спектральной области, причем чем больше коэффициент отражения, тем уже эта область.

Например, система из семи пленок для области 0,5 мкм дает коэффициент отражения r=96% (при коэффициенте пропускания 3,5% и коэффициенте поглощения

Источник: http://infofiz.ru/index.php/mirfiziki/formuly/337-interf

Интерференция света

Интерференция — взаимное усиление или ослабление двух или большего числа волн при их наложении друг на друга.

В результате интерференции происходит перерас­пределение энергии светового излучения в пространстве. Устойчивая (стационарная, постоянная во времени) интер­ференционная картина наблюдается при сложении коге­рентных волн.

Латинское слово «cohaerens» означает «находя­щийся в связи». И в пол­ном соответствии с этим значением под когерент­ностью понимают корре­лированное протекание во времени и простран­стве нескольких волно­вых процессов.

Требование когерентности волн — ключе­вое при рассмотрении интерференции. Разберем его на примере сложения двух волн одинаковой частоты. Пусть в некоторой точке пространства они возбуждают одинаково направленные (E̅1 ↑↑ E̅2) колебания: E̅1sin(ω̅t + φ1­) и E̅2sin(ω̅t + φ2­). Тогда величина амплитуды результирующе­го колебания E̅sin(ω̅t + φ) равна

где δ = φ1 — φ2. Если разность фаз δ постоянна во времени, то волны называются когерентными.

• Для некогерентных волн δ случайным образом изменяется во времени, поэтому среднее значение cosδ равно нулю. Поскольку интенсив­ность волны пропорциональна квадрату амплитуды, то в случае сложения некогерентных волн интенсивность результирующей волны I просто равна сумме интенсивно­стей каждой из волн:
• I = I1 + I2.
• При сложении же коге­рентных волн интенсивность результирующего колебания
• I = I1 + I2 + 2√(I1I2cosδ),

в зависимости от значения cosδ, мо­жет принимать значения и большие, и меньшие, чем I1 + I2. Так как значение δ в общем случае зависит от точки наблю­дения, то и интенсивность результирующей волны будет различной в разных точках. Именно это имелось в виду, ко­гда выше говорилось о перераспределении энергии в про­странстве при интерференции волн.

Плоская световая волна, падающая из воздуха на тонкую стеклянную пластину разделяется на две когерентные волны, которые собираются линзой на экране, расположенном в фискальной плоскости линзы. Если оптическая разность хода Δ = n(AB + BC) — AD + λ / 2 = mλ (m = 1, 2, 3 …), в точке наблюдается яркое пятно, если Δ = (2m + 1) λ / 2, то пятно кажется темным. В данном случае происходит деление амплитуды

Излучение с высокой степенью когерентности получают с помощью лазеров. Но если нет лазера, когерентные волны можно получить, разделив одну волну на несколько. Обыч­но используют два способа «деления» — деление волнового фронта и деление амплитуды.

При делении волнового фронта интерферируют волновые пучки, первоначально распространявшиеся от одного источника в разных напра­влениях, которые затем с помощью оптических приборов сводят в одной области пространства (ее называют полем интерференции).

Для этого используют бизеркала и би­призмы Френеля, билинзы Бийе и др.

Чтобы перечислить «цве­та» различных участков оптического диапазона в порядке убывания длины волны — красный, оран­жевый, желтый, зеленый, голубой, синий, фиолето­вый, достаточно вспом­нить фразу: «Каждый охотник желает знать, где сидит фазан».

При амплитудном де­лении волна разделяется на полупрозрачной границе двух сред. Затем, в результате последующих отражений и прело­млений, разделенные части волны встречаются и интерфе­рируют.

Именно так окрашиваются в разные цвета мыль­ные пузыри и тонкие масляные пленки на воде, крылья стрекозы и оксидные пленки на металлах и оконных стек­лах. Важно, что интерферировать должны дуги волн, испу­щенные в одном акте излучения атома или молекулы, т. е.

части волны должны «недолго» двигаться раздельно, иначе в точку встречи уже придут волны, испущенные раз­ными атомами. А так как атомы излучают спонтанно (если не созданы специальные условия, как в лазерах), то эти вол­ны будут заведомо некогерентны.

В лазерах работает вынужденное излучение и этим достигается высокая степень когерентности. Материал с сайта http://worldofschool.ru

Явление интерференции света в XVII в. исследовал Ньютон. Он наблюдал ин­терференцию света в тон­ком воздушном зазоре между стеклянной плас­тинкой и положенной на нее линзой.

Получающую­ся в таком опыте интерфе­ренционную картину так и называют — кольца Ньюто­на. Однако Ньютон не смог внятно объяснить по­явление колец в рамках своей корпускулярной те­ории света. Лишь в начале XIX столетия сначала Т. Юнг, а затем О.

Френель сумели объяснить образо­вание интерференцион­ных картин. И тот, и дру­гой были сторонниками волновой теории света.

В опыте Юнга (а) использовано деление волнового фронта. Два круглых или щелевидных отверстия служили источником когерентных волн. S — дуговая лампа; S0 — щель шириной 0,25 мм; S1 и S2 — щели шириной 0,1 мм на расстоянии 0,7 мм. На рис. (б) показана интерференционная картина, наблюдаемая по схеме Юнга На этой странице материал по темам:

Источник: http://WorldOfSchool.ru/fizika/optika/volnovaya/interferenciya/interferenciya-sveta

Интерференция света

Интерференция света – явление ослабления или усиления интенсивности света в зависимости от соотношения фаз складываемых световых когерентных волн, линейно поляризованных в одной плоскости. Для уровня школьной физики данное определение является излишним. По умолчанию, световые волны являются когерентными и линейно поляризованными.

Таким образом, для нас в задачах на интерференцию важно наличие нескольких (чаще всего двух) волн и разности фаз (разности хода) между ними.

В школьных задачах на интерференцию основным вопросом является результат интерференции в наблюдаемой точке (усиление или ослабление света).

Для математического описания явления интерференции вводят оптическую длину пути () — произведение показателя преломления среды, по которой проходит свет, на геометрическую длину пути, которую прошёл луч. Тогда для двух лучей (рис. 1):

• где
  • — оптическая разность хода,
  • ,  — показатели преломления двух сред,
  • ,  — геометрическая длина пути лучей.

Рис. 1. Интерференция

Пусть от точечного источника системой зеркал два луча развели по двум областям с различными показателями преломления ( и ). Пути лучей в этих системах  и соответственно. Затем, вышедшие из областей, лучи обратно свели в точку . За счёт того, что в средах с различным показателем преломления луч от одного и того же источника движется с разной скоростью, к одной и той же точке они приходят с ненулевой разностью хода (1).

Тогда результат интерференции (усиление или ослабление света) диктуется соотношениями:

• максимум интерференции (максимальное усиление):

(2)

• где
  • — оптическая разность хода,
  • — порядок максимума (счётчик),
  • — длина волны излучения.
• минимум интерференции (максимальное ослабление):

(3)

• где
  • — оптическая разность хода,
  • — порядок минимума (счётчик),
  • — длина волны излучения.

• Тогда для ответа на вопрос об усилении и ослаблении света можно анализировать приведённое уравнение (2):
• (4)
• Тогда, если полученное  целое или ближе к целому, то в точке  наблюдается усиление света, в случае, если  полуцелое или близко к полуцелому, в точке   — темнота.
• Вывод: фактически задачи на интерференцию сводятся к анализу уравнения (4) и поиску оптической длины пути для (1).

Пример: Оптическая разность хода волн от двух когерентных источников в некоторой точке пространства  мкм. Каков будет результат интерференции в этой точке, если длина волны будет:  нм,  нм.

1. Исходя из аналитической формулы (4):
2. (5)
3. (6)

Таким образом, получившийся параметр  получился целым числом, это говорит о том, что при данных параметрах в точке соединения лучей будет наблюдаться усиление света. Параметр  оказался ближе к полуцелому, таким образом, в исследуемой точке будет наблюдаться ослабление света.

Источник: https://www.abitur.by/fizika/teoreticheskie-osnovy-fiziki/optika/volnovaya-optika/interferenciya-sveta/

ИНТЕРФЕРЕ́НЦИЯ СВЕ́ТА

Авторы: E. Б. Александров

ИНТЕРФЕРЕ́НЦИЯ СВЕ́ТА, про­стран­ст­вен­ное пе­ре­рас­пре­де­ле­ние энер­гии све­то­во­го из­лу­че­ния при на­ло­же­нии двух или не­сколь­ких све­то­вых волн; ча­ст­ный слу­чай об­ще­го яв­ле­ния ин­тер­фе­рен­ции волн. Не­ко­то­рые яв­ле­ния И. с. ис­сле­до­ва­лись ещё И. Нью­то­ном в 17 в.

, но не мог­ли быть им объ­яс­не­ны с точ­ки зре­ния его кор­пус­ку­ляр­ной тео­рии. Пра­виль­ное объ­яс­не­ние И. с. как ти­пич­но вол­но­во­го яв­ле­ния бы­ло да­но в нач. 19 в. Т. Юн­гом и О. Фре­не­лем. Наи­бо­лее ши­ро­ко извест­на И. с.

, ха­рак­те­ри­зую­щая­ся об­ра­зо­ва­ни­ем ста­цио­нар­ной (по­сто­ян­ной во вре­ме­ни) ин­тер­фе­рен­ци­он­ной кар­ти­ны – ре­гу­ляр­но­го че­ре­до­ва­ния в про­стран­ст­ве об­лас­тей по­вы­шен­ной и по­ни­жен­ной ин­тен­сив­но­сти све­та, по­лу­чаю­щей­ся в ре­зуль­та­те на­ло­же­ния ко­ге­рент­ных све­то­вых пуч­ков, т. е. в ус­ло­ви­ях по­сто­ян­ной раз­но­сти фаз. Ре­же и толь­ко в спец. усло­ви­ях экс­пе­ри­мен­та на­блю­да­ют­ся яв­ле­ния не­ста­цио­нар­ной И. с., к ко­то­рым от­но­сят­ся све­то­вые бие­ния и эф­фек­ты кор­ре­ля­ции ин­тен­сив­но­стей. Стро­гое объ­яс­не­ние яв­ле­ний не­ста­цио­нар­ной И. с. тре­бу­ет учё­та как вол­но­вых, так и кор­пус­ку­ляр­ных свойств све­та и да­ёт­ся на ос­но­ве кван­то­вой элек­тро­ди­на­ми­ки.

Воз­ни­ка­ет при на­ли­чии ко­ге­рент­но­сти (оп­ре­де­лён­ной кор­ре­ля­ции фаз) на­ла­гаю­щих­ся волн.

Вза­им­но ко­ге­рент­ные све­то­вые пуч­ки мо­гут быть по­лу­че­ны пу­тём раз­де­ле­ния и по­сле­дую­ще­го све­де­ния лу­чей, ис­хо­дя­щих от об­ще­го ис­точ­ни­ка све­та.

Об­ра­зо­ва­ние ин­тер­фе­рен­ци­он­ной кар­ти­ны удоб­но про­сле­дить на идеа­ли­зи­ро­ван­ной схе­ме клас­сич. экс­пе­ри­мен­та Юн­га (рис. 1). То­чеч­ный ис­точ­ник $S$ све­та с дли­ной вол­ны $λ$ ос­ве­ща­ет два ма­лых от­вер­стия в эк­ра­не $A$, ко­то­рые ста­но­вят­ся вто­рич­ны­ми вза­им­но ко­ге­рент­ны­ми ис­точ­ни­ка­ми све­та (см.

 Ди­фрак­ция све­та). На эк­ра­не $B$ на­блю­да­ет­ся ин­тер­фе­рен­ци­он­ная кар­ти­на, вы­зван­ная ин­тер­фе­рен­ци­ей двух соз­дан­ных сис­тем волн.

В со­от­вет­ст­вии с су­пер­по­зи­ции прин­ци­пом на­пря­жён­ность элек­тро­маг­нит­но­го по­ля $E_Q$ в про­из­воль­ной точ­ке $Q$ эк­ра­на $B$ да­ёт­ся сум­мой на­пря­жён­но­стей по­лей $E_{1Q}$ и $E_2Q$, соз­дан­ных в этой точ­ке ис­точни­ка­ми 1 и 2.

На­блю­дае­мой ве­ли­чи­ной яв­ля­ет­ся ин­тен­сив­ность из­лу­че­ния, па­даю­ще­го на эк­ран, про­пор­цио­наль­ная ср. квад­ра­ту на­пря­жён­но­сти по­ля. Пред­став­ляя на­пря­жён­ность по­ля $E_i(t,, s)$ ка­ж­до­го ис­точ­ни­ка ($i=1,, 2$) гар­мо­нич.

функ­ци­ей вре­ме­ни $t$ и рас­стоя­ния $s$ вдоль на­прав­ле­ния рас­про­стра­не­ния $$E_i(t,, s)=Eicos [2π(νt+s/λ=φ_0)],$$ где $ν$ – час­то­та, $φ_0$ – на­чаль­ная фа­за све­то­вых ко­ле­ба­ний, мож­но вы­ра­же­ние для ин­тен­сив­но­сти све­та $I_Q$ по­лу­чить в ви­де: $$I_Q=I_1+I_2+2sqrt{I_1I_2} cos [2π(δ+δ_0)/λ].

quad  (*)$$ Здесь $I_1$ и $I_2$ – ин­тен­сив­но­сти све­та в точ­ке $Q$, соз­да­вае­мые ка­ж­дым ис­точ­ни­ком от­дель­но; $δ$ – оп­тич. раз­ность хо­да ин­тер­фе­ри­рую­щих лу­чей: $δ=n_1r_1-n_2r_2$; $r_1$ и $r_2$ – рас­стоя­ния от от­вер­стий 1 и 2 до точ­ки $Q$; $n_1$ и $n_2$ – по­ка­за­те­ли пре­лом­ле­ния сре­ды (в слу­чае воз­ду­ха $n_1 =n_2=1$); $δ_0$ – oптич. раз­ность хо­да лу­чей от ис­точ­ни­ка $S$ до то­чек 1 и 2.

Из фор­му­лы (*) сле­ду­ет, что ин­тен­сив­ность све­та в дан­ной точ­ке эк­ра­на от­ли­ча­ет­ся от сум­мы ин­тен­сив­но­стей $I_1+I_2$, соз­да­вае­мых ис­точ­ни­ка­ми 1 и 2 при не­за­ви­си­мом ос­ве­ще­нии ими эк­ра­на.

не ме­ня­ет пол­ной све­то­вой энер­гии, по­па­даю­щей на эк­ран $B$, а лишь пе­ре­рас­пре­де­ля­ет её с об­ра­зо­ва­ни­ем ха­рак­тер­ной ин­тер­фе­рен­ци­он­ной кар­ти­ны.

На эк­ра­не $B$ воз­ни­ка­ет сис­те­ма све­то­вых по­лос, ин­тен­сив­ность ко­то­рых в се­че­нии плос­ко­стью, про­хо­дя­щей че­рез ис­точ­ник и от­вер­стия 1 и 2, из­ме­ня­ет­ся, как по­ка­за­но гра­фи­че­ски сплош­ной ли­ни­ей на пра­вой час­ти рис. 1. Макс. ин­тен­сив­ность в ин­тер­ферен­ци­он­ной кар­ти­не на­блю­да­ет­ся при раз­но­сти хо­да, рав­ной чёт­но­му чис­лу по­лу­волн, ми­ни­маль­ная – при раз­но­сти хо­да, рав­ной не­чёт­но­му чис­лу по­лу­волн.

В ре­аль­ном опы­те ко­неч­ный раз­мер ис­точ­ни­ка све­та при­во­дит к па­де­нию кон­тра­ста ин­тер­фе­рен­ци­он­ной кар­ти­ны.

Это обу­слов­ле­но тем, что чуть сме­щён­ный от­но­си­тель­но $S$ то­чеч­ный ис­точ­ник $S′$ да­ёт сме­щён­ную ин­тер­фе­рен­ци­он­ную кар­ти­ну (штри­хо­вая ли­ния на рис. 1).

Сло­же­ние мно­же­ст­ва та­ких кар­тин от всех то­чек ис­точ­ни­ка при­во­дит к умень­ше­нию её рез­ко­сти.

Раз­брос длин волн $Δλ$ из­лу­че­ния ис­точ­ни­ка так­же яв­ля­ет­ся при­чи­ной сни­же­ния кон­тра­ста ин­тер­фе­рен­ци­он­ной кар­ти­ны, сни­же­ния тем боль­ше­го, чем вы­ше по­ря­док ин­тер­фе­рен­ции $η$, рав­ный це­лой час­ти от­но­ше­ния $δ/λ$.

При ос­ве­ще­нии бе­лым све­том на эк­ра­не вид­на бе­лая цен­траль­ная по­ло­са ну­ле­во­го по­ряд­ка с при­мы­каю­щи­ми к ней бы­ст­ро ис­че­заю­щи­ми ра­дуж­ны­ми по­ло­са­ми.

Су­ще­ст­ву­ет мно­го схем опы­тов и ес­те­ст­вен­ных си­туа­ций, в ко­то­рых на­блю­да­ет­ся И. с.

Их наи­бо­лее су­ще­ст­вен­ные раз­ли­чия свя­за­ны с раз­ли­чия­ми в спо­со­бах по­лу­че­ния ко­ге­рент­ных пуч­ков све­та и в чис­ле ин­тер­фе­ри­рую­щих лу­чей.

По спо­со­бам соз­да­ния ко­ге­рент­ных пуч­ков све­та вы­де­ля­ют схе­мы с де­ле­ни­ем вол­но­во­го фрон­та и с де­ле­ни­ем ам­пли­ту­ды.

При пер­вом спо­со­бе сво­дят­ся вме­сте све­то­вые пуч­ки, ис­ход­но раз­ли­чаю­щие­ся на­прав­ле­ни­ем рас­про­стра­не­ния от ис­точ­ни­ка. Та­кой прин­цип ис­поль­зу­ет­ся, напр., в опы­тах с при­ме­не­ни­ем би­лин­зы Бийе и др. Би­лин­за Бийе (рис.

 2) пред­став­ля­ет со­бой вы­пук­лую лин­зу, раз­ре­зан­ную по диа­мет­ру на две час­ти, не­мно­го раз­дви­ну­тые в на­прав­ле­нии, пер­пен­ди­ку­ляр­ном оп­тич. оси; они об­ра­зу­ют дей­ст­ви­тель­ные изо­бра­же­ния $S_1$ и $S_2$ то­чеч­но­го ис­точ­ни­ка $S$. Ин­тер­фе­рен­ци­он­ные по­ло­сы на­блю­да­ют­ся в мо­но­хро­ма­тич.

све­те в лю­бой плос­ко­сти об­лас­ти пе­ре­кры­тия рас­хо­дя­щих­ся пуч­ков от ис­точ­ни­ков $S_1$ и $S_2$ (по­ка­за­но штри­хов­кой). Из ин­тер­фе­рен­ци­он­ных уст­ройств с де­ле­ни­ем вол­но­во­го фрон­та боль­шое прак­тич. зна­че­ние в спек­тро­ско­пии име­ет ди­фрак­ци­он­ная ре­шёт­ка. Все схе­мы И. с.

с де­ле­ни­ем вол­но­во­го фрон­та предъ­яв­ля­ют жё­ст­кие тре­бо­ва­ния к ма­ло­сти уг­ло­во­го раз­ме­ра ис­точ­ни­ка све­та. Напр., в опы­те Юн­га при ос­ве­ще­нии от­вер­стий 1 и 2 пря­мым сол­неч­ным све­том, т. е.

В схе­мах И. с. с ам­пли­туд­ным де­ле­ни­ем вол­но­во­го по­ля из­лу­че­ние пер­вич­но­го ис­точ­ни­ка де­лит­ся по­лу­про­зрач­ны­ми гра­ни­ца­ми оп­тич. сред. Так, напр., воз­ни­ка­ет ши­ро­ко рас­про­стра­нён­ная в ес­те­ст­вен­ных ус­ло­ви­ях И. с.

в тон­ких плён­ках, обу­слов­ли­ваю­щая ра­дуж­ное ок­ра­ши­ва­ние мас­ля­ных пя­тен на во­де, мыль­ных пу­зы­рей, крыль­ев на­се­ко­мых, ок­сид­ных плё­нок на ме­тал­лах и др. Во всех этих слу­ча­ях име­ет ме­сто И. с., от­ра­жён­но­го дву­мя по­верх­но­стя­ми плё­нок.

В тон­ких плён­ках пе­ре­мен­ной тол­щи­ны при ос­веще­нии про­тя­жён­ным ис­точ­ни­ком све­та кар­ти­на ин­тер­фе­рен­ци­он­ных по­лос вос­при­ни­ма­ет­ся ло­ка­ли­зо­ван­ной на по­верх­но­сти плён­ки, при­чём дан­ная ин­тер­фе­рен­ци­он­ная по­ло­са со­от­вет­ст­ву­ет фик­си­ро­ван­ной тол­щи­не плён­ки (по­ло­сы рав­ной тол­щи­ны).

Яр­кое ин­тер­фе­рен­ци­он­ное ок­ра­ши­ва­ние воз­ни­ка­ет толь­ко для весь­ма тон­ких плё­нок тол­щи­ной по­ряд­ка дли­ны вол­ны, т. е. в низ­ких по­ряд­ках ин­тер­фе­рен­ции. Для бо­лее тол­стых плё­нок ин­тер­фе­рен­ци­он­ная кар­ти­на вид­на при ос­ве­ще­нии мо­но­хро­ма­тич. све­том, напр. в све­те на­трие­вой лам­пы низ­ко­го дав­ле­ния.

В тон­ких плён­ках стро­го по­сто­ян­ной тол­щи­ны (с точ­но­стью до ма­лых до­лей дли­ны вол­ны) оди­на­ко­вую раз­ность хо­да при­об­ре­та­ют при от­ра­же­нии от двух по­верх­но­стей плён­ки лу­чи, па­даю­щие на плён­ку под фик­си­ро­ван­ным уг­лом.

Эти лу­чи в фо­каль­ной плос­ко­сти лин­зы об­ра­зу­ют ин­тер­фе­рен­ци­он­ные по­ло­сы рав­но­го на­кло­на. Ме­тод де­ле­ния ам­пли­ту­ды ши­ро­ко при­ме­ня­ет­ся в разл. схе­мах ин­тер­фе­ро­мет­ров, в ко­то­рых для раз­де­ле­ния вол­но­вых по­лей ис­поль­зу­ют­ся спец. по­лу­про­зрач­ные зер­ка­ла.

Тре­бо­ва­ния к мо­но­хро­ма­тич­но­сти све­та не за­ви­сят от спо­со­ба де­ле­ния вол­но­во­го по­ля, а оп­ре­де­ля­ют­ся толь­ко по­ряд­ком ин­тер­фе­рен­ции. Как от­ме­ча­лось вы­ше, И. с. в низ­ких по­ряд­ках на­блю­да­ет­ся да­же в бе­лом све­те.

при прак­ти­че­ски не­ог­ра­ни­чен­ной раз­но­сти хо­да.

Поч­ти все упо­мя­ну­тые при­ме­ры И. с. от­но­си­лись к ти­пу двух­лу­че­вой ин­тер­фе­рен­ции, при ко­то­рой в ка­ж­дую точ­ку ин­тер­фе­рен­ци­он­ной кар­ти­ны свет от об­ще­го ис­точ­ни­ка при­хо­дит по двум пу­тям.

При этом ин­тен­сив­ность све­та в ин­тер­фе­рен­ци­он­ной кар­ти­не гар­мо­ни­че­ски за­ви­сит от раз­но­сти хо­да лу­чей $[∼cos^2(2πδ/λ )]$. Мно­го­лу­че­вая И. с. воз­ни­ка­ет при на­ло­же­нии мн. ко­ге­рент­ных волн, по­лу­чае­мых де­ле­ни­ем ис­ход­но­го вол­но­во­го по­ля с по­мо­щью мно­го­крат­ных от­ра­же­ний (напр.

, в ин­тер­фе­ро­мет­ре Фаб­ри – Пе­ро) или ди­фрак­ци­ей на мно­го­эле­мент­ных пе­рио­дич. струк­ту­рах (см.Ди­фрак­ци­он­ная ре­шёт­ка, Май­кель­со­на эше­лон). При мно­го­лу­че­вой И. с. яр­кость ин­тер­фе­рен­ци­он­ной кар­ти­ны яв­ля­ет­ся пе­рио­ди­че­ской, но не гар­мо­нич. функ­ци­ей $δ$ .

Рез­кая за­ви­си­мость яр­ко­сти ин­тер­фе­рен­ци­он­ной кар­ти­ны от $δ$ при мно­го­лу­че­вой И. с. ши­ро­ко ис­поль­зу­ет­ся для спек­траль­но­го ана­ли­за све­та.

Ес­ли для на­блю­де­ния И. с. от те­п­ло­вых ис­точ­ни­ков при­хо­дит­ся со­блю­дать ряд ог­ра­ни­че­ний (при­чём воз­ни­каю­щая ин­тер­фе­рен­ци­он­ная кар­ти­на обыч­но име­ет ма­лые яр­кость и раз­ме­ры), то при ис­поль­зо­ва­нии ла­зе­ров в ка­че­ст­ве ис­точ­ни­ков све­та яв­ле­ния И. с.

на­столь­ко яр­ки и ха­рак­тер­ны, что нуж­ны осо­бые ме­ры для по­лу­че­ния рав­но­мер­ной ос­ве­щён­ности. Чрез­вы­чай­но вы­со­кая ко­ге­рент­ность из­лу­че­ния ла­зе­ров при­во­дит к по­яв­ле­нию по­мех ин­тер­фе­рен­ци­он­но­го про­ис­хо­ж­де­ния при на­блю­де­нии объ­ек­тов, ос­ве­щён­ных ла­зе­ром.

При ла­зер­ном ос­ве­ще­нии про­из­воль­ной ше­ро­хо­ва­той по­верх­но­сти ак­ко­мо­ди­ро­ван­ный на бес­ко­неч­ность глаз вос­при­ни­ма­ет хао­тич. кар­ти­ну све­то­вых пя­тен, мер­цаю­щую при сме­ще­ни­ях гла­за (см. Спек­лы).

Это вы­зва­но тем, что ше­ро­хо­ва­тая по­верх­ность, рас­сеи­вая ла­зер­ное из­лу­че­ние, слу­жит ис­точ­ни­ком не­ре­гу­ляр­ной ин­тер­фе­рен­ци­он­ной кар­ти­ны, об­ра­зо­ва­нию ко­то­рой в обыч­ных ус­ло­ви­ях пре­пят­ст­ву­ет низ­кая про­стран­ст­вен­но-вре­мен­нáя ко­ге­рент­ность из­лу­че­ния те­п­ло­вых ис­точ­ни­ков.

К ней от­но­сят­ся све­то­вые бие­ния, на­блю­даю­щие­ся при на­ло­же­нии све­то­вых по­лей разл. час­тот.

В этом слу­чае воз­ни­ка­ет бе­гу­щая в про­стран­ст­ве ин­тер­фе­рен­ци­он­ная кар­ти­на, так что в за­дан­ной точ­ке про­стран­ст­ва ин­тен­сив­ность све­та пе­рио­ди­че­ски ме­ня­ет­ся во вре­ме­ни с час­то­той, рав­ной раз­но­сти час­тот ин­тер­фе­ри­рую­щих волн.

Бие­ния воз­ни­ка­ют в обыч­ных (не­ла­зер­ных) схе­мах И. с. при из­ме­не­нии во вре­ме­ни раз­но­сти хо­да ин­тер­фе­ри­рую­щих лу­чей. При­ме­ром мо­жет слу­жить ин­тер­фе­ро­метр Май­кель­со­на с пе­ре­мен­ной дли­ной од­но­го из плеч.

При пе­ре­ме­ще­нии вдоль лу­ча све­та од­но­го из зер­кал ин­тен­сив­ность све­та на вы­хо­де ин­тер­фе­ро­мет­ра пе­рио­ди­че­ски ме­ня­ет­ся, что мо­жет слу­жить сред­ст­вом из­ме­ре­ния ско­ро­сти очень мед­лен­ных пе­ре­ме­ще­ний. Напр., при дви­же­нии зер­ка­ла со ско­ро­стью 10–6 м/с ин­тен­сив­ность све­та ме­ня­ет­ся с час­то­той ок. 4 Гц.

Бие­ния мо­гут на­блю­дать­ся и в из­лу­че­нии не­за­ви­си­мых ис­точ­ни­ков све­та. Для это­го их яр­ко­сти и спек­траль­ные плот­но­сти из­лу­че­ния долж­ны быть очень ве­ли­ки.

Обе эти ха­рак­те­ри­сти­ки вы­ра­жа­ют­ся че­рез па­ра­метр вы­ро­ж­де­ния фо­то­нов $ρ$, рав­ный чис­лу фо­то­нов в объ­ё­ме ко­ге­рент­но­сти. При фо­то­элек­трич.

ре­ги­ст­ра­ции бие­ний па­ра­метр $ρ$ в про­из­ве­де­нии с кван­то­вым вы­хо­дом при­ём­ни­ка оп­ре­де­ля­ет ве­ли­чи­ну сиг­на­ла бие­ний по от­но­ше­нию к фо­ну фо­тон­но­го шу­ма.

Для те­п­ло­вых ис­точ­ни­ков обыч­но $ρ≪1$, по­это­му эф­фек­ты не­ста­цио­нар­ной И. с. в их из­лу­че­нии край­не ма­лы. Тем не ме­нее их уда­лось об­на­ру­жить в тон­ких экс­пе­ри­мен­тах по кор­ре­ля­ции ин­тен­сив­но­стей.

И. с. ис­поль­зу­ет­ся при спек­траль­ном ана­ли­зе све­та, для точ­но­го из­ме­ре­ния рас­стоя­ний, уг­лов, ско­ро­стей, в реф­рак­то­мет­рии. Боль­шое зна­че­ние ин­тер­фе­ро­мет­рия име­ет в оп­тич.

про­из­вод­ст­ве как сред­ст­во кон­тро­ля ка­че­ст­ва по­верх­но­стей и лин­зо­вых сис­тем. Ин­тер­фе­рен­ци­он­ные яв­ле­ния ис­поль­зу­ют­ся для соз­дания све­то­фильт­ров, вы­со­ко­ка­че­ст­вен­ных зер­кал, про­свет­ляю­щих по­кры­тий для оп­тич.

де­та­лей. И. с. со­став­ля­ет ос­но­ву оп­тич. го­ло­гра­фии.

Источник: https://bigenc.ru/physics/text/2015057