Существует несколько классификаций реакций, протекающих в неорганической и органической химии.
По характеру процесса
- Соединения
- Так называют химические реакции, где из нескольких простых или сложных веществ получается одно сложное вещество. Примеры:
- 4Na + O2 = 2Na2O
- P2O5 + 3H2O = 2H3PO4
- Разложения
- В результате реакции разложения сложное вещество распадается на несколько сложных или простых веществ.
Примеры:
- 2KMnO4 = K2MnO4 + MnO2 + 2O2
- Сa(OH)2 = CaO + H2O
- Замещения
- В ходе реакций замещения атом или группа атомов в молекуле замещаются на другой атом или группу атомов. Примеры:
- CuSO4 + Fe = FeSO4 + Cu
- 2KI + Cl2 = 2KCl + I2
- Обмена
- К реакциям обмена относятся те, которые протекают без изменения степеней окисления и выражаются в обмене компонентов между веществами. Часто обмен происходит анионами/катионами:
- 2KOH + MgCl2 = Mg(OH)2↓ + 2KCl
- AgF + NaCl = AgCl↓ + NaF

Окислительно-восстановительные реакции (ОВР)
Это те химические реакции, в процессе которых происходит изменение степеней окисления химических элементов, входящих в состав исходных веществ. ОВР подразделяются на:
- Межмолекулярные — атомы окислителя и восстановителя входят в состав разных молекул. Примеры:
- Внутримолекулярные — атомы окислителя и восстановителя в составе одного сложного вещества. Примеры:
- Диспропорционирование — один и тот же атом является и окислителем, и восстановителем
KMnO4 + HCl → KCl + MnCl2 + Cl2 + H2O K2SO3 + K2Cr2O7 + H2SO4 → K2SO4 + Cr2(SO4)3 + H2O
KMnO4 → K2MnO4 + MnO2 + O2 KClO3 → KCl + O2
KOH + Cl2 → (t) KCl + KClO3 + H2O KOH + Cl2 → KCl + KClO + H2O

Замечу, что окислителем и восстановителем могут являться только исходные вещества (а не продукты!) Окислитель всегда понижает свою СО, принимая электроны в процессе восстановления. Восстановитель всегда повышает свою СО, отдавая электроны в процессе окисления.
От обилия информации можно запутаться. Я рекомендую сформулировать четко: «Окислитель — понижает СО, восстановитель — повышает СО». Запомнив эту информацию таким образом, вы не будете путаться.

ОВР уравнивают методом электронного баланса, с которым мы подробно познакомимся в разделе «Решения задач».
Обратимые и необратимые реакции
Обратимые реакции — такие химические реакции, которые протекают одновременно в двух противоположных направлениях: прямом и обратном. При записи реакции в таких случаях вместо знака «=» ставят знак обратимости «⇆».
- Классическим примером обратимой реакции является синтез аммиака и реакция этерификации (из органической химии):
- N2 + 3H2 ⇆ 2NH3
- CH3COOH + C2H5OH ⇆ CH3COOC2H5 + H2O
Необратимые реакции протекают только в одном направлении, до полного расходования одного из исходных веществ. Главное отличие их от обратимых реакций в том, что образовавшиеся продукты реакции не взаимодействуют между собой с образованием исходных веществ.
Иногда сложно бывает отличить обратимую реакцию от необратимой, однако я дам несколько советов, которые советую взять на вооружение. В результате необратимых реакций:
- Образуются малодиссоциирующие вещества (например — вода, однако есть исключения — реакция этерификации)
- Реакция сопровождается выделение большого количества тепла
- В ходе реакции образуется газ или выпадает осадок
- Примеры необратимых реакций:
- BaCl2 + H2SO4 = BaSO4↓ + 2HCl (выпадает осадок)
- NaOH + HCl = NaCl + H2O (образуется вода)
- 2Na + 2H2O = 2NaOH + H2 (сопровождается выделением большого количества тепла)

Реакции и агрегатное состояние фаз
Фазой в химии называют часть объема равновесной системы, однородную во всех своих точках по химическому составу и физическим свойствам и отделенную от других частей того же объема поверхностью раздела. Фаза бывает жидкой, твердой и газообразной.
Все реакции можно разделить на гетеро- и гомогенные. Гетерогенные реакции (греч. heterogenes — разнородный) — реакции, протекающие на границе раздела фаз, в неоднородной среде. Скорость таких реакций зависит от площади соприкосновения реагирующих веществ.
К гетерогенным реакциям относятся следующие реакции (примеры): жидкость + газ, газ + твердое вещество, твердое вещество + жидкость. Примером такой реакции может послужить взаимодействие твердого цинка и раствора соляной кислоты:
Zn(тв.) + 2HCl(р-р.) = ZnCl2(р-р.) + H2(газ.)↑

Гомогенные реакции (греч. homogenes — однородный) — реакции, протекающие между веществами, находящимися в одной фазе.
К гомогенным реакциям относятся (примеры): жидкость + жидкость, газ + газ, твердое вещество + твердое вещество. Примером такой реакции может служить взаимодействие между растворами уксусной кислоты и едкого натра.
NaOH(р-р.) + CH3COOH(р-р.) = CH3COONa(р-р.) + H2O(р-р.)

Реакции и их тепловой эффект
Все реакции можно разделить на те, в ходе которых тепло поглощается, или, наоборот, тепло выделяется. Представьте пробирку, охлаждающуюся или нагревающуюся в вашей руке — это и есть тот самый тепловой эффект. Иногда тепла выделяется так много, что реакции сопровождаются воспламенением или взрывом (натрий с водой).
- Экзотермические реакции
- Эндотермические реакции
- 2HgO = Hg + O2 — Q
- 4NH3 + 5O2 = 4NO + 6H2O — Q
- CaCO3 = CaO + CO2↑ — Q
- С целью «запутывания» может быть дана энтальпия, она при таких реакциях всегда: ΔH > 0, так как внутренняя энергия веществ увеличивается. Например:
- CaCO3 = CaO + CO2↑ ; ΔH > 0 (значит реакция эндотермическая, так как внутренняя энергия увеличивается)
Экзотермические реакции (греч. exo — вне) — химические реакции, сопровождающиеся потерей энергии системой и выделением тепла (той самой энергии) во внешнюю среду. При написании химических реакций в конце экзотермических ставят «+ Q» (Q — тепло), иногда бывает указано точное количество выделяющегося тепла. Например: 2Mg + O2 = 2MgO + Q NaOH + HCl = NaCl + H2O + 56 кДж  К экзотермическим реакциям часто относятся реакции горения, соединения. Исключением является взаимодействие азота и кислорода, при котором тепло поглощается: N2 + O2 ⇄ 2NO — Q Как уже было отмечено выше, если тепло выделяется во внешнюю среду, значит, система реагирующих веществ потеряло это тепло. Поэтому не должно казаться противоречием, что внутренняя энергия веществ в результате экзотермической реакции уменьшается. Энтальпией называют (обозначение Н), количество термодинамической (тепловой) энергии, содержащееся в веществе. Иногда с целью «запутывания» в реакции вместо явного +Q при экзотермической реакции могут написать ΔH < 0. Например: 2Na + 2H2O = 2NaOH + H2; ΔH < 0 (это значит, что тепло выделяется — реакция экзотермическая)
К экзотермическим реакциям часто относятся реакции горения, соединения. Исключением является взаимодействие азота и кислорода, при котором тепло поглощается: N2 + O2 ⇄ 2NO — Q Как уже было отмечено выше, если тепло выделяется во внешнюю среду, значит, система реагирующих веществ потеряло это тепло. Поэтому не должно казаться противоречием, что внутренняя энергия веществ в результате экзотермической реакции уменьшается. Энтальпией называют (обозначение Н), количество термодинамической (тепловой) энергии, содержащееся в веществе. Иногда с целью «запутывания» в реакции вместо явного +Q при экзотермической реакции могут написать ΔH < 0. Например: 2Na + 2H2O = 2NaOH + H2; ΔH < 0 (это значит, что тепло выделяется — реакция экзотермическая) 
Эндотермические реакции (греч. ἔνδον — внутри) — химические реакции, сопровождающиеся поглощением тепла, в результате которых образуются вещества с более высоким энергетическим уровнем (их внутренняя энергия увеличивается). К таким реакциям наиболее часто относятся реакции разложения. При написании эндотермических реакций в конце ставят «-Q», либо указывают точное количество поглощенной энергии. Примеры таких реакций:

Замечу, что не все реакции разложения являются эндотермическими. Широко известная реакция разложения дихромата аммония («вулканчик») является примером экзотермического разложения, при котором тепло выделяется.

Источник: https://studarium.ru/article/160
Классификация химических реакций. Тепловой эффект химических реакций. Видеоурок. Химия 11 Класс
На уроке будут рассмотрены классификация и тепловой эффект химических реакций.
- Химическая реакция – это процесс, при котором из одних веществ получаются другие, отличающиеся от исходных веществ по составу или строению, по свойствам.
- Существует несколько классификаций химических реакций, основанных либо на параметрах самих реакций, либо на свойствах участвующих веществ.
- I. Классификация, основанная на агрегатном состоянии участвующих веществ
Реакция называется гомогенной (греч. «гомо-с» – одинаковый, «гениум» – рождать), т. е. одинаковый по рождению. Вещества, участвующие в реакции, находятся в одном агрегатном состоянии: газообразном, твердом или жидком. В понятие «жидкое агрегатное состояние» входят и растворы веществ. Но между веществами не должно быть границы раздела фаз.
- Гомогенные реакции подразделяют на
- · Газофазные
- · Жидкостные
- · Твердофазные
- Реакция называется гетерогенной (греч. «гетеро-с» – разный), если вещества находятся в различных агрегатных состояниях (жидкое и твердое, несмешивающиеся жидкости или смеси твердых веществ)
| Классификация по агрегатному состоянию участвующих веществ. | ||
| Гомогенные реакции | Гетерогенные реакции | |
| Газофазная | Жидкостная |
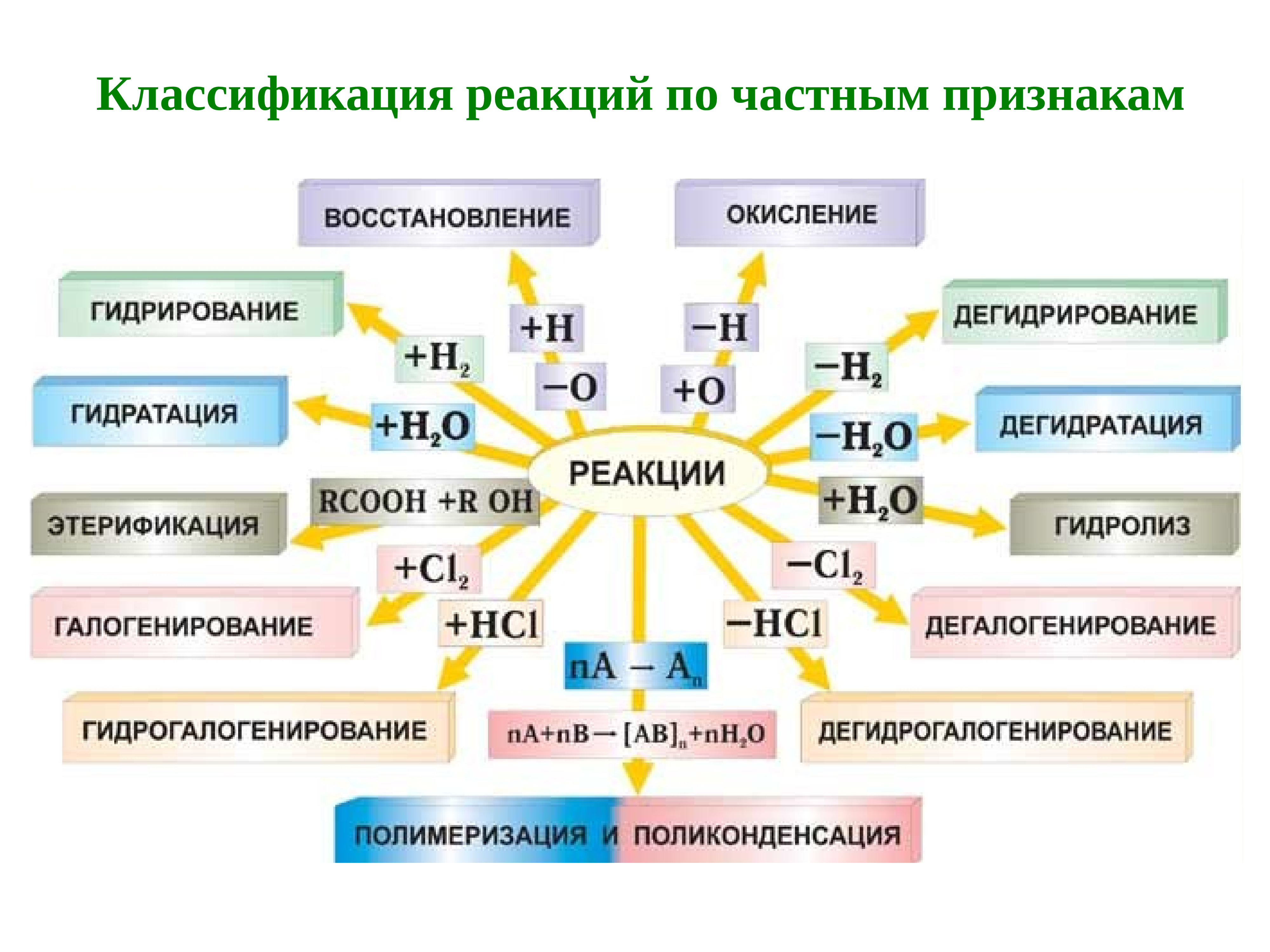
II. Классификация по изменению состава веществ или не изменению состава вещества
| Реакции, при которых не изменяется состав вещества: | |
 |
 |
| Реакция изомеризации пропил бензола в изопропилбензол | Переход между аллотропными модификациями (графит ↔ алмаз) |
- Табл. 2
- Реакции, происходящие с изменением состава веществ подразделяются на
- · соединения
- · разложения
- · замещения
- · обмена

В органической химии реакции присоединения обозначаются как гидрирование, гидратация, галогенирование, гидрогалогенирование, полимеризация.
Реакции разложения называют реакциями отщепления: дегидрирование, дегидратация, дегидрогалогенирование.
Реакции замещения в органической химии – это галогенирование алканов, замещение гидроксила на галоген в спиртах, галогенирование бензола.
В отдельную группу выделяют реакции, при которых происходит изменение степеней окисления в веществах. Это окислительно-восстановительные реакции.
- По константе равновесия, химические реакции делятся на обратимые и необратимые.
- В органической химии существует классификация реакций по типу атакующей частицы.

- III.Классификация по тепловому эффекту
- Одни химические реакции протекают с выделением теплоты, а другие – с поглощением.
- Количество теплоты, которое выделяется в результате реакции, называется тепловым эффектом химической реакции.
- По тепловому эффекту химические реакции делят на экзотермические и эндотермические.
Экзотермическими называются реакции, которые протекают с выделением теплоты. Например, реакция горения пропана.

Рис. 1. С3Н8 +О2→3СО2↑+4Н2О+Q
Эндотермическими называются реакции, которые протекают с поглощением теплоты. Например, реакция разложения гидроксида меди (II).
Сu(OH)2 СuО+Н2О — Q
Термохимические уравнения
Химические уравнения, в которых указан тепловой эффект реакции, называются термохимическими. В них указывается теплота процесса, соответствующая стехиометрическим коэффициентам.
Количество теплоты зависит от количества вещества. Ведь нельзя же обогреть помещение, сжигая одну спичку, а положив в камин несколько бревен – вполне. Хотя оба процесса – это горение древесины. Рис. 2.

Рис. 2. Горение древесины
Рассмотрим следующую задачу:
Задача 1. Вычислите массу и объём (н.у.) сгоревшего этилена, если в ходе реакции выделилось 2450 кДж теплоты. С2Н4(Г) + 3О2(Г)→2СО2(г)↑+ 2Н2О (ж) + 1400 кДж
- Решение:
- Согласно уравнению реакции, при сгорании 1 моль этилена выделяется 1400 кдж
- По условию задачи при сгорании х моль этилена выделяется 2450 кдж
- Составляем пропорцию:
![]()
- Ответ:
- Подведение итога урока
- На уроке рассмотрена классификация химических реакций по различным признакам, а также мы подробнее коснулись темы «Тепловой эффект химических реакций».
- Список литературы
1. Рудзитис Г.Е. Химия. Основы общей химии. 11 класс: учебник для общеобразовательных учреждений: базовый уровень / Г.Е. Рудзитис, Ф.Г. Фельдман. – 14-е изд. – М.: Просвещение, 2012.
2. Попель П.П. Химия: 8 кл.: учебник для общеобразовательных учебных заведений / П.П. Попель, Л.С.Кривля. – К.: ИЦ «Академия», 2008. – 240 с.: ил.
3. Габриелян О.С. Химия. 11 класс. Базовый уровень. 2-е изд., стер. – М.: Дрофа, 2007. – 220 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Internerurok.ru (Источник).
2. Hemi.nsu.ru (Источник).
3. Chemport.ru (Источник).
4. Химик (Источник).
Домашнее задание
1. №№1-3 (с. 48), решить з. 1, 2 (с. 48) Рудзитис Г.Е. Химия. Основы общей химии. 11 класс: учебник для общеобразовательных учреждений: базовый уровень / Г.Е. Рудзитис, Ф.Г. Фельдман. – 14-е изд. – М.: Просвещение, 2012.
2. Приведите примеры газофазной гомогенной реакции.
3. Что такое тепловой эффект химической реакции?
Источник: https://interneturok.ru/lesson/chemistry/11-klass/bklassifikaciya-himicheskih-reakcijb/klassifikatsiya-himicheskih-reaktsiy-teplovoy-effekt-himicheskih-reaktsiy
Типы химических реакций в органической химии
При протекании химических реакций происходит разрыв одних и возникновение других связей. Химические реакции условно делят на органические и неорганические.
Органическими реакциям принято считать реакции, в которых, по крайней мере, одно из реагирующих веществ является органическим соединением, изменяющим свою молекулярную структуру в процессе реакции. Отличием органических реакций от неорганических является то, что, как правило, в них участвуют молекулы.
Скорость таких реакции низка, а выход продукта обычно составляет всего лишь 50-80 %. Для повышения скорости реакции применяют катализаторы, повышают температуру или давление. Далее рассмотрим типы химических реакций в органической химии.
Классификация по характеру химических превращений
- Реакции замещения
- Реакции присоединения
- Реакция элиминирования (отщепления)
- Реакция изомеризации и перегруппировка
- Реакции окисления
- Реакции конденсации и поликонденсации
- Реакции разложения
Реакции замещения
В ходе реакций замещения один атом или группа атомов в начальной молекуле замещается на иные атомы или группы атомов, образуя новую молекулу. Как правило, такие реакции характерны для насыщенных и ароматических углеводородов, например:

Реакции присоединения
При протекании реакций присоединения из двух или более молекул веществ образуется одна молекула нового соединения. Такие реакции характерны для ненасыщенных соединений. Различают реакции гидрирования (восстановления), галогенирования, гидрогалогенирования, гидратации, полимеризации и т.п:
- Гидрирование – присоединение молекулы водорода:

- Галогенирование — присоединение молекулы галогена:

- Гидрогалогенирование — присоединение молекулы галогенводорода:
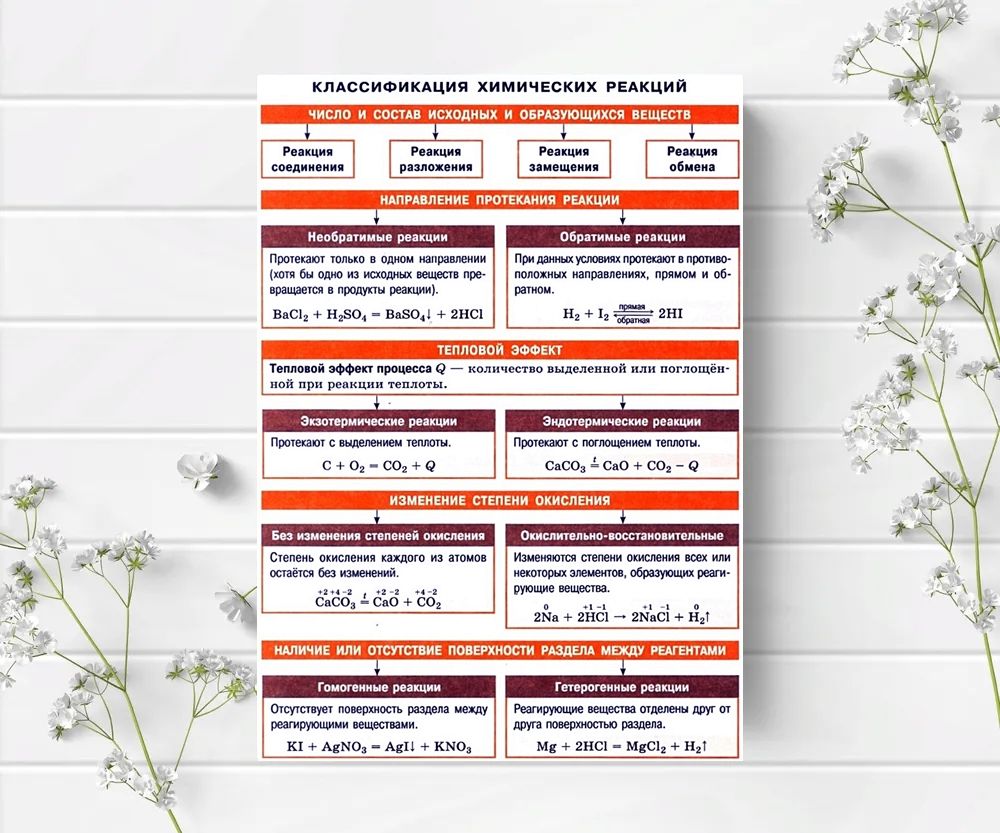
- Гидратация — присоединение молекулы воды:

- Полимеризация – образование высокомолекулярного соединения посредством многократного присоединения низкомолекулярного соединения, например:

Реакция элиминирования (отщепления)
В результате реакций отщепления органические молекулы теряют атомы или группы атомов, и образуется новое вещество, содержащее одну или несколько кратных связей. К реакциям элиминирования относятся реакции дегидрирования, дегидратации, дегидрогалогенирования и т.п.:
- Дегидрирование – отщепления молекулы водорода:

- Дегидратация – отщепление молекулы воды:

- Дегидрогалогенирования – отщепления молекулы галогеноводородов:

Реакции изомеризации и перегруппировка

- Реакции окисления
- В результате воздействия окисляющего реагента происходит повышение степени окисления углерода в органическом атоме, молекуле или ионе процесс за счет отдачи электронов, вследствие чего образуется новое соединение:
- Реакции конденсации и поликонденсации
- Заключаются во взаимодействии нескольких (двух и более) органических соединений с образованием новых С-С связей и низкомолекулярного соединения:
- Поликонденсация – образование молекулы полимера из мономеров, содержащих функциональные группы с выделением низкомолекулярного соединения. В отличие от реакции полимеризации, в результате которых образуется полимер, имеющий состав, аналогичный мономеру, в результате реакций поликонденсации состав образованного полимера отличается от его мономера:
- Реакции разложения
- Это процесс расщепления сложного органического соединения на менее сложные или простые вещества:
- С18H38 → С9H18 + С9H20
Классификация химических реакций по механизмам
Протекание реакций с разрывом ковалентных связей в органических соединениях возможно по двум механизмам (т.е. пути, приводящему к разрыву старой связи и образованию новой) – гетеролитическому (ионному) и гомолитическому (радикальному).
Гетеролитический (ионный) механизм
В реакциях, протекающих по гетеролитическому механизму образуются промежуточные частицы ионного типа с заряженным атомом углерода. Частицы, несущие положительный заряд называются карбкатионы, отрицательный – карбанионы. При этом происходит не разрыв общей электронной пары, а ее переход к одному из атомов, с образованием иона:
Склонность к гетеролитическому разрыву проявляют сильно полярные, например Н–O, С–О и легко поляризуемые, например С–Вr, С–I связи.
Реакции, протекающие по гетеролитическому механизму делят на нуклеофильные и электрофильные реакции. Реагент, располагающий электронной парой для образования связи называют нуклеофильным или электронодонорным. Например, HO—,RO—, Cl—, RCOO—, CN—, R—, NH2, H2O, NH3, C2H5OH, алкены, арены.
- Реагент, имеющий незаполненную электронную оболочку и способные присоединить пару электронов в процессе образования новой связи.называют электрофильным реагентам относятся следующие катионы: Н+, R3C+, AlCl3, ZnCl2, SO3, BF3, R-Cl, R2C=O
- Реакции нуклеофильного замещения
- Характерны для алкил- и арилгалогенидов:
- Реакции нуклеофильного присоединения
- Реакции электрофильного замещения
- Реакции электрофильного присоединения
- Гомолитический (радикальный механизм)
В реакциях, протекающих по гомолитическому (радикальному) механизму на первой стадии происходит разрыв ковалентной связи с образованием радикалов. Далее образовавшийся свободный радикал выступает в качестве атакующего реагента. Разрыв связи по радикальному механизму свойственен для неполярных или малополярных ковалентных связей (С–С, N–N, С–Н).
- Различают реакции радикального замещения и радикального присоединения
- Реакции радикального замещения
- Характерны для алканов
- Реакции радикального присоединения
- Характерны для алкенов и алкинов
- Таким образом, мы рассмотрели основные типы химических реакций в органической химии
Источник: http://zadachi-po-khimii.ru/organic-chemistry/tipy-ximicheskix-reakcij-v-organicheskoj-ximii.html
Классификация химических реакций в неорганической и органической химии
Классификацию химических реакций в неорганической и органической химии осуществляют на основании различных классифицирующих признаков, сведения о которых приведены в таблице ниже.


По изменению степени окисления элементов
Первый признак классификации — по изменению степени окисления элементов, образующих реагенты и продукты.
а) окислительно-восстановительные
б) без изменения степени окисления
Окислительно-восстановительными называют реакции, сопровождающиеся изменением степеней окисления химических элементов, входящих в состав реагентов.
К окислительно-восстановительным в неорганической химии относятся все реакции замещения и те реакции разложения и соединения, в которых участвует хотя бы одно простое вещество.
К реакциям, идущим без изменения степеней окисления элементов, образующих реагенты и продукты реакции, относятся все реакции обмена.

По числу и составу реагентов и продуктов
Химические реакции классифицируются по характеру процесса, т.е по числу и составу реагентов и продуктов.
- Реакциями соединения называют химические реакции, в результате которых сложные молекулы получаются из нескольких более простых, например:
4Li + O2 = 2Li2O - Реакциями разложения называют химические реакции, в результате которых простые молекулы получаются из более сложных, например:
CaCO3 = CaO + CO2 - Реакции разложения можно рассматривать как процессы, обратные соединению.
- Реакциями замещения называют химические реакции, в результате которых атом или группа атомов в молекуле вещества замещается на другой атом или группу атомов, например:
Fe + 2HCl = FeCl2 + H2
Их отличительный признак — взаимодействие простого вещества со сложным. Такие реакции есть и в органической химии.
Однако понятие «замещение» в органике шире, чем в неорганической химии.
Если в молекуле исходного вещества какой-либо атом или функциональная группа заменяются на другой атом или группу, это тоже реакции замещения, хотя с точки зрения неорганической химии процесс выглядит как реакция обмена.
— обмена (в том числе и нейтрализации).
Реакциями обмена называют химические реакции, протекающие без изменения степеней окисления элементов и приводящие к обмену составных частей реагентов, например:
AgNO3 + KBr = AgBr + KNO3 
По возможности протекать в обратном направлении
По возможности протекать в обратном направлении – обратимые и необратимые.
Обратимыми называют химические реакции, протекающие при данной температуре одновременно в двух противоположных направлениях с соизмеримыми скоростями. При записи уравнений таких реакций знак равенства заменяют противоположно направленными стрелками. Простейшим примером обратимой реакции является синтез аммиака взаимодействием азота и водорода:
- N2 +3H2↔2NH3
- Необратимыми называют реакции, протекающие только в прямом направлении, в результате которых образуются продукты, не взаимодействующие между собой. К необратимым относят химические реакции, в результате которых образуются малодиссоциированные соединения, происходит выделение большого количества энергии, а также те, в которых конечные продукты уходят из сферы реакции в газообразном виде или в виде осадка, например:
- HCl + NaOH = NaCl + H2O
- 2Ca + O2 = 2CaO
- BaBr2 + Na2SO 4 = BaSO4↓ + 2NaBr

По тепловому эффекту
Экзотермическими называют химические реакции, идущие с выделением теплоты. Условное обозначение изменения энтальпии (теплосодержания) ΔH, а теплового эффекта реакции Q. Для экзотермических реакций Q > 0, а ΔH < 0.
Эндотермическими называют химические реакции, идущие с поглощением теплоты. Для эндотермических реакций Q < 0, а ΔH > 0.
Реакции соединения как правило будут реакциями экзотермическими, а реакции разложения — эндотермическими. Редкое исключение — реакция азота с кислородом — эндотермическая:
N2 + О2 → 2NO – Q

По фазе
Гомогенными называют реакции, протекающие в однородной среде (однородные вещества, в одной фазе, например г-г, реакции в растворах).
Гетерогенными называют реакции, протекающие в неоднородной среде, на поверхности соприкосновения реагирующих веществ, находящихся в разных фазах, например, твердой и газообразной, жидкой и газообразной, в двух несмешивающихся жидкостях.
По использованию катализатора
- Катализатор – вещество ускоряющее химическую реакцию.
- Каталитические реакции протекают только в присутствии катализатора (в том числе и ферментативные).
- Некаталитические реакции идут в отсутствие катализатора.
По типу разрыва связей
- По типу разрыва химической связи в исходной молекуле различают гомолитические и гетеролитические реакции.
- Гомолитическими называются реакции, при которых в результате разрыва связей образуются частицы, имеющие неспаренный электрон — свободные радикалы.
- Гетеролитическими называют реакции, протекающие через образование ионных частиц — катионов и анионов.
- гомолитические (равный разрыв, каждый атом по 1 электрону получает)
- гетеролитический (неравный разрыв – одному достается пара электронов)
- Радикальными (цепными) называют химические реакции с участием радикалов, например:
- CH4 + Cl2 hv →CH3Cl + HCl
- Ионными называют химические реакции, протекающие с участием ионов, например:
- KCl + AgNO3 = KNO3 + AgCl↓
- Электрофильными называют гетеролитические реакции органических соединений с электрофилами — частицами, несущими целый или дробный положительный заряд. Они подразделяются на реакции электрофильного замещения и электрофильного присоединения, например:
- C6H6 + Cl2 FeCl3→ C 6 H 5 Cl + HCl
- H2C =CH2 + Br2 → BrCH2 –CH2Br
- Нуклеофильными называют гетеролитические реакции органических соединений с нуклеофилами — частицами, несущими целый или дробный отрицательный заряд. Они подразделяются на реакции нуклеофильного замещения и нуклеофильного присоединения, например:
- CH3Br + NaOH → CH3OH + NaBr
- CH3C(O)H + C2H5OH → CH3CH(OC2H5)2 + H2O
Классификация органических реакций
Классификация органических реакций приведена в таблице:

Таблицы по теме «Типы химических реакций»


Источник: http://himege.ru/klassifikaciya-ximicheskix-reakcij-v-neorganicheskoj-i-organicheskoj-ximii/
Урок 13. Типы химических реакций – HIMI4KA
Архив уроков › Химия 8 класс
В уроке 13 «Типы химических реакций» из курса «Химия для чайников» мы узнаем о типах химических реакций; подробно рассмотрим каждый тип и научимся их различать.
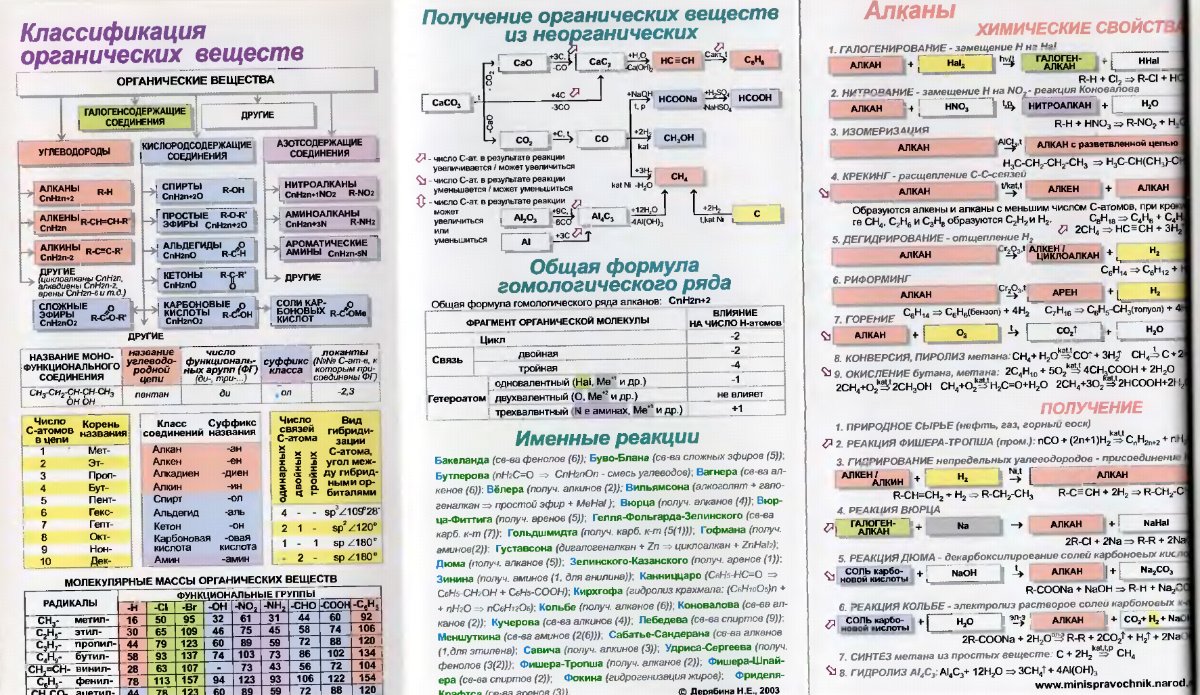
Мир химических реакций весьма разнообразен. Самые различные химические реакции постоянно происходят в природе, осуществляются человеком.
Можно ли классифицировать химические реакции? Что положить в основу их классификации? Сущность всякой химической реакции состоит в превращении веществ: разрушаются исходные вещества и образуются продукты реакций, меняется число и состав исходных веществ и продуктов реакции. Характер этих изменений и положен в основу классификации химических реакций.
Содержание
- Реакции соединения
- Реакции разложения
- Реакции замещения
Реакции соединения
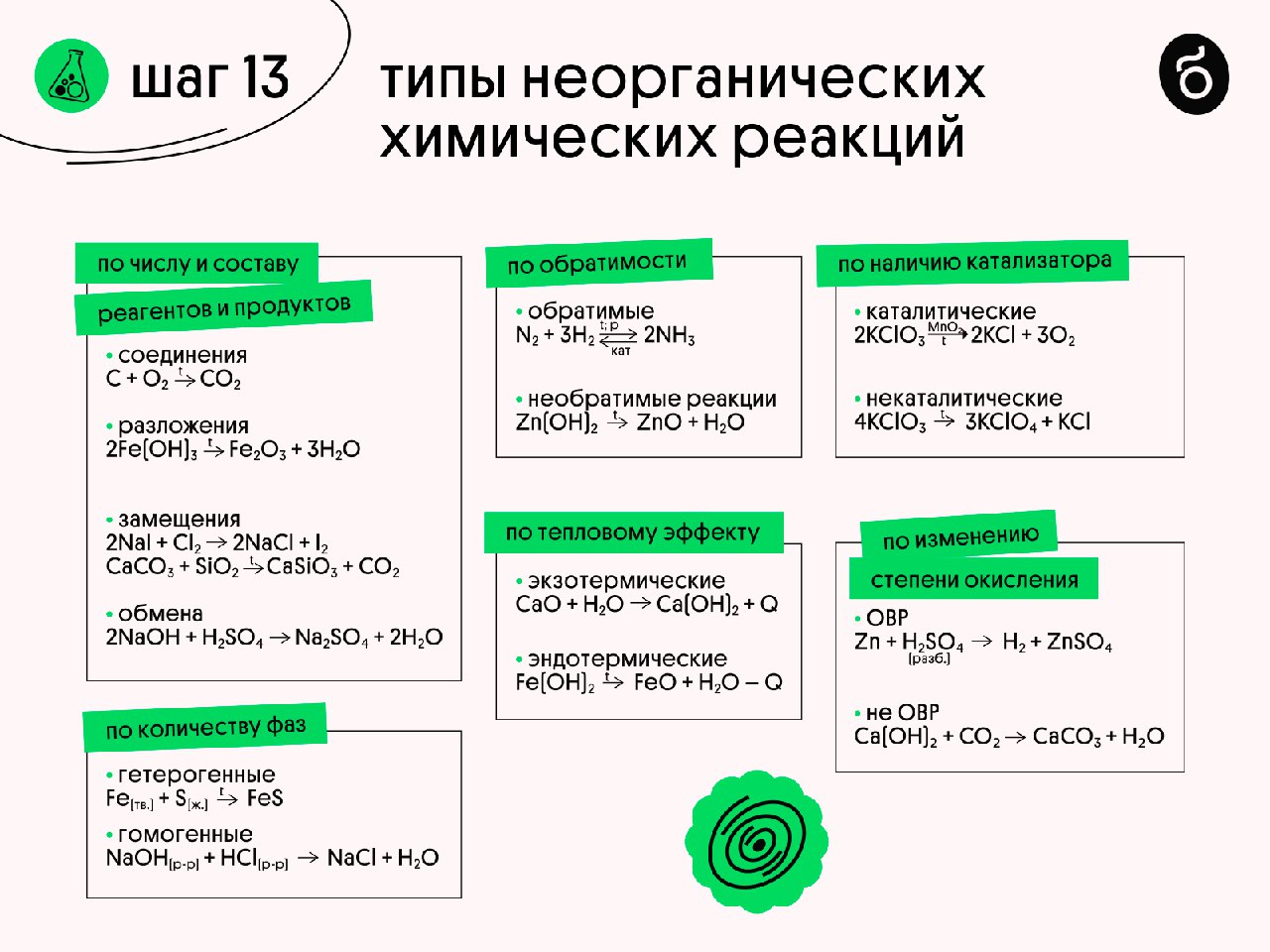
Рассмотрим уравнения следующих реакций (рис. 62):

Чем сходны данные реакции между собой? Тем, что в результате взаимодействия двух веществ получается только одно вещество. Такие реакции получили название реакций соединения.
Реакции соединения — это реакции, в результате которых из двух или нескольких веществ образуется одно новое сложное вещество.
В одних случаях из двух простых веществ получается одно сложное, в других — соединяются два и более простых или сложных веществ:
Реакции разложения
Рассмотрим уравнения следующих реакций:

Можно заметить, что из одного сложного вещества получается два или более новых веществ. Это реакции разложения. В них могут образовываться как простые, так и сложные вещества.
Реакции разложения — это реакции, в результате которых из одного сложного вещества образуется несколько новых веществ.
Для начала реакции разложения обычно необходимо нагреть исходные вещества. Например, негашеную известь CaO в промышленности получают нагреванием известняка CaCO3, реакция разложения происходит при температуре около 1000 °С. К такому типу реакций относится и реакция разложения метана CH4 (рис. 64) — составной части природного газа:

Реакции замещения
А могут ли взаимодействовать между собой два вещества: одно простое и одно сложное? Проверим это на опыте. В раствор медного купороса опустим небольшой кусочек железа — кнопку, гвоздь, канцелярскую скрепку с хорошо очищенной поверхностью.
Через 2—3 мин извлечем железо из раствора и увидим, что на его поверхности образовался темно-красный налет меди.
В химическую реакцию вступили простое (Fe) и сложное (CuSO4) вещества, и образовались новое простое (Cu) и новое сложное (FeSO4) вещества:
![]()
Из опыта и уравнения химической реакции хорошо видно, что атомы железа заместили атомы меди в сложном веществе (рис. 65). Такие химические реакции относятся к реакциям замещения.

Реакции замещения — это реакции, в результате которых атомы простого вещества замещают атомы одного из элементов в сложном веществе.
Для протекания таких реакций необходимо соблюдать некоторые особые условия. Не все простые вещества обязательно должны взаимодействовать со сложными веществами. В дальнейшем при изучении химии вы познакомитесь с этими условиями, а также с другими типами химических реакций.
Краткие выводы урока:
- Реакции соединения — это реакции, в результате которых из двух или нескольких веществ образуется одно новое сложное вещество.
- Реакции разложения — это реакции, в результате которых из одного сложного вещества образуется несколько новых веществ.
- Реакции замещения — это реакции, в которых атомы простого вещества замещают атомы одного из элементов в сложном веществе.
Надеюсь урок 13 «Типы химических реакций» был понятным и познавательным. Если у вас возникли вопросы, пишите их в комментарии. Если вопросов нет, то переходите к следующему уроку.
Источник: https://himi4ka.ru/arhiv-urokov/urok-13-tipy-himicheskih-reakcij.html
1.4.1 Классификация химических реакций в неорганической и органической химии
- Видеоурок: Типы химических реакций
- Лекция: Классификация химических реакций в неорганической и органической химии
- Виды химических реакций в неорганической химии
- А) Классификация по количеству начальных веществ:
- Разложение – вследствие данной реакции, из одного имеющегося сложного вещества, образуются два или несколько простых, а так же сложных веществ.
Пример: 2Н2O2 → 2Н2O + O2
Соединение – это такая реакция, при которой из двух и более простых, а также сложных веществ, образуется одно, но более сложное.
Пример: 4Al+3O2 → 2Al2O3
Замещение– это определенная химическая реакция, которая проходит между некоторыми простыми, а так же сложными веществами. Атомы простого вещества, в данной реакции, замещаются на атомы одного из элементов, находящегося в сложном веществе.
Пример: 2КI + Cl2 → 2КCl + I2
Обмен– это такая реакция, при которой два сложных по строению вещества обмениваются своими частями.
Пример: HCl + KNO2 → KCl + HNO2
Б) Классификация по тепловому эффекту:
Экзотермические реакции – это определенные химические реакции, при которых происходит выделение тепла. Примеры:
S +O2 → SO2 + Q
2C2H6 + 7O2 → 4CO2 +6H2O + Q
Эндотермические реакции – это определенные химические реакции, при которых происходит поглощение тепла. Как правило, это реакции разложения.
- Примеры:
- CaCO3 → CaO + CO2 – Q2KClO3 → 2KCl + 3O2 – Q
- Теплота, которая выделяется или поглощается в результате химической реакции, называется тепловым эффектом.
- Химические уравнения, в которых указан тепловой эффект реакции, называют термохимическими.
- В) Классификация по обратимости:
Обратимые реакции – это реакции, которые протекают при одинаковых условиях во взаимопротивоположных направлениях.
Пример: 3H2 + N2 ⇌ 2NH3
Необратимые реакции– это реакции, которые протекают только в одном направлении, а так же завершающиеся полным расходом всех исходных веществ. При этих реакциях выделяется газ, осадок, вода.Пример: 2KClO3 → 2KCl + 3O2 ↑
Г) Классификация по изменению степени окисления:
Окислительно — восстановительные реакции – в процессе данных реакций происходит изменение степени окисления.
Пример: Сu + 4HNO3 → Cu(NO3)2 + 2NO2 + 2H2O.
Не окислительно — восстановительные – реакции без изменения степени окисления.
Пример: HNO3 + KOH → KNO3 + H2O.
Д) Классификация по фазе:
Гомогенные реакции – реакции, протекающие в одной фазе, когда исходные вещества и продукты реакции имеют одно агрегатное состояние.
Пример: Н2(газ) + Cl2(газ) → 2HCL
Гетерогенные реакции– реакции, протекающие на поверхности раздела фаз, при которых продукты реакции и исходные вещества имеют разное агрегатное состояние.Пример: CuO+ H2 → Cu+H2O
Классификация по использованию катализатора:
Катализатор – вещество, которое ускоряет реакцию. Каталитическая реакция протекает в присутствии катализатора, некаталитическая – без катализатора.Пример: 2H202MnO2→ 2H2O + O2 катализатор MnO2Взаимодействие щелочи с кислотой протекает без катализатора.
Пример: КOH + HCl → КCl + H2O
Ингибиторы – вещества, замедляющие реакцию.Катализаторы и ингибиторы сами в ходе реакции не расходуются.
Виды химических реакций в органической химии
Замещение – это реакция, в процессе которой происходит замена одного атома/группы атомов, в исходной молекуле, на иные атомы/группы атомов. Пример: СН4 + Сl2 → СН3Сl + НСl
Присоединение– это реакции, при которых несколько молекул вещества соединяются в одну. К реакциям присоединения относятся:
- Гидрирование – реакция, в процессе которой происходит присоединение водорода по кратной связи.
Пример: СН3—СН = СН2 (пропен) + Н2 → СН3—СН2—СН3 (пропан)
- Гидрогалогенирование – реакция, присоединяющая галогенводород.
Пример: СН2 = СН2 (этен) + НСl → СН3—СН2—Сl (хлорэтан)
Алкины реагируют с галогеноводородами (хлороводородом, бромоводородом) так же, как и алкены. Присоединение в химической реакции проходит в 2 стадии, и определяется правилом Марковникова:
При присоединении протонных кислот и воды к несимметричным алкенам и алкинам атом водорода присоединяется к наиболее гидрогенизированному атому углерода.
Механизм данной химической реакции. Образующийся в 1 — ой, быстрой стадии, p- комплекс во 2 — ой медленной стадии постепенно превращается в s-комплекс — карбокатион. В 3 — ей стадии происходит стабилизация карбокатиона – то есть взаимодействие с анионом брома:

И1, И2 — карбокатионы. П1, П2 — бромиды.
Галогенирование – реакция, при которой присоединяется галоген. Галогенированием так же, называют все процессы, в результате которых в органические соединения вводятся атомы галогена. Данное понятие употребляется в «широком смысле». В соответствии с данным понятием, различают следующие химические реакции на основе галогенирования: фторирование, хлорирование, бромирование, йодирование.
Галогенсодержащие органические производные считаются важнейшими соединениями, которые применяются как в органическом синтезе, так и в качестве целевых продуктов. Галогенпроизводные углеводородов, считаются исходными продуктами в большом количестве реакций нуклеофильного замещения.
Что касается практического использования соединений, содержащих галоген, то они применяются в виде растворителей, например хлорсодержащие соединения, холодильных агентов — хлорфторпроизводные, фреоны, пестицидов, фармацевтических препаратов, пластификаторов, мономеров для получения пластмасс.
Гидратация – реакции присоединения молекулы воды по кратной связи.
Полимеризация – это особый вид реакции, при которой молекулы вещества, имеющие относительную невеликую молекулярную массу, присоединяются друг к другу, впоследствии образовывая молекулы вещества с высокой молекулярной массой.
| Предыдущий урок | Следующий урок |
Источник: https://cknow.ru/knowbase/754-141-klassifikaciya-himicheskih-reakciy-v-neorganicheskoy-i-organicheskoy-himii.html
Классификация химических реакций, с примерами
Наиболее часто под химическими реакциями понимают процесс превращения исходных веществ (реагентов) в конечные вещества (продукты).
Химические реакции записываются с помощью химических уравнений, содержащих формулы исходных веществ и продуктов реакции. Согласно закону сохранения массы, число атомов каждого элемента в левой и правой частях химического уравнения одинаково.
Обычно формулы исходных веществ записывают в левой части уравнения, а формулы продуктов – в правой.
Равенство числа атомов каждого элемента в левой и правой частях уравнения достигается расстановкой перед формулами веществ целочисленных стехиометрических коэффициентов.
Химические уравнения могут содержать дополнительные сведения об особенностях протекания реакции: температура, давление, излучение и т.д., что указывается соответствующим символом над (или «под») знаком равенства.
Все химические реакции могут быть сгруппированы в несколько классов, которым присущи определенные признаки.
Классификация химических реакций по числу и составу исходных и образующихся веществ
- Согласно этой классификации, химические реакции подразделяются на реакции соединения, разложения, замещения, обмена.
- В результате реакций соединения из двух или более (сложных или простых) веществ образуется одно новое вещество. В общем виде уравнение такой химической реакции будет выглядеть следующим образом:
- A + B (+D) = C
- Например:
- СаСО3 + СО2 + Н2О = Са(НСО3)2
- SO3 + H2O = H2SO4
- 2Mg + O2 = 2MgO.
- 2FеСl2 + Сl2 = 2FеСl3
Реакции соединения в большинстве случаев экзотермические, т.е. протекают с выделением тепла. Если в реакции участвуют простые вещества, то такие реакции чаще всего являются окислительно-восстановительными (ОВР), т.е.
протекают с изменением степеней окисления элементов. Однозначно сказать будет ли реакция соединения между сложными веществами относиться к ОВР нельзя.
- Реакции, в результате которых из одного сложного вещества образуется несколько других новых веществ (сложных или простых) относят к реакциям разложения. В общем виде уравнение химической реакции разложения будет выглядеть следующим образом:
- A= B+ C + D
- Например:
- CaCO3CaO + CO2 ↑ (1)
- 2H2O =2H2 ↑+ O2↑ (2)
- CuSO4 × 5H2O = CuSO4 + 5H2O (3)
- Cu(OH)2 = CuO + H2O (4)
- H2SiO3 = SiO2 + H2O (5)
- 2SO3 =2SO2 + O2 ↑ (6)
- (NH4)2Cr2O7 = Cr2O3 + N2↑ +4H2O (7)
Большинство реакций разложения протекает при нагревании (1,4,5). Возможно разложение под действием электрического тока (2).
Разложение кристаллогидратов, кислот, оснований и солей кислородсодержащих кислот (1, 3, 4, 5, 7) протекает без изменения степеней окисления элементов, т.е. эти реакции не относятся к ОВР.
К ОВР реакциям разложения относится разложение оксидов, кислот и солей, образованных элементами в высших степенях окисления (6).
- Реакции разложения встречаются и в органической химии, но под другими названиями — крекинг (8), дегидрирование (9):
- С18H38 = С9H18 + С9H20 (8)
- C4H10 = C4H6 + 2H2 ↑ (9)
- При реакциях замещения простое вещество взаимодействует со сложным, образуя новое простое и новое сложное вещество. В общем виде уравнение химической реакции замещения будет выглядеть следующим образом:
- A + BC = AB + C
- Например:
- 2Аl + Fe2O3 = 2Fе + Аl2О3 (1)
- Zn + 2НСl = ZnСl2 + Н2 (2)
- 2КВr + Сl2 = 2КСl + Вr2 (3)
- 2КСlO3 + l2 = 2KlO3 + Сl2 (4)
- СаСО3+ SiO2 = СаSiO3 + СО2 (5)
- Са3(РО4)2 + ЗSiO2 = ЗСаSiO3 + Р2О5 (6)
- СН4 + Сl2 = СН3Сl + НСl (7)
Реакции замещения в своем большинстве являются окислительно-восстановительными (1 – 4, 7). Примеры реакций разложения, в которых не происходит изменения степеней окисления немногочисленны (5, 6).
Реакциями обмена называют реакции, протекающие между сложными веществами, при которых они обмениваются своими составными частями. Обычно этот термин применяют для реакций с участием ионов, находящихся в водном растворе. В общем виде уравнение химической реакции обмена будет выглядеть следующим образом:
- АВ + СD = АD + СВ
- Например:
- CuO + 2HCl = CuCl2 + H2O (1)
- NaOH + HCl = NaCl + H2O (2)
- NаНСО3 + НСl = NаСl + Н2О + СО2↑ (3)
- AgNО3 + КВr = АgВr ↓ + КNО3 (4)
- СrСl3 + ЗNаОН = Сr(ОН)3 ↓+ ЗNаСl (5)
Реакции обмена не являются окислительно-восстановительными. Частный случай этих реакций обмена -реакции нейтрализации (реакции взаимодействия кислот со щелочами) (2). Реакции обмена протекают в том направлении, где хотя бы одно из веществ удаляется из сферы реакции в виде газообразного вещества (3), осадка (4, 5) или малодиссоциирующего соединения, чаще всего воды (1, 2).
Классификация химических реакций по изменениям степеней окисления
- В зависимости от изменения степеней окисления элементов, входящих в состав реагентов и продуктов реакции все химические реакции подразделяются на окислительно-восстановительные (1, 2) и, протекающие без изменения степени окисления (3, 4).
- 2Mg + CO2 = 2MgO + C (1)
- Mg0 – 2e = Mg2+ (восстановитель)
- С4+ + 4e = C0 (окислитель)
- FeS2 + 8HNO3(конц) = Fe(NO3)3 + 5NO↑ + 2H2SO4 + 2H2O (2)
- Fe2+ -e = Fe3+ (восстановитель)
- N5+ +3e = N2+ (окислитель)
- AgNO3 +HCl = AgCl ↓ + HNO3 (3)
- Ca(OH)2 + H2SO4 = CaSO4 ↓ + H2O (4)
Классификация химических реакций по тепловому эффекту
В зависимости от того, выделяется ли или поглощается тепло (энергия) в ходе реакции, все химические реакции условно разделяют на экзо – (1, 2) и эндотермические (3), соответственно.
Количество тепла (энергии), выделившееся или поглотившееся в ходе реакции называют тепловым эффектом реакции.
Если в уравнении указано количество выделившейся или поглощенной теплоты, то такие уравнения называются термохимическими.
- N2 + 3H2 = 2NH3 +46,2 кДж (1)
- 2Mg + O2 = 2MgO + 602, 5 кДж (2)
- N2 + O2 = 2NO – 90,4 кДж (3)
Классификация химических реакций по направлению протекания реакции
- По направлению протекания реакции различают обратимые (химические процессы, продукты которых способны реагировать друг с другом в тех же условиях, в которых они получены, с образованием исходных веществ) и необратимые (химические процессы, продукты которых не способны реагировать друг с другом с образованием исходных веществ).
- Для обратимых реакций уравнение в общем виде принято записывать следующим образом:
- А + В ↔ АВ
- Например:
- СН3СООН + С2Н5ОН↔ Н3СООС2Н5+ Н2О
- Примерами необратимых реакций может служить следующие реакции:
- 2КСlО3 → 2КСl + ЗО2↑
- С6Н12О6 + 6О2 → 6СО2↑+ 6Н2О
- Свидетельством необратимости реакции может служить выделение в качестве продуктов реакции газообразного вещества, осадка или малодиссоциирующего соединения, чаще всего воды.
Классификация химических реакций по наличию катализатора
С этой точи зрения выделяют каталитические и некаталитические реакции.
Катализатором называют вещество, ускоряющее ход химической реакции. Реакции, протекающие с участием катализаторов, называются каталитическими. Протекание некоторых реакций вообще невозможно без присутствия катализатора:
- 2H2O2 = 2H2O + O2 ↑ (катализатор MnO2)
- Нередко один из продуктов реакции служит катализатором, ускоряющим эту реакцию (автокаталитические реакции):
- MeO+ 2HF = MeF2 + H2O, где Ме – металл.
Примеры решения задач
Источник: http://ru.solverbook.com/spravochnik/ximiya/11-klass/klassifikaciya-ximicheskix-reakcij/




