 Студенты средних специальных и высших учебных заведений готовят по профильному предмету проекты. Чтобы защита была успешной, предварительно изучается ГОСТ содержания курсовой работы с образцами. При её написании студент проводит исследования, придерживаясь определённой структуры, последовательности изложения информации. Чтобы написать проект, потребуется около месяца.
Студенты средних специальных и высших учебных заведений готовят по профильному предмету проекты. Чтобы защита была успешной, предварительно изучается ГОСТ содержания курсовой работы с образцами. При её написании студент проводит исследования, придерживаясь определённой структуры, последовательности изложения информации. Чтобы написать проект, потребуется около месяца.
Принцип написания

Основные аспекты и стандарты, по которым регламентируется оформление содержания курсовых, считается ГОСТ 7 .32−2001. Правильное оформление оглавления курсовой работы помогает проверяющему ориентироваться в ней. Этот фактор учитывается при оценке студента. — план, по которому курсовик защищается. Его объём не должен превышать 1 страницу А4. Раздел располагают после титульного листа, но перед введением.
В оглавлении должны писаться:
- названия разделов и подразделов, описанных в проекте;
- номера страниц.
Запрещено ставить знак параграфа. Основа содержания — план исследования, написанный после изучения литературы по раскрываемой теме. С помощью такого плана студент может последовательно изучить проблему, соблюдая принятую структуру.
Чтобы правильно оформить проект, преподаватели советуют рассмотреть несколько примеров содержаний курсовых работ. Другие рекомендации научных руководителей:
 Разделы и подразделы нужно называть должным образом, придерживаясь тематики проекта.
Разделы и подразделы нужно называть должным образом, придерживаясь тематики проекта.- Нельзя в главах дублировать название самой работы.
- Каждая глава раскрывает определённый вопрос.
- Взаимосвязь между всеми разделами, подразделами и главами.
- Отсутствие одинаковых названий пунктов.
Титульный лист входит в нумерацию, но на нём номер страницы не проставляется. Оглавление размещается на второй страницы курсовика. Нумерацию нужно проставлять внизу страницы справа либо по центру.
Гост требования

Если придерживаться такого совета, оглавление будет структурированным и грамотным. Частая ошибка курсовиков — нумерация вводной и заключительной частей, перечня источников, приложения. По ГОСТу, нумерации подлежит только основной раздел работы.
Нумерация глав и подглав должна выглядеть следующим образом:
- Если номер главы — 3, подглавы нумерируют 3.1, 3.2, 3.3.
- Пункты подглав должны оформляться 3.1.1. , 3.1.2. , 3.1.3.
Научные руководители советуют брать примеры оглавлений курсовых работ из методических указаний. Проекты, которые можно скачать из глобальной сети, не всегда выполнены по ГОСТ стандартам.
Программа Word
Курсовые работы по любой теме оформляются с помощью компьютерной программы Microsoft Office Word. С учётом года выпуска различают несколько версий программы. На выбор Word прямое влияние оказывает Windows, установленный на рабочем компьютере. Несмотря на версию, принцип оформления содержания курсовой одинаковый.

Чтобы составить содержание, необходимо убедиться в том, что все разделы начинаются с нового листа формата А4. Этапы автоматической сборки готового текста:
- Нумерация страниц колонцифрами.
- Открывается вкладка «Вставка», расположенная вверху программы.
- Выбирается опция «Номер страницы».
- Появляется окно, в котором нужно определиться с местом расположения страницы (в методичках — это по центру внизу).
После автоматической нумерации листов окно колонтитулов закрывается.
Разделы и списки
Чтобы правильно оформить разделы, используется окно со стилями. Оно расположено справа. Предварительно выделяется соответствующий пункт. С учётом его значимости поэтапно применяется подходящий вариант:
- Названия глав оформляют с помощью «Заголовка 1».
- Для подразделов используется «Заголовок 2».

Во вкладке пользователь нажимает на «Автособираемое». Появляется список, составленный автоматически из выделенных названий разделов. Таким способом студент можно ознакомиться с условным образцом содержания курсовой работы, сформированным с помощью программы Word.
При оформлении учитывается тот факт, что оглавление размещается на одной странице. Его отделяют от основного текста работы. Для этого студенту потребуется выполнить следующие действия:
- Нажать на «Вставка».
- Слева щёлкнуть по строке «Разрыв страницы».
Корректировка и редактирование
Курсовые нужно не только грамотно писать, но и правильно их корректировать. Если изменился цвет либо шрифт, поправка вносится с помощью мышки. Курсор устанавливается на нужном заголовке. Нажав на правую кнопку мышки, появляется вкладка с разными действиями. Пользователь должен выбрать «Изменить».
Открывается окно с параметрами форматирования. Для заголовков различных уровней устанавливается соответствующий стиль. Во время написания курсовой студент сталкивается с разными проблемами: удаление и введение текста, изменение заголовка. При форматировании сдвигается нумерация страниц.

Выбирается подходящий ремонт коррекции. Содержимое обновляется мгновенно. Оглавление редактируется после правок проекта. Чтобы изъять оглавление, потребуется выполнить следующие действия: в панели инструментов выбирается «ссылки» — «оглавление» — «удалить».
Чтобы использовать навигацию по работе, нажимается клавиша Ctrl, курсором кликают по пункту списка. Для оформления листов с рамкой можно воспользоваться соответствующей функцией.
Практические советы
Научные руководители рекомендуют набирать заголовки в курсовых, придерживаясь полужирного стиля. Нельзя переносить слова, ставить знаки препинания в конце заголовка. С учётом профиля проекта используются автоматические сноски либо сноски в тексте в квадратных, круглых скобках.
Как правильно составлять литературный список, можно узнать из ГОСТа 7.1−2003. Курсовую пишут, используя информацию из книг, законодательных материалов, стандартов, диссертаций, учебников, методических материалов.
Чтобы верно оформить содержание курсовой работы, студент должно помнить о следующих правилах:
 Логическое соответствие содержания с темой проекта. Работу нужно писать последовательно: подразделы разделяют темы глав на несколько составляющих.
Логическое соответствие содержания с темой проекта. Работу нужно писать последовательно: подразделы разделяют темы глав на несколько составляющих.- Основная часть должны состоять минимум из двух глав.
- Иллюстрации и таблицы оформляются как приложения.
- Если нужно проиллюстрировать определённый раздел большим объёмом данных, используется приложение.
- Каждый раздел должен быть пронумерован. Если глава состоит из нескольких параграфов, номер страницы указывается напротив них.
Если написать и оформить курсовую, придерживаясь рекомендаций научного преподавателя и по ГОСТу, студент сможет избежать доработок.
Источник: https://100umov.com/oformlenie-soderzhanija-kursovoj/
Оглавление курсовой работы (образец, примеры, правила оформления)
При получении темы оглавление курсовой работы представляется самой простой частью в плане оформления. Но когда доходит до дела, среди студентов нередко возникает масса вопросов. Разъяснить их помогут государственные стандарты и инструкции по составлению студенческих работ.
Как писать оглавление в курсовой работе по ГОСТу
Общие требования по оформлению можно найти в ГОСТ 7.32. Сводятся они к следующему:
-
План располагается на второй странице, в верхней ее части по центру пишется слово «».
-
Далее следует список: «Введение», название глав и подглав, «Заключение», «Список использованной литературы» и «Приложения» при необходимости.
-
Наименование каждого раздела пишется прописными буквами, интервал полуторный.
-
Подглавы сдвигаются вправо на один отступ (1, 25).
- Заявка на курсовую
Напротив каждого пункта указывается страница.
-
Нумерация листа начинается с цифры 2. В зависимости от методических рекомендаций конкретного учебного заведения у страницы может быть не прописан номер.
-
Шрифт указывается Times New Roman, кегль 14.
-
Интервал между названием главы и номером заполняется точками.
-
Страницы нумеруются арабскими цифрами.
Многих волнует, какое наименование для курсовой работы правильное «Оглавление» или «». Первый вариант предпочтительнее, так как обозначает части работы, связанные тематически между собой. «» уместно, когда представлены отдельные труды. Обычно в курсовой допускаются оба варианта, но все же лучше ориентироваться на методические рекомендации ВУЗа
Как сделать оглавление курсовой в Ворде
Функционал Microsoft Office Word позволяет решить вопрос «Как быстро оформить оглавление в курсовой работе?» с помощью инструментов, расположенных во вкладке «Ссылки»:
-
Создается новый лист.
-
Во вкладке «Оглавление» выбирается «Ручное оглавление».
-
Появляется прямоугольник, в который вписываются названия конкретных глав.
Не всем удобно вручную вносить возникающие изменения. Поэтому, чтобы оформить содержание быстрее, некоторые используют автособираемую форму.
-
Нужно проследить, чтобы все заголовки были выполнены инструментами Word, листы правильно пронумерованы.
-
Далее надо отметить все главы.
-
Во вкладке «Стиль» выбрать подходящий заголовок.
-
После того, как название всех глав выглядит по регламенту, в разделе «Вставка» кликнуть на «Номер страницы» – «Закрыть окно колонтитулов».
-
Всем заголовкам присвоить уровень. Для этого нужно открыть вкладку «Ссылки», поставить курсор перед заголовком и нажать «Добавить текст».
-
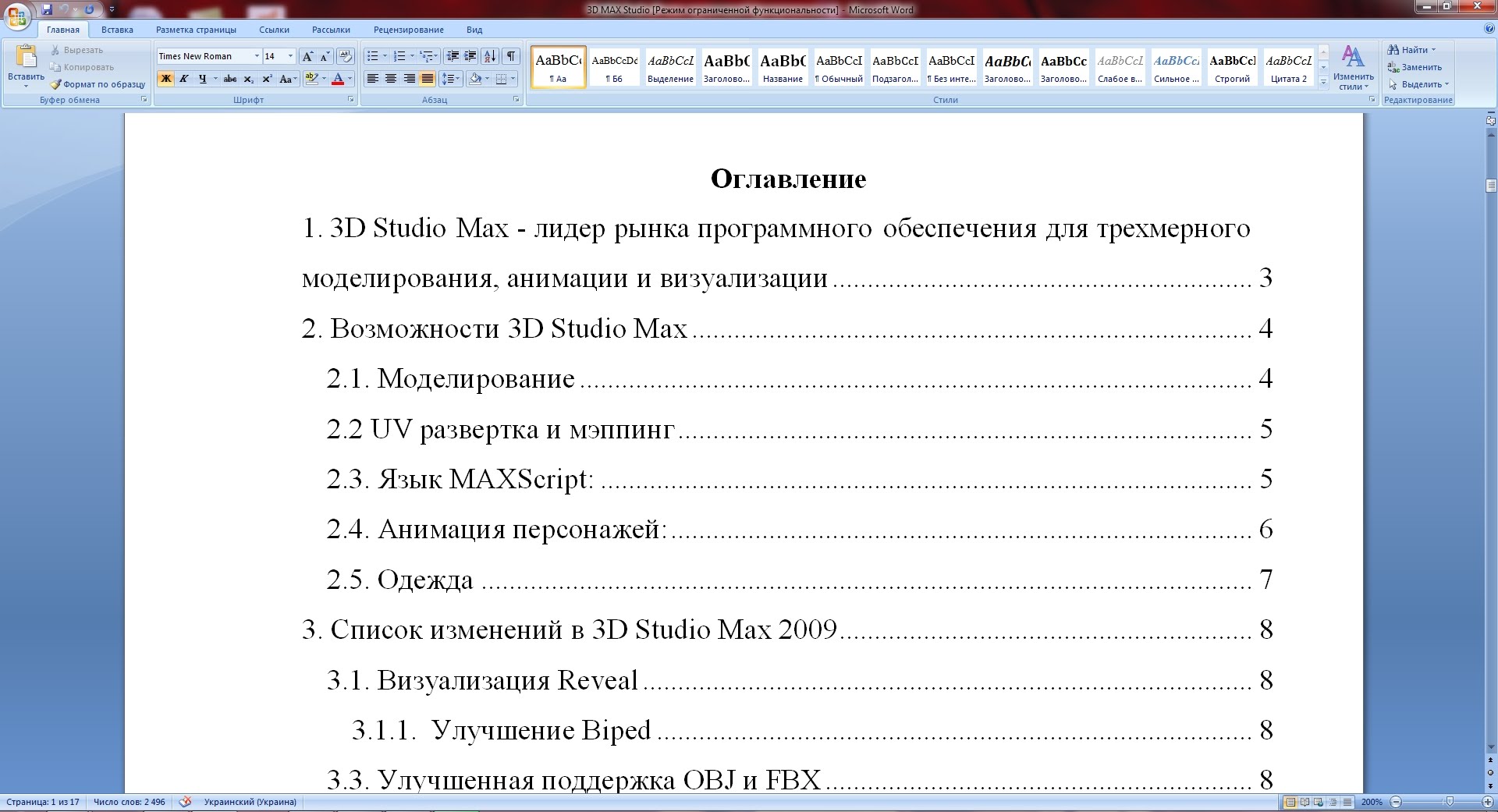
Для оформления оглавления курсовой работы необходимо установить курсор там, где будет расположен план, нажать на «Оглавление» – «Автособираемое оглавление».
Оформить содержание стоит таким образом, чтобы весь текст расположился на одной странице

Оформление оглавления курсовой работы вручную
Оглавление курсовой работы можно писать как автоматически, так и вручную. Обычно это делается так.
-
На новой странице пишется слово «» и выравнивается по центру.
-
На следующей строке указывается название раздела с соответствующим номером.
-
Расстояние заполняется точками.

Как видим из примера, столбик цифр получается неровным. Грамотно оформить столбец можно следующим образом:
-
Пишем слово «».
-
Переходим на новую строку и нажимаем «Нумерованный список».
-
Пишем название заголовка.
- Стоимость курсовой
Оставив курсор после последнего слова, выбираем «Разметка страницы» – «Абзац» – «Табуляция».
-
Выставляем параметры: сантиметры до номера, выравнивание по правому краю, заполнитель.
-
Печатая следующий заголовок, придерживайте «Tab», чтобы оказаться на месте, где прописывается номер страницы.
Образец оглавления курсовой работы
Пример оформления содержания курсовой работы.
Чтобы грамотно оформить содержание курсовой работы, необходимо в первую очередь ознакомиться с ГОСТом 7.32 и основными требованиями учебного заведения к курсовым работам, плюс хорошо ориентироваться в Microsoft Office Word. Также следует вручную проверять правильность нумерации и соответствие наименований глав в содержании тем, что указаны внутри работы.
Возврат к списку
Источник: https://tebestudent.ru/polezno-znat/kursovye-raboty/obrazets-oglavleniya-kursovoy-raboty/
Как написать содержание для курсовой работы любой специальности: советы и пример
– обязательная составляющая любого квалификационного проекта. По сути, оно представляет собой план, выведенный на отдельную страницу.
С вопросом, как написать содержание курсовой работы, рано или поздно приходится сталкиваться каждому студенту.
Без умения формировать грамотный и четкий план невозможно написать качественный квалификационный проект при переходе на следующий курс.
Четкая структура позволяет преподавателю определить, насколько раскрыта выбранная студентом тема и не пропустил ли он важные вопросы. Таким образом, содержание влияет на предварительную оценку работы. О том, как правильно структурировать курсовую и можно ли пропустить данный этап, читайте далее.
курсовой работы отражает ее структуру и рассмотренные автором вопросы. Для его размещения отводится отдельная страница после титульного листа. предоставляет возможность обзорно ознакомиться с сутью курсовой перед ее изучением.
Квалификационные проекты в высших учебных заведениях не принимаются без четкой структуры. Отсутствие содержания в курсовой работе является ошибкой, поэтому без соблюдения данного условия студент может не получить должную оценку даже, если выполнит остальные требования.
Важно! Многие учащиеся часто путают содержание и план, однако данные термины имеют разное обозначение. Чаще всего с подобной проблемой сталкиваются первокурсники, у которых отсутствует опыт в сдаче курсовых работ. действительно включает план, но имеет более широкое обозначение.
При несоответствии названий разделов и отсутствии разметки страниц просмотреть структуру работы без ее чтения невозможно. Поэтому, составляя содержание, следует придерживаться целого ряда правил.
курсовой работы составляется двумя способами: собственными силами или с использованием интернет-ресурсов. Даже опытные студенты испытывают трудности при написании квалификационной работы, ввиду чего им приходится обращаться к посторонней помощи. Специализированные сайты расскажут, как написать и оформить содержание курсовой работы.
Перед написанием проекта его образец должен быть утвержден научным руководителем. Если какой-то вопрос не будет согласован с преподавателем, при защите курсовой возникнут проблемы. С советами специалиста работа будет писаться гораздо проще, а вероятность получить за нее положительную оценку – намного выше.
Когда содержание будет оформляться, необходимо придерживаться следующих требований:
- Указать название «» или «Оглавление» прописными буквами.
- Убедиться, что поля имеют такие же размеры, как и во всей работе.
- Не указывать титульный лист.
- Вписывать название каждого пункта с новой строки.
- Рядом с каждым наименованием следует проставить номер страницы.
- Обозначить наличие прикладных материалов (таблиц, диаграмм, рисунков).
Обратите внимание! Многие студенты игнорируют перечисленные требования перед тем, как писать содержание курсовой работы, из-за чего допускают серьезную ошибку. Если не учесть правила структурирования, можно получить более низкую оценку за проект.
Чтобы узнать, как составить содержание курсовой работы, необходимо внимательно изучить общие нормы и рекомендации. При возникновении проблем Вы можете обратиться к нам и получить десятипроцентную скидку на написание и оформление любого проекта.
курсовой работы включает:
- Введение. В данном пункте студент должен определить актуальность выбранной темы, выделить цели и задачи исследования, после чего описать применяемые методы. Также во введении указываются источники, использованные при написании работы.
- Основной текст. Данный этап включает большую часть работы, в которой необходимо провести исследования, придя к планируемому результату. Курсовая схожа по структуре с диссертацией, поэтому она должна быть поделена не только на главы, но и подразделы. В отличие от реферата данный вид работы требует углубленного изучения темы.
- Заключение. Эта составляющая курсовой включает основные моменты исследования и его результаты.
- Список использованной литературы. Необходимо указать источники, которые были изучены в ходе написания работы.
- Приложения. Данный пункт не является обязательным и используется при проведении практического исследования. Если работа строится на основе теоретических рассуждений, в большинстве случаев приложения не требуются.
Для того, чтобы содержание было утверждено, в нем должна прослеживаться четкая последовательность. Некоторые студенты намерено пропускают сложную часть исследования, из-за чего аттестационная комиссия может задать дополнительные вопросы, которые негативно отразятся на оценке.
Следует убедиться, что пункты, указанные в содержание, имеют такие же названия, как и в тексте. Несоответствие оглавления по отношению к указанным разделам расценивается как нарушение норм.
Кроме того, в содержании не должно быть орфографических и пунктуационных ошибок, наличие которых ухудшает мнение аттестационной комиссии об авторе проекта. Придерживаясь аналогичных требований, составляется и дипломный проект. Если Вы испытываете трудности с тем, как писать содержание курсовой работы, можете ознакомиться с готовыми примерами:
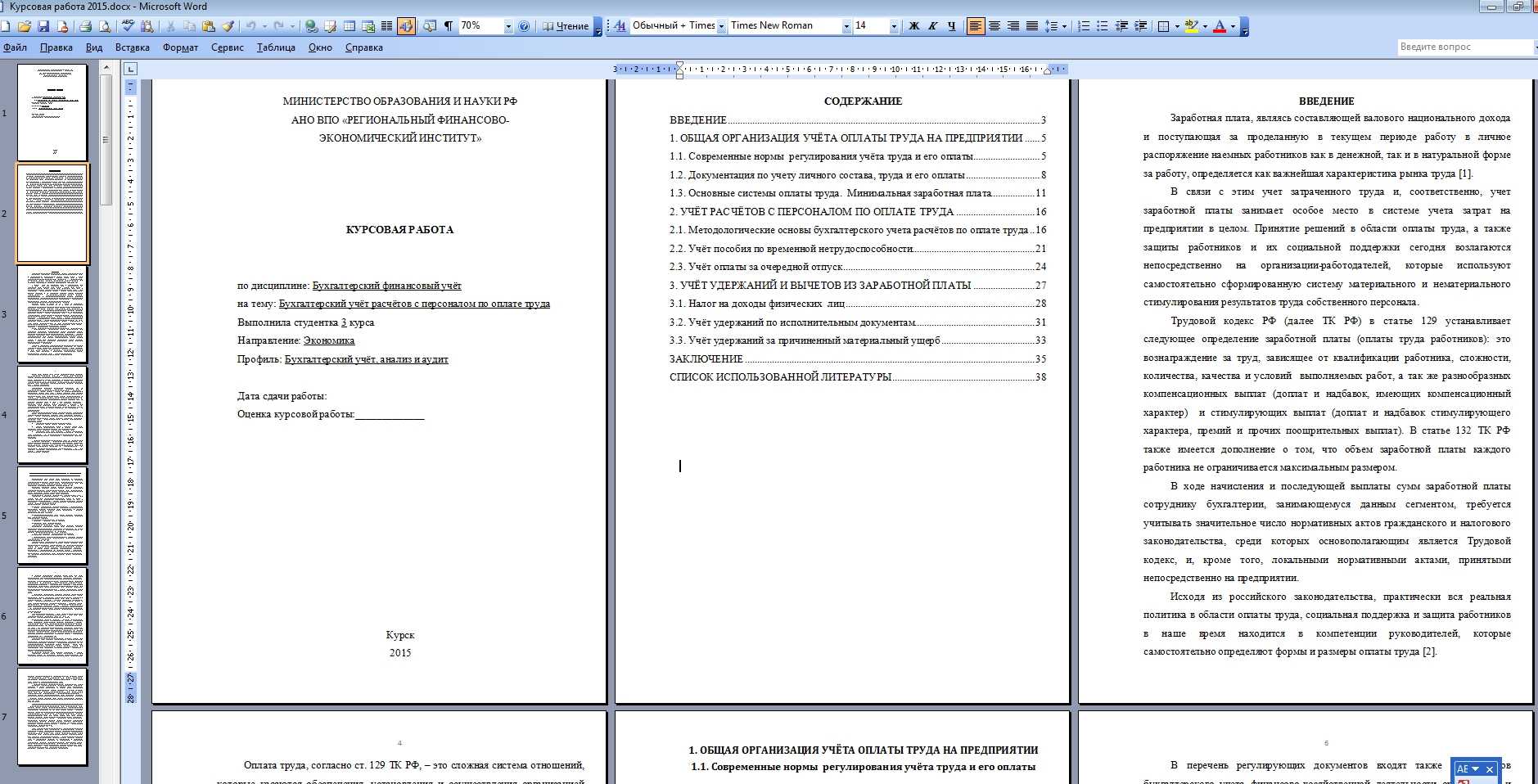

Большая часть ошибок, допускаемых студентами, связана с оформлением содержания. С данной проблемой сталкиваются учащиеся любых курсов, независимо от успеваемости и регулярности посещения лекций. Чтобы их избежать и написать правильное содержание, необходимо действовать строго по ГОСТу:
- Соблюдать последовательность и логику между разделами. Все пункты должны быть связаны и продолжать общее исследование.
- Использовать в разделе данные, соответствующие его названию. Не наполнять содержание главы лишней информацией для увеличения объема работы.
- Следить за тем, чтобы название каждого раздела не превышало больше одного предложения.
Внимание! Наименования глав в работе не должны совпадать.
Грамотно составленное содержание – важный шаг, от которого зависит успешная защита курсовой. Именно на структуру приемная комиссия в первую очередь обращает внимание. Если Вы беспокоитесь об ошибках, у нас можно заказать курсовую работу с готовым содержанием.
Источник: https://Studently.ru/blog/kursovye-raboty/soderzhanie-dlja-kursovoj-raboty/
Как оформить содержание в курсовой работе: пример правильного оглавления
Некоторые преподаватели очень любят аккуратность, поэтому часто снижают оценки только из-за помарок в оформлении. Одним из проблемных в оформлении мест является оглавление. Оглавление и титульный лист – это первое, что видит человек, взявший работу в руки.
Оглавление или содержание в курсовой
Многие студенты путают эти два понятия. Поэтому, чтобы избежать лишних помарок, следует знать, в чем их отличия, чтобы грамотно написать курсовую.
Определение 1
составляют тогда, когда разделы в работе не связаны между собой (например, в сборнике задач). Оглавление – когда главы соотносятся одна с другой.
Таким образом, понятно, что в курсовых необходимо писать «Оглавление».
Пример 1
Однако бывают курсовые работы, состоящие из разнородных частей (например, по бухгалтерскому учету преподаватель может предложить подготовить ответы на несколько теоретических вопросов и решить сквозную задачу по вымышленному предприятию) – тогда требуется оформление содержания курсовой работы.
- Оглавление включает в себя перечень всех разделов курсовой работы с указанием страниц, начиная с введения.
- Приведем несколько общих советов, как правильно оформить содержание в курсовой работе:
- Оглавление должно располагаться на второй странице сразу после титульного листа.
Пример 2
Иногда преподаватели требуют составить реферат по курсовой работе – своеобразную краткую характеристику, содержащую некоторые формальные сведения. В таком случае оглавление перемещается на третью страницу.
- Ответ на вопрос, что включает в себя содержание курсовой работы, однозначен: введение, главы и параграфы основной части, заключение, список использованных источников и приложения. Оглавление в курсовой работе не должно включать другие элементы, к примеру, титульный лист и реферат.
- Названия глав должны представлять собой законченную мысль. Перед тем, как сделать оглавление в курсовой работе, следует удостовериться, что названия глав и параграфов являются повествовательными предложениями. Вопросительные предложения в заголовках более типичны для публицистического, а не научного стиля.
Пример 3
Примеры названий параграфов в содержании курсовой работы: «Понятие монетарной политики» (а не «Что такое монетарная политика?»), «Виды монетарной политики» (а не «Какая бывает монетарная политика?»).
Оглавление должно отражать всю концепцию курсовой, весь ее план.
- После названий разделов точка не ставится. Это предусматривается требованиями оформления содержания курсовой по ГОСТу (точно так же, как точка не ставится после заголовка, размещенного в тексте работы).
- Правильное оформление курсовой работы предусматривает выравнивание текста по образцу: названия элементов – по левому краю (возможно делать отступы для отражения структуры – заголовки второго уровня с большим отступом, чем заголовки первого уровня), а названия страниц – по правому краю.
- Существуют и дискуссионные вопросы в том, как правильно оформить оглавление курсовой работы.
Пример 4
В некоторых вузах требуют использовать между названием структурного элемента и номером страницы заполнитель (обычно точки) для удобства чтения оглавления, в других настаивают на том, что место должно оставаться пустым.
Оформление автоматически собираемого оглавления курсовой работы
По тому, как выглядит содержание курсовой, можно сделать выводы об уровне владения ее автором текстовым редактором.
Разработчики популярных текстовых редакторов – MS Word, OpenOffice.Org Writer и подобных им – придумали, как оформлять содержание в курсовой с минимальными трудозатратами. Но не только студенты, но и преподаватели не всегда знают об этих возможностях, и продолжают выполнять оформление содержания в курсовой вручную.
Преимущества автоматического оглавления:
- Названия глав и параграфов будут выглядеть точно так же, как и в тексте. Программа не внесет опечаток и ошибок при копировании.
- Не возникает проблем с выравниванием названий слева, а номеров страниц справа. Линии начала и конца оглавления будут идеально прямыми.
- Осуществляется синхронизация текста и оглавления. Если вы внесли изменения в название элемента, или он переместился на другую страницу – это будет отражено соответствующим изменением в оглавлении. Правильность номеров страниц проверяется программой.
Поэтому решая, как оформлять оглавление в курсовой, отдавайте предпочтение использованию автоматизированных инструментов.
Как правильно оформляется содержание курсовой работы в MS Word
Для того, чтобы сделать в курсовой работе автоматически собираемое оглавление, следует провести предварительную работу. Проще всего это сделать на стадии написания текста, но если вы забыли об этом, можно и потом.
Чтобы текстовый редактор понял, какие части текста представляют собой заголовки (используемые в оглавлении), необходимо задать стили текста.
В MS Word есть стандартные стили заголовков – Заголовок 1, Заголовок 2 – но они не соответствуют обычным требованиям для оформления курсовых работ (используется выделение полужирным шрифтом, курсивом, цветом).
Можно изменить эти стили под требования вуза или создать собственные стили заголовков.

Рисунок 1. Стили заголовков в MS Word
Когда для всех заголовков установлен нужный стиль, остается перейти на вкладку Ссылки и выбрать инструмент Оглавление. 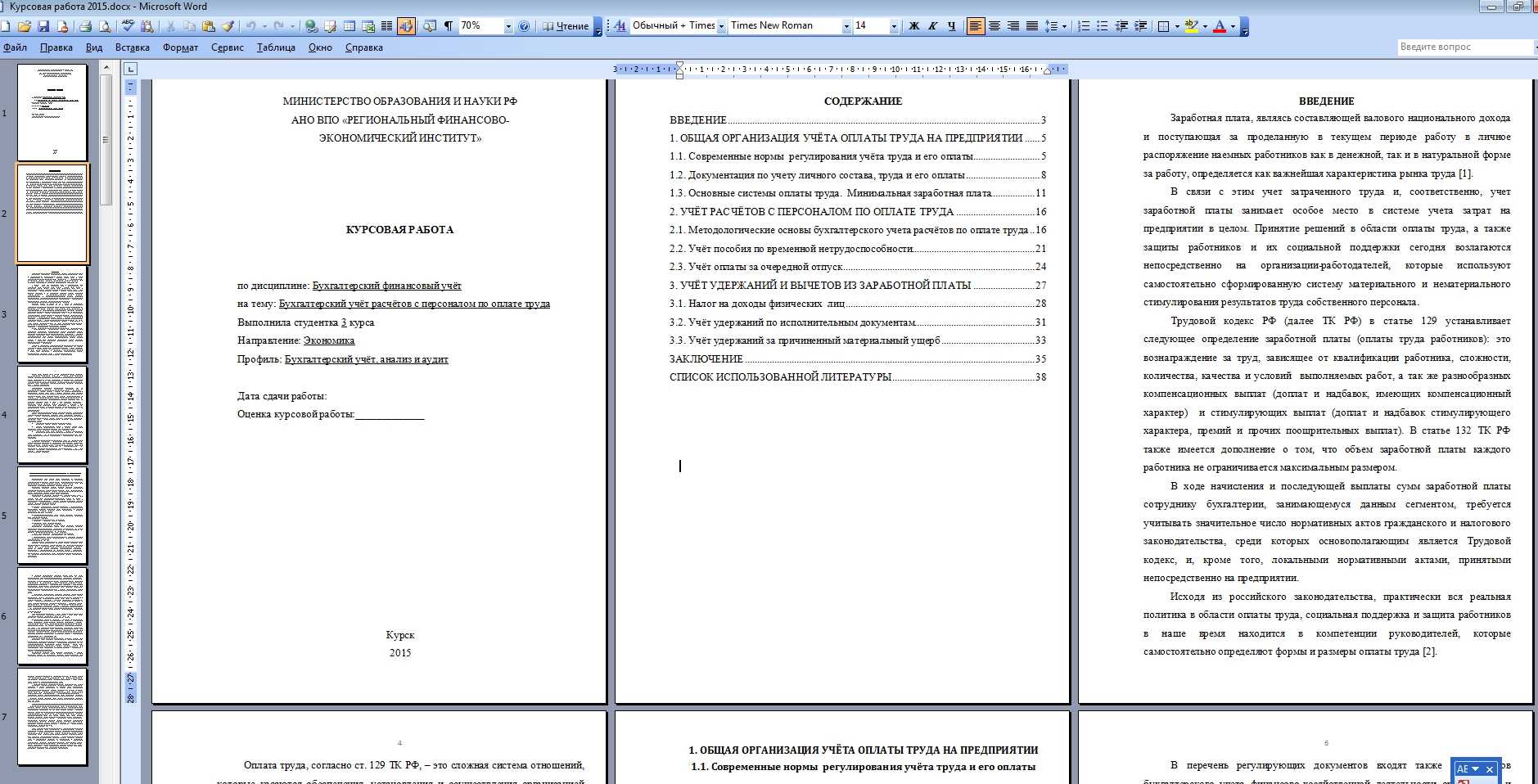
- Рисунок 2. Оформление содержания курсовой работы в MS Word
- Можно выбрать предлагаемый шаблон автособираемого оглавления или установить собственные параметры – перечень уровней заголовков, включаемых в оглавление, шрифт текста оглавления, абзацные отступы, заполнитель и некоторые другие.
Источник: https://spravochnick.ru/articles/kursovye_raboty/oglavlenie_kursovoj_raboty/
Образец содержания курсовой работы
 Каждая качественно выполненная курсовая работа начинается с составления чёткого плана, в пунктах которого должна отражаться логическая структура текста. Продуманная программа действий упростить работу над курсовой, что сделает выполнение задачи гораздо проще.
Каждая качественно выполненная курсовая работа начинается с составления чёткого плана, в пунктах которого должна отражаться логическая структура текста. Продуманная программа действий упростить работу над курсовой, что сделает выполнение задачи гораздо проще.
Научный руководитель – главный ориентир курсанта. Следует заботиться о подборе хорошего советчика как можно раньше. Если защита проекта поставлена на один из весенних месяцев, выслушать рекомендации и обсудить тему с научным руководителем следует уже осенью. Преподаватель обязан помочь в корректировке или составлении правильного плана работы. Научный руководитель направляет студента в нужное русло, даёт рекомендации по литературе, что следует изучить для грамотного выполнения курсовой работы. Но если приставленный к ученику научный руководитель не компетентен и требует замены, просьба поменять преподавателя – лучшее решение.
Обычно от студентов требуется выделение трех основных частей текста – вступительной, основной и завершающей. По стандарту основное содержание должно быть намного крупнее других частей, однако всем частям следует уделять достаточно внимания.
Введение отвечает на вопрос о том, почему студент выбрал ту или иную тему, а также указывает на актуальность и важность предмета обсуждения. Цели и задачи проекта – не менее важная часть. Помимо этого, вступление включает в себя методы изучения проблемы и ссылается на источники информации.
Основная часть включает в себя проведение анализа найденных результатов. Чаще всего здесь отмечается от двух до четырех основных глав, делящихся на небольшие части.
Заключение – результат проделанной курсовой работы. Завершающая часть подводит итог полученной информации по выбранной теме, раскрывает способности студента в составлении грамотного вывода.
Во время работы над планом проекта следует придерживаться нескольких правил.
А) Важно логически связывать разделы и части с помощью названий или текстовой составляющей.
Б) главы должно обобщаться одним названием, не повторяющимся в курсовой работе ранее. Отклоняться от темы раздела категорически запрещено.
В) Лишь одно предложение может называть главу или параграф.
Образец написания содержания курсовой работы по менеджменту
- Например, написанная с учетом этого устава курсовая работа по менеджменту зачастую пишется по такому плану:
- Часть I. ТЕОРИТИЧЕСКАЯ ЧАСТЬ (название раздела зависит от выбранного студентом аспекта менеджмента)
- § 1.1 Значение менеджмента и процессного подхода сейчас;
§ 1.2-1.4 Базовые знания менеджмента (зависят от выбранной темы);
- Часть II. ПРАКТИКА (проводится на примере конкретной организации)
- § 2.1 Основная информация об организации;
- § 2.2 Механизм управления организацией;
- § 2.3 Исследование внешних и внутренних условий;
- § 2.4 Мероприятия по улучшению механизмов управления;
- ЗАВЕРШАЮЩАЯ ЧАСТЬ
- ИСТОЧНИКИ
Обозначение небольших отрезков текста так же важно, как выделение ключевых частей. Основные разделы должны иметь несколько подразделов, что в свою очередь имеют несколько собственных «ответвлений» на более мелкие части. Для удобства использования плана рекомендуется использовать числовое упорядочивание пунктов – нумерацию.
Образец оформления курсовой работы по ГОСТу
Вводная часть
Часть I. ЭФФЕКТИВНОСТЬ УПРАВЛЕНИЯ
§ 1.1. Сущность, критерии и показатели эффективности управления;
§ 1.2. Экономическая эффективность управленческого труда;
§ 1.3. Пути повышения эффективности менеджмента в организации;
Часть II. АНАЛИЗ ЭФФЕКТИВНОСТИ МЕНЕДЖМЕНТА НА ПРЕДПРИЯТИИ
§ 2.1. Характеристика предприятия;
§ 2.2. Оценка экономической эффективности результатов работы менеджера предприятия;
- ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ
- ИСТОЧНИКИ
- ПРИЛОЖЕНИЯ
Результатом проделанного труда будет отражающий всю суть темы и полный полезным материалом проект с качественной структурой. Благодаря основательно продуманной программе действий, написанное не затратит много энергии ученика, облегчит задачу исполнителя.
Образец содержания
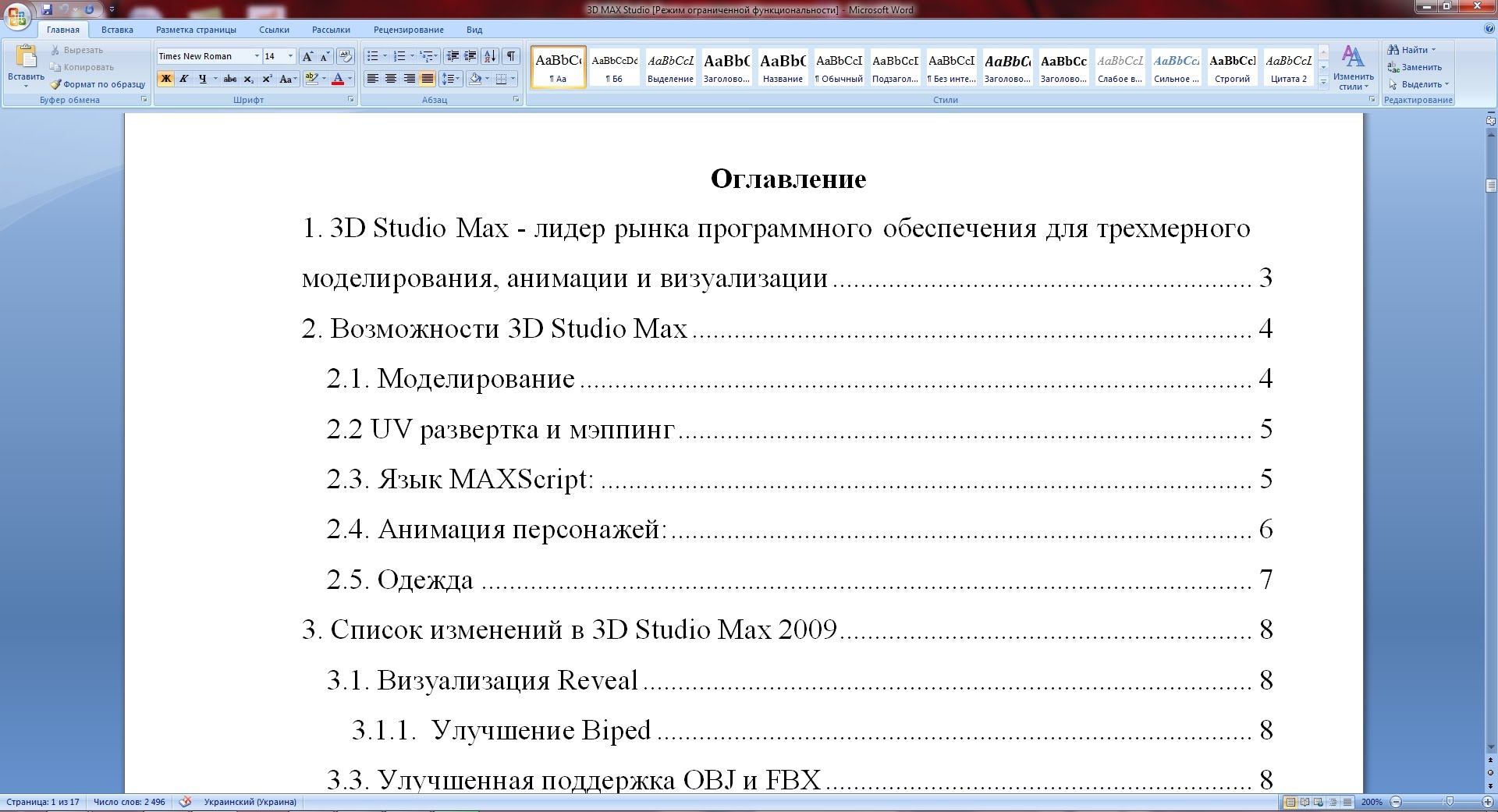
Источник: http://xn--b1agnqjgm2e.xn--p1ai/201-obrazec-soderzhaniya-kursovoj-raboty.html
16 советов, как составить содержание к реферату и курсовой работе *

Каждая студенческая работа имеет свою специфику. Безусловно, есть общие принципы – точность, логичность, верность оформления, обоснованность выбора источников.
Важным составляющим любой студенческой работы является составление и оформление содержания! В каждом отдельном случае оно должно быть подготовлено особым образом.
Сегодня расскажем, как составить содержание к реферату и к курсовой работе – дадим по 8 советов, отражающих специфику этих видов работ.
Как составить содержание к реферату? – 8 советов
Реферат – разновидность студенческой работы, в которой вы главным образом излагаете изученную информацию, ничего самостоятельно не изобретайте. Рекомендации по составлению содержания для реферата следующее:
Совет первый
Обязательно сделайте содержание к реферату! К сожалению, многие студенты забывают об этом простом правиле. И оставляют реферат без содержания, считая его слишком небольшой работой для таких тонкостей. Однако это не так! Реферат должен иметь содержание, иначе это уже не реферат, а эссе! Если не хотите снижения балла, делайте содержание!
Совет второй
Выбирайте небольшое количество глав! Не нужно указывать 10 или 15 разделов – это будет раздражать преподавателя, мельтешить перед глазами. Достаточно нескольких логичных и обоснованных глав!
Совет третий
Лучше, если глав будет три – это классическая схема оформления любой работы! В таком случае преподаватель на подсознательном уровне будет воспринимать ваш реферат как «правильный».
Совет четвертый
Не стоит делать параграфов, если преподаватель не попросил очень объемный реферат. Подразделы в реферате – лишнее! Однако если к этому есть особенные требования или преподаватель любит такой стиль оформления – не ленитесь и оформляйте.
Совет пятый
Помните о введении и заключении! Эти части рефераты также должны быть отдельно оформлены, а их названия обязательно вынесены в содержание.
Совет шестой
Приложения выносите в отдельный раздел! В реферате также могут использоваться картинки, схемы, таблицы. Их нужно размещать в конце работы, а страницу приложения указывать в содержании.
Совет седьмой
Придумайте каждой главе интересное название! В случае с рефератом, в отличие от того же диплома, вы можете проявить творчество. Не стоит делать названия слишком «газетными», но и скучными они быть не должны. Допустимо использовать метафоры и эпитеты!
Совет восьмой
Помните о списке литературы и вынесите его в отдельный раздел! В реферате вы в любом случае основывались на источниках, и очень важно это указать. Поэтому обязательно выносите в содержание список литературы.
Как составить содержание к курсовой работе? – 8 советов
Курсовая работа – студенческий проект, который выполняется на каждом курсе. Курсовая работа – подготовка к диплому, в ходе написания и защиты вы можете «обкатать» свои навыки написания и выступления с курсовой! К курсовой также нужно оформлять содержание. В целом, требования такие же, как и к диплому, но есть свои нюансы:
Совет первый
раздела соответствует названию! Частая ошибка студентов – выбирать непонятные названия! Преподаватель читает в содержании одно, а в тексте речь идёт абсолютно о другом. Даже если курсовая написана правильно, преподаватель воспринимает такое положение дел как «ошибку».
Совет второй
Разделы расположены последовательно! Очень часто студенты об этом забывают! И делают глупые ошибки в размещении глав. Это сразу отбирает баллы, которые можно набрать за курсовую работу.
Совет третий
Разделы должны быть связаны между собой! Информация в одном используется в другом. Это очень важно! У преподавателя должно сложиться ощущение «связного текста», а не набора разрозненных рассказов.
Совет четвертый
В названии раздела используйте только одно предложение! Два, три, четыре – ни в коем случае. Это название, а не текст. Оно должно быть ёмким, лаконичным и коротким.
Совет пятый
Главы пронумеруйте римскими цифрами, параграфы – арабскими! Это общепринятое правила из ГОСТа по оформлению студенческих работ. В случае если преподавателю что-то не понравится, всегда ссылайтесь на официальные документы.
Совет шестой
Узнайте, как именно нужно оформить курсовую работу в вашем ВУЗе! ВУЗ может устанавливать свои правила и их необходимо соблюдать! Ориентируясь только на ГОСТ, вы высказываете неуважение университету.
Совет седьмой
Не используйте одинаковых названий! Или тех, которые различаются всего одним словом. Читать такую работу просто неинтересно! Старайтесь проявить требования!
Совет восьмой
Если в институте нет особенных требований – ориентируйтесь на ГОСТ! Его можно найти в Интернете, или обратиться на кафедру. И в спорных ситуациях всегда ссылайтесь на официальные документы.
Теперь вы знаете специфику оформления содержания к курсовой работе и к реферату. Помните, что принципы оформления – общие, но нюансы в каждом случае свои! Если у вас нет времени возиться с оформлением содержания – не тяните до последнего, обращайтесь к профессионалам! Опытные специалисты помогут оформить содержание «на отлично».
Каждая студенческая работа имеет свою специфику. Безусловно, есть общие принципы – точность, логичность, верность оформления, обоснованность выбора источников.
Важным составляющим любой студенческой работы является составление и оформление содержания! В каждом отдельном случае оно должно быть подготовлено особым образом.
Сегодня расскажем, как составить содержание к реферату и к курсовой работе – дадим по 8 советов, отражающих специфику этих видов работ.
Как составить содержание к реферату? – 8 советов
Реферат – разновидность студенческой работы, в которой вы главным образом излагаете изученную информацию, ничего самостоятельно не изобретайте. Рекомендации по составлению содержания для реферата следующее:
Совет первый
Обязательно сделайте содержание к реферату! К сожалению, многие студенты забывают об этом простом правиле. И оставляют реферат без содержания, считая его слишком небольшой работой для таких тонкостей. Однако это не так! Реферат должен иметь содержание, иначе это уже не реферат, а эссе! Если не хотите снижения балла, делайте содержание!
Совет второй
Выбирайте небольшое количество глав! Не нужно указывать 10 или 15 разделов – это будет раздражать преподавателя, мельтешить перед глазами. Достаточно нескольких логичных и обоснованных глав!
Совет третий
Лучше, если глав будет три – это классическая схема оформления любой работы! В таком случае преподаватель на подсознательном уровне будет воспринимать ваш реферат как «правильный».
Совет четвертый
Не стоит делать параграфов, если преподаватель не попросил очень объемный реферат. Подразделы в реферате – лишнее! Однако если к этому есть особенные требования или преподаватель любит такой стиль оформления – не ленитесь и оформляйте.
Совет пятый
Помните о введении и заключении! Эти части рефераты также должны быть отдельно оформлены, а их названия обязательно вынесены в содержание.
Совет шестой
Приложения выносите в отдельный раздел! В реферате также могут использоваться картинки, схемы, таблицы. Их нужно размещать в конце работы, а страницу приложения указывать в содержании.
Совет седьмой
Придумайте каждой главе интересное название! В случае с рефератом, в отличие от того же диплома, вы можете проявить творчество. Не стоит делать названия слишком «газетными», но и скучными они быть не должны. Допустимо использовать метафоры и эпитеты!
Совет восьмой
Помните о списке литературы и вынесите его в отдельный раздел! В реферате вы в любом случае основывались на источниках, и очень важно это указать. Поэтому обязательно выносите в содержание список литературы.
Как составить содержание к курсовой работе? – 8 советов
Курсовая работа – студенческий проект, который выполняется на каждом курсе. Курсовая работа – подготовка к диплому, в ходе написания и защиты вы можете «обкатать» свои навыки написания и выступления с курсовой! К курсовой также нужно оформлять содержание. В целом, требования такие же, как и к диплому, но есть свои нюансы:
Совет первый
раздела соответствует названию! Частая ошибка студентов – выбирать непонятные названия! Преподаватель читает в содержании одно, а в тексте речь идёт абсолютно о другом. Даже если курсовая написана правильно, преподаватель воспринимает такое положение дел как «ошибку».
Совет второй
Разделы расположены последовательно! Очень часто студенты об этом забывают! И делают глупые ошибки в размещении глав. Это сразу отбирает баллы, которые можно набрать за курсовую работу.
Совет третий
Разделы должны быть связаны между собой! Информация в одном используется в другом. Это очень важно! У преподавателя должно сложиться ощущение «связного текста», а не набора разрозненных рассказов.
Совет четвертый
В названии раздела используйте только одно предложение! Два, три, четыре – ни в коем случае. Это название, а не текст. Оно должно быть ёмким, лаконичным и коротким.
Совет пятый
Главы пронумеруйте римскими цифрами, параграфы – арабскими! Это общепринятое правила из ГОСТа по оформлению студенческих работ. В случае если преподавателю что-то не понравится, всегда ссылайтесь на официальные документы.
Совет шестой
Узнайте, как именно нужно оформить курсовую работу в вашем ВУЗе! ВУЗ может устанавливать свои правила и их необходимо соблюдать! Ориентируясь только на ГОСТ, вы высказываете неуважение университету.
Совет седьмой
Не используйте одинаковых названий! Или тех, которые различаются всего одним словом. Читать такую работу просто неинтересно! Старайтесь проявить требования!
Совет восьмой
Если в институте нет особенных требований – ориентируйтесь на ГОСТ! Его можно найти в Интернете, или обратиться на кафедру. И в спорных ситуациях всегда ссылайтесь на официальные документы.
Теперь вы знаете специфику оформления содержания к курсовой работе и к реферату. Помните, что принципы оформления – общие, но нюансы в каждом случае свои! Если у вас нет времени возиться с оформлением содержания – не тяните до последнего, обращайтесь к профессионалам! Опытные специалисты помогут оформить содержание «на отлично».
Источник: https://disshelp.ru/blog/16-sovetov-kak-sostavit-soderzhanie-k-referatu-i-kursovoj-rabote/
к курсовой работе
—
Ни один курсовой проект не может обойтись без плана, а потому составление содержание – это немаловажный шаг, позволяющий расположить все разделы на своих местах и ничего при этом не перепутать.
Наличие четкого и продуманного плана избавит студента от ненужных и затратных действий, защитит текстовую часть от переполнения лишними материалами, найденными в ходе исследования, а также позволит качественно распланировать все работы по созданию курсового проекта.
Идеально, конечно, это посидеть с руководителем и обсудить тему работы, после чего ознакомиться с возможной литературой, а уже потом снова встретиться с преподавателем для уточнения название проекта и составления примерного плана. Позднее содержание все равно будет скорректировано или даже поменяно, но первоначальный набросок однозначно поможет студенту справиться с расстановкой приоритетов своего труда и уложиться в намеченные сроки написания.
По существу содержание – это кратко описанная логическая структура курсовой работы. План включает не только основные, но и малозначимые вопросы проекта, а потому в нем необходимо выделить как главные разделы, так и подразделы, делящиеся в свою очередь на еще более мелкие параграфы.
Глобально содержание делится на три раздела:
- — введение;
- — основная часть;
- — заключение.
Поскольку курсовая работа – это строго структурированный документ, потому он должен быть актуальным, последовательным, уникальным и корректно оформленным.
Естественно, что оформление не может обойтись без титульного листа, за которым следует страничка-другая с содержанием, и уже потом последовательно вся работа – введение, теоретический и практический разделы, заключение, литературные источники и приложения.
Теперь о том, как правильно написать содержание, которое, кстати, идет сразу после титулки, но при этом не нумеруется, хотя в общий объем работы входит на равных правах с остальными разделами.
Как уже говорилось, план в курсовой работе не занимает больше страницы, но при этом в нем следует аккуратно поместить точные название всех разнокалиберных глав с теми страницами, на которых дано название параграфа, подраздела и подпункта.
Также нумерации подлежит начало списка литературных источников, а вот приложения просто идет последней строкой и цифра с номером страницы рядом с ними не ставится.

Скачать пример (Тема — Анализ платежеспособности и ликвидности предприятия).
1. Разделы, подразделы и прочие более мелкие части работы не должны иметь наименований, идущих вразрез с темой, заявленной в теме курсового проекта, но при этом ни одна глава не может полностью дублировать названием курсовой работы.
2. Название каждой главы должно направлять на раскрытие определенной стороны изучаемой проблематики.
3. Каждый последующий раздел, подраздел, глава, параграф должен быть плавным продолжением предыдущего.
4. План курсовой работы не должен содержать пунктов с одинаковыми названиями.
5. Название каждого раздела, подпункта или главы должно состоять из одного предложения.
Вся информация по оформлению содержания курсовой работе обычно имеется в методических пособиях, выпускаемых на кафедре. Такую брошюру можно с легкостью получить или в деканате или у преподавателя, принимающего курсовую работу.
Если возникают какие-либо трудности или проблемы, то с вопросами следует обратиться к руководителю.
Мало того, что это поможет избежать неувязок на защите, так и преподаватель однозначно обратит внимание на думающего студента, что наверняка положительно скажется в будущем при выставлении оценки.
И еще одна подсказка: окончательный вариант содержания лучше всего писать уже по завершении основных разделов курсового проекта, после составления списка литературы, подбора приложений и дополнительных материалов. Когда все разделы уже не нуждаются в какой бы то ни было корректировке, тогда и получается самое лучшее содержание.
Примеры содержания:
курсовой работу по экономической теме.docx — Тема курсовой работы — Организация и пути повышения экономической эффективности использования сельскохозяйственных угодий
курсовой работы по ветеринарной теме.docx (табличная форма) — по теме ветеринарный контроль, мясная продукция.
курсовой работы по информационным технологиям.docx (строго по ГОСТу) — компьютеры, информатика, сети.
курсовой работы по технологии переработки.docx — технология переработки молока, производство масла и спредов.
курсовой работы по экономике сельского хозяйства.doc — экономика сельского хозяйства, молочное скотоводство.
Сборник содержаний к курсовым работам по экономике.docx — 6 шт.
Источник: https://xn——6kcbafd7dtbfpeiwcaco2t.xn--p1ai/soderzhanie.html
Образец содержания курсовой работы
Под «содержанием» в данном случае следует понимать оглавление, по правилам оформления курсовых работ располагающееся на второй странице — сразу после титульного листа.
Чтобы правильно оформить содержание курсовой, нужно знать несколько правил:
- курсовой работы должно соответствовать логике раскрытия темы. Это подразумевает некую последовательность: подразделы призваны разделить тему главы, к которой они относятся, на несколько составляющих с целью более глубокого и независимого погружения в каждую из них, при этом сама курсовая делится на главы аналогичным образом.
- Разумеется, исходя из первого, ни одна глава не должна дублировать название курсовой, и точно так же ни один подраздел не должен дублировать название главы.
- Исходя из общепринятых стандартов, все названия в курсовой работе — от названия самой курсовой до названий её глав и их подразделов — не должны быть больше одного предложения.
Гост содержания курсовой работы
Стандартом, регламентирующим оформление содержания курсовой работы, как и многих других её аспектов, традиционно считается ГОСТ 7.32–2001, но, несмотря на это, исчерпывающим руководством его назвать нельзя.
Наиболее полную информацию по любым вопросам оформления курсовой, как мы уже многократно говорили, можно получить только в методичке своего вуза, тем не менее, содержание — это раздел, к которому существуют общепринятые требования. Хоть и излагаются они во всех методичках по-разному, тем не менее, в большинстве случаев эти требования не имеют существенных отличий.
Как оформить содержание в курсовой работе
Требования к содержанию, распространённые в большинстве учебных заведений нашей страны, гласят, что обязательными разделами курсовой работы должны быть введение, основная часть, заключение и список литературы.
При этом основная часть предполагает наличие минимум двух глав (иногда допускается или даже требуется третья глава) — как правило, теоретической и практической, хоть это деление и условно, а в некоторых случаях и вовсе не требуется – всё зависит от логики вашего исследования.
Необязательным разделом является приложение — оно должно обязательно присутствовать в нескольких случаях:
- Если все иллюстрации и таблицы методичка в обязательном порядке требует оформлять как приложения (такое иногда бывает);
- Если вы ссылаетесь на собственное исследование или какую-либо информацию, которая не была опубликована (в таком случае пишется «См. приложение …»);
- Если вам необходимо проиллюстрировать какой-то раздел работы большим объёмом данных (результатами исследования, опроса и т.д.), но при этом размещение «в теле» курсовой повредило бы логике её повествования.
Разумеется, напротив каждого раздела пишется номер страницы, на которой он начинается. Если глава делится на несколько параграфов — что случается практически всегда — номер страницы пишется только напротив них, т.к. в тексте курсовой работы первый параграф всегда начинается сразу после объявления главы. Следовательно, дублировать номер страницы не нужно.
Ещё один вопрос, не имеющий точного ответа — как в содержании правильно отделяется название раздела от номера страницы. Раньше это чаще делалось точками, сейчас допускается отделение с помощью пробелов, что кажется гораздо привлекательней с эстетической точки зрения.
Пример содержания курсовой работы

курсовой работы — образец по ГОСТу (скачать)
Источник: https://journal.duplom.ru/kursovaya/obrazec-soderzhaniya-kursovoy-raboty/




