Формула инерции

Основные понятия и суть

Инерция — это способность тела сохранять приданную ей скорость движения при отсутствии какого-либо внешнего воздействия. Например, во время езды на общественном транспорте всем приходится держаться за поручни. Если этого не сделать, то при изменении скорости движения транспортного средства существует большая вероятность упасть вперёд или назад. Другими словами, возникает какая-то сила, влияющая на пассажира. Когда её действие заканчивается, движение человека всё равно продолжается.

Это свойство и описывается понятием инертность. Раньше изучали это явление известные учёные Галилей, Ньютон, Мах.

В соответствии с их исследованиями было установлено классическое правило момента вращения, физический смысл которого заключается в распределении массы в теле, определяемой суммой произведения простейшей массы на расстояние до начального множества в квадрате. Классическая формула, описывающая характеристику, выглядит следующим образом: Ja = Σmi*r2j. В ней:

• mi — масса в точке;
• rj — расстояние от точки до координаты.

То есть момент — это скалярная величина, являющаяся мерой инертности. В качестве единицы измерения по международной системе принято использовать произведение килограмма на квадратный метр (кг*м²).

Обозначают параметр латинской буквой I или J. При умножении момента инерции на угловое ускорение можно определить сумму моментов всех сил, приложенных к телу: M = I * E.

Фактически это уравнение является аналогом второго закона Ньютона.

М — это момент силы, оказывающий вращательное движение и воздействующий на ускорение тела, а E — угловое ускорение. Мера инертности тела отличается от массы тем, что вторая проявляется, когда его необходимо разогнать, а первая — при его раскручивании.

Вычисление параметра

Характеристика инерции тел зависит от их количественных показателей и формы. Для того чтобы найти характеристику, можно рассмотреть вращение материальной точки, находящейся на невесомой штанге, имеющей длину r и массу m. Для такой ситуации формулу момента инерции можно записать: I = m*r2. Длина r представляет собой радиус кольца, по которому происходит вращение объекта по оси. Таким образом, рассматриваемый момент зависит не только от массы тела, но и геометрических характеристик.

Любое тело можно описать совокупностью материальных точек. Для понятия процесса лучше всего рассмотреть простой пример. Пусть имеется невесомый цилиндр, способный вращаться по радиусу Rc.

На него намотана верёвка, к которой приложена сила F. На цилиндр будут насаживаться тела с различной формой.

Если известны его радиус и сила, с которой происходит раскручивание, то справедливо будет записать следующее выражение: M = F*Rc.

Допустим, на цилиндр помещены два тела. Одно имеет массу m1 и радиус вращения r1, а другое — m2 и r2. Используя основное уравнение динамики вращательного движения для первого тела с угловым ускорением ƹ1, момент силы можно определить как M1 = I1 * ƹ1. Соответственно, для второго предмета сила будет определяться по формуле: M1 = I2 * ƹ2.

Если эти два тела жёстко скрепить между собой, то они буду представлять собой составные части одного предмета, поэтому их угловые ускорения станут одинаковы (ƹ1 + ƹ2 = ƹ), а требующийся момент M станет равный сумме M1 + M2.

То есть нужный момент для тела, состоящего из совокупности точек, будет равен произведению суммы моментов инерции на угловое ускорение обоих тел.

Из сказанного можно сделать вывод, что момент инерции всего тела равен сумме моментов составных частей. Другим словами, он обладает свойством аддитивности. Используя это, можно составить алгоритм расчёта для любой формы.

Методика решения

Существует универсальный алгоритм, подходящий для расчёта параметра прямоугольника, треугольника, круга или другой фигуры произвольной формы. Допустим, есть сложное тело с заданной осью вращения. Необходимо найти момент его вращения. Для того чтобы решить поставленную задачу, используются два принципа:

• Аддитивность — свойство, обозначающее, что величина целого значения определяется суммой соответствующих ему частей.
• Формула нахождения момента для материальной точки I = m*r2.

Всё тело можно разделить на мельчайшие частички, которые представляют собой материальные точки. Номера этих кусков обозначают в виде i. Масса произвольной части будет определяться как дельта mi.

Пусть этот кусок находится на расстоянии ri от оси вращения O. Для этой части момент вращения находится с помощью выражения Ii = Δ mi*ri2.

Учитывая аддитивность, общий момент будет равен I = Σ Δ mi*ri2, где i принимает значение от 1 до n.

Эта формула является приближённой, так как точность зависит от массы частей и размера. Если кусочки, на которые разбивается тело, большие, считать их материальными точками нельзя.

Чем мельче части, тем точнее будет результат. В соответствии с математическим анализом такие задачи решаются с помощью интегрирования.

Понимая физический смысл момента инерции, можно отметить следующие зависимости:

• прямая пропорциональность массе;
• соответствие квадрату размера;
• изменение с учетом оси вращения.

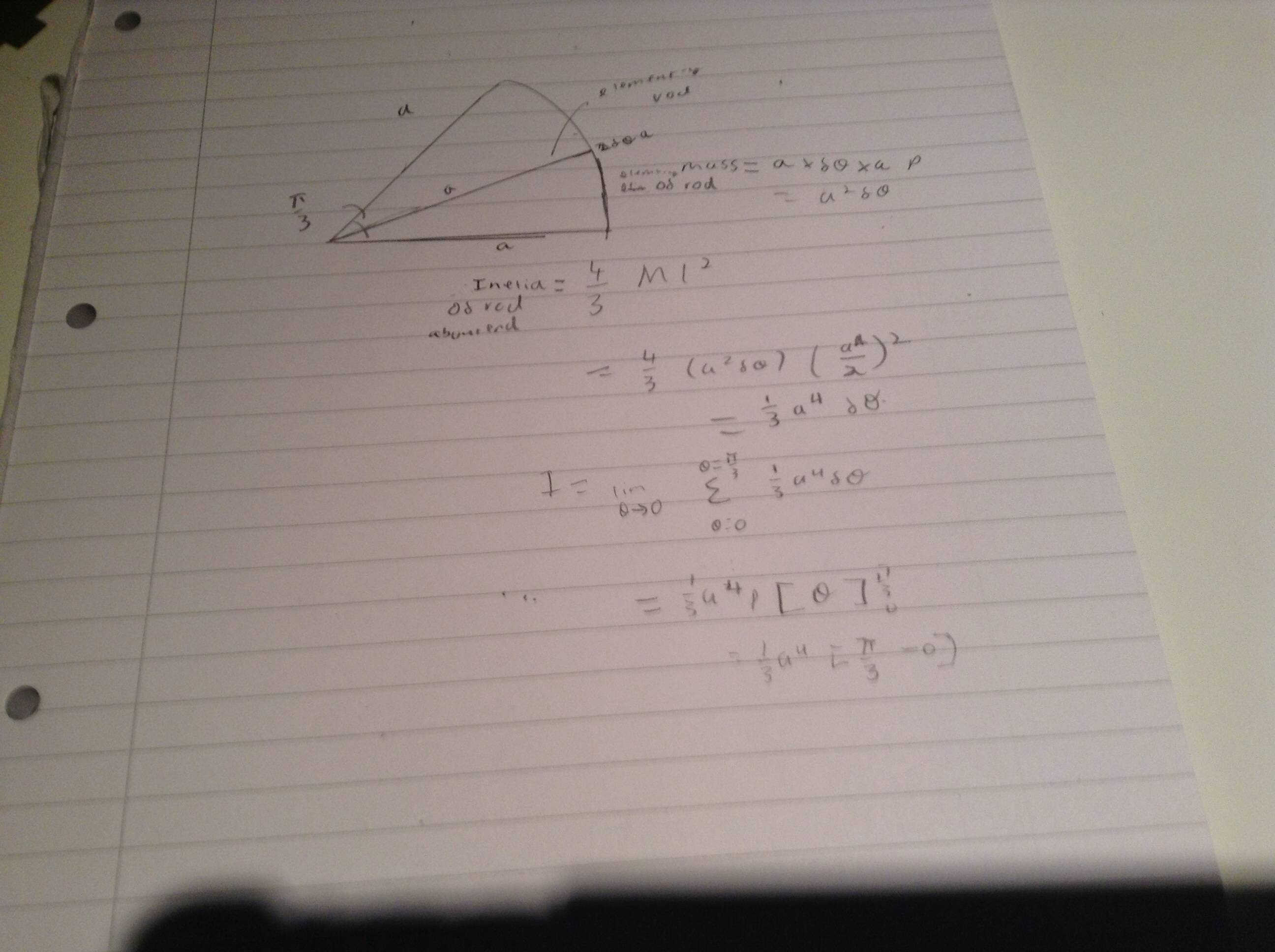
Роль последнего пункта огромна. Например, если рассмотреть два момента вращения велосипедной спицы диаметром 2 мм и длиной 30 сантиметров, то можно увидеть зависимость от выбранной оси поворота.

Относительно вертикальной оси вращение обозначим I1, горизонтальной — I2. Подставив в формулы выражения, используемые для расчётов, можно получить отношение I1/I2 = (m*l2/12) / ((m*d2/8).

После его упрощения будет верна запись I1/ I2 = (2/3)*(l/d)2. В итоге получится ответ 15000.

Моменты простейших объектов

Проведение интегрирования — довольно трудная операция, предполагающая хорошее знание высшей математики. Существует таблица, в которой собраны вычисления инерции для простейших геометрических фигур.

При взятии сведений из неё важно обращать внимание на то, относительно какой оси приводится момент вращения объекта.

Характеристика инерции для наиболее используемых объектов в физике имеет следующий вид:

1. Кольцо. Предположив, что точка имеет симметричное значение с противоположной стороны оси, можно утверждать, что формула не изменится. Если же точку распределить по плоскости перпендикулярной оси, то получится кольцо. Оно будет иметь такую же массу с кусками, находящимися на одинаковом расстоянии от центра r. Вычисление момента относительно оси вращения выполняют по той же формуле, что и для материальной точки: I = m * r2.
2. Тонкостенный цилиндр. Нарисовав такую фигуру и указав на ней ось вращения, массу и радиус, несложно будет увидеть, что формула для нахождения момента будет аналогична кольцу.
3. Диск. Вращение его происходит относительно оси, проходящей через его центр. Учитывая, что масса однородного диска распределена по всей его площади, то момент его будет меньше, чем у кольца. Проведённые расчёты показали, что момент диска будет меньше в два раза. Таким образом, формула выглядит как I = m*r2 / 2.
4. Сплошной цилиндр. Получают такую фигуру простым распределением массы сплошного диска вдоль оси. По аналогии с кольцом расчёт его характеристики инерции будет совпадать с однородным диском.
5. Шар. Момент проходящей оси через центр тяжести равен удвоенному произведению m*r2, разделенному на 5: I = (m*r2) * 2/5.
6. Сфера. Такой объект отличается от шара лишь тем, что внутри он полый. Направление вращения оси происходит через центр. Значение параметра для неё будет больше, чем шара, так как масса собрана не статически в одном месте, а размещена по всей поверхности. Расчёты показывают, что найти момент можно по формуле I =2*m*r2 /3.
7. Стержень. Момент вращения проходит через центр вдоль оси, перпендикулярной стержню: I = (1/12) * m*L2. L — длина стержня.

При использовании этих формул необходимо учитывать, что единицей измерения момента инерции является кг* м², поэтому при расчёте величины следует приводить значения к этим единицам.

Теорема Гюйгенса — Штейнера

Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей. Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:

1. Вычисления координаты центра масс: X = (m1*x1 + m2*x2+…+Mi*Xi) / (m1+m2+…+Mi) = (Σ Δ mi*ri 2)/ m.
2. Универсального расчёта инерции любого тела: I = Σ Δ mi*ri 2.

Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.

Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).

В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r'.

Находится ri'2 по формулам для прямоугольного треугольника, в котором один катет равняется yi, а другой — xi — Oц. Значение ri' совпадает с длиной гипотенузы. Таким образом, ri'2 = (xi — Oц)2 + yi2.

Подставив полученное равенство в формулу нахождения параметра момента в центре, можно получить следующую формулу: Io = Σ Δ mi* ((xi — Oц)2 + yi2).

После ряда подстановок и упрощения выражения в итоге получится равенство Io = I + m*x i2 — 2*m*xi2 = I — m*xi2.

Так как x центра масс совпадает с d, расстоянием между осями, одну из которых можно направить через центр, то формулу можно переписать как Io = I — m*d2. Выразив из выражения произвольный момент, формула Штейнера примет вид I = Io + m*d2.

Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.

Пример задачи

Допустим, есть монета с массой m и радиусом r. Вращение происходит вокруг оси, распложенной по касательной. Необходимо найти момент вращения.

Для этого нужно знать характеристику прямой, пересекающей центр монеты Io. Решение будет определяться суммой Io и расстоянием от центра до касательной, которая равняется диаметру монеты: I = Io + md2. Фактически задача состоит в нахождении Io. Определяется этот параметр согласно теореме о взаимно перпендикулярных осях.

Момент вращения относительно диска определяется с помощью выражения I1 = m* d2 / 2. Для решения задачи она будет выглядеть Io = m* d2 / 4. Подставив все данные, получим: I = (1m*d2 / 4) + (md)2 = 5*m*d2 /4.

Источник: https://nauka.club/fizika/moment-inertsii.html

Момент инерции: относительно оси вращения, материальной точки и твердых тел

В статье узнаете что такое момент инерции, как влияет ось вращения, а также момент вращения для материальной точки, множества частиц и для твердых тел.

Момент инерции, обозначенный буквой I, является физической величиной, характерной для вращательного движения тела. Это значение предполагает постоянное значение для данного тела и конкретной оси его вращения.

 Величина момента инерции зависит от веса тела, положения оси вращения, вокруг которой вращается тело и распределения его массы. Поэтому можно написать, что момент инерции тела информирует нас о том, как масса вращающегося тела распределяется вокруг фиксированной оси его вращения.

 Чем выше значение момента инерции, тем сложнее установить или изменить вращательное движение данного тела (например, уменьшить или увеличить его угловую скорость).

Момент инерции тела относительно оси вращения

На следующем рисунке показано, как выбор оси вращения тела влияет на значение момента его инерции и, следовательно, на легкость/сложность его вращения. На рисунках а) и б) показан однородный цилиндр с радиусом r и высотой h, который вращается вокруг продольной оси (рисунок а) и вокруг оси, перпендикулярной цилиндру, проходящему через его центр (рисунок б).

Ролик с радиусом r и высотой h вращается вокруг продольной оси (рисунок а) и оси, перпендикулярной цилиндру, проходящему через его центр (рисунок б)). Вес ролика в случае а) гораздо более сфокусирован вблизи его оси вращения, чем в случае б), поэтому цилиндр с рисунка а) вращать легче, чем ролик с рисунка б).

В обоих случаях мы имеем дело с одним и тем же телом, но в первом случае (рис. А) легче вращать ролик.

 Причиной такой ситуации является различное распределение веса цилиндра вокруг его оси вращения: при вращении цилиндра вокруг продольной оси масса ролика более сфокусирована вблизи оси вращения, чем во второй.

 В результате получается меньшее значение момента инерции цилиндра из рисунка а), а не цилиндра из рисунка б).

Если вы не хотите читать всю информацию советуем вам посмотреть видео про момент силы, в котором вы узнаете абсолютно все:

Момент инерции материальной точки

• Чтобы вычислить момент инерции и вращение отдельной частицы вокруг заданной оси вращения, используем следующее выражение:
• где m — масса частицы, r — расстояние частицы от оси вращения. 
• Момента инерции измеряется в кг ⋅ м2 в системе СИ.

Момент инерции сложного тела с частицами

Момент инерции тела, состоящего из n частиц, равен сумме моментов инерции каждой частицы относительно данной оси вращения.

 Например, для тела, состоящего из четырех частиц, имеем: 

где m1, m2, m3 и m4 — массы частиц, которые составляют тела, r1, r2, r3 и r4, расстояние от оси вращения соответственно частиц с массами m1, m2, m3 и m4.

Момент инерции твердого тела

Когда тело состоит из очень многих частиц, расположенных близко друг к другу, сумма моментов инерции в приведенном выше уравнении заменяется интегралом. Если расширенное тело разделено на бесконечно малые элементы с массой dm, удаленной от оси вращения на величину r, момент инерции I будет равен: 

На следующем рисунке показаны выбранные расширенные тела с их моментами инерции, рассчитанными для осей вращения, указанных на чертежах.

Момент инерции обода

Момент инерции обода будет равен I=mr2

Момент инерции шара

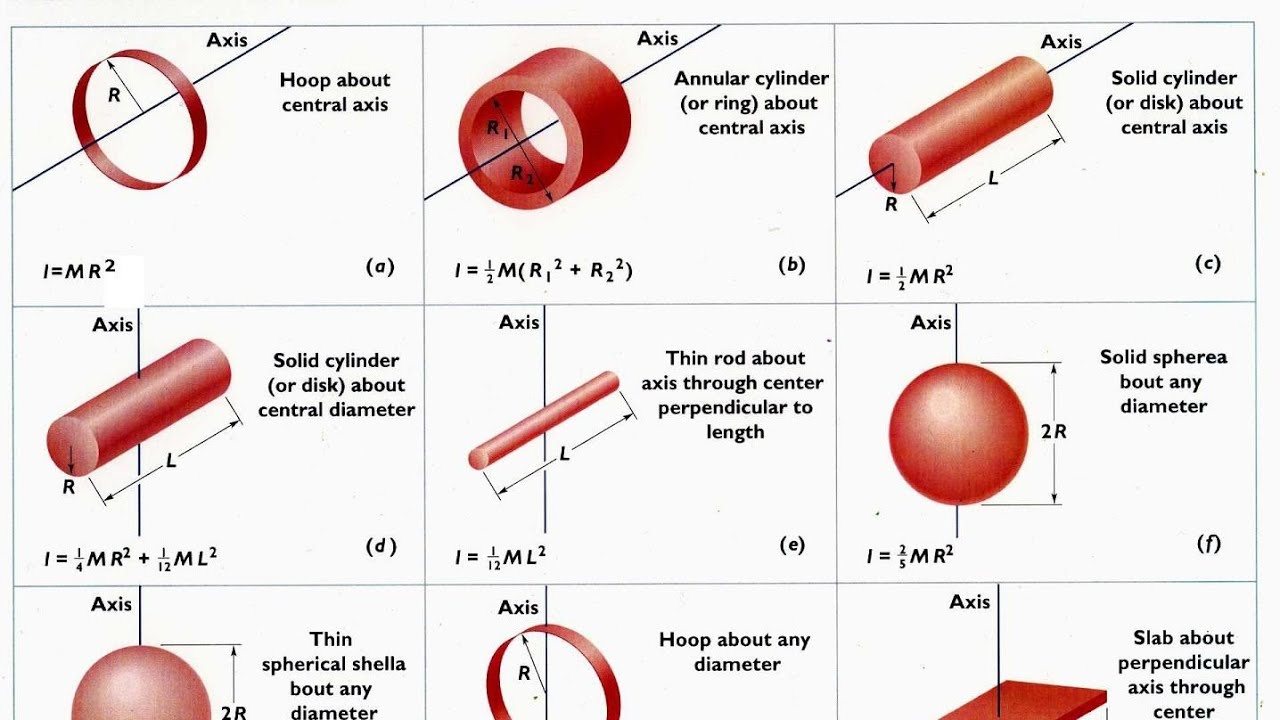
Момент инерции шара будет равен I=2/5mr2

Момент инерции сферы

Момент инерции сферы будет равен I=2/3mr2

Момент инерции к оси цилиндра

Момент инерции к оси цилиндра будет равен I=1/2mr2

Момент инерции к оси через центр цилиндра

Момент инерции к оси цилиндра, проходящей через центр цилиндра будет равен I=1/4mr2+1/12mh2

Момент инерции к оси перпендикулярной поверхности пластины

Момент инерции к оси перпендикулярной поверхности пластины, которая проходит через ее центр будет равен I=1/12m(x2+y2)

Важное примечание:при вводе значения момента инерции I для данного тела не забывайте всегда указывать ось вращения, для которой было рассчитано значение I.

Источник: https://meanders.ru/moment-inercii.shtml

Момент инерции: формула. Момент инерции тела :

Чтобы изменить скорость перемещения тела в пространстве, необходимо приложить некоторое усилие. Этот факт относится ко всем видам механического движения и связан с наличием инерционных свойств у объектов, имеющих массу. В данной статье рассматривается вращение тел и дается понятие об их моменте инерции.

Что такое вращение с точки зрения физики?

Ответ на этот вопрос может дать каждый человек, поскольку этот физический процесс ничем не отличается от его понятия в обиходе. Процесс вращения представляет собой перемещение объекта, обладающего конечной массой, по круговой траектории вокруг некоторой воображаемой оси. Можно привести следующие примеры вращения:

• Движение колеса автомобиля или велосипеда.
• Вращение лопастей вертолета или вентилятора.
• Движение нашей планеты вокруг оси и вокруг Солнца.

Какие физические величины характеризуют процесс вращения?

Перемещение по окружности описывается набором величин в физике, основные из которых перечислены ниже:

• r — расстояние до оси материальной точки массой m.
• ω и α — угловая скорость и ускорение, соответственно. Первая величина показывает, на сколько радиан (градусов) поворачивается тело вокруг оси за одну секунду, вторая величина описывает скорость изменения во времени первой.
• L — момент импульса, который подобен аналогичной характеристике при линейном движении.
• I — момент инерции тела. Эта величина рассматривается ниже в статье подробно.
• M — момент силы. Он характеризует степень изменения величины L, если приложена внешняя сила.

Перечисленные величины связаны друг с другом следующими формулами вращательного движения:

Первая формула описывает круговое движение тела в отсутствие действия внешних моментов сил. В приведенном виде она отражает закон сохранения момента импульса L. Второе выражение описывает случай ускорения или замедления вращения тела в результате действия момента силы M. Оба выражения часто используются при решении задач динамики по круговой траектории.

Как видно из этих формул, момент инерции относительно оси (I) в них используется в качестве некоторого коэффициента. Рассмотрим подробнее эту величину.

Откуда появляется величина I?

В этом пункте рассмотрим самый простой пример вращения: круговое перемещение материальной точки массой m, дистанция которой от оси вращения составляет r. Эта ситуация приведена на рисунке.

Согласно определению, момент импульса L записывается, как произведение плеча r на линейный импульс p точки:

L = r*p = r*m*v, поскольку p = m*v

Учитывая, что линейная и угловая скорость связаны друг с другом через расстояние r, это равенство можно переписать так:

v = ω*r => L = m*r2*ω

Произведение массы материальной точки на квадрат расстояния до оси вращения принято называть моментом инерции. Формула выше перепишется в таком случае следующим образом:

I = m*r2 => L = I*ω

То есть мы получили выражение, которое было приведено в предыдущем пункте, и ввели в использование величину I.

Общая формула для величины I тела

Выражение для момента инерции массой m материальной точки является базовым, то есть оно позволяет рассчитать эту величину для любого тела, имеющего произвольную форму и неоднородное распределение массы в нем.

Для этого необходимо разбить рассматриваемый объект на маленькие элементы массой mi (целое число i — номер элемента), затем, умножить каждый из них на квадрат расстояния ri2 до оси, вокруг которой рассматривают вращение, и сложить полученные результаты.

Описанную методику нахождения величины I можно записать математически так:

I = ∑i(mi*ri2)

Если тело разбито таким образом, что i->∞, тогда приведенная сумма заменяется интегралом по массе тела m:

I = ∫m(ri2*dm)

Этот интеграл эквивалентен другому интегралу по объему тела V, поскольку dV=ρ*dm:

Все три формулы используются для вычисления момента инерции тела. При этом в случае дискретного распределения масс в системе предпочтительнее пользоваться 1-м выражением. При непрерывном распределении массы применяют 3-е выражение.

Свойства величины I и ее физический смысл

Описанная процедура получения общего выражения для I позволяет сделать некоторые выводы о свойствах этой физической величины:

• она является аддитивной, то есть полный момент инерции системы можно представить, как сумму моментов отдельных ее частей;
• она зависит от распределения массы внутри системы, а также от расстояния до оси вращения, чем больше последнее, тем больше I;
• она не зависит от действующих на систему моментов сил M и от скорости вращения ω.

Физический смысл I заключается в том, насколько сильно система препятствует любому изменению скорости ее вращения, то есть момент инерции характеризует степень «плавности» возникающих ускорений.

Например, колесо велосипеда можно легко раскрутить до больших угловых скоростей и также легко его остановить, но чтобы изменить вращение маховика на коленвале автомобиля, понадобится приложить значительное усилие и некоторое время.

В первом случае имеет место система с маленьким моментом инерции, во втором — с большим.

Значение I некоторых тел для оси вращения, проходящей через центр масс

Если применить интегрирование по объему для любых тел с произвольным распределением массы, то можно получить для них величину I. В случае однородных объектов, которые имеют идеальную геометрическую форму, эта задача уже решена. Ниже приводятся формулы момента инерции для стержня, диска и шара массой m, в которых составляющее их вещество распределено равномерно:

• Стержень. Ось вращения проходит перпендикулярно ему. I = m*L2/12, где L — длина стержня.
• Диск произвольной толщины. Момент инерции с осью вращения, проходящей перпендикулярно его плоскости через центр масс, вычисляется так: I = m*R2/2, где R — радиус диска.
• Шар. В виду высокой симметрии этой фигуры, для любого положения оси, проходящей через ее центр, I = 2/5*m*R2, здесь R — шара радиус.

Далее приведем два примера решения задач на применение общей формулы для расчета I и на использование свойства аддитивности этой величины.

Задача на расчет значения I для системы с дискретным распределением массы

Представим себе стержень длиною 0,5 метра, который сделан из твердого и легкого материала. Этот стержень закреплен на оси таким образом, что она проходит перпендикулярно ему точно посередине. На этот стержень подвешены 3-и груза следующим образом: с одной стороны оси имеются два груза массами 2 кг и 3 кг, находящиеся на расстояниях 10 см и 20 см от его конца, соответственно; с другой стороны подвешен один груз массой 1,5 кг к концу стержня. Для этой системы необходимо рассчитать момент инерции I и определить, с какой скоростью ω стержень будет вращаться, если к одному из его концов приложить силу 50 Н в течение 10 секунд.

Поскольку массой стержня можно пренебречь, тогда необходимо рассчитать момент I для каждого груза и сложить полученные результаты, чтобы получить полный момент системы. Согласно условию задачи от оси груз массой 2 кг находится на расстоянии 0,15 м (0,25-0,1), груз 3 кг — 0,05 м (0,25-0,20), груз 1,5 кг — 0,25 м. Воспользовавшись формулой для момента I материальной точки, получаем:

I = I1+I2+I3 = m1*r12 + m2*r22 + m3*r32 = 2*(0,15)2+3*(0,05)2+1,5*(0,25)2 = 0,14 625 кг*м2.

Обратим внимание, что при выполнении вычислений все единицы измерения были переведены в систему СИ.

Чтобы определить угловую скорость вращения стержня после действия силы, следует применить формулу с моментом силы, которая была приведена во втором пункте статьи:

M = I*α

Поскольку α = Δω/Δt и M = r*F, где r — длина плеча, получаем:

r*F = I*Δω/Δt => Δω = r*F*Δt/I

Учитывая, что r = 0,25 м, подставляем числа в формулу, получаем:

Δω = r*F*Δt/I = 0,25*50*10/0,14625 = 854,7 рад/с

Полученная величина является достаточно большой. Чтобы получить привычную частоту вращения, следует поделить Δω на 2*pi радиан:

f = Δω/(2*pi) = 854,7/(2*3,1416) = 136 с-1

Таким образом, приложенная сила F к концу стержня с грузами за 10 секунд раскрутит его до частоты 136 оборотов в секунду.

Расчет значения I для стержня, когда ось проходит через его конец

Пусть имеется однородный стержень массой m и длиной L. Необходимо определить момент инерции, если ось вращения расположена на конце стержня перпендикулярно ему.

Воспользуемся общим выражением для I:

Разбивая рассматриваемый объект на элементарные объемы, заметим, что dV может быть записано, как dr*S, где S — площадь сечения стержня, а dr — толщина элемента разбиения. Подставляя это выражение в формулу, имеем:

I = ρ*S*∫L(r2*dr)

Этот интеграл вычислить достаточно просто, получаем:

I = ρ*S* (r3/3)∣0L => I = ρ*S*L3/3

Поскольку объем стержня равен S*L, а масса — ρ*S*L, то получаем конечную формулу:

Любопытно отметить, что момент инерции для того же стержня, когда ось проходит через его центр масс, в 4 раза меньше полученной величины (m*L2/3/(m*L2/12)=4).

Источник: https://www.syl.ru/article/428611/moment-inertsii-formula-moment-inertsii-tela

Что такое инерция?

Определение момента инерции

Формула момента инерции

Теорема Гюйгенса – Штейнера

Моменты инерции простейших объектов

Рекомендованная литература по теме и полезные ссылки

Момент инерции, видео

Что такое инерция?

Инерция в физике – способность тел определенное время сохранять состояние движения при отсутствии действия внешних сил. Впрочем, понятие инерции имеет частое применение не только в физике, но и в нашей повседневной жизни.

Так обычно «инертным» называют человека, который совершенно не проявляет никакой инициативы, делают только то, что ему скажут другие, и делает это крайне медленно, без какого-либо энтузиазма.

«Движется по инерции», – говорим мы, когда хотим подчеркнуть, что что-то делается без какого-либо смысла, а просто потому, что так было заведено когда-то или в силу наработанной годами привычки.

И если с понятием инерции все более-менее понятно, благодаря таким вот житейским примерам, то термин «момент инерции» требует более детального пояснения, чем мы и займемся в нашей статье.

Определение момента инерции

Со школьной программы по физике мы прекрасно знаем, что масса тела является мерой его инертности.

Например, если в супермаркете сильно толкнуть две тележки, одна из которых будет пустой, а вторая нагруженной разными товарами, то впоследствии остановить будет труднее тележку, нагруженную товарами в силу ее большей массы.

Другими словами, чем больше у тела масса, тем большее на него воздействие инерции и тем больше нужно сил, чтобы изменить движение такого тяжелого тела.

В приведенном примере тележка движется по прямой линии, то есть иными словами совершает поступательное движение. И если при поступательном движении какого-либо теле его масса является мерой его инерции, то при вращательном движении тела вокруг своей оси мерой его инерции будет величина, которая собственно и называется – момент инерции.

Момент инерции – скалярная физическая величина, мера инертности тела при его вращении вокруг оси. Обычно обозначается буквой J и измеряется в килограммах, умноженных на квадратный метр. Такое академическое определение того, что такое момент инерции.

Формула момента инерции

Как рассчитать точное значение момента инерции? Для этого есть общая формула, помогающая физикам определять момент инерции любого тела. Если тело разбить на бесконечно маленькие кусочки с массой dm, то момент инерции будет равным сумме произведения этих элементарных масс на квадрат расстояния до оси вращения. Формула будет иметь такой вид:

J – момент инерции, r – расстояние до оси вращения.

Для материальной точки массы m, которая вращается вокруг оси на расстоянии r, данная формула будет иметь такой вид:

Теорема Гюйгенса – Штейнера

• Говоря о моменте инерции невозможно не упомянуть о теореме двух математиков Гюйгенсе и Штейнере, которые дали формулировку определению характеристики параллельных осей.
• Теорема Гюйгенса – Штейнера гласит: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
• Если записать вышесказанное математической формулой, то получится следующее:

Где d – расстояние между осями

Эта теорема значительно облегчает решения многих физических задач, связанных с инерцией. К примеру, у Вас имеется объект произвольной формы, центробежная сила которого известна. При помощи формулы Штейнера можно вычислить момент инерции тела относительно любой оси параллельной линии, которая проходит через середину фигуры.

Моменты инерции простейших объектов

Несмотря на внешнюю простоту, вычисление моментов инерции для разных предметов предполагает знание интегралов, этих важных инструментов высшей математики. Для упрощения задачи создана таблица с вычислениями инерции для простых геометрических фигур: круга, квадрата, цилиндра и т. д.

Так выглядят математические расчеты вычисления моментов инерции для круга и кольца.

Аналогичным образом будет рассчитываться момент инерции цилиндра.

Предлагаем вашему вниманию более детальную таблицу с формулами для расчета момента инерции для основных геометрических фигур: шара, сферы, диска, цилиндров, и т. д.

Рекомендованная литература и полезные ссылки

• Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
• Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — DOI:10.1126/science.286.5437.77. — PMID 10506564.
• Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.)русск. : journal. — 2012. — Vol. 117. — DOI:10.1029/2012JE004161.
• Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
• Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
• Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
• Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3

Момент инерции, видео

1. И в завершение образовательное видео по теме нашей статьи.
3. Эта статья доступна на английском языке – Moment of Inertia.

Источник: https://www.poznavayka.org/fizika/moment-inertsii/

Формула инерции

В переводе с латыни инерция обозначает косность, вялость. В инерциальных системах отсчета тело стремится сохранить свое состояние покоя или равномерного прямолинейного движения без изменения, если на него не действуют другие тела или их действие взаимно компенсируется. Инерция – это свойство материи.

Мерой инерции служит масса. При вращательном движении в качестве меры инерции часто используют момент инерции.

Масса тела

• Масса является основной динамической характеристикой тела, выступает в качестве количественной характеристики его инертности, то есть возможности тела иметь определенное ускорение, которое придает ему сила. При этом для рассматриваемого тела ускорение () прямо пропорционально силе (), а коэффициент пропорциональности в данном случае это масса (m):
•    
• И так, инертной массой называют физическую величину, равную частному от деления величины силы на модуль ускорения тела:
•    

На сегодняшний момент пока нет четкого понимания, почему тела обладают массами, в чем состоит природа массы. Почему элементарные частицы обладают теми или иными массами. Однако определение массы в виде (2) дает возможность ее измерять. Кроме того, по найденной величине массы можно точно рассчитать движение того или иного тела. В чем и состоит основная задача механики.

1. Масса связана с таким параметром как количество вещества ():
2.    
3. где – молярная масса вещества.
4. При изучении движения тела следует учитывать не только совокупную массу тела, но и распределение масс в нем.
5. Следует заметить, что отношение силы к ускорению тела (2) , то есть масса, является постоянной величиной при относительно небольших скоростях. Если скорость тела увеличивается, то масса растет:
6.    
7. где m – релятивистская масса (или просто масса); – масса покоя; v – скорость движения тела; c – скорость света.

Момент инерции тела

• Инерцию тела во вращательном движении принято характеризовать при помощи такой физической величины как момент инерции тела (J). Момент инерции является скалярной (в общем случае тензорной) физической величиной, которую находят как сумму произведений масс материальных точек () (на которые следует провести разбиение рассматриваемого тела) на квадраты расстояний () от них до оси вращения:
•    
• Подробнее о моменте инерции можно прочитать в разделах «Момент инерции тела», «Момент инерции материальной точки», «Момент инерции, единицы измерения».

Закон инерции

Закон инерции, который мы знаем, сформулировал И. Ньютон: Каждое тело находится в состоянии покоя или движется равномерно и прямолинейно, относительно любой инерциальной системы отсчета, до того момента пока действие на него других тел не заставит его изменить свое состояние.

Закон инерции является важным и независимым законом. Он отображает возможность определить пригодность системы отсчета для рассмотрения движения в динамическом и кинематическом смыслах. Он стал первым шагом при установлении основных законов классической механики.

Движение по инерции является обязательно равномерным и прямолинейным.

Инерциальное движение – это движение по кратчайшему расстоянию, а кратчайшим расстоянием между двумя точками в свободном пространстве является прямая.

Такое движение можно считать аналогичным покою, так как всегда можно выбрать такую инерциальную систему отсчета, которая бы перемещалась со скоростью рассматриваемого тела и в ней тело будет покоиться.

Примеры решения задач по теме «Инерция»

Понравился сайт? Расскажи друзьям!

Источник: http://ru.solverbook.com/spravochnik/formuly-po-fizike/formula-inercii/

Техническая механика



При некоторых видах деформаций прочность и жесткость (способность противостоять деформации) элементов конструкций зависит не только от величины поперечного сечения, но и от формы этого сечения. Самый простой пример — обыкновенную школьную линейку можно легко изогнуть относительно широкой стороны поперечного сечения и совершенно невозможно изогнуть относительно его короткой стороны. При этом общая площадь сечения в обоих случаях одинакова. На основании этого примера становится очевидным, что на сопротивление некоторым видам деформации оказывает влияние (иногда — решающее) не только величина площади сечения бруса, но и его геометрическая форма. При изучении деформаций изгиба и кручения нам потребуется знание некоторых геометрических характеристик плоских сечений, которые оказывают влияние на способность конструкций сопротивляться деформациям относительно той или иной оси либо полюса (точки).

Чтобы понять суть явления и влияния этих геометрических характеристик на сопротивление бруса, например, изгибу, следует обратиться к основополагающим постулатам сопромата.

Как известно из установленного в 1660 году английским физиком Робертом Гуком закона, напряжение в сечениях бруса прямо пропорционально его относительному удлинению. Очевидно, что волокна, расположенные дальше от оси изгиба, растягиваются (или сжимаются) сильнее, чем расположенные вблизи оси.

Следовательно, и напряжения возникающие в них будут бόльшими. Можно привести условную сравнительную аналогию между напряжением в разных точках сечения бруса с моментом силы — чем больше плечо силы — тем больше ее момент (относительно оси или точки).

Аналогично — чем дальше от какого-либо полюса (оси) отстоит точка в сечении, тем большее напряжение в ней возникает при попытке изогнуть или скрутить брус относительно этого полюса (оси).

***

Статический момент площади

Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок (Si) на расстояния (ri)от них до этой оси.

Если упростить это определение, то статический момент инерции плоской фигуры относительно какой-либо оси (лежащей в той же плоскости, что и фигура) можно получить следующим образом:

• разбить фигуру на крохотные (элементарные) площадки (рис. 1);
• умножить площадь каждой площадки на расстояние ri от ее центра до рассматриваемой оси;
• сложить полученные результаты.

Статический момент площади плоской фигуры обозначают S с индексом оси, относительно которой он рассматривается: Sx, Sy, Sz.

Примечание: в разных учебниках или других источниках информации обозначение тех или иных физических величин может отличаться от приведенных на этом сайте. Как вы понимаете, от условного обозначения величин суть описываемых явлений и закономерностей не изменяется.

Sx = Σ y dA;        Sy = Σ x dA.

Анализ этих формул позволяет сделать вывод, что статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние от ее центра тяжести до этой оси. Из этого вывода следует еще один вывод — если рассматриваемая ось проходит через центр тяжести плоской фигуры, то статический момент этой фигуры относительно данной оси равен нулю.

Единица измерения статического момента площади — метр кубический (м3). При определении статического момента площади сложной фигуры можно применять метод разбиения, т. е. определять статический момент всей фигуры, как алгебраическую сумму статических моментов отдельных ее частей.

***

Полярный момент инерции

Полярным моментом инерции плоской фигуры относительно полюса (точки), лежащего в той же плоскости, называется сумма произведений элементарных площадок (Si) этой фигуры на квадрат их расстояний (r2i) до полюса. Полярный момент инерции обозначают Iρ (иногда его обозначают Jρ), а формула для его определения записывается так:

Iρ = Σ ρ2 dA.

Единица измерений полярного момента инерции — м4, из чего следует, что он не может быть отрицательным. Понятие полярного момента инерции понадобится при изучении деформаций кручения круглых валов, поэтому приведем формулы для определения полярного момента квадратного, круглого и кольцевого сечения.

Очевидно, что полярный момент инерции кольцевого сечения равен разности полярных моментов инерции большого и малого кругов, ограничивающих это сечение.

***

Осевой момент инерции

Осевым моментом инерции плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат расстояний от них до этой оси (рис).

Осевой момент инерции обозначается I (иногда — J)с индексом, соответствующим оси:

Ix = Σ y2 dA;        Iy = Σ x2 dA.

Если при этом площадь элементарных площадок принять стремящимися к минимуму, то можно использовать методы интегрального исчисления, заменив знак суммы Σ на знак интеграла ∫. Очевидно, что осевой и полярный момент инерции выражаются в одинаковых единицах — м4.

Осевой момент инерции величина всегда положительная и не равна нулю (м4 не может быть отрицательным, а площадь не может быть равной нулю, иначе пропадает и сама фигура, как площадка).

Если сложить осевые моменты инерции плоской фигуры относительно перпендикулярных осей, то получим полярный момент инерции этой фигуры относительно точки пересечения этих осей (начала координат), т. е. :

Ix + Iy = Iρ.

Так как интеграл суммы равен сумме интегралов, то момент инерции сложной фигуры можно вычислить как сумму моментов инерции простых фигур, на которые разбивают сложную фигуру. Понятие осевого момента инерции понадобится при изучении теории изгиба.

Приведем формулы для определения осевых моментов инерции наиболее часто встречающихся при расчетах форм сечений:

Для прямоугольника размером b × h:	Ix = bh3 /12
Для квадрата со стороной а:	Ix = a4 / 12
Для круга диаметром d:	Ix = Iy ≈ 0,05 d4
Для кольцевого сечения размером D × d:	Ix = Iy ≈ 0,05 (D4 — d4)

***

Момент инерции при параллельном переносе осей

Оси, проходящие через центр тяжести плоской фигуры, называют центральными осями. Момент инерции относительно центральной оси называется центральным моментом инерции.

• Теорема
• Момент инерции относительно какой-либо оси равен сумме момента инерции относительно центральной оси, параллельной данной, и произведения площади фигуры на квадрат расстояния между осями.

Для доказательства этой теоремы рассмотрим произвольную плоскую фигуру, площадь которой равна А, центр тяжести расположен в точке С, а центральный момент инерции относительно оси x будет Ix. Вычислим момент инерции фигуры относительно некоторой оси x1, параллельной центральной оси и отстоящей от нее на расстоянии а (рис. 2).

Ix1 = Σ y12 dA + Σ (y + a)2 dA = = Σ y2 dA + 2a Σ y dA + a2 Σ dA.

Анализируя полученную формулу, отмечаем, что первое слагаемое — осевой момент инерции относительно центральной оси, второе слагаемое — статический момент площади этой фигуры относительно центральной оси (следовательно, он равен нулю), а третье слагаемое после интегрирования может быть представлено в виде произведения a2 A, т. е. в результате получим формулу:

1. Ix1 = Ix + а2 А — теорема доказана.
2. На основании теоремы можно сделать вывод, что из ряда параллельных осей осевой момент инерции плоской фигуры будет наименьшим относительно центральной оси.
3. ***
4. Представим себе плоскую фигуру, моменты инерции которой относительно осей координат Ix и Iy, а полярный момент инерции относительно начала координат равен Iρ. Как было установлено ранее,
5. Ix + Iy = Iρ.



Если оси координат поворачивать в своей плоскости вокруг начала координат, то полярный момент инерции останется неизменным, а осевые моменты будут изменяться, при этом их сумма останется величиной постоянной.

Поскольку сумма переменных величин постоянна, то одна из них уменьшается, а другая увеличивается, и наоборот.

Следовательно, при определенном положении осей один из осевых моментов достигнет максимального значения, а другой — минимального.

Оси, относительно которых моменты инерции имеют минимальное и максимальное значения, называют главными осями инерции. Момент инерции относительно главной оси называется главным моментом инерции.

Если главная ось проходит через центр тяжести фигуры, она называется главной центральной осью, а момент инерции относительно такой оси — главным центральным моментом инерции. Можно сделать вывод, что если фигура симметрична относительно какой-нибудь оси, то эта ось всегда будет одной из главных центральных осей инерции этой фигуры.

***

Центробежный момент инерции

Центробежным моментом инерции плоской фигуры называют взятую по всей площади сумму произведений элементарных площадок на расстояние до двух взаимно перпендикулярных осей:

Ixy = Σ xy dA,

где x, y — расстояния от площадки dA до осей x и y. Центробежный момент инерции может быть положительным, отрицательным и равным нулю.

Центробежный момент инерции входит в формулы для определения положения главных осей несимметричных сечений. В таблицах стандартных профилей содержится характеристика, которая называется радиусом инерции сечения, вычисляемая по формулам:

где Ix, Iy — осевые моменты инерции сечения относительно центральных осей; А — площадь сечения. Эта геометрическая характеристика используется при изучении внецентрального растяжения или сжатия, а также продольного изгиба.

• ***
• Материалы раздела «Сопротивление материалов»:
• Растяжение и сжатие

Правильные ответы на вопросы Теста № 2

№ вопроса	1	2	3	4	5	6	7	8	9	10
Правильный вариант ответа	2	3	2	1	1	3	3	2	2	2

Источник: http://k-a-t.ru/tex_mex/1-sopromat_harakt_sech/

Вычисление моментов инерции

Моментом инерции материальной точки относительно оси называется число , где — масса точки, а — ее расстояние от оси. Аналогично определяется момент инерции относительно точки.

Пусть — материальная линия, линейная плотность которой во всех точках равна единице. Тогда масса элементарного участка этой линии равна его длине , а момент инерции такого участка относительно оси абсцисс равен . Интегрируя, получаем момент инерции относительно оси абсцисс всей линии:

. Так же доказывается, что и ,

где — момент инерции относительно начала координат. Отсюда следует, в частности, что .

Если линия задана параметрическими уравнениями , то

Аналогичные формулы справедливы для и

Моменты инерции криволинейной трапеции

Перейдем к вычислению моментов инерции криволинейной трапеции. Будем считать, что ее поверхностная плотность равна единице. Сначала найдем момент инерции прямоугольника со сторонами и относительно стороны .

Разобьем его на элементарные прямоугольники со сторонами и (см. рис. 61). Площадь (а потому и масса) каждого такого прямоугольника равна .

Значит, момент инерции элементарного прямоугольника относительно стороны равен , а момент инерции всего прямоугольника относительно этой стороны выражается формулой

Криволинейную трапецию разобьем на элементарные прямоугольники со сторонами и . Момент инерции каждого из этих прямоугольников относительно оси абсцисс выражается формулой . Интегрируя, получаем момент инерции всей криволинейной трапеции относительно оси абсцисс:

Аналогично доказывается, что момент инерции криволинейной трапеции относительно оси ординат выражается формулой

(момент инерции элементарного прямоугольника относительно оси ординат равен ).

Полярный момент инерции (т. е. момент относительно начала координат) в этом случае выражается формулой

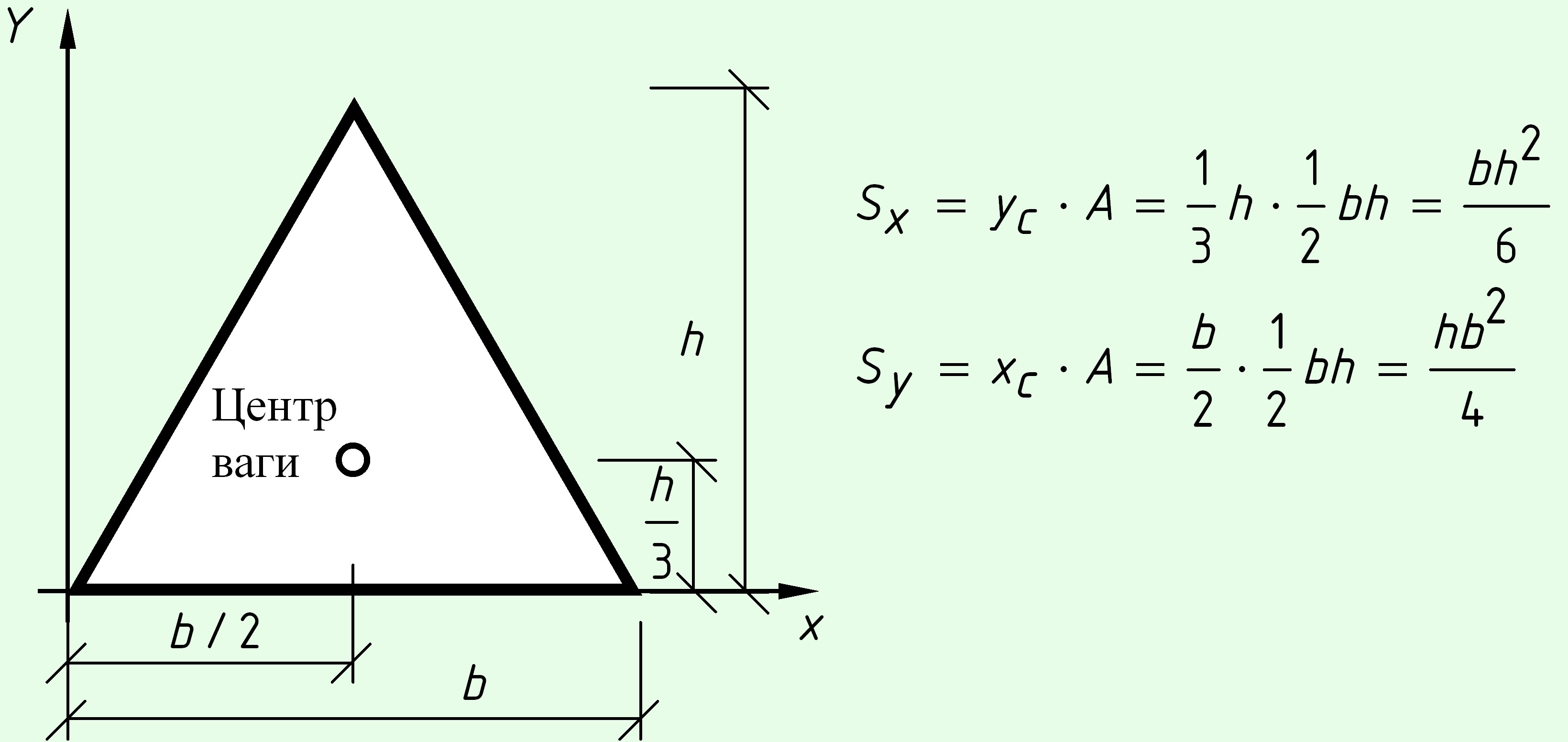
Пример 9. Вычислить момент инерции равнобедренного треугольника относительно его основания.

Решение. Расположим оси координат так, как показано на рисунке 65.

Ясно, что момент инерции треугольника относительно оси равен удвоенному моменту инерции треугольника относительно той же оси. Значит,

Источник: http://MathHelpPlanet.com/static.php?p=vychislenie-momentov-inertsii