Квадратные неравенства и их решение

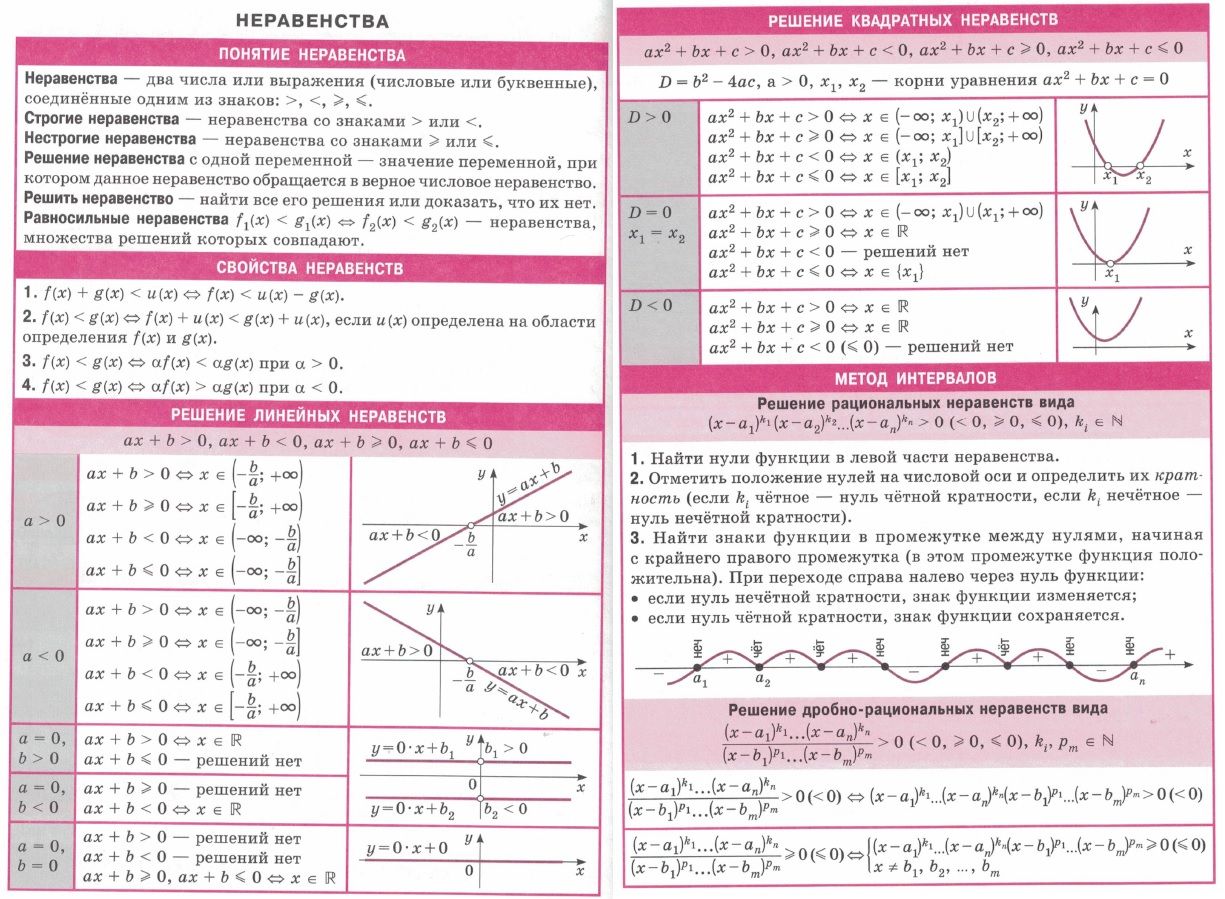
• Общий вид квадратного неравенства после переноса всех выражений на одну сторону неравенства представляет собой одну из следующих форм:
• $ax^2+bx+c > 0$ , либо   $ax^2+bx+c geq 0$  либо  $ax^2+bx+c < 0$ , либо  $ax^2+bx+c leq 0$       (1)
• Когда $a
  eq 0$ , а также $b, c in mathbb{R}$
• Решением каждого неравенства указанного выше, является нахождение всех действительных чисел, которыми можно заменить $x$ так, чтобы неравенство было верным.

Например, если мы заявляем, что $x = 1$ является одним из корней неравенства $x^2 — frac{1}{2} > 0$. Подставив 1 вместо всех переменных $x$ в неравенстве, мы получим, что $1^2 — frac{1}{2} > 0
ightarrow frac{1}{2} > 0$ ,
что всегда верно. Поэтому $x = 1$ является одним из решений данного неравенства.

1. Теперь мы научимся решать неравенства (1).
2. Во-первых, мы рассмотрим уравнение с двумя переменными, $y = ax^2+bx+c$, и предположим, что $ax^2+bx+c$ равно нулю. Тогда:
3. $ax^2+bx+c = 0
   ightarrow a(x^2+frac{b}{a}x+frac{c}{a}) = 0
   ightarrow^{a
   eq 0} x^2+frac{b}{a}x+frac{c}{a} = 0
   ightarrow$ $x^2+frac{b}{a}x+frac{c}{a}+frac{b^2}{4a^2}-frac{b^2}{4a^2} = 0
   ightarrow (x + frac{b}{2a})^2 — frac{b^2 — 4ac}{4a^2} = 0
   ightarrow$ $(x + frac{b}{2a})^2 = frac{b^2 — 4ac}{4a^2}
   ightarrow x + frac{b}{2a} = pm sqrt{frac{b^2 — 4ac}{4a^2}}
   ightarrow x + frac{b}{2a} = pm frac{sqrt{b^2 — 4ac}}{2a}
   ightarrow $
4. $x = frac{-b}{2a} pm frac{sqrt{b^2 — 4ac}}{2a}
   ightarrow x = frac{-b pm sqrt{b^2 — 4ac}}{2a}$
5. Из этого следует, что график квадратного уравнения пересекает ось x в точке $x_1 = frac{-b + sqrt{b^2 — 4ac}}{2a}$ и $x_2 = frac{-b — sqrt{b^2 — 4ac}}{2a}$

• Эти нули разделяют числовую прямую на три интервала:
•         $(-infty, x_1)$   ,   $[x_1,x_2]$   ,   $(x_2,+infty)$,
• допуская, что $x_1 < x_2$.
• Теперь пусть $Delta = b^2 — 4ac$.
• Мы можем рассмотреть три указанных ниже случая:

1. $Delta > 0$
2. $Delta = 0$
3. $Delta < 0$

Случай 1: Если $Delta > 0$,
тогда $ax^2+bx+c$ имеет два различных корня $(x_1
eq x_2)$.

Теперь, если $a>0$, то его график получается таким, как на «Рисунке а».

Если $a»Рисунке b». Поэтому, если $a>0$ и, если имеем $ax^2+bx+c geq 0 (ax^2+bx+c > 0)$, то тогда множество решений это: $(-infty, x_1] cup [x_2, +infty)$       $((-infty, x_1) cup (x_2, +infty))$ И если имеем $ax^2+bx+c leq 0 (ax^2+bx+c < 0)$, тогда множество решений это: $[x_1,x_2]$         $((x_1,x_2))$ С другой стороны, если $a < 0$, а также, если имеем $ax^2+bx+c geq 0 (ax^2+bx+c > 0)$, тогда множество решений это: $[x_1,x_2]$         $((x_1,x_2))$ А если имеем $ax^2+bx+c leq 0 (ax^2+bx+c < 0)$, тогда множество решений это:

$(-infty, x_1] cup [x_2, +infty)$       $((-infty, x_1) cup (x_2, +infty))$

Случай 2: Если $Delta = 0$,

тогда у $ax^2+bx+c = 0$ есть только один корень $(x_1 = x_2 = frac{-b}{2a})$. Теперь, если$a>0$, тогда его график выглядит, как показано на»Рисунке c», а если $a «Рисунке d».

Если $ax^2+bx+c geq 0$ и a > 0, то решениями являются все действительные числа.
Если a > 0 и $ax^2 + bx + c > 0$ (или a < 0 и $ax^2 + bx + c < 0$), тогда множество решений это $R — {frac{-b}{2a}}$(Все числа, за исключением ${frac{-b}{2a}}$) Понятно, что если a < 0 и $ax^2 + bx + c geq 0$(или a > 0 и $ax^2 + bx + c le 0$), тогда у неравенства только одно решение и оно ${frac{-b}{2a}}$, а также,

если a < 0 и $ax^2 + bx + c > 0$(или a > 0 и $ax^2 + bx + c < 0$), тогда у неравенства нет действительных решений.

Случай 3: Если $Delta < 0$,

тогда у $ax^2+bx+c=0$ нет решений. Теперь, если $a>0$, тогда график выглядит, как показано на «Рисунке e» ,а если $a»Рисунке f».

Если $ax^2 + bx + c ge 0$ или $ax^2 + bx + c > 0$ и $a > 0$(или $ax^2 + bx + c < 0$ и $a < 0$), тогда решениями являются все действительные числа.

Понятно, что если $ax^2 + bx + c > 0$ и $a < 0$(или $ax^2 + bx + c < 0$ и $a > 0$), то у квадратного неравенства нет действительных решений.

1. Пример 1: Найти множество решений неравенства $x^2 + 3x — 10 > 0$.
2. Решение: В соответствии с вышесказанным
3. $Delta = b^2 — 4ac
   ightarrow Delta = 3^2 — 4(1)(-10) = 9 + 40 = 49
   ightarrow Delta > 0
   ightarrow x^2 + 3x — 10$, значит есть два разных корня, которые можно найти, как:
4. $x_1 = frac{-b + sqrt{b^2 — 4ac}}{2a} = frac{-3 + sqrt{49}}{2 imes 1} = frac{-3 + 7}{2} = frac{4}{2} = 2$
5. $x_2 = frac{-b — sqrt{b^2 — 4ac}}{2a} = frac{-3 — sqrt{49}}{2 imes 1} = frac{-3 — 7}{2} = frac{-10}{2} = -5$
6. С другой стороны $a > 0$, поэтому множество решений неравенство согласно Случаю 1 и «Рисунку a» это:

• Пример 2: Найти множество решений $x^2 + 5x — 6 geq 0$.
• Решение: В соответствии с вышесказанным
• $Delta = b^2 — 4ac
  ightarrow Delta = 5^2 — 4(1)(-6) = 25 + 24 = 49
  ightarrow Delta > 0$
  $x^2 + 5x — 6 = 0$, значит есть два разных корня, которые можно найти, как:
• $x_1 = frac{-b + sqrt{b^2 — 4ac}}{2a} = frac{-5 + sqrt{49}}{2 imes 1} = frac{-5 + 7}{2} = frac{2}{2} = 1$
• $x_2 = frac{-b — sqrt{b^2 — 4ac}}{2a} = frac{-5 — sqrt{49}}{2 imes 1} = frac{-5 — 7}{2} = frac{-12}{2} = -6$
• С другой стороны $a > 0$, поэтому множество решений неравенство согласно Случаю 1 и «Рисунку a» это:

1. Пример 3: Найти множество решений $x^2 — 2x + 1 geq 0$.
2. Решение: В соответствии с вышесказанным
3. $Delta = b^2 — 4ac
   ightarrow Delta = (-2)^2 — 4(1)(1) = 4 — 4 = 0
   ightarrow Delta = 0$
   $x^2 — 2x + 1 = 0$, значит есть только один корень, который можно найти, как:
4. $x_1 = x_2 = frac{-b pm sqrt{b^2 — 4ac}}{2a} = frac{-(-2) pm sqrt{0}}{2 imes 1} = frac{2 pm 0}{2} = frac{2}{2} = 1$
5. С другой стороны $a > 0$, поэтому множество решений неравенство согласно Случаю 1 и «Рисунку c» это: $mathbb{R}$
6. Пример 4: Найти множество решений $x^2 — 2x + 1 < 0$.
7. Решение: В соответствии с вышесказанным
8. $Delta = b^2 — 4ac
   ightarrow Delta = (-2)^2 — 4(1)(1) = 4 — 4 = 0
   ightarrow Delta = 0$
   $x^2 — 2x + 1$, значит есть только один корень, который можно найти, как:
9. $x_1 = x_2 = frac{-b pm sqrt{b^2 — 4ac}}{2a} = frac{-(-2) pm sqrt{0}}{2 imes 1} = frac{2 pm 0}{2} = frac{2}{2} = 1$
10. С другой стороны $a > 0$, поэтому $x^2 — 2x + 1 geq 0$ , значит в соответствии со всем вышесказанным и графиком прошлого примера у $x^2 — 2x + 1 < 0$ нет решений в действительных числах.
11. Пример 5: Найти множество решений $-x^2 — 7x + 8 < 0$.
12. Решение: В соответствии с вышесказанным
13. $Delta = b^2 — 4ac
    ightarrow Delta = (-7)^2 — 4(-1)(8) = 49 + 32 = 81
    ightarrow Delta > 0$
    $-x^2 — 7x + 8$ , есть два разных корня, которые можно найти, как:
14. $x_1 = frac{-b + sqrt{b^2 — 4ac}}{2a} = frac{-(-7) + sqrt{81}}{2 imes (-1)} = frac{7 + 9}{-2} = frac{16}{-2} = -8$
15. $x_2 = frac{-b — sqrt{b^2 — 4ac}}{2a} = frac{-(-7) — sqrt{81}}{2 imes (-1)} = frac{7 — 9}{-2} = frac{-2}{-2} = 1$
16. С другой стороны $a > 0$, поэтому множество решений неравенство согласно Случаю 1 и «Рисунку a» это:

• Пример 6: Найти множество решений of $x^2 + 1 > 0$.
• Решение: В соответствии с вышесказанным
• $Delta = b^2 — 4ac
  ightarrow Delta = 0^2 — 4(1)(1) = 0 — 4 = -4
  ightarrow Delta < 0$ $x^2 + 1 = 0$, значит нет корней в действительных числах. С другой стороны $a > 0$, поэтому множество решений $x^2 + 1 > 0$ это $mathbb{R}$

Источник: https://www.math10.com/ru/algebra/kvadratnie-neravenstva.html

Решение квадратных неравенств с одной переменой

Сохрани ссылку в одной из сетей:

• Задание
  №13
• Решение
  квадратных неравенств с одной переменой.
• Неравенства
  вида
  где
  a,b,c
  –любые числа, называются
  квадратными неравенствами с одной
  переменной.
• Решить
  неравенство, значит найти такие значения
  переменной, при которых неравенства
  будут верными, или доказать, что таких
  значений нет.
• Решать
  такие неравенства можно различными
  способами.

1. Аналитически.

2. Графически.

3. Методом интервалов.

1.Находим корни квадратного трёхчлена.
Раскладываем на множители, используя
формулу

Пример:
решить неравенство

1. или
2. 
3. Решаю первую систему, получаю x>3.
   Вторая система даёт решение x0, значит две точки пересечения с числовой осью

• Выберу любое значение из левого интервала,
  например x=0. Вычислю
  значение квадратного трёхчлена при
  этом значении: ,
  в промежутке
  функция положительна (поставила знак
  +),
• Из второго промежутка взяла x=3, ,
  в промежутке
  функция отрицательна, (ставлю знак -),
• x=6 , в последнем интервале стоит знак +
• По условию задачи, неравенство должно
  быть неотрицательным, значит, ответ:
• Ответ: .
• 2)
• Решение:
• 1.D=100+96=196, два нуля функции
• 2.Числовая ось разбилась на три интервала

3. Найду знаки трёхчлена в каждом из них.

1. Ответ:(2;3)
2. 3)

1.D=36-84=-48, нулей функция не
имеет, ветви параболы направлены вверх,
значит, заданный трёхчлен принимает
положительные значения при любых
значениях переменной.

Ответ: пустое множество.

4) разделю
обе части неравенства на -1, изменю, знак
неравенства, получу равносильное
неравенство:

1.В
данном случае имеем сумму двух слагаемых,
первое из которых неотрицательно при
любых значениях переменной, а второе
положительное число, значит, сумма
всегда положительна.

• Ответ: пустое множество
• 5)

Источник: https://gigabaza.ru/doc/90055.html

Квадратные неравенства, формулы

Правило Определяется значением дискриминанта D = b2 — 4ac Правило 1 1.  D < 0.

1)  Если a > 0, то ax2 + bx + c = 0 при любом x;

2)  Если a < 0, то ax2 + bx + c < 0 при любом x.

Пример 3×2 + x + 4 ? 0.

D = -47 < 0;  a = 3 > 0,  значит 3×2 + x + 4 > 0 при любых x, т.е. исходное неравенство не имеет решений.

Ответ: нет решений.

Правило 2 2.  D = 0. Тогда ax2 + bx + c = a(x +   b  2a)2.

• 1)  Если a > 0, то ax2 + bx + c > 0 при любом x ? —   b  2a
• и ax2 + bx + c = 0 при x = —   b  2a.
• 2)  Если a < 0, то ax2 + bx + c < 0 при любом x ? —   b  2a
• и ax2 + bx + c = 0 при x = —   b  2a

Пример -x2 + 2x — 1 < 0 — (x — 1)2 < 0 — верно при любом x ? 1. Правило 3 3.  D > 0. Тогда ax2 + bx + c = a (a — x1) (x — x2).

где x1, x2 — действительные и различные корни квадратного трехчлена ax2 + bx + c. Пусть x1 < x2.

! В точках x1 и x2   ax2 + bx + c = 0.

Пример 2×2 — 13x + 15 ? 0.

D = 13×2 — 4 • 2 • 15 = 49 > 0;  x1 = 1,5;  x2 = 5,

значит 2×2 — 13x + 15 = 2(x — 1,5) (x — 5); a = 2 > 0. Правило

Где a ? 0, b, c — числа, x — переменная, символ ?? может означать любой из

знаков: >, . Примеры 1)  -4×2 + 3 ? 0;

1. 2)  6×2 — 5x + 13 < 0;
2. 3)  x2 + 1 ? 0;
3. 4)  -3×2 + x > 0.

Правило

• а
• б
• в
• г
• д
• е
• з
• и
• к
• л
• м
• н
• о
• п
• р
• с
• т
• у
• ф
• х
• ц
• ч
• э

© 2020 Все права защищеныПри использовании материалов данного сайта обязательно указывать ссылку на источник

Источник: https://formula-xyz.ru/kvadratnye-neravenstva.html

Квадратные неравенства

Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c , или ≥ в ответ выбираем интервалы со знаком +.

Если знак неравенства 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:

x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0

Это значит, что знак на интервале, в котором лежит точка 6 будет   +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .

Точки -3 и 4 будут в квадратных скобках, так как они жирные.

Ответ:   x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )

№2. Решить неравенство    − 3 x − 2 ≥ x 2 .

1. Решение:
2. Приводим квадратное неравенство к виду a x 2 + b x + c   ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
3. − 3 x − 2 ≥ x 2
4. − x 2 − 3 x − 2 ≥ 0
5. − x 2 − 3 x − 2 = 0
6. a = − 1, b = − 3, c = − 2
7. D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
8. D > 0 ⇒ будет два различных действительных корня
9. x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
10. x 1 = − 2, x 2 = − 1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:

− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2

Источник: https://epmat.ru/kvadratnye-neravenstva/

Квадратичные неравенства

Покажем, как с помощью графика функции y = ax2 + bx + c решать квадратные неравенства.

Квадратичная функция, или парабола, — это функция вида

Вспомним свойства этой функции:

• Если , ветви вверх
• Если , ветви вниз
• Точки пересечения с осью X: и
• где и — корни квадратного уравнения
• Точка пересечения с осью Y: М (0; с).
• Вспомним также, как выражение раскладывается на множители.
• где и — корни квадратного уравнения
• 1. Часто на тестировании мы предлагаем решить неравенство
• x2 < 400

Справляются далеко не все. Очень часто, не задумываясь, выдают «ответ»: x < ± 20.

Однако сама эта запись — абсурдна! Представьте, что вы слышите прогноз погоды: «Температура будет меньше плюс-минус двадцати градусов». Что, спрашивается, надеть — рубашку или шубу? ?

Давайте решим это неравенство с помощью графика. Изобразим схематично график функции y = x2 и отметим все значения x, для которых y < 400.

Теперь мы видим правильный ответ: x ∈ (−20; 20).

Запомним: извлекать корень из неравенства нельзя. Такого действия просто нет.

2. Следующее неравенство:

Переносим всё в левую часть неравенства. Раскладываем левую часть на множители.

Рисуем ось X. Рисуем параболу с ветвями вверх.

Эта парабола пересекает ось X в точках — 4 и 4. Отмечаем знаки выражения в левой части на каждом интервале.

Записываем ответ:

3. Решим неравенство: x2 − 3x − 10 ≥ 0.

Мы видим, что при x ∈ (−2; 5) значения функции отрицательны (график проходит ниже оси X). В точках −2 и 5 функция обращается в нуль, а при x < −2 и x > 5 значения функции положительны. Следовательно, наше неравенство выполняется при .

Обратите внимание, что для решения неравенства нам достаточно было схематично изобразить параболу. Ось Y вообще не понадобилась!

4. Ещё одно неравенство: x2 + 2x + 4 > 0.

Ветви параболы y = x2 + 2x + 4 направлены вверх. Дискриминант отрицателен, т. е. уравнение x2 + 2x + 4 = 0 не имеет корней. Стало быть, нет и точек пересечения параболы с осью X.

Раз ветви параболы направлены вверх и она не пересекает ось X — значит, парабола расположена над осью X.

Получается, что значения функции положительны при всех возможных x. Иными словами, решения нашего неравенства — это все действительные числа.

Ответ: .

Квадратные неравенства являются неотъемлемой частью ЕГЭ. Разберём типичные примеры из банка заданий ЕГЭ.

1. 5. Следующее квадратичное неравенство:
2. Разложим его левую часть на множители.
3. Получим:

И больше ничего не пишем. Рисуем ось X. Рисуем параболу с ветвями вверх.

Эта парабола пересекает ось X в точках 1 и 5. Отмечаем знаки выражения в левой части на каждом интервале.

• Записываем ответ:
• 6. Еще неравенство:

Квадратное уравнение не имеет решений — его дискриминант отрицателен. Это значит, что парабола нигде не пересекает ось X. Ветви этой параболы направлены вверх. Все значения функции положительны. Неравенство выполняется для всех действительных X.

Соберем в одну таблицу примеры решения различных квадратичных неравенств.

Источник: https://ege-study.ru/kvadratichnye-neravenstva/

Квадратные неравенства

• Квадратным неравенством называют неравенство вида 
• αx2 + bх + c > 0, где а ≠ 0
• Разберем графический способ решения квадратных неравенств

Графический способ

Графический способ – это один из самых простых методов решения неравенств. Суть графического способа решения неравенств следующая: рассматривают функцию y = f(x), строят её график в Декартовой системе координат и выясняют, на каких промежутках график расположен выше нуля, а на каких ниже. Те промежутки, на которых

• график функции f выше 0 являются решениями неравенства f(x) > 0;
• график функции f не ниже 0 являются решениями неравенства f(x) ≥ 0;
• график функции f ниже 0 являются решениями неравенства f(x) < 0;
• график функции f не выше 0 являются решениями неравенства f(x) ≤ 0.

Также скажем, что точки пересечения графика функции f(х) с осью абсцисс (осью х) являются решениями уравнения f(x) = 0.

Разберем на примере:

αx2 + bx + c < 0 (≤, >, ≥)

Графиком левой части неравенства является парабола. Дальше, согласно графическому способу решения неравенств, надо проанализировать, на каких промежутках график одной функции расположен выше или ниже оси Ох, что позволит записать искомое решение квадратного неравенства.

В зависимости от значений коэффициентов a, b и c возможны следующие шесть вариантов (для наших нужд достаточно схематического изображения, и можно не изображать ось Oy, так как ее положение не влияет на решения неравенства):

Вариант 1:

На этом чертеже мы видим параболу, ветви которой направлены вверх, и которая пересекает ось Ox в двух точках (x1 и x2). Этот чертеж отвечает варианту, когда коэффициент α – положительный (он отвечает за направленность вверх ветвей параболы), и когда положительно значение дискриминанта квадратного трехчлена αx2 + bx + c (при этом трехчлен имеет два корня, которые мы обозначили как x1 и x2).

Давайте для наглядности изобразим красным цветом части параболы, расположенные выше оси абсцисс, а синим цветом – расположенные ниже оси абсцисс и выясним, какие промежутки этим частям соответствуют. Определить их поможет следующий чертеж (в дальнейшем подобные выделения в форме прямоугольников будем проводить мысленно):

• Так на оси абсцисс оказались подсвечены красным цветом два промежутка(−∞, x1) и (x2, +∞), на них парабола выше оси Ox, они составляют решение квадратного неравенства αx2 + bx + c > 0.
• Синим цветом подсвечен промежуток (x1, x2), на нем парабола ниже оси Ox, он представляет собой решение неравенства αx2 + bx + c < 0. 
• Решениями нестрогих квадратных неравенств αx2 + bx + c≥0 и αx2 + bx + c ≤ 0 будут те же промежутки, но в них следует включить корни x1 и x2, отвечающие равенству αx2 + bx + c=0.

Вариант 2:

Здесь мы видим параболу, ветви которой направлены вверх, и которая касается оси абсцисс, то есть, имеет с ней одну общую точку, обозначим абсциссу этой точки как x0. Представленному случаю отвечает α > 0 (ветви направлены вверх) и D =0 (квадратный трехчлен имеет один корень x0). Для примера можно взять квадратичную функцию y= x2 − 4x + 4, здесь 

α = 1 > 0, D = (−4)2 − 4•1•4 = 0 и x0 = 2.

По графику отчетливо видно, что парабола расположена выше оси Ox всюду, кроме точки касания, то есть, на промежутках (−∞, x0), (x0, ∞). Для наглядности выделим на чертеже области по аналогии с предыдущим пунктом.

1. Делаем выводы: при α > 0 и D = 0
2. Решением квадратного неравенства 
3. Делаем выводы: при a>0 и D=0

• Решением квадратного неравенства αx2 + bx + c > 0 является(−∞, x0)∪(x0, +∞) или в другой записи x ≠ x0;
• Решением квадратного неравенства αx2 + bx + c ≥ 0 является (−∞, +∞) или в другой записи x ∈ R;
• Квадратное неравенство αx2 + bx + c < 0 не имеет решений (нет интервалов, на которых парабола расположена ниже оси Ox);
• Квадратное неравенство αx2 + bx + c ≤ 0 имеет единственное решение x = x0 (его дает точка касания), где x0 — корень квадратного трехчлена αx2 + bx + c > 0 является (−∞, x0)∪(x0, +∞) или в другой записи x ≠ x0;

Вариант 3:

В этом случае ветви параболы направлены вверх, и она не имеет общих точек с осью абсцисс. Здесь мы имеем условия α > 0 (ветви направлены вверх) и D < 0(квадратный трехчлен не имеет действительных корней). Для примера можно построить график функции y = 2×2 + 1, здесь α = 2 > 0, 

D = 02 − 4•2•1 = −8 < 0.

Очевидно, парабола расположена выше оси Ox на всем ее протяжении (нет интервалов, на которых она ниже оси Ox, нет точки касания).

И остаются три варианта расположения параболы с направленными вниз, а не вверх, ветвями относительно оси Ox. В принципе их можно и не рассматривать, так как умножение обеих частей неравенства на −1 позволяет перейти к равносильному неравенству с положительным коэффициентом при x2. 

Пример:

• а) x2 — 2x — 3 > 0
• б) x2 — 2x — 3 < 0
• в) x2 — 2x — 3 ≥ 0
• г) x2 — 2x — 3 ≤ 0
• Решение:

Рассмотрим параболу y = x2 — 2x — 3 на рисунке 1.

а) Решить неравенство x2 — 2x — 3 > 0 — это значит ответить на вопрос, при каких значениях xординаты точек параболы положительны. Замечаем, что y > 0, т. е. график функции расположен выше оси x, при x < -1 или при x > 3. Значит, решением неравенства служат все точки открытого луча (-∞; -1), а так же все точки открытого луча (3; +∞).

Используя знак  «U», ответ можно записать так: (-∞; -1)υ(3; +∞). Впрочем, ответ можно записать и так:

x < -1; x > 3.

б) Неравенство x2 — 2x — 3 < 0, или y < 0, где y = x2 — 2x — 3, также можно решить с помощью рис. 1: график расположен ниже оси x, если -1 < x < 3. Поэтому решениями данного неравенства служат все точки интервала (-1; 3).

в) Неравенство x2 — 2x — 3 ≥ 0 отличается от неравенства x2 — 2x — 3 > 0 тем, что в ответ надо включить и корни уравнения x2 — 2x — 3 = 0, т.е. точки x = -1 и x = 3. Таким образом, решениями данного неравенства являются все точки луча (-∞; -1], а также все точки луча [3; +∞).

г) Неравенство x2 — 2x — 3 ≤ 0 отличается от неравенства x2 — 2x — 3 < 0 тем, что в ответ надо включить и корни уравнения x2 — 2x — 3 = 0, т.е. x = -1 и x = 3. Следовательно, решениями данного неравенства служат все точки отрезка [-1; 3].

Алгоритм решения

Итогом всех предыдущих выкладок выступает алгоритм решения квадратных неравенств графическим способом:

• На координатной плоскости выполняется схематический чертеж, на котором изображается ось Ox (ось Oy изображать не обязательно) и эскиз параболы, отвечающей квадратичной функции            y = αx2 + bx + c . Для построения эскиза параболы достаточно выяснить два момента:
• Во-первых, по значению коэффициента a выясняется, куда направлены ее ветви (при a>0 – вверх, при a 0), касается ее в одной точке (при D = 0), или не имеет общих точек с осью Ox (при D < 0). Для удобства на чертеже указываются координаты точек пересечения или координата точки касания (при наличии этих точек), а сами точки изображаются выколотыми при решении строгих неравенств, или обычными при решении нестрогих неравенств.
• Когда чертеж готов, по нему на втором шаге алгоритма
• При решении квадратного неравенства a•x2+b•x+c>0 определяются промежутки, на которых парабола располагается выше оси абсцисс;
• При решении неравенства αx2 + bx + c ≥ 0 определяются промежутки, на которых парабола располагается выше оси абсцисс и к ним добавляются абсциссы точек пересечения (или абсцисса точки касания);
• При решении неравенства αx2 + bx + c < 0 находятся промежутки, на которых парабола ниже оси Ox;
• Наконец, при решении квадратного неравенства вида αx2 + bx + c ≤ 0 находятся промежутки, на которых парабола ниже оси Ox и к ним добавляются абсциссы точек пересечения (или абсцисса точки касания); они и составляют искомое решение квадратного неравенства, а если таких промежутков нет и нет точек касания, то исходное квадратное неравенство не имеет решений.

Источник: https://ya-znau.ru/znaniya/zn/128