Неравенство треугольника, формула и примеры

Подобный материал:

• Программа обсуждена на заседании кафедры Математики фнти, 38.01kb.
• План урока: Организационный момент. Рассказ сказка о медианах, высотах и биссектрисах., 161.11kb.
• Понятие юридических фактов, 989.45kb.
• Понятие юридических фактов, 366.24kb.
• Социальное неравенство в условия современной России 4 Глава, 325.02kb.
• Проект «Социальное неравенство и публичная политика» (СНиПП) «Неравенство доходов как, 804.89kb.
• Лекция 13. Индивидуальный и рыночный спрос 3 От индивидуального спроса к рыночному, 147.34kb.
• Тема: Измерение углов, 29.65kb.
• Ема урока. Свойство медианы равнобедренного треугольника, 39.45kb.
• Урок сказка по математике 6 класс «Умножение одночлена на многочлен», 304kb.

Математический кружок Русановского лицея Неравенство треугольника Неравенство треугольника – один из важнейших геометрических фактов.

Представляя собой одно из интуитивных свойств расстояния, оно нередко помогает в решении непростых геометрических и текстовых задач. С помощью неравенства треугольника представляется возможным отсеять часть из возможных вариантов расположения каких-либо элементов в громоздких геометрических задачах.

Часто именно невыполнение строгого неравенства треугольника (а именно – достижение в нем равенства) дает основание утверждать о принадлежности трех точек одной прямой.

Таким образом, неравенство треугольника является одновременно интуитивно понятным, даже очевидным, но весьма часто становится мощным инструментом при решении серьезных математических задач.

Несколько слов о неравенствах

Различают строгие и нестрогие неравенства.

Или же, переходя на язык отношений, строгое неравенство можно считать отношением строгого порядка на множестве действительных чисел (то есть отношением, которое обладает свойствами антирефлексивности, антисимметричности и транзитивности).

Если же речь идет о нестрогом неравенстве, то можно говорить о нем как об отношении нестрогого порядка на том же множестве (то есть рассматривать вместо антирефлексивности рефлексивность).

Напомним, что об отношениях как математическом объекте и их свойствах мы уже упоминали в Лекции 7 (были рассмотрены свойства отношения делимости). Более подробное их изучение нам предстоит в будущем, поскольку они довольно успешно систематизируют и обобщают ряд элементарных математических понятий. Теперь же мы приведем несколько примеров неравенств каждого из названных типов.

Строгими неравенствами называют такие неравенства:

• a < b – означает, что a меньше b;
• a > b – означает, что a больше b;
• a ≠ b – означает, что a не равно b или же что a и b различны.

К нестрогим неравенствам относят следующие математические отношения:

• a ≤ b – означает, что a меньше либо равно b или, что то же самое, a не больше (не превосходит, не превышает) b;
• a ≥ b – означает, что a больше либо равно b или, что то же самое, a не меньше b.

Пока что мы не будем утруждать себя более глубоким исследованием неравенств. Сегодня нам вполне хватит уже устоявшихся представлений о неравенствах.

• Неравенство треугольника
• Теорема (неравенство треугольника):
• Каждая сторона треугольника меньше суммы двух других его сторон.
• Замечание. Иногда используют также и несколько другую формулировку этой теоремы, подключая попутно и случай вырожденного треугольника:
• Длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон.

Заметим, что разница между двумя приведенными формулировками столь незначительна, что нет смысла рассматривать их отдельно. В дальнейшем при решении задач мы будем использовать как первую формулировку теоремы, так и вторую, не оговаривая это отдельно. Неравенство треугольника возникло, судя по всему, тогда же, когда человек научился ходить и хоть как-то мыслить. Известно, что одну из первых его формализаций приводит Евклид в знаменитых «Началах». Там он доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Из нее выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника. Вот такая вот непростая логическая цепочка для доказательства вполне очевидного, казалось бы, неравенства!

Рис. 1

Доказательство теоремы. Рассмотрим треугольник ABC и покажем, что AB < AC + BC. При доказательстве воспользуемся одним из видов дополнительных построений – откладыванием равных отрезков (метод спрямления).

В треугольнике ABC (рис. 1) на продолжении стороны BC отложим отрезок CD, равный AC. В равнобедренном треугольнике ACD . В треугольнике ABD угол ADB меньше угла BAD, значит, BD > AB, или BC + CD > AB. Но CD = AC, значит, AC + BC > AB.

1. Замечание. Обратите внимание, что, исходя из формулировки теоремы, следует записать сразу три неравенства:
2. AB < AC + BC;
3. AC < AB + BC;
4. BC < AB + AC.

Нередко, записав одно неравенство, о двух других почему-то забывают. Помните, что это может привести к довольно неприятным ошибкам.

Неравенство треугольника может служить одним из простых критериев принадлежности трех точек одной прямой. Три точки будут принадлежать одной прямой тогда и только тогда, когда в неравенстве треугольника достигается равенство. Естественно, равенство может достигаться лишь в одном из трех неравенств (см. замечание), поскольку одна из точек будет лежать четко между двумя другими.

Упражнение. Докажите, что в треугольнике каждая сторона больше разности двух других сторон.

Приведем в качестве примера использования неравенства треугольника несколько сравнительно несложных геометрических задач.

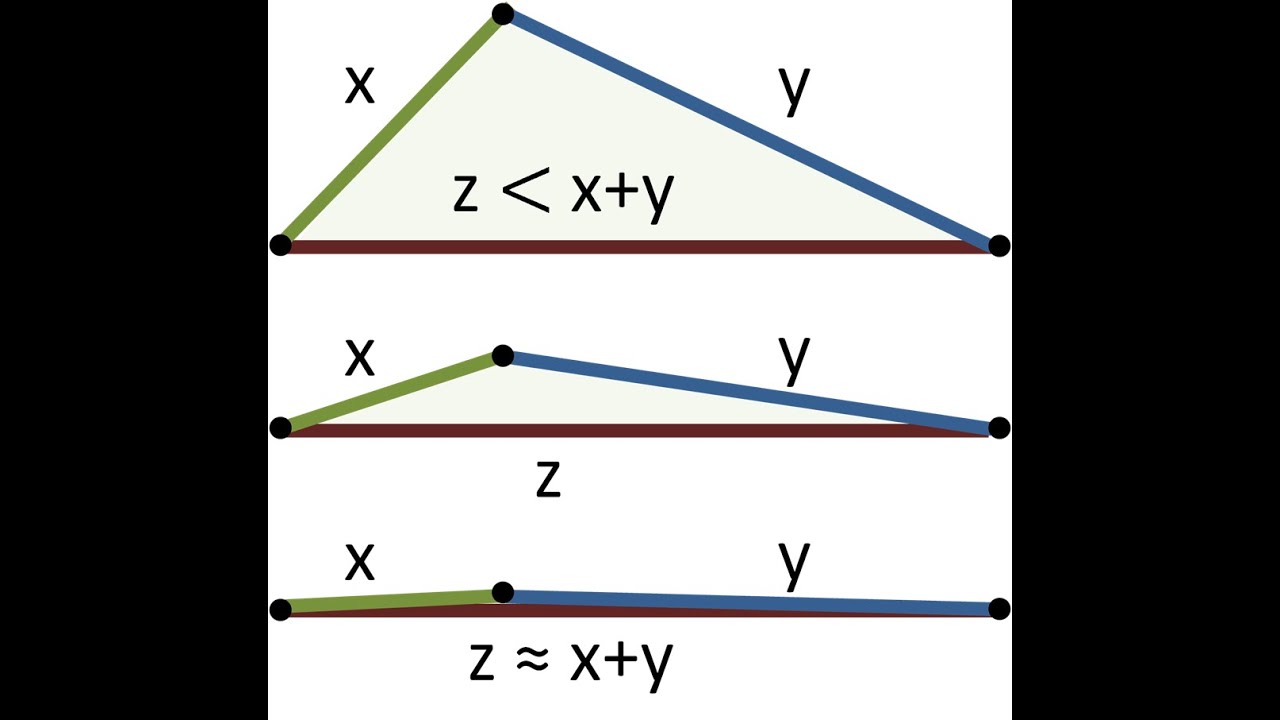
Задача 1. Докажите, что в произвольном четырехугольнике ABCD AB + CD < AC + BD.

Рис. 2

Решение. Пусть O – точка пересечения диагоналей четырехугольника ABCD (рис. 2). По неравенству треугольника:

• AO + OB > AB;
• CO + OD > CD.
• Рассмотрим сумму AC + BD:
• AC + BD = (AO + OC) + (BO + OD) =
• = (AO + BO) + (OC + OD) > AB + CD.

Задача 2. Докажите, что в треугольнике ABC выполнено неравенство (a, b, c – стороны треугольника ABC).

Решение. Воспользуемся следствием из неравенства треугольника (см. упражнение): (предполагаем, что ). Тогда, возведя в квадрат обе части неравенства, получим:

Аналогично:

.

Складывая все три неравенства, получим требуемое.

Упражнение. Докажите, что медиана AM в произвольном треугольнике ABC по длине меньше, чем .

Задача 3. На плоскости дан квадрат ABCD и точка O. Докажите, что расстояние от точки O до одной из вершин квадрата не превосходит суммы расстояний от O до трех других вершин квадрата.

Решение. Сложите неравенства треугольника AC + OC > OA и OB + OD > BD. Так как AC = BD, то, сокращая, получаем требуемое.

Задача 4. Найдите внутри выпуклого четырехугольника точку, такую, что сумма расстояний от нее до вершин минимальна.

Решение. Так как четырехугольник выпуклый, то его диагонали пересекаются в точке O внутри него. Обозначим вершины четырехугольника через A, B, C и D (по часовой стрелке). Тогда сумма расстояний от O до вершин равна сумме длин диагоналей AC и BD.

Но для любой другой точки P имеем, во-первых, что сумма расстояний от P до вершин не меньше AC + BD, а во-вторых, либо PA + PC > AC, либо PB + PD > BD. Значит, эта сумма равна AC + BD только если P совпадает с точкой O.

Значит, точка O – искомая.

Неравенство треугольника успешно применяется и в довольно запутанных текстовых задачах. Что интересно, в таких задачах многое может зависеть от того, насколько удачно Вы построите геометрическую интерпретацию.

Задача 5. В некоторой стране расположены 4 города: A, B, C и D. Два самолета одновременно вылетели из города A.

Маршрут первого самолета: A—B—D—C—A—D—B—C—A, а маршрут второго: A—B—C—D—A—B—C—D—A—B—C—D—A. Какой из самолетов раньше закончит свой маршрут, если их скорости одинаковы?

Не бойтесь экспериментировать! Если в задаче не задано конкретное расположение объектов, Вы вправе рисовать в своем решении всё, что не противоречит условию – оно ведь Ваше. В том числе, и города в Задаче 5 Вы можете расставить как угодно. Следует лишь помнить, что в некоторых задачах после разбора «нормального», общего случая, необходимо разобрать и некоторые «патологические», частные случаи. К примеру, в Задаче 5 может понадобиться рассмотрение случая, когда некоторые три города лежат на одной прямой – всё зависит от того, каково Ваше решение для общего случая.

Решение задачи 5. Запишем длины маршрутов каждого из самолетов в виде сумм расстояний между городами. Длина маршрута первого самолета будет равна

1. .
2. .
3. .
4. Докажем, что независимо от расположения точек A, B, C, D на плоскости (городов A, B, C, D в стране) выражение будет неположительным.

Второй же самолет пролетит расстояние Рассмотрим разность между расстоянием, которое пролетел первый самолет, и расстоянием, которое преодолел второй. Для этого следует рассмотреть два случая.

1. Предположим, что точки A, B, C, D создают на плоскости четырехугольник ABCD с диагоналями AC и BD. Тогда запишем последовательно неравенства треугольника для треугольников ABC, BCD, CDA и DAB (см. рис. 2):

• AB + BC > AC;
• BC + CD > BD;
• CD + DA > CA;
• DA + AB > DB.
• ;
• ;
• .

Сложив все четыре неравенства, получим

2. Рассмотрим случай, когда точки A, B, C, D создают на плоскости четырехугольник ACBD с диагоналями AB и CD (нарисуйте себе соответствующий рисунок). Заметим, что неравенства треугольника выполняются для тех же треугольников, что и в первом случае.

Оказывается, что решение задачи останется тем же, несмотря на то, что расположение точек на плоскости существенно изменилось. Это можно считать еще одной характерной чертой многих решений задач, использующих неравенство треугольника. Следовательно, первый самолет прилетит раньше, поскольку его маршрут короче маршрута второго. Заметьте, что решение Задачи 5 требует небольшого анализа, что является непременным качеством всех олимпиадных задач. Будьте внимательны – Ваше решение задачи будет правильным лишь тогда, когда Вы рассмотрите все возможные случаи, подходящие под условие. Следует также отметить, что зачастую на рисунке, изображающем условие задачи, не видно треугольника, применение неравенства треугольника для которого дало бы моментальное решение. В таком случае может помочь удачно подобранное геометрическое преобразование. Об этом мы поговорим несколько позже. Знакомство с неравенством треугольника на этом следует объявить законченным. Но новая встреча с ним уже не за горами. 7 класс Лекция 13. Неравенство треугольника

Источник: http://geum.ru/next/art-155722.php

Неравенство треугольника. Геометрические неравенства

Геометрические неравенства.

При изучении математики ученикам часто приходится сталкиваться с решением неравенств. Одними из наиболее сложных видов неравенств являются геометрические.

В школе на их решение отводится не достаточное количество времени, поэтому при работе с подобными неравенствами у учеников возникают трудности.

Однако на вступительных экзаменах в ВУЗы и на математических олимпиадах такого рода задания можно встретить достаточно часто. Рассмотрим некоторые из них.

• Неравенство треугольника
• Теорема (неравенство треугольника):
• Каждая сторона треугольника меньше суммы двух других его сторон.
• Замечание. Иногда используют также и несколько другую формулировку этой теоремы, подключая попутно и случай вырожденного треугольника:
• Длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон.

Заметим, что разница между двумя приведенными формулировками столь незначительна, что нет смысла рассматривать их отдельно. В дальнейшем при решении задач мы будем использовать как первую формулировку теоремы, так и вторую, не оговаривая это отдельно.

Неравенство треугольника возникло, судя по всему, тогда же, когда человек научился ходить и хоть как-то мыслить. Известно, что одну из первых его формализаций приводит Евклид в знаменитых «Началах». Там он доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного.

Из нее выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника.

Вот такая вот непростая логическая цепочка для доказательства вполне очевидного, казалось бы, неравенства!

Рис. 1

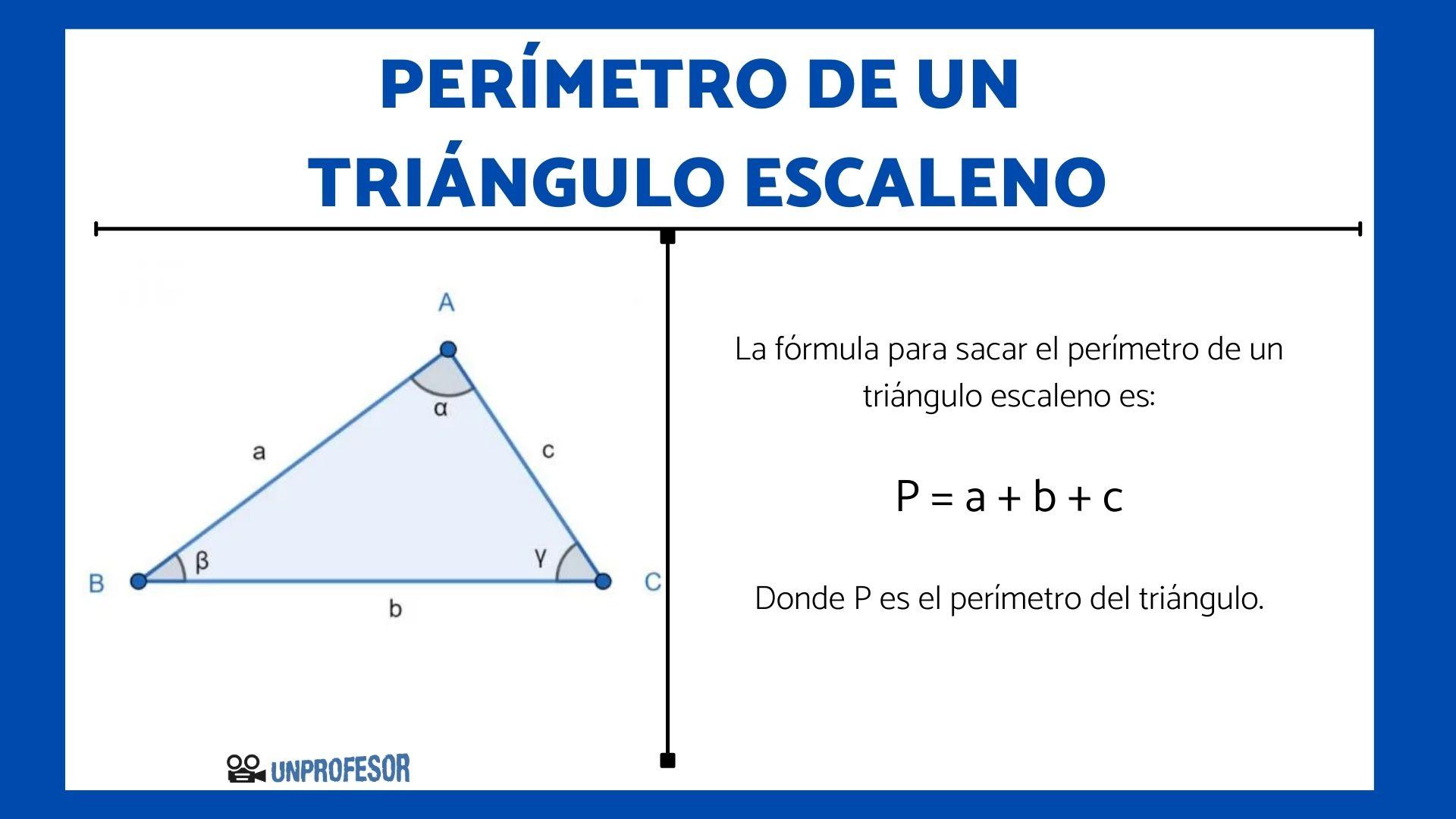
Доказательство теоремы. Рассмотрим треугольник ABC и покажем, что AB AC + BC. При доказательстве воспользуемся одним из видов дополнительных построений – откладыванием равных отрезков (метод спрямления).

В треугольнике ABC (рис. 1) на продолжении стороны BC отложим отрезок CD, равный AC. В равнобедренном треугольнике ACD . В треугольнике ABD угол ADB меньше угла BAD, значит, BD  AB, или BC + CD  AB. Но CD = AC, значит, AC + BC  AB.

1. Замечание. Обратите внимание, что, исходя из формулировки теоремы, следует записать сразу три неравенства:
2. ABAC + BC;
3. AC AB + BC;
4. BC AB + AC.

Нередко, записав одно неравенство, о двух других почему-то забывают. Помните, что это может привести к довольно неприятным ошибкам.

Неравенство треугольника может служить одним из простых критериев принадлежности трех точек одной прямой. Три точки будут принадлежать одной прямой тогда и только тогда, когда в неравенстве треугольника достигается равенство. Естественно, равенство может достигаться лишь в одном из трех неравенств (см. замечание), поскольку одна из точек будет лежать четко между двумя другими.

1. Докажите, что в треугольнике каждая сторона больше разности двух других сторон.

Приведем в качестве примера использования неравенства треугольника несколько сравнительно несложных геометрических задач.

1. В треугольнике длины двух сторон равны 5, 27 и 2, 79. Какой может быть длина третьей стороны, если известно, что она является целым числом.

2. Докажите, что в произвольном четырехугольнике ABCDAB + CD AC + BD.

3. Докажите, что в треугольнике ABC выполнено неравенство

 (a, b, c – стороны треугольника ABC).

1. Докажите, что медиана AM в произвольном треугольнике ABC по длине меньше, чем .

2. На плоскости дан квадрат ABCD и точка O. Докажите, что расстояние от точки O до одной из вершин квадрата не превосходит суммы расстояний от O до трех других вершин квадрата.

3. a, b и c — длины сторон произвольного треугольника.

   Докажите, что  a = y + z, b = x + z и c = x + y, где x, y и z — положительные числа. 

4. Пусть a, b, c – стороны треугольника. Докажите неравенство  a3 + b3 + 3abc c3.

5. a, b и c — длины сторон произвольного треугольника.

   Докажите, что  a2 + b2 + c2 ab + bc + ca). 

6. a, b и c — длины сторон произвольного треугольника.

   Докажите, что

a(b — c)2 + b(c — a)2 + c(a — b)2 + 4abca3 + b3 + c3.

1. a, b и c — длины сторон произвольного треугольника.

   Докажите, что

 +  + 3.

1. a, b, c – стороны треугольника. Докажите неравенство

2. a, b, c – длины сторон треугольника. Докажите, что

.

1. a, b и c — длины сторон произвольного треугольника.

   Докажите, что

(a + b — c)(a — b + c)(- a + b + c)  abc.

1. a, b и c — длины сторон произвольного треугольника. Докажите, что

a2b(a — b) + b2c(b — c) + c2a(c — a)  0.

1. Длины двух сторон треугольника a и b удовлетворяют условию a b, а длины соответствующих им высот равны haи hb.

Доказать неравенство a + ha≥ b + hbи определить, когда достигается равенство.

1. Докажите, что сумма длин любых двух медиан произвольного треугольника  а) не больше ¾ P, где P – периметр этого треугольника;   б) не меньше ¾ p, где p – полупериметр этого треугольника.

1. Отрезки AB и CD длины 1 пересекаются в точке O , причем  AOC=60o. Докажите, что AC+BD1. 

Решение

Построим отрезок CB1так, что четырехугольник ABB1C – параллелограмм, тогда AC=BB1.

Из треугольника BB1D получаем, что BB1+BD B1D и, следовательно, AC+BD B1D .

Остается заметить, что треугольник CB1D равносторонний ( CD=CB1=1, а  B1CD= AOC=60o), и, значит, B1D=1. Таким образом, получаем AC+BD1. 

1. Точки  C1, A1, B1 взяты на сторонах AB, BC, CA треугольника ABC так, что  BA1 =  . BC, CB1 =  . CA, AC1 =  . AB, причем  1/2  P треугольника ABC и периметр P1 треугольника A1B1C1 связаны неравенствами  (2-1)P P1 P. 

Решение

Возьмем на сторонах AB, BC, CA точки C2, A2, B2 так, что A1B2| AB, B1C2| BC, C1A2| CA (рис.). Тогда  A1B1 A1B2 + B2B1 = (1 — )AB + (2 — 1)CA.

Аналогично  B1C1 )BC + (2 — 1)AB и  C1A1 )CA + (2 — 1)BC. Складывая эти неравенства, получаем  P1 P. Ясно, что  A1B1 + A1C  B1C, т. е.  A1B1 + (1 — )BC   . CA. Аналогично  B1C1 + (1 — )CA   .

 AB и  C1A1 + (1 — )AB   . BC. Складывая эти неравенства, получаем  P1  (2 — 1)P. 

2

Источник: https://urokidoma.org/courses/podghotovka-k-olimpiadam-po-matiematikie-2017-1/lesson/nieravienstvo-trieughol-nika-gieomietrichieskiie-nieravienstva-1/

Неравенство треугольника

Теорема

Каждая сторона треугольника меньше суммы двух других сторон.

Доказательство:

• Дано: АВС.
• Доказать: АВВС + АС.
• Доказательство:

Сделаем дополнительное построение. Отложим на продолжении стороны ВС отрезок СD, равный стороне АС.

По построению СD = АС, следовательно, АСD — равнобедренный с основанием АD, тогда 1 = 2 (углы при основании), при этом в АВD ВАD2, следовательно, ВАD1.

В треугольнике против большего угла лежит большая сторона, значит, АВВD. При этом ВD = ВС + СD, а учитывая то, что по построению СD = АС получим, ВD = ВС + АС, поэтому АВВС + АС. Что и требовалось доказать.

Следствие

Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВАС+СВ, АСАВ+ВС, ВСВА+АС.

Каждое из неравенств АВАС+СВ, АСАВ+ВС, ВСВА+АС, называется неравенством треугольника.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

1. Теорема о сумме углов треугольника
2. Остроугольный, прямоугольный и тупоугольный треугольники
3. Теорема о соотношениях между сторонами и углами треугольника
4. Некоторые свойства прямоугольных треугольников
5. Признаки равенства прямоугольных треугольников
6. Уголковый отражатель
7. Расстояние от точки до прямой
8. Расстояние между параллельными прямыми
9. Построение треугольника по двум сторонам и углу между ними
10. Построение треугольника по стороне и двум прилежащим к ней углам
11. Построение треугольника по трем его сторонам
12. Соотношения между сторонами и углами треугольника

Правило встречается в следующих упражнениях:

• 7 класс
• Задание 249, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
• Задание 251, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
• Задание 292, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
• Задание 304*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
• Задание 305, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
• Задание 773, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
• Задание 801, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
• Задание 818, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
• Задание 858, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
• Задание 1176, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

1. © budu5.com, 2020
2. Пользовательское соглашение
3. Copyright
4. Нашли ошибку?
5. Связаться с нами

Источник: https://budu5.com/manual/chapter/3429

Урок по геометрии "Неравенство треугольника"

• Неравенство треугольника
• Цель урока: изучить теорему о неравенстве треугольника и показать ее применение при решении задач.
• Задачи:

• Образовательные:
  • относительно учащихся: научиться применять свойство «неравенство треугольника» и определять несуществующие треугольники;
  • относительно педагога: объяснить новую тему с первичным закреплением новых знаний; включить учеников в исследовательскую деятельность;
  • показать практическое применение полученных знаний; создать условия для формирования целостной картины мира.

• Развивающие:

  • развитие речи, мышления, сенсорной (восприятие внешнего мира через органы чувств) сферы личности и потребностно-мотивационной области;
  • развитие умственной деятельности (выполнять операции анализа, синтеза, способность наблюдать, делать выводы, выделять существенные признаки объектов, цели и способы деятельности, выдвигать гипотезы).

• Воспитательные:

  • повысить интерес к традициям края;
  • развивать самостоятельность, умение работать парами;
  • способствовать формированию коммуникативной компетенции.

Тип урока: урок изучения и первичного закрепления новых знаний.  

Оборудование: доска, компьютер, интерактивная доска или мультимедийный проектор, презентация, учебники, рабочие тетради 14 наборов полосок из картона по  5 см, 7 см (2 шт.), 9 см, 12 см, 14 см, 16 см, таблички с треугольниками, смайлики.

1. ХОД УРОКА
2. 1. Организационный этап
3. 2. Подготовка к основному этапу урока (обеспечение мотивации и принятия учащимися цели учебно-познавательной деятельности, актуализация опорных знаний)

– Посмотрите на рисунок, выполненный на доске. Как называется эта  фигура? (Это треугольник.) – Какая фигура называется треугольником? (Треугольник – фигура, состоящая из трех точек, не лежащих на одной прямой и трех отрезков, попарно соединяющих эти точки.

) – Что возникает в вашей памяти? Что вы можете рассказать об этом треугольнике? Если обозначить  треугольник АВС, назовите большую сторону. (Ребята отвечают на вопросы учителя.)– А почему именно эту фигуру я предложила вам вспомнить? (Будем изучать какие-то свойства треугольника.

) – Совершенно верно, сегодня мы будем изучать свойство «неравенство треугольника».

• 3.Усвоение новых знаний и способов действий
• Исследовательская работа
• – Перед вами лежат макеты сторон треугольников. Постройте, используя эти макеты треугольники со сторонами:
• а) 7, 12, 9; б) 7, 14, 7;
• в) 5, 16, 7.

В первой задаче треугольник построить легко. Во второй получился отрезок. Почему? (Т.к. три вершины лежат на одной прямой, а треугольник – это фигура,  составленная из трех точек, не лежащих на одной прямой, попарно соединенных отрезками. Длина большего отрезка равна сумме длин меньших.)

– Можно ли построить треугольник в третьем случае? (В третьем случае треугольник построить нельзя, так как длина большей стороны больше суммы длин меньших сторон.)

Учитель выслушивает версии учеников. В случае затруднения можно предложить детям сравнить длину стороны,  построенной первой и сумму двух других сторон треугольника.

Верная версия детей: «Если сторона, построенная первой, меньше суммы двух других сторон, то треугольник строится».

– Итак, треугольник, с какими сторонами мы смогли построить?

(Треугольник со сторонами 7, 12, 9.)

1. AB < BC + АС, так как 9 см < 7 см + 12 смВС < АВ + АС, так как 7 см < 9 см + 12 см
2. АС < АВ + ВС, так как 12 см < 9 см + 7 см.
3. Ученики обозначают стороны треугольника, записывают неравенства в тетради.

– Как называются выражения, записанные на доске? (Неравенства.)– Что связывают эти три неравенства? (Стороны треугольника.)– Какова тема урока? (Неравенство треугольника.)– Сформулируйте это свойство. (Каждая сторона треугольника меньше суммы двух других сторон.)– Молодцы ребята, хорошо поработали, но впереди еще серьезная работа по доказательству теоремы.

Физкультминутка.

Отложите ручки, повернитесь парами лицом друг другу. На счет «один», поднимите правую руку с вытянутым указательным пальцем. На счет «два», накройте левой ладонью указательный палец соседа. На счет «три», успейте убрать свою руку и схватить палец соседа. Начали!

Ребята с удовольствием выполняют упражнение,  которое снимает напряжение и создает доброжелательную атмосферу, повышает энергетический потенциал учащихся.

Доказательство теоремы

– Откройте учебник на стр. 74, прочитайте формулировку теоремы о неравенстве треугольника.

Ученики работают над формулировкой теоремы, выясняют, что дано и что требуется доказать, строят рисунок и доказывают теорему вместе с учителем в рабочих тетрадях. Отвечают на наводящие вопросы учителя.

Теорема. Каждая сторона треугольника меньше суммы двух других сторон.

Дано: Δ АВС. Доказать: АВ

Источник: https://infourok.ru/urok-po-geometrii-neravenstvo-treugolnika-1635635.html

§ 5. Неравенство треугольника

• Для произвольных
  векторов
  
  и
  
  евклидового пространства выполняется
  неравенство
• ,(2.7)
• называемое
  неравенством
  треугольника.

Для доказательства
справедливости (2.

7) заметим, что квад­рат
длины вектора
+равен
скалярному произведению вектора

png» width=»26″>
+

на самого себя, т. е.

. (2.8)

Обращаясь
последовательно к условию 2 в определении
евкли­дова пространства два раза, а
затем к условию 1, можем написать

.

Используя неравенство
Коши-Буняковского, получим

. (2.9)

Из сравнения (2.8)
и (2.9) следует справедливость (2.7). Заметим,
что если

png» width=»26″>
и

означают векторы, изученные ранее в
курсе геометрии, то неравенство (2.

7)
означает, что длина стороны треугольника
не больше суммы длин других его сторон.

§ 6. Угол между векторами

1. Вначале заметим,
   что на основании неравенства
   Коши-Буняковского можно утверждать,
   что величина
   меньше
   1.
2. Поэтому можно
   ввести следующее определение.
3. Определение
   1. Углом
   между векторами

   png» width=»26″>
   и
   
   
   называют такое
   число
   
   (от

   mAzB/img-36GRKC.png» width=»26″>до),
   для которого выпол­няется равенство

4. (2.10)
5. Определение
   2. Векторы
   

   png» width=»26″>
   и
   
   называются ортогональ­ными,
   если выполнено равенство

Если

png» width=»26″>
и

– оба ненулевые, то это определение
означает, что угол между

и

равен

mAzB/img-IceXtf.png» width=»32″>.
Нулевой вектор, по определению, счи­тается
ортогональным любому вектору.

Рассмотрим примеры.

Пример 1. В
пространстве векторов, изученных ранее
в курсе геометрии, скалярное произведение определено известным образом. Орты
попарно взаимно ортогональны.

Пример 2. В
евклидовом пространстве одностолбцовых
матриц, в котором ска­лярное произведение
определено равенством (2.3), векторы

и

ортогональны.

§ 7. Ортонормированный базис

Определение
1. Базис
евклидова
простран­ства

называется ортогональным, если векторы
базиса попарно ортогональны, т. е.

при

.

Если при этом все
векторы базиса единичные, т. е.

, ,

то базис называется
ортонормированным.

Теорема.
Во всяком -мерном
евклидовом прост­ранстве
имеются ортонормированные базисы.

Доказательство.
Доказательство проведем для слу­чая

.
Пусть

png» width=»82″>– произвольный базис пространства
.
Докажем, что с его помощью можно построить
ортонормированный базис. Положим

png» width=»247″>,
где

– некоторое ве­щественное число,
которое мы подберем так, чтобы векторы

png» width=»32″>
и

были ортогональны, то есть

Используя условия
2 и 3 определения евклидова
пространства,
получим

откуда получим
(так как
)

.(2.12)

Итак, если в качестве


взять число, определяемое равенством
(2.12), то векторы

png» width=»32″>
и

будут ортогональны, а так как векторы


и

mAzB/img-rZ05ao.png» width=»32″>
опреде­лим с помощью равенства

где вещественные
числа

и

определим так, чтобы вектор

mAzB/img-x8kGxu.png» width=»32″>
был ортогонален к векторам

и
,
т. е.

чтобы выполнялись ра­венства

Используя, как и
выше, условия 2 и 3 определения евклидова
пространства, можем написать

откуда, учитывая
ортогональность векторов

и

(т. е.

),
получим выражение для

и

mAzB/img-qVieCa.png» width=»35″>

, .(2.14)

Итак, если в качестве


и

взять числа, определяемые равен­ствами
(2.14), то вектор

png» width=»32″>
будет ортогонален векторам

и
,
так как векторы

png» width=»32″>,

,


линейно независимы, то вектор

png» width=»32″>
не может быть нулевым (вектор

выражается с помощью (2.13) в виде ли­нейной
комбинации векторов
,

mAzB/img-GdYqwG.png» width=»32″>,

).

Базис
,

,

–
ортогональный.

Но для того чтобы сделать
его ортонормированным, следует каждый
из векторов
,

,

png» width=»32″>
поделить на его длину. Векторы

• ; ;
• образуют искомый
  ортонормированный базис.
• Для случая
  этот
  процесс следует продолжать до тех пор,
  пока не найдем последний вектор.
• Примененный здесь
  способ получения ортонормированного
  ба­зиса из произвольного базиса носит
  название процесса
  ортогонализации.
  Естественно, что каждый вектор
  
  в
  -мерном
  евклидовом пространстве
  
  можно представить в виде
• , (2.15)
• где – некоторый ортонормированный базис,– координаты вектора в этом базисе.
  Отметим, что для координатимеют место равенства
• , ,

которые получатся,
если умножить обе части равенства (2.15)
на
.

Источник: https://studfile.net/preview/5301170/page:7/