Равновесие тел. виды равновесия

Статика — раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил и моментов.

• Абсолютно твердое тело – тело, которое не изменяет свою форму и размеры, какие бы силы не были к нему приложены.
• В статике все тела считаются абсолютно твердыми.
• Механическое равновесие — состояние тела, находящегося в покое, или движущегося равномерно, в котором сумма сил и моментов, действующих на него, равна нулю.
• Необходимое условие – равенство нулю равнодействующей всех сил, приложенных к телу:

Этого условия не всегда бывает достаточно. Например, при вращении колеса сумма сил равна нулю, но колесо не находится в покое, оно вращается.

Необходимое и достаточное условие равновесия – равенство нулю суммы сил и суммы моментов сил, действующих на тело, относительно произвольной оси:

В полном виде условие равновесия твердого тела можно сформулировать так:

Необходимым и достаточными условиями равновесия свободного твердого тела является равенство нулю векторной суммы всех внешних сил, действующих на тело, равенство нулю суммы всех моментов внешних относительно произвольной оси, равенство нулю начальной скорости поступательного движения тела и условие равенства нулю начальной угловой скорости вращения сил:

Моментом силы относительно оси вращения называется произведение силы на ее плечо.

Плечо силы – кратчайшее расстояние от линии действия силы до оси вращения.

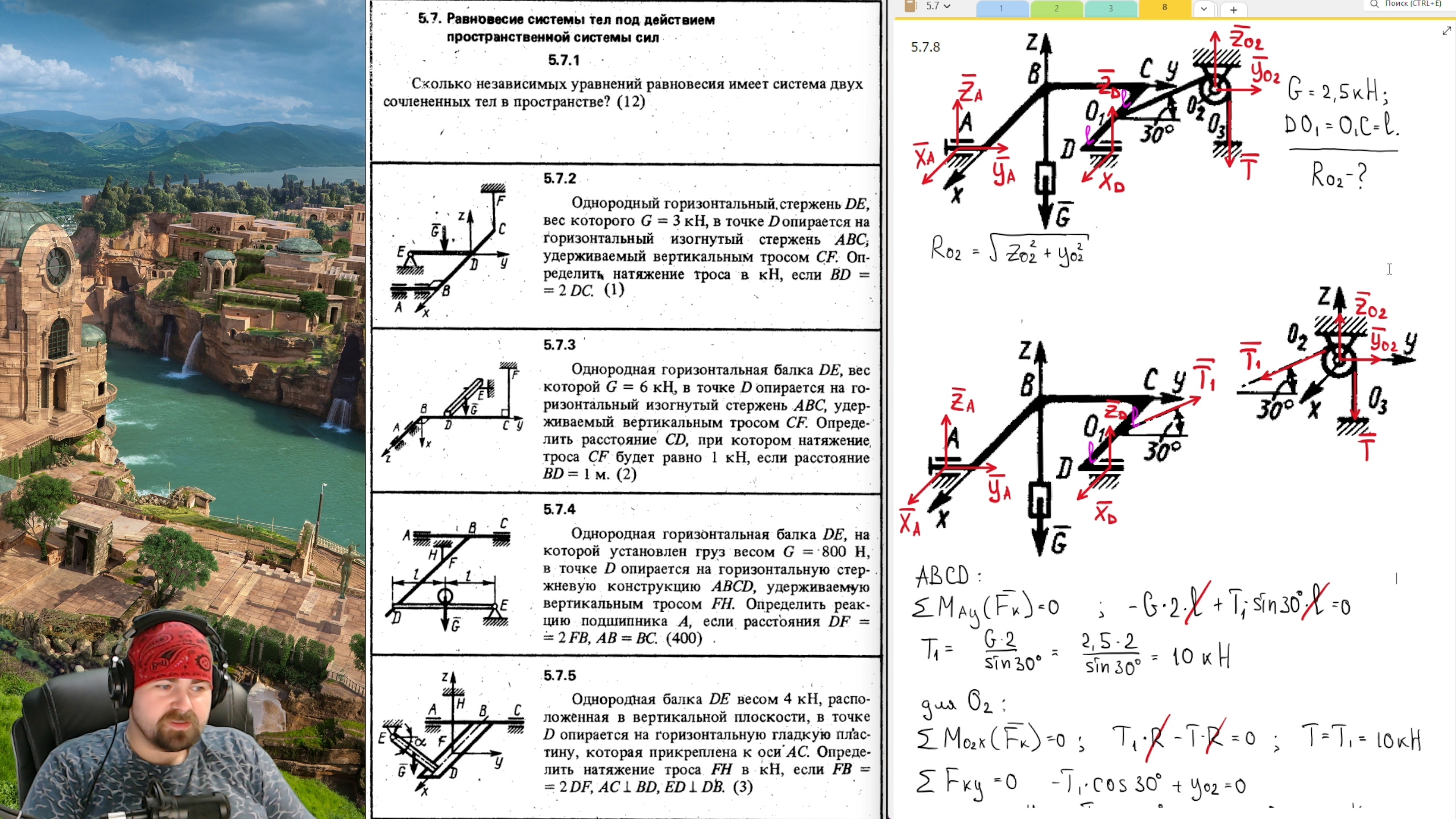
где d1 – плечо силы F1, а d2 – плечо силы F2.

Виды равновесияУстойчивое равновесие тела: при любых малых отклонениях от положения равновесия в системе возникают силы или моменты сил, стремящиеся возвратить тело в положение равновесия.

Это состояние соответствует минимуму потенциальной энергии тела.

Неустойчивое равновесие тела: при некоторых сколько угодно малых отклонениях от положения равновесия в системе возникают силы или моменты сил, стремящиеся еще больше отклонить тело от исходного положения равновесия.

Это состояние соответствует максимуму потенциальной энергии тела.

Безразличное равновесие тела: при любых малых отклонениях от положения равновесия тело не меняет своего положения.

Это состояние соответствует постоянному значению потенциальной энергии тела.

                                                      

Источник: http://light-fizika.ru/index.php/10-klass?id=95

Урок 14. статика. равновесие абсолютно твердых тел — Физика — 10 класс — Российская электронная школа

Физика, 10 класс

Урок 14. Статика. Равновесие абсолютно твёрдых тел

• Перечень вопросов, рассматриваемых на уроке:
• 1.Условия равновесия тела
• 2.Момент силы
• 3.Плечо силы
• 4. Центр тяжести
• Глоссарий по теме
• Статика – раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой
• Абсолютно твердое тело – модельное понятие классической механики, обозначающее совокупность точек, расстояния между текущими положениями которых не изменяются.
• Центр тяжести – центром тяжести тела называют точку, через которую при любом положении тела в пространстве проходит равнодействующая сил тяжести, действующих на все частицы тела.
• Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
• Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
• Устойчивое равновесие — это равновесие, при котором тело, выведенное из состояния устойчивого равновесия, стремится вернуться в начальное положение.
• Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.
• Безразличное равновесие системы — равновесие, при котором после устранения причин, вызвавших малые отклонения, система остается в покое в этом отклоненном состоянии
• Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017.– С. 165 – 169.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009.

Степанова Г.Н. Сборник задач по физике. 10-11 класс. — М.: Просвещение. 1999 г. С.48- 50.

Теоретический материал для самостоятельного изучения

Равновесие – это состояние покоя, т.е. если тело покоится относительно инерциальной системы отсчета, то говорят, что оно находится в равновесии.

Почему одни тела, выведенные из состояния равновесия, падают, а другие – нет? Выясним, при каком условии тело будет находиться в состоянии равновесия.

Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой. Статика является частным случаем динамики. В статике твердое тело рассматривается как абсолютно твердое, т.е. недеформируемое тело. Это означает, что деформация так мала, что её можно не учитывать.

Центр тяжести существует у любого тела. Эта точка может находиться и вне тела. Как же подвесить или подпереть тело, чтобы оно находилось в равновесии.

Подобную задачу в свое время решил Архимед. Им же были введены понятие плеча силы и момента силы.

1. Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
2. Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
3. После своих исследований Архимед сформулировал условие равновесия рычага и вывел формулу:

• Это правило является следствием 2-го закона Ньютона.
• Первое условие равновесия
• Для равновесия тела необходимо, чтобы сумма всех сил, приложенных к телу была равна нулю.

1. формула должна быть в векторном виде и стоять знак суммы
2. Второе условие равновесия
3. При равновесии твердого тела сумма моментов вcех внешних сил, действующих на него относительно любой оси, равна нулю.

Не менее важен случай, когда тело имеет площадь опоры. Тело, имеющее площадь опоры, находится в равновесии, когда вертикальная прямая, проходящая через центр тяжести тела, не выходит за пределы площади опоры этого тела.

Известно, что в городе Пизе в Италии существует наклонная башня. Несмотря на то, что башня наклонена, она не опрокидывается, хотя ее часто называют падающей.

Очевидно, что при том наклоне, которого башня достигла к настоящему времени, вертикаль, проведенная из центра тяжести башни, все еще проходит внутри ее площади опоры.

• В практике большую роль играет не только выполнение условия равновесия тел, но и качественная характеристика равновесия, называемая устойчивостью.
• Различают 3 вида равновесия: устойчивое, неустойчивое, безразличное.
• Если при отклонении тела от положения равновесия, возникают силы или моменты сил, стремящиеся вернуть тело в положение равновесия, то такое равновесие называется устойчивым.

Неустойчивое равновесие — это противоположный случай. При отклонении тела от положения равновесия, возникают силы или моменты сил, которые стремятся увеличить это отклонение.

Наконец, если при малом отклонении от положения равновесия тело все равно остается в равновесии, то такое равновесие называется безразличным.

Чаще всего необходимо, чтобы равновесие было устойчивым. Когда равновесие нарушается, то сооружение становится опасным, если его размеры велики.

Примеры и разбор решения заданий

1. Чему равен момент силы тяжести груза массой 40 кг, подвешенного на кронштейне АВС, относительно оси, проходящей через точку В, если АВ=0,5 м и угол α=450

Решение:

Момент силы – это величина равная произведению модуля силы на её плечо.

Сначала найдём плечо силы, для этого нам надо опустить перпендикуляр из точки опоры на линию действия силы. Плечо силы тяжести равно расстоянию АС. Так как угол равен 45°, то мы видим, что АС=АВ

Модуль силы тяжести находим по формуле:

1. После подстановки числовых значений величин мы получим:
2. F=40×9,8 =400 Н, М= 400 ×0,5=200 Н м.
3. Ответ: М=200 Н м.

2. Приложив вертикальную силу F, груз массой М — 100 кг удерживают на месте с помощью рычага (см. рис.). Рычаг состоит из шарнира без трения и однородного массивного стержня длиной L=8 м. Расстояние от оси шарнира до точки подвеса груза равно b=2 м. Чему равен модуль силы F, если масса рычага равна 40 кг.

Решение:

По условию задачи рычаг находится в равновесии. Напишем второе условие равновесия для рычага:

• После подстановки числовых значений величин получим
• F= (100×9,8 ×2 + 0,5×40×9,8×8)/8=450 Н
• Ответ: 450 Н.

Источник: https://resh.edu.ru/subject/lesson/4720/conspect/

Равновесие тел — Класс!ная физика

«Физика — 10 класс»

Вспомните, что такое момент силы. При каких условиях тело находится в покое?

Если тело находится в покое относительно выбранной системы отсчёта, то говорят, что это тело находится в равновесии. Здания, мосты, балки вместе с опорами, части машин, книга на столе и многие другие тела покоятся, несмотря на то что к ним со стороны других тел приложены силы.

Задача изучения условий равновесия тел имеет большое практическое значение для машиностроения, строительного дела, приборостроения и других областей техники. Все реальные тела под влиянием приложенных к ним сил изменяют свою форму и размеры, или, как говорят, деформируются.

Во многих случаях, которые встречаются на практике, деформации тел при их равновесии незначительны. В этих случаях деформациями можно пренебречь и вести расчёт, считая тело абсолютно твёрдым.

Вспомните определение абсолютно твёрдого тела.

Раздел механики, в котором изучаются условия равновесия абсолютно твёрдых тел, называется статикой.

В статике учитываются размеры и форма тел, в этом случае существенным является не только значение сил, но и положение точек их приложения.

Выясним вначале с помощью законов Ньютона, при каком условии любое тело будет находиться в равновесии. С этой целью разобьём мысленно всё тело на большое число малых элементов, каждый из которых можно рассматривать как материальную точку.

Как обычно, назовём силы, действующие на тело со стороны других тел, внешними, а силы, с которыми взаимодействуют элементы самого тела, внутренними (рис. 7.1). Так, сила 1,2 — это сила, действующая на элемент 1 со стороны элемента 2. Сила же 2,1 действует на элемент 2 со стороны элемента 1. Это внутренние силы; к ним относятся также силы 1,3 и 3,1, 2,3 и 3,2. Очевидно, что геометрическая сумма внутренних сил равна нулю, так как согласно третьему закону Ньютона

12 = -21, 23 = -32, 31 = -13 и т.д.

Статика — частный случай динамики, так как покой тел, когда на них действуют силы, есть частный случай движения ( = 0).

На каждый элемент в общем случае может действовать несколько внешних сил. Под 1, 2, 3 и т. д. будем понимать все внешние силы, приложенные соответственно к элементам 1, 2, 3, … . Точно так же через '1, '2, '3 и т. д. обозначим геометрическую сумму внутренних сил, приложенных к элементам 2, 2, 3, … соответственно (эти силы не показаны на рисунке), т. е.

'1 = 12 + 13 + … , '2 = 21 + 22 + … , '3 = 31 + 32 + … и т.д.

Если тело находится в покое, то ускорение каждого элемента равно нулю. Поэтому согласно второму закону Ньютона будет равна нулю и геометрическая сумма всех сил, действующих на любой элемент. Следовательно, можно записать:

1 + '1 = 0, 2 + '2 = 0, 3 + '3 = 0.         (7.1)

Каждое из этих трёх уравнений выражает условие равновесия элемента твёрдого тела.

Первое условие равновесия твёрдого тела.

Выясним, каким условиям должны удовлетворять внешние силы, приложенные к твёрдому телу, чтобы оно находилось в равновесии. Для этого сложим уравнения (7.1):

(1 + 2 + 3) + ('1 + '2 + '3) = 0.

В первых скобках этого равенства записана векторная сумма всех внешних сил, приложенных к телу, а во вторых — векторная сумма всех внутренних сил, действующих на элементы этого тела.

Но, как известно, векторная сумма всех внутренних сил системы равна нулю, так как согласно третьему закону Ньютона любой внутренней силе соответствует сила, равная ей по модулю и противоположная по направлению.

Поэтому в левой части последнего равенства останется только геометрическая сумма внешних сил, приложенных к телу:

1 + 2 + 3 + … = 0.         (7.2)

В случае абсолютно твёрдого тела условие (7.2) называют первым условием его равновесия.

• Оно является необходимым, но не является достаточным.
• Итак, если твёрдое тело находится в равновесии, то геометрическая сумма внешних сил, приложенных к нему, равна нулю.
• Если сумма внешних сил равна нулю, то равна нулю и сумма проекций этих сил на оси координат. В частности, для проекций внешних сил на ось ОХ можно записать:

F1x + F2x + F3x + … = 0.         (7.3)

Такие же уравнения можно записать и для проекций сил на оси OY и OZ.

Второе условие равновесия твёрдого тела.

Убедимся, что условие (7.2) является необходимым, но недостаточным для равновесия твёрдого тела. Приложим к доске, лежащей на столе, в различных точках две равные по модулю и противоположно направленные силы так, как показано на рисунке 7.2. Сумма этих сил равна нулю:

+ (-) = 0. Но доска тем не менее будет поворачиваться. Точно так же две одинаковые по модулю и противоположно направленные силы поворачивают руль велосипеда или автомобиля (рис. 7.3).

Какое же ещё условие для внешних сил, кроме равенства нулю их суммы, должно выполняться, чтобы твёрдое тело находилось в равновесии? Воспользуемся теоремой об изменении кинетической энергии.

Найдём, например, условие равновесия стержня, шарнирно закреплённого на горизонтальной оси в точке О (рис. 7.4). Это простое устройство, как вам известно из курса физики основной школы, представляет собой рычаг первого рода.

Пусть к рычагу приложены перпендикулярно стержню силы 1 и 2.

Вычислим работу, которую совершают внешние силы при повороте рычага на очень малый угол α. Точки приложения сил 1 и 2 пройдут пути s1 = ВВ1 и s2 = CC1 (дуги ВВ1 и СС1 при малых углах α можно считать прямолинейными отрезками).

Работа А1 = F1s1 силы 1 положительна, потому что точка В перемещается по направлению действия силы, а работа А2 = -F2s2 силы 2 отрицательна, поскольку точка С движется в сторону, противоположную направлению силы 2.

Сила 3 работы не совершает, так как точка её приложения не перемещается.

Пройденные пути s1 и s2 можно выразить через угол поворота рычага а, измеренный в радианах: s1 = α|ВО| и s2 = α|СО|. Учитывая это, перепишем выражения для работы так:

А1 = F1α|BO|,         (7.4) А2 = -F2α|CO|.

Радиусы ВО и СО дуг окружностей, описываемых точками приложения сил 1 и 2, являются перпендикулярами, опущенными из оси вращения на линии действия этих сил

Как вы уже знаете, плечо силы — это кратчайшее расстояние от оси вращения до линии действия силы. Будем обозначать плечо силы буквой d. Тогда |ВО| = d1 — плечо силы 1, а |СО| = d2 — плечо силы 2. При этом выражения (7.4) примут вид

А1 = F1αd1, А2 = -F2αd2.         (7.5)

Из формул (7.5) видно, что работа каждой из сил равна произведению момента силы на угол поворота рычага. Следовательно, выражения (7.5) для работы можно переписать в виде

А1 = М1α, А2 = М2 α,         (7.6)

а полную работу внешних сил можно выразить формулой

А = А1 + А2 = (М1 + М2)α. α,         (7.7)

Так как момент силы 1 положителен и равен М1 = F1d1 (см. рис. 7.4), а момент силы 2 отрицателен и равен М2 = -F2d2, то для работы А можно записать выражение

А = (М1 — |М2|)α.

Если работа внешних сил равна нулю, то кинетическая энергия тела не изменяется (остаётся равной нулю) и тело остаётся неподвижным. Тогда

М1 + М2 = 0.         (7.8)

Уравнение (7.8) и есть второе условие равновесия твёрдого тела.

При равновесии твёрдого тела сумма моментов всех внешних сил, действующих на него относительно любой оси, равна нулю.

Итак, в случае произвольного числа внешних сил условия равновесия абсолютно твёрдого тела следующие:

1 + 2 + 3 + … = 0,         (7.9) М1 + М2 + М3 + … = 0.

Второе условие равновесия можно вывести из основного уравнения динамики вращательного движения твёрдого тела. Согласно этому уравнению где М — суммарный момент сил, действующих на тело, М = М1 + М2 + М3 + … , ε — угловое ускорение. Если твёрдое тело неподвижно, то ε = 0, и, следовательно, М = 0. Таким образом, второе условие равновесия имеет вид М = М1 + М2 + М3 + … = 0.

Если тело не абсолютно твёрдое, то под действием приложенных к нему внешних сил оно может и не оставаться в равновесии, хотя сумма внешних сил и сумма их моментов относительно любой оси равны нулю.

Приложим, например, к концам резинового шнура две силы, равные по модулю и направленные вдоль шнура в противоположные стороны. Под действием этих сил шнур не будет находиться в равновесии (шнур растягивается), хотя сумма внешних сил равна нулю и нулю равна сумма их моментов относительно оси, проходящей через любую точку шнура.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Следующая страница «Примеры решения задач по теме «Равновесие твёрдых тел»» Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»

Статика — Физика, учебник для 10 класса — Класс!ная физика

Равновесие тел — Примеры решения задач по теме «Равновесие твёрдых тел»

Источник: http://class-fizika.ru/10_a40.html

Образовательный портал

Методическая разработка урока физики в 10-м классе

Равновесие тел. Виды равновесия

• Шмелева Гульджихан Равильевна, учитель лицея №384
• Кировского района Санкт-Петербурга

Контингент учащихся:10-й класс общеобразовательной школы, работающих по программе «Физика 10 класс»  авторы Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.

Технология: урок- исследование Техническое оснащение: мультимедийный проектор, ноутбук. Цели урока: 1. Обучающие: — закрепление полученных знаний по теме «Статика»; — совершенствование навыков работы с физическими приборами, умение измерять физические величины; — формирование умений оценивать результаты опытов, делать выводы, сравнивать результаты 2.

Развивающие: — развитие умения выстраивать логические цепочки, самостоятельно выявлять закономерности физических явлений, устанавливать связь между физическими явлениями; — развитие интереса к исследовательской деятельности в процессе решения экспериментальных задач 3.

Воспитывающие — раскрытие общекультурной значимости науки физики и формирование научного мировоззрения и мышления  учащихся; — развитие коммуникативных компетенций в ходе выполнения практической работы в парах. Дидактический тип урока: изучение нового материала Форма урока: урок- беседа с элементами исследования План урока: 1. Организационный момент 2. Повторение   материала 3.

Изучение нового материала 4. Исследовательская работа 5. Подведение итогов урока. Оборудование: 1.    Компьютерная презентация 2.    Проектор 3.    Демонстрационные опыты 4.    Фронтальные эксперименты 5.    Рабочие листы для оформления результатов исследования I. Актуализация знаний. Вспомним, что мы знаем о равновесии тел: 1. Что называется равновесием? 2.

Сегодня на уроке мы узнаем, как обеспечить устойчивость подъёмного крана, различных зданий и сооружений, рассмотрим в качестве примера памятник Петру I в нашем городе, проведём  исследование:  Каким образом Фальконе обеспечил равновесие скульптуры « Медный всадник»? Решение нашей проблемы разобьём на несколько этапов: найдём ответ на следующие вопросы — Что такое центр тяжести? — Какие  виды равновесия  различают?

1. — От чего зависит  устойчивость   тела, имеющего ось опоры и площадь опоры?
2. А)    Центр тяжести тела и его нахождение

Любое физическое  тело  – земной шар, жилой дом, автомобиль, человек и т.д. – обладает массой и на него действует сила тяжести. Каждая частица  тела  в отдельности также обладает массой, т.е. твердое  тело  находится под действием бесчисленного количества сил тяжести.

Все эти силы параллельны, поэтому их можно заменить одной суммарной силой. Точка приложения этой суммарной силы и называется центром тяжести.

Центр тяжести тела – это точка, через которую проходит равнодействующая всех параллельных сил тяжести, действующих на отдельные элементы тела (при любом положении тела в пространстве).У различных  тел  центр тяжести находится в разных местах, это зависит от их формы и однородности состава.

У абсолютно симметричных однородных фигур (прямоугольника, квадрата, круга, цилиндра) центр тяжести лежит в центре их осевых линий. Найти центр тяжести следующих фигур ( оформить ответ на рабочих листах) – проверить всем классом

Б) Виды равновесия тел

Теперь, уяснив для себя, что такое центр тяжести, вернёмся к понятию равновесия. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное.

Для того, чтобы выяснить при каком условии, тело находится в состоянии  устойчивого, неустойчивого и безразличного равновесия мы проведём практическую работу №1 «Наблюдение видов равновесия тела, имеющего ось опоры» Цель работы: выяснить условие устойчивого, неустойчивого и безразличного равновесия тела имеющего ось опоры. Т.к. мы исследуем 3 вида равновесия я попрошу вас разделиться на 3 группы.

Задание первой группе

Оборудование: цилиндр металлический, металлическая линейка, карандаш. 1. Положите линейку на стол, а на линейку цилиндр. 2. Сместите цилиндр вправо или влево и убедитесь, что в любом положении он сохраняет равновесие. 3.

Ответьте на вопросы: 1) Какие силы действуют на цилиндр? 2) Чему равен модуль равнодействующей этих сил? 3) Чему равна сумма моментов этих сил относительно оси опоры цилиндра? 4) Изменится ли высота центра тяжести цилиндра относительно нулевого уровня при его движении по горизонтальной линейке?

5) В равновесии ли находится цилиндр на горизонтальной линейке? Какое это равновесие?

Задание второй группе

Ответьте на вопросы: 1) Какие силы действуют на цилиндр? 2) Чему равен модуль равнодействующей этих сил? 3) Как направлена равнодействующая этих сил? 4) Почему цилиндр скатывается с выпуклой поверхности линейки при его смещении? 5) Как изменяется высота центра тяжести  относительно нулевого уровня

• 6) В каком равновесии находится цилиндр?
• Задание третьей  группе

Оборудование: цилиндр металлический, металлическая линейка, карандаш. 1. Изогните линейку, чтобы получилась вогнутая поверхность. Положите ци-линдр на нижнюю часть вогнутой поверхности. Сместите его влево и убеди-тесь, что он возвращается в исходное положение. 2.

Ответьте на вопросы: 1) Какие силы действуют на цилиндр? 2) Чему равен модуль равнодействующей этих сил? 3) Как направлена равнодействующая этих сил ? 4) Почему цилиндр возвращается в исходное положение? 5) Как изменяется высота центра тяжести  относительно  нулевого уровня

6) В каком равновесии находится цилиндр?

Какие силы действуют на цилиндр

Как направлена равнодействующая этих сил

Как ведёт себя цилиндр при смещении

Как изме-няется высота центра тяжести цилиндра относительно нулевого уровня

В каком равновесии находится цилиндр

Как изменяется Еп  относительно нулевого уровня

Отчёт представляете в виде таблицы. Каждая группа заполняет только одну строку таблицы и делает вывод по своей работе. Всю работу оформляете на рабочих листах. Таблица выводится на экран

1. Выводы из практической работы №1
2. —  Равновесие безразличное, если при отклонении от положения равновесия R=0 —  Равновесие неустойчиво, если при отклонении от положения равновесия возникает R, удаляющая тело от положения равновесия —  Равновесие устойчивое, если при отклонении от положения равновесия воз-никает R, возвращающая тело в состояние равновесия
3.     Условия возникновения трёх видов равновесия тела , имеющего ось опоры, справедливы и для тела, имеющего точку опоры, например шара, находящегося на горизонтальной, выпуклой и вогнутой поверхности (анимация) Как изменяется положение центра тяжести в состоянии: безразличного равновесия; неустойчивого равновесия устойчивого равновесия  В состоянии устойчивого равновесия центр тяжести шара занимает самое низкое положение. Напоминаю, что качественной характеристикой равновесия является его устойчивость
4. В) Условия устойчивого равновесия тела, имеющего площадь опоры

    Итак, мы с вами выяснили условие равновесия тела, имеющего ось опоры и точку опоры. Далее мы выясним условие устойчивого равновесия тела, имеющего площадь опоры.

Для этого мы проведём практическую работу №2 « Выяснение условия устойчивого равновесия тела, имеющего площадь опоры» Цель работы: 1) Выяснить при каком условии брусок находится в устойчивом                               равновесии?                         2) Какое положение бруска наиболее устойчивое? Почему?     Практическая работа проводится в парах.

Порядок выполнения работы размещён на рабочих листах, прочитайте его. Обращаю ваше внимание на порядок ваших действий 1) Найдите проекцию центра тяжести бруска на наибольшую его грань. Для этого на поверхности грани проведите две диагонали. 2) Поставьте брусок на линейку наименьшей гранью.

К бруску приставьте угольник так, чтобы точка пересечения диагоналей лежала на вертикальном катете. 3) Наклоняйте постепенно линейку, при этом угольник сдвигайте так, чтобы вертикальный катет  угольника всё время проходил через центр тяжести бруска. Заметьте положение вертикальной линии, проходящей через центр тяжести бруска, при котором брусок опрокидывается.

Пересекает ли вертикальная линия, проведённая через центр тяжести бруска, площадь опоры, когда брусок опрокидывается? 4)  Положите брусок на линейку другой гранью и повторите опыт 5) Сравните предельные углы наклона бруска в обоих опытах и положение его центра тяжести относительно стола После проведения работы класс делает выводы: 1) При каком условии брусок находится в устойчивом равновесии? (брусок находится в устойчивом состоянии только тогда, когда проекция центра тяжести проходит  через  площадь  опоры) 2) Какое положение бруска наиболее устойчивое? Почему?( Наиболее устойчиво тело, у которого больше площадь опоры, потому что возрастает вероятность того, что проекция центра тяжести попадёт на площадь опоры Вопрос: Как обеспечить состояние равновесия, если тело находится на двух точках опоры или линии опоры? Ответ: надо, чтобы проекция центра тяжести падала на линию опоры III. Проведение исследования. Мы рассмотрели теорию  и теперь попытаемся ответить на вопросы 1 Вопрос  Какой выход нашёл скульптор Фальконе, чтобы удержать вздыбленную лошадь на пьедестале? (добавил третью точку опоры, поместив змею под задними копытами коня, увеличив площадь опоры – в этом случае проще обеспечить попадание проекции центра тяжести на площадь опоры) 2 Вопрос Отливка монумента представляла исключительную трудность не только из-за его громадных размеров и сложной конфигурации, но еще и потому, что толщина бронзовых стенок в передней части статуи должна была быть значительно меньше толщины стенок в ее задней части. Почему? (Таким образом облегчалась передняя часть монумента, центр тяжести скульптуры смещался таким образом, чтобы он находился над площадью опоры. Это придавало всей группе необходимую устойчивость)

По расчётам скульптора для сохранения равновесия монумента передние стенки памятника должны были быть выполнены очень тонкими — не более сантиметра. От такой работы отказался даже специально приглашённый литейщик из Франции.

За три года скульптор в совершенстве овладел литьём. Отливать «Медного всадника» начали в 1774 году.

3 Вопрос: Каким образом скульптор понизил  общий центр тяжести всего памятника? Ответ: Установил пьедестал, который понижает  общий центр тяжести всего памятника. Степень  устойчивости  зависит и от того, как высоко расположен центр тяжести над опорой ( землёй): чем он выше, тем проще вывести тело из состояния равновесия, и наоборот, понижение центра тяжести  тела  ведет к увеличению его устойчивости .Прием понижения центра тяжести для придания различным предметам и конструкциям большей  устойчивости  применяется в разных областях. Например, для повышения  устойчивости  подъемного крана в его основании установлено несколько бетонных плит – это так называемый балласт, который приближает центр тяжести к  площади   опоры  (земле), тем самым повышая его  устойчивость. Чем больше грузоподъемность крана, тем мощнее и тяжелее должен быть его балласт. Постаменты памятников также служат для повышения  устойчивости . Представляя единую композицию со скульптурой, пьедестал понижает общий центр тяжести, обеспечивая памятнику более прочное положение.

• Вернёмся к цели нашего исследования: Каким образом Фальконе обеспечил равновесие скульптуры « Медный всадник»?
• Результаты  исследования:
• 1)    Увеличил площадь опоры для того, чтобы проекция центра тяжести проходила через площадь опоры ( поместив змею под задними копытами коня) 2)    Произвёл отливку таким образом, чтобы центр тяжести монумента  нахо-дился над площадью опоры ( передняя часть всадника была облегченной, а круп коня, его задние ноги и хвост более массивными) 3)    Понизил  общий центр тяжести всего памятника, установив пьедестал Итак, сегодня на уроке мы рассмотрели виды равновесия тел, выяснили условие устойчивого равновесия для тела, имеющего площадь опоры и линию опоры и применили результат нашего исследования, чтобы ответить на вопрос: Каким образом Фальконе обеспечил равновесие скульптуры « Медный всадник»
• В качестве домашнего задания  я предлагаю найти ответ на вопрос: Почему Пизанская башня стоит под наклоном и не падает?

You have no rights to post comments

Источник: http://ext.spb.ru/2011-03-29-09-03-14/96-2011-12-05-14-05-58/906—10-l-r.html

Занятие 27. Статика. Виды равновесий. Условия равновесия твёрдого тела

Главная задача статики заключается в нахождении состояния устойчивого равновесия тела, необходимого при строительстве сооружений, мостов и прочих объектов. Статика учитывает и возможные отклонения тела от положения равновесия (например, при толчках). Необходимо, чтобы тело при действии случайных сил снова вернулось в состояние устойчивого положения.

Продемонстрируем состояние устойчивого равновесия следующим рисунком, на котором изображён диск, подвешенный на нити в точке А.

Буквой С изображён центр тяжести диска, сила тяжести диска обозначена через Р.

Здесь тело находится в состоянии устойчивого равновесия — его центр тяжести С находится ниже точки подвеса А и лежит на одной вертикали с ней. Сила натяжения нити Т уравновешивает силу тяжести.

Если тело отклонить от положения равновесия, то сила тяжести Р создаст вращательный момент относительно точки подвеса, который вернёт диск в первоначальное положение.

Общим для всех видов устойчивого равновесия является то, что центр тяжести тела занимает наинизшее положение из всех возможных положений. Если тело упирается на плоскость, то оно будет находиться в состоянии устойчивого равновесия, когда вертикаль, проведённая через центр тяжести тела, будет находиться внутри площади опоры.

Запомним следующее.

Подумайте над решением следующих задач:

К.В. Рулёва Подписывайтесь на канал. Ставьте лайки.

Предыдущая запись: Занятие 26. Нахождение равнодействующей сил, приложенных к телу.

Следующая запись: Задачи 1 — 3 к занятиям 26 — 27

Занятие 15. Природа сил в механике.

Ссылки на другие занятия найдёте в Занятии 1.

Источник: https://zen.yandex.ru/media/id/5d94a74bc31e4900b2f962ce/zaniatie-27-statika-vidy-ravnovesii-usloviia-ravnovesiia-tverdogo-tela-5e59580e3f8d4a2b01fccbbf

Условия равновесия тел — виды, формулы и примеры — Помощник для школьников Спринт-Олимпиады

Раздел механики, изучающий условия равновесия тел, называют статикой. Методы науки используются в самых различных областях деятельности человека.

Архитекторы и инженеры рассчитывают силы, действующие на всевозможные конструкции, знание о поведении мышц позволяет лечить травмы.

Поэтому важным в физике является понимание условий, обеспечивающих телу состояние покоя, умение расчёта действующих сил. При этом единого способа решения задач не существует.

Общие сведения

Статика — это наука, изучающая силы, при которых положение тела не изменяется в пространстве. Такая ситуация называется равновесием. Особенность покоящихся тел в том, что в таком состоянии они не обладают ускорением и скоростью, а результирующая сила и момент равны нулю. Поэтому и кажется, что на тело не оказывается никакого воздействия, но на самом деле это не так.

В общем смысле под равновесием понимают состояние, которое может сохраняться сколько угодно долго, если нет внешних воздействий. Это утверждение справедливо для любого вида состояния покоя. Например, механического, теплового, экономического, политического и тому подобного.

При воздействии различных сил на материальную точку объект может вести себя трояко. В соответствии с этим различают три вида реакции физического тела на попытку вывести его из этого положения:

Устойчивое — после окончания воздействия возникают силы, которые возвращают объект в начальное состояние. Например, жёлоб с шариком. В исходном положении на объект действует сила тяжести и нормального давления (упругость лунки), направленные в противоположные стороны. Если шар переместить, то угол между воздействиями изменится. Их равнодействующая не будет нулевой, а её направление заставит тело вернуться в исходное состояние.

Неустойчивое — равновесие при малом отклонении, от которого возникают силы, удаляющие тело от положения покоя. Например, шар, находящийся на вершине выпуклой поверхности. Если его сдвинуть, то равнодействующая станет направленной от начального состояния, а тело скатится.

Безразличное — случай, при котором не возникают силы, приближающие или удаляющие материальную точку. Например, горизонтальная твёрдая поверхность.

Следует отметить, что для того чтобы узнать, какой вид равновесия присущ ситуации, необходимо вывести объект из положения покоя. При этом первостепенной задачей статики является изучение условий, которые приводят к одному из трёх состояний тела, и их математическое описание.

Центр тяжести и условия равновесия

Простейшим случаем, при котором материальная точка находится в равновесии, будет тот, когда нет вращения, а размерами тела можно пренебречь. В этом случае ускорение равняется нулю: a = 0.

Выяснить условия равновесия значит определить действующие силы. Согласно второму закону Ньютона, их равнодействующую можно найти из произведения массы на ускорение: F = m * a.

Отсюда следует, что в состоянии покоя F = 0.

Реальное тело имеет определённые размеры. Чтобы определить для такого случая условие, необходимо рассмотреть самый простой вид движения — поступательное. Им называют перемещение, при котором все точки в теле двигаются одинаково, то есть с одной и той же скоростью. А это значит, что ускорения для всех его частиц будет постоянным и равняться нулю.

Пусть имеется горизонтальная поверхность, на которой находится, например, тележка. Через неё можно провести условную прямую под любым наклоном к горизонту.

Места пересечения контуров тела с построенной линией будут точками A и B. К любой из них можно приложить силу F. Тележка начнёт двигаться.

Эту силу можно перенести вдоль линии к другой точке, не изменяя направления, то есть сменить место приложения. В результате никаких изменений не произойдёт.

Но предыдущих двух условий мало, чтобы можно было сформулировать достаточные условия. Например, пусть есть карандаш, лежащий на столе.

Таким образом, если тело находится в равновесии, для него должны выполняться три условия:

• равнодействующая всех сил, приложенных к объекту, равняется нулю: F = F1 + F2 +…+ Fn = 0;
• действие силы не изменяется при переносе точки её приложения вдоль линии действия;
• объект будет иметь неподвижную ось вращения лишь тогда, когда алгебраическая сумма моментов действующих на него сил относительно оси равна нулю: M = M1 + M1 +…+ Mn = 0.

Перечисленные условия являются необходимыми для нахождения тела в состоянии равновесия. Составив систему из уравнений, можно решать задачи с тремя неизвестными, что часто оказывается более чем достаточно, особенно для школьной программы.

Закреплённая ось вращения

Объект не будет вращаться, если равнодействующая приложенных к нему сил будет равняться нулю. Пусть имеется тело эллипсоидной формы. Чтобы оно не перемещалось поступательно, необходимо добиться одинакового движения точек.

В предмете можно сделать отверстие, которое будет обозначать ось вращения. Тогда центры перемещения точек находятся на этой линии.

К произвольно взятому месту A можно приложить силу F. Тело начнёт поворачиваться до тех пор, пока не наступит ситуация, при которой линия действия F начнёт проходить через ось. Тогда вращение прекратится. То есть произойдёт компенсирование реакцией оси. Кроме того, эти два действия не только лежат на одной линии, но и равны по модулю.

Из второго условия равновесия следует, что силу можно перемещать вдоль оси. Если это сделать, то к противоположной точке A окажется приложено две силы. Они будут равны по величине, но противоположны по направлению. Эта пара действует на закреплённую ось, поэтому предмет, необязательно эллипсоидной формы, вращаться не будет.

Таким образом, тело любого размера и массы с закреплённой осью будет находиться в равновесии, если линия действия приложенной к ней силы проходит через ось. Это простая ситуация.

Но может случиться так, что на тело будет оказываться воздействия одновременно с нескольких сторон. Причём они будут приложены к разным местам тела.

В этом случае, как и в первом, всё равно можно будет подобрать такую силу, которая будет действовать, как все существующие.

Но на самом деле этим правилом пользоваться неудобно, так как часто найти общее действие бывает довольно сложно. Поэтому используют плечо силы. Это кратчайшее расстояние до оси вращения. Физически величина равна произведению модуля действия на её плечо и называется моментом. Описывают её формулой: M = F * d, где первый член — модуль, а второй — плечо относительно оси вращения.

За единицу измерения момента принимают ньютон, умноженный на метр (Н * м). Причём эта величина может иметь как положительное, так и отрицательное значение. Выбор знака зависит от направления. Строго требования нет, но в математике вращение по часовой стрелке считают плюсовым, а против — минусовым.

Решение задач

Важно не только знать теоретический материал, но и уметь применять его на практике. Единого метода решения задач в статике не существует. В учебных классах по физике можно встретить плакаты, на которых изображён алгоритм вычислений, когда тело находится в инерциальной системе отсчёта (ИСО). Последовательность действий выглядит так:

Выбрать одно тело и изобразить на диаграмме все действующие на него силы и точки, к которым они приложены.

Использовать удобную систему координат, на которой можно разложить воздействия на составляющие.

Неизвестные обозначить буквами и составить уравнения для суммы всех сил и моментов, приравняв их к нулю.

Решить систему, найдя нужные величины.

Несомненно, самым трудным будет первый шаг. Вот один из примеров среднего уровня сложности. Однородная балка массой 1200 кг представляет собой весы. В конструкции убрали среднюю опору, но поставили две крайних.

На балку положили механизм весом 15 тонн. Определить силу, действующую на каждую из вертикальных опор. Учесть, что длина между колонами составляет 20 м, а расстояние от центра до груза равняется пяти метрам.

Вначале следует рассмотреть силы, действующие на концы балки. Они будут равны по величине действиям, с которыми концы главного стержня давят на опоры. Пусть это будет F1 и F2.

Сила тяжести балки приложена к центру масс, то есть приходится на середину. Так как условие равновесия для моментов можно записать относительно любой точки, то удобнее взять её в месте приложения F1.

Поскольку в этом случае она будет равняться нулю из-за значения плеча, то останется только одна неизвестная — F2.

Тогда условие ΣF = 0 будет выглядеть так: -(10 м) * (1200 кг) * (g) — (15 м) * (15000 кг) * (g) + (20 м) * F2 = 0. Отсюда F2 = (12000 кг) * (g) = 118000 H. Теперь силу F1 можно вычислить из условия равновесия: ΣFy = F1 — (1200 кг) * (g) — (15000 кг) * (g) + F2 = 0. Подставив в полученное выражение F2 = (12000 кг) * (g), верным будет записать: F1 = (4200 кг) * (g) = 41200 Н. Задача решена.

Таким образом, главное — правильно выбрать ось вращения, тем самым сделать расчёт более простым. Следует отметить, что в инженерии некоторые силы определяют с помощью специальных датчиков напряжения. Например, пьезоэлектрические датчики и тензодатчики. Их крепят как на саму конструкцию, так и на её модель.

ПредыдущаяСледующая

Источник: https://Sprint-Olympic.ru/uroki/fizika/121352-ysloviia-ravnovesiia-tel-vidy-formyly-i-primery.html

Равновесие тел. Виды равновесия. ЦЕЛЬ УРОКА: Изучить состояние равновесия тел, познакомиться с различными видами равновесия; выяснить условия, при которых. — презентация

1 Равновесие тел. Виды равновесия. ЦЕЛЬ УРОКА: Изучить состояние равновесия тел, познакомиться с различными видами равновесия; выяснить условия, при которых тело находится в равновесии.

2 Условия равновесия. I условие равновесия: Тело находится в равновесии, если геометрическая сумма внешних сил, приложенных к телу, равна нулю. F=0.

II условие равновесия: Сумма моментов сил, действующих по часовой стрелке, должна равняться сумме моментов сил, действующих против часовой стрелки. M по час. = M против час.

3 Условие равновесия рычага. F 1 l 1 = F 2 l 2 F1F1 F2F2 M 1 = M 2 O l2 l2 l1l1

4 Центр тяжести тела. Центр тяжести тела- это точка, через которую проходит равнодействующая всех параллельных сил тяжести, действующих на отдельные элементы тела. Найти центр тяжести данных фигур.

5 ВИДЫ РАВНОВЕСИЯ Устойчивое Неустойчивое Безразличное

6 Если на тело, имеющее опору, действуют уравновешивающие силы, то тело находится в положении равновесия.

7 При отклонении тела от положения равновесия нарушается и равновесие сил. Если тело под действием равнодействующей силы возвращается в исходное положение, то это — устойчивое равновесие. Если же тело под действием равнодействующей силы, ещё сильнее отклоняется от положения равновесия, то это — неустойчивое равновесие.

8 Возможен случай, когда при любом положении тела, равновесие сил сохраняется. Это состояние называется безразличным равновесием.

9 Вывод: Равновесие устойчиво, если при малом отклонении от положения равновесия есть сила, стремящаяся вернуть его в это положение. Устойчиво такое положение, в котором его потенциальная энергия минимальна.

10

11 Если центр тяжести находится выше точки опоры, то в этом случае осуществить равновесие сил практически невозможно. При малейшем отклонении карандаша от вертикального положения, его центр тяжести понижается и карандаш падает.

13 Равновесие тела, имеющего точку опоры ниже центра тяжести, неустойчиво. Но равновесие может восстанавливаться путём смещения точки опоры тела в сторону смещения центра тяжести.

14 Хождение на ходулях (две точки опоры или линия опоры) осуществляется путём непрерывного смещения центра тяжести относительно линии, соединяющей точки опоры(АВ).

15 По положению центра тяжести можно судить о виде равновесия. Например езда эквилибриста по канату на велосипеде с противовесом является примером устойчивого равновесия.

• 16
• 17 Вывод: Для устойчивости тела, находящегося на одной точке или линии опоры необходимо, чтобы центр тяжести находился ниже точки (линии) опоры.
• 18
• 19 Под площадью опоры понимают площадь соприкосновения тела с опорой или площадь, ограниченную возможными осями, относительно которых может происходить опрокидывание ( поворот) тела под действием внешних сил.

20 FтFт FтFт Если при отклонении тела, имеющего площадь опоры, происходит повышение центра тяжести, то равновесие будет устойчивым. При устойчивом равновесии вертикальная прямая, проходящая через центр тяжести, всегда будет проходить через площадь опоры.

21 FтFт FтFт FтFт FтFт FтFт Два тела, у которых одинаковы вес и площадь опоры, но разная высота, имеют разный предельный угол наклона. Если этот угол превысить, то тела опрокидываются. A = F т h

22 FтFт FтFт FтFт FтFт FтFт При более низком положении центра тяжести необходимо затратить большую работу для опрокидывания тела. Следовательно работа по опрокидыванию может служить мерой его устойчивости.

1. 23 FтFт FтFт FтFт FтFт FтFт Неустойчивое равновесие Устойчивое равновесие
2. 24 Чем ниже центр тяжести корабля, тем больше его устойчивость.
3. 25 Чтобы увеличить устойчивость машин на поворотах, полотно дороги наклоняют в сторону поворота.
4. 26

27 Вывод: 1. Устойчиво то тело, у которого площадь опоры больше. 2. Из двух тел одинаковой площади устойчиво то, у которого центр тяжести расположен ниже, т.к. его можно отклонить без опрокидывания на большой угол.

• 28 Почему Пизанская башня стоит под наклоном и не падает?
• 29 Почему «Ванька-встанька» возвращается в положение равновесия при любом наклоне игрушки?
• 30 Каким образом сохраняют равновесие велосипедисты и мотоциклисты?

31 Выводы урока: Существует три вида равновесия: устойчивое, неустойчивое, безразличное. Устойчиво положение тела, в котором его потенциальная энергия минимальна. Устойчивость тел на плоской поверхности тем больше, чем больше площадь опоры и ниже центр тяжести.

32 Автор урока: Махмутова А.Р. МОБУ Гимназия 17 г. Белорецк р. Башкортостан 2010г.

Источник: http://www.myshared.ru/slide/584077/