Теорема синусов для треугольника, формула и примеры

В данной публикации мы рассмотрим одну из главных теорем евклидовой геометрии, теорему синусов, которая определяет соотношение сторон в треугольнике, а также, научимся применять ее на практике для решения задач.

• Формулировка и формула теоремы
• Примеры задач

Формулировка и формула теоремы

1. Обычная теорема

Стороны треугольника пропорциональны синусам противолежащих углов.

2. Расширенная теорема

В произвольном треугольнике справедливо следующее соотношение:

R – радиус описанной вокруг треугольника окружности.

Примеры задач

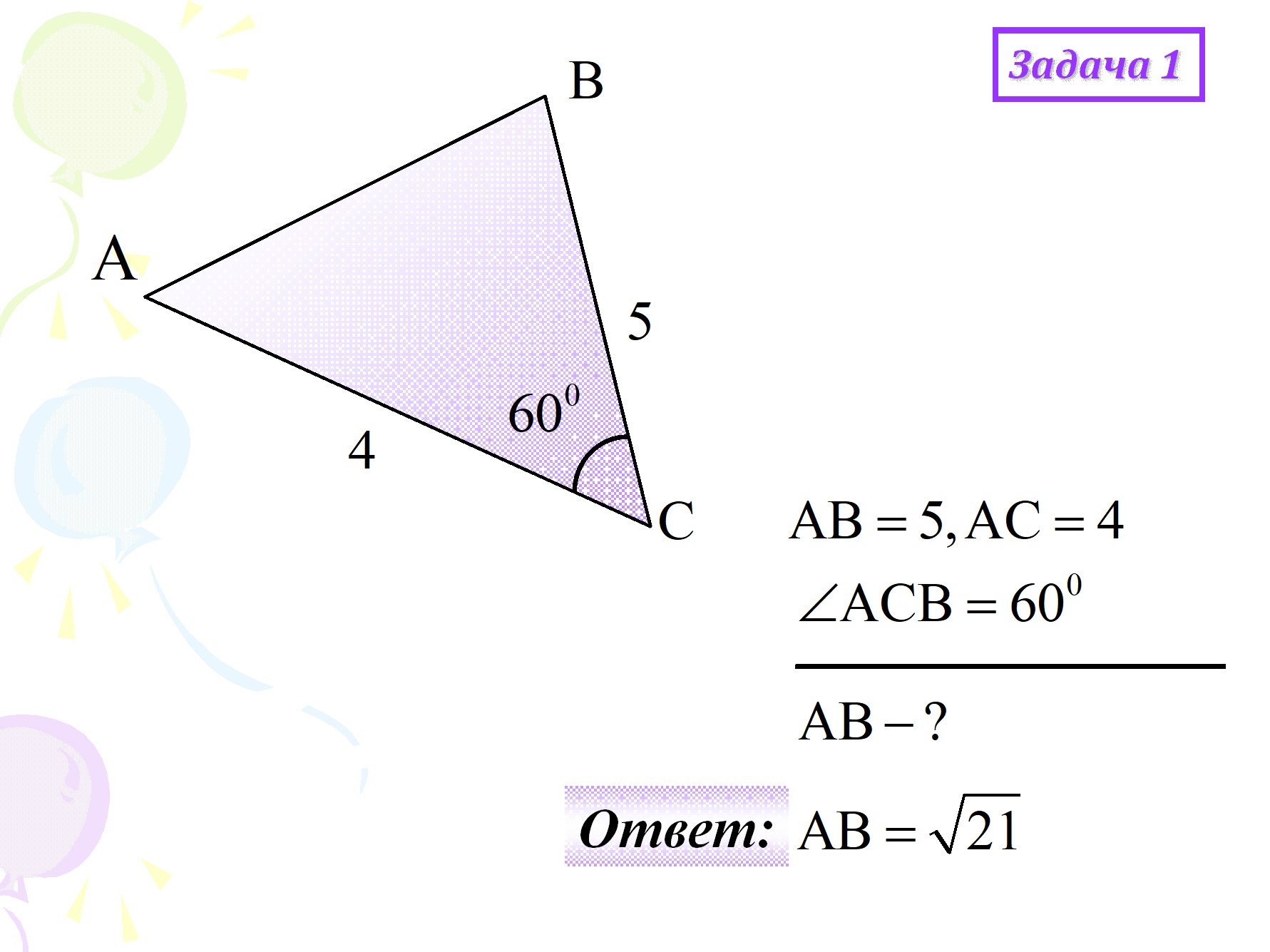
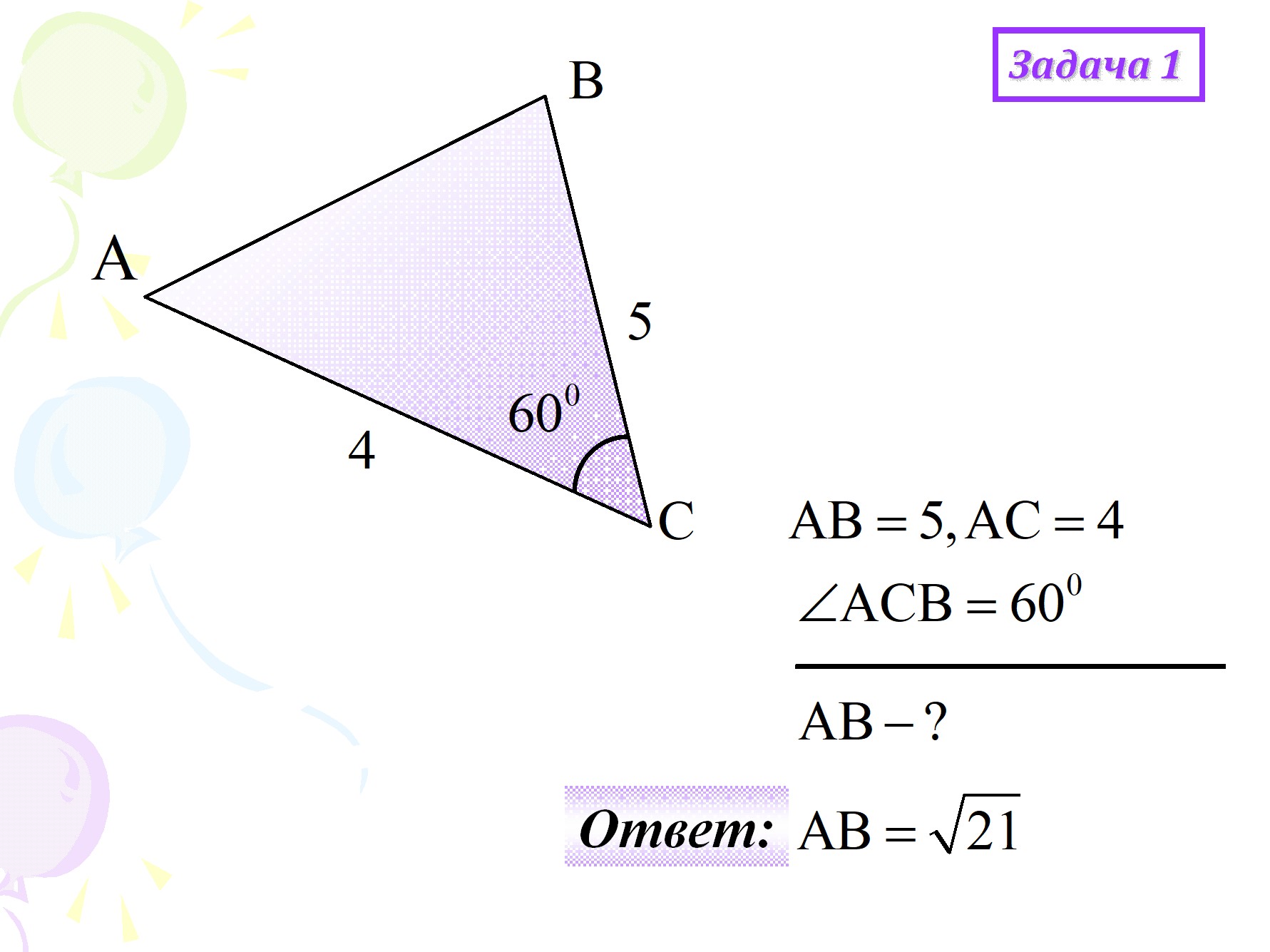
Задание 1
В треугольнике известна длина основания – 10 см, противолежащий основанию угол – 90°, а также, один из углов, прилегающих к нему – 45°. Найдите сторону напротив угла 45°.

Решение:
Примем неизвестную сторону за x и применим теорему синусов:

Следовательно:

Задание 2
Гипотенуза и один из катетов прямоугольного треугольника равны, соответственно, 10 и 8 см. Найти угол, расположенный напротив данного катета.

Решение:
Как мы знаем, в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. С учетом этого, соотношение сторон выглядит следующим образом:

Следовательно:

Значит x = arcsin (4/5) ≈ 53,1°.

Источник: https://MicroExcel.ru/teorema-sinusov/

Теорема синусов

Первая часть теоремы: стороны произвольного треугольника пропорциональный синусам противоположных углов, то есть:

Вторая часть теоремы: каждая дробь равна диаметру окружности, описанной около данного треугольника, то есть: .

Комментарий репетитора по математике: использование второй части теоремы синусов закладывается чуть ли не в каждой второй конкурсной задаче на окружность. Почему? Дело в том, что равенство позволяет находить радиус окружности имея в наличие только два элемента треугольника. Это очень часто используют составители сильных задач, которые специально так подбирают условие, чтобы никакие другие элементы треугольника (и всего рисунка) не находились бы вообше! «Картинка» при этом будет плавующей. Это обстоятельство сильно усложняет работу на экзамене, ибо не дает возможность действовать в обход заложенному свойству.

Доказательство теоремы синусов:

по учебнику Атанасяна
Докажем, что для любого треугольника со сторонами a, b, c и противолежащими углами A, B и С выполняется равенство: .
Проведем высоту BH из вершины В. Возможны два случая:

1) Точка H лежит на стороне AC (это возможно когда и  — острые).

По определению синуса острого угла в прямоугольном треугольнике ABH запишем
2) Пусть H лежит на продолжении стороны AC (например слева от А). Это произойдет, если – тупой. Аналогично по определению синуса острого угла А в треугольнике ABH запишем равенство , но так как синусы смежных углов равны, то заменив в этом равенстве на , получим как и в первом случае. Поэтому независимо от величин углов А и С равенство верное. После деления обеих его частей на получим . Аналогично доказывается равенство второй пары дробей

Доказательство теоремы синусов по учебнику Погорелова:

Применим формулу площади треугольника для двух углов A и C:

После приравнивания правых частей и сокращения на получим тоже самое равенство , как и в доказательстве первым способом. Из него тем же путем получаем равенство дробей.

Доказательство второй части теоремы синусов:

Опишем около данного треугольника окружность и через В проведем ее диаметр BD. Так как углы D и C опираются на одну дугу, то они равны (следствие из теоремы о вписанных углах). Тогда . Применим в треугольнике ABD определение синуса угла D: Что и требовалось доказать.

Задачи на вторую часть теоремы синусов:
1) В окружность радиуса 15 вписана трапеция. Длины диагонали и высоты трапеции соответственно равны 20 и 6. Найти боковую сторону.

2) Радиус окружность, описанной около трапеции, равен 25, а косинус ее тупого угла равен -0,28 (минус!!!). Диагональ трапеции образует с основанием угол . Найти высоту трапеции.

3) В окружность радиуса 10 вписана трапеция. Длины диагонали и средней линии трапеции соответственно равны 15 и 12. Найти длину боковой стороны трапеции.

4) Олимпиада в Финансовой академии 2009г. Хорды окружности пересекаются в точке Q. Известно, что а радиус окружности равен 4см. Найдите длину хорды PN. Олимпиада в Финансовой академии 2009г.

5) В треугольнике PST . Вокруг точки пересечения его биссектрис и вершин P и T описана окружность с радиусом 8см. Найдите радиус окружности, описанной около треугольника PST (авторская задача).

Если вам нужна подготовка к ЕГЭ по математике для сдачи экзамена не менее чем на 70 баллов — придется тренироваться в решении крепких планиметрических задач с номеров С4. В них теорему синусов часто применяют к вписанным треугольникам учитывая соотношение .

Помните об этом!

С уважением, Колпаков Александр Николаевич,
репетитор по математике

Источник: https://ankolpakov.ru/teorema-sinusov/

Теорема синусов

  Теорема

Стороны треугольника пропорциональны синусам противолежащих углов.

Доказательство

• Дано: АВС, АВ = , ВС = , АС = .
• Доказать: .
• Доказательство:

1. По теореме о площади треугольника:
2. , (1)      , (2)      . (3)
3. Из равенств (1) и (2) получим:
4. , откуда или .  (4)
5. Из равенств (2) и (3) получим:
6. , откуда или .   (5)
7. Из равенств (4) и (5) следует:
8. .
9. Теорема доказана.
10. Замечание

Доказательство

• Дано: окр(О, R)описана около АВС.
• Доказать: .
• Доказательство:
• Проведем диаметр ВА1 и рассмотрим треугольник А1ВС.

Угол С АВС опирается на диаметр ВА1, поэтому С — прямой, тогда (6) (смотри формулы для вычисления координат точки). Но . Действительно, если точка А1 лежит на дуге ВАС (см.

рисунок выше), то А1 = А, а если на дуге ВDС (см. рисунок ниже), то

А1 = 1800 — А. В обеих случаях .

Следовательно, учитывая (6), получим:

, при этом диаметр ВА1 = 2R, значит, , откуда . Что и требовалось доказать.

1. Из доказанного выше замечания получаем, что для любого АВС со сторонами АВ = , ВС = , АС = справедливы равенства
2. ,
3. где R — радиус описанной окружности.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Синус, косинус, тангенс, котангенс

Основное тригонометрическое тождество. Формулы приведения.

• Формулы для вычисления координат точки
• Теорема о площади треугольника
• Теорема косинусов
• Решение треугольников
• Измерительные работы
• Угол между векторами
• Скалярное произведение векторов
• Скалярное произведение в координатах
• Свойства скалярного произведения векторов
• Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

Правило встречается в следующих упражнениях:

1. 7 класс
2. Задание 1025, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
3. Задание 1026, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
4. Задание 1027, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
5. Задание 1029, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
6. Задание 1032, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
7. Задание 1037, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8. Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
9. Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
10. Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
11. Задание 1277, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

• © budu5.com, 2020
• Пользовательское соглашение
• Copyright
• Нашли ошибку?
• Связаться с нами

Источник: https://budu5.com/manual/chapter/3560

Теорема о площади треугольника, теоремы синусов и косинусов

Теорема 1

Площадь треугольника равна половине произведения двух сторон на синус угла между этими сторонами.

Доказательство.

Пусть нам дан произвольный треугольник $ABC$. Обозначим длины сторон этого треугольника как $BC=a$, $AC=b$. Введем декартову систему координат, так, что точка $C=(0,0)$, точка $B$ лежит на правой полуоси $Ox$, а точка $A$ лежит в первой координатной четверти. Проведем высоту $h$ из точки $A$ (рис. 1).

• Рисунок 1. Иллюстрация теоремы 1
• В этой системе координат, получаем, что
• Высота $h$ равняется ординате точки $A$, следовательно
• Тогда

Теорема синусов

Теорема 2

Стороны треугольника пропорциональны синусам противолежащих углов.

Доказательство.

Пусть нам дан произвольный треугольник $ABC$. Обозначим длины сторон этого треугольника как $BC=a$, $AC=b,$ $AC=c$ (рис. 2).

1. Рисунок 2.
2. Докажем, что
3. По теореме 1, имеем
4. Приравнивая их попарно, и получим, что

Теорема косинусов

Теорема 3

Квадрат стороны треугольника равен сумме квадратов двух других сторон треугольника без удвоенного произведения этих сторон на косинус угла между этими сторонами.

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

Доказательство.

Пусть нам дан произвольный треугольник $ABC$. Обозначим длины его сторон как $BC=a$, $AC=b,$ $AB=c$. Введем декартову систему координат, так, что точка $A=(0,0)$, точка $B$ лежит на положительной полуоси $Ox$, а точка $C$ лежит в первой координатной четверти (рис. 3).

• Рисунок 3.
• Докажем, что
• В этой системе координат, получаем, что
• Найдем длину стороны $BC$ по формуле расстояния между точками
• То есть

Пример задачи на использование данных теорем

Пример 1

Доказать, что диаметр описанной окружности произвольного треугольника равен отношению любой стороны треугольника к синусу противолежащего этой стороне угла.

Решение.

Пусть нам дан произвольный треугольник $ABC$. $R$ — радиус описанной окружности. Проведем диаметр $BD$ (Рис. 4).

1. Рисунок 4.
2. Докажем, что $frac{BC}{sinA}=2R$
3. Так как сторона $BD$ треугольника $DCB$ лежит на диаметре вписанной окружности, то он прямоугольный, следовательно, $sinD=frac{BC}{BD}=frac{BC}{2R}$.То есть
4. Следовательно,

[frac{BC}{sinD}=2R] [angle A={180}^0-angle D] [sinangle A={sin left({180}^0-angle D
ight) }={sin angle D }]
[frac{BC}{sinA}=2R]

ч. т. д.

Пример 2

• Найти третью сторону треугольника, если две его стороны равны 5 и 7, соответственно, а угол между ними равен ${60}^0.$
• Решение.
• Обозначим искомую сторону через $a$. Используя теорему 3, получим
• Ответ: $sqrt{39}$.

[a^2=25+49-70cos{60}^0=74-35=39] [a=sqrt{39}]

Источник: https://spravochnick.ru/matematika/sootnosheniya_mezhdu_storonami_i_uglami_treugolnika/teorema_o_ploschadi_treugolnika_teoremy_sinusov_i_kosinusov/

Теорема синусов

Развернуть структуру обучения

Свернуть структуру обучения

Примечание. В данной главе приводится формулировка и доказательство теоремы синусов. В уроках главы приведены задачи по геометрии с решениями на эту же тему. См. также Теорема косинусов.  

Теорема синусов устанавливает зависимость между величиной углов треугольника и противолежащих ему сторон. Формулировка теоремы синусов:

Стороны треугольника пропорциональны синусам противолежащих углов

или, где

R — радиус описанной вокруг треугольника окружности

a, b, c — стороны треугольника

α, β, γ

— величины противолежащих этим сторонам углов   Доказательство теоремы синусов происходит с помощью дополнительных построений.

Построим произвольный треугольник, вписанный в окружность. Обозначим его как ABC.

Дополнительно построим диаметр окружности, в который вписан произвольный треугольник, но так, чтобы он проходил через один из его углов. Диаметр равен двойному радиусу окружности (2R). Примем во внимание, что одним из свойств прямоугольного треугольника, вписанного в окружность является то, что его гипотенуза, является диаметром окружности, в которую он вписан. Обозначим диаметр для описанной окружности как BD. Образовавшийся треугольник BCD является прямоугольным, поскольку его гипотенуза лежит на диаметре описанной окружности (свойство углов, вписанных в окружность). 

Таким образом, дополнительно построенный треугольник, у которого одна общая сторона с построенным ранее произвольным треугольником, а гипотенуза совпадает с диаметром окружности — является прямоугольным. То есть треугольник DBC — прямоугольный.

  

• Для доказательства всей теоремы, поскольку размеры треугольника ABC выбраны произвольным образом, достаточно доказать, что соотношение одной произвольной стороны к противолежащему ей углу равно 2R.
• Пусть это будет 2R = a / sin α, то есть если взять по чертежу 2R = BC / sin A.
• Поскольку, углы, вписанные в окружность, опирающиеся на одну и ту же дугу, равны, то угол CDB либо равен углу CAB (если точки A и D лежат по одну сторону от прямой BC), либо равен π — CAB (в противном случае).

Обратимся к свойствам тригонометрических функций.  Поскольку sin( π − α ) = sin α, то указанные варианты построения треугольника все равно приведут к одному результату.

Вычислим значение 2R = a / sin α, по чертежу 2R = BC / sin A. Для этого заменим sin A на соотношение соответствующих сторон прямоугольного треугольника. 2R = BC / sin A 2R = BC / ( BC / DB ) 2R = DB А, поскольку, DB строился как диаметр окружности, то равенство выполняется. Повторив то же рассуждение для двух других сторон треугольника, получаем: Теорема синусов доказана.

Содержание главы:

• Задачи на решение с помощью теоремы синусов

• Теорема синусов (часть 2)

0  

 Синус | Описание курса | Задачи на решение с помощью теоремы синусов 

Источник: https://profmeter.com.ua/communication/learning/course/course7/chapter0551/

Теоретический материал: Соотношения между сторонами и углами прямоугольных треугольников

Алгебра

Глава 12. Тригонометрические функции и треугольники

12.1. Соотношения между сторонами и углами прямоугольных треугольников

Любой прямоугольный треугольник путем перемещения на плоскости можно расположить относительно системы координат. Обозначим через и острые углы и через и противолежащие им катеты; — прямой угол треугольника и — его гипотенуза.

Рис.1.

• Рассматриваем радиус-вектор , для которого ордината , абсцисса и длина радиус-вектора .
• Так как , , , то заменив , , на , , , получим: , , .
• Отсюда находим катеты: , , , и гипотенузу из первого и второго равенств:
• и .
• На основании свойства дополнительных углов и запишем: , , .

Получили тригонометрические соотношения между сторонами и углами прямоугольного треугольника: 1) и . Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла.

2) и . Катет равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к первому катету угла.

3) . Гипотенуза равна катету, деленному на синус противолежащего или косинус прилежащего к этому катету угла.

На этих правилах основаны следующие случаи решения прямоугольных треугольников.

1) Даны один из катетов и один из острых углов, например и . Требуется вычислить: , , .

Решение: ; ; .

2) Даны гипотенуза и острый угол, например . Определить: , , .

Решение: ; ; .

3) Даны гипотенуза и катет, например . Вычислить: , , .

Решение: ; ; .

4) Даны катеты и . , , =?

Решение: ; ; .

Источник: https://dl.bsu.by/mod/book/view.php?id=10174&chapterid=1248