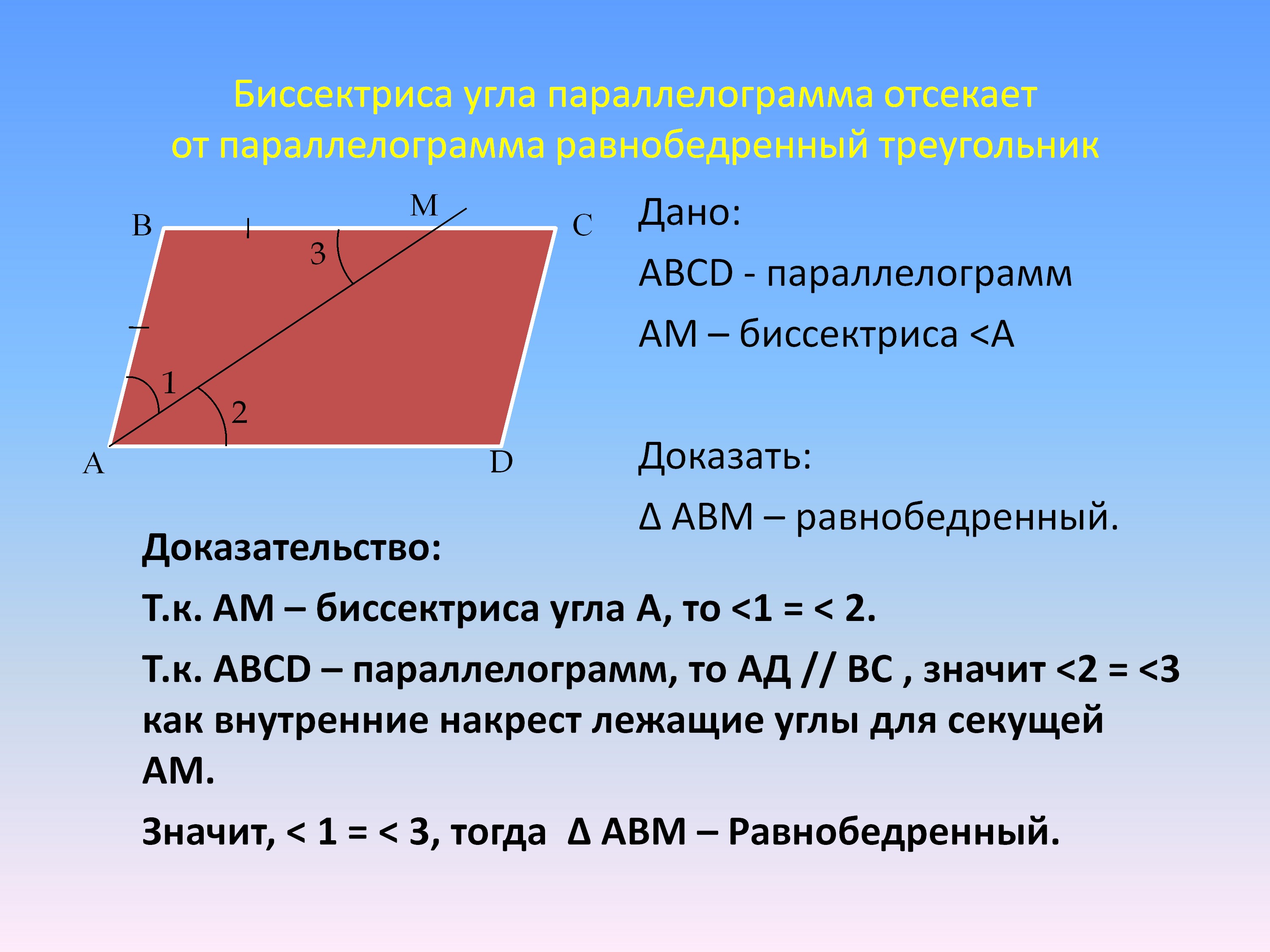
Определение 14. Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых 
Свойства параллелограмма: 
Теорема 22. Противоположные стороны параллелограма равны. Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠САВ=∠АСD, ∠АСВ=∠DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников: Теорема 23. Противоположные углы параллелограмма равны: ∠А=∠С и ∠В=∠D. Равенство первой пары идет из равенства треугольников АВD и CBD, а второй — АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠ОАD=∠ОСВ и ∠ОDА=∠ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д. Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠А=∠С и ∠В=∠D. Т.к. ∠А+∠В+∠С+∠D=360о, то ∠А+∠В=180о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению. Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом. Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник — параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.
В геометрии рассматривают частные случаи параллелограмма: прямоугольник, ромб, квадрат. Теорема 31. Площадь параллелограмма равна произведению стоны и проведенную к ней высоту.
Теорема 32. Площадь параллелограмма равна произведению двух смежных сторон и синуса угла между ними.
Теорема 33. Площадь параллелограмма равна половине произведения диагоналей и синуса угла между ними.
Теорема d2. (о сумме квадратов диагоналей параллелограмма): Сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон. Доказательство: Пусть ABCD — данный параллелограмм. Тогда: AB2 + BC2 + CD2 + AD2 = 2(AB2 + BC2) = = 2(AO2 + BO2 — 2AO·BO·cosAOB + + BO2 + CO2 — 2BO·CO·cosBOC) = = 2(2·(AO2 + BO2 — AO·BO(cosAOB — cosAOB))) = = 4(AO2+ BO2) = (2·AO)2 + (2·BO)2 = AC2 + BD2. Что и требовалось доказать.
Источник: http://methmath.ru/parall.html
7.2. Параллелограмм
- Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
- Высотой параллелограмма, проведенной к данной его стороне, называется перпендикуляр, опущенный из произвольной точки противолежащей стороны к прямой, содержащей данную сторону.
- Признаки параллелограмма.
Теорема 7.1.
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник – параллелограмм.
Пусть ABCD – данный четырехугольник. По условию AO = OC, BO = OD. Так как углы (AOB) и (COD) равны как вертикальные, то по теореме 4.1 треугольник AOB равен треугольнику COD, и, следовательно, углы (OAB) и (OCD) равны. Эти углы являются внутренними накрест лежащими при прямых (AB) и (CD) и секущей (AC) и по теореме 3.2 прямые (AB) и (CD) параллельны. Аналогично из равенства треугольников AOD и COB следует равенство углов (OAD) и (OCB) и по теореме 3.2 – параллельность прямых (AD) и (BC). Из полученных результатов следует, что четырехугольник ABCD – параллелограмм. Теорема доказана.
|
Теорема 7.2.
Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.
Пусть ABCD – данный четырехугольник и (AB) || (CD), AB = CD.
Проведем диагональ AC. Получившиеся треугольники ABC и ADC равны. Действительно, стороны AB и CD равны по условию, сторона AC – общая, углы ACD и BAC равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей AC. Из равенства треугольников следует равенство углов CAD и ACB. Данные углы являются внутренними накрест лежащими при прямых BC и AD и секущей AC. По теореме 3.2 прямые BC и AD параллельны. Следовательно, четырехугольник ABCD параллелограмм по определению. Теорема доказана. |
Теорема 7.3.
Если у четырехугольника противолежащие стороны попарно равны, такой четырехугольник – параллелограмм.
Пусть ABCD – данный четырехугольник, и AB = CD, BC = AD.
Проведем диагональ AC. Получившиеся треугольники ABC и CDA равны по трем сторонам. Действительно, AB = CD, BC = AD по условию, а сторона AC – общая. Тогда BCA = CAD и BAC = ACD. Первые два угла являются внутренними накрест лежащими при прямых BC и AD и секущей AC, а вторая пара – при прямых AB и CD и секущей AC. Из равенства внутренних накрест лежащих углов по теореме 3. 2 следует параллельность соответствующих прямых, а именно: из равенства углов BCA и CAD следует параллельность прямых BC и AD, а из равенства углов BAC и ACD – параллельность прямых AB и CD. Тогда по определению четырехугольник ABCD – параллелограмм. |
Теорема 7.4.
Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.
Пусть ABCD – данный четырехугольник, и B = D,A = C. Проведем диагональ AC.
Сумма углов четырехугольника равна сумме углов треугольника ABC и треугольника ACD. Так как сумма углов каждого треугольника – 180°, то A + B + C + D = 360°. С учетом условия получаем, что A +D = 180° и C + D = 180°. Углы A и D являются внутренними односторонними при прямых AB и CD и секущей AD, и, так как их сумма равна 180°, то по следствию 3.2 прямые AB и CD – параллельны. Аналогично углы C и D являются внутренними односторонними при прямых BC и AD и секущей CD, а сумма их равна 180°, и, следовательно, прямые BC и AD – параллельны. Таким образом, четырехугольник ABCD – параллелограмм по определению, что и требовалось доказать. |
Свойствa параллелограмма.
Теорема 7.5.
Диагонали параллелограмма пересекаются и точкой пресечения делятся пополам.
Пусть ABCD – данный параллелограмм. По определению (AB) || (CD) и (AD) || (BC). Пусть O – середина диагонали BD и на луче, дополняющем луч OA, отложен отрезок OC1, равный отрезку OA. По теореме 7.1 получившийся четырехугольник ABC1D – параллелограмм, и, следовательно, (BC1) || (AD) и (AB) || (C1D). С учетом условия – (BC) || (AD) и (AB) || (CD). В соответствии с теоремой 3.3 (BC) = (BC1) и (DC) = (DC1). Поэтому точки C и C1 совпадают. Следовательно, совпадают параллелограммы ABCD и ABC1D. Отсюда AO = OC и BO = OD. Теорема доказана.
|
Следствие 7.1.
Параллелограмм – выпуклый четырехугольник.
Теорема 7.6.
У параллелограмма противолежащие стороны равны, противолежащие углы равны.
Пусть ABCD – данный параллелограмм, т.е. (AB) || (CD) и (BC) || (AD) и O – точка пересечения диагоналей. Тогда AO = OC и BO = OD. Поскольку углы (AOB) и (COD) равны как вертикальные, то по теореме 4.1 треугольники AOB и COD равны, и, как следствие, AB = CD. Аналогично из равенства углов (AOD) и (COB) как вертикальных и равенства треугольников BOC и DOA следует равенство сторон AD и BC. В силу доказанного в треугольниках BAD, DCB AB = DC, AD = BC и BD – общая сторона и по теореме 4.8 Δ BAD = Δ DCB. Тогда BCD = BAD. Аналогично из равенства треугольников ABC и CDA следует равенство углов (ABC) и (CDA). Теорема доказана.
|
Прямоугольником называется параллелограмм, у которого все углы прямые.
| 7 |
| Рисунок 7.2.7.Прямоугольник |
Свойство прямоугольника задается следующей теоремой:
Теорема 7.7.
Диагонали прямоугольника равны.
Пусть ABCD – данный прямоугольник. Прямоугольные треугольники BAD и ABC равны по теореме 4.1, так как AD = BC, AB – общая сторона. BAD = ABC = 90°. Отсюда BD = AC. Теорема доказана.
|
| Hydra.center.onion |
| hydra.center.onion |
| web-onion.com |
Источник: https://mathematics.ru/courses/planimetry/content/chapter7/section/paragraph2/theory.html
Параллелограмм — это базовая геометрическая фигура с рядом важных свойств и признаков
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
В этой статье мы подробно расскажем о таком термине, как ПАРАЛЛЕЛОГРАММ.
С этой фигурой каждый из нас познакомился еще в школе – на уроках геометрии в 8 классе. Но если кто проболел в то время, прогулял занятия или просто не усвоил материал – мы поможем закрыть этот пробел.
Определение параллелограмма
Итак,
Параллелограмм – это геометрическая фигура, которая является разновидностью четырехугольника. У него противоположные стороны лежат на параллельных линиях, а соответственно, являются параллельными по отношению друг к другу.
Выглядит эта фигура вот так:
Это классический вид параллелограмма, который в учебниках приводят всегда в первую очередь. В данной фигуре сторона AD параллельна стороне ВС, а АВ параллельна CD.
Интересно, что более известные всем нам фигуры – квадрат, прямоугольник и ромб – также являются параллелограммами.
Можно даже дать такие определения:
- Квадрат – это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник – это параллелограмм, у которого стороны пересекаются под прямым углом, но при этом они не равны между собой.
- Ромб – это параллелограмм, у которого все стороны равны между собой, но при этом они не пересекаются под прямым углом.
Происхождение термина «параллелограмм»
Как и многие термины в математике, слово ПАРАЛЛЕЛОГРАММ пришло к нам из Древней Греции. И легко предположить, что оно как-то связано с самым известным в истории математиком – Евклидом.
Действительно, так и есть. Слово ПАРАЛЛЕЛОГРАММ впервые можно найти именно в трудах Эвклида, которые называются «Начала». Оно состоит из двух греческих слов – «Parallelos», что, естественно, означает «параллельный», и «Gramme» — «линия».
Таким образом, ПАРАЛЛЕЛОГРАММ можно перевести как «параллельные линии». Этот принцип и заложен в определении геометрической фигуры.
Еще любопытный факт, что именно Евклид поделил все четырехугольники на две большие категории. Первая – это параллелограммы, у которых противоположные стороны параллельны. И трапеции (что это?), у которых параллельна только одна пара сторон.
Свойства и признаки параллелограмма
Как понять, что перед нами ПАРАЛЛЕЛОГРАММ? Есть целый ряд признаков, который характерен только для этой геометрической фигуры.
Возьмем в качестве примера еще раз нашу фигуру:
Чтобы этот четырехугольник ABCD можно было считать параллелограммом, должно выполняться одно из следующих условий:
- Две противоположные стороны попарно параллельны.
- Две противоположные стороны попарно равны между собой.
- Две противоположные стороны и равны, и параллельны. В данном случае можно брать только одну пару сторон.
AD II BC и AD =BC. Или AB II CD и AB = CD
- Противоположные углы попарно равны между собой.
- Диагонали пересекаются в центре фигуры и делятся точкой пересечения на две равные части.
- Если сложить два соседних угла, то получится 180 градусов.
∠А + ∠В = ∠В + ∠С = ∠С + ∠D = ∠D + ∠А = 180
Это самые простые признаки параллелограмма. Есть еще некоторые признаки, смысл которых поясняется в этом видео:
Причем, для того чтобы удостовериться в подлинности фигуры, достаточно доказать только одно из них.
Правило действует и в обратную сторону – если хоть один из признаков параллелограмма верен, то автоматически верны и все остальные, и они не нуждаются в отдельном доказательстве.
Соответственно, если хоть один признак не получил подтверждения, то фигуру нельзя считать параллелограммом. И все остальное также не совпадет.
Как посчитать периметр параллелограмма
Для подсчетов длины периметра четырехугольников обычно просто складывают длины его сторон. Но в случае с параллелограммом все несколько проще, так как стороны у него попарно равны.
Снова возьмем для примера нашу фигуру:
Только для удобства обозначим стороны по-другому. AD и ВС будет просто «а», а АВ и CD – «b». Получится вот так:
Чтобы рассчитать периметр, надо просто сложить все стороны:
P = a + b + a + b
Но эту же формулу можно переиначить и по-другому:
P = 2a +2b
Или совсем просто:
P = (a + b) * 2
Это и есть формула периметра параллелограмма, которая записана во всех учебниках.
Как рассчитать площадь параллелограмма
С площадью геометрических фигур всегда чуть сложнее, чем с периметрами. Но параллелограмм в какой-то мере уникален, потому что для расчета его площади существует сразу несколько формул.
- Вычисление площади параллелограмма по высоте.
Напомним, высотой называют линию, которая выходит из вершины геометрической фигуры и идет под прямым углом к противоположному основанию.
- Вычисление площади параллелограмма по углам. Если известны длины сторон и хотя бы один угол, то можно применить следующую формулу.
- Вычисление площади параллелограмма по диагоналям. Для этого надо знать не только длину диагоналей, но и величину угла между ними. И тогда можно применять следующую формулу.
Источник: https://KtoNaNovenkogo.ru/voprosy-i-otvety/parallelogramm-chto-ehto-takoe-opredelenie-svojstva-priznaki-perimetr.html
Параллелограмм
Развернуть структуру обучения
Свернуть структуру обучения
Параллелограмм — четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. На приведенном рисунке параллелограмм обозначен синими линиями. Элементы параллелограмма, указанные на рисунке:
ABCD — параллелограмм, у которого противолежащие стороны попарно параллельны ( AB параллельна CD, а BC параллельна AD)
BH — высота параллелограмма, опущенная из точки B на основание AD (на рисунке обозначена красным цветом) AC и BD — диагонали параллелограмма.
- Противоположные стороны параллелограмма равны
- Противоположные углы параллелограмма равны
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Точка пересечения диагоналей называется центром симметрии параллелограмма
- Диагональ делит параллелограмм на два равных треугольника
- Сумма углов, прилежащих к одной стороне, равна 180°. (см. формулу ниже)
- Сумма всех углов равна 360°
- Средние линии параллелограмма пересекаются в точке пересечения его диагоналей и делятся этой точкой пополам
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон (см. формулу ниже)
Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:
- Противоположные стороны попарно равны
- Противоположные стороны попарно параллельны и равны
- Противоположные углы попарно равны
- Диагонали делятся в точке их пересечения пополам
- Сумма соседних углов равна 180 градусов
- Две стороны равны и параллельны
Формулы нахождения площади параллелограмма приведены ниже: То есть:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними. Как видно из чертежа, произведение b sin α равно высоте, опущенной на другую сторону, что в итоге дает нам предыдущую формулу
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
- Площадь параллелограмма также можно найти через формулу Герона, рассмотрев одну из диагоналей как треугольник и вычислив удвоенную площадь этого треугольника
- Для нахождения полупериметра треугольника из предыдущей формулы мы используем две стороны параллелограмма и его диагональ. Поскольку каждая диагональ разбивает его на два равных треугольника, то не имеет значения, какую из диагоналей мы выберем
Стороны параллелограмма можно найти через:
- Размеры диагоналей и угол между ними (формулы 1 и 2)
- Через длины диагоналей и одну из сторон можно найти вторую (формулы 3 и 4)
- Через высоту, опущенную на сторону и угол между сторонами (формулы 5 и 6)
- Через площадь и высоту, опущенную на заданную сторону, можно найти величину этой стороны (Формулы 7 и 8)
- Диагональ параллелограмма можно найти через длины его сторон и косинус угла между ними (Формулы 1-4)
- Также диагональ может быть найдена через длины сторон и размер второй диагонали (Формулы 5-6)
- Диагональ может быть найдена из площади, длины второй диагоналями и угла между ними (Формулы 7-8)
Периметр параллелограмма может быть найден:
- через его стороны (Формула 1)
- через одну из сторон и длину двух диагоналей (Формулы 2 и 3)
- через сторону, высоту и угол между сторонами (Формулы 4-6)
Задачи с решениями про параллелограмм смотрите в уроках ниже:
Содержание главы:
- Параллелограмм. Задачи про площадь и стороны
0
Трапеция, описанная вокруг окружности | Описание курса | Параллелограмм. Задачи про площадь и стороны
Источник: https://profmeter.com.ua/communication/learning/course/course7/chapter84/
Презентация к уроку по геометрии (8 класс) на тему: Параллелограмм. Свойства и признаки. | Социальная сеть работников образования
Слайд 1
Четырехугольники 8 класс геометрия Параллелограмм 1
Слайд 2
Цели: Ввести понятие параллелограмма. Рассмотреть свойства параллелограмма. Рассмотреть признаки параллелограмма. Решение базовых задач. 2
Слайд 3
3 А В С D ABCD – параллелограмм. AB II CD, DC II AD. Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
- Слайд 4
- 4 А В С D Свойства параллелограмма 1 В параллелограмме противоположные стороны равны и противоположные углы равны. ∠ A = ∠ C, ∠B = ∠D ВС = AD , АВ = С D
- Слайд 5
- 5 А В С D Свойства параллелограмма 2 Диагонали параллелограмма делятся точкой пересечения пополам. О ВО = О D , АО = ОС О – точка пересечения диагоналей
- Слайд 6
- 6 А В С D Свойства параллелограмма 3 В параллелограмме сумма углов, прилежащих к одной стороне, равна 180 °. ∠А + ∠ D = 180 ° , ∠ D + ∠ C = 180 ° , ∠А + ∠ B = 180 ° , ∠В + ∠ C = 180 ° ,
- Слайд 7
- 7 А В С D Признаки параллелограмма 1 Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм. Дано: Доказать: АВС D – четырехугольник, АВ = CD, АВ ∥ CD АВС D – параллелограмм
- Слайд 8
8 А В С D 1 Доказательство Пусть АВ = С D и АВ ∥ С D , проведем диагональ АС.
Рассмотрим треугольники ∆ А BC и ∆ ACD : ∆ А BC = ∆ ACD – по двум сторонам и углу между ними (АС – общая, АВ = С D – по условию, ∠1 = ∠ 2 как накрест лежащие при АВ ∥ С D и секущей АС. Поэтому ∠3 = ∠ 4 .
1 2 3 4 Но ∠3 и ∠ 4 – накрест лежащие углы при пересечении прямых ВС и AD секущей – АС. Следовательно ВС∥ AD. Таким образом, если в четырехугольнике противоположные стороны параллельны, то этот четырехугольник АВС D — параллелограмм.
- Слайд 9
- 9 А В С D Признаки параллелограмма 2 Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм. Дано: Доказать: АВС D – четырехугольник, АВ = CD, ВС = А D АВС D – параллелограмм
- Слайд 10
10 А В С D 2 АВС D — четырехугольник, АВ = CD, ВС = А D . Доказательство Рассмотрим треугольники ∆ А BC и ∆ ACD : ∆ А BC = ∆ ACD – по трем сторонам (АС – общая, АВ = С D , ВС = А D – по условию).
1 4 3 2 Поэтому ∠1 = ∠ 2 как накрест лежащие при секущей АС. Отсюда следует, что АВ ∥ С D . Проведем диагональ АС.
Так как АВ ∥ С D и АВ = С D , то по признаку 1 четырехугольник АВС D – параллелограмм (если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм).
- Слайд 11
- 11 А В С D 3 О Признаки параллелограмма Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм. Дано: Доказать: АВС D – четырехугольник, ВО = О D, АО = ОС АВС D – параллелограмм
- Слайд 12
12 А В С D 3 О АВС D – четырехугольник, ВО = О D, АО = ОС. Доказательство 1 2 3 4 Проведем диагонали АС и BD.
Рассмотрим треугольники ∆ АО B и ∆ C О D : ∆ АО B = ∆ C О D – по первому признаку равенства треугольников (ВО = О D, АО = ОС – по условию, ∠ АО B = ∠ C О D – как вертикаль.) Поэтому АВ = CD и ∠1 = ∠2. Из ∠1 = ∠2 следует, что АВ ∥ CD .
Так как в четырехугольнике АВС D стороны АВ = CD и АВ ∥ CD , то по 1 признаку четырехугольник АВС D – параллелограмм (если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм).
Слайд 13
13 Дано : Доказать : 1 АВС D – четырехугольник, ∠ B А C = ∠ ACD, ∠CAD =∠BCA АВС D – параллелограмм. Доказательство Рассмотрим треугольники ∆ А BC и ∆ ACD : 1.
∠ B А C = ∠ ACD, ∠CAD =∠BCA – по условию, АС – общая; следовательно ∆ А BC = ∆ ACD – по стороне и двум прилежащим углам; поэтому ВС = AD. А В С D 2 .Так как ∠ B А C = ∠ ACD – накрест лежащие углы при параллельных прямых ВС, AD и секущей — АС, то ВС ∥ AD . 3.
Так как ВС = AD и ВС ∥ AD , то по 1-му признаку параллелограмма АВС D – параллелограмм, что и требовалось доказать. Задача
Слайд 14
14 Ответить на вопросы: Спасибо за внимание! Какая фигура называется параллелограммом? Докажите, что в параллелограмме противоположные стороны и углы равны. Докажите, что в параллелограмме диагонали точкой пересечения делятся пополам. Сформулируйте и докажите признаки параллелограмма.
Источник: https://nsportal.ru/shkola/geometriya/library/2017/10/30/parallelogramm-svoystva-i-priznaki
