Таблица сложения чисел, формулы и примеры

Сложение является одним из часто выполняемых математических действий. Результат сложения часто представляют в таблице сложения. Ниже представлен один из способов ее оформления.

Таблица сложения до 10 для распечатывания

Для скачивания можно нажать на правую кнопку мышки над картинкой и выбрать «сохранить как».

Или скачать файлы ниже.

В первом столбце и в первой строке записаны слагаемые, в ячейках на пересечении соответствующих столбцов и строк записаны результаты.
Например, если первое слагаемое равно 4, а второе равно 3, то сумма будер равна 7:

Другие варианты, в том числе до 20, таблицу в другом цветовом оформлении можно найти и скачать для распечатывания в конце статьи. Кроме таблиц для удобного счета с древних времен используют также и другие способы, они описаны в соответствующем разделе, в этой же статье речь пойдет прежде всего о таблицах.

Прежде чем приступать к описанию этой темы, следует определиться с основными понятиями.

Например, что значит запись «4 + 5 = 9», и как это отразить в таблице сложения. В большинстве современных книг по математике приняты определенные названия для каждого из этих чисел. Мы будем применять на этой странице наиболее распространенные на сегодняшний день.

Согласно общепринятой терминологии, в вышеприведенном примере 4 и 5 – это слагаемые, 9 – сумма. Сложение также иногда называют прибавлением и суммированием, нахождением суммы. Также в математике есть термин «операция сложения».

Слагаемые иногда называют суммируемыми, а результат — результатом сложения или результатом суммирования.

Часто начинают изучение со сложения простых чисел. Первым этапом является сложение чисел до 10, далее от 10 до 20.

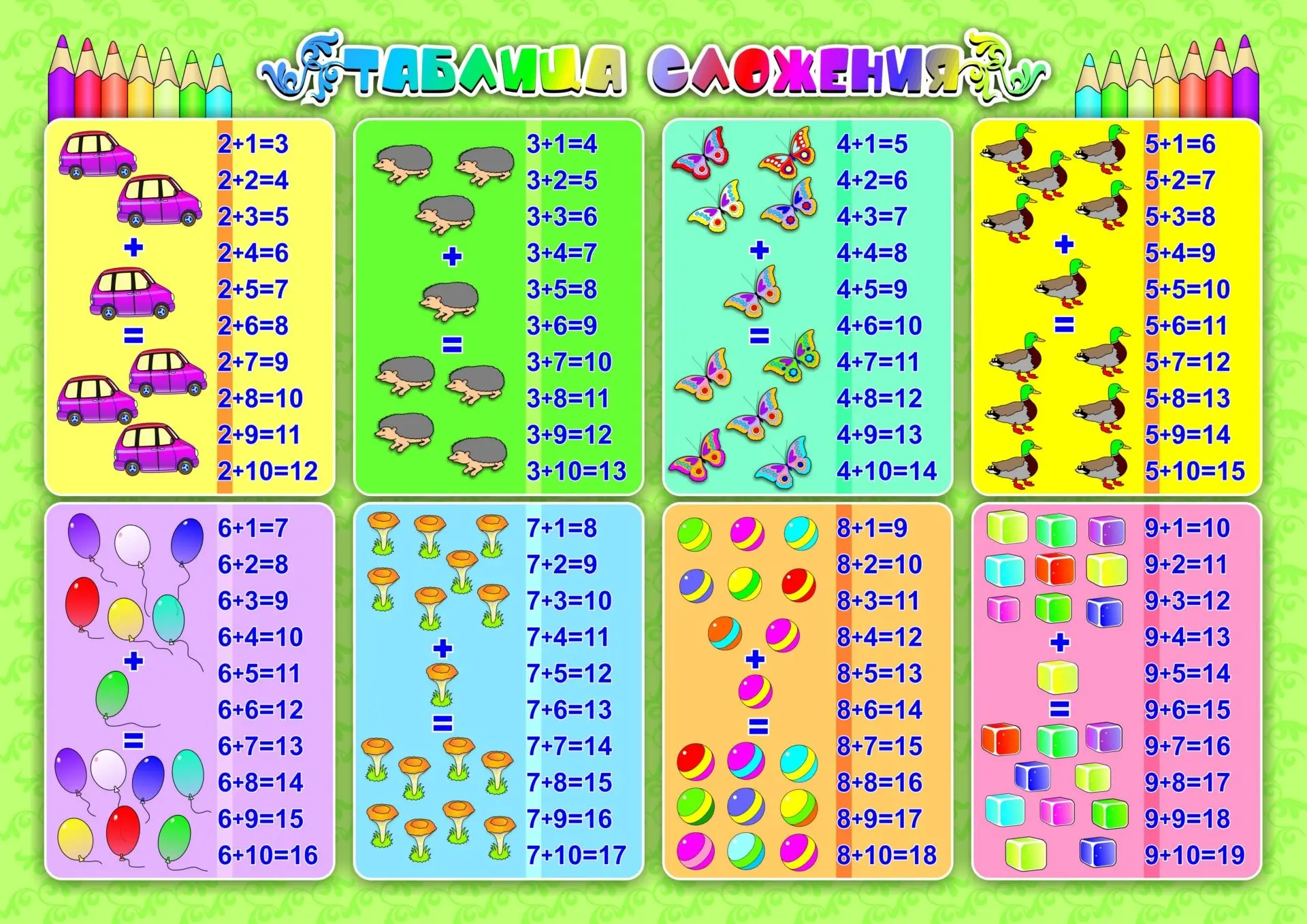
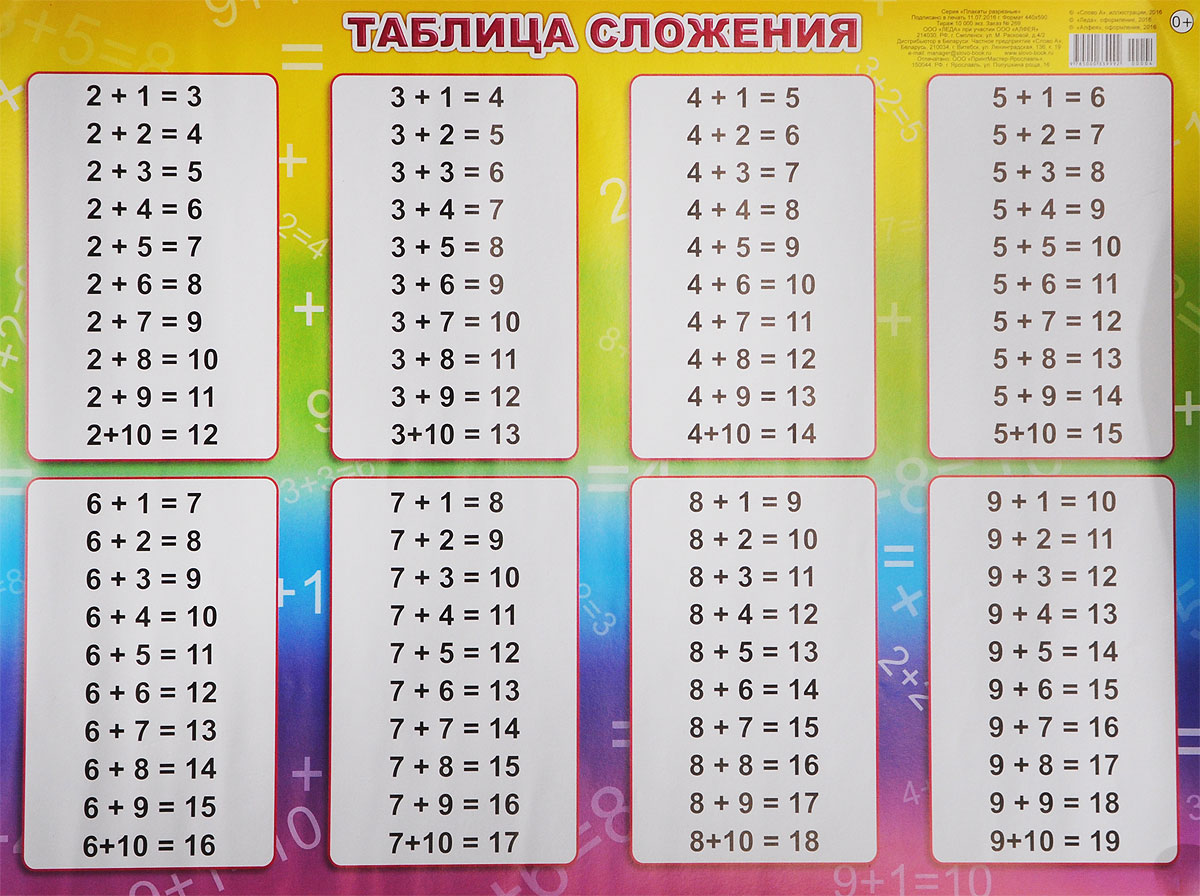
Первый – это, собственно говоря, не совсем таблица, а скорее сгруппированные простые равенства.

Таблица сложения равенства.

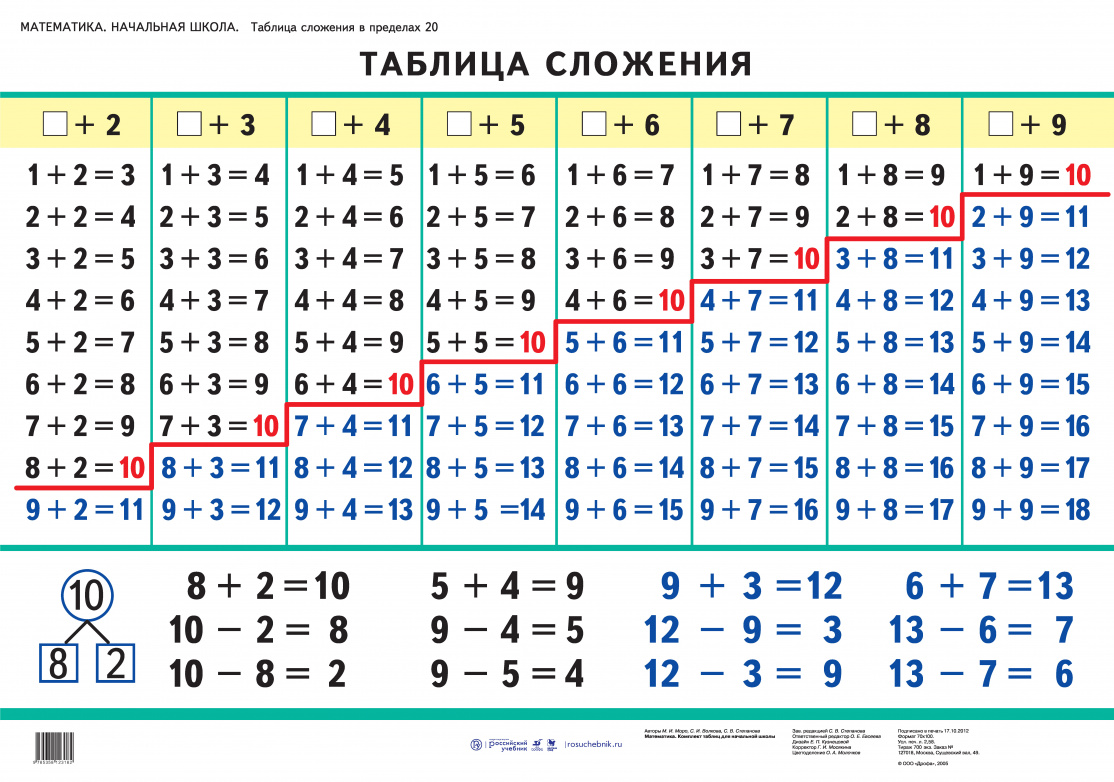
Расширенный вариант обычно представляют в следующем виде.

Таблица сложения до 20

Отсюда вытекает одно из свойств, справедливых для суммы чисел. Звучит оно так: «От перестановки мест слагаемых сумма не меняется». Это свойство справедливо и для большего количества слагаемых. Разберемся в вопросе о том, можно ли данной таблицей пользоваться в случае сложения нескольких слагаемых. Ответ: можно, но до определенных значений. В этом случае действия нужно производить постепенно. Сначала складываем первые два слагаемых, получаем некое число. Если это простое число, которое входит в таблицу, то мы находим его и к нему прибавляем оставшееся и так далее. То есть, ориентируемся на наличие значений в таблице. Например, 4+5+6. Начала находим результат для действия 4 + 5, в ячейке на пересечении их столбца и строки находится 9. Далее выполняем действие 9+6. Находим в таблице 9 и 6. Далее все аналогично. Для больших чисел обычно таблицы не составляются. Таблица вычитания. Этой же таблицей можно пользоваться и для операции вычитания. В этом случае производим обратные действия. В самой таблице находим значение, из которого нужно вычесть число. Затем проводим линию до того числа, которое вычитается, остается мысленно дойти до оставшегося значения. Оно и будет искомым. Совсем просто это можно осуществить при помощи линейки. В данном случае линейка подставляется от вычитаемого числа сначала вертикально, затем горизонтально. Или наоборот. Для быстрого устного счета часто запоминают результаты сложения, и со временем уже нет необходимости наличия таблицы перед глазами.

Для ознакомления также ниже представлены более старые варинты таблицы.
 

Таблицы сложения значительно упрощают повседневный счет, поэтому много лет назад люди начали их использовать и некоторые из них мы можем видеть в сохранившихся книгах. Например, так выглядела таблица сложения в книге «Арифметика» Магницкого Л. Ф. 1703 года издания.

(на картинке как раз фотография тоже сканированной версии переиздания 1914 года).

Источник: https://tablica-umnozheniya.ru/tablica-slozheniya

Арифметические операции в позиционных системах счисления — урок. Информатика, 10 класс

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам.

Правила выполнения арифметических операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление уголком. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.

Таблицы сложения в любой позиционной системе счисления легко составить, используя правило счета:

Если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд.

https://www.youtube.com/watch?v=Os22o9h3BXA

Таблица сложения в двоичной системе:

Таблица сложения в восьмеричной системе:

Пример:

1) Сложим числа (15) и (6) в различных системах счисления.

Решение. Переведем числа (15) и (6 )в двоичную и восьмеричную системы счисления и выполним сложение, используя таблицы сложения (см. выше).

Ответ: 15+6=2110=101012=258

2) Вычислим сумму чисел 438 и 5616. Результат представим в восьмеричной системе счисления.

Решение: переведем число 5616  в восьмеричную систему счисления, используя поразрядный способ перевода разложением на тэтрады и триады:

Пользуясь правилами сложения в восьмеричной системе счисления, получаем:

Ответ: 438 + 5616 = 1718

Вычитание осуществляется по тем же правилам, что и в десятичной системе счисления.

При вычитании из меньшего числа большего производится заем из старшего разряда.

Пример:

Вычислим разность (X — Y) двоичных чисел, если (X =)10101002 и (Y =)10000102. Результат представим в двоичном виде.

Решение:

Ответ: 100102

Замечание. Если вам трудно складывать или вычитать в системах счисления, отличных от десятичной, можете перевести числа в десятичную систему счисления, выполнить арифметические действия, а затем результат перевести в требуемую в ответе систему счисления.

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Таблица умножения в двоичной системе:

Таблица умножения в восьмеричной системе:

Умножение многоразрядных чисел в различных позиционных системах счисления происходит по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.

Пример:

Перемножим числа (15) и (12).

Ответ: 15⋅12=18010=101101002=2648

Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. Следует только грамотно пользоваться теми цифрами, которые входят в алфавит используемой системы счисления.

Обрати внимание!

При выполнении любых арифметических операций над числами, представленными в разных системах счисления, следует предварительно перевести их в одну и ту же систему.

Источники:

Угринович Н. Д. Информатика и ИКТ. Профильный уровень : учебник для 10 класса / Н. Д. Угринович. — 3-е изд. испр. — М. : БИНОМ. Лаборатория знаний, 2008, стр. 140-142

Самылкина Н. Н. Информатика : все темы для подготовки к ЕГЭ. (В помощь старшекласснику). М. : Эксмо, 2011, стр. 33-36

Источник: https://www.yaklass.ru/p/informatika/10-klass/informatciia-i-informatcionnye-protcessy-11955/predstavlenie-chislovoi-informatcii-v-kompiutere-11901/re-47e97f24-6602-46d5-a9e4-e07fc025ae49

Таблица сложения до 20: скачать и распечатать — 3mu.ru

С первого класса от детей требуют научится складывать до 20-ти. Предлагаем скачать таблицу сложения, которую можно распечатать и использовать в обучении.

Скачать таблицу сложения от 1 до 10

Таблица представляет из себя 10 столбиков, в которых содержатся решения складываемых чисел от 1 до 10, с максимальным решением в 20. Если необходимо что-либо исправить в таблице, скачайте DOC, для распечатки без изменений, можно скачать бесплатно PDF версию таблицы.

Скачать карточки сложения на 1 и 2

Распечатав данный лист на формате А4, разрежьте карточки, отделив ответ от примера сложения.

Скачать карточки сложения на 3 и 4

Скачать карточки сложения на 5 и 6

Скачать карточки сложения на 7 и 8

Скачать карточки сложения на 9 и 10

Источник: http://3mu.ru/?p=2907

Как написать формулу в Excel

Редактор таблиц Microsoft Excel имеет очень широкий набор возможностей для решения задач самой разной сложности в различных сферах деятельности. Именно благодаря этому Эксель стал таким популярным среди пользователей по всему миру.

Одним из базовых навыков работы с программой является проведение простейших вычислений и математических операций. В этой статье подробно разберём, как выполнять сложение, вычитание, умножение и деление в Excel.

Давайте же начнём! Поехали!

Математические операции выполняются без использования калькулятора

Все расчёты в Экселе основаны на построении простых формул, с помощью которых программа и будет производить вычисления. Для начала необходимо создать таблицу со значениями. Обратите внимание на то, что каждая ячейка таблицы имеет свой адрес, который определяется буквой и цифрой. Каждая буква соответствует столбцу, а каждая цифра — строке.

Начнём с самых простых операций — сложения и вычитания. Для сложения чисел можно использовать, так называемую функцию «Автосумма». Ей удобно пользоваться в случаях, когда необходимо посчитать сумму чисел, которые стоят подряд в одной строке, столбце либо в выделенной вами области.

Чтобы воспользоваться этим инструментом, перейдите во вкладку «Формулы». Там вы обнаружите кнопку «Автосумма». Выделив участок таблицы со значениями, которые нужно сложить, кликните по кнопке «Автосумма». После этого появится отдельная ячейка, содержащая результат вычисления.

Это был первый подход.

Второй подход заключается в том, что формула для расчёта вводится вручную. Допустим, перед вами стоит задача вычислить сумму чисел, разбросанных по таблице. Для этого сделайте активной (кликните по ней левой кнопкой мыши) ячейку, в которую желаете поместить результат вычисления.

Затем поставьте знак «=» и по очереди вводите адрес каждой ячейки, содержимое которой нужно просуммировать, не забывая ставить знак «+» между ними. К примеру, у вас должно получиться: «=A1+B7+C2+B3+E5». После того как будет введён адрес последней ячейки, нажмите на клавиатуре «Enter» и вы получите сумму всех отмеченных чисел. Необязательно вводить каждый адрес вручную.

Достаточно кликнуть по определённой ячейке и в поле для формул сразу отобразится её адрес, ставьте после него «+» и переходите к следующей.

Существует ещё один подход — использование функции «Специальная вставка». Этот способ удобен тем, что позволяет суммировать данные из нескольких отдельных таблиц, при условии, что все их графы одинаковые. Для начала создайте сводную таблицу, в которую вы будете вставлять скопированные данные.

Выделите числа одной таблицы и вставьте их в сводную, далее поступите так же со значениями второй таблицы, только в этот раз кликните по ячейке правой кнопкой мыши и выберите пункт «Специальная вставка». В открывшемся окне в разделе «Вставить» отметьте «Значения», а в разделе «Операция» выберите сложить.

В результате все данные просуммируются.

Вычитание в Excel выполняется таким же способом, как и сложение. Вам понадобится ввести формулу, указав необходимые ячейки, только вместо знака «+» между адресами ставится «–».

Чтобы умножить числа в Экселе, напишите формулу, отмечая нужные данные и ставя между ними знак «*». Формула будет иметь следующий вид: «=A3*A7*B2».

Деление производится аналогичным образом, только используется знак «/». Также вы можете выполнять несколько арифметический операций сразу. Формулы строятся по математическим правилам. Например: «=(B2-B4)*E8/(A1+D1)*D4». Построенная вами формула может быть любой сложности, главное, не забывать основные математические правила, чтобы расчёт был выполнен верно.

Владея навыками простых арифметических вычислений в программе Microsoft Excel, вы уже сможете упростить себе процесс решения некоторых задач и сэкономить время. Эксель позволяет решать сложные уравнения, выполнять инженерный и статистический анализ.

Постепенно овладевая базовыми функциями и инструментами программы, вы научитесь выполнять всё больше операций в редакторе Excel.

Пишите в х помогла ли вам статья разобраться с возникшими вопросами и делитесь своим опытом с другими пользователями.

Источник: https://nastroyvse.ru/programs/review/prostye-raschyoty-excel.html

Табличное сложение

Прежде чем познакомиться с таблицами сложения чисел, мы рассмотрим случаи сложения разных видов.

Например, 7 + 6 = ?

Мы видим, что сумма будет больше 10, потому что 10 — это 7 и 3. Мы будем прибавлять число 6 по частям.

• Сначала прибавляем столько, чтобы полу­чить 10:   7 + 3 = 10.
• Дальше мы вспоминаем, что 6 — это 3 и 3.
• Число 3 мы уже прибавили, значит, надо прибавить ещё 3:  10 + 3 = 13.
• Тогда наш пример 7 + 6 можно записать по-другому: 

или так:

Значит, 7 + 6 = 13

Рассуждая так, можно решить любой пример на сложение в пределах 20.

Случаи табличного сложения

1. 11 — это 1 и 10
2. 11 — это 2 и 9
3. 11 — это 3 и 8
4. 11 — это 4 и 7
5. 11 — это 5 и 6
6. 12 — это 2 и 10
7. 12 — это 3 и 9
8. 12 — это 4 и 8
9. 12 — это 5 и 7
10. 12 — это 6 и 6
11. 13 — это 3 и 10
12. 13 — это 4 и 9
13. 13 — это 5 и 8
14. 13 — это 6 и 7
15. 14 — это 4 и 10
16. 14 — это 5 и 9
17. 14 — это 6 и 8
18. 14 — это 7 и 7
19. 15 — это 5 и 10
20. 15 — это 6 и 9
21. 15 — это 7 и 8
22. 16 — это 6 и 10
23. 16 — это 7 и 9
24. 16 — это 8 и 8
25. 17 — это 7 и 10
26. 17 — это 8 и 9
27. 18 — это 8 и 10
28. 18 — это 9 и 9
29. 19 — это 9 и 10

Таблицы сложения

Таблица сложения нужна, чтобы научиться быстрому сложению чисел.

Существует несколько таблиц сложения чисел. Одна из первых таблиц такого рода — таблица сложения в пределах 10, но если ты хорошо знаешь состав чисел, тебе она не понадобится.

Как пользоваться такой таблицей?

Например, тебе нужно узнать, сколько будет 4 + 5.

Есть очень простая таблица сложения чисел с переходом через десяток. Вот она.

Пользоваться ею, конечно, очень легко.

Но наиболее полная таблица сложения чисел в от 1 до 20 представлена ниже.

Как ею пользоваться? Очень просто.

Например, тебе нужно к 7 + 6:

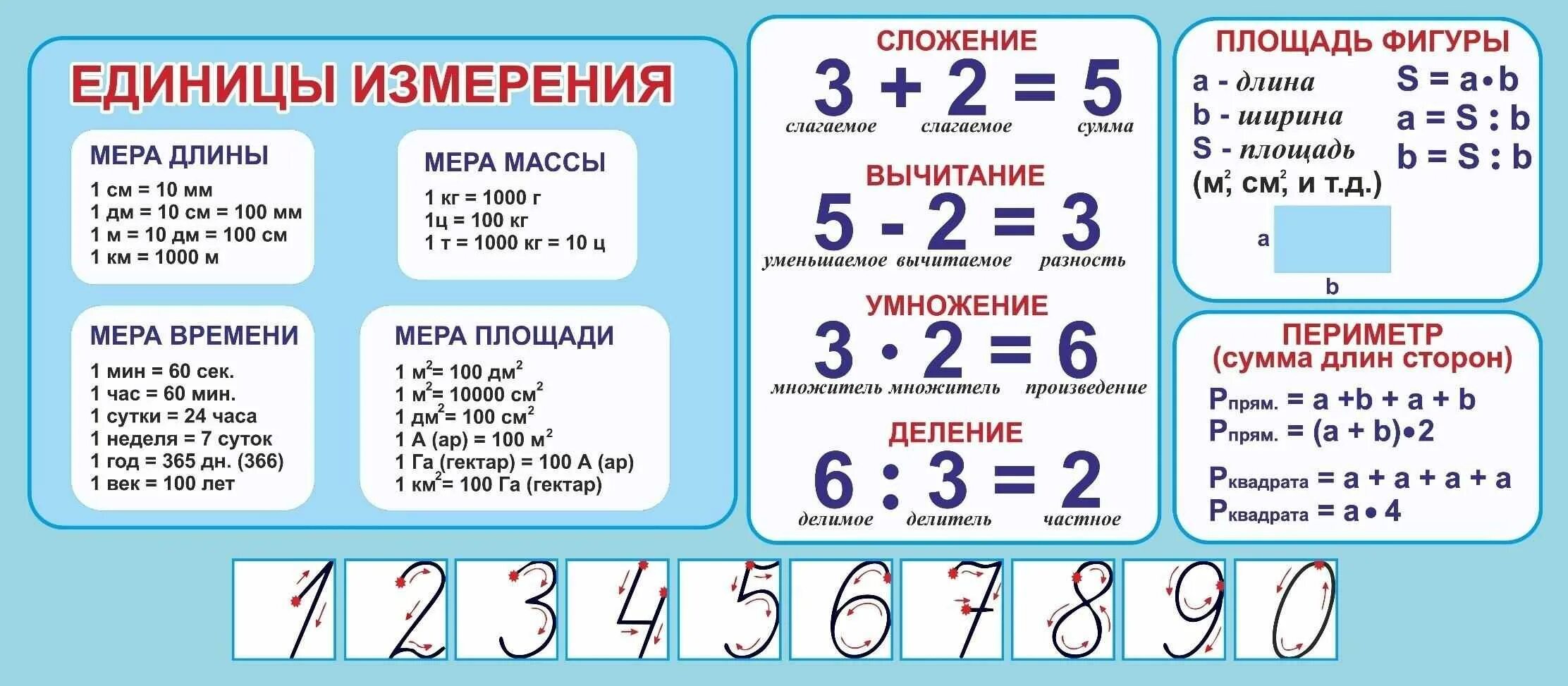
А это сводная таблица, которой можно прользоваться, пока не заучишь её наизусть.

А такими таблицами можно пользоваться при заучивании результатов сложения наизусть.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Письменное сложение в столбик

Сложение

Правило встречается в следующих упражнениях:

1 класс

Страница 42. Вариант 1. № 1, Волкова, Проверочные работы

Страница 50. Вариант 1. № 2, Волкова, Проверочные работы

1. Страница 76, Моро, Волкова, Степанова, Учебник, 2 часть
2. Страница 77, Моро, Волкова, Степанова, Учебник, 2 часть
3. Страница 85, Моро, Волкова, Степанова, Учебник, 2 часть
4. Страница 104, Моро, Волкова, Степанова, Учебник, 2 часть
5. Страница 12, Моро, Волкова, Рабочая тетрадь, 2 часть
6. Страница 38, Моро, Волкова, Рабочая тетрадь, 2 часть
7. Страница 40, Моро, Волкова, Рабочая тетрадь, 2 часть
8. Страница 44, Моро, Волкова, Рабочая тетрадь, 2 часть
9. 2 класс
10. Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
11. Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
12. Задание 2, Моро, Волкова, Рабочая тетрадь, 1 часть
13. Задание 52, Моро, Волкова, Рабочая тетрадь, 1 часть
14. Задание 132, Моро, Волкова, Рабочая тетрадь, 1 часть
15. Задание 144, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 6. Вариант 1. № 2, Моро, Волкова, Проверочные работы

• Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
• Страница 98, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
• Страница 48, Моро, Волкова, Рабочая тетрадь, 2 часть
• 3 класс
• Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
• Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
• Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
• Страница 31, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
• Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
• Страница 6, Моро, Волкова, Рабочая тетрадь, 1 часть
• Страница 11, Моро, Волкова, Рабочая тетрадь, 1 часть
• Страница 4, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
• Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
• Страница 7, Моро, Волкова, Рабочая тетрадь, 2 часть
• 5 класс
• Упражнение 166, Мерзляк, Полонский, Якир, Учебник

1. © budu5.com, 2020
2. Пользовательское соглашение
3. Copyright
4. Нашли ошибку?
5. Связаться с нами

Источник: https://budu5.com/manual/chapter/1159

Сложение и вычитание отрицательных и положительных чисел — правило, формулы и примеры

Впервые знакомство с отрицательными числами происходит в школьном курсе в 6 классе, иногда раньше. Число со знаком «+» называется положительным, противоположное — отрицательным.

Чтобы понять, что такое сложение и вычитание положительных и отрицательных чисел, достаточно воспользоваться координатной прямой. Например, сумма чисел -18 и 2. Сначала отмечаем на координатном отрезке число (-18), откладываем от него вправо, соответствующие масштабу, 2 единичных отрезка, и получаем на координатном луче число -16.

Правило сложения отрицательных чисел и чисел с разными знаками

Для суммирования двух отрицательных чисел, необходимо:

• суммировать их модули;
• перед полученной суммой поставить знак «минус».

• Например, сложение чисел -9 и -6 будет выглядеть следующим образом:
• -9 + (-6) = -15
• В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«. 

1. Сложение рациональных или дробных чисел выполняется аналогичным способом:
2. -26,35 + (-25,35) = -(26,35 + 25,35) = -51,75

К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».

Для суммирования натуральных чисел со знаками «+» и «-», надо:

• из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;
• перед полученным результатом поставить знак того слагаемого, которое имело большее значение.

• Пример:
• 61,2 + (-31,5) = + (61,2 — 31,5) = 30,5
• Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:
• -81 + 35 = -(81 — 35) = 46
• Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.

Как вычитать отрицательные и положительные числа

1. Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.
2. Наглядно данное действие лучше представить в виде формулы:
3. a — b = a + (-b)
4. То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.

• Примеры:
• -20 — 14 = -20 + (-14) = -34;
• -6,1 + 5,6 = 5,6 + (-6,3) = 0,5.

Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.

Примеры:

• 15 — 6 = 15 + (-6) = 9 — уменьшаемое 15, больше вычитаемого, поэтому ответ положительный;
•  -15 — 6 = -15 + (-6) = -21 — уменьшаемое -15, меньше вычитаемого, следовательно, ответ отрицательный. 

1. Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».
2. Пример:
3. 10 — (-5) = 10 + 5 = 15;
4. — 10 — (-5) = -10 + 5 = 5 — 10 = -5.

Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».

Например, чтобы задать число -81,73, надо в следующем порядке нажать кнопки: «8», «1», «,», «7». «3», «+/-». А решать пример с отрицательными числами следует в том же порядке, что и с положительными. 

Заключение

Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма. 

Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.

Источник: https://nauka.club/matematika/slozhenie-i-vychitanie-polozhitelnykh-i-otritsatelnykh-chisel.html

Самый быстрый технологический приём запоминания таблицы сложения или состава чисел

Здравствуйте, сегодня расскажу о самом удобном, быстром способе запоминания состава чисел, либо таблицы сложения и вычитания (как в пределах 10, так и в пределах 20)

В предыдущих статьях я рассказывала о самых продуктивных играх по математике для 1 класса.

Игры играми, а когда приходит время и просто необходимо уже знать таблицу сложения вашему ребёнку, тогда и помогут вам тренировки с СОРБОНКАМИ.

Так вы и не знаете, КАКИЕ ИМЕННО ВАРИАНТЫ ПРИМЕРОВ ОН НЕ ВЫУЧИЛ. И у ребенка стресс- он никак не может это выучить! Неправда!. Что-то же он знает! Вот это «что-то» и надо найти, похвалить и учить не всё подряд снова, а только то, что не знает. Вот таким «методом исключения» и тренируем ребенка с помощью сорбонок.

Ещё чем хороши сорбонки?? Примеры всегда перед глазами, ответы тоже, в процессе игры- ребенок всё выучит.

В этом приёме содержится мониторинг с корректировкой результатов.

Сорбонки — это небольшие карточки из плотной бумаги, на одной стороне записан вопрос (слово), а на другой ответ(картинка, перевод). Сорбонки- от названия Парижского университета Сорбон. Может использоваться на любых уроках. В начальных классах очень удобно применять в математике и при изучении иностранных слов.

Подписывайтесь на канал, вас ждт ещё много интересного, ставьте «ВО!», если статья понравилась, комментируйте, спрашивайте, отвечу!м. На длинной стороне пишем пример и знак =, на короткой -ответ. Либо просто два числа на длинной стороне как состав числа, которое написано справа . Заворачиваем ответы вниз.

Играем-тренируемся. Складываем стопкой примеры. Показываем их по очереди. Если ребёнок ответил правильно, показываем ответ и откладываем в одну сторону сорбонку, если неправильно, разворачиваем ответ и откладываем в другую сторону.

Считаем, сколько примеров ребенок знает. Хвалим до небес. А те, что не знает, надо выучить.

Учим тут же. Теперь берем ТОЛЬКО те сорбонки, которые ребёнок только что учил. Опять играем точно так же.

Осталось меньше примеров, которые никак не запоминаются? Ура! Берём только их для заучивания. Заучиваем, разворачивая сорбонки. И так играем до тех пор, пока не останется ни одной сорбонки, которые ребёнок не знает. Выучили? УРА! Играем и завтра, уже веселее !.

А в дальнейшем играем просто, чтобы показать знания ребёнка. Для удовольствия. Можно играть в классе на перемене с друзьями.

Подписывайтесь на канал, вас ждёт ещё много интересного, ставьте «ВО!», если статья понравилась, комментируйте, спрашивайте, отвечу!

Источник: https://zen.yandex.ru/media/id/5d69c96b1d656a00ad00be79/5d84f6c2c31e4900aef07d76

Составляем таблицу сложения

Середина урока

Предложите учащимся разделиться на группы и продолжить работу. Каждой группе следует дать задание составить фрагмент таблицы сложения. Для этого первоклассникам необходимо раздать разли­нованные листы бумаги формата А4. На листе дети запишут по 1 столбцу примеров из таблицы сложе­ния. Всего 9 столбцов.

Распределите задание в зависимости от количе­ства созданных групп. Дифференцируйте задание с учетом уровня подготовки школьников. Например, в классе может быть образовано 9 групп по 3 человека, тогда каждой группе будет поручено составить свой столбец таблицы сложения. Если ко­личество групп учащихся 3 или 4, то группам можно дать задание составить по 2—3 столбца.

После создания таблицы сложения объедините все листы в единый справочник и разместите его на вид­ном месте. Поблагодарите подопечных за проделанную работу и сообщите, что они могут пользоваться данным справочником, который создали все вместе, пока не запомнят значения примеров на сложение однозначных чисел в пределах 10.

Исследуй таблицу сложения. Предложите перво­классникам рассмотреть, из каких столбцов состоит таблица сложения. Назовите основной принцип рас­пределения столбцов в зависимости от второго сла­гаемого при сложении.

Ответ

• Число 2.
• Число 10.
• 8 примеров имеют ответ 9:

• + 1; 7 + 2; 6 + 3; 5 + 4; 4 + 5; 3 + 6; 2 + 7; 1 + 8.

Подумай. Выполните задание со всем классом. Предложите детям найти в таблице сложения при­меры, результатом которых станет число 10.

Ответы

9 + 1; 8 + 2; 7 + 3; 6 + 4; 5 + 5; 6 + 4; 7 + 3; 2 + 8; 1 + 9.

Реши. Организуйте работу в парах. Предложите учащимся назвать компоненты сложения и решить примеры, используя таблицу сложения. Распредели­те ребят таким образом, чтобы они могли оказывать друг другу содействие. Предложите им фиксиро­вать ответы к примерам на ламинированных листах, которые можно показывать одноклассникам при вза­имопроверке.

Задание содержит примеры, демонстрирующие переместительный закон сложения. Основные выво­ды по применению данного свойства будут сдела­ны позже в этом разделе. Пока следует отмечать их в виде наблюдения за взаимодействием чисел.

Учебник:

Составляем таблицу сложения, с. 76—77.

Рабочая тетрадь:

Рабочий лист 73 «Применяй таблицу сложения», с. 75.

Рабочий лист 74 «Решай по таблице сложения», с. 76.

Ресурсы:

• маркеры;
• листы ламинированной бумаги формата А4 для работы в группах и для каждого человека;
• демонстрационная таблица сложения.

Источник: https://kopilkaurokov.ru/matematika/uroki/sostavliaiem_tablitsu_slozhieniia