Данная тема посвящена механическим волнам и их основным характеристикам.
Ранее говорилось о колебаниях и колебательных системах. Колебательная система — это физическая система, в которой при отклонении от положения равновесия возникают и существуют колебания.
Реальные колебательные системы практически всегда расположены в какой-либо среде. Поэтому колебательная система может отдавать энергию частицам среды, непосредственно прилегающим к ней, вызывая их вынужденные колебания. Например, движение качелей происходит в воздухе, и, стоя возле них, можно ощущать движение воздуха.
Между молекулами вещества существуют силы взаимодействия, которые определяют его упругие свойства.

Если какие-то частицы в упругой среде выводятся из положения равновесия, то силы взаимодействия со стороны соседних частиц препятствуют этому и одновременно сами смещают соседние частицы. Вследствие взаимодействия между частицами колебательное движение передается от одной частицы к другой, и колебательный процесс распространяется в среде.

Процесс распространения колебаний в упругой среде, называется механической волной.
А тела, которые вызывают распространяющиеся в среде упругие механические волны, называются источниками волн или вибраторами.
В качестве модели возникновения и распространения механической волны можно рассмотреть движение двух поплавков на поверхности воды. Погрузим один из них в воду так, чтобы поплавок начал колебаться вверх-вниз.
Вместе с поплавком смещаются соприкасающиеся с ним частицы воды, которые вовлекают в движение ближайшие к ним другие частицы, и от поплавка по всем направлениям распространяются волны.
Эти волны вовлекают в колебательное движение второй поплавок, и от него появляются такие же волны.

Обратите внимание на то, что оба поплавка только колеблются возле положения равновесия, а волны распространяются от них во всех направлениях.
Рассмотрим модель еще более простой механической волны, которая распространяется только в одном направлении. Для этого возьмем резиновый шнур с нанизанными на него бусинами, один конец закрепим, а второй конец будем периодически двигать вверх-вниз возле положения равновесия

В качестве источника колебаний выступает рука, и пусть ее колебания, а, следовательно, колебания ближайшей от нее бусины, происходят вдоль оси Oy по закону синуса.

В записанном уравнении A — это амплитуда колебания бусины, которая подвержена нашим воздействиям, аргумент синуса — это фаза колебания, а T — период колебаний.
На рисунке видны положения бусин на шнуре через определенную часть периода колебаний.

- Из рисунка видно, что при распространении волны, во-первых, смещение каждой точки шнура от положения равновесия происходит с течением времени периодически; а во-вторых, смещения всех точек шнура в каждый момент времени периодически изменяются от точки к точке, то есть являются периодической функцией координат.
- Иногда говорят, что при распространении волны происходит перемещение фазы колебания от точки к точке с определенной скоростью.
- Фазовой скоростью называется скорость распространения какой-либо фазы от одной точки среды к другой.
- Геометрическое место точек среды, колеблющихся в одинаковых фазах, образуют волновую поверхность.

- А волновая поверхность, отделяющая колеблющиеся частицы среды от частиц, которые еще не начали колебаться, называют фронтом волны.
- В зависимости от формы фронта волны, различают волны плоские, сферические и так далее.
- В плоской волне волновые поверхности представляют собой плоскости, перпендикулярные к направлению распространения волны.
А в сферической волне волновые поверхности представляют собой концентрические сферы. Такая волна распространяется с одинаковой скоростью по всем направлениям.

Распространение колебательного движения в среде с определенной скоростью называется бегущей волной.
Рассмотрим ее более подробно. Пусть волна вдоль шнура распространилась до точки с координатой х. Бусина в этой точке имеет такую же фазу колебаний, как и первая, но в более поздний момент времени распространения волны, то есть отстает во времени на x/v.

Следовательно, уравнение колебаний бусины вдоль оси Oy около положения ее равновесия, имеющего координату x, будет повторять уравнение колебаний первой бусины, но с соответствующим отставанием по фазе.

Это уравнение называют уравнением плоской бегущей монохроматической волны, при этом полагают, что затуханием волны в процессе ее распространения можно пренебречь.
Важно понимать, что при распространении бегущей механической волны частицы среды не перемещаются вместе с волной, а только совершают колебания около своих положений устойчивого равновесия. Поэтому бегущая волна не переносит вещество, а переносит энергию колебательного движения.
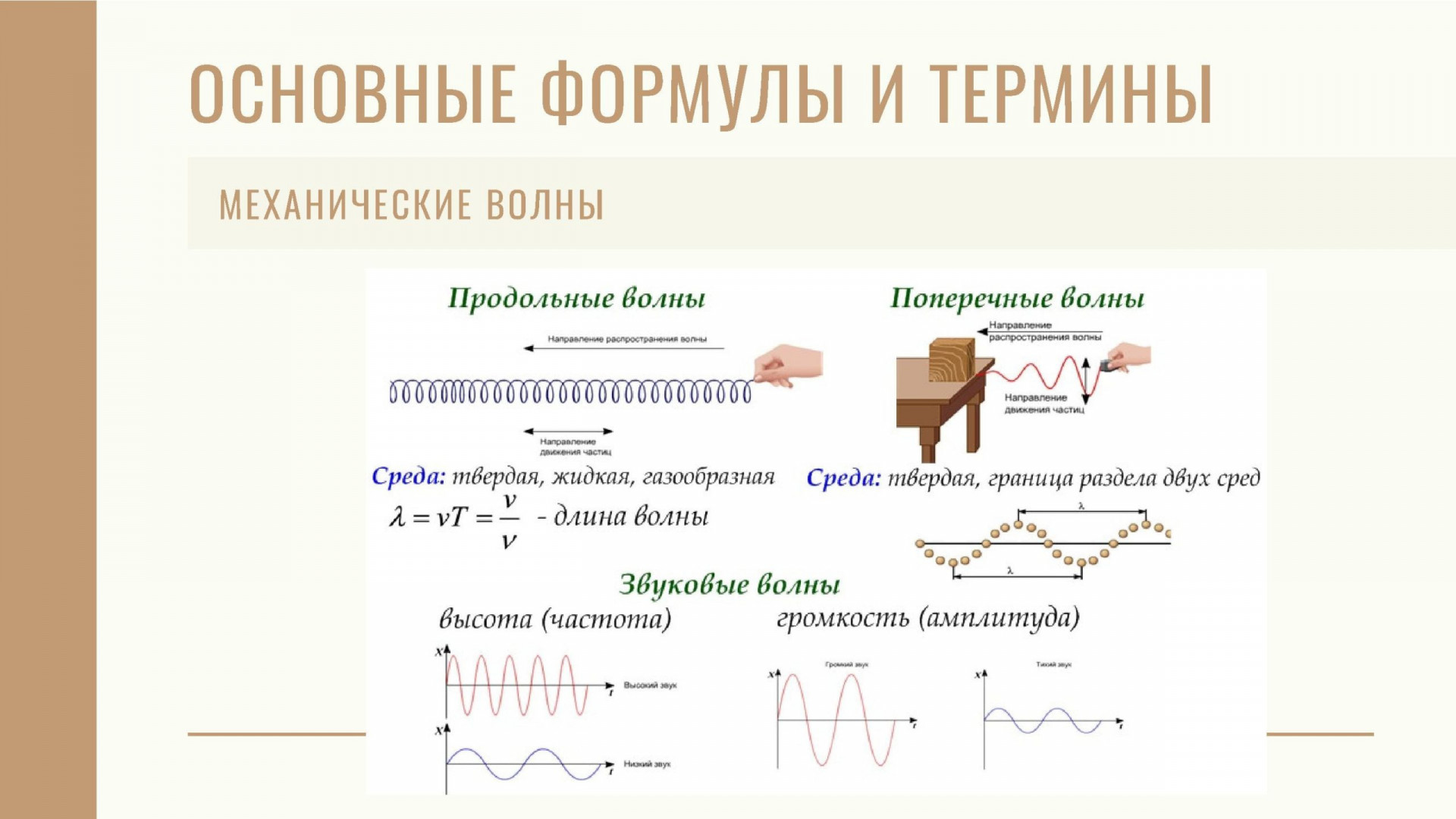
В зависимости от направления колебаний частиц среды относительно направления распространения волны, различают поперечные и продольные волны.
Поперечной волной называется распространение колебательного процесса в среде, при котором частицы среды колеблются перпендикулярно направлению распространения волны. Рассмотренный пример колебаний шнура является моделью возникновения и распространения поперечной волны.
Продольной волной называется распространение колебательного процесса в среде, при котором частицы среды колеблются вдоль направления распространения волны. Примером продольных волн может служить распространение колебательного процесса вдоль ряда шариков, которые скреплены друг с другом одинаковыми пружинками.
Вид волны зависит от вида деформации среды. Продольные волны обусловлены деформацией растяжения и сжатия, поперечные — деформацией сдвига.
Поэтому в газах и жидкостях, в которых упругие силы возникают только при сжатии, распространение поперечных волн невозможно.
А продольные волны могут возникать и распространяться в веществе, находящимся в любом состоянии: твердом, жидком и газообразном.
Необходимо отметить, что распространение механических волн определяется передачей энергии колебательного движения от одной частицы к другой. Эта переносимая волной энергия равна сумме кинетических энергий колеблющихся частиц и потенциальной энергии упругой деформации среды.
И так, механическая волна — это процесс распространения колебательного движения в среде от частицы к частице, обусловленный взаимодействием между ними. Следовательно, скорость распространения механических волн в среде должна зависеть от сил взаимодействия между частицами среды.
При рассмотрении механических деформаций говорилось, что силы взаимодействия в веществе зависят от свойств молекул или атомов и расстояний, на которых они находятся. А опыты по изучению механических волн показывают, что скорость их распространения в однородной среде тем больше, чем меньше плотность вещества и чем более упругим оно является.
- Так как различные виды упругой деформации характеризуются количественно отличающимися коэффициентами, то поэтому, например, в твердых телах продольные волны распространяются быстрее, чем поперечные.
- Волне присущи все характеристики, которые соответствуют колебательному движению: амплитуда, период колебания и частота.
- Амплитуда — это максимальное смещение тела от положения равновесия.
- Промежуток времени, в течение которого тело совершает одно полное колебание — это период.
- А число колебаний в единицу времени называется частотой колебаний.
- Также для характеристики волн применяют понятие «длина волны», которое можно ввести двумя способами:
- И так, длиной волны называется расстояние, на которое распространяется колебательный процесс в среде за время, равное периоду колебаний ее частиц;
- Или длина волны — это расстояние между двумя ближайшими точками бегущей волны, которые колеблются в одинаковой фазе.
- В том, что эти два варианта определения длины волны равноправны, легко убедиться, проанализировав развитие волнового процесса, представленного на рисунке.
- Если известны период и скорость распространения волны, то, согласно первому варианту определения, длины волны равна произведению ее скорости и периода.
- Период волны определяется источником колебаний, а скорость обусловлена свойствами среды, поэтому при распространении колебательного процесса из одной среды в другую изменяются и скорость, и длина волны, а вот частота и период не изменяются.
- Также механическим волнам присущи явления интерференции и дифракции, которые являются характерными признаками волновых процессов любой природы.
- Интерференция представляет собой явление увеличения или уменьшения амплитуды результирующей волны в результате сложения двух или нескольких волн с одинаковыми периодами колебаний.
- Для наблюдения интерференционного максимума, то есть увеличения амплитуды, необходимо, чтобы разность хода волн равнялась целому числу длин волн.
- А для наблюдения минимума, разность хода должна равняться нечетному числу длин полуволн.
- При этом необходимым условием интерференции является когерентность двух источников, то есть они должны испускать волны одинаковой частоты с постоянной разностью фаз.
Дифракция представляет собой явление отклонения волн от прямолинейного распространения и огибание ими препятствий. При этом следует помнить, что явление дифракции проявляется только тогда, когда размеры препятствий соизмеримы с длиной волны.
Волны, как и колебания, не могут существовать бесконечно долго. В окружающем мире мы часто наблюдаем возникновение и исчезновение (затухание) волн.
Затуханием волны называется уменьшение ее амплитуды в процессе распространения.
Колебательному движению частиц среды препятствуют силы сопротивления, в результате этого энергия колебательного движения частиц переходит во внутреннюю энергию вещества, и волны затухают.
Основные выводы:
Вспомнили, что называют механической волной. Рассмотрели особенности распространения волн. А также повторили виды волн и их основные характеристики.
Источник: https://videouroki.net/video/42-miekhanichieskiie-volny-i-ikh-osnovnyie-kharaktieristiki.html
Механические волны
- Механические волны
- .
- Выполнила
- учитель физики
Бондаренко Л.П.

- Цель исследования:
- установить с научной точки зрения, что такое звук.
- Задачи исследования :
1. Изучить физическую теорию звука.
2. Исследовать историю изучения людьми звука.
3. Проверить некоторые свойства звука в школьной лаборатории.

Механические волны
- Волна — это колебания, распространяющиеся в пространстве с течением времени.
- Механической волной — называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии колеблющегося тела от одной точки упругой среды к другой.

- Виды волн
- поперечные волны
- продольные волны
- волна называется поперечной , если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волн.
- волна называется продольной , если колебания частиц среды происходят в направлении распространения волны.

- Физические характеристики волны
- длина волны
- это расстояние, на которое распространяется волна за время, равное одному периоду колебаний.
 v=λν=λ/Т [ λ ]=[м]; [ v ]=[м/с ] » width=»640″
v=λν=λ/Т [ λ ]=[м]; [ v ]=[м/с ] » width=»640″
скорость распространения волны
- это скорость, с которой перемещаются в среде волновой фронт (точки волны одинаковой фазы, т.е. горбы или впадины). Фазовая скорость волны зависит от механических свойств среды, в которой волна распространяется.
- Связь между длиной волны λ ,
- фазовой скоростью волны v ,
- частотой ν и периодом Т волны: λ = vT= v / ν = v=λν=λ/Т [ λ ]=[м]; [ v ]=[м/с ]

- Распространение волн в упругих средах
- сферическая волна
- плоская волна
- это волна, фронт которой представляет собой сферическую поверхность с радиусом, совпадающую с направлением распространения волны.
- это волна , у которой направление распространения одинаково во всех точках пространства

Звук
- Мир наполнен самыми разнообразными звуками: тиканьем часов и гулом моторов, шелестом листьев и завыванием ветра, пением птиц и голосами людей.
- С помощью речи люди общаются, с помощью звука люди и животные получают информацию об окружающем мире.
- Звуки – наши неизменные спутники. Они по-разному воздействуют на человека: информируют нас о чем-то, предупреждают, об опасности, радуют и раздражают, успокаивают и пугают своей неожиданностью.
- Из биологии мы знаем, что есть звуки, которые мы, люди, не слышим, однако многие животные и птицы пользуются этими звуками (например, дельфины общаются с помощью этих звуков)

Что такое звук?
- Звук — это распространяющиеся в упругих средах:
газах, жидкостях и твердых телах — механические колебания, воспринимаемые органами слуха.
- Восприимчивость человека к звукам избирательна, поэтому мы говорим о слышимых и неслышимых звуках.
- Ультразвуки и инфразвуки имеют очень важную роль и в живом мире.
- Для того чтобы тело издавало звук (и наше ухо воспринимало звук) тело должно совершать колебания с частотой от 20 до 20.000 Гц

Механизм распространения звука
- Струна музыкального инструмента передает свои колебания окружающим частицам воздуха, эти колебания будут распространяться все дальше и дальше, а достигнув, уха, вызовут колебания барабанной перепонки звук.
- Наличие упругой среды – обязательное условие для возникновения звуковых волн !!!
- В вакууме звук не распространяется !!!
Приемники звуковых волн
Естественный приемник
- у человека – это ухо;
- у рыб — для этой цели приспособлен плавательный пузырь.
Технический приемник — микрофон.
Микрофон преобразует звуковые колебания в электрические .
Тип звуковых волн
- Продольные механические волны большей длины волны называют инфразвуковыми , а волны меньшей длины – ультразвуковыми .
- Излучение звуковых волн сильно зависит от формы колеблющегося тела.
- Яркий пример – камертон.
Характеристики звуковых волн
- Высота тона звуковой волны зависит от частоты колебаний источника звука:
— чем больше частота колебаний, тем выше звук;
— чем меньше частота колебаний, тем звук ниже.
- Громкость звука зависит от амплитуды колебаний источника звука:
- чем больше амплитуда, тем громче звук.
- чем больше амплитуда, тем громче звук.
- Восприятие громкости звука зависит от: высоты тона (высокий звук кажется громче низкого); индивидуальных особенностей слуха; длительности звука
- высоты тона (высокий звук кажется громче низкого);
- индивидуальных особенностей слуха;
- длительности звука
- Эхо
- Эхо — это физическое явление, заключающееся в принятии наблюдателем отражённой от препятствий волны.
- Звуковое эхо — отражённый звук.
- Эхо обусловлено тем, что звуковые волны могут отражаться твердыми поверхностями, это связано с динамической картиной разрежений и уплотнений воздуха вблизи отражающей поверхности.
- Если источник звука находится на достаточном расстоянии от отражающей поверхности, а кроме источника звука поблизости нет никаких дополнительных звуковых источников, то эхо становится наиболее отчетливым.
- Существует два вида эхо:
- Однократное эхо — это волна, отражённая от препятствия и принятая наблюдателем.
- Многократное эхо — это эхо, возникающее при каком-нибудь громком звуке, что порождает не один, а несколько следующих друг за другом звуковых откликов.
В зависимости от рельефа местности, места и ориентации наблюдателя, погодных условий, времени года и суток эхо изменяет свою громкость, тембр, длительность; меняется число его повторений. Кроме того, может измениться и частота звукового отклика; она может оказаться более высокой или, напротив, более низкой по сравнению с частотой исходного звукового сигнала.
Звуковые волны в различных средах
- чаще всего звуковые волны достигают наших ушей по воздуху.
- звук распространяется в воде и твердых телах. (нырнув под воду, вы можете услышать звук например, удара двух камней).
Хорошо проводит звук земля.
- (Дмитрий Донской перед Куликовской битвой, приложив ухо к земле, услышал топот копыт конницы противника, когда она еще не была видна).
Это интересно
Источник: https://multiurok.ru/files/miekhanichieskiie-volny-1.html
Механические волны
| Волна — распространяющиеся колебания. Волнами называются всякие возмущения состояния вещества или поля, распространяющиеся в пространстве с течением времени. |
|
| Основное свойство волны — перенос энергии без переноса вещества. | |
Виды волновых процессов:
|
  |
| Распространение механических волн Распространение продольных волн проиллюстрировано на рисунке:  |
 |
|
 |
Внимание!
|
|
|
|
Луч- линия, перпендикулярная волновой поверхности. Показывает направление распространения волны (переноса энергии). |
 |
| Для сферической волны амплитуда колебаний и энергия через единицу поверхности уменьшаются с ростом расстояния от источника, при этом амплитуда уменьшается обратно пропорционально расстоянию от точки наблюдения до источника, а энергия – обратно пропорционально квадрату этого расстояния. Для плоской волны — амплитуда колебаний и энергия через единицу площади поверхности не меняются при отсутствии трения. |
Источник: https://www.eduspb.com/node/1785
Механические волны. Продольные и поперечные волны — Класс!ная физика
Волны могут быть разной природы: механические, электромагнитные и т.д. Мы будем рассматривать механические волны.
МЕХАНИЧЕСКИЕ ВОЛНЫ
Волна- это колебания, распространяющиеся в пространстве в течениие времени. Механические волны могут распространяться только в какой- нибудь среде (веществе): в газе, в жидкости, в твердом теле. В вакууме механическая волна возникнуть не может.
Источником волн являются колеблющиеся тела, которые создают в окружающем пространстве деформацию среды.

Для возникновения волны нужна деформация (наличие Fупр) среды. Для распространения волны нужна упругая среда. Бегущая волна — волна, где происходит перенос энергии без переноса вещества. Бегущая упругая волна- волна, где есть перенос энергии и возникает F упругости в среде распространения.
- Среди механических волн мы будем рассматривать бегущие упругие волны.
- Механические волны делятся на:
- а) продольные
![]()
— колебания среды происходят вдоль направления распространения волн, при этом возникают области сжатия и разрежения среды.

— возникают в любой среде (жидкости, в газах, в тв. телах).
б) поперечные

-колебания среды происходят перпендикулярно направлению их распространения, при этом происходит сдвиг слоев среды. — возникают только в твердых телах.

- СДЕЛАЙ САМ
- -попробуй сам смоделировать на тренажере продольную или поперечную волну, жми здесь.
- ПРОСТОЙ ОПЫТ
- Стоячая волна

В стеклянную трубку диаметром 4-5 см, длиной около 50 см, закрытую с одного конца, насыпьте мелко накрошенную пробку, так что бы она рассыпалась по трубке тонкой ленточкой, затем слегка поверните трубку по оси так, что бы крошка осталась на стенке, не сползая вниз, закрепите трубку горизонтально и к открытому концу поднесите звучащий камертон. Крошка осыплется, оставшись только в узлах стоячей волны.
КНИЖНАЯ ПОЛКА
Пловец и волны. Что знали о волнах моря (в 1912г.)?
ЭТО ИНТЕРЕСНО

Волны на поверхности жидкости не являются ни продольными, ни поперечными. Если бросить на поверхность воды небольшой мяч, то можно увидеть, что он движется, покачиваясь на волнах, по круговой траектории. Таким образом, волна на поверхности жидкости представляет собой результат сложения продольного и поперечного движения частиц воды.
ЗНАЕТЕ ЛИ ВЫ
… что скорость продольных и поперечных волн в одном и том же вещества, как правило, неодинакова.
Следующая страница «Длина волны. Скорость распространение волн»
Механические колебания и волны — Класс!ная физика
Колебательное движение — Величины, характеризующие колебательное движение — Затухающие и вынужденные колебания. Превращения энергии при колебательном движении — Волны — Длина волны.
Скорость распространение волн — Звуковые волны — Интересное о звуковых волнах — Интересные факты о звуковых волнах — Забавно о звуковых волнах — Распространение звука.
Скорость звука — Как бороться с шумом, и хорошо ли без него — Отражение звука. Эхо
Источник: http://class-fizika.ru/9_24.html
Поперечные и продольные волны — урок. Физика, 9 класс
При возникновении волн в пружине колебания её витков происходили вдоль направления распространения волны в ней (рис. (1)).

Рис. (1)
Волны, в которых колебания происходят вдоль направления их распространения, называются продольными волнами.
Кроме продольных волн существуют и поперечные волны.
Проведём опыт.
Возьмём длинный резиновый шнур. Один конец этого шнура закрепим, другой конец приведём в колебательное движение в вертикальной плоскости (перпендикулярно горизонтально расположенному шнуру).
Благодаря силам упругости, возникающим в шнуре, колебания будут распространяться вдоль шнура.
В нём возникают волны, причём колебания частиц шнура происходят перпендикулярно направлению распространения волн (рис. (2)).

Рис. (2)
Волны, в которых колебания происходят перпендикулярно направлению их распространения, называются поперечными волнами.
Движение частиц среды, в которой образуются как поперечные, так и продольные волны, можно наглядно продемонстрировать с помощью волновой машины (рис. (3), (4)).
На рисунке (3) показана продольная волна, а на рисунке (4) — поперечная. Обе волны распространяются в горизонтальном направлении.

Рис. (3)

Рис. (4)
На волновой машине представлен только один ряд шариков. Но, наблюдая за их движением, можно понять, как распространяются волны в сплошных средах, протяжённых во всех трёх направлениях (например, в некотором объёме твёрдого, жидкого или газообразного вещества).
Для этого представим, что каждый шарик является частью вертикального слоя вещества, расположенного перпендикулярно к плоскости рисунка.
При распространении поперечной волны эти слои, подобно шарикам, будут сдвигаться друг относительно друга, совершая колебания в вертикальном направлении (рис. (5)). Поэтому поперечные механические волны являются волнами сдвига.

Продольные волны — это волны сжатия и разрежения. В этом случае деформация слоёв среды состоит в изменении их плотности, так что продольные волны представляют собой чередующиеся уплотнения и разрежения (рис. (7)).

Обрати внимание!
Упругие силы при сдвиге слоев возникают только в твёрдых телах. В жидкостях и газах смежные слои свободно скользят друг по другу без появления противодействующих упругих сил. Раз нет упругих сил, то и образование упругих волн в жидкостях и газах невозможно. Поэтому поперечные волны могут распространяться только в твёрдых телах.
При сжатии и разрежении (т. е. при изменении объёма участков тела) упругие силы возникают как в твёрдых телах, так и в жидкостях и газах. Поэтому продольные волны могут распространяться в любой среде — твёрдой, жидкой и газообразной.
Источник: https://www.yaklass.ru/p/fizika/9-klass/mekhanicheskie-kolebaniia-i-volny-zvuk-18755/poperechnye-i-prodolnye-volny-dlina-volny-260612/re-ca5c6006-b2cb-4517-86b2-da5fdb26ab43
Волновые явления — Механические волны
Каждый из нас наблюдал, как от камня, брошенного на спокойную поверхность пруда или озера, кругами разбегаются волны (рис. 6.1). Многие следили за морскими волнами, набегающими на берег.
Все читали рассказы о морских путешествиях, о чудовищной силе морских волн, легко раскачивающих большие корабли. Однако при наб.
тюдении этих явлений не всем известно, что звук всплеска воды доносится до нашего уха волнами в том воздухе, которым мы дышим, что свет, с помощью которого мы зрительно воспринимаем окружающее, тоже представляет собой волновое движение.
Волновые процессы чрезвычайно широко распространены в природе. Различны физические причины, вызывающие волновые движения. Но, подобно колебаниям, все виды волн описываются количественно одинаковыми или почти одинаковыми законами. Многие трудные для понимания вопросы становятся более ясными, если сравнивать различные волновые явления.

Что же называют волной? Почему возникают волны? Отдельные частицы любого тела -твердого, жидкого или газообразного — взаимодействуют друг с другом. Поэтому если какая-либо частица тела начинает совершать колебательные движения, то в результате взаимодействия между частицами это движение начинает с некоторой скоростью распространяться во все стороны.
Волна — это колебания, распространяющиеся в пространстве с течением времени.
В воздухе, твердых телах и внутри жидкостей механические волны возникают благодаря действию сил упругости. Эти силы осуществляют связь между отдельными частями тела. Образование волн на поверхности воды вызывают сила тяжести и сила поверхностного натяжения.
Наиболее отчетливо главные особенности волнового движения можно увидеть, если рассматривать волны на поверхности воды. Это могут быть, например, волны, которые представляют собой бегущие вперед округлые валы.
Расстояния между валами, или гребнями, примерно одинаковы.
Однако если на поверхности воды, по которой бежит волна, находится легкий предмет, например лист с дерева, то он не будет увлекаться вперед волной, а начнет соверпгать колебания вверх и вниз, оставаясь почти на одном месте.
При возбуждении волны происходит процесс распространения колебаний, но не перенос вещества. Возникшие в каком-то месте колебания воды, например от брошенного камня, передаются соседним участкам и постепенно распространяются во все стороны, вовлекая в колебательные движения все новые и новые частицы среды. Течение же воды не возникает, перемещаются лишь локальные формы ее поверхности.
Скорость волны. Важнейшей характеристикой волны является скорость ее распространения. Волны любой природы не распространяются в пространстве мгновенно. Их скорость конечна.
Можно себе, например, представить, что над морем летит чайка, причем так, что она все время оказывается над одним и тем же гребнем волны. Скорость волны в этом случае равна скорости чайки.
Волны на поверхности воды удобны для наблюдения, так как скорость их распространения сравнительно невелика.
Поперечные и продольные волны. Нетрудно также наблюдать волны, распространяющиеся вдоль резинового шнура. Если один конец шнура закрепить и, слегка натянув шнур рукой, привести другой его конец в колебательное движение, то по шнуру побежит волна (рис. 6.2).
 Скорость волны будет тем больше, чем сильнее натянут шнур. Волна добежит до точки закрепления шнура, отразится и побежит назад. В этом опыте при распространении волны происходят изменения формы шнура. Каждый участок шнура колеблется относительно своего неизменного положения равновесия.
Скорость волны будет тем больше, чем сильнее натянут шнур. Волна добежит до точки закрепления шнура, отразится и побежит назад. В этом опыте при распространении волны происходят изменения формы шнура. Каждый участок шнура колеблется относительно своего неизменного положения равновесия.

Обратим внимание на то, что при распространении волны вдоль шнура колебания совершаются в направлении, перпендикулярном направлению распространения волны. Такие волны называются поперечными (рис. 6.3).
В поперечной волне смещения отдельных участков среды происходят в направлении, перпендикулярном направлению распространения волны. При этом возникает упругаядеформация, называемая деформацией сдвига. Отдельные слои вещества сдвигаются относительно друг друга.
При деформации сдвига в твердом теле возникают силы упругости, стремящиеся вернуть тело в исходное состояние. Именно силы упругости и вызывают колебания частиц среды1.
Сдвиг слоев относительно друг друга в газах и жидкостях не приводит к появлению сил упругости. Поэтому в газах и жидкостях не могут существовать поперечные волны. Поперечные волны возникают в твердых телах.
Но колебания частиц среды могут происходить и вдоль направления распространения волны (рис. 6.4). Такая волна называется продольной. Продольную волну удобно наблюдать на длинной мягкой пружине большого диаметра.
Ударив ладонью по одному из концов пружины (рис. 6.5, а), можно заметить, как сжатие (упругий импульс) бежит по пружине.
С помощью серии последовательных ударов можно возбудить в пружине волну, представляющую собой последовательные сжатия и растяжения пружины, бегущие друг за другом (рис. 6.5, б).
Итак, в продольной волне происходит деформация сжатия. Силы упругости, связанные с этой деформацией, возникают как в твердых телах, так и в жидкостях и газах.
1Когда мы говорим о колебаниях частиц среды, то имеем в виду колебания малых объемов среды, а не колебания молекул.

Эти силы вызывают колебания отдельных участков среды. Поэтому продольные волны могут распространяться во всех упругих средах. В твердых телах скорость продольных волн больше скорости поперечных.
Это учитывается при определении расстояния от очага землетрясения до сейсмической станции. Вначале на станции регистрируется продольная волна, так как ее скорость в земной коре больше, чем поперечной.
Спустя некоторое время регистрируется поперечная волна, возбуждаемая при землетрясении одновременно с продольной.
Зная скорости продольных и поперечных волн в земной коре и время запаздывания поперечной волны, можно определить расстояние до очага землетрясения.
Энергия волны. При распространении механической волны движение передается от одних частиц среды к другим. С передачей движения связана передача энергии. Основное свойство всех волн независимо от их природы состоит в переносе ими энергии без переноса вепцества. Энергия поступает от источника, возбуждающего колебания начала шнура, струны и т. д.
, и распространяется вместе с волной. Через любое поперечное сечение, например шнура, передается энергия. Эта энергия слагается из кинетической энергии движения частиц среды и потенциальной энергии их упругой деформации.
Постепенное уменьшение амплитуды колебаний частиц при распространении волны связано с превращением части механической энергии во внутреннюю.
Волна — это колебания, распространяющиеся в пространстве с течением времени. Скорость волны конечна. Волна переносит энергию, но не переносит вещество среды.
Источник: https://www.sites.google.com/site/mehaniceskie4volny/volnovye-avlenia
11 класс
- Физика
- Пройдите тест по явлению ЭМИ!
- Пройдите тест по природе света!

Электродинамика
Магнитное поле
Взаимодействие токов. Магнитное поле. Магнитная индукция. Вихревое поле
Сила Ампера. Электроизмерительные приборы. Громкоговоритель. Сила Лоренца
Электромагнитная индукция. Открытие ЭМИ. Магнитный поток
Самоиндукция. Индуктивность. Энергия магнитного поля
- Магнитные свойства вещества
- Уравнения Максвелла*
- Механические колебания
- Свободные и вынужденные колебания. Условия возникновения колебаний
- Динамика колебательного движения. Энергия колебательного движения
Сложение гармонических колебаний. Резонанс. Автоколебания
- Электромагнитные колебания
- Свободные и вынужденные электромагнитные колебания. Колебательный контур
- Переменный электрический ток. Активное, ёмкостное, индуктивное сопротивление в цепи переменного тока
- Электрический резонанс. Мощность в цепи с активным сопротивлением
Генерирование электрической энергии. Трансформаторы. Производство, передача и использование электрической энергии
Механические волны
Механические волны. Длина волны. Скорость волны. Свойства волн
Звуковые волны. Звук. Эффект Допплера
Электромагнитные волны
Электромагнитные волны. Экспериментальное обнаружение и свойства электромагнитных волн
Изобретение радио А.С. Поповым. Принцип радиосвязи. Модуляция и детектирование. Простейший детекторный приёмник
Распространение радиоволн. Радиолокация. Телевидение. Развитие средств связи

- Оптика
- Геометрическая оптика
- Развитие взглядов на природу света
- Основные понятия геометрической оптики. Фотометрия
Принцип Гюйгенса и Ферма. Закон отражения. Закон преломления света. Полное отражение
- Плоское зеркало. Сферическое зеркало
- Задачи на сферическое зеркало
- Линза
- Линза. Формула тонкой линзы
- Построение изображений, даваемой линзой
- Оптические приборы
- Волновая оптика
- Скорость света
- Дисперсия света. Интерференция света
- Дифракция света. Дифракционная решётка
- Поляризация света
- Основы теории относительности
- Законы электродинамики и принцип относительности
- Постулаты теории относительности. Релятивисткой закон сложения скоростей
- Зависимость массы тела от скорости его движения. Связь между массой и энергией
- Основы квантовой физики
- Излучения и спектры
- Виды излучений. Источники света
- Спектры и спектральный анализ
- Инфракрасное, ультрафиолетовое и рентгеновское излучение
- Шкала электромагнитных излучений
- Световые кванты
- Физические истоки квантовой теории
- Теория фотоэффекта. Применение фотоэффекта
Фотоны. Давление света. Гипотеза де Бройля
- Атомная физика
- Опыт Резерфорда. Ядерная модель атома
- Квантовые постулаты Бора. Модель атома водорода по Бору
- Атом водорода в квантовой механике
- Вынужденное излучение света. Лазеры
- Открытие радиоактивности. Альфа-, Бета-, гамма- излучения
- Методы наблюдения и регистрации радиоактивных излучений
- Радиоактивные превращения
Закон радиоактивного распада. Период полураспада. Изотопы
Ядерная физика
Открытие нейтрона. Состав ядра атома
Ядерные силы. Энергия связи атомных ядер. Ядерные спектры
Ядерные реакции. Энергетический выход ядерных реакций
Деление ядер урана. Цепные ядерные реакции. Ядерный реактор
- Термоядерные реакции. Применение ядерной энергии
- Получение радиоактивных изотопов и их применение. Биологическое действие радиоактивных излучений
- Физика элементарных частиц
- Стандартная модель элементарных частиц
- Открытие позитрона. Античастицы
- Современная физическая картина мира
- Современная физическая картина мира

- Строение Вселенной
- Строение Вселенной
- Солнечная система
- Звёзды и источники их энергии. Современные представления о происхождении и эволюции Солнца и звёзд
- Наша галактика и другие галактики
- Пространственные масштабы наблюдаемой Вселенной
- Применимость законов физики для объяснения природы космических объектов
- «Красное смещение» в спектрах галактик
- Современные взгляды на строение и эволюцию Вселенной
- Наблюдение солнечных пятен, звёздных скоплений, туманностей и галактик
- Медиаматериалы
- Магнитное поле
- Дисперсия света
- Виды излучений и спектры
- Загадки спектра
- Инфракрасное и ультрафиолетовое излучение
Источник: http://light-fizika.ru/index.php/11-klass?layout=edit&id=138
Механические волны
- Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
- Темы кодификатора ЕГЭ: механические волны, длина волны, звук.
- Механические волны — это процесс распространения в пространстве колебаний частиц упругой среды (твёрдой, жидкой или газообразной).
Наличие у среды упругих свойств является необходимым условием распространения волн: деформация, возникающая в каком-либо месте, благодаря взаимодействию соседних частиц последовательно передаётся от одной точки среды к другой. Различным типам деформаций будут соответствовать разные типы волн.
Продольные и поперечные волны
Волна называется продольной, если частицы среды колеблются параллельно направлению распространения волны. Продольная волна состоит из чередующихся деформаций растяжения и сжатия. На рис.
1 показана продольная волна, представляющая собой колебания плоских слоёв среды; направление, вдоль которого колеблются слои, совпадает с направлением распространения волны (т. е.
перпендикулярно слоям).
 |
| Рис. 1. Продольная волна |
Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Поперечная волна вызывается деформациями сдвига одного слоя среды относительно другого. На рис. 2 каждый слой колеблется вдоль самого себя, а волна идёт перпендикулярно слоям.
 |
| Рис. 2. Поперечная волна |
Продольные волны могут распространяться в твёрдых телах, жидкостях и газах: во всех этих средах возникает упругая реакция на сжатие, в результате которой появятся бегущие друг за другом сжатия и разрежения среды.
Однако жидкости и газы, в отличие от твёрдых тел, не обладают упругостью по отношению к сдвигу слоёв. Поэтому поперечные волны могут распространяться в твёрдых телах, но не внутри жидкостей и газов*.
Важно отметить, что частицы среды при прохождении волны совершают колебания вблизи неизменных положений равновесия, т. е. в среднем остаются на своих местах. Волна, таким образом, осуществляет
перенос энергии, не сопровождающийся переносом вещества.
Наиболее просты для изучения гармонические волны. Они вызываются внешним воздействием на среду, меняющимся по гармоническому закону. При распространении гармонической волны частицы среды совершают гармонические колебания с частотой, равной частоте внешнего воздействия. Гармоническими волнами мы в дальнейшем и ограничимся.
Рассмотрим процесс распространения волны более подробно. Допустим, что некоторая частица среды (частица ) начала совершать колебания с периодом . Действуя на соседнюю частицу она потянет её за собой. Частица в свою очередь, потянет за собой частицу и т. д. Так возникнет волна, в которой все частицы будут совершать колебания с периодом .
Однако частицы имеют массу, т. е. обладают инертностью. На изменение их скорости требуется некоторое время. Следовательно, частица в своём движении будет несколько отставать от частицы , частица будет отставать от частицы и т. д. Когда частица пустя время завершит первое колебание и начнёт второе, своё первое колебание начнёт частица , находящаяся от частицы на некотором расстоянии .
Итак, за время, равное периоду колебаний частиц, возмущение среды распространяется на расстояние . Это расстояние называется длиной волны. Колебания частицы будут идентичны колебаниям частицы колебания следующей частицы будут идентичны колебаниям частицы и т.
д. Колебания как бы воспроизводят себя на расстоянии можно назвать пространственным периодом колебаний; наряду с временным периодом она является важнейшей характеристикой волнового процесса.
В продольной волне длина волны равна расстоянию между соседними сжатиями или разрежениями (рис. 1). В поперечной — расстоянию между соседними горбами или впадинами (рис. 2).
Вообще, длина волны равна расстоянию (вдоль направления распространения волны) между двумя ближайшими частицами среды, колеблющимися одинаково (т. е. с разностью фаз, равной ).
- Скоростью распространения волны называется отношение длины волны к периоду колебаний частиц среды:
- .
- Частотой волны называется частота колебаний частиц:
- .
- Отсюда получаем связь скорости волны, длины волны и частоты:
- . (1)
| На поверхности жидкости могут существовать волны особого типа, похожие на поперечные — так называемые поверхностные волны. Они возникают под действием силы тяжести и силы поверхностного натяжения. |
Звук
Звуковыми волнами в широком смысле называются всякие волны, распространяющиеся в упругой среде. В узком смысле звуком называют звуковые волны в диапазоне частот от 16 Гц до 20 кГц, воспринимаемые человеческим ухом. Ниже этого диапазона лежит область инфразвука, выше — область ультразвука.
К основным характеристикам звука относятся громкость и высота.
Громкость звука определяется амплитудой колебаний давления в звуковой волне и измеряется в специальных единицах -децибелах (дБ). Так, громкость 0 дБ является порогом слышимости, 10 дБ — тиканье часов, 50 дБ — обычный разговор, 80 дБ — крик, 130 дБ — верхняя граница слышимости (так называемый болевой порог).
Тон — это звук, который издаёт тело, совершающее гармонические колебания (например, камертон или струна). Высота тона определяется частотой этих колебаний: чем выше частота, тем выше нам кажется звук. Так, натягивая струну, мы увеличиваем частоту её колебаний и, соответственно, высоту звука.
Скорость звука в разных средах различна: чем более упругой является среда, тем быстрее в ней распространяется звук. В жидкостях скорость звука больше, чем в газах, а в твёрдых телах — больше, чем в жидкостях.
Например, скорость звука в воздухе при равна примерно 340 м/с (её удобно запомнить как «треть километра в секунду»)*.
В воде звук распространяется со скоростью около 1500 м/с, а в стали — около 5000 м/с.
Заметим, что частота звука от данного источника во всех средах одна и та же: частицы среды совершают вынужденные колебания с частотой источника звука.
Согласно формуле (1) заключаем тогда, что при переходе из одной среды в другую наряду со скоростью звука изменяется длина звуковой волны.
| Если хочешь найти расстояние до грозовых туч в километрах, посчитай, через сколько секунд после молнии придёт гром, и раздели полученное число на три. |
Источник: https://ege-study.ru/ru/ege/materialy/fizika/mexanicheskie-volny/




