Аксиомы планиметрии и следствия из них

ТЕМА 1. АКСИОМЫ ПЛАНИМЕТРИИ

I. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки плоскости можно провести прямую, и только одну.

II. Из трёх точек, лежащих на прямой, одна и только одна лежит между двумя другими.

III. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

IV. Любая прямая разбивает плоскость на две полуплоскости.

V. Каждый угол имеет определённую градусную меру, большую нуля. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между сторонами этого угла. Градусная мера развёрнутого угла равна 180°.

VI. На любой полупрямой, от её начальной точки можно отложить отрезок заданной длины, и только один.

VII. От любой полупрямой от её начальной точки в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.

VIII. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

IX. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

§ 1. Прямая и отрезок.

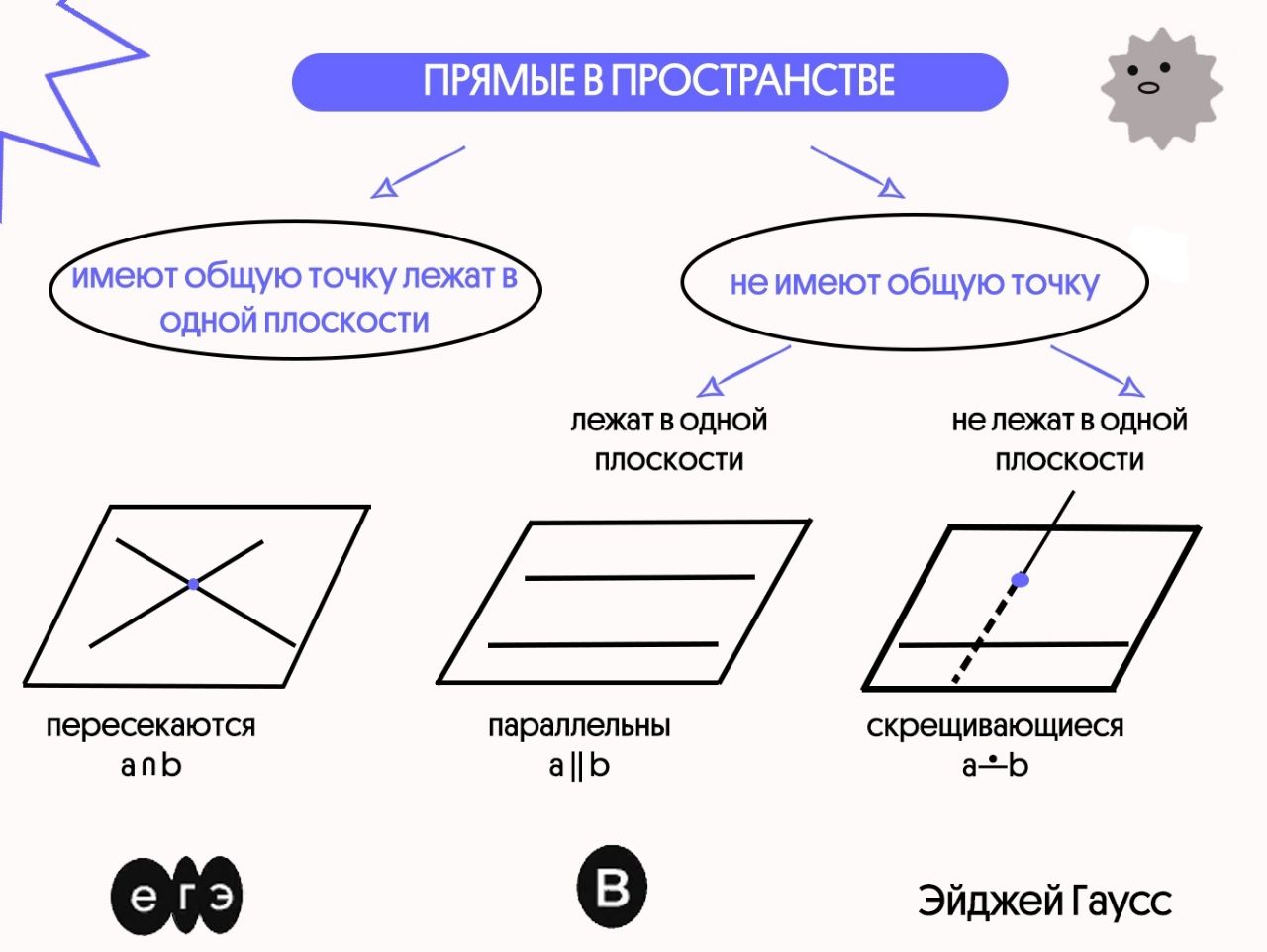
1. Пересекаются ли отрезки ABи CD?

2. Пересекаются ли прямые ABи CD?

3. Отметьте точку М так, чтобы она лежала на прямой CD, но не лежала ни на отрезке AB, ни на отрезке CD.

4. Отметьте точку N, которая лежит на прямойCD между точками A иB. Как вы назовёте такую точку?

1. Пересекает ли прямая KL отрезок EF?

2. Пересекает ли прямая KL прямую EF?

3. Отметьте точку А, которая лежит на прямой EF, но не лежит на прямой KL.

4. Существуют ли точки, которые одновременно лежат на отрезке EFи прямой LK?

1. Сколько существует различных отрезков с концами в точках A, B, Cи D?

2. Пересекаются ли прямые ABи CD?

3. Какая из точек, Aили D, лежит между точками Bи C?

4. Отметьте точку М, которая лежит на прямой AD,но не лежит на отрезке BC.

5. Проведите прямую, проходящую через точку Е, которая пересекает прямые ABиBC, но не пересекает отрезок AD.

1. Сколько существует различных отрезков с концами в точках E, F, Mи N?

2. Пересекаются ли прямые ENи FM?

3. Какая из точек, Aили N, лежит между точками Eи F?

4. Отметьте точку B, которая лежит на отрезке MN,но не лежит на прямой EF.

5. Проведите прямую, проходящую через точку A, которая пересекает прямые EFиMN, но не пересекает отрезок FM.

1. Начертите две пересекающиеся прямые и расположите на них два отрезка, не имеющие общих точек.

2. Сколько точек надо взять между точками A иB, чтобы вместе с отрезком ABполучилось шесть различных отрезков?

3. Даны отрезок AB, точка E, не лежащая на прямой AB, и точка C, лежащая на прямой AB. Каково взаимное расположение прямой EC и отрезка AB?

4. Можно ли провести прямую, не проходящую через точку A, так, чтобы она пересекала одновременно прямые AB, AC и AD.

1. Начертите две пересекающиеся прямые и расположите на них два непересекающиеся отрезка так, чтобы точка пересечения прямых принадлежала одному из них.

2. Проведите прямую, которая пересекает некоторые из указанных на рис. 1 отрезков, так, чтобы вместе с данными отрезками образовалось шесть отрезков.

3. Дана прямая EF, A∉EF, B∉EF. Может ли прямая AB не пересекать отрезок EF?

4. Может ли прямая, не проходящая через точку O, одновременно пересекать прямые OA, OB, OC и OD (рис. 2)?

1. Сколько различных прямых можно провести через 4 точки? Сделайте чертежи.

2. По рисунку определите число отрезков с концами в обозначенных точках.

1. Сколько точек пересечения могут иметь четыре попарно пересекающиеся прямые? Для каждого случая сделайте рисунок.

2. По рисунку определите число отрезков с концами в обозначенных точках.

§ 2. Луч и угол.

1. а) Сколько лучей с началом в точке О изображено на рисунке?

б) Сколько углов изображено на этом рисунке?

в) Постройте луч ОМ так, чтобы угол АОМ был развёрнутым.

1. Начертите угол. Отметьте точку М, которая лежит на стороне угла, точку N, лежащую во внутренней области угла, и точку Е, принадлежащую его внешней области.

1. а) Сколько лучей с началом в точке О изображено на рисунке?

б) Сколько углов изображено на этом рисунке?

в) Постройте луч ОА так, чтобы угол АОNбыл развёрнутым.

1. Начертите угол. Изобразите отрезок: а) все точки которого лежат во внутренней области угла; б) все точки которого лежат во внешней области угла; в) часть точек которого лежит во внутренней области угла.

1. а) Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?

б) Проведите лучи с началом в точке В, один из которых пересекал бы луч АС, а другой не пересекал бы его.

1. Даны угол MEFи точка А, лежащая в его внутренней области (рис. 2). Проведите луч с началом в точке Е так, чтобы образовались два угла, такие, что точка А не принадлежала бы их внутренним областям.

1. а) Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?

б) Начертите луч CD, проведите два луча с началом в точке A, один из которых пересекал бы луч CD, а другой не пересекал бы его.

1. Даны угол EKLи точка M, не лежащая в его внутренней области (рис. 2). Проведите из точки К луч так, чтобы образовалось ещё два угла, такие, что точка М не лежала бы в их внутренней области.

1. Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?

2. С началом в точке Е (рис. 2) проведите лучи, один из которых пересекает луч СА, а другой не пересекает луч ВС. Рассмотрите возможные варианты.

3. Дан неразвёрнутый угол АВС. Проведите лучи с началом в точке В, чтобы образовались при этом шесть углов, из которых один был бы развёрнутым.

1. Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?

2. С началом в точке Е (рис. 2) проведите лучи, один из которых пересекает луч ВС, а другой не пересекает луч АС. Рассмотрите возможные варианты.

3. Через заданную точку проведите столько прямых, чтобы при их пересечении образовалось шесть углов.

1. Углы AOB, BOC, COD, DOEи EOA имеют общую вершину О. Прямая а, не проходящая через точку О, пересекает не менее двух лучей, которые являются сторонами этих углов. Рассмотрите все возможные случаи. Сделайте чертежи.

2. Углы MAF, FAK, KAP, PAQ и QAM имеют общую вершину О. Прямая а, не проходящая через точку О, пересекает не менее трёх лучей, которые являются сторонами этих углов. Рассмотрите все возможные случаи. Сделайте чертежи.

§ 3. Сравнение отрезков и углов.

1. На рис. 1 CB = BE, DE AC. Сравните отрезки AB и DB.

2. На рис. 2 ∠AOB = ∠DOC. Есть ли ещё на рисунке равные углы?

1. На рис. 1 EO = NO, OK OL. Сравните отрезки EK и NL.

2. На рис. 2 ∠MOL = ∠KON. Есть ли ещё на рисунке равные углы?

1. На прямой а от точки А в одном направлении отложены два отрезка АВ и АС (АС АВ). От точки С на этой прямой отложите такой отрезок СЕ, чтобы АС = ВЕ. Что вы можете сказать о длине отрезка СЕ?

2. ∠AOC = ∠BOD, OM – биссектриса ∠АОВ. Докажите, что OM – биссектриса ∠COD.

1. На прямой m от точки А отложены два отрезка так, что АС АВ и точка А лежит между точками В и С. От точки С отложен отрезок СМ так, что ВМ = АС. Сравните отрезки МС и АВ.

2. На рисунке ∠AOC = ∠BOС и∠AOЕ = ∠BOF. Является ли луч ОС биссектрисой угла EOF?

1. Если на прямой даны точки A, B, C, D (точка С лежит между А и В) так, что AB = CD, то является ли середина отрезка AD также серединой отрезка ВС? Обоснуйте ответ.

2. На рисунке ОВ – луч, принадлежащий внутренней области угла АОС. Как нужно провести луч ОЕ, чтобы ∠AOC = ∠BOЕ? Покажите на рисунках возможные варианты.

1. АВ и АС – отрезки одной прямой (А лежит между точками В и С), точка М – середина отрезка АВ, N – середина АС. Верно ли, что BC = 2MN? Ответ обоснуйте.

2. На рисунке ОС – луч, принадлежащий внутренней области угла АОВ. Как нужно провести луч OD, чтобы ∠AOD = ∠COB? Покажите на рисунке возможные варианты.

1. На прямой а от точки А отложены два отрезка АВ и АС, причём ABAC1,99AB. Сравните отрезки ВС и АВ. Ответ обоснуйте.

2. На рисунке ∠AOC = ∠BOD, OMи ON – биссектрисы углов АОВ и COD. Сравните углы MONи AOC.

1. На прямой m от точки А отложены два отрезка АВ и АС, причём 0,51ABACAB. Сравните отрезки ВС и АС. Ответ обоснуйте.

2. На рисунке OMи ON – биссектрисы углов AOBи COD, ∠MON = ∠AOC. Сравните углы АОС иBOD.

§ 4. Измерение отрезков и углов.

1. На прямой m лежат точки M, NиK, причём MN = 85 мм, NK =1,15 дм. Какой может быть длина отрезка MK в сантиметрах?

2. ∠AOВ = 90°. Проведите луч ОС так, чтобы угол АОС равнялся 45° (рассмотрите два случая).

1. Чему равен угол СОВ?

2. Каким углом: острым, тупым или развёрнутым является угол СОВ?

3. Является ли луч ОС биссектрисой угла АОВ?

1. Точки А, В и С лежат на прямой а, причём АВ = 5,7 м, ВС = 730 см. Какой может быть длина отрезка АС в дециметрах?

2. ∠AOВ = 120°. Проведите луч ОС так, чтобы угол АОС равнялся 60° (рассмотрите два случая).

1. Чему равен угол СОВ?

2. Каким углом: острым, тупым или развёрнутым является угол СОВ?

3. Является ли луч ОС биссектрисой угла АОВ?

1. На отрезке MN, равном 8 дм, лежат точки А и В по разные стороны от середины С отрезка MN, СА = 7 см, СВ = 0,24 м. Найдите длины отрезков AN иBN в дециметрах.

2. ∠AOВ = 80°. Луч ОС делит этот угол на два угла так, что ∠AOС = 4∠СОВ.

1. Найдите эти углы.

2. Найдите угол DOB, если луч OD проведён так, что ОА – биссектриса угла DOB. Каким углом: острым или тупым является этот угол?

1. Точка M – середина отрезка EF, длина которого равна 1,2 м. От точки М, по разные стороны от неё, отложены два отрезка MP = 1,6 дм и MQ = 40 см. Найдите длины отрезков EP и QF в сантиметрах.

2. ∠AOВ = 100°. Луч ОЕ делит этот угол на два угла так, что ∠ВОЕ = 3∠АОЕ.

1. Найдите эти углы.

2. Найдите угол AOF, если луч OF проведён так, что ОE – биссектриса угла FOB. Каким углом: острым или тупым является этот угол?

1. На отрезке АВ, равном 192 дм, дана точка С, такая, что АС:СВ = 1:3. На отрезке АС отложен отрезок CD, равный ВС. Найдите расстояние между серединами отрезков ADи CB.

2. Угол АОВ расположен во внутренней области угла COD. ОЕ иOF – биссектрисы углов СОА и BOD соответственно. Объясните, почему угол EOF прямой, если ∠COD + ∠AOВ = 180°.

3. На прямой отложены два равных отрезка АС и СВ. На отрезке СВ дана точка D, такая, что 5СD = 4DB. Найдите длину отрезка, концами которого являются середины отрезков АС и DB, если CD= 12 м.

4. Угол АОВ принадлежит внутренней области угла COD; ∠COD = 140°, а ∠АОВ = 100°. Найдите угол, образованный биссектрисами углов AOC иBOD, если луч ОВ принадлежит внутренней области угла AOD.

1. Длина отрезка АВ равна 14 см. Найдите на прямой АВ все такие точки D, для которых DA= 3DB.

2. Прямой угол разделён лучом, исходящим из его вершины, на два угла, такие, что половина одного угла трети другого. Найдите эти углы.

1. Длина отрезка АВ равна 12 см. Найдите на прямой АВ все такие точки М, для которых МА = 2МВ.

2. Прямой угол двумя лучами, исходящими из его вершины, разделён на три угла, один из которых равен разности двух других углов. Найдите величину большего из этих углов.

8

Источник: https://multiurok.ru/index.php/files/aksiomy-planimietrii-1.html

Урок 3. введение в стереометрию — Геометрия — 10 класс — Российская электронная школа

• Геометрия, 10 класс
• Урок №3. Введение в стереометрию
• Перечень вопросов, рассматриваемых в теме

1. определение стереометрии;
2. понятие пространства;
3. аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве, а также следствия из них.

1. Глоссарий по теме
2. Геометрия— это наука о свойствах геометрических фигур.
3. Планиметрия— это раздел геометрии, в котором изучаются свойства фигур на плоскости.
4. Стереометрия— это раздел геометрии, в котором изучаются свойства фигур в пространстве.
5. Простейшими (основными) фигурами в пространстве являются точки, прямые и плоскости.
6. Обязательная литература:

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии. 10 кл. Москва.: Просвещение, 2013 г. С. 1-4

Дополнительная литература:

Зив Б. Г. Геометрия. 10 класс. Дидактические материалы.: Москва, Просвещение, 2013 г. С.4, 14, 24

Открытый электронный ресурс:

Решу ЕГЭ. Открытый образовательный портал. https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Мы закончили изучать и повторять раздел геометрии, который называется планиметрией.

Сегодня мы начинаем изучать новый раздел геометрии, который называется стереометрией.

Обратите внимание на данные фигуры. Как вы заметили- они объемные.

• И их все объединяет раздел геометрии Стереометрия.
• Что же такое стереометрия?
• По аналогии с планиметрией мы можем вывести следующее определение:
• Стереометрия- это раздел геометрии, в котором изучаются свойства фигур в пространстве.
• Простейшими (основными) фигурами в пространстве являются точки, прямые и плоскости.

Вместе с этими фигурами рассматриваются геометрические тела и их поверхности. Представления о геометрических телах дают нам: кристаллы (составлен из многоугольников) – многогранники; куб; капли жидкости в невесомости – шар; футбольный мяч (шар); консервная банка (цилиндр).

Многогранники:

Куб:

Шар:

Цилиндр:

Изучая свойства геометрических фигур, мы получаем представления о геометрических свойствах реальных предметов. В этом и состоит практическое значение геометрии, в частности стереометрия, широко используется в строительстве, архитектуре, машиностроении, геодезии, в науке и технике.

В планиметрии основными фигурами были точки и прямые. В стереометрии наряду с ними рассматривается ещё одна основная фигура – плоскость.

Представление плоскости нам дает любая гладкая поверхность. Она безгранична.

В стереометрии:

1. точки обозначаются прописными латинскими буквами: А, В, С и т. д.
2. прямые – строчными латинскими буквами: а, b, с и т. д. или двумя большими латинскими буквами: АВ, ВС и т. д.
3. плоскости – греческими буквами: α, β, γ и т. д.

Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.

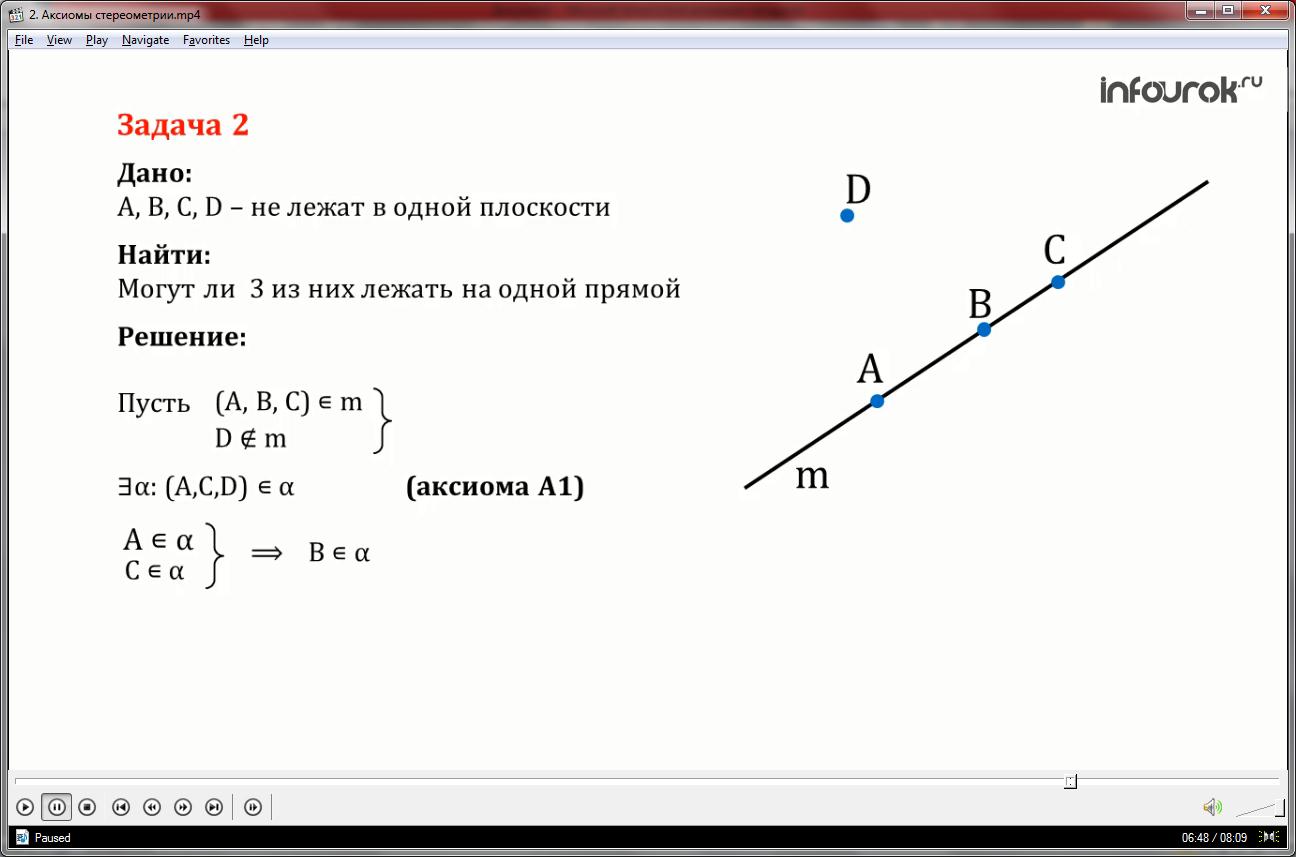
А1: Через 3 точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

1. ТочкиА α, В α, С α.
2. Если взять четыре произвольные точки, то через них может не проходить ни одна плоскость.
3. А2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
4. В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.
5. Это свойство используется при проверке “ровности” линейки.
6. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
7. А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
8. В этом случае говорят, что плоскости пересекаются по прямой.
9. Пример: пересечение пола и стены
10. В пространстве существует бесконечно много плоскостей, и в каждой плоскости справедливы все аксиомы и теоремы планиметрии.
11. Некоторые следствия из аксиом.
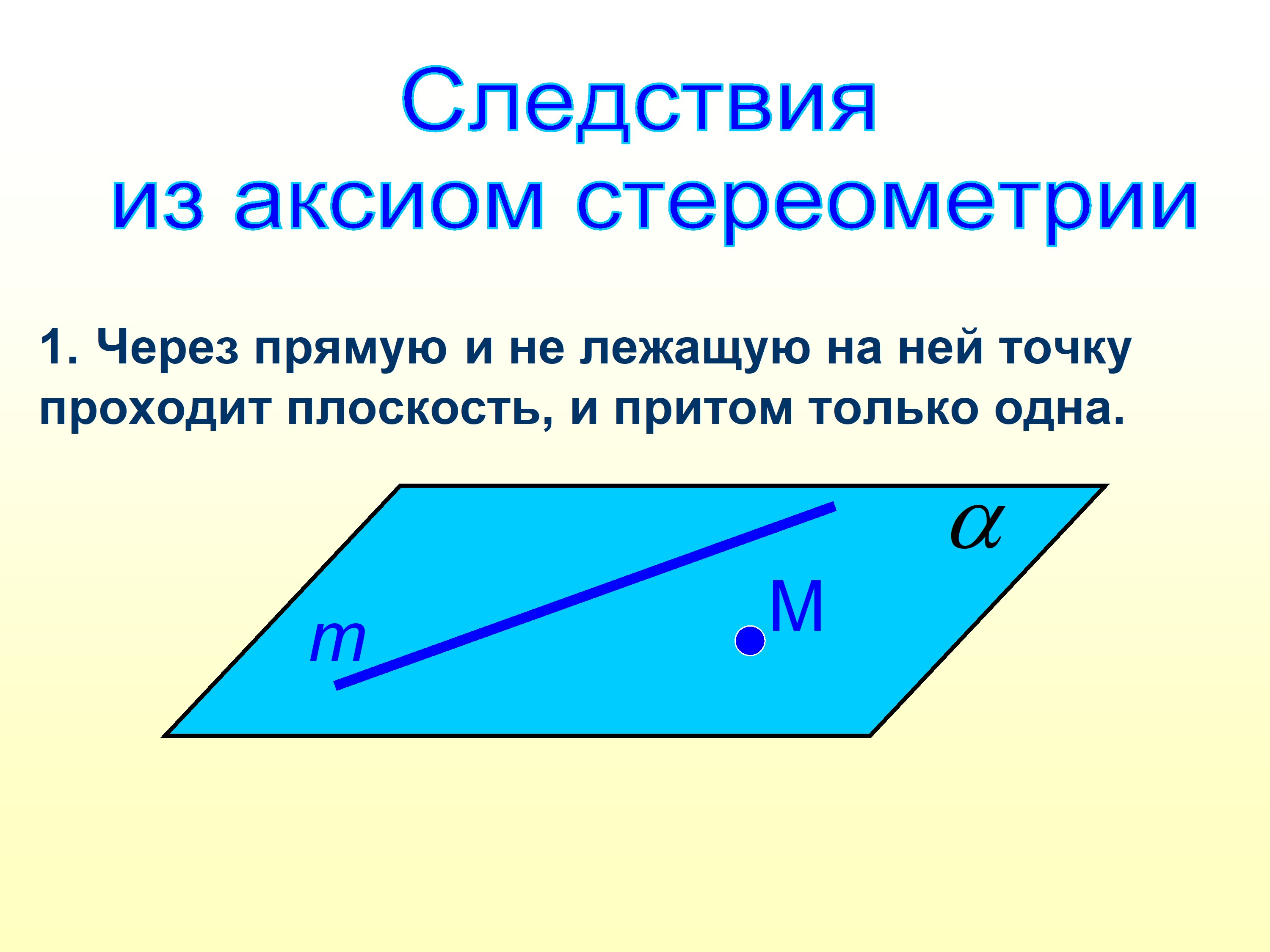
12. Теорема 1: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
13. Дано: а – прямая, точка М ∉ а.
14. Доказать: 1) существует α: а α.
15. 2) α – единственная.
16. Доказательство:

1) Дополнительные построения: т. В а, т. С а.

2) В, С, М не лежат на одной прямой, следовательно, по первой аксиоме существует плоскость α.

3) т. к.

4) Единственность α. следует из того, что любая плоскость, проходящая через прямую а и т. М, проходит через М, В, С. Значит, она совпадает с α (по Аксиоме 1). Теорема доказана.

• Теорема 2: Через две пересекающиеся прямые проходит плоскость, и, причём только одна.
• Дано: а ∩ b в точке М
• Доказать: существование плоскости α, а α, b α.
• Доказательство:
• 1) Дополнительные построения: N Є b, N∉ a.
• 2) Существует α : N α, a α.
• 3)

4) Из 2) и 3) следует α. проходит через прямые а и b.

5) Единственность α следует из того, что любая плоскость, проходящая через прямые а и b, проходит через точку N, значит она совпадает с α (по Теореме 1). Теорема доказана.

1. Разбор решения заданий тренировочного модуля
2. №1.
3. Тип задания: выделение цветом
4. Прямая MN пересекает плоскость:
5. 1) (АА1В1);
6. 2) (ABC);
7. 3) (AA1D1).
8. Разбор решения:
9. Внимательно рассмотрите рисунок, как вы видите прямая MN пересекает плоскости ABC и A1B1С1, рассмотрим варианты ответов, среди них есть вариант 2) (ABC), он и является верным.
10. Ответ: 2) (ABC);
11. №2.
12. Тип задания: смежный граф
13. Пользуясь данным рисунком
14. назовите три плоскости, содержащие прямую DС1 (нижний индекс записываете цифрой после буквы, без пробела)
15. Решение: Внимательно рассмотрите прилагающийся рисунок, определите, где на нем располагается прямая DС1, как вы видите из рисунка он располагается в плоскостях:
16. 1)DD1С1С
17. 2)D1С1С
18. 3) DСС1
19. Их и запишем в ответ.
20. Ответ: 1)DD1С1С; 2)D1С1С; 3) DСС1

Источник: https://resh.edu.ru/subject/lesson/4756/conspect/

Аксиомы планиметрии (стр. 1 из 3)

• МОУ “ООШ №16″
• Доклад на тему:
• “Аксиомы планиметрии”
• Выполнила:
• Ученица 7 класса
• Аулова Евгения
• Астрахань 2010
• Из истории аксиом

Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике.

Аксиоматический метод построения научной теории заключается в следующем: выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них. Основные понятия выделяются следующим образом.

Известно, что одно понятие должно разъясняться с помощью других, которые, в свою очередь, тоже определяются с помощью каких-то известных понятий. Таким образом, мы приходим к элементарным понятиям, которые нельзя определить через другие. Эти понятия и называются основными.

Когда мы доказываем утверждение, теорему, то опираемся на предпосылки, которые считаются уже доказанными. Но эти предпосылки тоже доказывались, их нужно было обосновать. В конце концов, мы приходим к недоказываемым утверждениям и принимаем их без доказательства. Эти утверждения называются аксиомами.

Набор аксиом должен быть таким, чтобы, опираясь на него, можно было доказать дальнейшие утверждения. Выделив основные понятия и сформулировав аксиомы, далее мы выводим теоремы и другие понятия логическим путём. В этом и заключается логическое строение геометрии. Аксиомы и основные понятия составляют основания планиметрии.

Так как нельзя дать единое определение основных понятий для всех геометрий, то основные понятия геометрии следует определить как объекты любой природы, удовлетворяющие аксиомам этой геометрии. Таким образом, при аксиоматическом построении геометрической системы мы исходим из некоторой системы аксиом, или аксиоматики.

В этих аксиомах описываются свойства основных понятий геометрической системы, и мы можем представить основные понятия в виде объектов любой природы, которые обладают свойствами, указанными в аксиомах. После формулировки и доказательства первых геометрических утверждений становится возможным доказывать одни утверждения (теоремы) с помощью других.

От латинского названия «Начал» произошёл термин «элементарная геометрия». Несмотря на то, что сочинения предшественников Евклида до нас не дошли, мы можем составить некоторое мнение об этих сочинениях по «Началам» Евклида. В «Началах» имеются разделы, логически весьма мало связанные с другими разделами.

Появление их объясняется только тем, что они внесены по традиции и копируют «Начала» предшественников Евклида. «Начала» Евклида состоят из 13 книг. 1 — 6 книги посвящены планиметрии, 7 — 10 книги — об арифметике и несоизмеримых величинах, которые можно построить с помощью циркуля и линейки. Книги с 11 по 13 были посвящены стереометрии.

«Начала» начинаются с изложения 23 определений и 10 аксиом. Первые пять аксиом — «общие понятия», остальные называются «постулатами». Первые два постулата определяют действия с помощью идеальной линейки, третий — с помощью идеального циркуля. Четвёртый, «все прямые углы равны между собой», является излишним, так как его можно вывести из остальных аксиом.

Последний, пятый постулат гласил: «Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то, при неограниченном продолжении этих двух прямых, они пересекутся с той стороны, где углы меньше двух прямых».

Пять «общих понятий» Евклида являются принципами измерения длин, углов, площадей, объёмов: «равные одному и тому же равны между собой», «если к равным прибавить равные, суммы равны между собой», «если от равных отнять равные, остатки равны между собой», «совмещающиеся друг с другом равны между собой», «целое больше части». Далее началась критика геометрии Евклида.

Критиковали Евклида по трём причинам: за то, что он рассматривал только такие геометрические величины, которые можно построить с помощью циркуля и линейки; за то, что он разрывал геометрию и арифметику и доказывал для целых чисел то, что уже доказал для геометрических величин, и, наконец, за аксиомы Евклида. Наиболее сильно критиковали пятый постулат, самый сложный постулат Евклида. Многие считали его лишним, и что его можно и нужно вывести из других аксиом. Другие считали, что его следует заменить более простым и наглядным, равносильным ему: «Через точку вне прямой можно провести в их плоскости не более одной прямой, не пересекающей данную прямую».

Критика разрыва между геометрией и арифметикой привела к расширению понятия числа до действительного числа. Споры о пятом постулате привели к тому, что в начале XIX века Н.И. Лобачевский, Я. Бойяи и К.Ф. Гаусс построили новую геометрию, в которой выполнялись все аксиомы геометрии Евклида, за исключением пятого постулата.

Он был заменён противоположным утверждением: «В плоскости через точку вне прямой можно провести более одной прямой, не пересекающей данную». Эта геометрия была столь же непротиворечивой, как и геометрия Евклида. Модель планиметрии Лобачевского на евклидовой плоскости была построена французским математиком Анри Пуанкаре в 1882 г. На евклидовой плоскости проведём горизонтальную прямую.

Фигура на плоскости Лобачевского — фигура открытой полуплоскости, лежащей выше абсолюта (F). Неевклидово движение является композицией конечного числа инверсий с центром на абсолюте и осевых симметрий, оси которых перпендикулярны абсолюту. Два неевклидовых отрезка равны, если один из них неевклидовым движением можно перевести в другой.

Таковы основные понятия аксиоматики планиметрии Лобачевского. Все аксиомы планиметрии Лобачевского непротиворечивы. Определение прямой следующее: «Неевклидова прямая — это полуокружность с концами на абсолюте или луч с началом на абсолюте и перпендикулярный абсолюту».

Таким образом, утверждение аксиомы параллельности Лобачевского выполняется не только для некоторой прямой и точки A, не лежащей на этой прямой, но и для любой прямой и любой не лежащей на ней точки A.

За геометрией Лобачевского возникли и другие непротиворечивые геометрии: от евклидовой отделилась проективная геометрия, сложилась многомерная евклидова геометрия, возникла риманова геометрия (общая теория пространств с произвольным законом измерения длин) и др. Из науки о фигурах в одном трёхмерном евклидовом пространстве геометрия за 40 — 50 лет превратилась в совокупность разнообразных теорий, лишь в чём-то сходных со своей прародительницей — геометрией Евклида.

1. Аксиомы планиметрии
2. Аксиомы принадлежности
3. — Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
4. — Через любые две точки можно провести прямую, и только одну.
5. Аксиомы расположения
6. — Из трех точек на прямой одна и только одна лежит между двумя другими.
7. — Прямая разбивает плоскость на две полуплоскости.
8. Аксиомы измерения

— Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумму длин частей, на которые он разбивается любой его точкой.

— Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 градусов. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

• Аксиомы откладывания
• — На любой полупрямой от ее начальной точки можно отложить отрезок, заданной длины, и только один.
• — От любой полупрямой в заданную полуплоскость можно отложить угол заданной градусной мерой, меньшей 180 градусов, и только один.
• — Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.
• Аксиома параллельности
• — Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
• Евклид
• Биография

Евклид (иначе Эвклид) – древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения о Евклиде крайне скудны. Известно лишь, что учителями Евклида в Афинах были ученики Платона, а в правление Птолемея I (306-283 до н.э.) он преподавал в Александрийской академии.

Евклид – первый математик александрийской школы. Евклид – автор ряда работ по астрономии, оптике, музыке и др. Арабские авторы приписывают Евклиду и различные трактаты по механике, в том числе сочинения о весах и об определении удельного веса. Умер Евклид между 275 и 270 до н. э.

Начала Евклида

Источник: https://mirznanii.com/a/313546/aksiomy-planimetrii

Билет №1 аксиомы планиметрии

Билет №1

• аксиомы планиметрии:
• Аксиомы стереометрии.
• Стереометрия — раздел геометрии, в котором изучаются фигуры в пространстве.
• С1: какова бы ни была плоскость, существует точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

1.

какова бы ни была прямая, существуют точки, принадлежащие этой прямой и точки не принадлежащие ей. Через любые две точки можно провести прямую и только одну. 2. из трех точек на прямой одна о только одна лежит между двумя другими. 3. каждый отрезок имеет определенную длину, большую нуля.

Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой. 4. прямая разбивает плоскость на две полуплоскости. 5. каждый угол имеет определенную градусную меру, большую нуля. Градусная мера угла равна сумме градусных мер углов на которые он разбивается любым лучом, проходящим между его сторонами. 6.

на любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один. 7. от любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180, и только один. 8. каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой. 9.

С2: если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Этой аксиомой утверждается, что если две различные плоскости a и b имеют общую точку, то существует прямая с , принадлежащая каждой из этих плоскостей. При этом если точка С принадлежит обеим плоскостям, то она принадлежит прямой с.

С3: если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну. Это значит, что если две различные прямые a и b имеют общую точку С, то существует плоскость a, содержащая прямые a и b. Плоскость, обладающая этим свойством, единственна.

Теорема 15.1: через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

Доказательство: пусть АВ — данная прямая и С — не лежащая на ней точка. Проведем через точки А и С прямую (аксиома 1). Прямые АВ и АС различны, так как точка С не лежит на прямой АВ. Проведем через прямые АВ и АС плоскость a (аксиома С3). Она проходит через прямую АВ и точку С.

Докажем, что плоскость a, проходящая через прямую АВ и точку С, единственна. Допустим, существует другая плоскость a1, проходящая через прямую АВ и точку С. По аксиоме С2 плоскости a и a1 пересекаются по прямой. Эта прямая должна содержать точки А, В и С. Но они не лежат на одной прямой.

Мы пришли к противоречию. Теорема доказана.

Параллелепипед, его элементы.

Если основание призмы — параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани — параллелограммы. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. Бывает прямой и наклонный. Прямой параллелепипед: основание — прямоугольник. У него все грани — прямоугольники. Прямоуг параллеп, у которого все ребра равны, называется кубом. Длины непараллельных ребер прямоуг параллеп называются его линейными размерами (измерениями). У прямоуг параллеп три измерения.

Теорема 19.3: диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

Дано: параллелепипед АВСДА1В1С1Д1., О — точка пересечения диагоналей С1А и ВД1.

Доказательство: рассмотрим какие-нибудь две диагонали параллелепипеда, например АС1 и ВД1. Так как четырехугольники АВСД и ДД1С1С — параллелограммы с общей стороной СД, то их стороны АВ и Д1С1 параллельны друг другу, а значит, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым АД1 и ВС1.

Следовательно, четырехугольник ВАД1С1 — параллелограмм. Диагонали параллелепипеда АС1 и ВД1 являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения О делятся пополам. Аналогично доказываются другие диагонали. Отсюда заключаем, что все четыре диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

Билет №2.

Параллельные прямые.

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.

Теорема 16.1: через точку вне данной прямой можно провести прямую, параллельную данной и только одну.

Замечание: утверждение единственности в теореме 16.1 не является простым следствием аксиомы параллельных, так как этой аксиомой утверждается единственность прямой, параллельной данной в данной плоскости. Поэтому она требует доказательства.

Доказательство: пусть а — данная прямая и А — точка, не лежащая на этой прямой. Проведем через прямую и точку плоскость a. Проведем через точку А в плоскости a прямую а1, параллельную а. Докажем, что прямая а1, параллельная а, единственна.

Допустим, что существует другая прямая а2, проходящая через точку А и параллельная прямой а. Через прямые а и а2 можно провести плоскость a2. Плоскость a2 проходит через прямую а и точку А, следовательно по теореме 15.1 она совпадает с a.

Теперь по аксиоме параллельных прямые а1 и а2 совпадают. Теорема доказана.

Площадь сферы. (вывод формулы).

Площадь поверхности сферы — предел отношения объема слоя, покрывающего поверхность, к толщине этого слоя, если толщина этого стремиться к нулю.

Билет №3.

Прямая, параллельная плоскости.

Пряма и плоскость называются параллельными, если они не пересекаются.

Теорема 16.3: если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

Доказательство: пусть a — плоскость и а — не лежащая в ней прямая и а1 — прямая в плоскости a, параллельная прямой а. Проведем плоскость b через прямые а и а1. Плоскости a и b пересекаются по прямой а1.

Если бы прямая а пересекала плоскость a, то точка пересечения принадлежала бы прямой а1. Но это невозможно, так как прямые а и а1 параллельны. Итак, прямая а не пересекает плоскость a, а значит, параллельна плоскости a.

ЧТД.

1. Вывод формулы объема конуса.
2. Билет №4.
3. Параллельные плоскости.

Конусом (а точнее круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга, — вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Прямой конус — прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. Две плоскости называются параллельными, если они не пересекаются.

Теорема 16.4: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство: пусть a и b — данные плоскости, а1 и а2 — прямые в плоскости a, пересекающиеся в точке А, в1 и в2 — соответственно параллельные им прямые в плоскости b.

Допустим, что плоскости a и b не параллельны, т.е. пересекаются по некоторой прямой с. По теореме 16.

3 прямые а1 и а2 , как параллельные прямым в1 и в2, параллельны плоскости b, и поэтому они не пересекают лежащую в этой плоскости прямую с.

Таким образом, в плоскости a через точку А проходят две прямые (а1 и а2), параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД.

• Вывод формулы объема пирамиды.
• Билет №5.
• Теорема об отрезках параллельных прямых, заключенных между двумя параллельными плоскостями.

Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Действительно, согласно определению параллельные прямые — это прямые, которые лежат в одной плоскости и не пересекаются. Наши прямые лежат в одной плоскости — секущей плоскости. Они не пересекаются, так как не пересекаются содержащие их параллельные плоскости. Значит, прямые параллельны. ЧТД.

Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны. Действительно, пусть a и b — параллельные плоскости, а и в — пересекающие их параллельные прямые, А1, А2,и В1, В2 — точки пересечения прямых с плоскостями (см рисунок).

Проведем через прямые а и в плоскость. Она пересекает плоскости a и b по параллельным прямым А1В1 и А2В2. Четырехугольник А1В1В2А2 — параллелограмм, т.к. у него противолежащие стороны параллельны. А у параллелограмма противолежащие стороны равны. Значит А1А2=В1В2. ЧТД.

Касательная плоскость — плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А.

Теорема 20.5: касательная плоскость имеет с шаром только одну общую точку — точку касания.

Доказательство: пусть a — плоскость, касательная к шару, и А — точка касания. Возьмем произвольную точку Х плоскости a, отличную от А. Так как ОА — перпендикуляр, а ОХ — наклонная, то ОХ>ОА=R. Следовательно точка Х не принадлежит шару. Теорема доказана.Прямая в касательной плоскости шара, проходящая через точку касания, называется касательной к шару в этой точке. Так как касательная плоскость имеет с шаром только одну общую точку, то касательная прямая тоже имеет с шаром только одну общую точку — точку касания.

Билет №6.

Прямая, перпендикулярная плоскости.

Две прямые называются перпендикулярными, если угол между ними равен 900. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой в этой плоскости.

Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения.

Теорема 17.2: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.

Доказательство:

Площадь боковой поверхности пирамиды.

Теорема 19.6: боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.

Билет №7.

Теорема о трех перпендикулярах.

Теорема 17.5: если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Доказательство: пусть АВ — перпендикуляр к плоскости a, АС — наклонная и с — прямая в плоскости a, проходящая через основание С наклонной. Проведем прямую СА1, параллельную прямой АВ. Она перпендикулярна плоскости a. Проведем через прямые АВ и А1С плоскость b.

Прямая с перпендикулярна прямой СА1. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости b, а значит, и прямой АС.

1. Вывод формулы объема шара.
2. Билет №8.
3. Перпендикулярные плоскости.

Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Теорема 17.6: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство: пусть a — плоскость, в — перпендикулярная ей прямая, b — плоскость, проходящая через прямую в, с- прямая, по которой пересекаются плоскости a и b. Докажем, что плоскости a и b перпендикулярны.

Проведем в плоскости a через точку пересечения прямой в с плоскостью a прямую а, перпендикулярную прямой с. Проведем через прямые а и в плоскость g. Она перпендикулярна прямой с, т.к. прямая с перпендикулярна прямым а и в. Т.к.

прямые а и в перпендикулярны, то плоскости a и b перпендикулярны. ЧТД.

• Призма — многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.
• Прямая призма — боковые ребра призмы перпендикулярны основаниям.
• Боковая поверхность призмы (площадь боковой поверхности) — сумма площадей боковых граней.

Теорема 19.1: боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т.е. на длину бокового ребра.

Доказательство: боковые грани прямой призмы — прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Отсюда следует, что боковая поверхность призмы равна……

1. задача о боковой поверхности наклонной призмы: боковая поверхность наклонной призмы равна произведению периметра перпендикулярного сечения и бокового ребра.
2. Билет №9.
3. Теорема о двух прямых, перпендикулярных плоскости.

Теорема 17.4: две прямые, перпендикулярные одной и той же плоскости, параллельны.

Доказательство: пусть а и в — две прямые, перпендикулярные плоскости a. Допустим, что прямые а и в не параллельны. Тогда существует некая прямая в1 параллельная а. Выберем на прямой в точку С, не лежащую в плоскости a.

Проведем через точку С прямую в1, параллельную а. Прямая в1 перпендикулярна плоскости a (теорема 17.3). пусть В и В1 — точки пересечения прямых в и в1 с плоскостью a. Тогда прямая ВВ1 перпендикулярна пересекающимся прямым в и в1. А это невозможно.

Мы пришли к противоречию. ЧТД.

Прямоугольный параллелепипед — параллелепипед, у которого основанием является прямоугольник. У прямоугольного параллелепипеда все грани — прямоугольники. Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями).

Теорема 19.4: в прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.

Доказательство:

Билет № 10.

Теорема 17.3: если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

Доказательство: пусть а1 и а2 — две параллельные прямые и a — плоскость, перпендикулярная прямой а1. Докажем, что эта плоскость перпендикулярна и прямой а2. Проведем через точку А2 пересечения прямой а2 с плоскостью a произвольную прямую х2 в плоскости a. Проведем в плоскости a через точку А1 пересечения прямой а1 с a прямую х1, параллельную прямой х2.

Так как прямая а1 перпендикулярна плоскости a, то прямые а1 и х1 перпендикулярны. По теореме 17.1(если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны) параллельные им пересекающиеся прямые а2 и х2 тоже перпендикулярны. Таким образом, прямая а2 перпендикулярна любой прямой х2 в плоскости a.

А это значит, что прямая а2 перпендикулярна плоскости a.

Теорема о противолежащих гранях параллелепипеда.

Источник: http://uz.denemetr.com/docs/294/index-41681-12.html