Деформации твердых тел, с примерами задач

В данной теме будут рассмотрены решения задач, связанных с использованием закона Гука. А также порешаем задачи на тепловое расширение тел.

Задача 1. Для измерения глубины моря с корабля спустили гирю на стальном тросе. Плотность стали 7800 кг/м3, плотность морской воды 1030 кг/м3. Если предел прочности стали равен 5 ∙ 108 Па, то какова максимальная глубина, которую можно измерить этим методом? Массой гири пренебречь.

ДАНО:

РЕШЕНИЕ Равнодействующая сил Выталкивающая сила Масса троса Тогда равнодействующая сил Предел прочности Искомая глубина Проверим размерности

Ответ: максимальная глубина, которую можно измерить этим методом равна 7,5 км.

Задача 2. Между стенами закреплен брус, площадь поперечного сечения которого 10 см2, модуль Юнга 2,1 ∙ 1011 Па, а коэффициент линейного расширения равен 1,2 ∙ 10−5 К−1. С какой силой будет давить брус на стены, если его нагреть на 20 оС?

ДАНО:

РЕШЕНИЕ В результате нагревания бруса происходит его удлинение на величину Dl Удлинение бруса можно определить как Чтобы длина бруса, вследствие его нагревания, не изменилась, очевидно, что к нему необходимо приложить силу, которую можно найти из закона Гука Жёсткость бруса Тогда сила упругости Согласно III закону Ньютона Проверим размерности

Ответ: брус будет давить на стены с силой 50,4 кН.

Задача 3. Определите модуль упругости хрящевой ткани, поперечное сечение которой 1,5 см2, если растяжение ткани силой 130 Н вызывает ее относительное удлинение 3,9%.

ДАНО:

СИ

РЕШЕНИЕ Изобразим хрящевую ткань в виде кубика, и силы, действующие на нее. На ткань действуют следующие силы — это растягивающая сила (ее мы направим вправо) и сила упругости хрящевой ткани, которая препятствует ее удлинению Условие равновесия Сила упругости по закону Гука равна Коэффициент жёсткости хрящевой ткани Тогда сила упругости Модуль Юнга

Ответ: Е = 22,2 МПа.

Задача 4. К медной проволоке длиной 1 м и радиусом поперечного сечения 1 мм подвесили груз массой 100 кг. Чему равна работа по растяжению проволоки?

ДАНО:

СИ

РЕШЕНИЕ Работа по растяжению проволоки Условие равновесия Из закона Гука Тогда условие равновесия Из условия равновесия удлинение проволоки Жёсткость проволоки Тогда работа по растяжению проволоки

Ответ: работа по растяжению проволоки равна 1,3 Дж.

Задача 5. В медный калориметр с площадью дна 200 см2 и высотой 12 см налит до краев керосин при температуре 20 оС. Сколько керосина по массе выльется, если его нагреть до 100 оС?

ДАНО:

СИ

РЕШЕНИЕ Поскольку коэффициент объемного расширения жидкостей всегда больше коэффициента объемного расширения твердых тел, то при нагревании на одинаковое число кельвин приращение объема керосина будет больше приращения объема калориметра, и часть керосина из него выльется. Масса влившегося керосина Массы керосина Объем керосина при начальной и конечной температурах Как правило, в таблицах не дают значений коэффициентов объемного расширения твердых тел. Поэтому при решении задач принято считать, что коэффициент объемного расширения твердого тела в три раза больше коэффициента его линейного расширения. Тогда Плотности керосина при начальной и конечной температурах Изменения температур Тогда масса вылившегося керосина

Ответ: из калориметра выльется 16,4 г керосина.

Источник: https://videouroki.net/video/14-dieformatsiia-vidy-dieformatsii-tvierdykh-tiel-miekhanichieskoie-napriazhieniie-zakon-guka.html

Деформация твёрдого тела: её виды, измерение

Подробности Категория: Молекулярно-кинетическая теория Опубликовано 17.11.2014 18:20 Просмотров: 10881

Под воздействием внешних сил твёрдые тела меняют свою форму и объем, т.е. деформируются.

В результате действия приложенных к телу сил частицы, из которых оно состоит, перемещаются. Изменяются расстояния между атомами, их взаимное расположение. Это явление называют деформацией.

Если после прекращения действия силы тело возвращает свою первоначальную форму и объём, то такая деформация называется упругой, или обратимой. В этом случае атомы снова занимают положение, в котором они находились до того, как на тело начала действовать сила.

Если мы сожмём резиновый мячик, он изменит форму. Но тут же восстановит её, как только мы его отпустим. Это пример упругой деформации.

Если же в результате действия силы атомы смещаются от положений равновесия на такие расстояния, что межатомные связи на них уже не действуют, они не могут вернуться в первоначальное состояние и занимают новые положения равновесия. В этом случае в физическом теле происходят необратимые изменения.

Сдавим кусочек пластилина. Свою первоначальную форму он не сможет вернуть, когда мы прекратим воздействовать на него. Он деформировался необратимо. Такую деформацию называют пластичной, или необратимой.

Например, когда детали и узлы каких-то агрегатов во время работы испытывают серьёзные механические нагрузки, а также подвергаются значительному нагреву, в них со временем наблюдается деформация ползучести.

Под воздействием одной и той же силы тело может испытывать упругую деформацию, если сила приложена к нему на короткое время. Но если эта же сила будет воздействовать на это же тело длительно, то деформация может стать необратимой.

Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а само тело восстановит свою форму после снятия нагрузки, называется пределом упругости. При значениях выше этого предела тело начнёт разрушаться. Но разрушить твёрдое тело не так-то просто. Оно сопротивляется. И это его свойство называется прочностью.

Когда два автомобиля, соединённые буксировочным тросом, начинают движение, трос подвергается деформации. Он натягивается, а его длина увеличивается. А когда они останавливаются, натяжение ослабевает, и длина троса восстанавливается. Но если трос недостаточно прочный, он просто разорвётся.

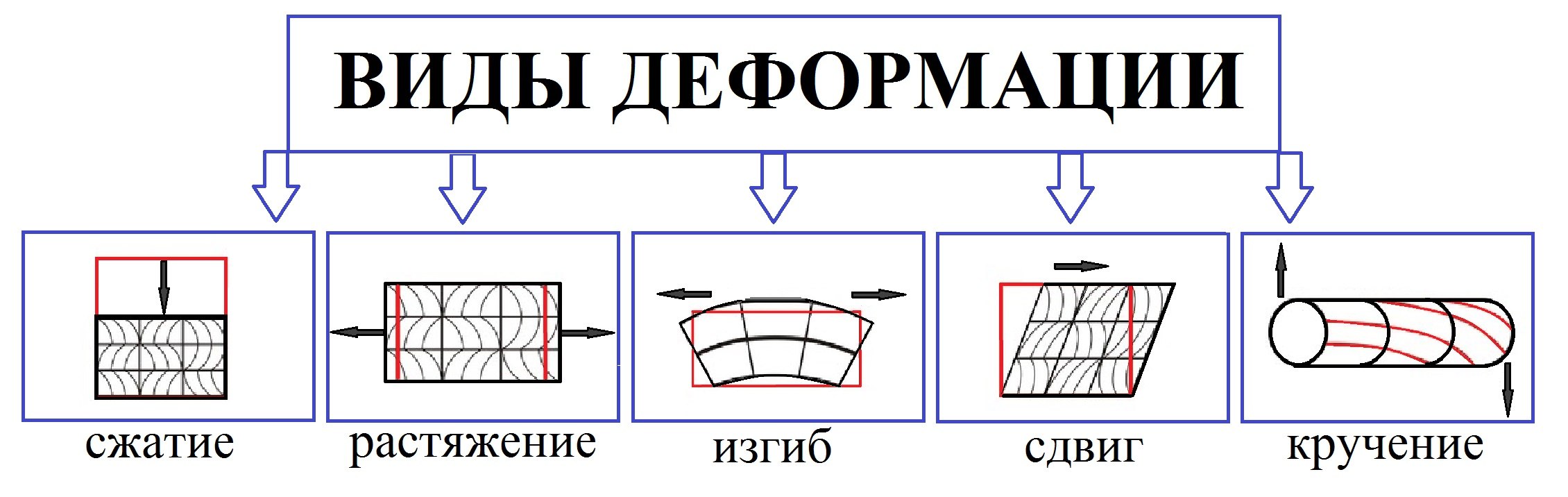
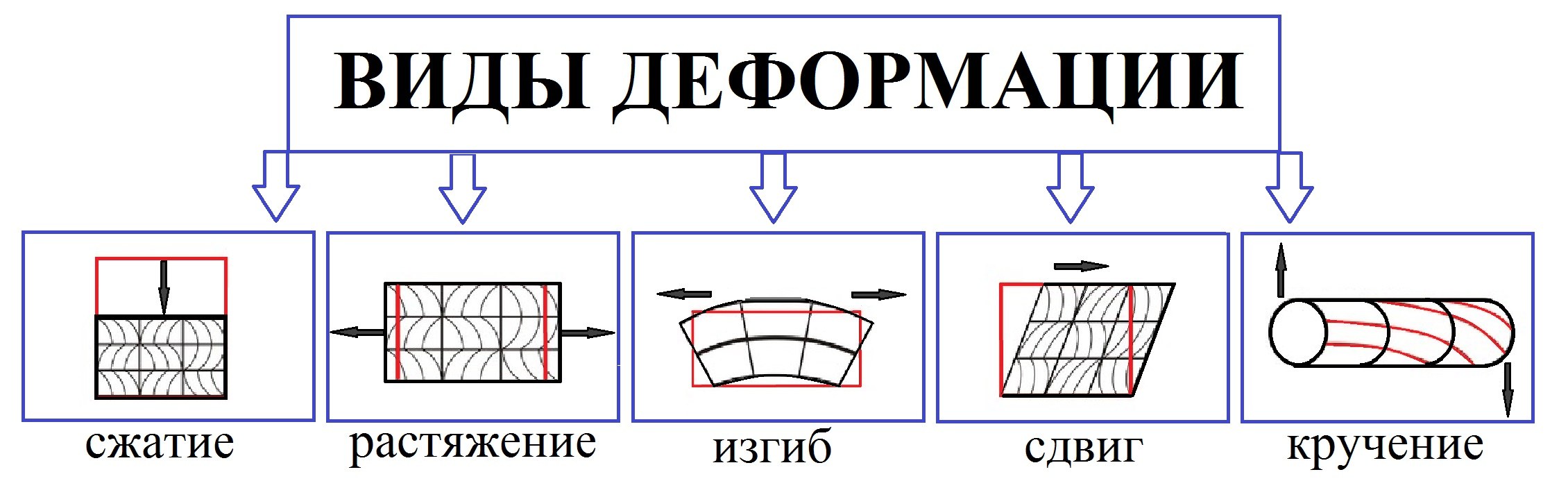
Типы деформации

В зависимости от того, как приложена внешняя сила, различают деформации растяжения-сжатия, сдвига, изгиба, кручения.

Деформация растяжения-сжатия

 

Деформация растяжения-сжатия вызывается силами, которые приложены к концам бруса параллельно его продольной оси и направлены в разные стороны.

Под действием внешних сил частицы твёрдого вещества, колеблющиеся относительно своего положения равновесия, смещаются. Но этому процессу пытаются помешать внутренние силы взаимодействия между частицами, старающиеся удержать их в исходном положении на определённом расстоянии друг от друга. Силы, препятствующие деформации, называются силами упругости.

Деформацию растяжения испытывают натянутая тетива лука, буксировочный трос автомобиля при буксировке, сцепные устройства железнодорожных вагонов и др.

Когда мы поднимается по лестнице, ступеньки под действием нашей силы тяжести деформируются. Это деформация сжатия. Такую же деформацию испытывают фундаменты зданий, колонны, стены, шест, с которым прыгает спортсмен.

Деформация сдвига

Если приложить внешнюю силу по касательной к поверхности бруска, нижняя часть которого закреплена, то возникает деформация сдвига. В этом случае параллельные слои тела как бы сдвигаются относительно друг друга.

Представим себе расшатанный табурет, стоящий на полу. Приложим к нему силу по касательной к его поверхности, то есть, попросту потянем верхнюю часть табурета на себя. Все его плоскости, параллельные полу, сместятся друг относительно друга на одинаковый угол.

Такая же деформация происходит, когда лист бумаги разрезается ножницами, пилой с острыми зубьями распиливается деревянный брус и др. Деформации сдвига подвергаются все крепёжные детали, соединяющие поверхности, — винты, гайки и др.

Деформация изгиба

Такая деформация возникает, если концы бруса или стержня лежат на двух опорах. В этом случае на него действуют нагрузки, перпендикулярные его продольной оси.

Деформацию изгиба испытывают все горизонтальные поверхности, положенные на вертикальные опоры. Самый простой пример — линейка, лежащая на двух книгах одинаковой толщины. Когда мы поставим на неё сверху что-то тяжёлое, она прогнётся. Точно так же прогибается деревянный мостик, перекинутый через ручей, когда мы идём по нему.

Деформация кручения

Кручение возникает в теле, если приложить пару сил к его поперечному сечению. В этом случае поперечные сечения будут поворачиваться вокруг оси тела и относительно друг друга. Такую деформацию наблюдают у вращающихся валов машин. Если вручную отжимать (выкручивать) мокрое бельё, то оно также будет подвергаться деформации кручения.

Закон Гука

Наблюдения за различными видами деформации показали, что величина деформации тела зависит от механического напряжения, возникающего под действием приложенных к телу сил.

Эту зависимость описывает закон, открытый в 1660 г. английским учёным Робертом Гуком, которого называют одним из отцов экспериментальной физики.

Виды деформации удобно рассматривать на модели бруса. Это тело, один из трёх размеров которого (ширина, высота или длина), гораздо больше двух других. Иногда вместо термина «брус» употребляют термин «стержень». У стержня длина намного превышает его ширину и высоту.

Рассмотрим эту зависимость для деформации растяжения-сжатия.

Предположим, что стержень первоначально имеет длину L. Под действием внешних сил его длина изменится на величину ∆l. Она называется абсолютным удлинением (сжатием) стержня.

• Для деформации растяжения-сжатия закон Гука имеет вид:
• F — сила, сжимающая или растягивающая стержень; k — коэффициент упругости.
• Сила упругости прямо пропорциональна удлинению тела до некого предельного значения.

Е — модуль упругости первого рода или модуль Юнга. Его величина зависит от свойств материала. Это теоретическая величина, введённая для характеристики упругих свойств тел.

1. S — площадь поперечного сечения стержня.
2. Отношение абсолютного удлинения к первоначальной длине стержня называют относительным удлинением или относительной деформацией.
3. При растяжении его величина имеет положительное значение, а при сжатии отрицательное.
4. Отношение модуля внешней силы к площади поперечного сечения стержня называется механическим напряжением.
5. Тогда закон Гука для относительных величин будет выглядеть так:
6. Напряжение σ прямо пропорционально относительной деформации ε.
7. Считается, что сила, стремящаяся удлинить стержень, является положительной (F ˃ 0), а сила, укорачивающая его, имеет отрицательное значение (F ˂ 0).

Измерение деформации

При проектировании и эксплуатации различных механизмов, технических объектов, зданий, мостов и других инженерных сооружений очень важно знать величину деформации материалов.

Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью. Для этого используют приборы, называемые тензометрами.

Тензометр состоит из тензометрического датчика и индикаторов. В него также может быть включено регистрирующее устройство.

В зависимости от принципа действия тензометры бывают оптические, пневматические, акустические, электрические и рентгеновские.

В основу оптических тензометров положено измерение деформации нити из оптоволокна, приклеенной к объекту исследования. Пневматические тензометры фиксируют изменение давления при деформации.

В акустических тензометрах с помощью пьезоэлектрических датчиков проводятся измерения величин, на которые изменяются скорость звука и акустическое затухание при деформации. Электрические тензометры вычисляют деформацию на основе изменений электрического сопротивления.

Вплоть до 80-х годов ХХ века сигналы датчиков регистрировались самописцами на обыкновенной бумажной ленте. Но когда появились компьютеры и начали бурно развиваться современные технологии, стало возможным наблюдать деформации на экранах мониторов и даже подавать управляющие сигналы, позволяющие изменить режим работы тестируемых объектов.

Источник: http://ency.info/materiya-i-dvigenie/molekulyarno-kineticheskaya-teoriya/360-deformatsiya-tvjordogo-tela-ejo-vidy-izmerenie

Физика

В СИ за единицу механического напряжения принимают 1Па = 1Н/м2. 

Закон Гука (1635-1703): при малых деформациях напряжение прямо пропорционально относительному удлинению (б = Е • е). На рис.33 представлен график зависимости механического напряжения от относительного удлинения.

Участок 0А — область пропорциональности: на этом участке выполняется закон Гука. Точке А соответствует напряжение бпроп, называемое пределом пропорциональности.

• Предел пропорциональности бпроп — максимальное напряжение, при котором закон Гука еще выполняется.
• Предел упругости бупр — напряжение, при котором тело полностью утрачивает упругость (участок АВ).
• На участке ВС наблюдается явление «текучести» материала: удлинение тела нарастает при незначительном росте деформирующей силы.
• При дальнейшем увеличении удлинения тело вновь обретает способность сопротивляться деформации; напряжение в нем вновь увеличивается, достигая максимума в точке D, которой соответствует начало разрушения.

Предел прочности бпроч — наибольшее напряжение, возникающее в теле перед началом разрушения. Участку DE соответствует постепенное разрушение тела.

Все детали машин и механизмов изготавливаются со значительным, но разумным запасом прочности.

Отношение предела прочности материала (или предела текучести для пластичных тел) к фактически действующему напряжению называют коэффициентом запаса прочности (k). Например, в строительном деле коэффициент запаса прочности стальных балокустановлен не менее 2,5 — 2,6, а для балок из хрупких материалов (чугун, бетон) не менее 3 — 9.

Механические свойства материалов различны. Такие материалы, как резина или сталь, обнаруживают упругие свойства при сравнительно больших напряжениях и деформациях. Их называют упругими.

Материалы, у которых незначительные нагрузки вызывают пластические деформации, называют пластичными (пластилин, свинец).

Большое значение на практике имеет такое свойство твердых тел, как хрупкость. Материалы называют хрупкими, если они разрушаются при небольших деформациях (чугун, фарфор).

Важной характеристикой материалов является твердость. Она характеризует способность материала оказывать сопротивление проникновению в него другого тела, т. е. способность противодействовать вдавливанию или царапанью.)

Деформация и напряжение. Деформацию сжатия и растяжения можно характеризовать абсолютным удлинением Δl, равным разности длин образца до растяжения l0 и после него l :

.

   Отношение абсолютного удлинения  к длине образца  называется относительным удлинением :

. (30.1)

При деформации тела возникают силы упругости. Физическая величина, равная отношению модуля силы упругости к площади сечения тела, называется механическим напряжением :

. (30.2)

За единицу механического напряжения в СИ принят паскалъ (Па). .

Модуль упругости. При малых деформациях напряжение прямо пропорционально относительному удлинению:

. (30.3)

Коэффициент пропорциональности Е в уравнении (30.3) называется модулем упругости. Модуль упругости одинаков для образцов любой формы и размеров, изготовленных из одного материала:

. (30.4)

Из формулы (30.4) следует, что

. (30.5)

Сравнив выражение (30.5) с законом Гука, получим, что жесткость k стержня пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.

Диаграмма растяжения. Зависимость напряжения  от относительного удлинения  является одной из важнейших характеристик механических свойств твердых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси ординат откладывается механическое напряжение , по оси абсцисс — относительное удлинение  (рис. 102).

Закон Гука выполняется при небольших деформациях. Максимальное напряжение , при котором еще выполняется закон Гука, называется пределом пропорциональности. За пределом пропорциональности (точка А) напряжение перестает быть пропорциональным относительному удлинению; до некоторого напряжения после снятия нагрузки размеры тела восстанавливаются полностью. Такая деформация называется упругой.Максимальное напряжение , при котором деформация еще остается упругой, называется пределом упругости(точка В). Большинство металлов испытывает упругую деформацию до значений .   При напряжениях, превышающих предел упругости , образец после снятия нагрузки не восстанавливает свою форму или первоначальные размеры. Такие деформации называются остаточными или пластическими.

   В области пластической деформации (участок CD) деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала.

   Материалы, у котерых область текучести CD значительна, могут без разрушения выдерживать большие деформации. Если же область текучести материала почти отсутствует, он без разрушения сможет выдержать лишь небольшие деформации. Такие материалы называются хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун.

   За пределом текучести кривая напряжений поднимается и достигает максимума в точке Е. Напряжение, соответствующее точке Е, называется пределом прочности . После точки Е кривая идет вниз и дальнейшая деформация вплоть до разрыва (точка К) происходит при все меньшем напряжении.

Дефекты в кристаллах. Способы повышения прочности твердых тел. Кристаллическими телами являются все металлические изделия — стальные каркасы зданий и мостов, рельсы железных дорог, линии электропередач, станки, машины, поезда, самолеты.

   Одной из важнейших задач науки и техники является создание прочных и надежных машин, станков и зданий с минимальной затратой металлов и других материалов.

   Сравнение реальной прочности кристаллов со значениями, полученными на основании теоретических расчетов, обнаруживает весьма существенные расхождения. Теоретический предел прочности в десятки и даже в сотни раз превосходит значения, получаемые при испытаниях реальных образцов.

   Оказалось, что причина расхождения теории и эксперимента заключается в наличии внутренних и поверхностных дефектов в строении кристаллических решеток.

   Самые простые дефекты в идеальной кристаллической решетке — точечные дефекты — возникают при замещении собственного атома чужеродным, внедрении атома в пространство между узлами решетки или при отсутствии атома в одном из узлов кристаллической решетки (рис. 103).

Другой вид дефектов — линейные дефекты — возникает при нарушениях в порядке расположения атомных плоскостей в кристаллах. Пример такого нарушения в структуре кристалла представлен на рисунке 104.

Деформация и разрушение кристалла с линейным дефектом облегчаются потому, что вместо одновременного разрыва всех связей между атомами двух плоскостей становится возможным поочередный разрыв небольшого числа связей между атомами с постепенным перемещением дефекта в кристалле.

   Для получения кристаллических материалов с высокой прочностью нужно выращивать монокристаллы без дефектов. Это очень сложная задача, и поэтому в практике этот путь пока широкого распространения не получил.

   Большинство современных методов упрочнения материалов основано на другом способе. Для упрочнения кристалла с дефектами в решетке можно создать условия, при которых перемещение дефектов в кристалле затрудняется.

Препятствием для перемещения дефектов в кристалле могут служить другие дефекты, специально созданные в кристаллической решетке. Так, для увеличения прочности стали применяется легирование стали — введение в расплав небольших добавок хрома, вольфрама и других элементов.

Внедрение атомов чужеродных элементов в решетку кристаллов железа затрудняет перемещение линейных дефектов при деформации кристаллов, прочность стали повышается при этом примерно в три раза.

Дополнительные дефекты в кристаллической решетке создаются при протяжке, дробеструйной обработке металлов. Эти виды обработки могут повышать прочность материалов примерно в два раза.

Источник: https://www.sites.google.com/site/fizika486486/

Виды деформаций твердых тел

• Известно, что при деформации твердые тела прояв­ляют упругие свойства. Так, было установ­лено, что растяжение или сжатие тела вы­зывает силу упругости, значение которой пропорционально величине деформации (за­кон Гука):
• Fупр = -kx,
• где x — величина деформации тела, k — ко­эффициент пропорциональности, характе­ризующий жесткость материала.

Жесткость металла k опреде­ляется значением силы F, ко­торую нужно приложить к телу, чтобы деформировать его на единицу длины (1 мм, 1 см или 1 м). В СИ она изменяется в Н/м.

Рис. 3.14. Продольная деформация рас­тяжения и сжатия

Различают разные виды деформации. Ес­ли сила, приложенная к телу, вызывает его растяжение или сжатие в одном из на­правлений (длины, ширины или высоты), то такая деформация называется продоль­ным растяжением или сжатием.

Например, растяжение или сжатие стержня длиной l под действием силы F, приложенной к его концам (рис. 3.14), приведет к дефор­мации растяжения или сжатия.

Сила уп­ругости, которая будет возникать при этом, имеет противоположное направление и по закону Гука будет пропорциональна сме­щению Δl.

Рис. 3.15. Деформация изгиба

Приложение силы перпендикулярно оси стержня (рис. 3.15) вызовет его прогибание, вследствие чего возникнет сила упругости, которая будет уравновешивать действующую силу. Этот вид деформации называется де­формацией изгиба. В данном случае сила упругости так же пропорциональна смеще­нию Δh: Fynp ~ Δh.

Рис. 3.16. Деформация кручения (а) и сдвига (б)

Существуют и другие виды деформации, например деформация кручения, когда под действием приложенных сил различные слои тела смещаются относительно оси, или дефор­мация сдвига, когда различные слои тела под действием силы сдвигаются друг относи­тельно друга (рис. 3.16). Материал с сайта http://worldofschool.ru

Любая из этих деформаций вызывает внутри тела силы, противодействующие ей. Если после прекращения действия внешних сил тело возобновляет свою первоначаль­ную форму и объем, то деформация на­зывается упругой.

Тем не менее, не всегда можно этого достичь. То есть после прекращения действия сил тело может сохранить (частично или полностью) деформированное состоя­ние. Это свойство твердых тел называют пластичностью.

Остаточная деформация, имею­щая место после снятия ме­ханических нагрузок, называет­ся пластической деформацией.

Учитывание упругих и пласти­ческих деформаций является основой конструирования де­талей машин, строительства, обработки материалов и т. д.

На этой странице материал по темам: Вопросы по этому материалу:

Источник: http://WorldOfSchool.ru/fizika/mehanika/sploshnyh-sred/deformacii/vidy-deformacij-tverdyh-tel

Деформация: виды деформации, пределы упругости и прочности

Частицы, из которых состоят твердые тела (как аморфные, так и кристаллические) постоянно совершают тепловые колебания около положений равновесия. В таких положениях энергия их взаимодействия минимальная.

Если расстояние между частицами уменьшается, начинают действовать силы отталкивания, а если увеличиваться – то силы притяжения.

Определение 1

Если твердое тело изменяется под воздействием внешних сил, то частицы, из которых оно состоит, меняют свое внутреннее положение. Такое изменение называется деформацией.

Виды деформации

Различают деформации нескольких видов. На изображении показаны некоторые из них.

Рисунок 3.7.1. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия.

Первый вид – растяжение или сжатие – является наиболее простым видом деформации.

В таком случае изменения, происходящие с телом, можно описать при помощи абсолютного удлинения Δl, которое происходит под действием сил, обозначаемых F→.

Взаимосвязь, существующая между силами и удлинением, обусловлена геометрическими размерами тела (в первую очередь толщиной и длиной), а также механическими свойствами вещества.

Определение 2

Если мы разделим величину абсолютного удлинения на первоначальную длину твердого тела, мы получим величину его относительного удлинения (относительной деформации).

Обозначим этот показатель ε и запишем следующую формулу:

ε=∆ll.

Определение 3

Относительная деформация тела растет при его растяжении и соответственно уменьшается при сжатии.

Если учесть, в каком именно направлении внешняя сила действует на тело, то мы можем записать, что F будет больше нуля при растяжении и меньше нуля при сжатии.

Механическое напряжение

Определение 4

• Механическое напряжение твердого тела σ – это показатель, равный отношению модуля внешней силы к площади сечения твердого тела.
• σ=FS.
• Величину механического напряжения принято выражать в паскалях (Па) и измерять в единицах давления.

Важно понимать, как именно механическое напряжение и относительная деформация связаны между собой. Если отобразить их взаимоотношения графически, мы получим так называемую диаграмму растяжения. При этом нам нужно отмерить величину относительной деформации по оси x, а механическое напряжение – по оси y.

На рисунке ниже представлена диаграмма растяжения, типичная для меди, мягкого железа и некоторых других металлов.

Рисунок 3.7.2. Типичная диаграмма растяжения для пластичного материала. Голубая полоса – область упругих деформаций.

В тех случаях, когда деформация твердого тела меньше 1% (малая деформация), то связь между относительным удлинением и механическим напряжением приобретает линейный характер. На графике это показано на участке Oa. Если напряжение снять, то деформация исчезнет.

Определение 5

Деформация, исчезающая при снятии напряжения, называется упругой.

Линейный характер связи сохраняется до определенного предела. На графике он обозначен точкой a.

Определение 6

Предел пропорциональности – это наибольшее значение σ=σпр, при котором сохраняется линейная связь между показателями σ и ε.

1. На данном участке будет выполняться закон Гука:
2. ε=1Eσ.
3. В формуле содержится так называемый модуль Юнга, обозначенный буквой E.

Если мы продолжим увеличивать напряжение на твердое тело, то линейный характер связи нарушится. Это видно на участке ab. Сняв напряжение, мы также увидим практически полное исчезновение деформации, то есть восстановление формы и размеров тела.

Предел упругости

Определение 7

Предел упругости – максимальное напряжение, после снятия которого тело восстановит свою форму и размер.

После перехода этого предела восстановления первоначальных параметров тела уже не происходит. Когда мы снимаем напряжение, у тела остается так называемая остаточная (пластическая) деформация.

Определение 8

Обратите внимание на участок диаграммы bc, где напряжение практически не увеличивается, но деформация при этом продолжается. Это свойство называется текучестью материала.

Предел прочности

Определение 9

Предел прочности – максимальное напряжение, которое способно выдержать твердое тело, не разрушаясь.

В точке e материал разрушается.

Определение 10

Если диаграмма напряжения материала имеет вид, соответствующий тому, что показан на графике, то такой материал называется пластичным. У них обычно деформация, при которой происходит разрушение, заметно больше области упругих деформаций. К пластичным материалам относится большинство металлов.

Определение 11

Если материал разрушается при деформации, которая превосходит область упругих деформаций незначительно, то он называется хрупким. Такими материалами считаются чугун, фарфор, стекло и др.

Деформация сдвига имеет аналогичные закономерности и свойства. Ее отличительная особенность состоит в направлении вектора силы: он направлен по касательной относительно поверхности тела.

Для поиска величины относительной деформации нам нужно найти значение Δxl, а напряжения – FS (здесь буквой S обозначена та сила, которая действует на единицу площади тела).

Для малых деформаций действует следующая формула:

∆xl=1GFS

Буквой G в формуле обозначен коэффициент пропорциональности, также называемый модулем сдвига. Обычно для твердого материала он примерно в 2-3 раза меньше, чем модуль Юнга. Так, для меди E=1,1·1011 Н/м2, G=0,42·1011 Н/м2.

Когда мы имеем дело с жидкими и газообразными веществами, то важно помнить, что у них модуль сдвига равен 0.

При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях

∆VV=1Bp

Для твердого тела, изготовленного из стали, значение этого параметра равно 0,025 %, то есть оно меньше в 70 раз. Это подтверждает, что твердые тела благодаря жесткой кристаллической решетке обладают гораздо меньшей сжимаемостью по сравнению с жидкостью, в которой атомы и молекулы связаны между собой не так плотно.

Газы могут сжиматься еще лучше, чем тела и жидкости.

От значения модуля всестороннего сжатия зависит скорость, с которой звук распространяется в данном веществе.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Источник: https://Zaochnik.com/spravochnik/fizika/molekuljarno-kineticheskaja-teorija/deformatsija/

Урок "Виды деформаций твердых тел"

• План – тезис урока.
• Предмет: физика.
• Класс: 10.
• Преподаватель: Подольская Людмила Ивановна.
• Тема урока: Виды деформаций твердых тел.
• Эпиграф: Душа науки – это практическое применение ее открытий.
• У. Томсон
• Цели урока:
• обучающая: 1) Сформировать у учащихся представления о свойствах твердых тел;
• 2) Расширить понятие деформации и рассмотреть различные виды деформаций;
• 3) Показать границы применимости физических законов в профессии.
• развивающая:1) развивать познавательную активность учащихся с помощью проблемных вопросов и исторического материала;
• 2) способствовать развитию навыков работы с дополнительной литературой;
• воспитательная: показать связь физики с профессией, способствовать формированию научного мировоззрения и любознательности учащихся.
• Форма проведения урока: комбинированный урок.
• Межпредметные связи: электроматериаловедение, история физики, математика,
• спецтехнология.
• Оборудование:1) модель твердого тела, состоящая из параллельных пластин;
• 2) Пружина, закрепленная в штативе;
• 3) Набор грузов;
• 4) Ластик ученический, расчерченный с обеих сторон в клетку;
• 5) Резиновый жгут с длинным штрихом:
• 6) Раздаточный материал – таблица для записи
• результатов наблюдений и опытов упругих деформаций.
• МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ.

Урок разработан для учащихся 1курса в соответствии с программой по физике и с учетом требований стандарта образования. Урок изучения нового материала по теме «Твердые тела», способствует развитию познавательной активности учащихся путем привлечение дополнительных источников информации.

1. Урок в основном направлен на развитие любознательности учащихся, на формирование научного мировоззрения и на осознание существующих проблем.
2. На уроке рассмотрены вопросы профессиональной направленности:
3. 1) понятие деформации;
4. 2) виды деформаций;
5. 3) учет деформаций в промышленности;
6. 4) применение закона Гука в профессии.
7. Урок способствует формированию глубоких знаний, как по физике, так и по предметам профессионально – технического цикла.
8. Урок предусматривает использование наглядного материала и оборудования, что способствует развитию познавательного интереса.
9. Учащиеся должны знать:

• Понятие деформации.
• Виды деформаций.
• Как учитываются свойства твердых тел в технике.

Учащиеся должны уметь:

• Определять вид деформации.
• Проводить эксперимент по наблюдению деформаций различных видов.
• Отбирать необходимый материал для подготовки докладов по данным темам.

ЭТАПЫ УРОКА:

1. Организационный момент (2 мин.).

Цель: Подготовить учащихся к восприятию материала.

1. Введение (сообщение учителя). (7 мин.).

Цель: постановка проблемного вопроса на уроке, активизация учащихся.

1. Выступления учащихся с докладами. (15 мин.).

Цель: донести до учащихся исторические сведения об открытии закона Гука.

1. Объяснение нового материала и эксперименты учащихся. (19 – 20 мин.)

Цель: показать виды деформаций и объяснить возникновение деформации на молекулярном уровне.

1. Подведение итогов (слово учителя). (5 мин.).

Цель: обобщение знаний полученных на уроке, решение поставленной проблемы.

1. Домашнее задание. (1- 2 мин.).

• Цель:
• Итого 40 мин.
• Ход урока.

2. Введение. Слово преподавателя.

— Подготовка учащихся к восприятию материала.

Фронтальный опрос: Какими свойствами обладают твердые тела? Как расположены атомы в твердых телах? Что такое деформация?

— Постановка проблемного вопроса на уроке:

Атомы и молекулы твердых тел занимают определенное положение и совершают колебания около этого положения. При уменьшении расстояния между молекулами появляются силы отталкивания, а при увеличении силы притяжения. Этими силами объясняются упругие свойства твердых тел.

Недеформируемых тел в природе не существует. В то же время мы часто встречаемся с малыми деформациями, которые сами и не замечаем.

Изучение деформаций и свойств твердых тел дает возможность предварительно определять изменения, возникающие в конструкциях при нагрузке. Инженеры, которые проектируют конструкцию, интересуются свойствами материалов и определяют, какую нагрузку может выдержать конструкция.

Твердые тела могут изменить свою форму под действием внешних сил приложенных к ним. Изменение формы или объема тела называется деформацией. Деформации бывают двух видов: 1) упругая деформация – деформация, которая полностью исчезает после прекращения действия внешних сил. Упругую деформацию испытывают пружина, резиновый шнур.

При деформации возникает сила упругости, которая направлена в сторону противоположную смещению частиц тела.

2) пластическая деформация – деформация, которая не исчезает после прекращения действия внешних сил. Пластическую деформацию испытывают пластилин, глина, воск, свинец.

1. Существует несколько видов упругих деформаций, которые мы будем наблюдать с помощью оборудования: 1) модель твердого тела, состоящая из параллельных пластин;
2. 2) Пружина, закрепленная в штативе;
3. 3) Набор грузов;
4. 4) Ластик ученический, расчерченный с обеих сторон в клетку;
5. 5) Резиновый жгут с длинным штрихом:
6. Доклад открытие Гука.
7. Учащиеся получают бланки для выполнения экспериментальной работы, где необходимо ответить на вопросы о проделанных опытах.
8. Преподаватель показывает опыты:

1) по растяжению резинового жгута, на котором насажен картонный круг, если потянуть за жгут, то круг сползет вниз. Деформация растяжения характеризуется абсолютным и относительным удлинением. Абсолютное удлинение показывает, на сколько изменилась длина тела.

• ∆ℓ = ℓ — ℓ0
• Относительное удлинение показывает, во сколько раз изменилась длина тела.
• ε = ∆ℓ/ℓ0 , где ℓ0 – начальная длина, ℓ — конечная длина стержня.

При малых деформациях справедлив закон Гука, который говорит о том, что чем больше сила действует на тело, тем большую деформацию тело получает. Для описания большей деформации используется диаграмма растяжения и вводится понятие механического напряжения.

Механическое напряжение это отношение силы упругости к площади поперечного сечения тела: σ =F/S. За единицу напряжения принимается 1 Па = 1 Н/м2 . График зависимости напряжения от относительного удлинения строится по результатам опытов по растяжению тела и называется диаграмма растяжения.

Закон Гука: при малых деформациях напряжение прямо пропорционально относительному удлинению. Закон Гука записывается в виде: σ = E|ε|. Коэффициент пропорциональности E, входящий в закон Гука, называется модулем Юнга. Для большинства материалов модуль Юнга определен экспериментально, он характеризует сопротивляемость материала упругой деформации.

Например, модуль Юнга стали 21 * 1010 Па, а модуль Юнга

При некотором напряжении удлинение нарастает практически без увеличения нагрузки. Это явление называют текучестью материала. Напряжение, при котором происходит разрыв образца, называется пределом прочности. Эта величина зависит от материала и от качества его обработки.

Диаграмма растяжения дает достаточно полную информацию о механических свойствах материала и позволяет оценить прочность.

Учащиеся делают опыт самостоятельно и делают выводы.

2) Показать опыт по деформации сдвига с помощью модели твердого тела, состоящего из параллельных пластин. Деформация сдвига характеризуется относительным смещением слоев тела.

Учащиеся наблюдают деформацию сдвига с помощью ластика и отвечают на вопросы.

3) Показать опыт по деформации изгиба с помощью модели твердого тела, состоящего из параллельных пластин. Деформация изгиба характеризуется стрелой прогиба.

Поскольку слои близкие к нейтральному слою испытывают меньшую деформацию, то детали машин и конструкций, работающие на изгиб, выгодно делать полыми.

Это дает экономию материала и снижает массу конструкции без ухудшения механических свойств.

Учащиеся наблюдают деформацию изгиба с помощью ластика.

4) Показать опыт по деформации кручения с помощью резинового жгута, на котором сделан длинный штрих. Деформация кручения характеризуется углом закручивания.

Учащиеся наблюдают деформацию кручения с помощью ластика.

Вывод с урока: В любом деформированном теле действует сила упругости, которая направлена в сторону противоположную смещению частиц и препятствует разрушению тела.

1. Наблюдение упругих деформаций твердых тел.
2. Вид деформаций
3. Вопросы
4. Ответы

1. Деформация растяжения – сжатия.

ОПЫТ: Резиновый ластик расчерчен карандашом в клетку. Растяните и сожмите ластик.

1. Как направлена сила упругости при растяжении или сжатии ластика?

При растяжении ластика

При сжатии ластика

2. Как изменится длина и площадь поперечного сечения ластика при растяжении и сжатии?

При растяжении ластика

При сжатии ластика

3. Нарисовать новую форму, которую приобрели ластик и сетка в результате растяжения и сжатия.

• При растяжении ластика
• При сжатии ластика
• 4. Привести примеры деформации растяжения
• и сжатия тел.
• Деформацию растяжения испытывают:
• Деформацию сжатия испытывают:

2. Деформация сдвига.

ОПЫТ: действуя на ластик руками, получите деформацию сдвига.

1. Как смещаются слои ластика при деформации?

2. Сделайте рисунок, показав, как меняется форма квадратов и ластика в результате деформации.

3. Как изменится деформация сдвига при увеличении нагрузки?

4. Приведите примеры деформации сдвига.

3. Деформация изгиба.

ОПЫТ: действуя на ластик руками, получите деформацию изгиба.

1. Какие деформации, и в каких слоях возникают в результате изгиба?

2. Сделайте рисунок, показав, как

меняется форма квадратов и ластика в результате деформации.

3. Приведите примеры деформации изгиба.

4. Деформация кручения.

ОПЫТ: действуя на ластик руками, получите деформацию кручения.

1. Из каких деформаций состоит деформация кручения?

2. Сделайте рисунок, показав, как

меняется форма квадратов и ластика в результате деформации.

3. Приведите примеры деформации кручения.

1. Приведите примеры, где и когда нужно учитывать деформации в вашей профессии?
2. Какие виды деформаций испытывают: 1) тросы подъемного крана, 2) струна, 3) шуруп, 4) пружина, 5) дверной ключ, 6) провода линии электропередач, 7) стул.
3. Доклад по теме: «Открытие Гука».

В 1676 году Роберт Гук объявил о своем открытии. Это был простой закон, но ему была предназначена важная роль в физике и технике. Гук был в восторге от своего открытия, но своим коллегам он не доверял и боялся, как бы кто – нибудь не приписал это открытие себе.

Поэтому Гук придал своему открытию закона о растяжении пружин вид анаграммы: c e i i i n o s s s t t u v. Это было своеобразное патентование открытия.

Он выждал два года, чтобы конкуренты могли сделать заявки о своих открытиях, связанных с пружинами, а затем дал расшифровку своей анаграммы: «ut tension, sic vis», или «каково удлинение, такова и сила».

Гук открыл, что при растяжении возрастающей силой удлинение изменяется прямо пропорционально этой силе. Как известно из практики, это соотношение выдерживается для стальных пружин с высокой точностью в широком диапазоне удлинений. Оно справедливо также для пружин из других материалов.

С поведением материалов по закону Гука мы встречаемся во многих случаях растяжения, сжатия, скручивания, изгиба, упругой деформации любых видов.

Закон Гука открывает перед инженерами возможность предварительно определять упругие изменения, возникающие при нагрузке в конструкциях. Он может вычислить прогиб моста, прежде чем мост построен, или определить закручивающую силу на валу винта, измеряя малые деформации при закручивании. Инженеры интересуются свойствами материалов за пределами закона Гука.

Источник: https://infourok.ru/urok-vidi-deformaciy-tverdih-tel-486143.html

Деформация твердых тел

Слайд 1

« Первые шаги в науку » «Деформация твердых тел» Гейн Александр обучающийся 10 класса Руководитель: Жалнина Е.А., учитель физики Образовательное учреждение: МБОУ Мучкапская СОШ Мучкапского р-на Секция «Физика»

Слайд 2

Актуальность Вопрос, почему любое твердое тело вообще способно сопротивляться приложенной к нему нагрузке, издавна занимал умы ученых. Мы не проваливаемся сквозь пол, и это для нас настолько обычно, что мы над этим никогда не задумываемся. Первый существенный вклад в решение проблемы внесли такие выдающиеся умы, как Галилей (1564–1642) и Гук (1635–1702).

• Слайд 3
• Цель работы Изучение физического явления – деформации твердого тела, экспериментального исследования силы упругости, возникающей при деформации пружины.
• Слайд 4
• Задачи: изучить и проанализировать теоретический материал по выбранной теме; рассмотреть различные виды деформации твердых тел; определить особенности деформирования тела при малых деформациях; исследовать зависимость силы упругости, возникающей при деформации пружины, от ее удлинения;
• Слайд 5

Гипотеза Любое твердое тело сопротивляется приложенной к нему нагрузке. Деформация твердых тел происходит неравномерно .

1. Слайд 6
2. ДЕФОРМАЦИЯ УПРУГАЯ ПЛАСТИЧЕСКАЯ растяжение сжатие изгиб кручение сдвиг
3. Слайд 7

РОБЕРТ ГУК Родился 18 июля 1635 г. в местечке Фрешуотер на английском острове Уайт в семье настоятеля местной церкви. В истории физики он известен как первый, кто установил связь силы упругости и деформации

• Слайд 8
• Закон Гука Сила упругости, возникающая при упругой деформации тела, прямо пропорциональна величине деформации) и направлена в сторону противоположную перемещению частиц тела при деформации.
• Слайд 9

Закон Гука хорошо выполняется только при малых деформациях. При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе, а при очень больших деформациях тело разрушается.

1. Слайд 10
2. ДЕФОРМАЦИИ В ЖИЗНИ СРЕЗ
3. Слайд 11

Результат исследования Зависимость прогиба деревянной линейки от силы, действующей на неё . Зависимость прогиба деревянной линейки от её длины. Зависимость прогиба деревянной линейки от её ширины Зависимость прогиба железной линейки от силы, действующей на неё Зависимость прогиба железной линейки от её длины.

• Слайд 12
• РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ В ходе исследования было отмечено, что существует зависимость деформаций от геометрических размеров, длина и толщина образца влияют в большей степени при изгибе, чем ширина; Деформации зависят от материала образцов; Существует предел упругих деформаций; Наблюдается остаточная деформация у всех образцов, но в разной степени; Практические результаты качественно согласуются с теорией деформации изгиба: При измерениях у меня получилась погрешность из-за того, что я не учитывал вес самих образцов и маленькую остаточную деформацию при проведении повторных опытов.
• Слайд 13

Гипотеза о том, что деформация физических тел происходит неравномерно, подтверждается только при больших деформациях. Закон Гука хорошо выполняется только при малых деформациях. При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе, а при очень больших деформациях тело разрушается. Вывод

Слайд 14

ЗАКЛЮЧЕНИЕ Проведённая работа мне очень понравилась, потому что во время неё я узнал много нового. Интересен был процесс исследования и достаточно труден процесс измерения: например, надо было подумать, как установить лучше прибор, и как сделать так, чтобы измерения были точнее.

Результаты получились неожиданными; измерения получились верные, но не очень точные, хотя они сопоставимы с теоретическими данными. Я думаю, что такие исследовательские работы нужны в процессе изучения любого предмета это поможет лучше понять предмет и подавить страх перед ним.

Слайд 15

Источник: https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2014/11/12/deformatsiya-tverdykh-tel