Формула n-го члена геометрической прогрессии

Геометрической прогрессией называют числовую последовательность, каждый следующий член которой получается из предыдущего умножением его на постоянное число, не равное нулю

Это число называют знаменателем геометрической прогрессии и обозначают буквой (q).

Например, последовательность (3); (6); (12); (24); (48)… является геометрической прогрессией, потому что каждый следующий элемент отличается от предыдущего в два раза (иначе говоря, может быть получен из предыдущего умножением его на два):

Как и любую последовательность, геометрическую прогрессию обозначают маленькой латинской буквой. Числа, образующие прогрессию, называют ее членами (или элементами). Их обозначают той же буквой, что и геометрическую прогрессию, но с числовым индексом, равным номеру элемента по порядку

Например, геометрическая прогрессия (b_n = {3; 6; 12; 24; 48…}) состоит из элементов (b_1=3); (b_2=6); (b_3=12) и так далее. Иными словами:

порядковый номер элемента	(1)	(2)	(3)	(4)	(5)	…
обозначение элемента	(b_1)	(b_2)	(b_3)	(b_4)	(b_5)	…
значение элемента	(3)	(6)	(12)	(24)	(48)	…

Если вы поняли вышеизложенную информацию, то уже сможете решить большинство задач на эту тему.

Пример (ОГЭ): Геометрическая прогрессия задана условиями (b_1=-2); (q=7). Найдите (b_4). Решение:

	Зная первый член и знаменатель, последовательно вычисляем элементы, пока не дойдем до нужного.
	Можно писать ответ.

Ответ: (-686).

Пример (ОГЭ): Даны первые три члена прогрессии (324); (-108); (36)…. Найдите (b_5). Решение:

	Чтобы продолжить последовательность, нам нужно знать знаменатель. Найдем его из двух соседних элементов: на что нужно умножить (324), чтоб получилось (-108)?
(324·q=-108)	Отсюда без проблем вычисляем знаменатель.
(q=-) (frac{108}{324})(=-) (frac{1}{3})	Теперь мы легко находим нужный нам элемент.
	Готов ответ.

• Ответ: (4).
• Пример:  Прогрессия задана условием (b_n=0,8·5^n). Какое из чисел является членом этой прогрессии:
• а) (-5)      б) (100)     в) (25)     г) (0,8) ?

Решение: Из формулировки задания очевидно, что одно из этих чисел точно есть в нашей прогрессии. Поэтому мы можем просто вычислять ее члены по очереди, пока не найдем нужное нам значение.

Так как у нас прогрессия задана формулой n-го члена, то вычисляем значения элементов, подставляя разные (n): (n=1);  (b_1=0,8·5^1=0,8·5=4) – такого числа в списке нет. Продолжаем.

(n=2);  (b_2=0,8·5^2=0,8·25=20) – и этого тоже нет.

1. (n=3);   (b_3=0,8·5^3=0,8·125=100) – а вот и наш чемпион!
2. Ответ: (100).

Пример (ОГЭ): Даны несколько идущих последовательно друг за другом членов геометрической прогрессии …(8); (x); (50); (-125)…. Найдите значение элемента, обозначенного буквой (x).

Решение:

	Найти (x), можно, например, умножив (8) на знаменатель прогрессии. Однако мы его не знаем, поэтому сначала найдем знаменатель из двух известных соседних членов.
(50·q=-125)
(q=-) (frac{125}{50})(=-)(2,5)	Теперь вычисляем икс, умножая (8) на (-2,5).
	Задача решена.

Ответ: (-20).

Пример (ОГЭ): Прогрессия задана условиями (b_1=7), (b_{n+1}=2b_n). Найдите сумму первых (4) членов этой прогрессии.

Решение:

(b_1=7), (b_{n+1}=2b_n)	Мы знаем первый элемент и имеем рекуррентное соотношение — формулу для вычисления следующего элемента по предыдущему. Вот и найдем необходимые нам первые (4) элемента, подставляя разные (n).
(n=1);   (b_{1+1}=2b_1 :: ⇔ :: b_2=2·7=14) (n=2);   (b_{2+1}=2b_2 :: ⇔ :: b_3=2·14=28) (n=3);   (b_{3+1}=2b_3 :: ⇔ :: b_4=2·28=56)	Теперь найдем сумму.
(S_4=b_1+b_2+b_3+b_4=) (=7+14+28+56=105)	Ответ готов.

Ответ: (105).

Пример (ОГЭ): Известно, что в геометрической прогрессии (b_6=-11), (b_9=704). Найдите знаменатель (q).

Решение:

	Из схемы слева видно, что чтобы «попасть» из (b_6) в (b_9) – мы делаем три «шага», то есть три раза умножаем (b_6) на знаменатель прогрессии. Иными словами (b_9=b_6·q·q·q=b_6·q^3).
(b_9=b_6·q^3)	Подставим известные нам значения.
(704=(-11)·q^3)	«Перевернем» уравнение и разделим его на ((-11)).
(q^3=) (frac{704}{-11})(::: ⇔ ::: )(q^3=-) (64)	Какое число в кубе даст (-64)? Конечно, (-4)!
(q=-4)	Ответ найден. Его можно проверить, восстановив цепочку чисел от (-11) до (704).
	Все сошлось — ответ верен.

Ответ: (-4).

Как видите, большинство задач на геометрическую прогрессию можно решать чистой логикой, просто понимая суть (это вообще характерно для математики). Но иногда знание некоторых формул и закономерностей ускоряет и существенно облегчает решение. Мы изучим две такие формулы.

Формула (n)-го члена: (b_n=b_1·q^{n-1}), где (b_1) – первый член прогрессии; (n) – номер искомого элемента; (q) – знаменатель прогрессии; (b_n) – член прогрессии с номером (n).

С помощью этой формулы можно, например, решить задачу из самого первого примера буквально в одно действие.

Пример (ОГЭ): Геометрическая прогрессия задана условиями (b_1=-2); (q=7). Найдите (b_4). Решение:

(b_4=b_1·q^3)	Нам нужен четвертый член, вот и вычисляем его сразу, напрямую, не находя всех промежуточных.
(b_4=(-2)·7^3=(-2)·343=-686).	Готов.

Ответ: (-686).

Этот пример был простым, поэтому формула нам облегчила вычисления не слишком сильно. Давайте разберем задачку чуть посложнее.

Пример: Геометрическая прогрессия задана условиями (b_1=20480); (q=frac{1}{2}). Найдите (b_{12}). Решение:

(b_{12}=b_1·q^{11})	Действуем как в предыдущей задаче.
(b_4=20480·(frac{1}{2})^{11}=20480·frac{1}{2048}=10.)	Есть ответ.

Ответ: (10).

Конечно, возводить (frac{1}{2}) в (11)-ую степень не слишком радостно, но всё же проще чем (11) раз делить (20480) на два.

Сумма (n) первых членов: (S_n=)( frac{b_1·(q^n-1)}{q-1}), где (b_1) – первый член прогрессии; (n) – количество суммируемых элементов; (q) – знаменатель прогрессии; (S_n) – сумма (n) первых членов прогрессии.

Пример (ОГЭ): Дана геометрическая прогрессия (b_n), знаменатель которой равен (5), а первый член (b_1=frac{2}{5}). Найдите сумму первых шести членов этой прогрессии. Решение:

(S_6=)( frac{b_1·(q^6-1)}{q-1})	Все данные есть, сразу вычисляем ответ.
(S_6=)( frac{frac{2}{5}·(5^6-1)}{5-1})(=)( frac{frac{2}{5}·15624}{4})(=) (=)( frac{2·15624}{5·4})(=)(frac{15624}{10})(=1562,4)	Ответ готов.

Ответ: (1562,4).

И вновь мы могли решить задачу «в лоб» – найти по очереди все шесть элементов, а затем сложить результаты. Однако количество вычислений, а значит и шанс случайной ошибки, резко возросли бы.

Для геометрической прогрессии есть еще несколько формул, которые мы не стали рассматривать тут из-за их низкой практической пользы. Вы можете найти эти формулы здесь.

Если же (q) меньше единицы, но при этом положителен (то есть, лежит в пределах от нуля до единицы), то каждый следующий элемент будет меньше чем предыдущий. Например, в прогрессии (4); (2); (1); (0,5); (0,25)… знаменатель (q) равен (frac{1}{2}).

Эти прогрессии называются убывающими. Обратите внимание, что ни один из элементов такой прогрессии не будет отрицателен, они просто становятся всё меньше и меньше с каждым шагом. То есть, мы будем постепенно приближаться к нулю, но никогда его не достигнем и за него не перейдем. Математики в таких случаях говорят «стремиться к нулю».

Отметим, что при отрицательном знаменателе элементы геометрической прогрессии будут обязательно менять знак. Например, у прогрессии (5); (-15); (45); (-135); (675)… знаменатель (q) равен (-3), и из-за этого знаки элементов «мигают».

Источник: http://cos-cos.ru/math/244/

Урок «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии»

Бесплатно

Видеоурок «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии» дает представление о геометрической прогрессии, ее элементах, формирует умения решать задачи, в которых используются геометрические прогрессии. Задача данного видеоурока – представить учебный материал в наглядном виде, повысить эффективность обучения на уроках математики.

В видеоматериале используются элементы, помогающие удерживать внимание учеников на изучаемом материале, помогать запоминать понятия и определения, способствовать глубокому пониманию материала. Такими инструментами являются анимационные эффекты, выделение цветом, заключение важных материалов в рамки для запоминания и записи в тетради.

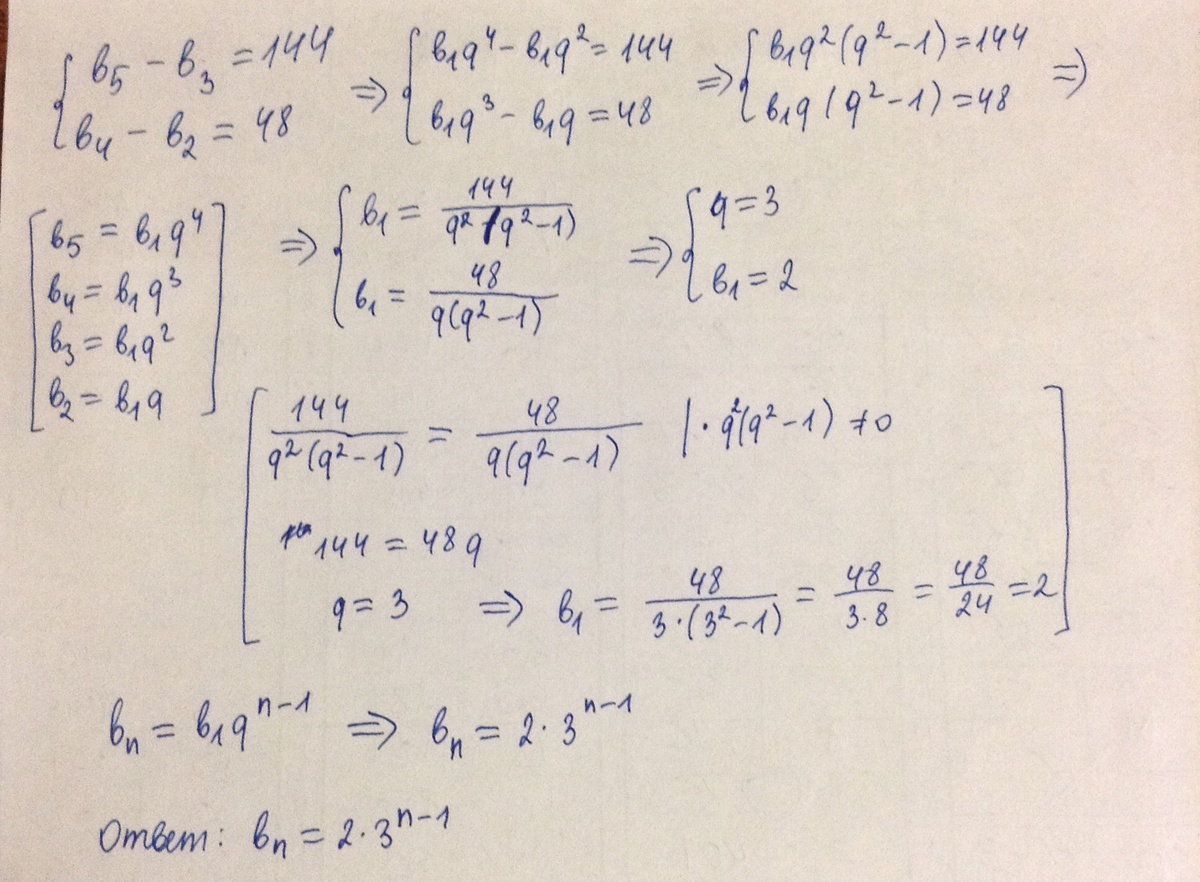
Урок начинается с представления темы. Вначале предлагается рассмотреть последовательность чисел, которые представляют собой степень с одинаковым основанием и показателем степени. Возрастающем с каждым членом на единицу: 2, 22, 23, 24… Отмечается, что каждый член данной прогрессии, кроме первого, образован умножением на 2  предыдущего члена.

Такая последовательность называется геометрической прогрессией. Название прогрессии выделено для запоминания в рамку. Далее демонстрируется определение геометрической прогрессии, которая представляет собой последовательность чисел, не равных нулю, которые образуются умножением предыдущего члена на некоторое одно и то же число, начиная со второго члена.

На следующем кадре представлен общий вид геометрической прогрессии (bn), которая определяется тем, что для каждого натурального nбудет bn≠0, а bn+1= bn·q, где q – некоторое число.

Рассматривается, каким образом определяется геометрическая прогрессия, описанная в начале урока 2, 22, 23, 24… Если данную последовательность обозначить через (bn), то ее каждый член, больший первого, можно представить равенством bn+1= bn·2. Число q, на которое умножается каждый член прогрессии, здесь равняется 2.

Далее вводится понятие знаменателя геометрической прогрессии, который равен уже выделяемому числу q. Для этого указывается, что при делении любого члена геометрической прогрессии на предыдущий член bn+1/bnполучается данное число q, которое неравно 0. Оно и является знаменателем прогрессии. Задание некоторой геометрической прогрессии сводится к указанию ее первого члена и знаменателя.

Приводятся примеры, в которых необходимо определить геометрическую прогрессию, в которой указаны первый член и знаменатель. Описывается геометрическая прогрессия 1; 0,1; 0,01; 0,001; 0,0001,… с первым членом b1=1 и q=0,1, прогрессия с первым отрицательным членом b1=-4 и знаменателем q=3: -4; -12; -36;…, прогрессия с отрицательным знаменателем q=-2 и первым членом b1=6: 6; 6;…

На основе рассмотренных примеров делается обобщение, каким образом можно найти любой член геометрической прогрессии: b2= b1q, b3= b2q= b1q2 и т.п.

Из данных формул видно, что следующий член образуется умножением первого на qn-1. На экран выводится формула bn=b1qn-1.

Отмечается, что данная формула есть формулой n-го члена геометрической прогрессии, ее необходимо запомнить, так как она далее будет использоваться в решении задач.

Рассматривается пример, в котором описывается нахождение 5-го члена геометрической прогрессии, в которой первый член b1=8 и знаменателем прогрессии является q=1/2.

Напоминается изученная формула n-го члена, которая для 5-го члена будет звучать таким образом: b5=b1q5-1.

После подстановки чисел, являющихся значениями первого члена и знаменателя, вычисляется 5-й член прогрессии: b5=8·(1/2)4=1/2.

Второй пример демонстрирует нахождение 6-го члена геометрической прогрессии, в которой известен первый и третий члены: b1=64 и b3=16. Для поиска третьего члена прогрессии формула приобретает вид: b3=b1q2.

Зная, что каждый следующий член образуется умножением предыдущего на знаменатель, определяем квадрат знаменателя q2= b3/b1=16/64=1/4. Очевидно, что q может принимать значения ½ или -1/2. Решение сводится к вычислению значения 6-го члена в случае, когда знаменатель равен ½ и -1/2.

В первом случае b6=b1q5=64·(1/2)5=2, а во втором b6=b1q5=64·(-1/2)5=-2. Поэтому значение 6-го члена может быть 2 или -2.

Демонстрируется пример, каким образом используются математические знания о геометрической прогрессии в решении практических задач. Предлагается рассмотреть решение задачи о возрастании суммы банковского вклада за 5 лет, если процент роста составляет 4%, а начальная сумма 6000 рублей.

Так как рост вклада за первый год составит 4%, то сумма будет 6000·1,04 р., значение этой суммы за два года будет составлять (6000·1,04)·1,04 или 6000·1,042. Таким образом мы получаем геометрическую прогрессию, в которой каждый последующий член умножается на 1,04.

Она будет состоять из чисел 6000, 6000·1,04; 6000·1,042; … Накопления, которые будут на счете через 5 лет, представляют собой 6-й член геометрической прогрессии. По формуле b6=b1q5 находим его значение 6000·1,045≈7300. Это и будет приближенным значением суммы.

Задачи подобного типа называются задачами со сложными процентами. Они нередко появляются в экономике, банковском секторе.

На экран для запоминания выведено еще одно полезное правило. Оно утверждает, что квадрат любого члена геометрической прогрессии, кроме первого, будет равен произведению предыдущего и последующего членов. Данное утверждение подтверждается, если рассмотреть некоторую прогрессию (bn). В ней n-й член равен bn= bn-1q. А n+1-й член определяется bn+1= bnq.

Так как все члены геометрической прогрессии не равны нулю, можно их представить отношением bn/bn-1=bn+1/bn. Отсюда значение квадрата будет bn2= bn-1·bn+1. Также отмечается, что к данному утверждению верно и обратное.

То есть равенство произведения предыдущего и последующего членов квадрату данного члена означает, что эта последовательность – геометрическая прогрессия.

Обращается внимание учеников на то, что модуль любого члена геометрической прогрессии является средним геометрическим последующего и предыдущего членов. Это подтверждается простой демонстрацией: bn2=bn-1·bn+1, следовательно, | bn|=√(bn-1·bn+1).

Видеоурок «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии» может быть использован как наглядный материал или полноценная часть урока в школе. Он хорошо раскрывает данную тему, поэтому может быть полезен для самостоятельного изучения, может быть полезен в ходе дистанционного обучения.

Источник: https://urokimatematiki.ru/urok-opredelenie-geometricheskoy-progressii-formula-ngo-chlena-geometricheskoy-progressii-671.html

Геометрическая прогрессия на примерах

Геометрическая прогрессия не менее важная в математике по сравнению с арифметической. Геометрической прогрессией называют такую последовательность чисел b1, b2,…

, b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число.

Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначают

Для полного задания геометрической прогрессии кроме знаменателя необходимо знать или определить первый ее член. Для положительного значения знаменателя прогрессия является монотонной последовательностью, причем если это последовательность чисел является монотонно убывающей и при монотонно возрастающей. Случай, когда знаменатель равен единице на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса

Общий член геометрической прогрессии вычисляют по формуле

Сумма n первых членов геометрической прогрессии определяют по формуле

Рассмотрим решения классических задач на геометрическую прогрессию. Начнем для понимания с простейших.

Пример 1. Первый член геометрической прогрессии равен 27, а ее знаменатель равен 1/3. Найти шесть первых членов геометрической прогрессии.

Решение: Запишем условие задачи в виде

Для вычислений используем формулу n-го члена геометрической прогрессии

• На ее основе находим неизвестные члены прогрессии
• Как можно убедиться, вычисления членов геометрической прогрессии несложные. Сама прогрессия будет выглядеть следующим образом

Пример 2. Даны три первых члена геометрической прогрессии : 6; -12; 24. Найти знаменатель и седьмой ее член.

1. Решение: Вычисляем знаменатель геомитрической прогрессии исходя из его определения
2. Получили знакопеременную геометрическую прогрессию знаменатель которой равен -2. Седьмой член вычисляем по формуле
3. На этом задача решена.

Пример 3. Геометрическая прогрессия задана двумя ее членами . Найти десятый член прогрессии.

• Решение:
• Запишем заданные значения через формулы
• По правилам нужно было бы найти знаменатель, а затем искать нужное значение, но для десятого члена имеем
• Такую же формулу можно получить на основе нехитрых манипуляций с входными данными. Разделим шестой член ряда на другой, в результате получим
• Если полученное значение умножить на шестой член, получим десятый
• Таким образом, для подобных задач с помощью несложных преобразований в быстрый способ можно отыскать правильное решение.
• Пример 4. Геометрическая прогрессия задано рекуррентными формулами
• Найти знаменатель геометрической прогрессии и сумму первых шести членов.
• Решение:
• Запишем заданные данные в виде системы уравнений
• Выразим знаменатель разделив второе уравнение на первое
• Найдем первый член прогрессии из первого уравнения
• Вычислим следующие пять членов для нахождения суммы геометрической прогрессии
• Поскольку найти сумму в данном случае не составляет большого труда, то обходя простые выкладки сводим все слагаемые под общий знаменатель

В общем случае, при нахождении суммы знакопеременных рядов следует выделять их положительную часть и отрицательную и найти отдельно их суммы по приведенным выше формулам. Наконец найденные значения добавить.

Примеры на геометрическую прогрессию не так сложны если знать несколько базовых формул. Все остальное сводится к простым математическим манипуляциям. Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными.

Источник: https://yukhym.com/ru/matematika/geometricheskaya-progressiya.html

Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии. — презентация

1 Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии

2 ЦЕЛЬ УРОКА : Формирование понятия геометрической прогрессии, используя сопоставление и противопоставления понятию арифметической прогрессии. Познакомить со свойствами геометрической прогрессии и формулой n- го члена. Закрепить на примерах решения задач.

3 Содержание урока: 1. Самостоятельная работа с проверкой в классе. 2. Организация изучения понятия геометрической прогрессии и введение формулы n-го члена геометрической прогрессии. 3. Первичное применение знаний и умений. 4. Подведение итогов работы на уроке.

4 Самостоятельная работа Самостоятельная работа

Продолжите числовую последовательность, записав еще 2 члена: 1;2;4;… 1. двадцать третий член, если первый член -9 и разность сумму десяти первых членов, если а = 4n+2, n – натуральное число. 3. сумму семи первых членов прогрессии -5;-3;-1;… 4.

Продолжите числовую последовательность, записав еще 2 члена: -2;6;-18;…

• 6 Ответы к самостоятельной работе: 1 ВАРИАНТ ; 32 2 ВАРИАНТ ;-162
• 7 Изучение понятия геометрической прогрессии и вывод формулы n-го члена геометрической прогрессии.
• 8 4 задание 1 вариант 2 вариант 1; 2; 4; 8; 16; ; 6; -18; 54; -162; ( -3) 6 ( -3) -18 ( -3) 54 ( -3)
• 9 Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число.

10 Определение d Числовая последовательность, в которой каждый следующий член получается из предыдущего прибавлением одного и того же числом d,называется арифметической прогрессией. q Числовая последовательность отличных от нуля чисел, в которой каждый следующий член получается из предыдущего умножением на одно и тоже число q, называется геометрической прогрессией.

11 d разностью Число d – называется разностью арифметической прогрессии. q знаменателем Число q – называется знаменателем геометрической прогрессии.

1. 12 Обозначение Арифметическая прогрессия Геометрическая прогрессия
2. 13 Допустимые значения Арифметическая прогрессия любые числа Геометрическая прогрессия числа неравные нулю
3. 14 Рекуррентная формула Арифметическая прогрессия Геометрическаяпрогрессия
4. 15 Нахождение разность арифметической разность арифметической прогрессии прогрессии знаменатель геометрической прогрессии знаменатель геометрической прогрессии
5. 16 Используя рекуррентную формулу, получим формулу общего члена геометрической прогрессии.
6. 17 Итак,
7. 18 Формула n-го члена арифметическая прогрессия геометрическая прогрессия
8. 19 Характеристическое свойство арифметическая прогрессиягеометрическая прогрессия или
9. 20 Геометрическая прогрессия в геометрии:
10. 21 Решение задач Решение задач
11. 22 Задача 1 Найдите первые 5 членов геометрической прогрессии, если первый член -2, а знаменатель Ответ: -2; 1; -0,5; 0,25; — 0,125

23 Задача 2. В правильный треугольник, сторона которого равна 16 см, вписан второй треугольник так, что его вершинами являются середины сторон первого. Во второй треугольник таким же способом вписан третий и т.д. Найдите периметр пятого треугольника.

24 Ответ: 3 см.

25 Задача 3 (решить двумя способами) Найдите знаменатель геометрической прогрессии, если ее четвертый член 25, а шестой член 16. Ответ:

26 Задача 4. Между числами и 27 вставьте четыре числа, чтобы получилась геометрическая прогрессия. Найдите эти числа. Ответ: ; 1; 3; 9

27 Задача 5. Дана геометрическая прогрессия ( ), в которой и Найти первый член геометрической прогрессии. Ответ: 12 или

28 Итог урока Итог урока

29 Домашнее задание Придумать задачу, где используется геометрическая прогрессия.Придумать задачу, где используется геометрическая прогрессия.

Источник: http://www.myshared.ru/slide/1189560/