Формулы площади круга и примеры применения

Содержание

Формулы площади коуга

Площадь пруга:

R — радиус; D — диаметр; с — длина дуги окружности.
Формула площади круга
Определение

Круговой сектор — это часть круга, лежащая внутри соответствующего центрального угла.

R — радиус круга; a0 или a — радиан, соответствующий центральный угол; l — длина дуги сектора.
Формула кругового сектора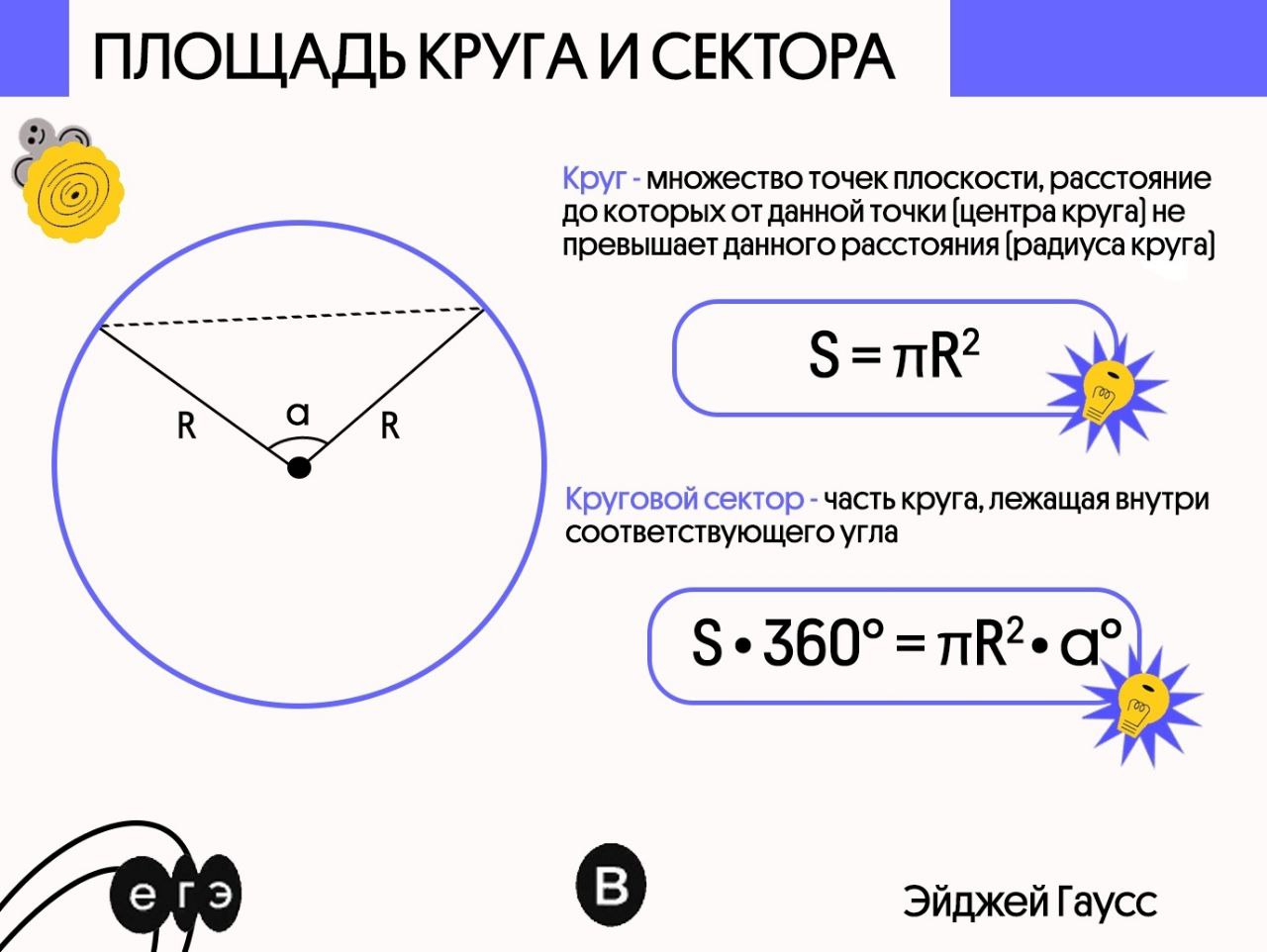
Определение Круговой сегмент — это часть круга, ограниченная дугой окружности и стягивающая ее хордой. R — радиус круга; a0 или a радиан — дуга сегмента (угол AOB).
Свойство 1

a0 < 180? (a < ?):

Формула сегмента:
Свойство 2

a0 > 180? (a > ?):

Формула сегмента:
Свойство 3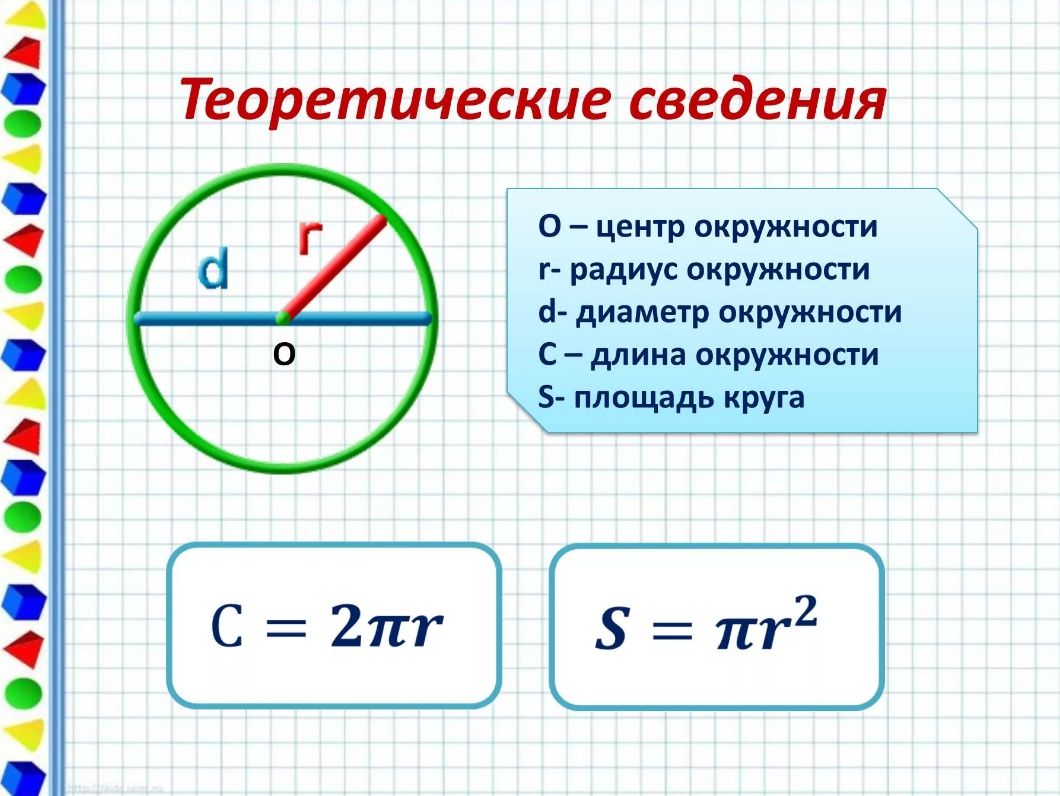

a0 = 180? (a = ?):

Формула сегмента:

Источник: https://formula-xyz.ru/ploshchad-kruga-i-ego-chastej.html

Как найти площадь круга

В этом докладе рассказывается о таком важном математическом понятии, как площадь круга. В работе приводятся исторические выкладки и рассматривается очень интересный и наглядный метод расчета площади круга. Наш доклад написан на языке понятном для шестиклассников.

А вот в статье, приведенной ниже, мы решили углубиться в исследование этой интересной темы.

Возможно к этой статье ребенок сможет вернуться, будучи в старших классах, а возможно, многое поймет уже и сейчас. Многие интересные, красивые, но и трудные теоремы связаны с окружностью.

Тот, кто не изучил ее свойства или не умеет их применять, еще не знает геометрии. Так что окружность можно назвать своего рода «колесом геометрии».

К тому же одно из свойств колеса – его ось остается все время на неизменном расстоянии от поверхности, по которой оно катиться, — в математической формулировке превращается в определение окружности.

Окружность – это множество точек плоскости, удаленных от некоторой точки, ее центра, на одно и то же расстояние, или радиус (от лат. Radius– «спица колеса», «луч»). Радиус окружности — это отрезок, соединяющий центр с точками окружности.

Два свойства окружности выделяют ее среди других замкнутых линий. Прежде всего она ограничивает наибольшую площадь по сравнению со всеми замкнутыми кривыми той же длины (т.е. периметра).

Это так называемое изопериметрическое свойство окружности.

Далее окружность может скользить по самой себе, причем ее произвольная точка может совместиться с любой другой. Кроме окружности это свойство присуще только одной линии – прямой, но она не замкнута.

А потому, для того чтобы кривая сабля точно входила в ножны, она должна быть изогнута по окружности. Часть плоскости, заключенная внутри окружности (т.е.

состоящая из точек, удаленных от центра окружности на расстояние, не большее радиуса) называется кругом.

Хорда – это отрезок, соединяющий любые две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Он вдвое длиннее радиуса и является наибольшим возможным расстоянием между точками окружности.

Любая хорда, а значит и любой отрезок между точками круга, целиком принадлежит кругу; другими словами, круг – выпуклая фигура. Прямая имеет не более двух общих точек с окружностью. Если таких точек две, прямая называется секущей, а если одна – касательной.

Две окружности не могут иметь более двух общих точек. Если таких точек две – говорят, что окружности пересекаются, если же одна, -что они касаются друг друга. Причем касание бывает внешним, когда окружности расположены одна вне другой, или внутренним, когда одна лежит внутри другой.

Если у окружностей нет общих точек, но есть общий центр, то они называются концентрическими.

Длина окружности и площадь круга

Формулы 2πR для величины окружности радиуса R и, πR² для вычисления площади ограниченного ею круга, известны многим. Они пользовались особым вниманием математиков и вычислителей на протяжении тысячелетий.

Интерес к все более точному определению постоянной π долгое время поддерживался надеждами осуществить квадратуру круга – построить циркулем и линейкой квадрат, равновеликий данному кругу, а еще более – стремлением опровергнуть ложные «решения» этой задачи.

В дальнейшем уточнение значения числа π стало своего рода математическим спортом, а в наше время – еще и способом продемонстрировать достоинства компьютерных программ и самих компьютеров.

Собственно, же формулы просто выражают тот факт, что длина окружности пропорциональна ее радиусу, а площадь круга – квадрату радиуса, причем первый коэффициент пропорциональности вдвое больше второго. Указанные свойства следуют из определений длины окружности и площади круга.

Но сами эти определения не столь просты, как в случае длины отрезка или площади многоугольника. Ведь здесь нам приходиться иметь дело с «кривыми» фигурами. Площади криволинейных фигур определяют, строя все более близкие к ним по форме многоугольники.

Детали определений могут отличаться, но в любом случае их суть сводиться к следующему предложению.

Если последовательность многоугольников mₓ, содержащихся в данной фигуре Ф, и последовательность многоугольников Мₓ, содержащих ее таковы, что разность площадей Мₓ и mₓ становиться сколь угодно малой с ростом x, то площади многоугольников обеих последовательностей стремятся к одному и тому же предельному значению, которое и принимается за площадь Ф.

Скачать бесплатно и без регистрации:

Ploshad_kruga.pdf

173 Скачивания

Другие интересные презентации по этому предмету:

Презентация «Старинные меры длины»

Источник: http://www.school-present.ru/shestoj-klass/matematika/30-doklad-ploshchad-kruga.html

Как находить площадь круга

Большое количество точек расположенных на равном расстоянии от центра и находящиеся на одном расстоянии — образуют круг, плоскую фигуру.

Радиус круга — это прямая которая соединяет середину круга с любой из точек находящейся в его окружности. При этом в одной окружности, какая бы точка не была, радиус будет одинаков.

Диаметр круга — это отрезок исходящий от любой точки окружности, проходящий через середину круга и заканчивающийся в параллельной точке той же окружности.

Как находить площадь круга? Площадь круга находится с помощью формулы в которой участвует число ?.

Интересный факт: Числом ? представляется отношение между длиной окружности и длиной диаметра этой же окружности. При этом имеет постоянную величину. А как нам известно ?= 3,1415926 и стало применяться с 1737 года.

Заметка: Ни как не можете определиться, какую машину выбрать? В автосалоне москва автомобили с пробегом (http://center-carauto.ru/), вы сможете в комфортных условиях подобрать наилучший вариант и при этом сэкономить. Согласитесь, заманчивое предложение!

Как рассчитать площадь круга? Как и говорилось выше благодаря формуле, в которой участвует число ? и радиус, записывается так:

S = ?R2

Разберем для наглядности
Найдем площадь круга с помощью его радиуса который равен 4 см.

Площадь круга равна:
S= 3,14 * 42 = 3,14 * 16 = 50,24 кв/см
Так же площадь круга через диаметр находиться по формуле

Решение

S = (?/4)d2

Разберем для наглядности
Найдем площадь круга с помощью его диагонали. Возьмем радиус равный 4 см.

Решение
S =(3,14/4) * 82 = 0,785 * 64 = 50,24

1) Вычислим диаметр, который больше радиуса в два раза.
d=2R
d = 2 * 4 =8
2) Подставляем значения в формулу
Если сверить полученный ответ с предыдущим, то они равны.

Когда мы ищем площадь сегмента круга или сектора, очень помогает знание основных формул. С их помощью них можно узнавать не известные значения.
Сегментом — называется ограниченная часть круга, которую ограничивают хорда и дуга данного круга.

Как нам уже известно расчет площади круга вычисляется с использованием числа ? умноженного на радиус в квадрате. Используя длину окружности, мы сможем найти радиус.

R = (l/2)?

Если подставить эту формулу в формулу расчета площади., у нас получится:

S = ? ((l/2)?)2 = l2/4?

Разберем для наглядности
Найти площадь круга с окружностью равной 8 см.
Решение
Используем формулу S= 82/4*3,14 = 64 / 12,56 = 5 см

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Источник: https://reshit.ru/Kak-nakhodit-ploshhad-kruga

Площадь круга: формула. Чему равна площадь круга, описанного и вписанного в квадрат, прямоугольный и равнобедренный треугольник, прямоугольную, равнобедренную трапецию?

Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.

Содержание

Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
Площадь круга, вписанного в квадрат: формула, примеры решения задач
Площадь круга, описанного около квадрата: формула, примеры решения задач
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Видео: Математика | Вычисление площадей круга и его частей

Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.

Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач

Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.

Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач

Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.

Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.

Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.

Формула нахождения площади круга через радиус:

Площадь круга: формула через радиус

Примеры решения заданий по нахождению S-площади круга через R-радиус:
————————————————————————————————————————
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².

Формула нахождения S-площади круга через D-диаметр:

Площадь круга: формула через диаметр

Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².

Нахождение S круга, если известна длина окружности:

Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.

Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².

Площадь круга, вписанного в квадрат: формула, примеры решения задач

Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.

Формула нахождения площади круга, вписанного в квадрат:

Площадь круга, вписанного в квадрат: формула

Примеры решения задач по нахождению площади круга, вписанного в квадрат:

———————————————————————————————————————

Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности

Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————

Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см

Решайте так: Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².

Площадь круга, описанного около квадрата: формула, примеры решения задач

Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.

Формула нахождения S круга, описанного около квадратной фигуры:

Площадь круга, описанного около квадрата: формула

Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:

Задача

Площадь круга, описанного около квадрата: примеры решения задач

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач

Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.

Формула нахождения площади круга, вписанного в равнобедренный треугольник:

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула

Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².

Формула нахождения площади круга, вписанного в прямоугольный треугольник:

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник

Примеры решения заданий:

Задача №1

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: примеры решения задач

Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²

Задача №2

Площадь круга, вписанного в равнобедренный треугольник: примеры решения задач

Решение:

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: примеры

Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.

Задача №3

Площадь круга, вписанного в треугольник: примеры решения задач

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач

Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.

Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула

Примеры решения задач:

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: примеры решения задач

Вот еще пример решения задачи с использованием формулы Герона.

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: примеры

Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач

У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.

Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.

Для решения этой задачи нужно использовать такие формулы:

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула

Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию

Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.

Примеры решения задач:

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: примеры решения задач

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач

Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула

Примеры решения задач:

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: примеры решения задач

Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.

Ответ: Радиус равен 6.

В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.

Видео: Математика | Вычисление площадей круга и его частей

Источник: https://heaclub.ru/ploshhad-kruga-formula-chemu-ravna-ploshhad-kruga-opisannogo-i-vpisannogo-v-kvadrat-pryamougolnyj-i-ravnobedrennyj-treugolnik-pryamougolnuyu-ravnobedrennuyu-trapeciyu

Площадь круга

Круг — часть плоскости, ограниченная окружностью. Круг радиуса с центром содержит точку и все точки плоскости, которые находятся от точки на расстоянии, не большем .

Впишем в окружность, ограничивающую круг, правильный — угольник А1А2А3….An:

Так как данный многоугольник целиком содержится в данном круге, то площадь данного круга больше площади данного многоугольника. Если мы в данный многоугольник впишем окружность радиуса , то площадь круга, ограниченного этой окружностью, меньше площади данного многоугольника , потому что данный круг полностью содержится в многоугольнике. Значит, мы можем записать, что

(1)

Теперь неограниченно будем увеличивать число сторон многоугольника. Нам известно, что радиус вписанной в правильный многоугольник окружности, можно вычислить по формуле .

Если стремится к бесконечности, то отношение будет стремится к нулю, а значит будет стремится к единице, а значит, радиус вписанной окружности будет стремиться к радиусу описанной окружности .

Другими словами, при неограниченном увеличении числа сторон многоугольника вписанная в него окружность «стремится» к описанной окружности, а значит, площадь круга, ограниченного вписанной окружностью, стремится к площади круга, ограниченного описанной окружностью, , значит, учитывая неравенство (1), получим, что при неограниченном увеличении числа сторон многоугольника, площадь многоугольника стремится к площади круга , ограниченного описанной около данного многоугольника окружностью.

Пусть — периметр многоугольника А1А2А3….An, тогда площадь данного многоугольника вычисляется по формуле

Так как при неограниченном увеличении сторон многоугольника радиус вписанной окружности стремится к радиусу описанной окружности , а периметр данного многоугольника стремится к длине окружности , а площадь многоугольника стремится к площади круга . Значит,
Итак, площадь круга радиуса вычисляется по формуле:

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Правильный многоугольник
Окружность, описанная около правильного многоугольника
Окружность, вписанная в правильный многоугольник
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Построение правильных многоугольников
Длина окружности
Площадь кругового сектора
Длина окружности и площадь круга

Правило встречается в следующих упражнениях:

7 класс
Задание 1119, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1145, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1218, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1220, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1222, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1246, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1253, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1290, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Пользовательское соглашение
Copyright
Нашли ошибку?
Связаться с нами

Источник: https://budu5.com/manual/chapter/3575