Таблица значений тригонометрических функций

Тригонометрия

• Таблица значений основных тригонометрических функций
• 
• Значения аргумента из первой четверти: (0º-90º)

x (град)

0º

15º

18º

22,5º

30º

36º

45º

54º

60º

67,5º

72º

75º

90º

x (рад)

0

sinx

0

1

cosx

1

0

tgx

0

1

***

ctgx

***

1

0

Значения аргумента из второй четверти: (90º-180º)

x (град)

90º

105º

108º

112,5º

120º

126º

135º

144º

150º

157,5º

162º

165º

180º

x (рад)

p

sinx

1

0

cosx

0

-1

tgx

***

-1

0

ctgx

0

-1

***

Значения аргумента из третьей четверти: (180º-270º)

x (град)

180º

195º

198º

202,5º

210º

216º

225º

234º

240º

247,5º

252º

255º

270º

x (рад)

π

sinx

0

-1

cosx

-1

0

tgx

0

1

***

ctgx

***

1

0

Значения аргумента из четвертой четверти: (270º-360º)

x (град)

270º

285º

288º

292,5º

300º

306º

315º

324º

330º

337,5º

342º

345º

360º

x (рад)

2π

sinx

-1

0

cosx

0

1

tgx

***

-1

0

ctgx

0

-1

***

При отрицательных значениях аргумента можно использовать формулы:
cos(-x) = cos(x)	sin(-x) = — sin(x)
tg(-x) = — tg(x)	ctg(-x) = — ctg(x)

В данных таблицах перечислены почти все положительные значения аргумента x, для которых значения основных тригонометрических функций выражаются точно через радикалы (достаточно компактным образом). Однако это далеко не полный перечень значений аргументов с подобными свойствами. Например, синус и косинус шести градусов также могут быть выражены через радикалы:

Более полная таблица значений тригонометрических функций с 30 углами из первой четверти, изменяющимися с шагом в три градуса, приведена в файле компьютерной программы Maple.

, содержащем также решения 9 заданий по математике из «Сборника задач по Математике для поступающих во ВТУЗы» под редакцией М.И.Сканави. Задачи из «СКАНАВИ» посвящены преобразованиям тригонометрических выражений, в которых используются нестандартные углы 18, 36 54 градуса и др.

Решения задач получены двумя способами: в аналитическом виде (при помощи формул из школьной тригонометрии) и средствами программы Maple.

Расширенная таблица значений тригонометрических функций

Web Design: Kurilin A.V. 2003-2014

Источник: http://web-tutor.narod.ru/Pages_1024x768/Trigtables.htm

Тригонометрический круг. Основные значения тригонометрических функций

• Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы,  или вы совсем нетерпеливы,  – то вот он, тригонометрический круг:
• 
• Мы же здесь будем все подробно разбирать шаг за шагом.

Тригонометрический круг – не роскошь, а необходимость

 

1. Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций,  столько формул…  А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
2. Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.
3. Если вы постоянно смотрите в таблицу со значениями тригонометрических формул,  давайте избавляться от этой привычки!

Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!

К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул, чему равен синус, скажем, 300 градусов, или -45.

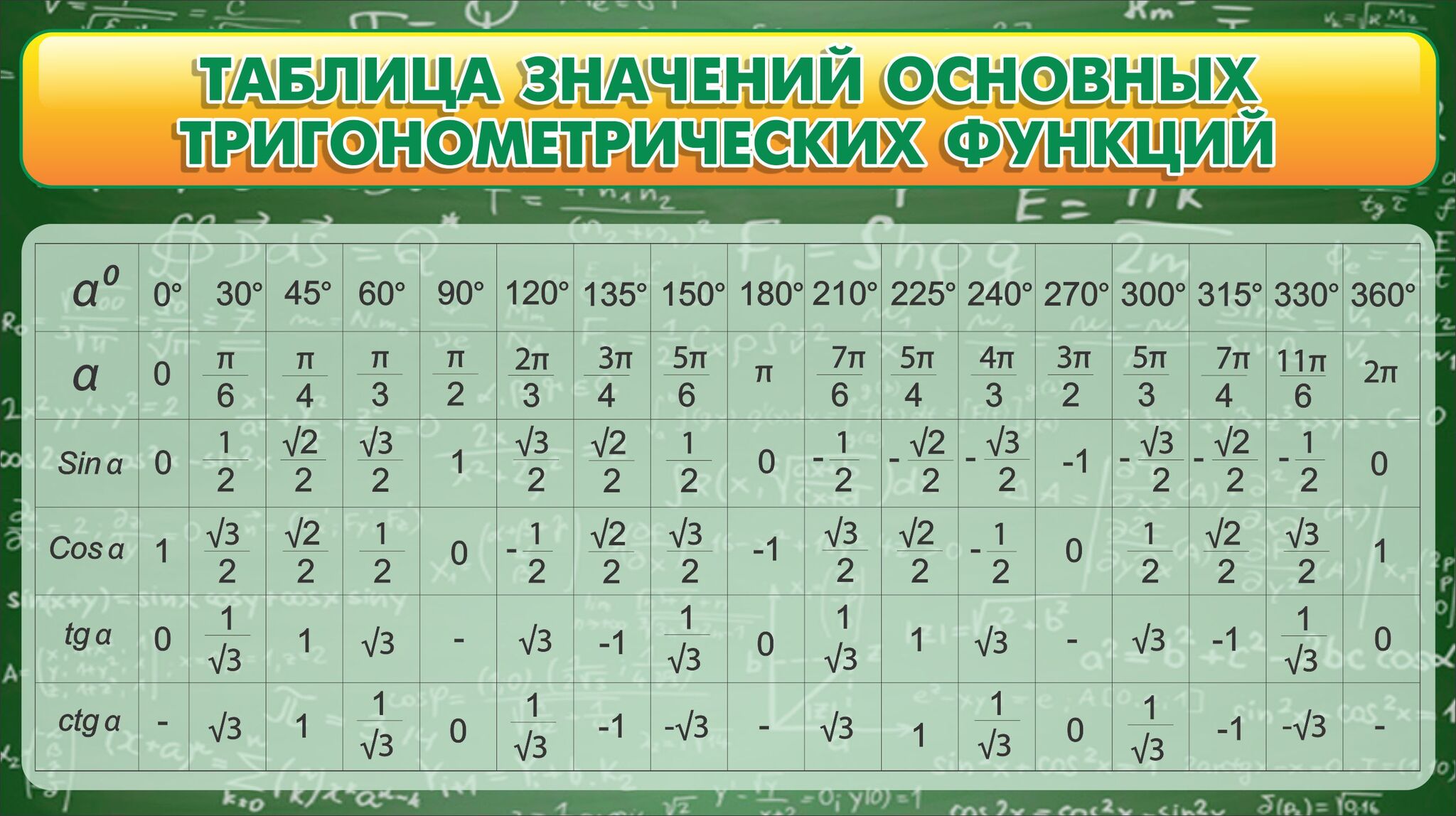
Никак?.. можно, конечно, подключить формулы приведения…  А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!

А при решении тригонометрических уравнений и неравенств   без тригонометрического круга  – вообще никуда.

Знакомство с тригонометрическим кругом

Давайте по порядку.

Сначала выпишем вот такой ряд чисел:

А теперь такой:

И, наконец, такой:

Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».

• И зачем оно нам?
• Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
• Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).

Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.

Это почему же, спросите вы?

Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.

Треугольник АОВ – прямоугольный, в нем  . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).

1. Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
2. Надеюсь, уже что-то становится понятно?
3. Наконец, что такое синус, косинус в прямоугольном треугольнике?
4. Так вот точка  В и будет соответствовать  значению , а точка М – значению
5. Аналогично с остальными значениями первой четверти.

Как вы понимаете, привычная нам ось (ox) будет осью косинусов, а ось  (oy) – осью синусов.   Про тангенс и котангенс позже.

• Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
• Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг, без которого никуда в тригонометрии.
• А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.

 

Источник: https://egemaximum.ru/trigonometricheskiy-krug/

Значения тригонометрических функций основных углов

Найдём значения тригонометрических функций для углов в 30°, 45° и 60°.

1) Для угла в 30°

Возьмём прямоугольный треугольник с острым углом в 30°. Обозначим длину гипотенузы АВ через с и выразим длины катетов.

• ВС = с/2, как катет, лежащий против угла в 30°.
• Катет АС найдём по теореме Пифагора.
• Тогда
• sin30o = ( frac{BC}{AB}=frac{frac{c}{2}}{c}=frac{1}{2}=0,5 )
• tg30o = ( frac{BC}{AC}=frac{frac{c}{2}}{frac{csqrt3}{2}}=frac{1}{sqrt3}=frac{sqrt3}{3}approx 0,5774 )
• cos30o= ( frac{AC}{AB}=frac{frac{csqrt3}{2}}{c}=frac{sqrt3}{2}approx 0,8660 )
• 2) Для угла в 45°.
• Возьмём прямоугольный треугольник с острыми углами по 45°.

$$ AC = sqrt{AB^2 — BC^2} = sqrt{c^2 — frac{c^2}{4}} = sqrt{frac{3c^2}{4}} = frac{csqrt3}{2} $$

1. Обозначим длину гипотенузы AB через c и выразим длины катетов. АС = BC, следовательно, по теореме ПифагораAB2 = 2BC2, откуда $$ BC^2 = frac{AB^2}{2} = frac{2AB^2}{4} = frac{2c^2}{4} $$
2. Значит, (BC = sqrt{frac{2c^2}{4}} = frac{csqrt2}{2}), одновременно и (AC = frac{csqrt2}{2})
3. sin 45° = ( frac{BC}{AB} = frac{frac{csqrt2}{2}}{c} = frac{sqrt2}{2} approx 0,7071 )
4. tg 45°= ( frac{BC}{AC} = 1 )
5. cos 45°= ( frac{BC}{AB} = frac{sqrt2}{2} approx 0,7071 )
6. 3) Для угла в 60°
7. Значения тригонометрических функций для угла в 60° можно найти из того же треугольника, из которого нашли значения тригонометрических функций для угла в 30°, так как если ∠A = 30°, то ∠В = 60°.
8. Тогда
9. sin 60° = ( frac{AC}{AB} = frac{sqrt3}{2} approx 0,8660 )
10. tg 60° = ( frac{AC}{BC} = sqrt3 approx 1,7321 )
11. cos 60° = ( frac{BC}{AB} = frac{1}{2} = 0,5)
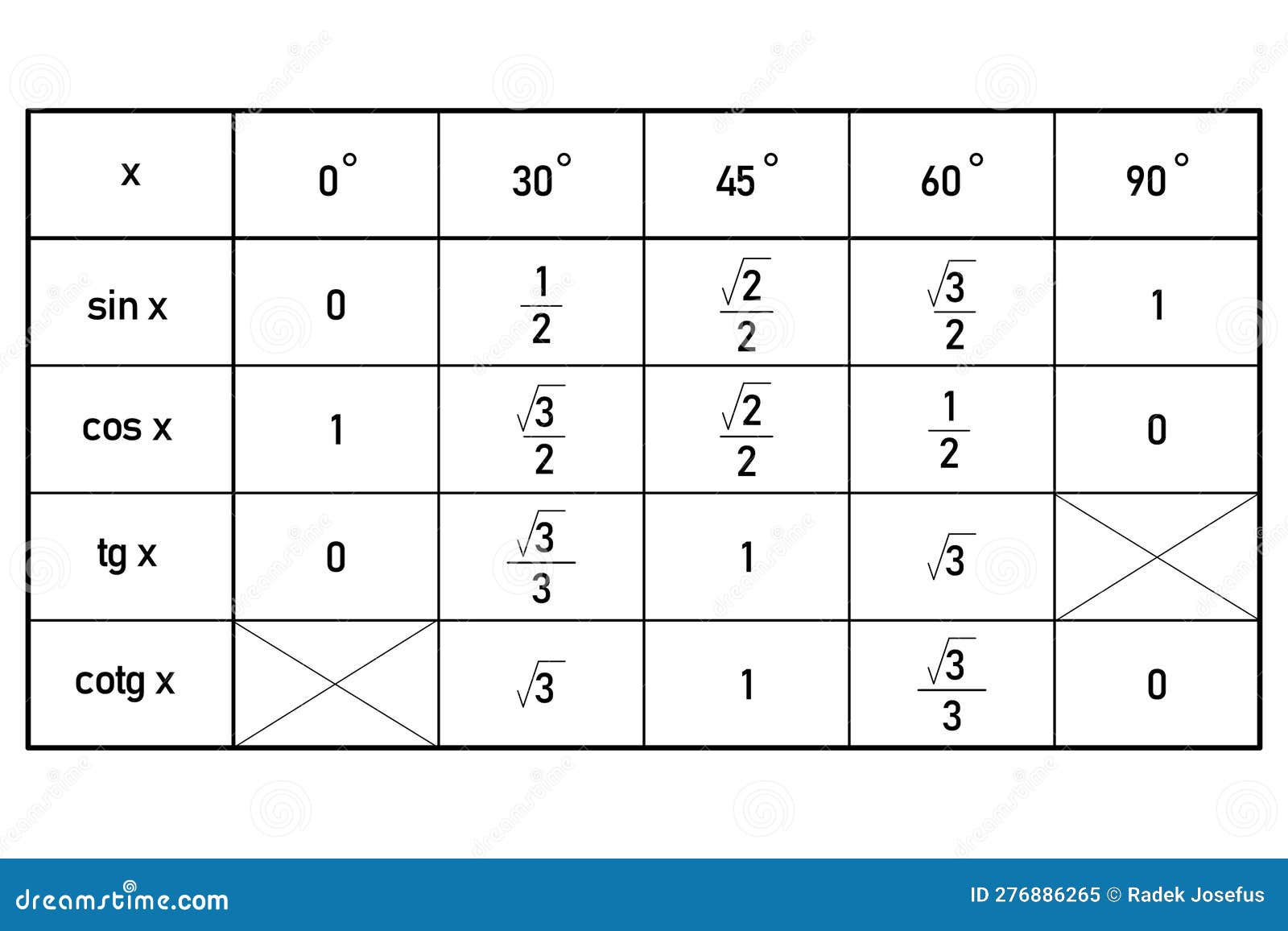
12. Таблица значений тригонометрических функций для углов в 30°, 45° и 60°.

УГОЛ	СИНУС	КОСИНУС	ТАНГЕНС
30о	( frac{1}{2}=0,5 )	( frac{sqrt3}{2}approx 0,8660 )	( frac{sqrt3}{3}approx 0,5774 )
45о	( frac{sqrt2}{2}approx 0,7071 )	( frac{sqrt2}{2}approx 0,7071 )	1
60о	( frac{sqrt3}{2}approx 0,8660 )	( frac{1}{2}=0,5 )	( sqrt3 approx 1,7321 )

Рассматривая эту таблицу, можно заметить, что синус и тангенс острого угла возрастают при увеличении угла, а косинус при увеличении угла убывает. При уменьшении угла синус и тангенс убывают, а кoсинус возрастает.

Дополнительными углами называются два угла, которые в сумме составляют 90°. Такими углами, в частности, являются острые углы прямоугольного треугольника.

Углы А и В в прямоугольном треугольнике ACB являются дополнительными углами, так как

∠A + ∠B = 90°; ∠A = 90° — ∠B; ∠В = 90° — ∠A

Рассмотрим соотношения между тригонометрическими функциями дополнительных углов.

1) ( sinA = frac{a}{c}; cosB = frac{a}{c} ), т. e. синус данного угла равен косинусу дополнительного угла.

2) ( cosA = frac{b}{c}; sinB = frac{b}{c} ), т.е. косинус данного угла равен синусу дополнительного угла.

3) ( tgA = frac{a}{b}; ctgB = frac{a}{b} ), т.е. тангенс данного угла равен котангенсу дополнительного угла.

4) ( ctgA = frac{b}{a}; tgB = frac{b}{a} ), т.e. котангенс данного угла равен тангенсу дополнительного угла.

Знание соотношений между тригонометрическими функциями дополнительных углов важно для понимания устройства тригонометрических таблиц.

Источник: http://razdupli.ru/teor/52_znacheniya-trigonometricheskih-funkcij-osnovnyh-uglov.php

Тригонометрическая таблица

Тригонометрическая таблица представляет собой таблицу значений тригонометрических функций. Эта тригонометрическая таблица содержит углы в градусах и радианах, что очень удобно для перевода градусов в радианы и наоборот, радианов в градусы.

Таблица тригонометрических значений функций составлена с корнями квадратными и дробями, что позволяет сокращать дроби при решении школьных примеров. В таблице представлены синус sin, косинус cos, тангенс tg, котангенс ctg, секанс sec, косеканс cosec.

Таблица значений тригонометрических функций углов 0, 30, 45, 60, 90, 180, 270 и 360 градусов, 0 пи, пи на 6, пи на 4, пи на 3, пи на 2, пи, 3 пи на 2, 2 пи.» id=»BLOGGER_PHOTO_ID_5475701195873439474″ src=»http://4.bp.blogspot.com/_JwbCNIxiifg/S_2ZOeQ3zvI/AAAAAAAAAOg/mWZTXqx1g0Q/s400/trig1-1.PNG»>

Специально для самых умных умников сообщаю. Это правильная таблица. Где-то между роддомом и сегодня, вы учили свойства дробей. Так вот, с тех самых пор ничего не изменились. Что для школьных малявок, что для здоровых дядек и теток, свойства дробей одинаковы. Даже президент Путин не в состоянии ничего поменять. Одно из волшебных свойств дроби гласит: если числитель и знаменатель дроби умножить на одно и то же число, дробь не изменится. И ни какое стадо депутатов этот закон отменить не в состоянии. Математика — это не соседей или собственный народ грабить. Даже Боги могут только пользоваться законами математики, но не изменять их. Хотя, дуракам закон не писан.

Свойства дробей

 Чтобы облегчить жизнь блондинки Ксю, мы еще не раз будем разбирать эту тригонометрическую таблицу на строчки синусов, косинусов, тангенсов, котангенсов, секансов и косекансов, на столбики градусов и радиан, на отдельные квадратики значений тригонометрических функций.

В тригонометрической таблице представлены синус угла sin 0, 30, 45, 60, 90, 180, 270 и 360 градусов или 0, пи/6, пи/4, пи/3, пи/2, пи, 3пи/2, 2пи радиан. Значения синуса угла sin 0, 1/2, корень из 2 деленный на 2, корень из 3 деленный на 2, единица и минус единица. Строчка напротив буквочек sin називается еще таблица синусов.

Таблица значений тригонометрических функций содержит косинус угла cos 0, 30, 45, 60, 90, 180, 270, 360 градусов.

Если перевести эти углы в радианы, мы получим 0 пи, пи на 6, пи на 4, пи на 3, пи на 2, пи, 3 пи на 2, 2 пи радиан.

Таблица косинусов этих углов представляет собой строчку напротив букв cos, в которой записаны единица, корень из трех деленный на два, корень из двух деленный на два, одна вторая, ноль и минус единица.

Первых две строчки этой таблицы sin и cos — это таблица синусов и косинусов.

Таблица тангенсов спряталась ниже таблицы синусов и косинусов в строчке с двумя буковками tg. Как это ни странно, но здесь присутствуют те же тангенс угла tg 0, 30, 45, 60, 90, 180, 270, 360 градусов. И в радианы они переводятся точно так же 0 пи, пи / 6, пи / 4, пи / 3, пи / 2, пи, 3 пи / 2, 2 пи радиан.

Значения тангенсов этих углов составляют ноль, единица деленная на корень из трех, единица, корень из трех и черточка, которую иногда заменяют знаком бесконечности. Это означает, что математики не могут определить значение тригонометрической функции тангенс для углов 90 и 270 градусов.

Так что, блондинки, не отчаивайтесь, даже математики могут не всё!

Еще ниже находится таблица котангенсов. Повторим еще раз те углы, для которых в тригонометрической таблице записан котангенс ctg: 0, 30, 45, 60, 90, 180, 270, 360 градусов.

И еще раз потренируемся переводить градусы в радианы: 0 пи, пи / 6, пи / 4, пи / 3, пи / 2, пи, 3 пи / 2, 2 пи радиан.

Две средние строчки тригонометрической таблицы складываются в таблицу тангенсов и котангенсов.

Две последние строчки тригонометрической таблицы занимают секанс, который обозначается sec, и косеканс, который обозначается cosec. Поскольку эти тригонометрические функции обратны косинусу и синусу соотвественно, то и значения этих функций обратны значениям косинуса и синуса.

Обращаю ваше особое внимание на то, что математики в очередной раз попытались запутать блондинок, нарушив логику применения приставки КО. У них получилось, что секанс — это тригонометрическая функция, обратная КОсинусу, а КОсеканс — обратная синусу.

Естественно, что для секанса и косеканса есть углы, значения функций для которых не определены.

• В завершение наших блужданий по тригонометрической таблице Блондинка Ксю споет нам песню «Вместо жизни» — тангенс пи пополам!
• Найти значение:
• Таблица тригонометрических функций основных углов — в тригонометрической таблице приведены самые распространенные в учебниках и примерах углы.
• Таблица косинуса синуса тангенса и котангенса бесплатно — все эти функции здесь собраны в одну кучку и смотреть на них можно совершенно бесплатно.
• Тригонометрическая таблица sin cos tg ctg — а еще здесь есть sec и cosec, в градусах и радианах.
• Тангенс пи на 4 — как же только не извращаются математики, чтобы замаскировать обыкновенную единичку.

Синус 180 градусов равен — а вот так математики могут замаскировать обыкновенный ноль. Прямо не математика, а женская сумочка какая-то — покуда что-нибудь найдешь…

sin нуля — ну вот, ещё один ноль они спрятали, правда не очень далеко, но коварно — в cos 0 за нулем прячется единица. Попробуй тут не запутаться.

Таблица синусов и косинусов в радианах — ну, здесь не самая большая таблица, но кое-какие радианы имеются. Нужно будет соорудить что-нибудь монументальное, в духе Зураба Церетели.

Таблица часто встречающихся значений синуса косинуса тангенса котангенса — здесь есть нужные вам значения. Если вы считаете, что другие значения встречаются чаще, сообщите мне об этом, я исправлю досадное недоразумение.

ctg 225 градусов — равен единице (1). В таблице для ботаников этого нет, приходится самим додумывать. Плохая тригонометрическая таблица, нужно другую нарисовать, специально для серии «Тригонометрия для блондинок».

Таблица синусов и косинусов в дробях — да, именно в виде дроби записаны значения шести тригонометрических функций для некоторых углов в таблице на рисунке.

Таблиця косинусів синусів тангенсів котангенсів — вау! в Украине тоже изучают тригонометрическую таблицу! А я считал, что там только выборами занимаются. Наверное, они по этим таблицам прогнозы выборов считают.

Школьная таблица тангенса — есть здесь и тангенс в виде дроби, специально для школьников.

Вычислить cosekans — здесь есть косекансы в таблице. Хотя, в сокращенном виде косеканс пишется как «cosec», а по-английски это пишется «cosecant».

Таблица тангенсов с использованием пи — за неимением лучшей, пока могу предложить только эту таблицу.

Источник: http://www.webstaratel.ru/2010/02/blog-post_06.html

Таблицы тригонометрических функций

• Из тригонометрических определений функций $sin$, $cos$, $ an$ и $cot$ можно узнать их значения для углов $0$ и $90$ градусов:
• $sin⁡0°=0$, $cos0°=1$, $ an 0°=0$, $cot 0°$ не определяется;
• $sin90°=1$, $cos90°=0$, $cot90°=0$, $ an 90°$ не определяется.
• В школьном курсе геометрии при изучении прямоугольных треугольников находят тригонометрические функции углов $0°$, $30°$, $45°$, $60°$ и $90°$.

Найденные значения тригонометрических функций для указанных углов в градусах и радианах соответственно ($0$, $frac{pi}{6}$, $frac{pi}{4}$, $frac{pi}{3}$, $frac{pi}{2}$) для удобства запоминания и использования заносят в таблицу, которую называют тригонометрической таблицей, таблицей основных значений тригонометрических функций и т.п.

При использовании формул приведения, тригонометрическая таблица может быть расширена до угла $360°$ и соответственно $2pi$ радиан:

Применяя свойства периодичности тригонометрических функций, каждый угол, который будет отличаться от уже известного на $360°$, можно рассчитать и записать в таблицу. Например, тригонометрическая функция для угла $0°$ будет иметь такое же значение и для угла $0°+360°$, и для угла $0°+2 cdot 360°$, и для угла $0°+3 cdot 360°$ и т.д.

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

С помощью тригонометрической таблицы можно определить значения всех углов единичной окружности.

В школьном курсе геометрии предполагается запоминание основных значений тригонометрических функций, собранных в тригонометрической таблице, для удобства решения тригонометрических задач.

Использование таблицы

В таблице достаточно найти необходимую тригонометрическую функцию и значение угла или радиан, для которых эту функцию нужно вычислить. На пересечении строки с функцией и столбца со значением получим искомое значение тригонометрической функции заданного аргумента.

На рисунке можно увидеть, как найти значение $cos⁡60°$, которое равно $frac{1}{2}$.

Аналогично используется расширенная тригонометрическая таблица. Преимуществом ее использования является, как уже упоминалось, вычисление тригонометрической функции практически любого угла. Например, легко можно найти значение $ an 1 380°= an (1 380°-360°)= an(1 020°-360°)= an(660°-360°)= an300°$:

Таблицы Брадиса основных тригонометрических функций

Возможность расчета тригонометрической функции абсолютно любого значения угла для целого значения градусов и целого значения минут дает использование таблиц Брадиса. Например, найти значение $cos⁡34°7'$. Таблицы разделены на 2 части: таблицу значений $sin$ и $cos$ и таблицу значений $ an$ и $cot$.

Таблицы Брадиса дают возможность получить приближенное значение тригонометрических функций с точностью до 4-х знаков после десятичной запятой.

Использование таблиц Брадиса

Используя таблицы Брадиса для синусов, найдем $sin⁡17°42'$. Для этого в столбце слева таблицы синусов и косинусов находим значение градусов – $17°$, а в верхней строке находим значение минут – $42'$. На их пересечении получаем искомое значение:

$sin17°42'=0,304$.

Для нахождения значения $sin17°44'$ нужно воспользоваться поправкой в правой части таблицы. В данном случае к значению $42'$, которое есть в таблице, нужно добавить поправку для $2'$, которая равна $0,0006$. Получим:

$sin17°44'=0,304+0,0006=0,3046$.

Для нахождения значения $sin17°47'$ также пользуемся поправкой в правой части таблицы, только в этом случае за основу берем значение $sin17°48'$ и отнимаем поправку для $1'$:

$sin17°47'=0,3057-0,0003=0,3054$.

Для значений тангенса до $90°$ и котангенса малого угла поправок нет. Например, найдем $ an 78°37'$, который по таблице равен $4,967$.

1. Найдем $cot 2°13'=25,83$.

Источник: https://spravochnick.ru/matematika/trigonometricheskie_funkcii/tablicy_trigonometricheskih_funkciy/