- Если ТС – однородное рабочее тело, то в расчетах применяются относительные теплоемкости:
- — удельная теплоемкость – теплоемкость, отнесенная к 1 кг вещества с=С/m, Дж/кгК;
- — молярная теплоемкость – теплоемкость, отнесенная с 1 молю вещества , Дж/мольК;
- — объемная теплоемкость – теплоемкость, отнесенная к 1м3 вещества , Дж/м3К.
- Теплоемкость – функция процесса и зависит от рода рабочего тела, характера процесса и параметров состояния. Так, теплоемкость в процессе с постоянным давлением называется изобарной теплоемкостью:

где H, Дж – энтальпия.
Теплоемкость в процессе с постоянным объемом называется изохорной теплоемкостью:

где U, Дж – внутренняя энергия.
Теплоемкость идеального газа не зависит от температуры и давления и зависит только от числа степеней свободы движения молекул и в соответствии с законом о равном распределении энергии по степеням свободы движения молекул теплоемкость:  , где — вращательные степени свободы, равные для одноатомного газа нулю , для двухатомного газа — =2 и для трехатомных газов =3; Дж/мольК – молярная газовая постоянная. Теплоемкость определяется по уравнению Майера:
, где — вращательные степени свободы, равные для одноатомного газа нулю , для двухатомного газа — =2 и для трехатомных газов =3; Дж/мольК – молярная газовая постоянная. Теплоемкость определяется по уравнению Майера:
Для одноатомного газа и , для двухатомного газа и , для трех и более атомных газов и .
Теплоемкость реальных газов зависит от давления и температуры. В ряде случаев можно пренебречь влиянием давления на теплоемкость и принять, что теплоемкость реальных газов зависит только от температуры: C=f(t). Эта зависимость определяется экспериментально.
Эмпирическая зависимость удельной истинной теплоемкости от температуры может быть представлена в виде многочлена:
, Дж/кгК,
где при температуре t=00C. Для двухатомных газов можно ограничиться двумя слагаемыми: , или , где .
- Для конечного участка процесса 1-2 количество теплоты равно:
- .
- Тогда средняя теплоемкость на этом участке процесса будет равна:
- , Дж/кгК.
В области низких температур при Т
Источник: http://fiziku5.ru/uchebnye-materialy-po-fizike/uravnenie-majera
Уравнение Майера
Так как данный раздел посвящен уравнению Майера, а это уравнение, связывающее теплоемкости идеального газа в двух изопроцессах, то напомним само определение теплоемкости.
Определение
Количество теплоты, переданное телу с целью нагреть его на $1К$ — теплоемкость тела (системы). Обычно обозначается «C»:
[С=frac{delta Q}{dT}left(1
ight).]
Теплоемкость единицы молярной массы тела:
[c_{mu }=frac{C}{
u } left(2
ight)-]
молярная теплоемкость.
Теплоемкость не является функцией состояния, она — характеристика двух бесконечно близких состояний системы (начального и конечного) или скорее функция бесконечно малого процесса, который совершается в системе. Что это значит в количественном выражении? Из уравнения (1) и при использовании первого начала термодинамики в дифференциальной форме запишем:
[С=frac{delta Q}{dT}=frac{dU+pdV}{dT}left(3
ight).]
Три параметра термодинамической системы
Термодинамическая система однозначно определяется тремя параметрами (p,V,T). Между ними существует соотношение — уравнение состояния. Для идеального газа, например, уравнение Менделеева — Клайперона. В общем виде функциональная связь:
[p=pleft(T,V
ight) или T=Tleft(p,V
ight), V=V(p,T)]
- в зависимости от выбора. Если в качестве независимых переменных выбраны V и T, то внутренняя энергия системы будет функцией U=U(T,V), тогда полный дифференциал от внутренней энергии будет иметь вид:
- Подставим (4) в (3), получим:
- Из формулы (5) очевидно, что теплоемкость зависит от процесса. Так, если процесс изохорный, то
- Тогда теплоемкость в изохорном процессе имеет вид:
- Если процесс изобарный, то теплоёмкость для изобарного процесса будет иметь вид:
- Рассмотрим в качестве исследуемой системы идеальный газ. Малое приращение внутренней энергии идеального газа можно записать в виде:
- Следовательно,
- Состояние идеального газа описывается уравнением Менделеева — Клайперона:
- Значит:
- Подставим (10) и (11) в (7), получим:
- Уравнение (12) называется соотношением Майера.
- Или для молярных теплоемкостей:
[dU={left(frac{partial U}{partial T}
ight)}_VdT+{left(frac{partial U}{partial V}
ight)}_TdVleft(4
ight).] [С=frac{{left(frac{partial U}{partial T}
ight)}_VdT+{left(frac{partial U}{partial V}
ight)}_TdV+pdV}{dT}={left(frac{partial U}{partial T}
ight)}_V+left[p+{left(frac{partial U}{partial V}
ight)}_T
ight]frac{dV}{dT}left(5
ight).] [frac{dV}{dT}=0.] [C_V={left(frac{partial U}{partial T}
ight)}_Vleft(6
ight).] [C_p={left(frac{partial U}{partial T}
ight)}_V+left[p+{left(frac{partial U}{partial V}
ight)}_T
ight]{left(frac{partial V}{partial T}
ight)}_p=C_V+left[p+{left(frac{partial U}{partial V}
ight)}_T
ight]{left(frac{partial V}{partial T}
ight)}_pleft(7
ight).] [dU=frac{i}{2}
u RdT left(8
ight).] [{left(frac{partial U}{partial V}
ight)}_T=0 left(9
ight).] [pV=
u RT left(10
ight).] [{left(frac{partial V}{partial T}
ight)}_p=frac{
u R}{p} left(11
ight).] [C_p=C_V+left[p+0
ight]frac{
u R}{p}=C_V+
u R left(12
ight).] [с_{mu p}=с_{mu V}+R left(13
ight).] 
Ничего непонятно?
Попробуй обратиться за помощью к преподавателям
Пример 1
- Задание: Найти удельную теплоемкость смеси 16 грамм кислорода и 10 грамма гелия в процессе при постоянном давлении.
- Решение:
- Если $Q$ — количество тепла, которое получает смесь газов в процессе, то
- где $m$ — масса смеси, $c_p$- удельная теплоемкость смеси при постоянном давлении.
- $Q_{O_2}$ — количество тепла, которое получает кислород:
- $m_{O_2}$ — масса кислорода, ${c_p}_{O_2}$- теплоемкость кислорода при постоянном давлении.
- Для гелия аналогично:
- Кроме того, мы знаем, что:
- Масса смеси находится по закону сохранения массы:
[Q=c_pm riangle T left(1.1
ight),] [Q_{O_2}={c_p}_{O_2}m_{O_2} riangle T left(1.2
ight).] [Q_{He}={c_p}_{He}m_{He} riangle T left(1.3
ight).] [Q=c_pm riangle T=Q_{O_2}+Q_{He}={c_p}_{O_2}m_{O_2} riangle T+{c_p}_{He}m_{He} riangle T (1.4)] [m=m_{O_2}+m_{He} left(1.5
ight).]
Выразим теплоемкость смеси $c_p$из (1.4), учитывая (1.5), получим:
[c_p=frac{{c_p}_{O_2}m_{O_2}+{c_p}_{He}m_{He} }{m_{O_2}+m_{He}}left(1.6
ight).]
- Зная, что молярная теплоемкость с удельной связана, как:
- Если $с_{mu V}=frac{i}{2}R$, следовательно из соотношения Майера ($с_{mu p}=с_{mu V}+R$):
- Удельные теплоемкости в таком случае:
- В результате, формула для удельной теплоёмкости смеси:
- Проведем расчет
- Ответ: Удельная теплоемкость смеси 2,56 $frac{Дж}{гК}$.
[с_{mu }=сcdot mu o с=frac{с_{mu }}{mu } left(1.7
ight).] [с_{mu p}=frac{i+2}{2}R left(1.8
ight).] [i_{He}=3, i_{O_2}=5] [{c_p}_{He}=frac{frac{5}{2}R}{{mu }_{He}}, {c_p}_{O_2}=frac{frac{7R}{2}}{{mu }_{O_2}} left(1.9
ight).] [c_p=frac{frac{frac{7R}{2}}{{mu }_{O_2}}m_{O_2}+frac{frac{5}{2}R}{{mu }_{He}}m_{He} }{m_{O_2}+m_{He}} left(1.10
ight)] [c_p=frac{frac{3,5cdot 8,31cdot 16}{32}+frac{2,5cdot 8,31cdot 10}{4} }{26}=frac{14,5+51,94}{26}=2,56 (frac{Дж}{гК})]
Пример 2
Задание: В своих опытах Джоуль получил, что $с_{mu p}-с_{mu V}=1,986frac{кал}{Кcdot моль}$. Газовая постоянная измеренная в механических единицах $R=8,314cdot {10}^7frac{эрг}{К моль}$. Определите, как соотносятся 1 кал, эрг и Дж.
- Решение:
- В качестве основы решения примем уравнение Майера:
- Тогда получаем:
- Ответ: $1кал=4,18cdot {10}^7эрг=4,18 Дж$.
[с_{mu p}=с_{mu V}+R o с_{mu p}-с_{mu V}=R left(2.1
ight).] [с_{mu p}-с_{mu V}=1,986frac{кал}{Кcdot моль}=8,314cdot {10}^7frac{эрг}{К моль} o 1кал=4,18cdot {10}^7эрг=4,18 Дж.]
Источник: https://spravochnick.ru/fizika/termodinamika/uravnenie_mayera/
Первое начало термодинамики 1.внутренняя энергия. работа и теплота 2.теплоёмкость идеального газа. уравнение майера 3. теплоёмкости одноатомных и многоатомных. — презентация
1 ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ 1. Внутренняя энергия. Работа и теплота 2.Теплоёмкость идеального газа. Уравнение Майера 3. Теплоёмкости одноатомных и многоатомных газов 4. Закон о равномерном распределении энергии по степеням свободы 5. Применение первого начала термодинамики к изопроцессам идеальных газов
2 1. Внутренняя энергия. Работа и теплота Наряду с механической энергией любое тело (или система) обладает внутренней энергией. Она складывается из -теплового хаотического движения молекул, -потенциальной энергии их взаимного расположения, — кинетической и потенциальной энергии электронов в атомах, нуклонов в ядрах и др.
3 В термодинамике важно знать не абсолютное значение внутренней энергии, а её изменение.
В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой энергии недостаточно, чтобы изменить строение атома, а тем более ядра).
Следовательно, фактически под внутренней энергией в термодинамике подразумевают энергию теплового хаотического движения молекул.
4 Внутренняя энергия U одного моля идеального газа равна: или Таким образом, внутренняя энергия зависит только от температуры. Внутренняя энергия U является функцией состояния системы независимо от предыстории
5 Понятно, что в общем случае термодинамическая система может обладать как внутренней, так и механической энергией и разные системы могут обмениваться этими видами энергии. Обмен механической энергией характеризуется совершённой работой А, а обмен внутренней энергией – количеством переданного тепла Q.
6 Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и на совершение телом работы: – это первое начало термодинамики или закон сохранения энергии в термодинамике. Учитывая правило знаков, первое начало термодинамики можно записать в виде: – изменение внутренней энергии тела равно разности сообщаемой телу теплоты и произведённой телом работы.
- 7
- 8 Закон сохранения энергии для малого изменения состояния системы будет иметь вид: U – функция состояния системы; dU – её полный дифференциал, а δQ и δА таковыми не являются.
- 9 В каждом состоянии система обладает определенным и только таким значением внутренней энергии, поэтому можно записать Так как U – функция состояния, то Этот справедливо для любой функции состояния.
10 Теплота Q и работа А зависят от того, каким образом совершен переход из состояния 1 в состояние 2 (изохорический, адиабатический), а внутренняя энергия U не зависит. При этом нельзя сказать, что система, обладает определенным для данного состояния значением теплоты и работы. Количество теплоты Q выражается в тех же единицах, что работа и энергия, т.е. в джоулях [Q] = Дж.
11 Особое значение в термодинамике имеют круговые или циклические процессы, при которых система, пройдя ряд состояний, возвращается в исходное.
12 Если то согласно первому началу термодинамики т.е. нельзя построить периодически действующий двигатель, который совершал бы большую работу, чем количество сообщенной ему извне энергии. Вечный двигатель первого рода невозможен. К недостаткам первого начала следует отнести то, что: первое начало термодинамики не указывает, в каком направлении идут процессы изменения состояния.
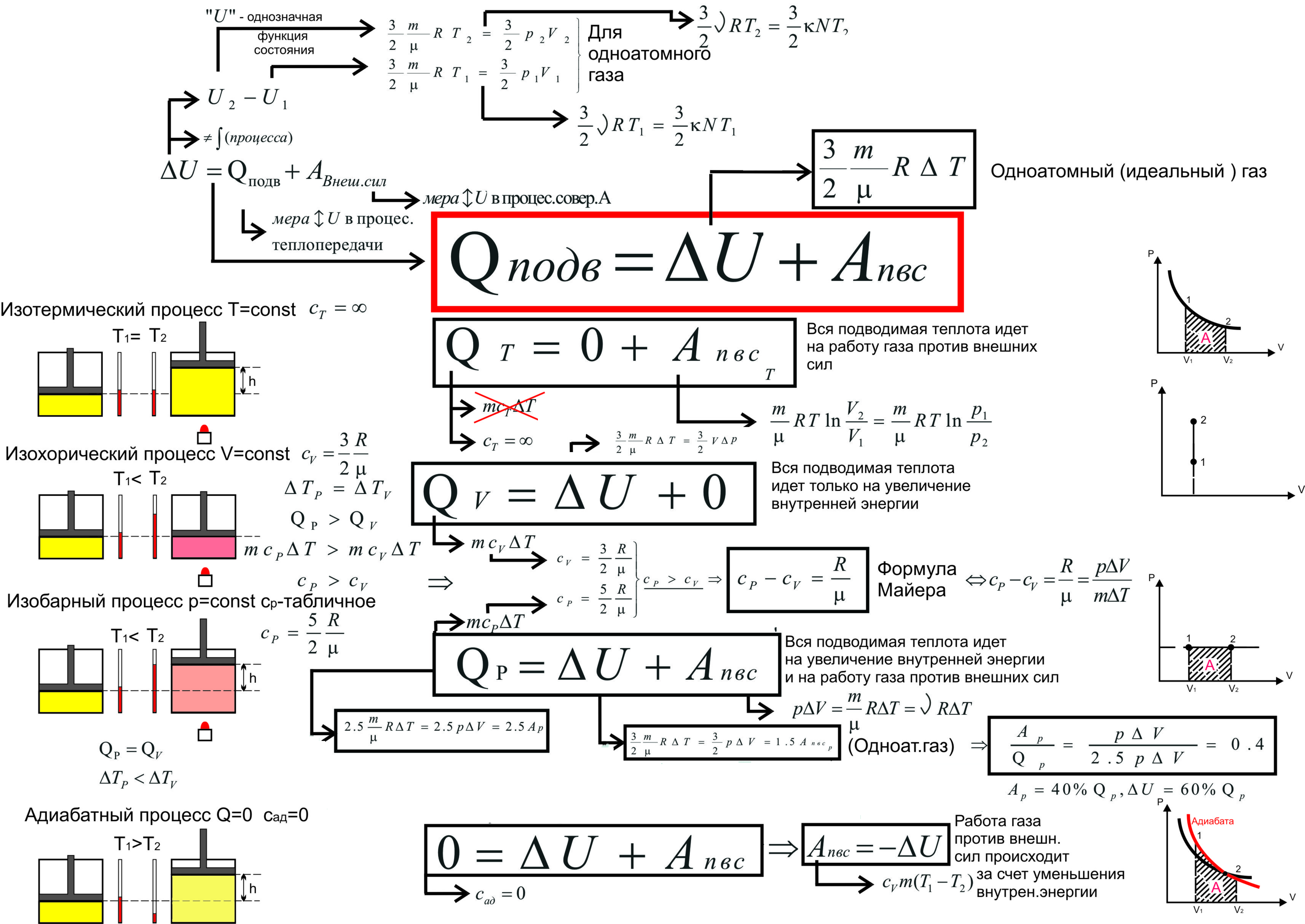
13 2. Теплоёмкость идеального газа Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус Размерность теплоемкости: [C] = Дж/К. Теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.
14 Удельная теплоёмкость С уд – количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [C уд ] = Дж/К. Молярная теплоемкость С μ количество теплоты, необходимое для нагревания 1 моля газа на 1 градус [C μ ] = Дж / (моль К).
15 Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании. Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при постоянном объёме С V
16 С Р – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу.
17 Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Следовательно Q и С не являются функциями состояния. Величины С Р и С V оказываются связанными простыми соотношениями. Найдём их.
18 Пусть мы нагреваем один моль идеального газа при постоянном объёме. Тогда, первое начало термодинамики, запишем в виде: т.е. бесконечно малое приращение количества теплоты равно приращению внутренней энергии. Теплоемкость при постоянном объёме будет равна:
- 19 В общем случае так как U может зависеть не только от температуры. В случае идеального газа справедлива формула Из этого следует, что
- 20 Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобным), поэтому формула справедлива для любого процесса. Для произвольной массы идеального газа:
- 21 При изобарическом процессе кроме увеличения внутренней энергии происходит совершение работы газом: Из основного уравнения молекулярно- кинетической теории При изобарическом процессе Р = const. Тогда получим:
22 Это уравнение Майера для одного моля газа. Из него следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус при изобарическом процессе. Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.
23 3. Теплоёмкости одноатомных и многоатомных газов Внутренняя энергия одного моля идеального газа равна
24 — постоянная адиабаты (коэффициент Пуассона)
25 Так как Тогда Из этого следует, что (4.3.5) Кроме того, где i – число степеней свободы молекул.
26 Подставив в выражение для внутренней энергии, получим: а так как, то внутреннюю энергию можно найти по формуле: (4.3.6)
27 Опыты с двухатомными газами такими как азот, кислород и др. показали, что Для водяного пара и других многоатомных газов (СН 3, СН 4, и так далее) То есть молекулы многоатомных газов нельзя рассматривать как материальные точки. Необходимо учитывать вращательное движение молекул и число степеней свободы этих молекул.
28 Числом степени свободы называется число независимых переменных, определяющих положение тела в пространстве и обозначается i i = 3 Как видно, положение материальной точки (одноатомной молекулы) задаётся тремя координатами, поэтому она имеет три степени свободы: i = 3
29 Многоатомная молекула может ещё и вращаться.
Например, у двухатомных молекул вращательное движение можно разложить на два независимых вращения, а любое вращение можно разложить на три вращательных движения вокруг взаимно перпендикулярных осей.
Но для двухатомных молекул вращение вокруг оси x не изменит её положение в пространстве, а момент инерции относительно этой оси равен нулю
- 30 i = 6 i = 5i = 3
- 31 4. Закон о равномерном распределении энергии по степеням свободы Больцман доказал, что, средняя энергия, приходящаяся на одну степень свободы равна Для i степеней свободы i = i п + i вр + i кол для одноатомной молекулы i = 3, для двухатомной молекулы i = 5 для трёхатомной молекулы i = 6
- 32 Для молярной теплоемкости Для удельной теплоемкости
- 33
34 Для одноатомных газов это выполняется в очень широких пределах, а для двухатомных газов только в интервале от К. Отличие связано с проявлением квантовых законов.
При низких температурах вращательное движение как бы «вымерзает» и двухатомные молекулы движутся поступательно, как одноатомные; равны их теплоёмкости.
При увеличении температуры, когда Т > 1000 К, начинают сказываться колебания атомов молекулы вдоль оси z (атомы в молекуле связаны не жёстко, а как бы на пружине).
35 Одна колебательная степень свободы несет энергии, так как при этом есть и кинетическая и потенциальная энергия, то есть появляется шестая степень свободы – колебательная. При температуре равной 2500 К, молекулы диссоциируют.
На диссоциацию молекул тратится энергия раз в десять превышающая среднюю энергию поступательного движения. Это объясняет сравнительно низкую температуру пламени.
Кроме того, атом – сложная система, и при высоких температурах начинает сказываться движение электронов внутри него.
- 36
- 37 Название процесса Изохорический ИзобарическийИзотермический Адиабатический Условие протекания процесса V =constP =constT =const Связь между параметрами состояния 5. Применение первого начала термодинамики к изопроцессам идеальных газов δQ = 0 Закон Шарля Закон Гей-Люссака Закон Бойля – Мариотта
- 38 Работа в процессе δA = PdV = dU А = U = C V (T 1 T 2 ) Количество теплоты, сообщённое в процессе Q = С V (T 2 T 1 ) δQ = δA Q = A δQ = δA Q = A δQ = 0Q = 0δQ = 0Q = 0 Изменение внутренней энергии dU = δQU = QdU = δQU = Q dU = С V dT U = С V (T 2 T 1 ) dU = 0U = 0dU = 0U = 0 dU = δA= С V dT U =A=С V (T 2 T 1 ) Теплоёмкость C Т = С ад = 0
- 39
- 40
41 Политропный процесс – такой процесс, при котором изменяются все основные параметры системы, кроме теплоемкости, т.е. С = const. Уравнение политропы n – показатель политропы.
42 С помощью показателя n можно легко описать любой изопроцесс: 1. Изобарный процесс Р = const, n = 0 2. Изотермический процесс Т = const, n = 1, 3. Изохорный процесс V = const,
43 4. Адиабатический процесс Q = 0, n = γ, С ад = 0. Во всех этих процессах работу можно вычислить по одной формуле:
44 Молярные теплоемкости при температуре 20 °С и давлении 1 атм Вещество С V, кал/(моль К) С P, кал/(моль К) СP/CVСP/CV Одноатомный газ He Ar 2,98 4,97 1,67 Двухатомный газ H 2 N 2 4,88 4,96 6,87 6,95 1,41 1,40 Многоатомный газ СО 2 NH 3 6,80 6,65 8,83 8,80 1,30 1,31
45
Источник: http://www.myshared.ru/slide/1025098/
Большая Рнциклопедия Нефти Рё Газа
Cтраница 1
Уравнение Майера является одним из основных соотношений в теории теплоемкости. [1]
Теоретически уравнение Майера — Боголюбова содержит бесконечно большое число членов вириального СЂСЏРґР° РІ правой его части Рё РїСЂРё этом является абсолютно точным РїСЂРё любых параметрах Рї РїСЂРё любом агрегатном состоянии данного реального газа. Практически же анализ его позволяет выявить следующую закономерность: чем меньше плотность газа, тем меньшее число членов вириального СЂСЏРґР° обеспечивают приемлемую точность этого уравнения. [2]
Физический смысл уравнения Майера заключается в том, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для такого же изохорного нагревания. Разность теплот должна быть равна работе, совершенной [ азом при изобарном расширении. [3]
Физический смысл уравнения Майера заключается в том, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для такого же изохор-ного нагревания. Разность теплот должна быть равна работе, совершенной газом при изобарном расширении. [4]
Рто соотношение называется уравнением Майера. [5]
Полученная формула называется уравнением Майера.
[6]
Выражение (53.6) называется уравнением Майера; оно показывает, что С, всегда больше Су на величину молярной газовой постоянной. [7]
Соотношение (2.20) называется уравнением Майера и является одним из основных в технической термодинамике идеальных газов. [9]
Рто соотношение называется уравнением Майера. [10]
Рта зависимость называется уравнением Майера. [11]
Выражение (53.6) называется уравнением Майера; оно показывает, что Ср всегда больше Су на величину молярной газовой постоянной.
Рто объясняется тем, что РїСЂРё нагревании газа РїСЂРё постоянном давлении требуется еще дополнительное количество теплоты РЅР° совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. [12]
Рто соотношение называется уравнением Майера. [13]
Полученная формула называется уравнением Майера.
Р�Р· уравнения Майера РІРёРґРЅРѕ, что удельная теплоемкость РїСЂРё постоянном давлении больше удельной теплоемкости РїСЂРё постоянном объеме РЅР° величину газовой постоянной R — работы расширения 1 РєРі газа РїСЂРё нагреве его РЅР° 1 РЎ РІ процессе СЂ const. Так как R РЅРµ зависит РѕС‚ параметров состояния, то теплоемкость идеального газа РїСЂРё СЂ const РЅРµ зависит РѕС‚ давления Рё объема. РћРЅР° зависит только РѕС‚ температуры газа. [14]
Рто уравнение РЅРѕСЃРёС‚ название уравнения Майера. [15]
Страницы: 1 2 3 4
Источник: https://www.ngpedia.ru/id541149p1.html
ПОИСК
Обычно уравнение Боголюбова—Майера представляется в общем виде [31 [c.20]
Теплоемкости идеального газа связаны с газовой постоянной уравнением Майера [c.114]
Используя уравнение первого начала термодинамики, можно вывести формулу Майера в несколько другом виде, чем выражение (П.5), а именно [c.32]
Вириальное уравнение состояния Боголюбова—Майера [c.19]
Если теплоемкость выражена в ккал/(кг-°С), а удельная газовая постоянная в кгс-м/(кг-°С), то уравнение Майера имеет вид [c.26]
С помош,ью уравнения (1.2) не всегда удается с достаточной точностью описать поведение реальных газов. В реальных газах существует межмолекулярное взаимодействие и сами молекулы занимают некоторый собственный объем. При высоких давлениях все газы следует рассматривать как реальные. Реальность газа следует учитывать также при низких и средних давлениях для многоатомных газов при температурах, близких к критическим. Сложный характер межмолекулярного взаимодействия не позволяет получить уравнение состояния конкретного реального газа чисто теоретическими методами. Более целесообразным является получение уравнения состояния в виде интерполяционной фс рмулы, описывающей экспериментальные данные. Существует много эмпирических или полуэмпирических уравнений состояния реального газа. Одно из них, называемое уравнением Майера—Боголюбова, можно представить в следующем наиболее общем виде [c.13]
Уравнение Боголюбова—Майера (1.50) разрешено в явном виде только относительно давления и коэффициента сжимаемости. Поэтому для определения плотности это уравнение приходится решать относительно р итеративным путем, привлекая процедуру определения давления [c.33]
Если использовать для расчета разложение, предложенное Майером и Гепперт-Майер (уравнения (11.74) и (11.75)), то у = 0,0008494 и для 5000° К [c.92]
Определение энтальпии. Энтальпия вещества по уравнению Боголюбова—Майера определяется в соответствии с изложенной выше методикой. Так как уравнение состояния имеет вид р = / (Т, V), то необходимо использовать выражение (111). Из (1.32) находим подынтегральную функцию второго члена правой части выражения (1.11), заметив, что V 1/р и т Т/Т р-. [c.20]
Достоинствами уравнения Битти—Бриджмена являются возможность его представления в форме Боголюбова—Майера н наличие простой и удобной методики комбинирования коэффициентов прн расчете смесей. Коэффициенты к уравнению Битти—Бриджмена более чем за 50 лет его существования получены для очень многих газов, что расширяет возможности его применения. [c.19]
Уравнения БВР и Старлинга также могут быть представлены в форме Боголюбова—Майера, однако они имеют остаточный член, содержащий экспоненту. Это сопряжено с изменением программы расчетов, так как необходимо вводить соответствующие поправки в алгоритм. [c.19]
Сопоставление уравнения Боголюбова—Майера (1.32) и полученных на его основе выражений для калорических параметров [c.31]
Процедуры определения термических и калорических параметров по уравнению Боголюбова—Майера. Представление зависимостей, определяющ,их термические и калорические величины по уравнению Боголюбова—Майера, в операторной форме позволяет запрограммировать их в виде системы вложенных операторов. В этом случае оператором низшего ранга является оператор определения величины ПП,Л1 для любой комбинации индексов I и J. Его можно записать в виде процедуры-функции [c.32]
Оценка точности метода условных температур. Для оценки точности метода условных температур выполнялись численные расчеты с использованием уравнения состояния Боголюбова— Майера (1.
32) применительно к хладагенту R12, свойства которого наиболее сильно отличаются от свойств идеального газа [17].
Расчетной проверке подвергались политропные процессы, соответствующие адиабатному сжатию с потерями, протекающие в непосредственной близости от линии насыщения. В этой области [c.116]
Коэффициенты Ь1) уравнения Боголюбова—Майера для некоторых хладагентов [38 [c.21]
Что касается формальной теории, то большинству специалистов ясно, как рассчитывать вириальные коэффициенты классическим способом или с помощью квантовомеханической теории. С этой точки зрения теорию можно считать в основном законченной, допуская лишь незначительное уточнение некоторых ее вопросов.
Это не значит, что не осталось нерешенных проблем, представляющих интерес. Например, очень важен вопрос о сходимости вириального разложения при высоких плотностях, особенно для теории конденсированного состояния, которая была развита Майером и другими исследователями [23, 24].
Однако этот вопрос, как и другие нерешенные проблемы, выходит за рамки настоящей работы, и теорию можно считать окончательной в той части, где речь идет о межмолекулярных силах. Поэтому в гл. 2 дается только обзор существующей теории и приводятся основные допущения и результаты.
Более подробно останавливаться на теории вириального уравнения нецелесообразно, так как уже имеется ряд превосходных обзоров и монографий, посвященных этому вопросу [23—28]. [c.14]
Вследствие того что уравнение Битти—Бриджмена дает хорошие результаты в сравнительно широком диапазоне изменения давления и плотности, а его константы получены для большого числа веществ, оно в течение долгого времени применяется в технике.
Несмотря на то, что сейчас ведутся интенсивные исследования веществ с целью определения для них коэффициентов к уравнению Боголюбова—Майера, этих данных пока еще меньше, чем констант к уравнению Битти—Бриджмена, поэтому оно не утрачивает актуальности и в настоящее время, хотя в дальнейшем, по мере накопления экспериментальных данных по уравнению Боголюбова—Майера, постепенно выйдет из употребления. [c.37]
Естественное желание инженера использовать при расчетах параметров реального газа уравнение состояния одного вида, в котором изменяться будут только числовые константы, может быть удовлетворено и при использовании уравнения Битти-Бриджмена, если принять во внимание, что оно может быть представлено в вириальной форме Боголюбова—Майера [3] [c.37]
Так как при использовании уравнения Боголюбова—Майера S = / (р. Т) и t = / (р, Т), то в качестве величины при итерациях принята температура Т (рис. 3.7).
Ее начальное значение Ti задается минимально возможным, а начальное значение шага DT (DT) выбрано равным одной трети разности критической и начальной температур DT = (Т р — Ti)/3. Поиск решения ведется шаговым методом.
Сначала по известным температуре Ti и энтропии S определяется энтальпия в точке 1. Если она оказывается меньше заданной энтальпии i (точка А на рис. 3.7), то температура [c.110]
Подставим эти производные в уравнение (2.58) и получим закон Р. Майера [c.37]
Задание. На основе полученных соотношений установите связь молярных теплоемкостей , и Су идеального газа (формула Р. Майера). Для этого подставьте в формулу теплоемкости при постоянном давлении выражение энтальпии и используйте уравнение состояния 1 моль идеального газа. [c.65]
Эта зависимость называется уравнением Майера. [c.26]
V — оо уравнение Майера—Боголюбова превращается в уравнение Менделеева—Клапейрона. [c.14]
В другом цикле, предложенном Майером (1930), используются энергии сублимации галогенидов шелочных металлов, энергии диссоциации их газообразных молекул и некоторые другие термохимические величины, уже фигурировавшие в цикле Габера — Борна. Для Na l этот цикл дает AG = 75(5 кДж-м оль .
Таким образом, можно полагать, что энергия решетки хлорида натрия должна лежать в пределах от 760 до 790 кДж-моль , куда попадают значения, подсчитанные по уравнениям. (1.23) и (1.25) величину 762 кДж-моль- можно считать наиболее вероятным значением энергии решетки Na l. [c.
46]
Групповые интегралы более высокого порядка достаточно трудно записать в удобной форме, потому что они состоят из большого числа членов. Другими словами, комбинаторная проблема для больших / не является простой.
Решение этой проблемы может быть существенно упрощено применением простых диаграмм, с помощью которых указанная проблема формулируется как задача теории линейных графов. Такие групповые диаграммы были введены Майером для классического случая и затем обобщены на случай квантовой статистики [23].
Хотя метод групповых диаграмм представляет большой интерес для ряда проблем, выходящих за рамки вириального уравнения состояния, эти диаграммы не будут рассматриваться, так как их применение особенно важно лишь для исследования явлений конденсации с помощью высших bj и высших вириальных коэффициентов [21, 24].
С точки зрения изучения межмолекулярных сил нам необходимы первые несколько коэффициентов, которые легко могут быть найдены без использования групповых диаграмм. [c.39]
Силы отталкивания возникают вследствие взаимного проникновения электронных облаков атомов. Это явление (вместе с запретом Паули) препятствует слишком сильному сближению атомов.
Попытки выразить в математической форме возникающие силы отталкивания встречают чрезвычайно большие трудности. Эти силы быстро возрастают с уменьшением расстояния между атомами, но закономерность, которой они подчиняются, имеет сложный характер.
Однако в ряде случаев можно пользоваться упрощенными уравнениями.
При расчетах энергий решеток ионных кристаллов галоидных солей щелочных металлов и окислов щелочноземельных металлов хорошие результаты были получены при применении предложенного Борном и Майером [14] простого выражения, описывающего зависимость потенциальной энергии от сил отталкивания. Оно имеет следующий вид [c.26]
Теплоемкости Сру и идеального газа, у которого йу < 1, отрицательны, поэтому изобары и изохоры идут в Sy — Ту-диа-грамме с понижением Ту (рис. 3.8), так как подводимая теплота dq >0. При этом изобары идут круче изохор, так как ку = Сру с. у < < 1 и, значит, I Сру I < I с-,у . По мере увеличения давления изобары смещаются вниз в сторону уменьшения условных температур.
Для такого идеального газа справедливы уравнения Майера (3.40) и уравнения термодинамики, если заменить в них термодинамическую температуру условной. Энтальпия и внутренняя энергия идеального газа с < I отрицательны, но так как при изобарном или изохорном подводе теплоты величина Ту умень шается, то эти параметры в конце процесса больше, чем в начале т. е. dq = di > u. [c.
120]
Из уравнения Майера (11.13) имеем [c.58]
Отношение констант ионизацииможет быть выражено с помощью равновесия изотопного обмена, константа которого в принципе может быть вычислена по уравнению Бигелейзена —Майера [уравнение (17)], где числа симметрии сокращены [96, 97]. [c.90]
Примепеинс каждого из уравнений определяется характером поставленной задачи и требуемой точностью расчетов. При расчете процессов сжатия перегретого пара при средних и малых давлениях и илотиостях, не превышающих критической плотности, инженерная точность вполне может быть обеспечена с помощью уравнений Битти—Бриджмена, Старлинга, БВР.
Существенным преимуществом этпх уравнений является возможность расчета параметров смесей реальных газов, которые часто являются рабочими веществами компрессоров в химическом и нефтехимическом производствах. Если необходима высокая точность расчетов, то применяют уравнения Боголюбова—Майера, Клёцкого и др.
Отметим, что по существу почти псе известные уравнения состояния являются математическими аппроксимациями двумерных термодинамических поверхностей, описывающих термические свойства реальных газов. Поэтому точность р—V—Г-зависимостей определяется главным образом степенью полинома, который входит в уравнение состояния.
Так, уравнение Битти—Бриджмена является уравнением третьей степени по температуре и плотности, уравнение БВР — пятой степени по плотности и третьей степени по температуре, уравнение Старлинга — пятой степени и по плотности и по температуре.
В некоторых случаях таких значений степени недостаточно для получений нужной точности, тогда принимают уравнение Боголюбова—Майера, которое теоретически представляет собой бесконечный ряд по степеням температуры и плотности. Однако на практике даже для прецизионного описания термических свойств редко приходится применять степени выше восьмой. [c.18]
Уравнение Боголюбова—Майера представляет собой наиболее обгцую форму уравнения состояния с вириальными коэффициентами и имеет теоретическое обоснование.
Вследствие этого оно признано сейчас основным уравнением состояния, что значительно облегчает программирование и выполнение расчетов на ЭВМ, так как переход от од Юго рабочего вещества к другому осуществляется без изменения алгоритма простой заменой одного массива коэффициентов аппроксимации на другой. Недостатками уравнения Боголюбова—Майера являются отсутствие коэффициентов аппрок- [c.18]
После работ Боголюбова и Майера вириальное уравнение состояния приобрело особое значение как единственное из известных уравнений состояння, имеющих строгую теоретическую основу. Оно имеет вид [c.19]
И. И. Перельштейн и Е. Б. Парушин [38] преобразовали обобщенное уравнение состояния Битти—Бриджмена в вириаль-ную форму Боголюбова—Майера, придав ему вид [c.40]
Для теплоемкостей в состоянии чдеального газа справедливо уравнение Майера [c.41]
Теоретическое развитие вириального уравнения состояния было начато гораздо позже его применения для описания экспериментальных данных. Правда, это не относится к теории второго вириального коэффициента.
Строгое теоретическое обоснование уравнения состояния представляло огромные трудности даже после того, как в 1927 г. Урселом [12] была математически обоснована форма разложения в виде степенного ряда. И только после работ Майера [13], выполненных в 1937 г., теория уравнения состояния получила свое развитие.
Формальную теорию и в классической, и в квантовой механике теперь можно рассматривать как в основном законченную теорию, хотя все еще существуют трудности, связанные с точным численным расчетом высших вириальных коэффициентов.
В отличие от общей теории вириального разложения теоретическое обоснование второго вириального коэффициента известно уже давно. Причиной является то, что это частный случай вириального разложения для низких плотностей, который можно было решить сравнительно просто.
Несколько разных математических методов было использовано для развития теоретической интерпретации второго вириального коэффициента. Возможно, самым старым и простым из них является расчет давления при рассмотрении потока момента через воображаемую единицу площади поверхности в газе [14].
Второй вириальный коэффициент является тогда дополнительным членом, учитывающим двойное взаимодействие. Этот кинетический метод очень трудно применить к вычислению высших вириальных коэффициентов, исключая некоторые модели молекул, например жесткие сферы [15]. Более общие методы [c.12]
Иногда эту модель называют потенциалом Гершфельда—Ген-перта-Майера в честь исследователей, использовавших его для изучения уравнения состояния одномерной жидкости [30]. Из уравнения (4.
1) следует, что этот потенциал не дает максимума для второго вириального коэффициента В(Т), так как и О при г>а.
Однако во всех других отношениях он достаточно удачен, так как содержит три параметра, причем глубину [c.181]
Изобарная и изохорная теплоемкости взаимосвязаны соотношением, называелшм уравнением Ю. Р. Майера (1814—1878), [c.55]
Это уравнение носит название формулы Майера. Согласно (11.64) ири постоянстве Ср в том же диапазоие температур должна быть постоянна и величина v- Таким образом, понятие идеального газового состояния до-полняется еще в том смысле, что величины Ср ж Су не зависят от температуры и давления. [c.42]
Идеальные газы не удовлетворяют третьему закону термодинамики. Для идеального газа справедливо уравнение Майера Ср— v=R.
Но так как срфсу и ЯфО, то можно заключить, что уравнение состояния идеального газа (pV=RT), с помощью которого и получено уравнение Майера, не позволяет теплоемкостям Ср и v ни прн каких условиях быть равными нулю.
Это указывает на то, что идеальный газ при низких температурах должен вести себя не в соответствии с уравнением Клапейрона. Это положение было названо вырождением идеального газа. [c.188]
Источник: https://www.chem21.info/info/91614/
Уравнение Майера
| Наименование параметра | Значение |
| Тема статьи: | Уравнение Майера |
| Рубрика (тематическая категория) | Физика |
Получим отношения к через число степеней свободы:
- показатель адиабаты
- Состояние газа характеризуется тремя параметрами: Т, P, V.
- Термодинамический процесс — ϶ᴛᴏ переход системы из одного состояния в другое, в результате которого изменяются параметры P, V, T.
- Термодинамика базируется на двух базовых законах, называемых началами термодинамики.
Уравнение Майера — понятие и виды. Классификация и особенности категории «Уравнение Майера» 2017, 2018.
Сравнение между собой Ср и СV приводит к уравнению Майера: . Это уравнение показывает, что Ср больше, чем СV на величину универсальной газовой постоянной R. Это объясняется тем, что при изобарном нагревании газа, в отличие от изохорного нагревания, требуется дополнительное… [читать подробнее].
Теплоемкостьютела называется величина, равная количеству теплоты, которое нужно сообщить телу, чтобы повысить его температуру на 1 К. Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: . Молярная… [читать подробнее].
Уравнение Майера связывает между собой теплоемкости идеального газа в процессах p=const и v=const. Для удельных теплоемкостей сp и сv эта связь получается из рассмотрения формулы, являющейся определением функции состояния-энтальпии: , Дж/кг. Тогда дифференциал , а… [читать подробнее].
Молярная теплоемкость при постоянном объеме Записав первое начало термодинамики и учитывая, что , , для 1-го моля газа получим . (9.8) При V = const, pdV = 0, поэтому сообщаемая газу извне теплота идет только на увеличение его внутренней энергии: . (9.9) Таким образом, молярная… [читать подробнее].
Источник: http://referatwork.ru/category/fizika/view/507410_uravnenie_mayera




