Уравнение равномерного движения

Содержание

Тема урока:
«Скорость равномерного прямолинейного движения»
«Уравнение прямолинейного равномерного движения»
Цели урока: сформулировать признаки равномерного движения.
Ход урока.

Организационный момент.
Проверка домашнего задания

Что называется перемещением точки?
Что называется телом отсчета?
Каким способом можно задать положение точки?
Что называется радиус – вектором?

Изучение нового материала.

Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Дадим определение скорости.

Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.

При прямолинейном движении скорость не изменяется по направлению. Движение называется равномерным прямолинейным, если траектория- прямая линия и точка за любые равные промежутки времени проходит равные перемещения.

Равномерное прямолинейное движение – движение, при котором любые равные промежутки времени тело совершает равные перемещения.

Если начальный момент времени t0 принять равным нулю, то

Отсюда

Последнее уравнение и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени.

Вместо векторного уравнения можно записать три эквивалентных ему уравнения в проекциях на оси координат. Радиус-вектор является суммой двух векторов: радиус-вектора и вектора .

Следовательно, проекции радиус-вектора на оси координат должны быть равны сумме проекций этих двух векторов на те же оси. Выберем оси координат так, чтобы тело двигалось по какой-либо оси, например по оси ОХ. Тогда векторы и будут составлять с осями ОY и ОZ, прямой угол.

Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора на оси ОY и ОZ.

Так как проекции радиус-вектора на координатные оси равны координатам его конца, то rx = x и r0x = x0. Поэтому в проекциях на ось ОХ уравнение можно записать в виде

Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.

Строго говоря, равномерного прямолинейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значение скорости слегка изменяется.

Незначительная неровность шоссе, порыв ветра, чуть-чуть большее нажатие на педаль газа и другие причины вызывают небольшие изменения скорости. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью.

Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения. Графическое представление равномерного прямолинейного движения. Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график зависимости проекции скорости от времени. Это прямая, параллельная оси времени.

Площадь прямоугольника ОАВС, заштрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть , а сторона ОС — время движения t, поэтому .

На рисунке ниже приведены примеры графиков зависимости координаты от времени для трех различных случаев равномерного прямолинейного движения. прямая 1 соответствует случаю х0 = 0, vх1 0;
прямая 2 — случаю х0 0;
прямая 3 — случаю х0 0, vх3
Угол наклона α2 прямой 2 больше, чем угол наклона α1 прямой 1.
За один и тот же промежуток времени t1 точка, движущаяся со скоростью vх2, проходит большее расстояние, чем при движении ее со скоростью vх1.
Во втором случае скорость vх больше, чем в первом.
Скорость определяет угол наклона прямой к оси t.
Очевидно, скорость vх численно равна тангенсу угла α. В случае 3 α3

Решение задач

1. Движение грузового автомобиля описывается уравнением х1=-270+12t, а движение пешехода по обочине того же шоссе — уравнением х2=-1,5t. Сделать пояснительный рисунок (ось Х направить вправо), на котором указать положение автомобиля и пешехода в начальный момент времени. С какими скоростями и в каком направлении они двигались? Когда и где они встречались?

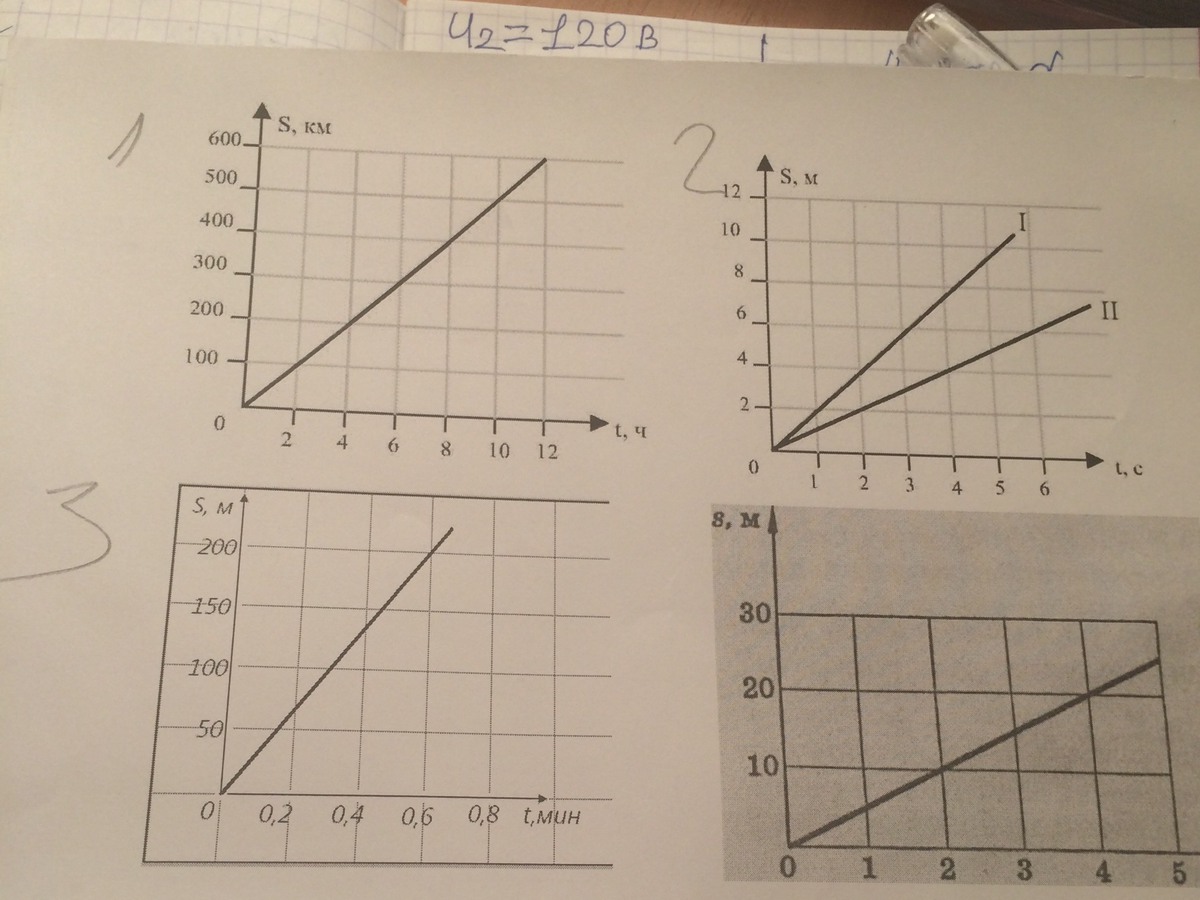
2. По заданным графикам найти начальные координаты тел и проекции скоростей их движения. Написать уравнения Х(t). По графику найти время и место встречи.

Домашняя работа §9-10, стр.27 упр.1(1)

Источник: https://kopilkaurokov.ru/fizika/uroki/skorost-priamolinieinogho-ravnomiernogho-dvizhieniia-uravnieniie-priamolinieinogho-ravnomiernogho-dvizhieniia

Прямолинейное равномерное движение

ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
Прямолинейное движение— траектория представляет собой прямую линию. Прямолинейным равномерным движением называется механическое движение, при котором тело за любые равные промежутки времени t1 = t2 = t3 = … совершает одинаковые перемещения
Следовательно: — эта величина является характеристикой движения.
— скорость прямолинейного равномерного движения.
Скорость прямолинейного равномерного движения — это векторная физическая величина, численно равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Скорость показывает, какое перемещение совершает тело за единицу времени, двигаясь прямолинейно и равномерно. Например, если модуль скорости равна 5 м/с, это значит, что за каждую секунду своего движения тело, двигаясь прямолинейно и равномерно, перемещается на 5 м.
Для описания прямолинейного равномерного одного тела достаточно одной оси координат. По правилам действия с векторами Из чертежа видим: , где — проекция вектора скорости на координатную ось x.
Решение основной задачи механики для прямолинейного равномерного движения:
Следовательно: Если движение сонаправлено с осью координат, то. Если движение против оси координат, то .
Графическое представление равномерного прямолинейного движения
1.График зависимости проекции скорости от времени Площадь под графиком скорости численно равна перемещению. (Справедливо для любого движения)
2. График зависимости проекции перемещения от времени и — движение сонаправлено с осью, — движение против оси.
3. График зависимости координаты от времени. 1, 2, 4 — движение сонаправлено с осью, 3, 5 — движение против оси.

Источник: https://www.eduspb.com/node/1665

Равномерное прямолинейное движение. Скорость

В прошлой теме говорилось о механическом движении, которое представляет собой изменение положения тел (или частей одного и того же тела) относительно друг друга в пространстве с течением времени.

Для описания механического движения необходимо выбрать тело отсчета, то есть тело или группу тел, которое в данном случае принимают за неподвижное и относительно которого рассматривается движение других тел, и связать с ним систему координат.

Так же было установлено, что для определения положения тела в какой-то момент времени, нужно знать вектор его перемещения. Действительно, для того, чтобы сказать, как переместилось тело, необходимо знать не только расстояние от начальной точки, но и направление, в котором тело переместилось.

Также довольно важной характеристикой любого движения является скорость. В данной теме разговор пойдёт о скорости при равномерном прямолинейном движении тела.

Равномерное прямолинейное движение — это самый простой вид движения. При таком движении тело двигается только по прямой и за любые равные промежутки времени совершает равные перемещения.

То есть это движение с постоянной по модулю и направлению скоростью.

Обратите внимание на то, что всегда необходимо задавать направление скорости. В прошлых темах было показано, что выбор системы отсчёта имеет решающее значение, а в разных системах отсчета скорости могут быть направлены по-разному.

Вообще скоростью называется физическая векторная величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения. Иными словами, это производная радиус-вектора точки по времени.

Уравнение скорости для равномерного прямолинейного движения имеет вид

По формулам, написанным в векторном виде, вычисления вести нельзя. Ведь векторная величина имеет не только численное значение, но и направление.

При вычислениях удобно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат, так как над проекциями можно производить алгебраические действия. И так, как же рассчитать проекцию скорости? Рассмотрим простой пример.

Пусть в начальный момент времени координата тела была равна x0, а в момент времени t – x.

Тогда за промежуток времени ∆tؚ, равный tؚ — tؚ0, координата тела изменилась на величину равную разности между конечной и начальной координатой тела. Тогда проекция скорости тела в этом случае будет равна отношению изменения координаты тела к промежутку времени, в течении которого это изменение произошло.

Из записанной формулы, воспользовавшись известными математическими приемами, можно получить уравнение зависимости координаты тела от времени.

Полученное уравнение называют кинематическим уравнением равномерного движения.

Известно, что разность между начальной и конечной координатой тела есть ни что иное, как проекция перемещения на выбранную координатную ось.

Воспользуемся основным свойством пропорции, чтобы выразить проекцию перемещения.

Полученное уравнение называется уравнением перемещения.

При равномерном прямолинейном движении направление вектора скорости не изменяется, а значит путь и модуль проекции перемещения тела равны. На основании этого, получим уравнение пути при равномерном прямолинейном движении тела.

Обратите внимание, что проекция скорости тела взята под знак модуля. Это объясняется тем, что путь не может быть отрицательным, а вот знак проекции вектора скорости, как и проекции перемещения, будет зависеть от выбора направления координатной оси.

Рассмотрим графические зависимости скорости, координаты, пути и перемещения от времени при равномерном прямолинейном движении.

При равномерном движении скорость постоянна, поэтому график зависимости скорости от времени будет представлять собой прямую линию, параллельную оси времени.

Иными словами, при равномерном движении скорость не зависит от времени, так как является величиной постоянной.

Из графика скорости видно, что проекция скорости тел для оранжевой и зелёной прямых больше нуля, так как они располагаются выше оси времени. В случае с синей прямой, наблюдается противоположная картина: значит, тело двигается в обратном направлении, поэтому проекция скорости отрицательная.

Если рассмотреть конечный промежуток времени, то получим ограниченную область, имеющую форму прямоугольника. Площадь этого прямоугольника будет являться ничем иным, как изменением координаты «Икс», а, следовательно, пройденным телом путем. Действительно, ведь длина одной из сторон прямоугольника — это скорость, а длина другой — это промежуток времени.

Следующим рассмотрим график зависимости проекции перемещения от времени. Для этого еще раз вспомним уравнение перемещения:

Из уравнения видим, что проекция перемещения линейно зависит от времени. Следовательно, при равномерном движении графиком перемещения является прямая линия.

Направление и угол наклона графика зависимости проекции перемещения к оси времени будет зависеть от проекции вектора скорости на координатную ось.
Из рисунка видно, что тело 1 и тело 3 движутся в положительном направлении оси х, при этом скорость первого тела больше скорости третьего.
Тело 2 движется в направлении, противоположном направлению оси х, поэтому график перемещения располагается под осью времени.
Рассмотрим зависимость пройденного пути от времени.

Для равномерного движения график зависимости пути от времени представляет собой прямую линию, так как зависимость пути от времени, как и в случае с перемещением тела, линейная.

Однако графики зависимости пути от времени для всех трех тел располагаются выше оси времени.

Это объясняется тем, что пройденный путь — это длина траектории, а, следовательно, путь не может быть отрицательным.

Наклон графика пути к оси времени, как и в случае с графиком перемещения, зависит от модуля скорости: чем больше скорость движения тела, тем больший угол наклона.
Рассмотрим графики зависимости координаты от времени (их еще называют графиками движения).

На рисунке представлены три прямые, каждая из которых описывается одним и тем же уравнением. Точки пересечения этих графиков с осью x соответствуют значениям начального положения. Как видно из графика, для первого тела x00.

Так же на графике хорошо видно, что проекции скоростей для первого и третьего тел больше нуля. Действительно, ведь значение координаты x увеличивается с течением времени. Значит, тело двигается в направлении, совпадающем с положительным направлением оси икс. Это соответствует положительному перемещению, а, значит, положительной проекции скорости.

В случае с синей прямой, наблюдается противоположная картина: значит второе тело двигается в обратном направлении, поэтому его проекция скорости отрицательная.

Кроме того, из графиков можно судить о модуле скорости. Очевидно, что тело, движение которого описано оранжевой прямой, двигается быстрее остальных, так как за один и тот же промежуток времени оно проходит большее расстояние. Используя этот же аргумент, можно сказать, что модуль скорости второго тела больше, чем модуль скорости тела номер три.

При этом, как и в случае с перемещением, угол наклона графика к оси времени зависит от скорости тела. Из этих наблюдений можно сделать следующий вывод: чем больше угол между прямой и осью времени, тем больше скорость движения тела.

В случае прямолинейного равномерного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).
С помощью графика движения можно определить:
1) координаты тела в любой момент времени;
2) путь, пройденный телом за некоторый промежуток времени;
3) время, за которое пройден какой-то путь;
4) кратчайшее расстояние между телами в любой момент времени;
5) момент и место встречи тел;
6) и так далее.
Необходимо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.

Очень часто наблюдаются довольно сложные типы движения, когда тело движется относительно системы отсчёта, которая в тоже время движется относительно Земли. На прошлых уроках говорилось о том, что любое механическое движение относительно, то есть в разных системах отсчета будут различны вид траектории, значение скорости, перемещения и других физических величин.

Было установлено, что в случае, когда тело участвует одновременно в нескольких движениях, результирующее перемещение тела равно векторной сумме перемещений, совершаемых им в каждом из движений.

В рассматриваемом примере очевидно, что все перемещения произошли за один и тот же промежуток времени.

Разделив каждое перемещение в уравнении на этот промежуток времени, получим классический закон сложения скоростей, установленный Галилеем: скорость тела относительно неподвижной системы отсчета равна геометрической сумме скорости тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной.

Здесь следует помнить, что данный закон справедлив и для неравномерного движения. В этом случае вектора скорости — это мгновенные скорости, то есть скорости в данный момент времени или в данной точке траектории.

Основные выводы:

В данной теме были повторены некоторые важные понятия кинематики. Поговорили о равномерном прямолинейном движении тел и способах описания такого движения. Еще раз затронули относительность движения и вывели классический закон сложения скоростей.

Источник: https://videouroki.net/video/3-ravnomiernoie-priamolinieinoie-dvizhieniie-skorost.html

Основное уравнение равномерного движения

Равномерным движением называется установившееся движение, при котором скорости частиц жидкости не изменяются вдоль траекторий. При равномерном движении жидкости в водопроводах, а также в открытых руслах живые сечения, средние скорости течения и глубины по длине потока остаются постоянными.

Выведем основное уравнение равномерного движения, на основании которого выявим факторы, влияющие на величину гидравлических потерь по длине трубопровода.

Рассмотрим поток жидкости произвольной формы площадью , имеющий по длине постоянное живое сечение и наклоненный к горизонту под углом (рис. 5.1). Выделим в потоке сечениями 1-1 и 2-2 отсек длиной l. Действие отброшенной жидкости слева и справа заменим давлениями р1 и р2, которые создают внешние силы, приводящие жидкость в движение: ; . К ним относятся и сила тяжести отсека жидкости:

Рис.5.1

На жидкость действуют также силы сопротивления движению. Эти силы приложены вдоль поверхности стенок. Обозначим через удельную силу трения, через – длину смоченного периметра. Тогда сила трения

Составим уравнение равновесия сил, действующих на выделенный отсек.

По условию равномерного движения, внешние силы, приводящие жидкость в движение, должны быть равны силам сопротивления, т.е. если спроектировать все силы на ось потока, получим

Тогда получим

Сравним выражение (5.1) с уравнением Бернулли для потока реальной жидкости:

Так как V1 = V2, то

разделим левую и правую часть выражения (5.3) на l:

Выражения (5.2), (5.3) и (5.4) являются уравнениями равномерного движения.

Не нашли то, что искали? Воспользуйтесь поиском:

Источник: https://studopedia.ru/6_158749_osnovnoe-uravnenie-ravnomernogo-dvizheniya.html

Равномерное прямолинейное движение – FIZI4KA

ОГЭ 2018 по физике ›

1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.

Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.

2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.

Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.

Если за время ( t ) тело совершило перемещение ( vec{s} ), то скорость его движения ( vec{v} ) равна ( vec{v}=frac{vec{s}}{t} ).

Единица скорости: ( [,v,]=frac{[,s,]}{[,t,]} ); ( [,v,]=frac{1,м}{1,с}=1frac{м}{с} ). За единицу скорости принимается 1 м/с — скорость такого равномерного движения, при котором тело за 1 с совершает перемещение 1 м.

Зная скорость равномерного движения, можно найти перемещение за любой промежуток времени: ( vec{s}=vec{v}t ). Вектор скорости и вектор перемещения направлены в одну сторону — в сторону движения тела.

3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.

Пусть ( vec{s} ) — перемещение тела (рис. 11). Направим координатную ось ОХ по направлению перемещения. Найдем проекцию перемещения на координатную ось ОХ. На рисунке ( x_0 ) — координата начальной точки перемещения, ( x ) — координата конечной точки перемещения.

Проекция перемещения равна разности координат конечной и начальной точек: ( vec{s}_x=x-x_0 ). С другой стороны, проекция перемещения равна проекции скорости, умноженной на время, т.е. ( vec{s}_x=vec{v}_xt ). Откуда ( x-x_0=vec{v}_xt ) или ( x=x_0+vec{v}_xt ).

Если начальная координата ( x_0 ) = 0, то ( x=vec{v}_xt ).

Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.

Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае ( x>x_0 ). Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае ( xv_2>v_3 ) 3) ( v_1

Источник: https://fizi4ka.ru/ogje-2018-po-fizike/ravnomernoe-prjamolinejnoe-dvizhenie.html

Величины равномерного движения, уравнения и формулы равномерного движения

Скорость
Путь
Закономерности равномерного движения, расчеты
Уравнение движения с постоянной скоростью

Одним из наиболее распространенных видов движения в механике является равномерное движение. На самом деле встретить в быту этот вид движения очень сложно. Это своего рода модель, на основе которой построено изучение движущихся тел.

Равномерное движение — это вид механического движения, изучаемый в кинематике, при котором физическое тело проходит за одинаковый временной период, одинаковый путь.
Потому для вывода формулы этого вида движения используют следующие физические величины, характерные для движущегося материального тела: скорость физического тела; время; расстояние, пройденное телом.
Чем выше скорость рассматриваемого предмета, тем больше будет расстояние, которое оно пройдет за промежуток времени.
Как следствие, получается прямо пропорциональная зависимость расстояния от скорости движения.
В итоге получается зависимость, выражаемая формулой:

Скорость

Как видно из формулы, скорость физического тела — это один из главных элементов при изучении движения.

Координата тела х определяет положение тела, в результате чего, функция зависимости выглядит следующим образом: t — x(t), где t — время, за которое тело прошло путь.

Физической величиной быстроты при равномерном движении является скорость, которую очень просто можно вычислить. Также нельзя забывать о том, что скорость является векторной физической величиной, имеющей направление. И при решении задач это условие обязательно следует учитывать.

Скоростью при этой форме движения, называют величину, показывающую какое расстояние проходит предмет за определенный временной промежуток. Обычно ее называют путевой скоростью.

Расстояние, пройденное телом, обозначают буквой S, скорость v, а промежуток времени t.

Формула расчета выглядит так:

Это соотношение мы получили из зависимости S = vt.
Скорость — это отношение пути к промежутку времени, за который оно пройдено.
В чем же измеряется скорость?
В системе измерений СИ — это метры в секунду (м/с), но чаще всего в повседневной жизни используют другую размерность — километры в час (км/ч).
Эта единица измерения не является основной, но в быту мы может чаще о ней слышать.
Пройденный путь пропорционален времени, потому отношение пути к этой величине не находится в зависимости от интервала времени.

Путь

Пройденное расстояние определяет насколько передвинулось тело, но это величина не показывает направленность передвижения.
Чтобы это определить нужно ввести еще координаты, которые позволяют выявить насколько сместилось тело в пространстве.
Для этого применяют формулу:
Δx=x−x0
В данной функции х — координата физического тела в данный момент, а х0 — в начальный.
Если значение координаты увеличивается она становится положительной.
Если уменьшается — отрицательной, в следствие этого Δx — это величина, показывающая направленность движущегося тела.
Пройденный путь тела во время движения в одном направлении, будет равен изменению его координаты.
То есть наблюдается такая зависимость, выражаемая формулой:

Исходя из этого, скорость будет равна отношению изменения координаты тела к времени, за которое они произошли.

Расстояние — это длина траектории.

Не нужно путать понятия траектории и перемещения. Траектория — это длина линии, по которой тело перемещалось, она может быть как кривой, так и прямой.

Перемещение — это векторная физическая величина, которая начинается от начальной координаты тела и заканчивается в конечной. По сути это вектор, длина этого вектора и есть перемещение.

Вычисление равномерного движения

Равномерное движение — это движение, при котором модуль скорости не зависит от промежутка времени, т.е. скорость постоянна:

Расстояние обозначается латинской буквой S. Между расстоянием и временем наблюдается линейная зависимостью:

Выводим уравнение

Формула скорости будет выглядеть следующим образом:
При , уравнение будет таким:
Запишем уравнение равномерного движения в векторной форме:
Таким образом находится радиус-вектор, определяющий, где находится точка в пространстве в различные временные промежутки.
Чтобы это определить достаточно знать скорость тела и его исходное положение в пространстве.

Начальное положение тела задается величиной

Для записи уравнения равномерного движения применяют координатную форму.
Чтобы верно решить поставленную задачу, для определения нахождения точки в пространстве, используют дополнительные координаты х, у, z.
Уравнения зависимости приобретают вид:
В данных уравнениях — это начальные координаты тела в пространстве, а — это проекции векторов скорости на соответствующие оси координат.
Уравнение равномерного прямолинейного движения.
Равномерное прямолинейное движение — это движение определяемое следующими характеристиками:

движение тела по ровной линии;
за равные промежутки времени тело проходит один и тот же путь;
тело перемещается одинаково.

Одним из разновидностей равномерного движения является движение тела по окружности. Это движение также является моделью, на основе которой происходит изучение более сложных видов движения.

В этом случае тело проходит углы поворота за одинаковое время.

При этом движении радиус-вектор будет иметь на любом участке пути одинаковое значение.

Для изучения этого вида движения вводится величина, которую называют угол поворота. Она определяет перемещение тела, которое вращается по окружности, за очень маленький промежуток времени.

Ее обозначают греческой буквой φ.
Двигаясь по окружности, тело приобретает мгновенную угловую скорость равную средней угловой скорости.
В случае равномерного движения тела по окружности угол поворота радиус-вектора вычисляется по формуле:

Источник: https://sciterm.ru/spravochnik/velichini-ravnomernogo-dvizheniya-uravneniya-i-formuli-ravnomernogo-dvizheniya/

Урок «Равномерное движение тел. Скорость. Уравнение равномерного движения»

Поурочный план. Физика, 10 класс. Мякишев Г.Я, Буховцев Н.Н., Сотский Н.Н. – М.: Просвещение, 2013. 2 ч. в неделю

Урок 3/2

Тема: Равномерное движение тел. Скорость. Уравнение равномерного движения. Решение задач.

Цели урока: ∙ повторение, углубление и систематизация имеющихся у учащихся сведений о равномерном движении тела и о его скорости при равномерном движении;
∙ формирование неформальных знаний в усвоении понятия «скорость» и уравнения равномерного прямолинейного движения тел в векторной и координатной формах;
∙ воспитывать сознательное отношение к учебе и заинтересованность в изучении физики.
Оборудование: Желоб, штатив, шарик, деревянный брусок, нить.
Ход урока:
Проверка домашнего задания.
∙ Опрос по материалу учебника § 3–6.
Изучение нового материала.
Повторение:
∙ Равномерное движение точки (определение).
∙ Виды траектории при равномерном движении.
∙ Равномерное прямолинейное движение – самый простой вид движения.
Основной материал:
∙ Скорость – важная (вторая) кинематическая величина, характеризующая движение точки.
∙ Скорость – векторная физическая величина (имеет модуль и направление).
∙ Определение и формула расчета скорости.
∙ Смысл модуля скорости (расстояние, пройденное точкой за единицу времени).
∙ Уравнение равномерного прямолинейного движения точки:
а) в векторной форме;
б) в координатной форме.
∙ Примеры практически равномерных прямолинейных движений.
Демонстрации:
∙ Неравномерное прямолинейное движение шарика, скатывающегося по наклонному желобу.
∙ Равномерное прямолинейное движение деревянного бруска по деревянной линейке.
Закрепление материала.
Разбор вопросов и задач:
— с учебника:
∙ контрольные вопросы 1,2 к § 8;

∙ упр.1 (1).

— со сборника М.Е. Тульчинский (№ 8, с.7):

∙ Чему равно перемещение какой-нибудь точки, находящейся на краю диска радиусом R при его повороте относительно подставки на 60°? на 180°? (Решить задачу в системах отсчета, связанных с подставкой и диском).

— Тестовые задания со сборника Тулькибаевой Н.Н. и др. – Челябинск: ЧГПУ, 2004 (с. 10, 11).

— Дополнительные вопросы и задания:

∙ Что мы знаем, если скорость равномерного прямолинейного движения точки задана как вектор? (знаем, какое расстояние проходит эта точка в единицу времени и в каком направлении она движется).

Подведение итогов урока.

Домашнее задание: § 7, 8 (1). Упр. 1 (2).

Источник: https://xn--j1ahfl.xn--p1ai/library/ravnomernoe_dvizhenie_tel_skorost_uravnenie_ravnom_141713.html