Внешний угол треугольника, формула и примеры

Инфоурок › Математика ›Презентации›Сумма углов треугольника. Внешний угол треугольника

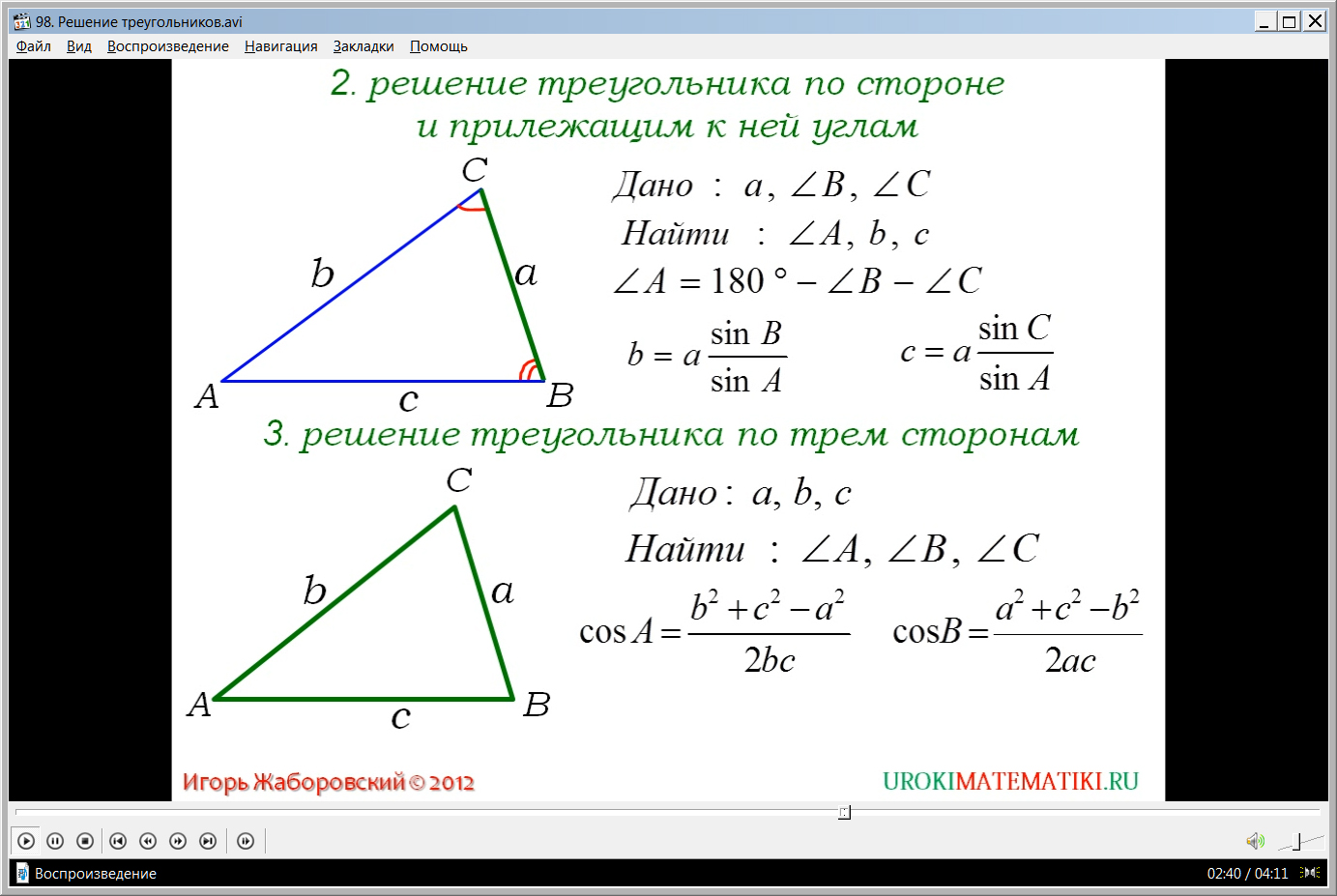
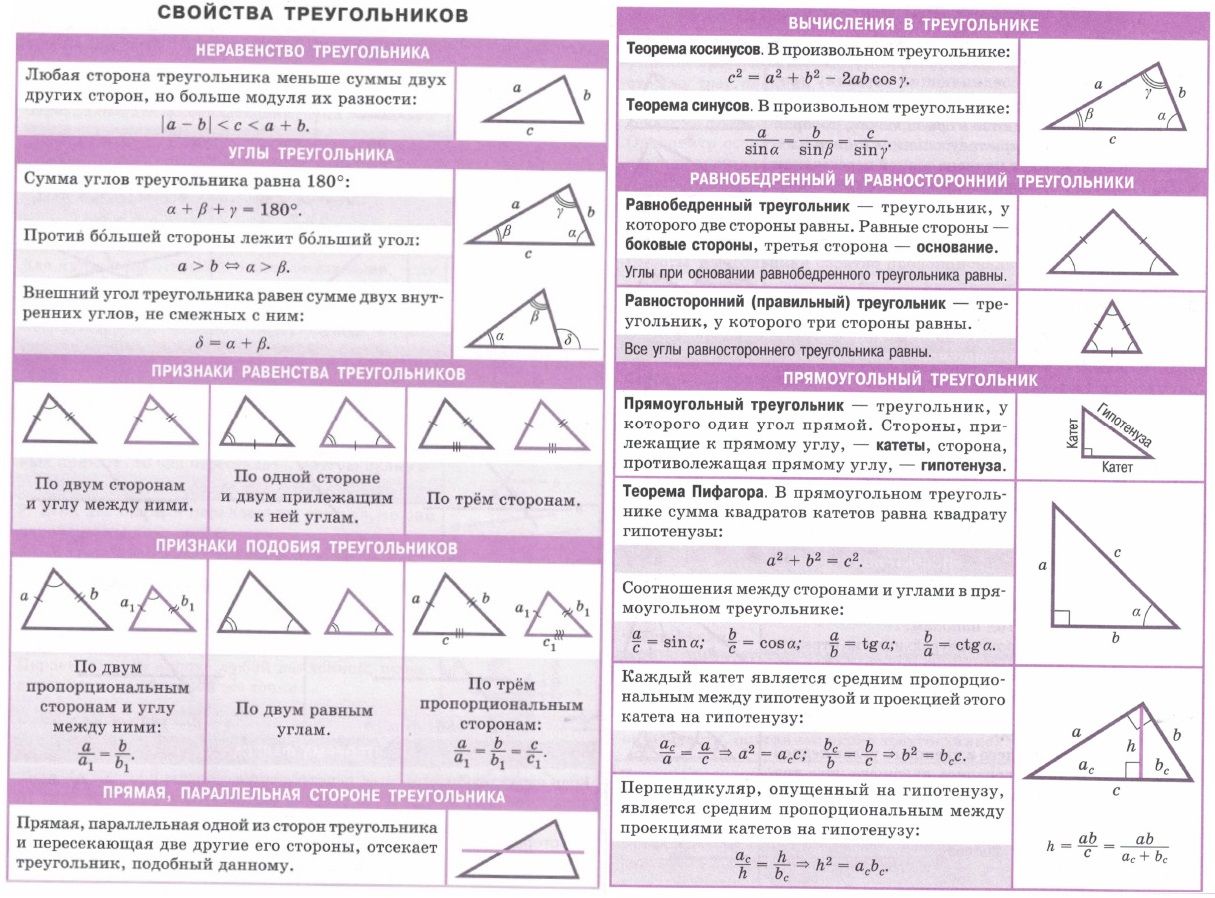
Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Классная работа «Сумма углов треугольника» «Внешние углы треугольника»

2 слайд Описание слайда:

Сумма углов треугольника Сумма углов треугольника равна 180 А+В+С=180 А В С

3 слайд Описание слайда:

Дано: треугольник АВС Доказать: А+В+С=180 Доказательство: 1. Пусть АВС данный треугольник. 2.Проведем через вершину В прямую а II АС, 3.1и4;3и5-накрест лежащие. 4.Поэтому1=4;3=5.4+2+5=180, а значит 1+2+3=180 Следствие: у любого треугольника хотя бы два угла острые А В С а 1 3 2 4 5

4 слайд Описание слайда:

ВНЕШНИЙ УГОЛ Угол смежный с каким-нибудь углом треугольника называется внешним углом треугольника __ 4 А В С 4 1 2 3 Д

5 слайд Описание слайда:

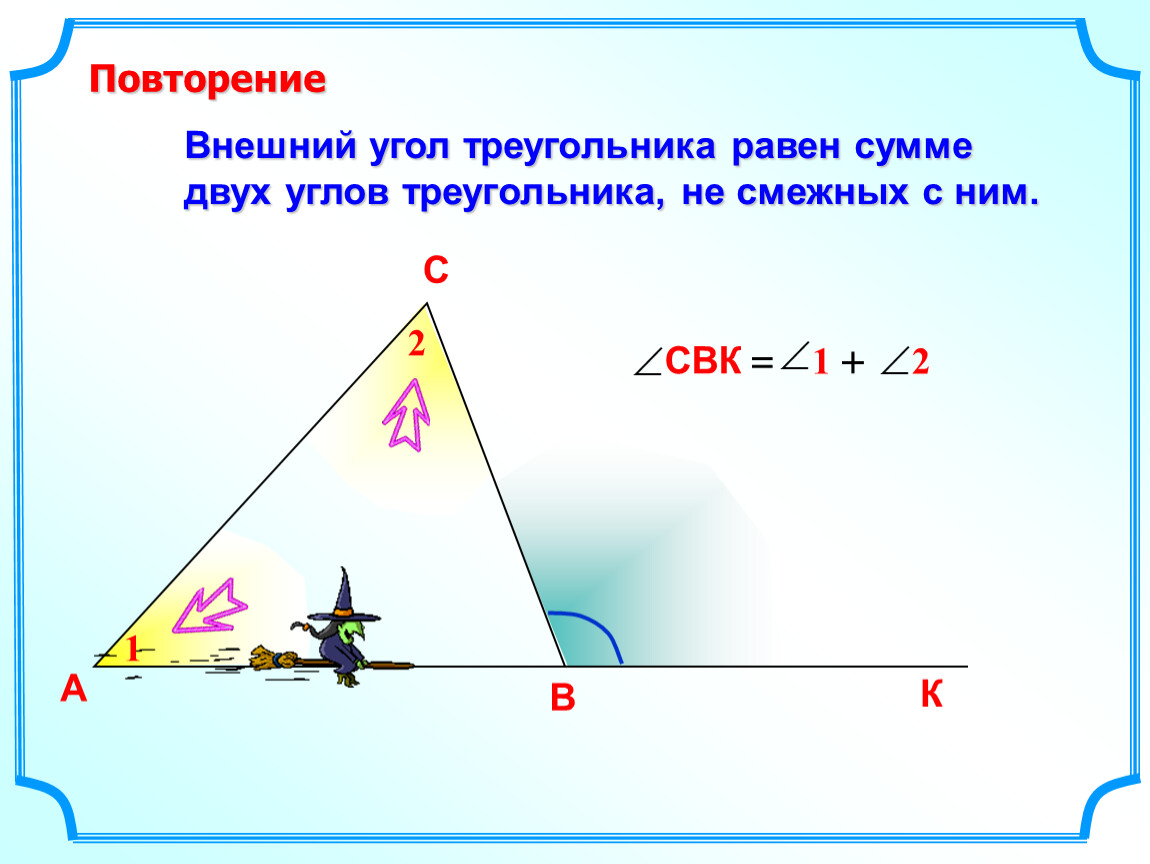
Теорема: Свойство внешнего угла Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: 4=1+2 А В С 4 1 2 3

6 слайд Описание слайда:

Доказательство: 1.Пусть АВС- данный треугольник. 2.По теореме о сумме углов треугольника 1+2+3=180 3. Отсюда следует, что 1+2=180-3, следовательно 4=1+2

7 слайд Описание слайда:

ВИДЫ ТРЕУГОЛЬНИКОВ ОСТРОУГОЛЬНЫЙ ТРЕУГОЛЬНИК ( все углы острые) А В С

8 слайд Описание слайда:

ВИДЫ ТРЕУГОЛЬНИКА Тупоугольный треугольник (один из углов тупой, два других острые) А В С

9 слайд Описание слайда:

ВИДЫ ТРЕУГОЛЬНИКА Прямоугольный треугольник (один из углов прямой, а два других острые) АВ,АС катеты ВС гипотенуза А В С

10 слайд Описание слайда:

Соотношения между сторонами и углами треугольника

11 слайд Описание слайда:

12 слайд Описание слайда:

СЛЕДСТВИЯ 1. В прямоугольном треугольнике гипотенуза больше катета. Если в треугольнике два угла равны, то треугольник равнобедренный( признак равнобедренного треугольника).

13 слайд Описание слайда:

Прямоугольный треугольник

14 слайд Описание слайда:

Прямоугольный треугольник – треугольник, у которого есть прямой угол. катет гипотенуза

15 слайд Описание слайда:

ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ(свойства) 1. Сумма двух острых углов прямоугольного треугольника равна 90. 2. Катет прямоугольного треугольника, лежащий против угла в 30, равен половине гипотенузы. 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30.

16 слайд Описание слайда:

Сумма двух острых углов прямоугольного треугольника равна 90. В А С В+С=90.

17 слайд Описание слайда:

Катет прямоугольного треугольника, лежащего против угла в 30, равен половине гипотенузы. Рассмотрим треугольник АВС, где А=90, В=30 и С=60. Докажем, что АС=½ВС. Приложим к треугольнику АВС равный ему треугольник АВД. Получим треугольник ВСД, В=Д=60, поэтому ДС = ВС, но АС= ½ ДС, значит АС = ½ ВС. 6 В Д С А 30 30 60 60

18 слайд Описание слайда:

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30.

Рассмотрим прямоугольный треугольник АВС, у которого катет АС равен половине гипотенузы ВС.

Докажем, что АВС=30 Приложим к треугольнику АВС равный ему треугольник АВД, получим равно- сторонний треугольник ВСД, где Д=С=ДВС=60. ДВС=2АВС, следовательно, АВС=30. 1 В С А Д 1 2 3 4

19 слайд Описание слайда:

Скрыть

Важно! Узнайте, чем закончилась проверка учебного центра «Инфоурок»?

Краткое описание документа:

Общая информация

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Источник: https://infourok.ru/material.html?mid=37980

Внешний угол треугольника

Внешний угол треугольника. Продолжаем рассматривать задачи на решение прямоугольного треугольника. Такие типы заданий имеются в прототипах открытого банка заданий по математике.

Некоторые примеры мы уже рассмотрели в статьях «Прямоугольный треугольник. Часть 1» и «Прямоугольный треугольник. Часть 2».

В этой статье разберём задачи, в которых необходимо определить значения тригонометрических функций внешнего угла треугольника (или внутреннего, когда дано значение внешнего).

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине

• 
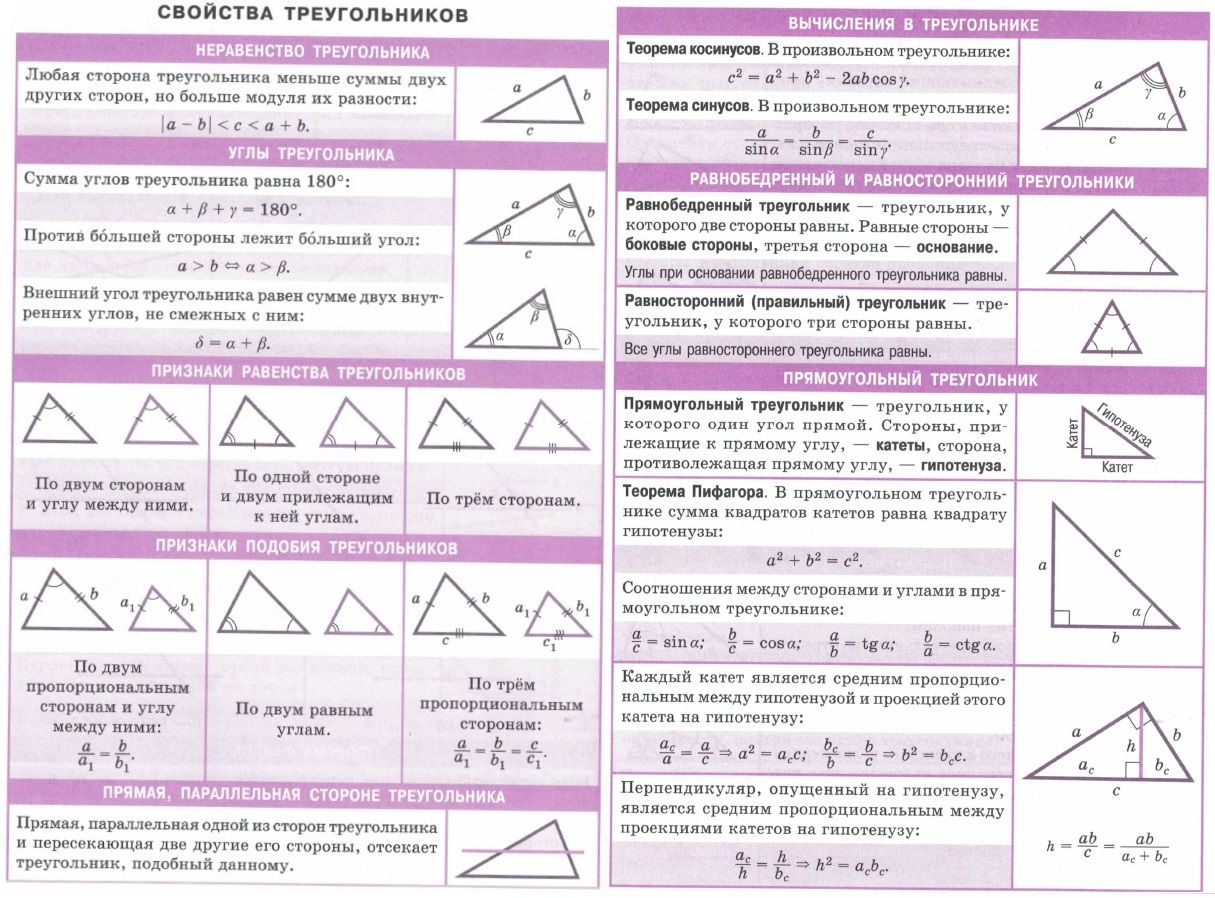
• Угол DAB является внешним.
• Стоит повторить определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике, также основные тригонометрические формулы для решения прямоугольного треугольника.  Вспомним основные из них:
• 
• 

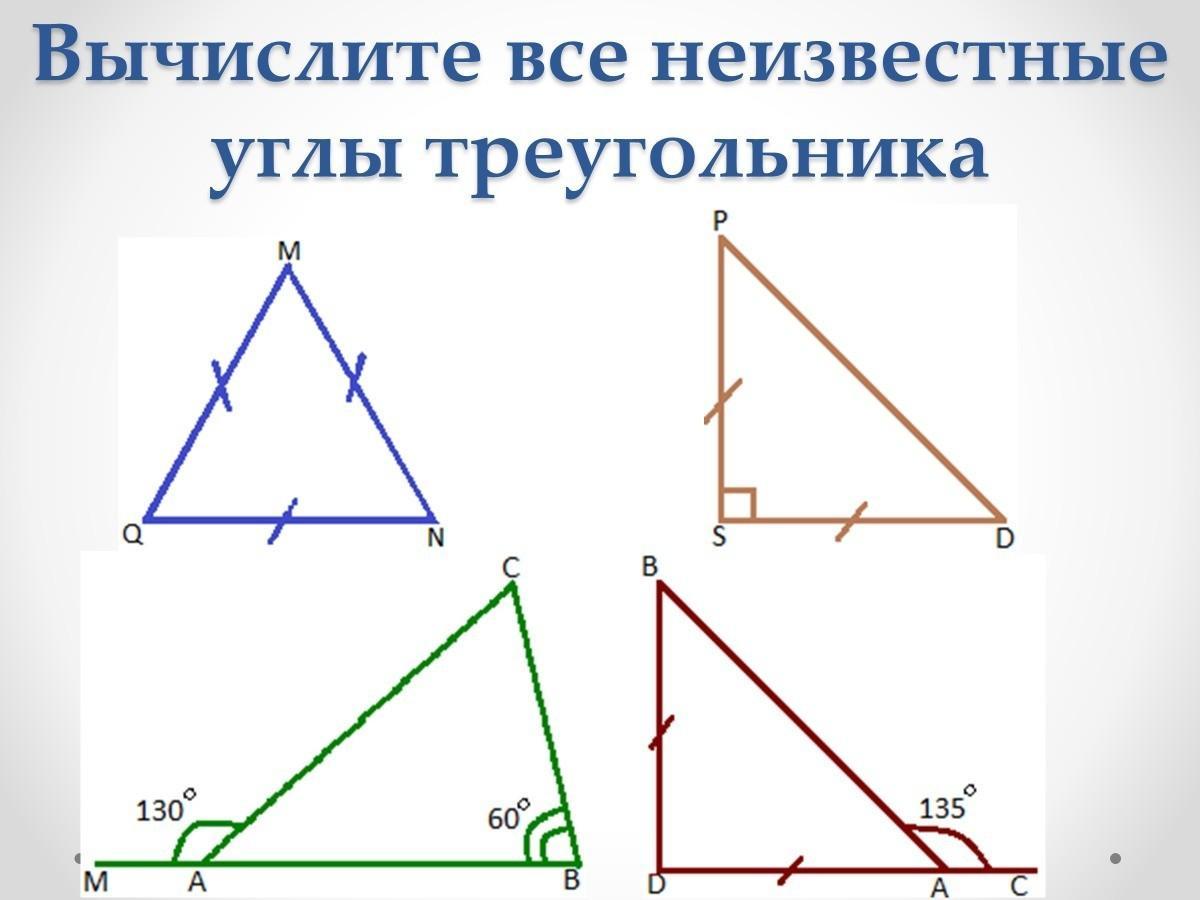
А также формулы приведения (не все). Отмечу одну типичную ошибку, которую допускают (из-за невнимательности). При решении подобных задач часто используется формула основного тригонометрического тождества:

1. 
2. Из  неё мы получаем:
3. 
4. *Запись с ошибкой (её часто допускают — теряют квадрат):
5. 
6. Будьте внимательны!
7. Рассмотрим задачи:
8. 

В треугольнике ABC угол C равен 900, sin A = 0,27. Найдите синус внешнего угла при вершине А.

• 
• Углы ВАС и BAD смежные, значит:
• 
• По свойству синуса:
• А лучше раз и навсегда запомнить сам факт того, что синусы смежных углов равны, и вам даже не будет необходимости что-то записывать при решении такой задачи, ответ вы озвучите сразу.
• Ответ: 0,27
• Решите самостоятельно:
• Посмотреть решение 

В треугольнике ABC угол C равен 900, . Найдите тангенс внешнего угла при вершине A.

1. Углы ВАС и BAD смежные, значит:
2. Значит по свойству тангенса (используем формулу приведения):
3. То есть необходимо найти тангенс угла ВАС.  Известно, что:

Синус угла ВАС нам известен. Найдём его косинус.

• Из основного тригонометрического тождества:
• Вычисляем тангенс:
• Таким образом  tg BAD = – tg BAC = – 0,3
• Ответ: – 0,3
• Решите самостоятельно:
• Посмотреть решение 
• Посмотреть решение 

В треугольнике ABC угол C равен 900, АВ = 6, .  Найдите косинус внешнего угла при вершине A.

1. Углы ВАС и BAD смежные, значит:
2. По свойству косинуса:
3. Найдём cos BAC   Для этого необходимо найти сторону АС. По теореме Пифагора:
4. Значит АС = 3.
5. По определению косинуса:
6. Таким образом, cos DAB = – cos BAC = – 0,5.   
7. Ответ: – 0,5
8. Решите самостоятельно:
9. Посмотреть решение 
10. Посмотреть решение 

В треугольнике ABC угол C равен 900, косинус внешнего угла при вершине A равен  . Найдите sin A.

• Углы ВАС и BAD смежные, значит:
• В данной задаче можем найти косинус угла ВАС, а затем используя основное тригонометрическое тождество синус этого угла.
• По свойству косинуса (используем формулу приведения):
• Значит
• Найдём sin BAC.  Из основного тригонометрического тождества получим:
• Ответ: 0,9

В треугольнике ABC угол C равен 900, тангенс внешнего угла при вершине A равен  –2/9.  Найдите tg = B.

1. Из свойств прямоугольного треугольника мы знаем, что tg ABC = ctg BAC.
2. Найдём ctg BAC. Известно, что tg BAC ∙ ctg BAC = 1, значит

Тангенс угла ВАС найти не сложно. Углы BAC и BAD смежные. Это  значит, что

• По свойству тангенса:   
• Значит
• Таким образом:
• Ответ: 4,5

В треугольнике ABC угол C равен 900, косинус внешнего угла при вершине A  равен  – 0,7; АВ = 20. Найдите AC.

1. Найти АС мы сможем, если нам будет известен косинус угла ВАС. Так как по определению косинуса в прямоугольном треугольнике:
2. Найдём косинус. По его свойству:
3. *Использовали формулу приведения.
4. Значит
5. Таким образом:
6. Ответ: 14
7. Решите самостоятельно:
8. Посмотреть решение 
9. Посмотреть решение 
10. Посмотреть решение 
11. Посмотреть решение 

В треугольнике ABC АС = ВС, АВ = 12, тангенс внешнего угла при вершине A равен  . Найдите AC.

• Построим  высоту CH.
• Найдём  тангенс внутреннего угла.  По свойству тангенса:

Сторона АС является гипотенузой в прямоугольном треугольнике АСН. В этом треугольнике зная тангенс острого угла и один катет мы без труда можем найти второй катет.

1. Высота проведённая к основанию равнобедренного треугольника является медианой, то есть АН = ВН, a АВ = 2АН:
2. Рассмотрим прямоугольный треугольник ACH: по определению тангенса в прямоугольном треугольнике:
3. Следовательно:
4. В прямоугольном треугольнике  нам известны катеты АН и СН.
5. По теореме Пифагора мы можем найти гипотенузу АС:
6. Таким образом, АС = 9.
7. Ответ: 9
8. Решите самостоятельно:
9. Посмотреть решение

В будущем будем рассматривать другие задачи, не пропустите! Успехов Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник: https://matematikalegko.ru/praymougolni-treugolnik/zadachi-s-vneshnim-uglom-treugolnika.html

Теорема о внешнем угле треугольника

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине. Чтобы не путать угол треугольника при данной вершине с внешним углом треугольника при этой же вершине, его иногда называют внутренним углом. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

• Отсюда следует, что внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
• Задача по теме «Признаки равенства треугольников».

Задача по теме «Площадь».

Теорема о средней линии трапеции (формулировка и пример).

Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме. Пример.

Теорема о сумме углов выпуклого многоугольника.

Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. Сумма углов выпуклого п-угольника равна 180° — (п — 2).

Задача по теме «Признаки равенства треугольников».

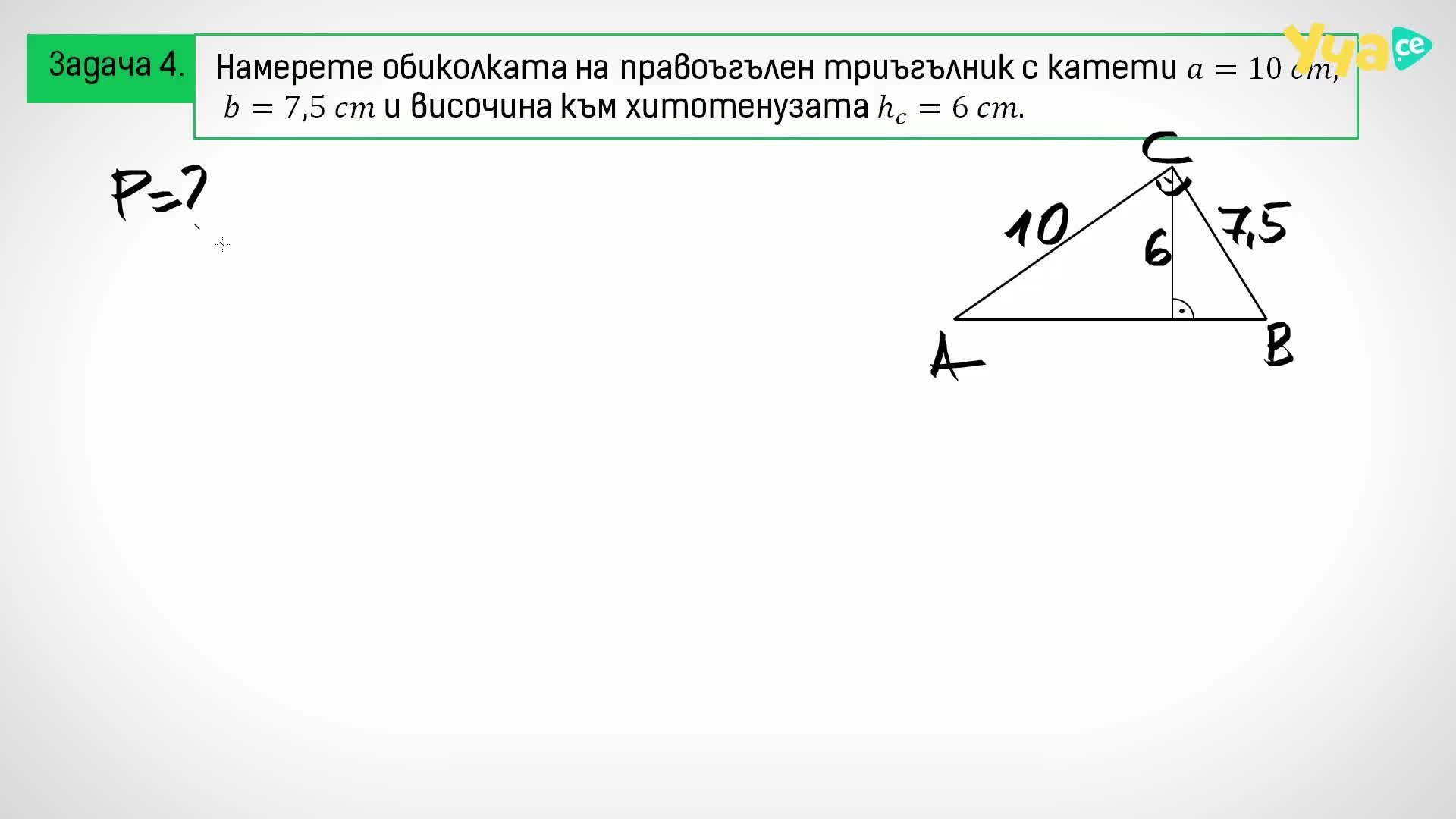
Задача по теме «Решение прямоугольных треугольников».

Формулы для радиусов вписанных и описанных окружностей правильного n-угольника (формулы и примеры).

Свойство диагоналей ромба.

Дано: ABCD — ромб, АС и BD — диагонали, О — точка пересечения диагоналей. Доказать: AC BD, АС и BD — биссектрисы углов ромба.

Доказательство. Рассмотрим ромб ABCD (см. рис. 61). По свойству параллелограмма АО = ОС. Значит, в треугольнике ABC отрезок ВО является медианой. Так как ABCD — ромб, то АВ = ВС и треугольник ABC — равнобедренный.

По свойству равнобедренного треугольника медиана, проведенная к его основанию, является биссектрисой и высотой. А это значит, что диагональ BD является биссектрисой угла В и перпендикулярна диагонали АС. Аналогично рассматривается AABD.

Теорема доказана.

Задача по теме «Равнобедренный треугольник».

Задача по теме «Подобие треугольников».

В треугольнике из всех вершин проведены высоты, каждая из которых разбивает его на два треугольника. Докажите, что любые два из этих треугольников, имеющие общую вершину с данным, подобны.

Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырехугольника, правильного шестиугольника (формулы и примеры).

Примеры. 1. Найдите радиус окружности, вписанной в правильный треугольник, если сторона треугольника равна 5 см.

1. Решение:
2. Решение:

2. Радиус окружности, вписанной в квадрат, равен 1 см. Найдите радиус описанной окружности. Решение: 3. Радиус окружности, описанной около правильного шестиугольника, равен 7 см. Найдите сторону правильного шестиугольника.

Источник: https://megaobuchalka.ru/16/9380.html

Внешний угол при вершине треугольника

Очередная задача про равнобедренный треугольник:

В тре­уголь­ни­ке АВС АС=ВС. Внеш­ний угол при вер­ши­не В равен 122 градуса. Най­ди­те угол. Ответ дайте в гра­ду­сах. Можно мне все подробно?

Постараюсь объяснить как можно подробнее. Почему я сразу сказал, что задача про равнобедренный треугольник? У обычных треугольников все стороны разной длинны. Их даже так и называют — разносторонние.

Берем картинку со страницы про виды треугольников, отрезаем ненужное и начинаем разукрашивать. Геометрия — это та же детская разукрашка, только проще. В задаче обычно всегда говорится, что именно и как вы должны разукрашивать.

Разукрасим нашу картинку с видами треугольников по размерам сторон синенькими буквами вершин равнобедренного треугольника.

Виды треугольников

Теперь нужно разобраться, что такое внешний угол при вершине треугольника. По моему глубокому убеждению, это мусор, которым математики засоряют вам мозги. Ведь чем больше всякого мусора в учебнике, тем больше часов нужно на его изучение и тем больше сможет заработать учитель. Чем запутаннее предмет, тем легче репетиторам найти работу. Это похоже на продажу овощей на вес — чем больше в них грязи, тем больше денег заработает продавец. И так, открываем «умную» книжку и начинаем копаться в математической грязи. В книжке написано буквально следующее:

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.

По умолчанию предполагается, что мы уже должны знать, что такое смежный угол. Не знаю, как вы, а я уже давно забыл, что это за фигня такая — «смежный угол». Ведь все нормальные люди пользуются нормальными углами. Хорошо, что к определению внешнего угла треугольника картинка прилагается, которая проясняет, как именно он выглядит.

Внешний угол

Я никогда не пойму, зачем к треугольнику лепить внешний угол, если у него уже есть обычные, внутренние, углы. Я так понимаю, что одни дураки когда-то учили других, а те тупо повторяют действия учителей. Своими мозгами пользоваться их так никто и не научил. Кстати, величайшим достижением современного образования можно считать отсутствие в учебной программе научной теории о трех китах и Земле, которая на них держится. И это только потому, что данная теория не относится к математике. А ведь если в учебной программе что-то записано, то учить это обязательно для получения хорошей оценки.

Ладно, по возмущался и хватит. Вернемся к наше задаче. Читаем внимательно: Внеш­ний угол при вер­ши­не В равен 122 градуса. Собственно, картинка внешнего угла — это то, что доктор прописал. Обычный угол треугольника получается путем вычитания из 180 градусов внешнего угла. У равнобедренного треугольника углы при основании равны. Рисуем картинку и сразу решение.

Внешний угол при вершине

Кажется, я догадываюсь, откуда в математике могли появиться внешние углы. Когда европейцы увидели пирамиды древнего Египта, они были потрясены увиденным. Им захотелось измерить эти грандиозные сооружения. Вот только внутренний угол пирамиды измерить не представляется возможным. Можно измерить внешний угол и высчитать внутренний. Математики увидели, что делают другие, и записали в свою Математическую Библию определение внешнего угла треугольника. Вот с тех пор это Священное Писание переписывается из учебника в учебник.

Источник: http://www.webstaratel.ru/2014/02/vneshnij-ugol-pri-vershine.html

Свойства внешнего угла треугольника

Внешний угол треугольника редко используется при решении геометрических задач. Однако при этом свойства внешнего угла лучше знать, потому как задача на применение этих свойств рано или поздно попадется каждому ученику.

Внешний угол треугольника это угол, смежный с внутренним. Внутренних углов в треугольнике три, и их сумма равняется 180 градусам. Смежными углами зовутся углы, одна из сторон которых лежит на одной прямой, а вторая является общей.

Что нужно сделать, чтобы увидеть внешний угол треугольника? Для этого придется выполнить некоторые дополнительные построения. Чтобы увидеть внешний угол треугольника необходимо продолжить его сторону. При каждой вершине две стороны, соответственно продолжить можно две прямых и смежных углов будет два.

Рис. 1. Внешние углы треугольника.

Итого в треугольнике получается 6 внешних углов.

Нежелательно на рисунке строить два внешних угла при одной вершине одновременно. Это усложнит построение и, чаще всего, не принесет никакого положительного результата.

Свойств у внешних углов треугольника не так много и все они связаны с определением внешнего угла.

Основное свойство гласит, что внешний угол треугольника равен сумме двух внутренних углов не смежных с ним. Свойство доказывается достаточно просто. Сумма смежных углов равна 180. Сумма углов в треугольнике все те же 180. Тогда, если обозначить внутренние углы а,в,с, внешний угол d, то:

• а+в+с=180
• а+d=180
• Вычтем из первого выражения второе и получим:
• а+в+с-(а+d)=180-180
• в+с-d=0
• d=в+с – вот и все доказательство.

Рис. 2. Рисунок к доказательству.

Есть еще несколько дополнительных свойств внешних углов:

• Если решение задачи требует одновременного существования двух внешних углов при одной вершине на чертеже, то можно заметить, что эти внешние углы будут равны, как вертикальные.
• Сумма трех внешних углов, по одному при каждой из вершин, равняется 360 градусам.
• Так как внешний и внутренний углы треугольника смежные, то их сумма равняется 180 градусам.

Особенное значение имеют внешние углы при решении тупоугольных треугольников. Дело в том, что в тупоугольном треугольнике одна из высот всегда внешняя. Найти эту высоту можно через тригонометрические функции. Для этого и нужно знать угол, который для тупоугольного треугольника будет внешним, а для достроенного прямоугольного треугольника – внутренним.

Рис. 3. Внешний угол тупоугольного треугольника.

Мы привели определение внешнего угла треугольника. Посчитали количество внешних углов треугольника, определили особенности построения внешних углов при решении задачи. Рассказали, где чаще всего применяются свойства внешних углов треугольника.

Средняя оценка: 4.6. Всего получено оценок: 232.

Источник: https://obrazovaka.ru/geometriya/vneshniy-ugol-treugolnika-opredelenie-svoystvo.html