









ДИФФЕРЕНЦИАЛЬНАЯ ФОРМУЛА ВЫНУЖДЕННЫХ КОЛЕБАНИЙ Общая дифференциальная формула вынужденных колебаний • Для механических колебаний (пружинный маятник) • Для электромагнитных колебаний В установившемся режиме вынужденные колебания происходят с частотой и являются гармоническими, амплитуда и фаза колебаний, так же
зависят от циклической частоты. Если период вынуждающей силы не равен периоду свободных колебаний системы, то в начале происходит несколько биений, а затем устанавливаются вынужденные колебания с постоянной амплитудой.
АМПЛИТУДА И НАЧАЛЬНАЯ ФАЗА ВЫНУЖДЕННЫХ КОЛЕБАНИЙ Установившиеся вынужденные колебания можно считать гармоническими, то есть для механических колебаний, приблизительно можно считать: Если вывести значения скорости и ускорения то дифференциальное уравнение колебаний: Сократим все части уравнения на ния: и ведём обозначе- ,
В результате получим: Правую часть уравнения можно рассматривать как уравнение некоторого гармонического колебания, получившегося от сложения трёх гармонических колебаний, определяемых левой частью равенства. Для сложения воспользуемся методом векторных диаграмм, так x что. Отсюда можно определить амплитуду А: Амплитуда установившихся вынужденных колебаний прямо пропорциональна вынуждающей силе.
– сдвиг фаз между скоростью колебаний и вынуждающей силой.
РЕЗОНАНС Если , , не изменяются, то амплитуда А зависит от соотношения и. 1) Если , то , и смещение равно статической деформации. 2) Если , то есть нет затухания, тогда А будет расти при увеличении , и при , а затем будет убывать 3) Если затухания существуют, то А достигает максимального значения, когда знаменатель минимален, то есть:
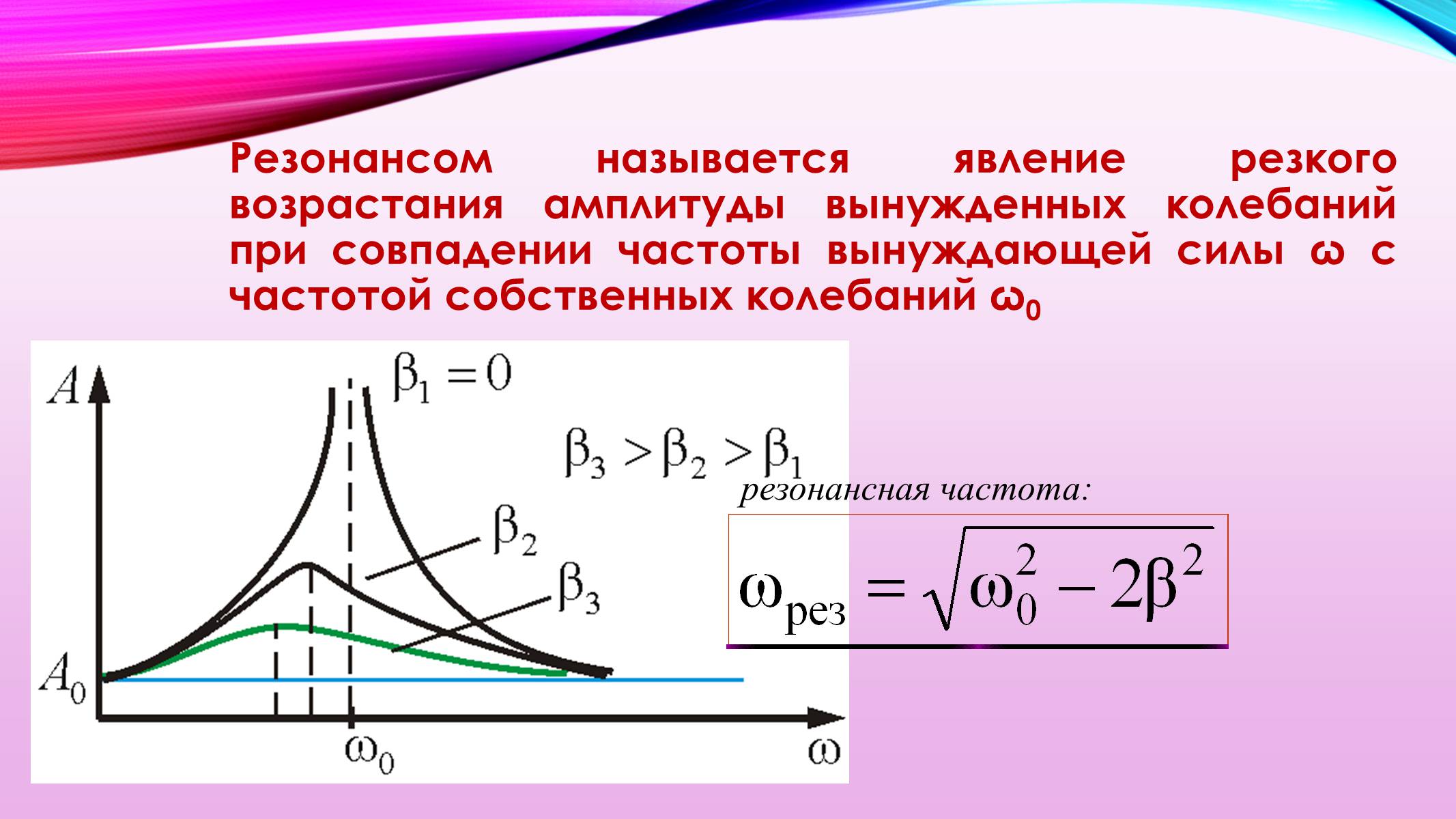
Введем понятие – резонансная частота, — частота, при которой амплитуда смещения достигает своего максимума: Явление резкого возрастания амплитуды вынужденных колебаний, приближении частоты возбуждающей силы (частоты вынуждающего переменного напряжения)к частоте называется – РЕЗОНАНС.
ВОЛНЫ
СПЛОШНАЯ СРЕДА– среда непрерывно распределенная в пространстве и обладающая упругими свойствами. ВОЛНОВОЙ ПРОЦЕСС – процесс распространения колебаний в сплошной среде. Колеблющееся материальное тело, помещенное в упругую среду, увлекает за собой, и приводит в состояние колебания прилегающие к нему, частицы среды.
Те, в свою очередь воздействуют на соседние частицы и приводят их в колебательное движение. При распространении волны, частицы среды не движутся вместе с волной, а колеблются около своего положения равновесия. Вместе с волной передаются лишь состояние колебательного движения и его энергия.
Основным свойством всех волн независимо от их природы является: перенос энергии без переноса вещества.
ВОЛНОВАЯ ПОВЕРХНОСТЬ – совокупность точек колеблющихся в одинаковой фазе. ФРОНТ ВОЛНЫ – поверхность которая отделяет колеблющиеся частицы, от частиц ещё не пришедших в колебательное движение, или, иначе говоря, геометрическое место точек до которого дошли колебания в момент времени.
Волновых поверхностей огромное количество, но волновой фронт только один, и он так же является волновой поверхностью. Волновые поверхности могут быть любой формы, в простейшем случае представляют собой совокупность плоскостей параллельных другу, или совокупность концентрических сфер.
Соответственно волны бывают плоскими или сферическими.
ВИДЫ ВОЛН Волны бывают различных типов: • Волны на поверхности жидкости • Электромагнитные волны • Механические (упругие) волны и т. д. Упругие (механические) волны – механические возмущения распространяющиеся в упругой среде. ПРОДОЛЬНЫЕ ВОЛНЫ – частицы среды колеблются в направлении распространения волны. ПОПЕРЕЧНЫЕ ВОЛНЫ – перпендикулярны направлению распространения колебаний.
ГАРМОНИЧЕСКИЕ ВОЛНЫ
Упругая волна называется – ГАРМОНИЧЕСКОЙ ВОЛНОЙ, если соответствующие ей колебания частиц являются гармоническими.
Представленная на рисунке гармоническая поперечная волна распространяется вдоль оси со скоростью то есть приведена зависимость между смещением частиц среды участвующих в волновом процессе и расстояния от этих частиц (В) до источника колебаний (О) в момент времени.
Приведенный график похож, но принципиально отличается от графика гар-монических колебаний, так как выражает зависимость смещения всех частиц среды от расстояния до источ-ника колебаний, а график
колебания данной частицы от времени. ДЛИНА ВОЛНЫ – расстояние между ближайшими частицами, колеблющимися в одинаковой фазе. Она равна тому расстоянию, на которое распространяется определённая фаза колебания за период.
ЧАСТОТА КОЛЕБАНИЙ (ВОЛНЫ) – СКОРОСТЬ РАСПРОСТРАНЕНИЯ ВОЛНЫ – Пусть частица в начальной точке О совершает колебания , до некоторой точки В волна дойдет за время.
Колебания в точке В начнутся с опозданием тем большим, чем дальше она отстоит от исходной точки О.
Смещение точки В в момент времени , будет равно смещению точки О в момент времени Уравнение плоской волны распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию: – амплитуда волны – циклическая частота волн – начальная фаза колебаний (определяемая выбором начала отсчета, ).
– фаза плоской волны – волновое число Иная форма записи уравнения плоской волны Представим, что в волновом процессе фаза постоянна: , продифференцируем: , разделим на и получим Скорость распространения волны – это скорость перемещения фазы, и её называют ФАЗОВОЙ СКОРОСТЬЮ.
Выше был рассмотрен случай плоской волны, уравнение СФЕРИЧЕСКОЙ ВОЛНЫ – волновые поверхности которой имеют форму концентрических сфер, записывается как : – расстояние от центра волны до рассматриваемой точки В случае сферической волны, даже если среда не поглощает энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием ( справедливо для тех случаев, когда расстояния много больше размеров источника сигнала.
ВОЛНОВОЕ УРАВНЕНИЕ Распространение волн в однородной изотропной среде, в общем случае записывается ВОЛНОВЫМ УРАВНЕНИЕМ – специальным дифференцированным уравнением в частных производных. – оператор Лапласа – фазовая скорость Решением этого уравнения является уравнение любой волны (любого типа волн) Волновое уравнение для одномерного (вдоль оси х) распространения волны.
ПРИНЦИП СУПЕРПОЗИЦИИ ГРУППОВАЯ СКОРОСТЬ
ПРИНЦИП СУПЕРПОЗИЦИИ Если среда, в которой одновременно распространяются несколько волн, линейна, то есть её свойства не изменяются под действием возмущений создаваемых волной, то к этим волнам применим ПРИНЦИП СУПЕРПОЗИЦИИ (НАЛОЖЕНИЯ) ВОЛН.
При наложении в линейной среде нескольких волн, каждая из них распространяется независимо от других, как будто иные волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагаемых волновых процессов.
Суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства называется – волновым пакетом.
Пусть имеется волновой пакет из двух расположенных вдоль оси х горизонтальных волн с одинаковыми амплитудами, близкими частотами и волновыми числами т. е. : . Тогда: Эта волна отличается от гармонической тем, что её амплитуда есть медленно изменяющаяся функция координаты и времени :
ГРУППОВАЯ СКОРОСТЬ Результат сложения колебаний двигающихся в одном направлении определяется соотношением фаз этих колебаний. Если фазы противоположны, то результирующая амплитуда минимальна, если совпадают то максимальна.
Каждый момент времени максимальной амплитуды группы волн, соответствует тому участку пространства в котором сосредоточен максимум энергии волны. Эта точка называется центром группы волн, и так как фазы группы волн со временем меняются, то и центр группы волн, за некоторое время , перемещается с некоторой скоростью.
Иначе говоря: За ГРУППОВУЮ СКОРОСТЬ принимают скорость перемещения максимума амплитуды волн.
Для уравнений выполняется условие: Рассмотрим связь между групповой скоростями. и фазовой Если фазовая скорость не зависит от фазы , то есть нет дисперсии, то.
Понятие групповой скорости определяет скорость распространения сигнала который можно уловить каким либо прибором. В теории относительности доказывается что групповая скорость.
В то время как для фазовой скорости ограничений не существует.
ИНТЕРФЕРЕНЦИЯ ВОЛН
Согласованное во времени и пространстве протекание нескольких волновых или колебательных процессов наблюдается только в том случае, если волны имеют одинаковую частоту. КОГЕРЕНТНЫЕ ВОЛНЫ – волны которые имеют одинаковую частоту и постоянную разность фаз.
При положении в пространстве нескольких когерентных волн происходит перераспределение энергии волн, то есть в разных точках происходит усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Данное явление называется – ИНТЕРФЕРЕНЦИЯ.
Рассмотрим наложение двух когерентных сферических волн, возбуждаемых источниками и , колеблющихся с одина-
ковыми амплитудами янной разностью фаз. и частотами , а так же посто- – расстояния от источников волн, до рассматриваемой точки В – начальные фазы обеих складывающихся сферических волн – волновое число Амплитуда результирующей волны в точке В:
Так как для когерентных источников , то результат наложения двух волн в различных точках зависит от разности хода волн. • Там где – интеференционный максимум, амплитуда результирующего колебания • Если – интеференционный минимум, амплитуда результирующего колебания – порядок интерференционного максимума или минимума.
СТОЯЧИЕ ВОЛНЫ
СТОЯЧИЕ ВОЛНЫ – волны образованные при наложении двух бегущих волн, распространяющихся навстречу другу, с одинаковыми частотами и амплитудами. Пусть две волны распространяются навстречу другу без затухания, с одинаковыми амплитудами и частотами, вдоль оси х. При фазы. Уравнение стоячей волны: – волновое число – амплитуда стоячей волны – длина волны узел пучность
• Если туда максимальна • Если – ампли. – ПУЧНОСТЬ. . – УЗЕЛ. . –
Источник: https://present5.com/lekciya-7-svobodnye-zatuxayushhie-kolebaniya-svobodnye/
Затухающие и вынужденные колебания. Резонанс
На прошлых уроках мы с вами знакомились с колебательным
движением и простейшими колебательными системами — математическим и пружинным
маятниками. При этом мы считали, что их колебания являются свободными (то есть
происходят только под действием внутренних сил), и подчиняются гармоническому
закону.
Напомним, что системы, на которые не действуют внешние силы,
— это замкнутые системы. А, мы уже знаем, что в замкнутой системе полная
механическая энергия остаётся постоянной и равной той энергии, которую мы
изначально ей сообщили. Поэтому свободные колебания — это колебания с
постоянной амплитудой. А маятник, выведенный из положения равновесия, должен
колебаться вечно!
Иногда действительно можно наблюдать колебания, длящиеся
достаточно долго. Например, если очень длинный маятник отклонить на небольшой
угол, то он сможет в течение многих часов совершать колебания с постоянной
амплитудой.
Однако, как бы долго ни продолжались свободные колебания, маятник в
конце концов все-таки останавливается. Говорят, что колебания затухают.
«Виновата» в этом сила трения, которая в реальных земных условиях действует на
всё, что движется.
Колебания с уменьшающейся амплитудой называются
затухающими колебаниями. Причём чем больше силы сопротивления движению, тем
быстрее прекращаются колебания. Например, в воде колебания затухают гораздо
быстрее, чем в воздухе.

Конечно же затухающие колебания нельзя считать свободными,
поскольку свободные колебания — это колебания, происходящие с постоянной
амплитудой.
— Каким же образом можно добиться того, чтобы колебания не
затухали?
Очевидно, что необходимо восполнять потери энергии за каждый
период колебаний. Для этого нужно воздействовать на колеблющееся тело
периодически изменяющейся силой. Например, если каждый раз подталкивать маятник
в такт его колебаниям, то он сможет качаться сколь угодно долго.

Такие колебания, то есть колебания, происходящие под
действием внешней периодически изменяющейся силы, называются вынужденными
колебаниями.
А периодическая сила, вызывающая такие колебания,
называется вынуждающей силой.
Таким образом, колебательная система, на которую действует
внешняя периодическая сила, совершает вынужденные колебания, частота которых
равна частоте вынуждающей силы.
При этом амплитуда вынужденных колебаний
при данной частоте вынуждающей силы не изменяется, даже если на систему
будут действовать силы сопротивления, так как потери энергии компенсируются
работой вынуждающей силы.
Давайте выясним, зависит ли амплитуда вынужденных колебаний
от соотношения между частотой вынуждающей силы и собственной частотой колебательной
системы. Для этого проведём такой опыт. Подвесим на нитях, прикреплённых к
общей перекладине два маятника — маятник один и маятник два, имеющий массу
существенно больше.

Длина нити первого маятника постоянна, а длину второго можно
изменять, подтягивая свободный конец нити, при этом будет изменяться и его
собственная частота колебаний. Если привести в движение маятник большей массы,
то он через перекладину будет действовать на маятник один с некоторой
вынуждающей силой, изменяющейся с такой же частотой, с какой колеблется маятник
два.
Если мы будем уменьшать длину второго маятника частота его
колебаний увеличится. При этом увеличится и частота вынуждающей силы, действующей
на первый маятник, при этом начнёт увеличиваться и его амплитуда. Увеличение
амплитуды будет продолжаться до тех пор, пока длины маятников не станут
равными.
Когда длины маятников становятся равными, то есть когда
частота вынуждающей силы совпадает с частотой собственных колебаний первого
маятника, его амплитуда колебаний резко возрастает. При дальнейшем уменьшении
длины маятника два частота вынуждающей силы оказывается больше собственной
частоты маятника один и амплитуда его колебаний уменьшается.

Явление резкого возрастания амплитуды вынужденных
колебаний при равенстве частот вынуждающей силы и собственной частоты
колебательной системы называется резонансом.
Явление резонанса можно продемонстрировать и на таком опыте.
Подвесим на рейку несколько маятников разной длины.

Пусть центральный маятник будет массивным, а остальные —
лёгкими. Приведём центральный маятник в движение в плоскости, перпендикулярной
рейке. Он будет совершать свободные колебания, периодически действуя с
некоторой силой на рейку. Рейка будет передавать это воздействие остальным
маятникам, которые начнут совершать вынужденные колебания с частотой колебаний
массивного маятника.

Обратите внимание, что маятники 2 и 3 останутся почти
неподвижными, так как их собственные частоты значительно отличаются от частоты
массивного маятника. Амплитуды маятников 4 и 5 будут больше, а маятники 6 и 7,
имеющие ту же длину нити, что и массивный маятник, начнут колебаться с очень
большой амплитудой, то есть войдут в резонанс с массивным маятником.
В чем причина явления резонанса? Почему растёт амплитуда
колебаний, когда частота вынуждающей силы приближается к частоте собственной?
Дело в том, что совпадение частот означает, что
равнодействующая силы тяжести и силы упругости нити в самой системе действует
«в такт» с вынуждающей силой.
Если равнодействующая и вынуждающая силы в
какие-то моменты действуют в одном направлении, то они складываются и их
действие усиливается.
И даже если вынуждающая сила мала, она всё равно приведёт
к росту амплитуды, так как она добавляется к равнодействующей силе каждый
период.


Явление резонанса может быть полезным, поскольку оно
позволяет получить даже с помощью малой силы большое увеличение амплитуды колебаний.
Например, тяжёлый язык большого колокола можно раскачать, действуя сравнительно
небольшой силой с частотой, равной собственной частоте колебаний колокола.
С другой стороны, резонансные явления могут вызвать
необратимые разрушения в различных механических системах. Известны случаи,
когда вследствие резонанса в воздухе рассыпался на части самолёт, ломались
гребные винты у кораблей, разрушалась железная дорога.
Что бы не допустить резонанса, изменяют собственную частоту
системы или частоту вынуждающей силы. Для этого, например, поезда переезжают
мосты или очень медленно, или с максимальной скоростью, что бы частота ударов
колёс о стыки была либо меньше, либо больше собственной частоты колебаний
моста.
А солдаты, переходя через мост, идут не в ногу, а сбивают шаг. Иначе,
если частота их шагов совпадёт с частотой собственных колебаний моста, он может
разрушится. Так произошло в 1850 году вблизи города Анже во Франции, когда
через мост Бас-Шен, висящий на цепях, проходил отряд солдат.
В результате
обрушения погибло 226 человек.
Похожий случай произошёл и в Петербурге в январе 1905 года,
при переходе кавалерийского эскадрона по Египетскому мосту через реку Фонтанка.
По счастливой случайности, никто из людей не погиб.
А 7 ноября 1940 года сильный порыв ветра вызвал резонансные
колебания Такомского моста в США, что привело к его разрушению.
В тех случаях, когда резонанс может нанести ущерб, принимают
меры к тому, чтобы не допустить его возникновения. Например, многие заводские
станки, отдельные части которых совершают периодические движения, устанавливают
на массивном фундаменте или амортизаторных пружинах, препятствующих
возникновению колебаний всего станка.
На явлении резонанса основано действие частотомера, с помощью
которого измеряют частоту колебаний.

Закрепления материала.

Источник: https://videouroki.net/video/24-zatuhayushchie-i-vynuzhdennye-kolebaniya-rezonans.html
Магнитомеханические явления. Электромагнитная индукция. Гармонические колебания. Затухающие колебания (Главы 4-7 учебного пособия по общей физике), страница 16
![]()
Мы вновь получили однородное дифференциальное уравнение
второго порядка.
Данное уравнение ничем не отличается
от того, которое было получено для пружинного маятника в предыдущем разделе.
Следовательно, его решение имеет такой же вид: ![]() , где
, где ![]() .
.
Это означает, что в
колебательном контуре с потерями энергии могут происходить затухающие
колебания.
7.3. Характеристики затухающих
колебаний
Из решения
дифференциального уравнения видно, что амплитуда затухающих колебаний
уменьшается с течением времени по закону . Чем
больше коэффициент b,
тем быстрее уменьшается амплитуда колебаний. Поэтому его называют коэффициентом
затухания.
Поскольку , постольку колебания затухают тем быстрее,
чем больше коэффициент трения r и чем меньше масса колеблющегося груза m.
Этот вывод достаточно легко
понять – чем больше трение, которое препятствует всякому движению, тем быстрее
пре-кратится колебательное движение реального осциллятора. Умень-шение массы
означает, что уменьшается запас кинетической энергии осциллятора и поэтому при
равном трении энергия будет быстрее израсходована на его преодоление.
Если обозначить символом t время, за которое амплитуда колебаний
уменьшится в е раз, то , т. е. bt = 1 и .
- Таким образом, b есть величина, обратная времени, за
которое амплитуда уменьшается в е раз. - Время t называют временем релаксации
- В качестве характеристики
затухания колебаний используется также логарифмический декремент затухания

- где A(t) –
амплитуда колебания в некоторый момент t; A(t + T) –
амплитуда колебания через один период затухающего колебания. - Из последнего соотношения
следует, что l = bT. - Целесообразность использования такой
характеристики видна из следующего.
Поскольку l = bT, а
b = 1/t, постольку .
Но Т – это время, за которое совершается одно колебание, а t – время, за которое произойдёт, в
общем случае, несколько колебаний*.
Тогда

- где Nе – число
колебаний, в ходе которых амплитуда уменьшится в е раз. - Таким образом, b и l являются характеристиками затухания, дополняющими друг друга:
b показывает, как быстро затухают
колебания, но при этом не содержит информации о количестве колебаний; l же показывает, за сколько колебаний
амплитуда уменьшится в е раз, но ничего не говорит о времени, за которое
произойдёт это уменьшение. - Из решения
дифференциального уравнения также следует, что частота затухающих колебаний w меньше частоты колебаний идеального
маятника wо: .
.
Циклические частоты w и wо соотносятся
следующим образом. Допустим, маятник совершает затухающие колебания с частотой w; если избавиться от трения, он будет
совершать гармонические колебания с частотой wо.
- Поскольку , где r – коэффициент трения, с
ростом трения частота затухающих колебаний уменьшается. - Колебания, совершаемые
пружинным маятником с трением, не являются гармоническими. - ____________________________
- * В ходе этих колебаний амплитуда как
раз и уменьшится в е раз.
Они также не являются и
периодическими. Однако в физике принято использовать так называемый период
затухающих колебаний ; при этом под Т
подразумевают время, за которое совершается одно колебание.
7.4. Критическое затухание
На качественной основе в
разд. 7 было показано, что при достаточно большом трении колебания станут
невозможны. Выведенная из положения равновесия колебательная система просто
вернётся в него.
 |

В этом случае решение
диффе-ренциального уравнения принимает такой вид:
![]()
т. е. х от времени зависит экс-поненциально, колебаний
нет. Система, которую вывели из положения равновесия, действительно постепенно
возвращается в него (см. рисунок).
Затухание, при котором , называют критическим. При таком (и
большем) затухании колебания в системе невозможны.
Источник: https://vunivere.ru/work23450/page16
7.7.Затухающие колебания
Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают — их амплитуда постепенно уменьшается.
Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости.
Эти силы, независимо от их происхождения, называют силами сопротивления.
| (7.17) |
или
| |
(7.18) |
![]()
![]()
| |
(7.19) |
![]()
Таким образом, в случае малого сопротивления среды , решением уравнения (7.19) будет функция
| (7.20) |
График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину называют собственной циклической частотой колебаний диссипативной системы.
Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения.
Величину обычно называют периодом затухающих колебаний, правильнее — условным периодом затухающих колебаний,
- Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.
- Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда
- откуда
Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.
- Пусть N — число колебаний, после которых амплитуда уменьшается в е раз, Тогда
- Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз
Источник: https://physics-lectures.ru/mexanicheski-kolebaniya-i-volny/7-7-zatuxayushhie-kolebaniya/
Затухающие колебания в физике
Причина затухания заключается в том, что во всякой колебательной системе, кроме возвращающей силы, всегда действуют разного рода силы трения, сопротивление воздуха
и т. п., которые тормозят движение. При каждом размахе часть полной колебательной энергии (потенциальной и кинетической) расходуется на работу против сил трения. В конечном итоге на эту работу уходит весь запас энергии, сообщенный колебательной системе первоначально.
Рассматривая свободные гармонические колебания, мы имели дело с идеальными, строго периодическими собственными колебаниями. Описывая при помощи такой модели реальные колебания, мы сознательно допускаем неточность в описании.
Однако подобное упрощение является пригодным в силу того, что у многих колебательных систем затухания колебаний, вызванные трением, действительно малы: система успевает совершить много колебаний прежде, чем их амплитуда уменьшится заметным образом.
Графики затухающих колебаний
При наличии затухания собственное колебание (рис.1) перестает быть гармоническим.
Более того, затухающее колебание перестает быть периодическим процессом — трение влияет не только на амплитуду колебаний (то есть является причиной затухания), но и на продолжительность размахов.
С увеличением трения время, необходимое системе для совершения одного полного колебания, увеличивается. График затухающих колебаний представлен на рис. 2.

Рис.1. График свободных гармонических колебаний

Рис.2. График затухающих колебаний
Характерной чертой колебательных систем является то, что небольшое трение влияет на период колебаний в гораздо меньшей степени, чем на амплитуду. Это обстоятельство сыграло огромную роль в усовершенствовании часов.
Первые часы с маятником построил голландский физик и математик Христиан Гюйгенс в 1673 г. Этот год можно считать датой рождения современных часовых механизмов.
Ход часов с маятником мало чувствителен к изменениям, обусловленным трением, которые в общем случае зависят от многих факторов, в то время как скорость хода предшествующих безмаятниковых часов очень сильно зависела от трения.
На практике возникает потребность как в уменьшении, так и в увеличении затухания колебаний. К примеру, при конструировании часовых механизмов стремятся уменьшить затухание колебаний балансира часов.
Для этого ось балансира снабжают острыми наконечниками, которые упираются в хорошо отполированные конические подпятники, выполненные из твердого камня (агата или рубина).
Наоборот, во многих измерительных приборах очень желательно, чтобы подвижная часть устройства устанавливалась в процессе измерений быстро, но совершая большого числа колебаний. Для увеличения затухания в этом случае применяют различные демпферы – устройства, увеличивающие трение и, в общем случае, потерю энергии.
| Понравился сайт? Расскажи друзьям! |
Источник: http://ru.solverbook.com/spravochnik/mexanika/mexanicheskie-kolebaniya-i-volny/zatuxayushhie-kolebaniya/
Колебания. Затухающие и незатухающие
Повторяющиеся процессы определяют нашу жизнь. Зима сменяет лето, день сменяет ночь, вдох сменяет выдох. Бежит время, и его мы тоже отмеряем повторяющимися процессами. Повторяющиеся процессы и есть колебания.
Колебаниями называются повторяющиеся во времени изменения физической величины.
Если эти изменения повторяются через определенный интервал времени, то колебания называются «периодическими». Наименьший интервал времени T, через который повторяются значения физической величины A(t), называется периодом ее колебаний A(t + Т) = A(t).
Число колебаний в единицу времени v называется частотой колебаний. Частота колебаний и период связаны соотношением v = 1 / Т. Колебания системы, которые совершаются в отсутствие внешнего воздействия, называются свободными.
Для возбуждения колебаний необходимо внешнее воздействие. Системе извне сообщается запас энергии, за счет которой и происходят колебания.
Это внешнее воздействие выводит систему из положения равновесия, и в дальнейшем она совершает движение около положения равновесия, уходя и возвращаясь к нему, по инерции проскакивая его. И так повторяется раз за разом. Движение в данном контексте означает изменение состояния.
В механических системах это может быть перемещение в пространстве или изменение давления, в электрических — изменение величины заряда или напряженности поля. Существует бесконечное множество различных движений и соответствующих им колебательных процессов.
Любую систему, совершающую колебательное движение, именуют «осциллятор» (в пер. с лат. oscillo — «колеблюсь»), соответственно и слово «колебания» часто заменяют термином «осцилляции».
- Если амплитуда колебаний не меняется во времени, гармонические колебания называются незатухающими.
- Дифференциальное уравнение, описывающее гармонические незатухающие колебания, имеет вид:
- d2A(t) / dt2 + ω02A(t) = 0.
- Производную по времени в физике принято обозначать точкой над дифференцируемой функцией. Тогда уравнение записывается:
- Ȧ + ω02A = 0.
- Если амплитуда уменьшается с течением времени, колебания называются затухающими.
- Часто встречающийся пример затухающих колебаний — колебания, в которых амплитуда уменьшается по закону
- A0(t) = a0e-βt.
- Коэффициент затухания β > 0.
В системе СИ время измеряется в с, а частота соответственно в обратных секундах (с-1). Эта единица измерения имеет специальное название «герц», 1 Гц = 1 с-1. Немецкий физик Генрих Рудольф Герц много занимался изучением электромагнитных колебаний и волн. «Генрих Герц» — первые слова, посланные с Земли в космос. Материал с сайта http://worldofschool.ru
 |
| Затухающие периодические колебания |
 |
| Затухающие апериодические колебания |
На этой странице материал по темам:
Источник: http://WorldOfSchool.ru/fizika/volnovaya/t-kolebanij/kolebaniya.-zatuhayushhie-i-nezatuhayushhie
Затухающие колебания — урок. Физика, 9 класс
При рассмотрении вопроса о превращениях энергии во время колебаний математического и пружинного маятников мы допустили, что потери энергии на преодоление сил трения при движении маятника пренебрежимо малы.
Тогда, согласно закону сохранения энергии, полную механическую энергию маятника в любой момент времени можно считать одинаковой и равной той потенциальной энергии, которую мы изначально сообщили маятнику, выведя его из положения равновесия.
При этом маятник мог бы совершать колебания сколь угодно долго с постоянной амплитудой. Так было бы, если бы при колебаниях маятника не было никаких потерь энергии.
Но реально потери энергии всегда есть. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха, переходя при этом во внутреннюю энергию. Амплитуда колебаний постепенно уменьшается, и через некоторое время колебания прекращаются. Такие колебания называются затухающими.
Затухающие колебания — это колебания, энергия которых уменьшается с течением времени.
Обрати внимание!
Чем больше силы сопротивления движению, тем быстрее прекращаются колебания.
Пример:
в воде (график (1)) колебания затухают быстрее, чем в воздухе (график (2)).
Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии.
Обрати внимание!
При наличии трения колебания идут медленнее:
Tзат>T0.
Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.
Амплитуда затухающих колебаний — величина не постоянная, а изменяющаяся со временем. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить.
При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.
Источники:
Физика. 9 кл.: учебник / Перышкин А. В., Гутник Е. М. — М.: Дрофа, 2014. — 319 с.www.studfiles.ruwww.alterozoom.comwww.ru.wikipedia.org
www.cankri.ru
Источник: https://www.yaklass.ru/p/fizika/9-klass/mekhanicheskie-kolebaniia-i-volny-zvuk-18755/zatukhaiushchie-kolebaniia-vynuzhdennye-kolebaniia-rezonans-158009/re-9bcce91b-d3d7-4a6e-88a6-4b4be6250934




