Формула второго закона кирхгофа

  Второй закон (правило) Кирхгофа — алгебраическая сумма напряжений на элементах контура электрической цепи равна нулю.

Контур электрической цепи — замкнутый проводящий ток путь образованный элементами электрической цепи.
Рассмотрим схему на рисунке 1:

Рисунок 1 — Схема с одним контуром

В этой схеме присутствуют: источник ЭДС и резисторы R1, R2 и R3; эти элементы образуют замкнутый путь проводящий ток т.е. контур. Напряжение на источнике ЭДС равно E и направлено так как показано на рисунке 1 стрелочкой справа от источника.

Стрелка на условном обозначении источника направлена в сторону противоположную направлению напряжения на источнике ЭДС (иногда это запутывает при расчёте схем но так принято обозначать источник ЭДС). Направления падений напряжений на резисторах указаны стрелками (рис. 1).

Для составления уравнения, по второму закону Кирхгофа, необходимо выбрать направление обхода контура (по часовой стрелке или против). В схеме на рисунке показано направление по часовой стрелке. Запишем уравнение по второму закону Кирхгофа:

Напряжения резисторов вошли в левую часть уравнения со знаком плюс т.к. направление обхода контура совпадает с направлениями напряжений на резисторах.

Напряжение источника ЭДС E вошло в правую часть со знаком плюс т.к. направление обхода контура не совпадает с направлением напряжения источника.

Можно также записать напряжение источника в левой части уравнения со знаком минус (что, в принципе, тоже самое):

Уравнение (2) больше подходит для определения второго закона Кирхгофа приведенного выше.

Напряжения совпадающие по направлению с обходом контура записаны со знаком плюс а напряжение источника не совпадающее с обходом контура — со знаком минус и вся эта алгебраическая сумма равна нулю. Теперь, из выражения (2), зная три каких либо напряжения можно найти четвёртое.

Обычно расчёт цепи сводится к нахождению токов во всех ветвях или потенциалов всех узлов т.к. зная эти величины (токи ветвей или потенциалы узлов), сопротивления всех элементов и напряжения источников ЭДС (и токи всех источников тока) можно найти напряжение на любом элементе и ток любого элемента.

В схеме на рисунке 1 для определения напряжений U1, U2 и U3 достаточно знать ток I т.к. он одинаков для всех элементов цепи (R1, R2, R3, E).

Умножением тока I на сопротивление R1 находится напряжение U1, умножением тока I на сопротивление R2 находится напряжение U2, умножением тока I на сопротивление R3 находится напряжение U3. Учитывая это можно привести уравнение (1) к виду:

Из уравнения (3) можно найти ток I. Т.к. контур один то и ток в уравнении один но если схема содержит больше одно контура то и токов будет больше.

Вынеся ток I за скобки и поделив обе части уравнения на сумму сопротивлений R1, R2 и R3 получаем уравнение для нахождения тока I, но этот ток можно найти и другим способом например заменой последовательного соединения резисторов R1, R2 и R3 одним резистором R123 и делением напряжения E на сопротивление резистора R123.

Сопротивление резистора R123 равно сумме сопротивлений резисторов R1, R2 и R3. Ток находится из уравнения:

     Если в контуре содержится больше одного источника ЭДС то уравнение, по второму закону (правилу) Кирхгофа, составляется аналогично.

Рисунок 2 — Схема с двумя источниками ЭДС

Запишем уравнение, по второму закону Кирхгофа, для контура в схеме на рисунке 2:

Напряжение E2 источника E2 записано в правой части уравнения со знаком минус т.к. оно совпадает по направлению с обходом контура. Заменяя напряжения на резисторах произведениями тока I на сопротивления резисторов получим уравнение:

Из уравнения (6) может быть найден ток I.

Если схема имеет больше одного контура то Закон (правило) Кирхгофа все равно выполняется для всех контуров. Уравнения по второму закону Кирхгофа, в таком случае, составляются аналогично тому как в примерах выше.

 Отличие будет только в том что необязательно для всех элементов будет один и тот же ток. В случае если схема имеет больше одного контура можно считать что через каждый элемент течет свой ток.

Напряжение на элементе, в таком случае, находится умножением сопротивления этого элемента (если этот элемент например резистор) на ток данного элемента.

Рисунок 3 — Часть схемы имеющей больше одного контура

Рисунок 4 — Часть схемы имеющей больше одного контура и ветвь из двух элементов

Рисунок 4 — Часть схемы имеющей больше одного контура, ветвь из двух элементов и элементы напряжения на на которых имеют направления не совпадающие с выбранным направлением обхода контура

О том что такое узлы и ветви можно узнать из предыдущей статьи.

При составлении уравнений по второму закону Кирхгофа не стоит слишком много времени уделять выбору направлений обходов контуров и направлений токов (они (направления обходов и токов) выбираются произвольно) так как реальные направления токов определяются при решении этих уравнений.

Пример:

Направление напряжения на элементе R1 такое же как и направление тока этого элемента по тому что принято считать что ток течёт от большего потенциала к меньшему а напряжение направлено также (от большего потенциала к меньшему).

Источник: http://electe.blogspot.com/2012/01/blog-post_29.html

2. Второй закон Кирхгофа

Второй закон Кирхгофа

Давайте посмотрим на нашу последовательную схему с другой стороны. На этот раз мы пронумеруем все точки схемы, чтобы к ним можно было привязать напряжения:

Если мы подключим вольтметр к точкам 1 и 2 (красный щуп к точке 2, а черный — к точке 1), то он зарегистрирует напряжение +45 В. Обычно дисплей цифрового электроизмерительного прибора знак «+» не показывает, но так как в рамках нашей статьи полярность напряжения имеет очень важное значение, мы будем  показывать положительные числа с этим знаком:

Когда рядом с напряжением указываются два символа (символы «2-1» в обозначении U2-1), это означает, что напряжение в первой точке (2) измеряется по отношению ко второй точке (1). Напряжение обозначенное как «Ucd» скажет нам о том, что красный щуп измерительного прибора подсоединяется к точке «с», а черный — к точке «d», то есть это напряжение измеряется в точке «c» относительно точки «d»:

Если мы теперь возьмем тот же самый вольтметр и измерим напряжения на каждом резисторе цепи, обходя ее по часовой стрелке (подсоединяя при этом красный щуп к первой точке, а черный — ко второй), то получим следующие показания:

Ранее вы познакомились с одним из принципов последовательной цепи, который гласит что общее напряжение такой цепи складывается из напряжений ее отдельных участков. Но, если при измерении напряжения мы будем учитывать его полярность (математический знак), то пред нами откроется новый аспект этого принципа — суммарное напряжение цепи будет равно нулю:

Этот принцип известен как Второй Закон Кирхгофа или Закон напряжений Кирхгофа (открыт в 1847 году немецким физиком Густавом Кирхгофом), и гласит он следующее:

«Алгебраическая сумма всех напряжений любой замкнутой цепи должна равняться нулю» 

Здесь под словом «алгебраическая» понимается учет математического знака (полярности) напряжения, а под словом «замкнутой цепи» — понимается последовательный путь, проложенный вокруг этой цепи из одной ее точки к другим точкам, и обратно к первой точке.

В приведенном выше примере замкнутая цепь сформирована последовательностью точек 1-2-3-4-1. Не имеет абсолютно никакого значения с какой точки мы начнем и в каком направлении мы будем двигаться; сумма напряжений все равно будет равняться нулю.

В качестве еще одного примера можно подсчитать напряжение в последовательности точек 3-2-1-4-3 этой же схемы:

Все это будет более понятно, если перерисовать нашу последовательную цепь таким образом, чтобы все ее компоненты находились на одной линии:

Перед вами все та же последовательная цепь, только ее компоненты расположены иным способом.

Обратите внимание на полярность напряжений резисторов относительно батареи: напряжение последней отрицательно слева и положительно справа, тогда как напряжения на всех резисторах ориентированы в другую сторону (положительны слева и отрицательны справа). Различия в полярности обусловлены тем, что резисторы сопротивляются потоку электронов, производимому батареей.

На следующем рисунке вы можете увидеть показания цифровых вольтметров на каждом компоненте этой цепи:

Если мы произведем замеры напряжения на группах компонентов, начиная с левой стороны цепи (с резистора R1), то увидим, что напряжения складываются алгебраически (к нулевому результату):

То, что напряжения последовательной цепи складываются, является очевидным фактом, и в этом сложении очень важную роль играет полярность напряжения.

 Измеряя напряжение на резисторах R1, R1—R2, R1—R2—R3 (символ двойного тире «—» используется для того, чтобы показать последовательное соединение между резисторами R1, R2, и R3) мы видим, что его величина (хоть и отрицательная) последовательно увеличивается от начальной точки к каждому последующему резистору.

Такое увеличение является следствием одинаковой ориентации (полярности) напряжения на всех резисторах («+» слева, «-» справа).

  Сумма напряжений на резисторах R1, R2, и R3 нашей схемы будет равна 45 вольт, что аналогично напряжению на выводах батареи, за тем исключением, что полярность батареи («-» слева, «+» справа) противоположна полярности суммарного напряжения резисторов. Таким образом, общее напряжение на всей линейке компонентов схемы будет равно нулю (45В + (-45В) = 0).

Полученное в результате суммирования итоговое напряжение, величиной 0 вольт, вполне закономерно.

Поскольку непосредственно связанные точки являются электрически общими по отношению друг к другу, напряжение между ними должно быть равно нулю.

• Второй закон Кирхгофа будет работать не только на последовательной конфигурации цепи, но и на любой другой. Посмотрите как он работает на следующей параллельной цепи:
• В параллельной цепи, как вы знаете, напряжение на каждом резисторе равно напряжению батареи, которое в нашем случае составляет 6 вольт. Подсчитав напряжение в последовательности точек 2-3-4-5-6-7-2, мы получим:

Обратите внимание, суммарное напряжение мы обозначили как U2-2. А обозначили мы его так из за того, что начали измерения в точке 2, и закончили в этой же точке. Алгебраическая сумма напряжений в этом случае будет равна напряжению между точками 2-2, которое конечно-же равно нулю.

Тот факт, что эта цепь параллельная а не последовательная, никак не влияет на справедливость второго закона Кирхгофа. Любая схема вообще может быть «черным ящиком», а ее конфигурация может быть полностью скрыта от нашего взгляда. При этом, если контрольные точки этой схемы будут открыты, то замеры напряжения между ними подтвердят верность данного закона:

Попробуйте в вышеприведенной схеме измерить напряжения любой последовательностью шагов между любыми ее точками (возвращаясь при этом в исходную точку), и вы увидите, что алгебраическая сумма напряжений всегда равна нулю.

Последовательность точек, к которой можно применить закон, не обязательно должна соответствовать реальному потоку электронов.

Единственным условием, которое необходимо выполнить, является то, что последовательность должна начинаться и заканчиваться в одной точке цепи, при этом полярность при проведении замеров должна неукоснительно соблюдаться.

Давайте рассмотрим абсурдный пример, замерив напряжения в последовательности точек 2-3-6-3-2 этой же цепи:

1. Второй закон Кирхгофа можно использовать для определения неизвестного напряжения сложной цепи, в которой остальные напряжения выбранной последовательности точек известны. Возьмем в качестве примера следующую сложную цепь (представляющую две последовательные цепи, основания которых соединены проводом):

Для упрощения задачи мы опустим значения сопротивлений, оставив только значения напряжений на каждом резисторе.

Так как две изображенные на рисунке последовательные схемы имеют общий провод (провод 7-8-9-10), у нас появляется возможность измерить между ними напряжение.

Если мы хотим определить напряжение между точками 4 и 3, то его нужно подставить в уравнение Второго закона Кирхгофа как неизвестное:

Таким образом, напряжение от точки 9 до точки 4 оказалось положительным +12 вольт, так как красный щуп подключался к точке 9, а черный — к точке 4. Напряжение от точки 3 до точки 8 так же положительно + 20 вольт (красный щуп к точке 3, черный — к точке 8).

И напряжение от точки 8 до точки 9 имеет нулевое значение, потому что эти две точки являются электрически общими.

1. Итак, окончательным ответом для напряжения от точки 4 до точки 3 будет  -32 вольта. Именно такое напряжение покажет вольтметр, если мы подключим его красный щуп к точке 4, а черный — к точке 3:
2. Если бы наше уравнение начиналось с U3-4 вместо U4-3, то последовательность измерений проводилась бы при противоположной ориентации тестовых проводов мультиметра. В этом случае окончательный ответ был бы следующим — U3-4=+32 В:

Здесь важно понять, что оба подхода являются правильными. В обоих случаях мы достигаем правильной оценки напряжения между точками 3 и 4.

Источник: http://www.radiomexanik.spb.ru/5.-shemyi-deliteley-i-zakonyi-kirhgofa/2.-vtoroy-zakon-kirhgofa.html

Законы Кирхгофа

Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников. Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.

1.1 Резисторы и подводящие провода

• Проводник, обладающий сопротивлением R, мы называем резистором и изображаем следующим образом (рис. 1):
• 
• Рис. 1 Резистор

Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.

Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.

1. Пусть положительный заряд q перемещается по цепи из точки a в точку b, проходя через резистор R (рис. 2):
2. 
3. Рис.2  U = φa – φb

Стационарное поле совершает при этом положительную работу A = q(φa − φb). Так как q > 0 и A > 0, то и φa − φb > 0, т. е. φa > φb.

Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: U = φa − φb.

Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если φa − φb = IR и R = 0, то φa = φb (рис. 3):

Рис.3   φa = φb

Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение.

А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным.

В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.

1.2 Последовательное соединение

При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.

Рассмотрим два резистора R1 и R2, соединённых последовательно и подключённых к источнику постоянного напряжения U (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

• 
• Рис.4 Последовательное соединение
• Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере:

• При последовательном соединении проводников сила тока в них одинакова. В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
• Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике. Действительно, напряжение Uab на участке ab — это работа поля по переносу единичного заряда из точки a в точку b; напряжение Ubc на участке bc — это работа поля по переносу единичного заряда из точки b в точку c. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки a в точку c, то есть напряжение U на всём участке: U = Uab + Ubc.

Можно и более формально, без всяких словесных объяснений: U = Uac = φa − φc = (φa − φb) + (φb − φc) = Uab + Ubc.

• Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника. Пусть R — сопротивление участка ac. По закону Ома имеем:

что и требовалось.

Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения S, но с разными длинами l1 и l2.

Сопротивления проводников равны:

Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.

Доказательство этого даётся с помощью закона Ома, как показано выше.

Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.

1.3 Параллельное соединение

При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.

Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).

Рис.5 Параллельное соединение

Резисторы подсоединены к двум точкам: a и b. Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от b к a (по направлению тока) называется неразветвленной частью цепи.

Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов:

• Напряжение на каждой ветви одинаково и равно напряжению на неразветвленной части цепи. В самом деле, оба напряжения U1 и U2 на резисторах R1 и R2 равны разности потенциалов между точками подключения:

U1 = U2 = φa − φb = U.

Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.

• Сила тока в неразветвленной части цепи равна сумме сил токов в каждой ветви. Пусть, например, в точку a за время t из неразветвленного участка поступает заряд q. За это же время t из точки a к резистору R1 уходит заряд q1, а к резистору R2 — заряд q2. Ясно, что q = q1 + q2. В противном случае в точке a накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:

что и требовалось.

• Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей. Пусть R — сопротивление разветвлённого участка ab. Напряжение на участке ab равно U; ток, текущий через этот участок, равен I. Поэтому:

1. 
2. Сокращая на U, получим:
3. 1/R = 1/R1 + 1/R2 ,                                                 (1)
4. что и требовалось.
5. Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.

Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами l, но разными поперечными сечениями S1 и S2. Тогда это соединение можно рассматривать как проводник той же длины l, но с площадью сечения S = S1 + S2. Имеем:

• Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
• Из соотношения (1) можно найти R:
• R = R1R2/(R1 + R2) .                                               (2)
• К сожалению, в общем случае n параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением

1/R = 1/R1 + 1/R2 + . . . + 1/Rn .                               (3)

Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех n резисторов одинаковы и равны R1. Тогда:

Мы видим, что сопротивление участка из n параллельно соединённых одинаковых проводников в n раз меньше сопротивления одного проводника.

1.4 Смешанное соединение

Смешанное соединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.

Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.

Рассмотрим пример смешанного соединения проводников (рис. 6).

Рис. 6 Смешанное соединение

Пусть U = 14 В, R1 = 2 Ом, R2 = 3 Ом, R3 = 3 Ом, R4 = 5 Ом, R5 = 2 Ом. Найдём силу тока в цепи и в каждом из резисторов.

1. Наша цепь состоит из двух последовательно соединённых участков ab и bc. Сопротивление участка ab:
2. Сопротивление цепи: R = Rab + Rbc = 1,2 + 1,6 = 2,8 Ом.
3. Теперь находим силу тока в цепи:
4. I = U/R = 14/2,8 = 5 A.
5. Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
6. Uab = IRab = 5 · 1,2 = 6 B;
7. Ubc = IRbc = 5 · 1,6 = 8 B.

(Заметим попутно, что сумма этих напряжений равна 14 В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)

• Оба резистора R1 и R2 находятся под напряжением Uab, поэтому:
• Стало быть, через резистор R5 течёт ток I5 = I − I3 = 5 − 1 = 4 A

Законы Кирхгофа – правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году.

В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле.

Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.

Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю

Давайте разбираться. Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i1 и i2.

Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i1-i2=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i1 и i2 i=i1+i2.

Но если бы, например, ток i2 входил в узел, тогда бы ток I определялся как i=i1-i2. Важно учитывать знаки при составлении уравнения.

Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает.

Второй закон Кирхгофа – алгебраическая сумма ЭДС, действующая в замкнутом контуре, равна алгебраической сумме падений напряжения в этом контуре

1. Напряжение выражено как произведение тока на сопротивление (по закону Ома).

В этом законе тоже существуют свои правила по применению. Для начала нужно задать стрелкой направление обхода контура.

Затем просуммировать ЭДС и напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E2 и Е3 совпадают с ней по направлению, значит знак плюс, а Е1 направлено в противоположную сторону, значит знак минус.

Теперь смотрим на напряжения, ток I1 совпадает по направлению со стрелкой, а токи I2 и I3 направлены противоположно. Следовательно:

— E1 + E2 + E3 = I1R1 — I2R2 — I3R3

Источник: http://razmishlyajem.ru/o-raznom-vsyakom/prochee/dlya-studentov/zakony-kirxgofa

Второй закон Кирхгофа

Господа, всем привет!

Сегодня мы рассмотрим второй закон Кирхгофа. Он чуть сложнее, чем первый закон Кирхгофа, который мы уже рассматривали ранее, поэтому я сперва дам общую формулировку, а потом мы постараемся аккуратно разобраться во всем этом деле. 

Итак, второй закон Кирхгофа гласит, что алгебраическая сумма ЭДС, действующих в контуре равна алгебраической сумме падений напряжения в ветвях контура.

Может быть сложновато для восприятия, если вы читаете это в первый раз, не спорю. Но сейчас попробуем разобраться более детально во всем этом. Для начала давайте определим, что же такое контур электрической цепи, где эти самые ЭДС действуют.

Пожалуй, это тот случай, когда проще нарисовать картинку, чем объяснять словами. Взглянем на рисунок 1.

Рисунок 1 – Контура в схеме

На нем мы можем видеть три контура: я обозначил их красным, оранжевым и синим цветами. То есть контур –  это некоторая замкнутая часть электрической цепи, состоящая из нескольких ветвей.

То есть что говорит второй закон Кирхгофа? У нас есть большая и сложная электрическая схема. В ней много различных контуров. Будем рассматривать подробно один из этих контуров, любой на выбор.

И вот если мы в этом контуре сложим ЭДС всех источников, какие там есть, то их сумма будет равна сумме падений напряжения на всех сопротивлениях этого контура. И это верно для любого контура в нашей схеме. Довольно интересный факт.

И если про первый закон Кирхгофа можно говорить, что он интуитивно очевиден, то здесь, вообще говоря, это не совсем так. А поскольку он не очевиден на первый взгляд, тем больше поводов показать его верность математически.

Господа, прошу обратить внимание на рисунок 2. На нем изображен один из контуров какой-то сложной электрической схемы.

Рисунок 2 – Контур схемы

Почему он именно такой, можете вы спросить? Да просто так! Я рисовал его так, как подскажет фантазия в тот момент. Вы можете смело заявить, что ваша фантазия лучше и нарисовать какой-либо другой контур с другими компонентами. Потом повторите все действия, которые я буду производить над этим контуром, и в конечном счете у вас должен получиться точно такой же результат, как и у меня.

Первым делом давайте зададимся направлением обхода контура. Это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода контура у нас по часовой стрелке, и я показал его синей стрелочкой на рисунке 2.

Следующим шагом нам надо расставить предполагаемое направление токов в каждой ветви. Тут опять же все целиком отдается вашей фантазии. На данном этапе можно рисовать любое направление токов. Если мы угадали – отлично, если нет – в конце всех расчетов получим ток с другим знаком. Я расставил на рисунке 2 все токи черными стрелками и рядом с ними подписал их величины (I1…I4).

А теперь внимание, господа. Пришло время вспомнить то выражение, ради получения которого я написал предыдущую статью. На всякий случай, если вдруг кто забыл, напоминаю его

Оно означает, что если потенциалы на концах ветви равны φ1 и φ2, то их разность равна ЭДС источника в ветви минус произведение тока в ветви на сопротивление в ветви.

Применим это выражение для каждой ветви нашего контура, изображенного на рисунке 2. Поскольку у нас в контуре четыре ветви, то всего мы получим четыре уравнения. Резонный вопрос – а как быть со знаками при записи этих уравнений? Правила тут два.

• Если направление работы источника напряжения совпадает с направлением обхода контура, то берем его со знаком плюс. Если не совпадает – со знаком минус. Совсем просто: если стрелка в источнике напряжения совпадает со стрелкой обхода, то Е в уравнении пишется без изменения знака, если стрелки в разные стороны – то надо поставить минус перед E.
• Если направление тока, которое мы сами выбрали чуть раньше, совпадает с направлением обхода, то в нашем уравнении перед произведением тока на сопротивление так и остается знак минус. Если они направлены в разные стороны, то знак минус меняем на плюс.

Пользуясь этими простыми правилами, запишем уравнения для каждой ветви.

Очевидно, что если в цепи нет источника ЭДС, то у нас не будет первого слагаемого в правой части. А если нет сопротивления, то не будет второго слагаемого в правой части. Собственно, это и видно из составленных уравнений.

Господа, надеюсь вы помните, что с уравнениями в одной системе можно творить всякие интересные штуки? Например, можно все их сложить между собой (правые и левые части). Легко заметить, что при сложении всех этих четырех уравнений в левой части будет нолик, то есть все потенциалы волшебным образом самоликвидируются. Сделаем это! Получим

А теперь давайте перенесем все слагаемые с ЭДС в одну сторону, а с током и сопротивлением – в другую. Имеем

А имеем мы, собственно, второй закон Кирхгофа. Все честно, как я и писал в начале – алгебраическая сумма ЭДС, действующих в контуре равна алгебраической сумме падений напряжения в ветвях контура.

Надеюсь, господа, после статьи про закон Ома у вас не возникает вопросов, почему произведение тока на сопротивление – это падение напряжения на сопротивлении?  Если возникает – срочно, очень срочно, прямо сейчас пройдитесь по этой ссылке и разрешите эти вопросы!

А что же все-таки тут понимается под словом алгебраическая сумма? Это словосочетание нам уже встречалось. Это значит, что складывать надо с учетом знака.

А как выбирать правильно этот самый знак? Господа, взгляните еще разок на рисунок 2. Там у нас задано направление обхода контура и направление токов. Все это мы выбирали (я бы даже сказал придумывали) сами.

Ну и направление работы источника еще видно по его графическому изображению.

Так вот, если направление работы источника ЭДС совпадает с направлением обхода контура, то мы ему приписываем знак плюс, а если не совпадает – минус. Аналогично и для правой части. Если направление тока совпадет с направлением обхода, то мы пишем произведение тока на сопротивление со знаком плюс. Иначе – со знаком минус.

Специально для труЪ-математиков привожу запись второго закона Кирхгофа с использованием хитрых значков суммирования. Вне всякого сомнения, если вы будете использовать эту запись, то произведете впечатление человека, который шарит в теме!

Здесь у нас N источников c ЭДС Ei и M ветвей с сопротивлениями Rj и токами Ij. Разумеется, суммирование идет все так же с учетом знаков.

Может возникнуть резонный вопрос: «Как же так? Получается, я сам все придумываю: и направление обхода, и направление токов и это значит, что знак может получиться любой.

Поверну стрелку тока в другую сторону и сразу знак у слагаемого поменяется! Но ведь в реальной схеме токи всегда текут в своем направлении вне зависимости от того, что я там нарисую на листочке! Какое-то противоречие!» Господа, вопрос весьма справедливый. Но предлагаю разобраться в нем в следующей статье.

Сохраним некоторую интригу на текущий момент, как принято во всяких этих сериальчиках . А сейчас – спасибо, что прочитали статью, огромной вам всем удачи, и пока!

Источник: http://myelectronix.ru/postoyannyy-tok/34-vtoroy-zakon-kirkhgofa

Уравнения Кирхгофа для электрических цепей

Уравнения, или правила, Кирхгофа относят к основным законам электрических цепей.

Они вытекают из таких фундаментальных законов как, закон сохранения заряда и безвихревости электростатического поля, в своё время описанных уравнениями Максвелла.

Уравнения Кирхгофа довольно часто используются благодаря своей универсальности, пригодности для решения многих задач в теории электротехники, в том числе и связанных с расчётами сложных электрических цепей, практичности.

Применяя правила Кирхгофа к линейной электрической цепи можно получить систему линейных уравнений, из которых в свою очередь, можно найти значения токов на всех ветвях цепи и все межузловые напряжения.

В правилах Кирхгофа применяют такие понятия электрической цепи, как: узел, ветвь, контур.

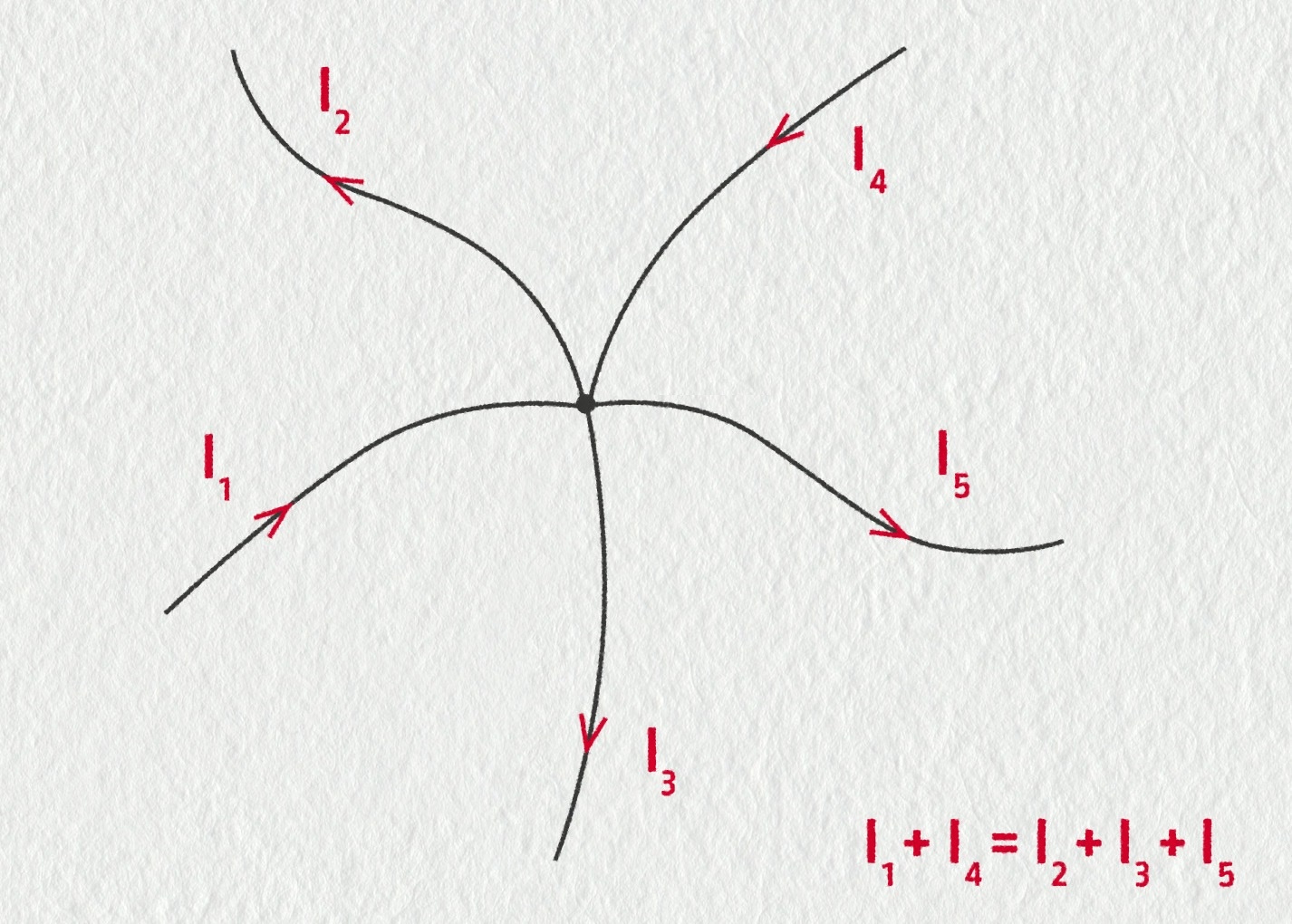
  Участок электрической цепи с одним и тем же током называют ветвью, например отрезок 1-4, на рисунке 1, с протекающим по нему током i1 , есть ветвь.

Точку, соединяющую три и более ветви называют узлом, например точки 1,2,3,4 на рисунке 1 есть узлы. Замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи называют контуром.

Начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, и возвратившись в исходный узел, мы пройдём путь, который и называют замкнутым. Проходимые при таком обходе ветви и узлы принято называть принадлежащими данному контуру, при этом надо принимать во внимание, что ветвь и узел могут принадлежать одновременно нескольким контурам.

Рисунок 1

• Первое правило Кирхгофа построено на основании утверждения о непрерывности электрического тока для любого узла электрической цепи или замкнутого контура.
• Первое правило Кирхгофа трактует, что алгебраическая сумма токов ветвей , для любого узла или замкнутого сечения электрической цепи, равна нулю:

Выше сказанное говорит о том, что электрические заряды в узле (например, S2 на рисунок 1) или сечении (например, S14  на рисунке 1) любой электрической цепи накапливаться не могут. Иными словами, сколько тока втекает в узел, столько из него и вытекает.

1. Второе правило Кирхгофа основано на утверждении, что любая электрическая цепь является потенциальной, а работа по перемещению электрических зарядов в замкнутом контуре равна нулю:
2. где U – работа(электрическое напряжение), k – число источников выполняющих работу;

Рассмотрим цепь, изображённую на рисунке1, образованную двухполюсными элементами, где ветви в местах соединений образуют узлы 1,2,3,4 и где направления напряжений и токов в ветвях совпадают.

Для составления уравнений Кирхгофа выберем произвольно узел  S2 , замкнутое сечение S14 (”несколько узлов”) и замкнутый контур 1, направление обхода которого изображено на рисунке 1.

• Если принять, что выходящие из сечений и узлов токи считать положительными, а входящие отрицательными, то тогда уравнения составленные по первому правилу Кирхгофа будут иметь вид:
• 
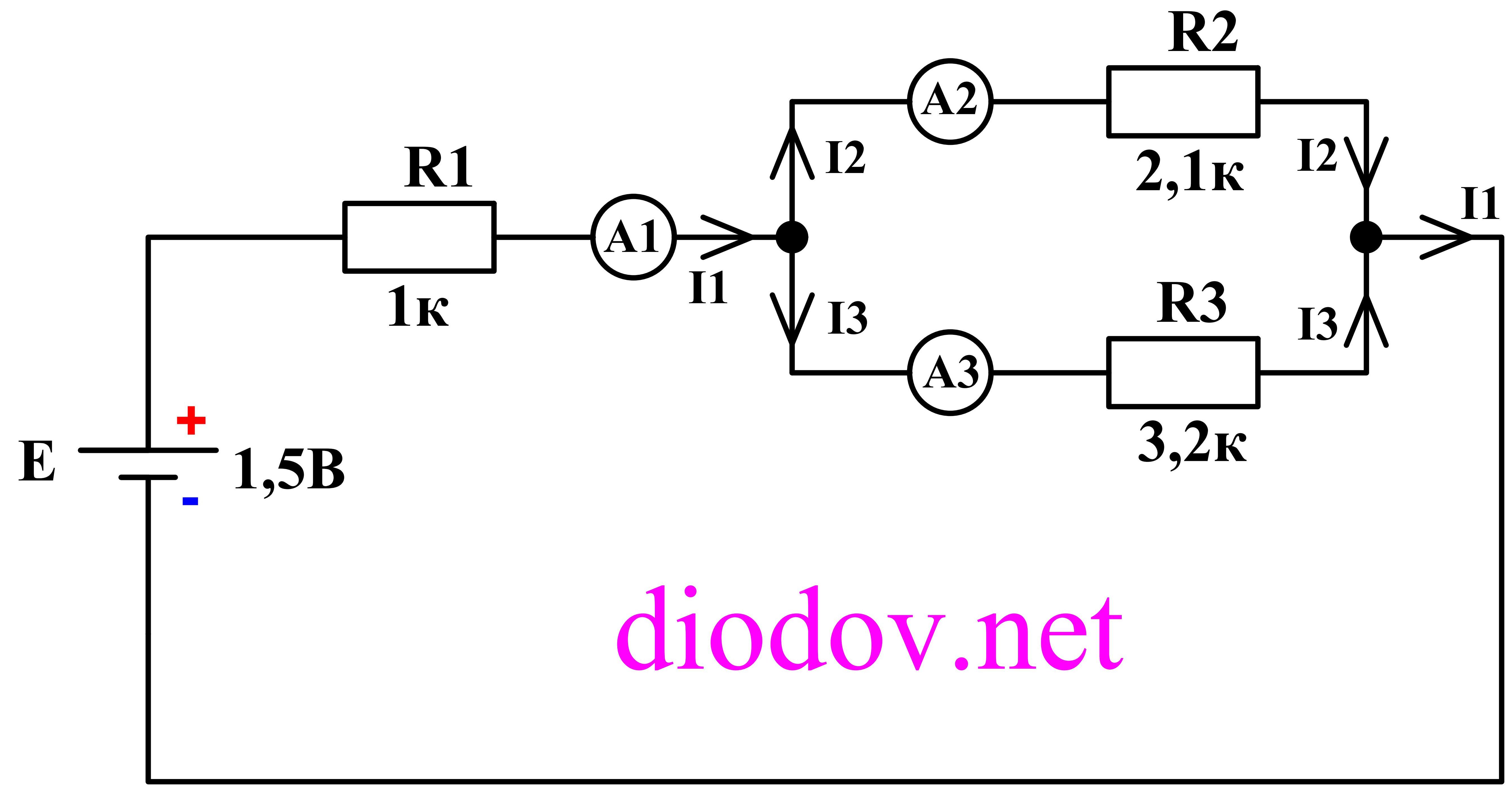
• Для составления уравнения по второму правилу Кирхгофа, напряжения совпадающие с направлением обхода контура считаем положительными, а не совпадающие отрицательными. При этом уравнение примет вид:
• 
• Рассмотрим второе правило Кирхгофа на более наглядном примере (рисунке 2, см. ниже) и с более понятной для практического применения трактовкой, утверждающей что: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре
• 
• где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.

Рисунок 2

1. Применяя второе правило Кирхгофа составляем уравнение для замкнутого контура схемы(рисунок 2) :
2. 
3. При составлении полученного уравнения знаки учитывались как:
4. — ЭДС (E) положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
5. — падение напряжения (IR) на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Мы рассмотрели применение правил Кирхгофа на простых примерах цепей постоянного тока и напряжений. На самом деле электрические цепи бывают значительно сложнее и состоять из различных элементов (источников ЭДС и тока , нелинейных и т.п.).

Например, для второго правила Кирхгофа физическое представление уравнения для переменного тока уже будет иметь вид:

Следует отметить, что для цепей синусоидального(переменного) тока правила Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений. Чтобы решать уравнения Кирхгофа для цепей синусоидального тока их составляют в комплексной форме, в которой учитываются ”мгновенные” изменения значений токов и напряжений.

Но какие сложные уравнения не приходилось бы составлять и решать, следует помнить, что физически второе правило(закон) Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Источник: https://elenergi.ru/uravneniya-kirxgofa-dlya-elektricheskix-cepej.html

Второй закон Кирхгофа

Законы Кирхгофа являются важной частью электротехники, их можно использовать для теоретических расчетов и с практической пользой в случае электрических цепях разветвленного и произвольного типа.

Первый закон и второй закон Кирхгофа пользуются особым спросом благодаря своего универсального применения и возможности решить различного рода задач. Они работают, так как для линейных цепей, так и для нелинейных, где ток может быть переменным или постоянным.

В некоторых источниках законы Киргофа принято называть правилами, так как выводы были сделаны на основе длительного наблюдения за определенными процессами.

• До того как понять, что собой представляет второй закон Кирхгофа стоит вспомнить, что именно гласит первый закон, так как между ними определенно должна быть какая-то связь, учитывая, в том числе последовательность их появления. Несмотря на то какая формулировка, первый закон Кирхгофа гласит одну истину:
• Первая формулировка : Сумма всех токов, которые сводятся в один узел, равна нулю.
• Вторая формулировка: Сумма тех токов, которые являются втекающими и вытекающими из единого узла представляет собой одно и то же значение, то есть эти два значения равны.

Речь именно об алгебраической сумме этих токов. Данный закон появился как производное от закона сохранения заряда. Другими словами первый закон указывает на непрерывность тока.

Первый закон может быть сформулирован по-разному, но вне зависимости от этого он будет означать то же самое понятие.

Если первый закон гласит, что сумма всех токов входящие в один узел равна сумме всех токов выходящих из этого узла, то не составит труда сформулировать на основе этого и второе неопровержимое правило Кирхгофа.

Понимание правил Кирхгофа можно упростить, если удостовериться, что такие простые понятия как ветвь, узел, контур и электрическая цепь являются понятными и доступными.

Разъяснение можно начать с самого простого понятия – ветвь, что представляет собой некую часть электрической цепи с одинаковым током по всей длине. Узел более сложное понятие, так как он может состоять из определенного количества ветвей, которые объединены в одной точке.

Понятие контур уже некий замкнутый электрический путь, который может состоять из разного количества ветвей и узлов. Путь обязательно закрытый и подразумевает возврат в исходную точку после прохождения всех элементов электрической цепи.

Несколько контуров могут существовать бок о бок и делить между собой свои элементы, так как ветви и узлы. Все эти значения обозначают второй закон Кирхгофа.

Второй закон Кирхгофа и его определение

В едином замкнутом контуре алгебраическая сумма ЭДС будет равняться на значение, которое суммирует изменения напряжения на всеобщее количество резистивных элементов данного контура.

Второе правило Кирхгофа актуально в сетях с постоянным и/или переменным током. В формулировке закона используется именно понятие алгебраическая сумма, так как она может быть указана со знаком плюс или минус. Точное определение возможно в таком случае только посредством простого, но эффективного алгоритма.

Для начала надо подобрать какое-то направление для обхода контура, по/против часовой стрелке, на собственное усмотрение. Само направление тока подбирается только через элементы цепи. После следует определить знаки «+» и «-» для напряжениях и ЭДС. Напряжения нужно записывать с отрицательным знаком, когда ток не соответствует обходу контура в плане направления и с плюсом в случае совпадения.

То же самое правило нужно использовать и в том случае, когда необходимо отметить ЭДС.

Второй закон Кирхгофа — практическое применение

На практике второй закон Кирхгофа применяется успешно для расчета электрических цепей. Благодаря его разъяснению можно рассчитать необходимые параметры в сложных электрических цепях.

Когда присутствует необходимость рассчитать значение тока и/или направление всегда выручит второй закон Кирхгофа. Невзирая на то, что правила Кирхгофа были сформулированы в далеком 1845 году, они показали себя как рабочие и не вызывают вопросы ни у кого.

Теория электрических цепей была бы неполной без наличия этих законов, которые так хорошо подходят для решения различных уравнений в этой области.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Источник: https://reshit.ru/vtoroj-zakon-kirxgofa

Второй закон Кирхгофа

23 августа 2013. Категория: Электротехника.

Падение напряжений в замкнутом контуре

При расчете электрических цепей нам часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы, то есть источники напряжений. На рисунке 1 представлен участок сложной электрической цепи.

Задана полярность всех электродвижущих сил (э. д. с.). Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим участок АБ.

На этом участке происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).

Рисунок 1. Участок сложной электрической цепи

• На участке АБ:
• φА + E1 – I1 × r1 = φБ .
• На участке БВ:
• φБ – E2 – I2 × r2 = φВ .
• На участке ВГ:
• φВ – I3 × r3 + E3 = φГ .
• На участке ГА:
• φГ – I4 × r4 = φА .
• Складывая почленно четыре приведенных уравнения, получим:
• φА + E1 – I1 × r1 + φБ – E2 – I2 × r2 + φВ – I3 × r3 + E3 + φГ – I4 × r4 = φБ + φВ + φГ + φА
• или
• E1 – I1 × r1 – E2 – I2 × r2 – I3 × r3 + E3 – I4 × r4 = 0.
• Перенеся произведения I × r в правую часть, получим:
• E1 – E2 + E3 = I1 × r1 + I2 × r2 + I3 × r3 + I4 × r4.
• В общем виде

Это выражение представляет собой второй закон Кирхгофа. Формула второго закона Кирхгофа показывает, что во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжений.

Бывают случаи, когда в замкнутом контуре отсутствуют источники э. д. с., тогда применимо другое определение второго закона Кирхгофа – алгебраическая сумма падений напряжений в замкнутом контуре равна нулю.

Видео 1. Второй закон Кирхгофа

Рассмотрим простой замкнутый контур (рисунок 2).

Рисунок 2. Простой замкнутый контур

По второму закону Кирхгофа

1. откуда
2. E = I × r0 + I × r = I × (r0 + r),
3. откуда
4. Мы получили формулу закона Ома для всей цепи.

Применение первого и второго законов Кирхгофа для расчета электрических цепей

Рисунок 3. Электрическая цепь – к примеру 1

Решим несколько задач, используя закон Ома и оба закона Кирхгофа.

Пример 1. Дана электрическая цепь (рисунок 3). Найти ее ток. Выберем произвольно положительное направление тока. Обходя контур по часовой стрелке, пишем уравнение второго закона Кирхгофа:

– E1 + E2 = I × r1 + I × r2;     – 1,9 + 1,3 = I × (2 + 3);    – 0,6 = 5 × I;I = – 0,12

Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.

Пример 2. Дана электрическая цепь (рисунок 4). Определить токи на отдельных участках.

• Произвольно выбираем положительные направления токов.
• Рисунок 4. Электрическая цепь – к примеру 2
• Для контура абде:
• Для контура авге:

6 – 2 = 2 × I1 – 4 × I2;     2 = I1 – 2 × I2.

(2)

Для точки Б по первому закону Кирхгофа:

Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I3 из уравнения (3) в уравнение (1), получим:

1. 6 = 2 × I1 + 5 × I1 + 5 × I2;
2. Сложим уравнения для двух контуров почленно:
3. (6 = 7 × I1 + 5 × I2) + (2 = I1 – 2 × I2)
4. или
5. (12 = 14 × I1 + 10 × I2) + (10 = 5 × I1 – 10 × I2).
6. Сложив два последних уравнения, имеем:
7. 22 = 19 × I1, откуда I1 = 1,156 А,
8. подставляем значение I1 в уравнение (1):
9. 6 = 2 × 1,156 + 5 × I3,

• Подставляем значение I1 в уравнение (2):
• 2 = 1,156 – 2 × I2,
• откуда

Знак минус показывает, что действительное направление тока I2 обратно принятому нами направлению.

Источник: Кузнецов М. И., «Основы электротехники» – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.

Источник: https://www.electromechanics.ru/electrical-engineering/542-kirchhoffs-second-law.html

Формула второго закона Кирхгофа

Какой бы сложной не была электрическая цепь, она имеет элементы двух видов: узлы и замкнутые контуры. Узлом цепи называют точку разветвления цепи, в которой сходятся три или более проводника с током.

Расчеты в любой самой сложной цепи можно провести, используя закон Ома и закон сохранения заряда.

Для упрощения расчетов цепей постоянного тока используют правила (законы) Кирхгофа, которые позволяю составить линейные уравнения вычисления сил токов, текущих в элементах цепи.

Падение напряжения это произведение силы тока на сопротивление (). Если в цепи источников ЭДС будет несколько, то следует ЭДС суммировать, учитывая знаки.

ЭДС принято считать положительной, если при обходе контура первым встречается отрицательный полюс источника. Направление обхода контура выбирают произвольно, (по часовой стрелке или против нее).

Теперь к самой формуле, отображающей второй закон Кирхгофа:

   

Формула второго закона Кирхгофа говорит о том, что сумма произведений силы токов (I) (с учетом знака) на внешние и внутренние сопротивления всех участков замкнутого контура равны сумме величин ЭДС () источников, которые включены в данный контур (суммирование ЭДС происходит с учетом знаков). При составлении и уравнений с использованием формулы второго закона Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС.

Система уравнений, которая получается при использовании первого и второго правил Кирхгофа является полной и дает возможность отыскать все токи.

При составлении уравнений, используя правила Кирхгофа, надо следить за тем, чтобы новое уравнение имело хотя бы одну величину, которая еще не вошла в предыдущие уравнения.

Кроме того, необходимо, чтобы система уравнений имела число уравнений равное количеству неизвестных.

Второе правило Кирхгофа следует из того, что электрическое напряжение по замкнутому контуру равно нулю, то есть это правило является следствием основного свойства электростатического поля, которое заключается в том, что работа поля при движении заряда по замкнутой траектории равна нулю.

Примеры решения задач по теме «Второй закон Кирхгофа»

Понравился сайт? Расскажи друзьям!

Источник: http://ru.solverbook.com/spravochnik/formuly-po-fizike/formula-vtorogo-zakona-kirxgofa/