









Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Четырехугольники Пискунова И.В. учитель математики ГБОУ лицея №299
2 слайд Описание слайда:
Найди четырехугольники B C D E M N K S O P L H A B C D M N O K R T F Q H Z I R Какая буква лишняя?
3 слайд Описание слайда:
Четырехугольник Фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. А B C D
4 слайд Описание слайда:
Основные элементы четырехугольника A, B, C, D — вершины четырехугольника A и B — соседние вершины AD, BC, CD, BA – стороны многоугольника AD и CD — смежные стороны многоугольника AB и CD — несмежные стороны AC, BD – диагонали многоугольника А B C D
5 слайд Описание слайда:
Сумма углов выпуклого многоугольника Сумма углов выпуклого четырехугольника А B C D
6 слайд Описание слайда:
Выпуклость четырехугольника
7 слайд Описание слайда:
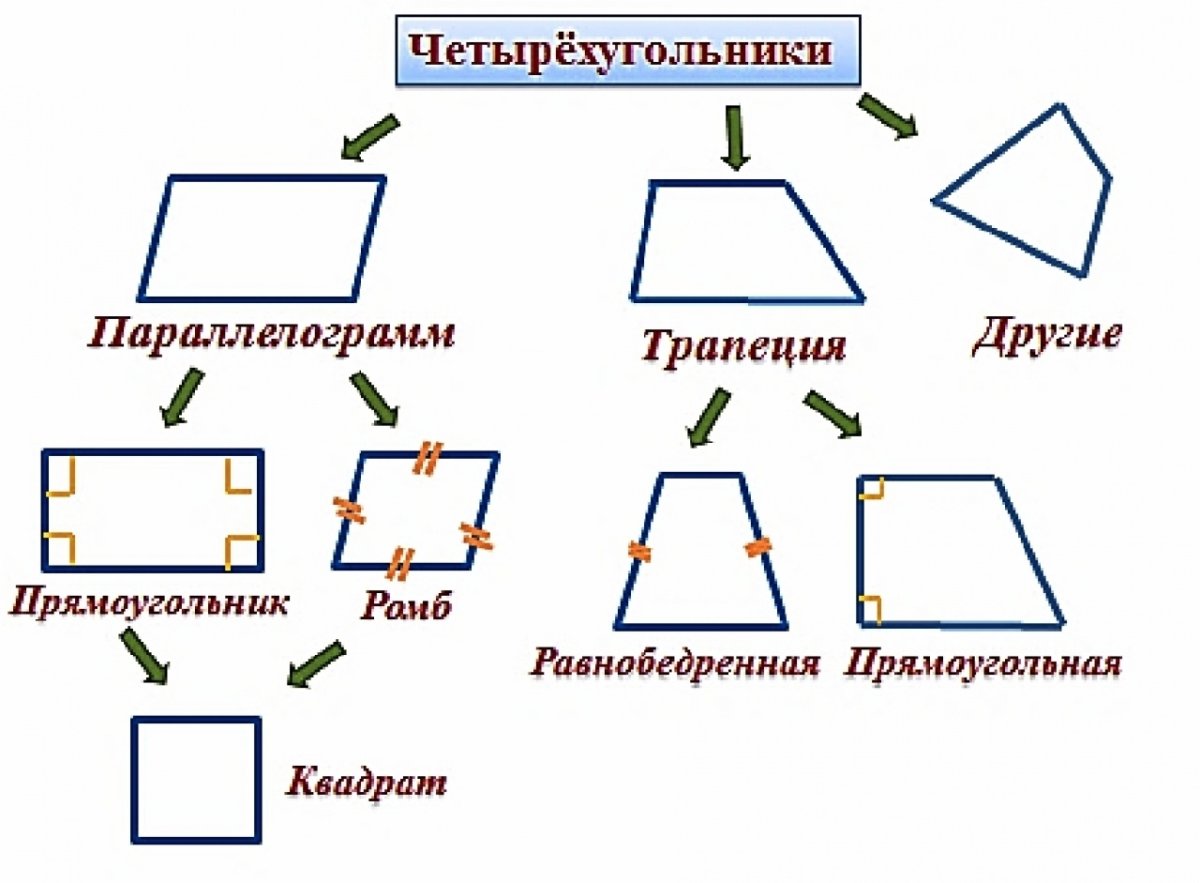
Виды четырехугольников Трапеция Четырехугольник Параллелограмм Квадрат Прямоугольник Ромб
8 слайд Описание слайда:
Параллелограмм четырехугольник, у которого противоположные стороны попарно параллельны. A B C D
9 слайд Описание слайда:
Свойства параллелограмма
10 слайд Описание слайда:
Площадь параллелограмма
11 слайд Описание слайда:
Прямоугольник Прямоугольник — параллелограмм, у которого все углы прямые.
12 слайд Описание слайда:
Свойства прямоугольника Замечание: Справедливы также обратные утверждения. Их называют признаками прямоугольника.
13 слайд Описание слайда:
Окружность, описанная около прямоугольника
14 слайд Описание слайда:
Площадь прямоугольника
15 слайд Описание слайда:
Ромб Ромб — параллелограмм, у которого все стороны равны.
16 слайд Описание слайда:
Свойства ромба
17 слайд Описание слайда:
Окружность, вписанная в ромб
18 слайд Описание слайда:
Площадь ромба
19 слайд Описание слайда:
Квадрат Квадрат— прямоугольник, у которого все стороны равны,
20 слайд Описание слайда:
Свойства квадрата
21 слайд Описание слайда:
Окружность, описанная около квадрата
22 слайд Описание слайда:
Окружность, вписанная в квадрат
23 слайд Описание слайда:
Площадь квадрата
24 слайд Описание слайда:
Трапеция — четырехугольник, у которого ровно одна пара противолежащих сторон параллельна. Трапеция
25 слайд Описание слайда:
Окружность, описанная около трапеции
26 слайд Описание слайда:
Окружность, вписанная в трапецию
27 слайд Описание слайда:
Площадь трапеции
Скрыть
Важно! Узнайте, чем закончилась проверка учебного центра «Инфоурок»?
Общая информация
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Источник: https://infourok.ru/chetirehugolniki-osnovnie-priznaki-i-svoystva-1448464.html
Четырехугольники. Основные теоремы, формулы и свойства. Виртуальный справочник репетитра по математике
Здесь ученики и репетиторы по математике и могут найти основные свойства и формулы площадей четырехугольников, изучаемых в школе по основной программе.
Регулярно пользуюсь этими теоретическими сведениями на тематических и обзорных занятиях по геометрии (планиметрии), а также при подготовке к ЕГЭ по математкие.
Все математические понятия и факты иллюстрированы с цветовыми выделениями главных особенностей изучаемого.
1) Площади четырехугольников
Площадь параллелограмма

![]()
произведение основания на высоту
![]()
пороизведение сторон на синус угла между ними
![]()
полупроизведение диагоналей на синус угла между ними
Площадь трапеции

![]()
произведение полусуммы оснований на высоту
![]()
произведение средней линии на высоту
![]()
полупроизведение диагоналей на синус угла между ними
Площадь произвольного четырехугольника
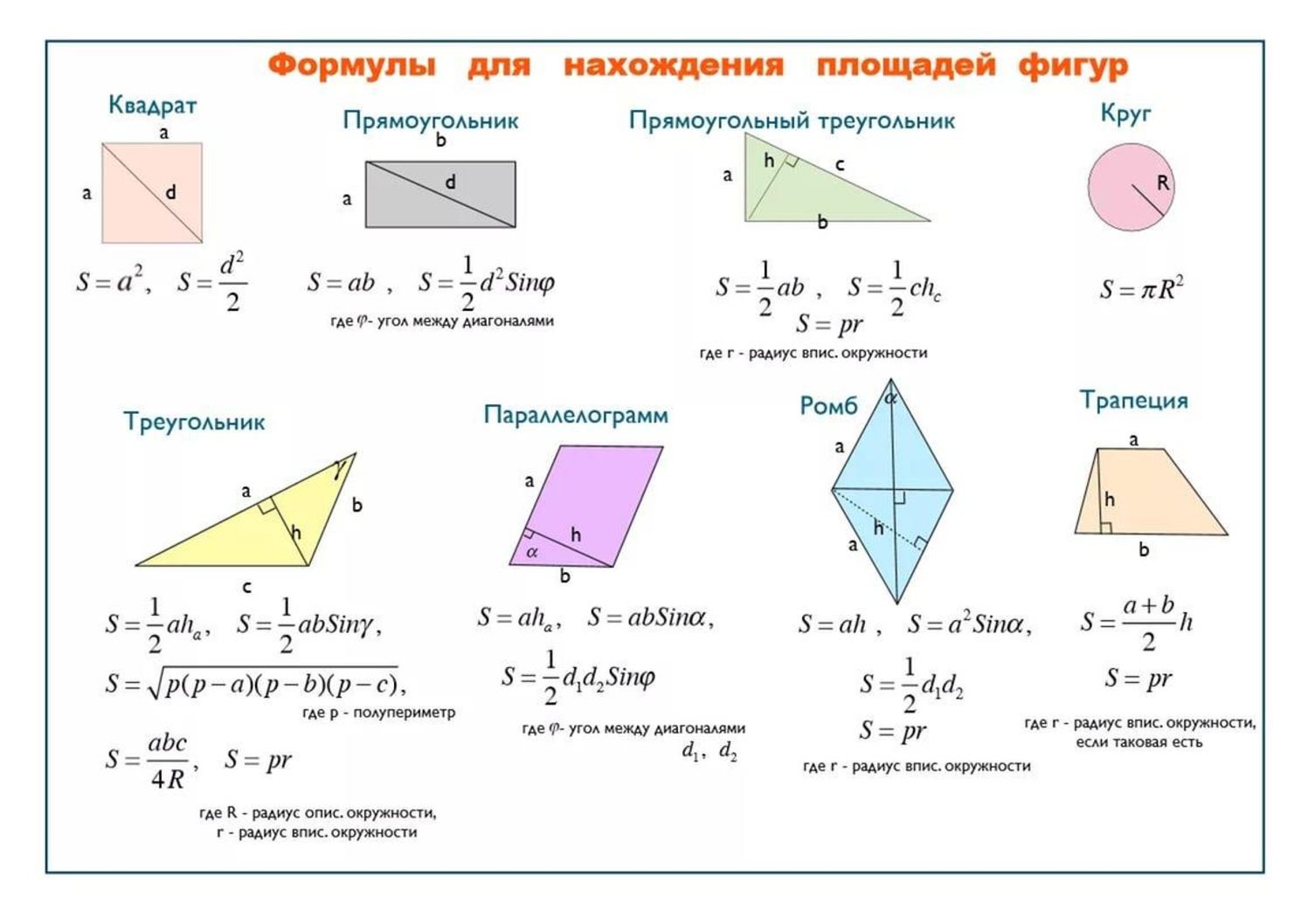
![]()
Площадь произвольного четырехугольника равна полупроизведению его диагоналей на синус угла между ними
- 2) Свойства параллелограмма
- В параллелограмме:
противолежащие стороны и углы равны - диагонали пересекаются и в точке пересечения делятся пополам
- 3) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, то есть
- 3) Cредняя линия в трапеции
Теорема о средней линии: Средняя линия трапеции параллельна основаниям и равна их полусумме.
То есть и - 4) Средняя линия в равнобедренной трапеции
- Средняя линия в равнобедренной трапеции равна отрезку нижнего основания, соединяющему вершину основания с снованием проведенной к ней высоты.
- То есть
- 5) Теорема с сдвиге диагонали в трапеции
- Теорема: Если в трапеции через вершину В, как показано на рисунке слева , провести отрезок параллельный одной из диагоналей, то окажутся верными следующие факты:
- трапеция — равнобедренная равнобедренный
- 6) Четыре замечательные точки в трапеции
- Теорема: В любой трапеции точка пересечения диагоналей, точка пеерсечения продолжений боковых сторон и середины оснований лежат на одной прямой.
- То есть точки M, N, K и P лежат на одной прямой
Комментарий репетитора по математкие: Знаний этих свойств по четырехугольникам вполне достаточно для решения задачи С4 на ЕГЭ, то есть ничего сверх этих фактов по четырехугольникам абитуриент знать не обязан.
Однако сильным ученикам для решения сложных задач части С или олимпиадных геометрических задач, а также для качественной подготовки к экзамену по математике в МГУ необходимо расширить список.
Я бы не советовал репетиторам ограничиваться только задачами на применение этих свойств, так как составителями ЕГЭ по математике закладывается проверка сразу нескольких навыков работы с теорией.
В течении всего времени подготовки к ЕГЭ репетитору по математкие необходимо отбирать тренировочные задачи на одновременное использование этих свойств с другими планиметрическими фактами внутри одной задачи, ибо на экзамене может встретиться многоходовая комбинация.
Колпаков Александр Николаевич. Репетитор по математике.
Источник: https://ankolpakov.ru/2010/10/11/chetyrexugolniki-osnovnye-teoremy-formuly-i-svojstva-virtualnyj-spravochnik-repetitra-po-matematike/
Виды четырехугольников
Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

Свойство. В параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство. Диагонали параллелограмма точкой пересечения делятся пополам.

1 признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2 признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
3 признак параллелограмма. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Трапеция
Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны называются основаниями.

Трапеция называется равнобедренной (равнобочной), если ее боковые стороны равны. В равнобедренной трапеции углы при основаниях равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Средняя линия параллельна основаниям и равна их полусумме.

Прямоугольник
Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойство. Диагонали прямоугольника равны.
Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Ромб
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
Свойство. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Квадрат
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Квадрат есть частный вид прямоугольника, а также частный вид ромба. Поэтому он имеет все их свойства.
Свойства: 1. Все углы квадрата прямые
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Источник: http://fizmat.by/math/chetyrehugoln/vidy
Документ без названия
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки.
Различают выпуклые и невыпуклые и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла.
Четырехугольник, у которого угол больше развернутого называется невыпуклым
- Виды четырёхугольников
- Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны; Прямоугольник — четырёхугольник, у которого все углы прямые; Ромб — четырёхугольник, у которого все стороны равны; Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны; Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
- (Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)
- Свойства
- Сумма углов четырёхугольника равна 2 π = 360°.
- Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
- Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
- Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
- Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
- Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
- Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
Теорема Вариньона Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника. или сокращённо
Середины сторон произвольного четырёхугольника — вершины параллелограмма
Доказательство
Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников и . По теореме о средней линии, отрезки будут параллельны диагонали, а, значит, и друг другу. Повторив аналогичные рассуждения для диагонали BD, получаем, что противоположные стороны четырёхугольника EFGH параллельны, и, по определению, это — параллелограм.
Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ проходит внутри четырёхугольника. Тогда площадь треугольника равна , где — высота треугольника , проведённая из вершины . Аналогично, площадь треугольника равна . Тогда площадь всего четырёхугольника равна ![]() . Но
. Но ![]() — это сумма расстояний до прямой от точек и , то есть в точности высота параллелограмма . А поскольку сторона параллелограмма вдвое меньше , то и площадь параллелограмма равна половине площади ,
— это сумма расстояний до прямой от точек и , то есть в точности высота параллелограмма . А поскольку сторона параллелограмма вдвое меньше , то и площадь параллелограмма равна половине площади ,
- Теорема Эйлера
- в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями

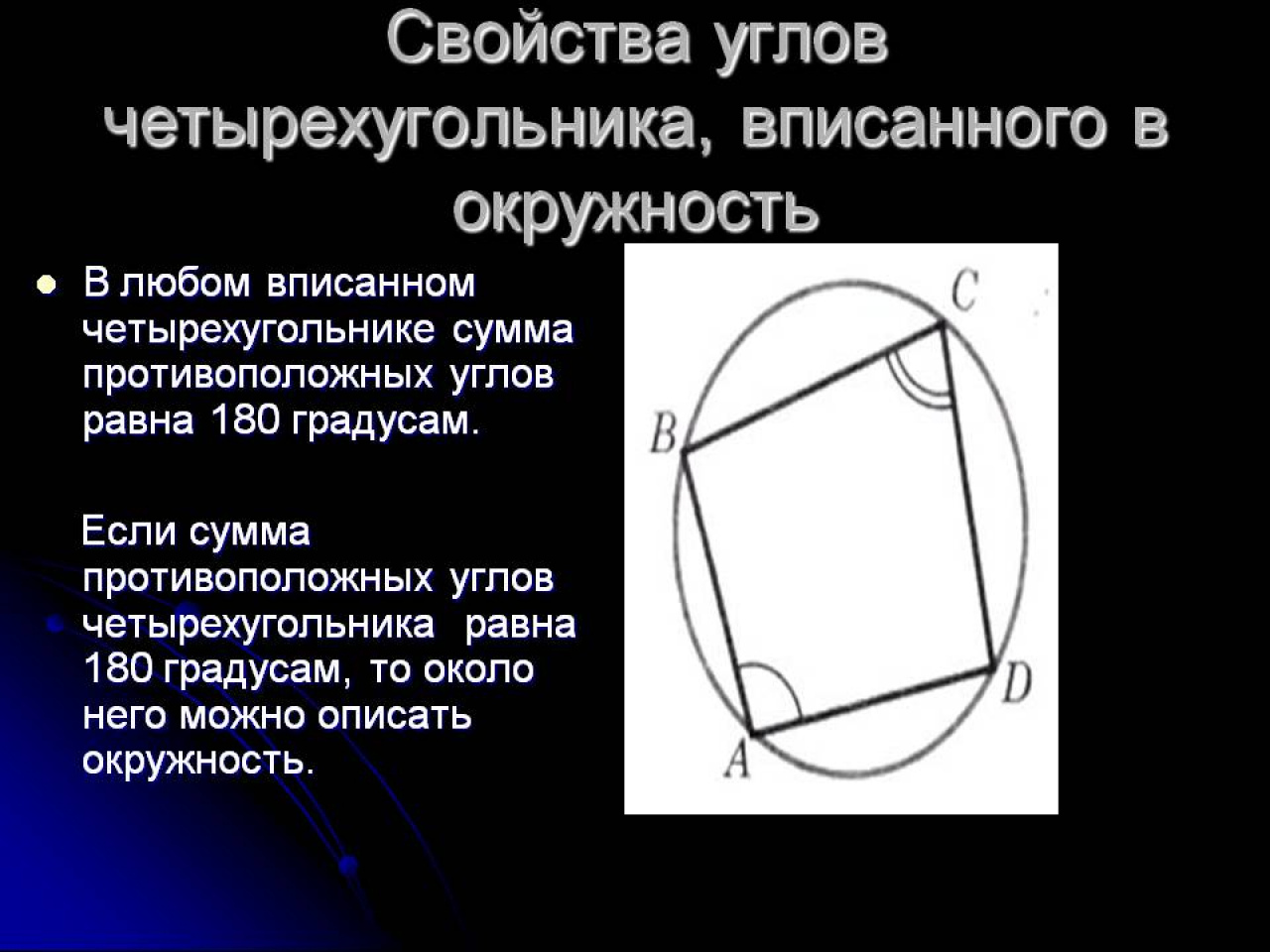 Следствие: Сумма квадратов длин равна диагоналей параллелограмма равна сумме квадратов длин его сторон
Следствие: Сумма квадратов длин равна диагоналей параллелограмма равна сумме квадратов длин его сторон - Теорема Птолемея Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC
-


- Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)
Если a, b, c, d – длины сторон четырёхугольника, – его полупериметр, а α – сумма его противоположных углов, то площадь Sчетырёхугольника равна . В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид: ; это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: . 
Источник: http://www.ra-scorpion.narod.ru/geometry/10/index.html
Четырехугольники, вписанные в окружность. Теорема Птолемея
| Справочник по математике | Геометрия (Планиметрия) | Четырехугольники |
| Вписанные четырехугольники и их свойства |
| Теорема Птолемея |
Определение 1. Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником.

Рис.1
Теорема 1. Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Доказательство. Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC.
Угол ADC является вписанным углом, опирающимся на дугу ABC. Поэтому величина угла ADC равна половине угловой величины дуги ABC.
Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180°.
Если рассмотреть углы BCD и BAD, то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A, B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Рис.2
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E, и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180°.
При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC.
Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC, не смежного с ним.
- Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
- Теорема 2 доказана.
- Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство |
| Окружность, описанная около параллелограмма |  |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба | 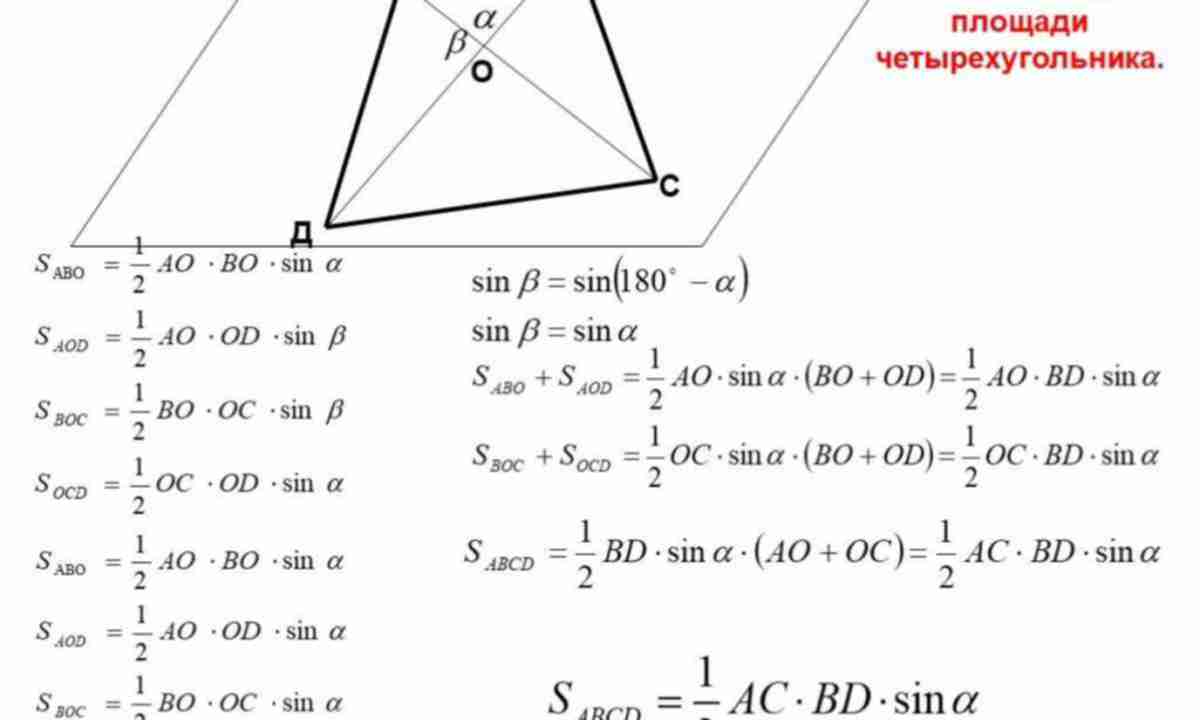 |
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции |  |
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |  |
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник | Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:где a, b, c, d – длины сторон четырёхугольника,а p – полупериметр, т.е. |
| Окружность, описанная около параллелограмма |
| Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба |
| Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции |
| Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |
| Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник |
| Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:где a, b, c, d – длины сторон четырёхугольника,а p – полупериметр, т.е. |
| Окружность, описанная около параллелограмма |
| Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба |
| Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции |
| Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |
| Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник |
| Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:где a, b, c, d – длины сторон четырёхугольника,а p – полупериметр, т.е. |
Теорема Птолемея
Теорема Птолемея. Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Доказательство. Рассмотрим произвольный четырёхугольник ABCD, вписанный в окружность (рис.3).
- Рис.3
- Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
Рис.4
Заметим, что треугольник ABD подобен треугольнику BCE. Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
| (1) |
Заметим, что треугольник ABE подобен треугольнику BCD. Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
| (2) |
Складывая равенства (1) и (2), получаем:
Теорема Птолемея доказана.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник: https://www.resolventa.ru/spr/planimetry/ofcircle.htm
Четырёхугольник
- Главная
- Справочник
- Геометрия
- Фигуры
- Четырёхугольник
Сегодня рассмотрим геометрическую фигуру — четырехугольник. Из названия этой фигуры уже становится понятно, что у этой фигуры есть четыре угла. А вот остальные характеристики и свойства этой фигуры мы рассмотрим ниже.
Что такое четырех угольник
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Площадь четырехугольника равна полупроизведению его диагоналей и угла между ними.
Четырехугольник — это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.
Четырехугольник — это геометрическая фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, последовательно соединенная отрезками.
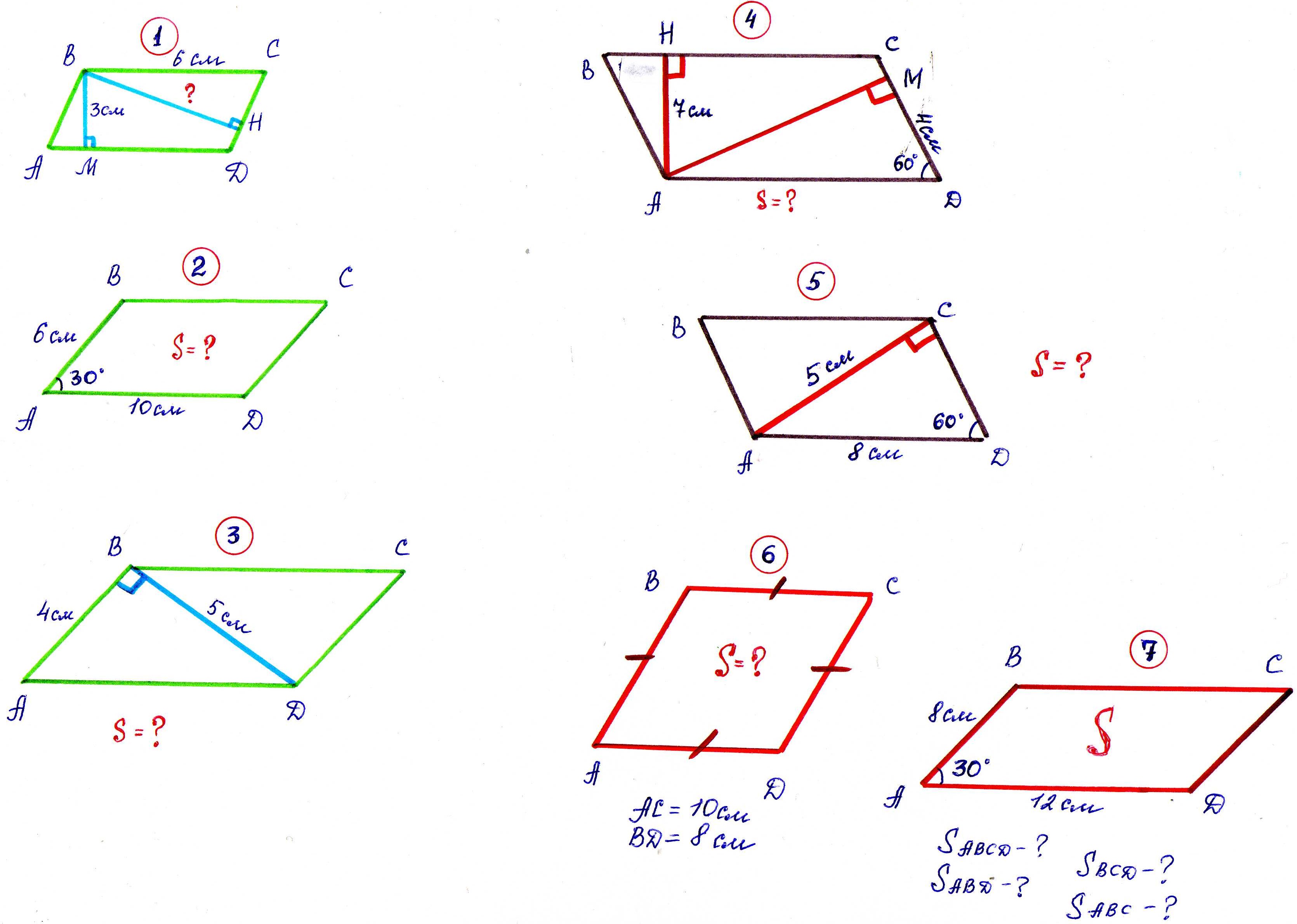
Виды четырехугольников
- Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
- Четырехугольник, у которого две противоположные стороны параллельны, а две другие − нет, называется трапецией.
- Четырехугольник, у которого все углы прямые, является прямоугольником.
- Четырехугольник, у которого все стороны равны, является ромбом.
- Четырехугольник, у которого все стороны равны и все углы прямые, называется квадратом.
Четырехугольник может быть:
Самопересекающимся

Невыпуклым

Выпуклым
- Самопересекающийся четырехугольник — это четырехугольник, у которого любые из его сторон имеют точку пересечения (на рисунке синим цветом).
- Невыпуклый четырехугольник — это четырехугольник, в котором один из внутренних углов более 180 градусов (на рисунке обозначен оранжевым цветом).
- Сумма углов любого четырехугольника, который не является самоперсекающимся всегда равна 360 градусов.
Особые виды четырехугольников
Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:
- Параллелограмм
- Ромб
- Прямоугольник
- Квадрат
- Трапеция
- Дельтоид
- Контрпараллелограмм
Четырехугольник и окружность
- Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).
- Главное свойство описанного четырехугольника:
- Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.
- Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)
- Главное свойство вписанного четырехугольника:
- Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.
Свойства длин сторон четырехугольника
- Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.
- |a — b| ≤ c + d
- |a — c| ≤ b + d
- |a — d| ≤ b + c
- |b — c| ≤ a + d
- |b — d| ≤ a + b
- |c — d| ≤ a + b
Важно.
Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.
- В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны.
- a ≤ b + c + d
- b ≤ a + c + d
- c ≤ a + b + d
- d ≤ a + b + c
Важно. При решении задач в пределах школьной программы можно использовать строгое неравенство (
Источник: https://calcsbox.com/post/cetyrehugolnik.html
Самая удобная и увлекательная подготовка к ЕГЭ
1. В параллелограмме противоположные стороны и углы попарно равны.
2. Диагональ делит параллелограмм на два равных треугольника.
3. Диагонали точкой пересечения делятся пополам.
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
5. Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
6. В параллелограмме биссектрисы углов, прилежащих к одной стороне (соседних углов), пересекаются под углом в $90°$.
- Пример:
- Определите синус острого угла параллелограмма, если его большая высота равна $7$, а стороны $10$ и $14$.
- Решение:
- Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
- $S=a·b·sinα$, из этой формулы можем выразить синус угла.
- $sinα={S}/{a·b}$
Стороны параллелограмма нам известны, осталось вычислить площадь. Площадь параллелограмма можно вычислить как произведение высоты на основание. Нам известна большая высота параллелограмма, а большая высота опускается к меньшей стороне параллелограмма, следовательно, $S=7·10=70$.
- Подставим все известные данные в формулу синуса:
- $sinα={S}/{a·b}={70}/{14·10}=0.5$
- Ответ: $0.5$
Прямоугольник — это параллелограмм, у которого все углы прямые.
- Площадь прямоугольника равна половине произведения смежных (соседних) сторон.
- $S=a·b$, где $а$ и $b$ — смежные стороны.
- Ромб — это параллелограмм, у которого все стороны равны.
Свойства ромба:
- Все свойства параллелограмма.
- Диагонали ромба пересекаются под прямым углом. $BD⊥AC$.
- Диагонали ромба являются биссектрисами углов.
Площадь ромба:
- Площадь ромба равна половине произведения его диагоналей. $S={d_1·d_2}/2$, где $d_1$ и $d_2$ — диагонали ромба
- Площадь ромба равна произведению квадрата стороны на синус острого угла ромба. $S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Все свойства прямоугольника.
- Все свойства ромба.
Площадь квадрата:
- $S=a^2$, где $а$ — сторона квадрата.
- $S={d^2}/{2}$, где $d$ — диагональ квадрата.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие нет.
- Параллельные стороны называются основаниями: $ВС$ и $AD$ — основания.
- Непараллельные стороны называются боковыми сторонами: $АВ$ и $CD$ – боковые стороны.
- Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
- Свойства средней линии трапеции:
1. Средняя линия параллельна основаниям трапеции.
$MN││BC; MN││AD.$
2. Средняя линия равна полусумме оснований.
$MN={BC+AD}/{2}$
3. Диагональ делит среднюю линию на две части, каждая из которых является средней линией получившихся треугольников.
- $МК$ — средняя линия треугольника $ABD; MK={AD}/{2}$.
- $KN$ — средняя линия треугольника $BCD; KN={BC}/{2}$.
- Трапеция, у которой боковые стороны равны, называется равнобедренной.
Свойства равнобедренной трапеции:
1. Углы при основаниях равны.
$∠А=∠D; ∠B=∠C.$
2. Диагонали в равнобедренной трапеции равны.
$BD=AC.$
3. Основание высоты равнобедренной трапеции, опущенной из меньшего основания, делит другое основание на отрезки, больший из которых равен полусумме оснований.
$АС_1={BC+AD}/{2}.$
4. Основания высот равнобедренной трапеции, опущенных из меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований.
$BC=B_1C_1;$
$AB_1=C_1 D={AD-BC}/{2}.$
5. Если трапеция является равнобедренной, то около неё можно описать окружность.
6. Если в равнобедренной трапеции диагонали пересекаются под прямым углом, то высота рана длине средней линии данной трапеции.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
Около четырехугольника не всегда можно описать окружность. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
- $∠В+∠D=180°$
- $∠A+∠C=180°$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Биссектриса – это линия, которая делит угол пополам.
Свойства биссектрисы:
1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
$AD=DC$
3. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
Теорема Пифагора
- В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
- $AC^2+BC^2=AB^2$
- Соотношение между сторонами и углами в прямоугольном треугольнике:
- В прямоугольном треугольнике $АВС$, с прямым углом $С$
- Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
- Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Теорема косинусов
- Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
- $a^2=b^2+c^2-2·b·c·cosα;$
- $b^2=a^2+c^2-2·a·c·cosβ;$
- $c^2=b^2+a^2-2·b·a·cosγ.$
Источник: https://examer.ru/ege_po_matematike/teoriya/chetirehugolniki
Четырехугольники и их свойства Геометрия. 8 класс Учитель: Еремина В.А. — презентация
1
2 Четырехугольники и их свойства Геометрия. 8 класс Учитель: Еремина В.А.
3 Названия четырехугольников. Параллелограмм Трапеция ПрямоугольникРомбКвадрат
4 Из каких четырехугольников построен домик ? Из каких четырехугольников построен домик ? трапеция прямоугольник параллелограмм ромб квадрат
5 Элементы параллелограмма.
6 противоположные стороны смежные стороны противоположные углы односторонние углы диагонали ABCD O точка пересечения диагоналей отрезки диагонали AC сумма углов (360 0 ) периметр (сумма длин всех сторон) AB и CD — AB и AD — B и D — B и D — A и B — A и B — AC и BD — О -О -О -О — AO и OC — A + B + A + B + C + D — C + D — P -P -P -P —
7 Помогите Незнайке исправить двойку. Ребята, я сделал пять ошибок! Помогите их найти ! А я проверю ваши ответы!
8 AC и BD — AO и OC — A + B = A + B = P -P -P -P — A + B + A + B + C + D — C + D — противоположные стороны диагонали диагонали сумма углов (180 0 ) периметр (сумма всех углов) (360 0 ) диагонали отрезки диагонали AC сторон ) ABCD O
9 Незнайка исправил двойку! Спасибо, ребята! Вы молодцы!
10 Определения четырехугольников. Определения четырехугольников.
- 11 Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны Н 4-х У К П С Попарно
- 12 Прямоугольником называется параллелограмм, у которого все углы прямые Н У К В П
- 13 Ромбом называется параллелограмм, у которого все стороны равны Н У К В С
14 Квадратомназываетсяпрямоугольник, у которого у которого все стороны равны. равны. Н У К В С
- 15 Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны Н 4-х У К 2 С А 2 Д Не
- 16 Н 4-х У К П С Попарно Н У К В П Н У К В С = Н Н 4-х У К 2 С А 2 Д Не
- 17 Свойства четырехугольников.
18 ABCD O В параллелограмме : 1. Противоположные стороны равны. П С = 2.Противоположные углы равны. П = 3.Диагонали в точке пересечения делятся пополам. делятся пополам. Д В ·П : П
19 ABCD O В прямоугольнике : П С = П = Д В ·П : П 4.Все углы прямые. 5.Диагонали равны. Д = В П
20 В ромбе: П С = П = Д В ·П : П 3.Все стороны равны. В С = 5.Диагонали взаимно перпендикулярны. перпендикулярны. Д В 6.Диагонали делят углы пополам. пополам. Д : П ABCD O
21 В квадрате: П С = П = Д В ·П : П В П Д = В С = Д В Д : П ABCD O
22 В П П = П С = ДВ ·П:П Д = В С = Д В Д : П
23 Диктант. У каких четырехугольников: 1.Все стороны равны? В С = 2.Диагонали в точке пересечения делятся пересечения делятся пополам? пополам? ДВ ·П:П 3. Противоположные стороны равны? стороны равны? П С =
24 4.Противоположные углы равны? углы равны? П = 5.Все углы прямые? В П 6.Диагонали взаимно перпендикулярны? перпендикулярны? Д В 7.Диагонали равны? Д = 8.Диагонали делят углы пополам? пополам? Д : П
- 25 Проверка результатов диктанта в парах. Критерии оценок: без ошибок «5» 1-2 ошибки «4» 3-4 ошибки «3» > 4 ошибок «2»
- 26 В С = ДВ ·П:П П С = П = В П Д В Д = Д : П
- 27 Игра «Конструктор»
- 28 Сложите из треугольников прямо- угольник, параллелограмм, ромб, трапецию.
- 29 Исторические сведения О происхождении геометрических терминов.
30 Термин параллелограмм греческого происхождения, был введен Евклидом. В «Началах» Евклида доказана теорема: «в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам». Термин диагональ происходит от сочетания двух греческих слов « диа » (через) и « гониос » (угол), т.е. прямая, проходящая через вершины углов.
31 Слово ромб тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу. Слово квадрат в переводе с греческого «тетрагон» — четырехугольник. Трапеция греческое слово, означавшее в древности столик.
32 Спасибо за урок!
Источник: http://www.myshared.ru/slide/603473/
Четырёхугольник — это… Что такое Четырёхугольник?
| ┌─────────────┼────────────┐ | ||
| невыпуклый | выпуклый | самопересекающийся |
| ┌─────────────┼─────────────┐ | ||
| Вписанный | трапеция | описанный |
| | ┌───────────┤ | | | |
| равнобедренная трапеция равнобокая |
параллелограмм стороны параллельны |
выпуклый ромбоид (дельтоид) диагонали перпендикулярны |
| └─────┬─────┘ | └─────┬─────┘ | |
| прямоугольник прямые углы |
Ромб равнобедренный |
|
| └──────────┬─────────┘ | ||
| квадрат |
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники (см. рис.).
Виды четырёхугольников
- Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
- Прямоугольник — четырёхугольник, у которого все углы прямые;
- Ромб — четырёхугольник, у которого все стороны равны;
- Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
- Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
- Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.
Четырёхсторонник
Хотя такое название может быть эквивалентно четырёхугольнику, в него часто вкладывают дополнительный смысл.
Четвёрка прямых, никакие две из которых не параллельны и никакие три не проходят через одну точку, называется четырёхсторонником.
Такая конфигурация встречается в некоторых утверждениях евклидовой геометрии (например, теорема Менелая, прямая Гаусса, прямая Обера и др.), в которых часто все прямые являются взаимозаменяемыми.
Свойства
- Сумма углов четырёхугольника равна 2 π = 360°.
- Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
- Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
- Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
- Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
- Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
- Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
- См. также свойства центроида четырёхугольника.
- Шесть расстояний между четырьмя произвольными точками плоскости, взятыми попарно, связаны соотношением:
.
Его можно представить ещё в виде:
Площадь
- Площадь произвольного четырёхугольника с диагоналями , и углом между ними (или их продолжениями), равна:
- Площадь произвольного выпуклого четырёхугольника равна:
- , где , — длины диагоналей, a, b, c, d — длины сторон.
- , где p — полупериметр. Из этой формулы для вписанных 4-угольников следует формула Брахмагупты.
Особые случаи
Если 4-угольник и вписан, и описан, то .
История
В древности египтяне и некоторые другие народы использовали в качестве площади четырёхугольника неверную формулу — произведение полусумм его противоположных сторон a, b, c, d[1]: .
См. также
Примечания
- ↑ Г. Г. Цейтен История математики в древности и в средние века, ГТТИ, М-Л, 1932.
Источник: https://dic.academic.ru/dic.nsf/ruwiki/6741




