Свойства параллельных прямых, с примерами

С помощью данного видеоурока вы сможете самостоятельно изучить тему «Свойства параллельных прямых». В ходе него вам предстоит параллельные прямые, рассмотреть их свойства, а также сформулировать одну из самых важных аксиом геометрии.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»

Определение:

Две прямые на плоскости называются параллельными, если они не пересекаются (Рис. 1). Обозначается это так: .

Рис. 1

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной(Рис. 2).

• 
• Рис. 2
• Следствие1:
• Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

1. Рис. 3
2. Дано:.
3. Доказать:.
4. Доказательство:

Будем доказывать от противного. Предположим, что с не пересекает прямую b(Рис. 4). 

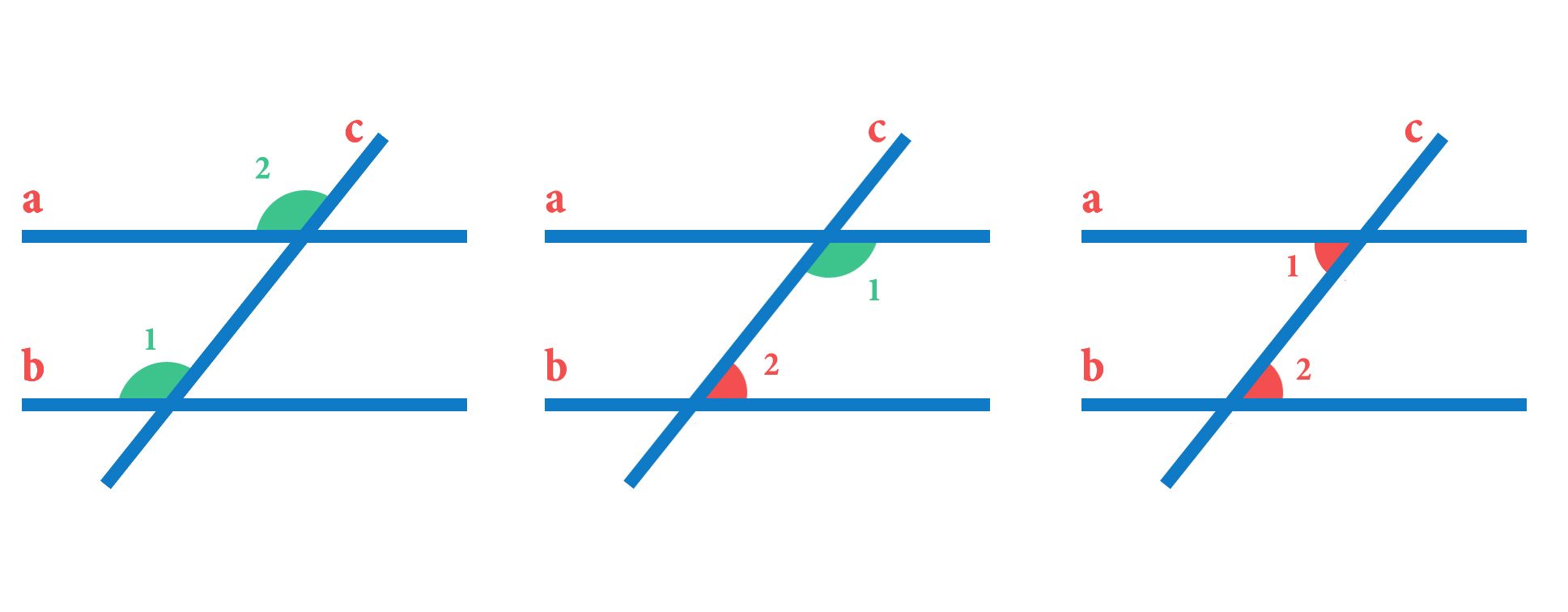
Рис. 4

Тогда:(по условию), (по предположению). То есть через точку М проходят две прямые (а и c), параллельные прямой b. А это противоречит аксиоме. Значит, наше предположение неверное. Тогда прямая c пересечет прямую b.

Следствие 2:

Если две прямые параллельны третьей прямой, то они параллельны(Рис. 5).

• Рис. 5
• Дано:.
• Доказать:.
• Доказательство:

Будем доказывать от противного. Предположим, что прямые a и bпересекаются в некоторой точке М (Рис. 6).

Рис. 6

Таким образом, получаем противоречие с аксиомой: через точку М проходят две прямые, одновременно параллельные третьей прямой.

Следовательно, наше предположение неверно. Тогда .

Теорема 1:

Если две прямые пересечены секущей, то накрест лежащие углы равны(Рис. 7).

1. 
2. Рис. 7
3. Дано:.
4. Доказать:.
5. Доказательство:

Будем доказывать от противного. Предположим, что: .

Тогда от луча MNможно отложить единственный угол ∠PMN, который будет равен ∠2 (Рис. 7).

Но тогда ∠PMNи ∠2 – накрест лежащие и равны. Тогда прямые PMи b–  параллельны.

Тогда через точку М проходят две прямые, параллельные третьей. А именно:

Получаем противоречие с аксиомой. Значит, наше предположение неверно. То есть: .

• Следствие:
• Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй.
• 
• Рис. 8
• Дано:
• Доказать:
• Доказательство:

1.      с пересекает а, а значит, и пересекает параллельную ей прямую, то есть b. Тогда с – секущая по отношению к а и b.

2.      поскольку они являются накрест лежащими. Тогда . То есть.

1. Теорема 2:
2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
3. Рис. 9
4. Дано: – секущая.

Доказать: (Рис. 9).

Доказательство:

Если , то из предыдущей теоремы следует, что накрест лежащие углы равны. То есть .

• Тогда, по свойству вертикальных углов, .
• Значит, , что и требовалось доказать.
• Теорема 3:
• Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
• Рис. 10
• Дано: – секущая.
• Доказать:.
• Доказательство:

Из того, что , вытекает, что ∠1 = ∠3, в силу предыдущей теоремы. Но по свойству смежных углов. Тогда , что и требовалось доказать.

Список рекомендованной литературы

1. Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. – М.: Просвещение.
3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

Рекомендованные ссылки на интернет-ресурсы

1. Свойства углов. Свойства параллельных прямых (Источник).
2. Свойства параллельных прямых (Источник).
3. Признаки параллельности двух прямых (Источник).

Рекомендованное домашнее задание

1. На стороне угла АВС взята точка А. Через нее проведена прямая, параллельная ВС. Найдите меры углов при вершине А, если .
2. Докажите, что если одна секущая с двумя прямыми образует равные соответственные углы, то и любая другая секущая будет образовывать с ними равные соответственные углы.
3. Если прямые образуют с секущей неравные соответственные углы, то они пересекаются. Докажите это.

Источник: https://interneturok.ru/lesson/geometry/7-klass/parallelnye-pryamye/svoystva-parallelnyh-pryamyh

Параллельные прямые — YouClever.org

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Параллельные прямые…Прежде всего: что это такое?

Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали.

Вот, как рельсы

Принято обозначение:

– читается как   параллельна  .

Самым важным фактом, который нужно принять без доказательства (не только тебе, но и любому математику) для того, чтобы вся геометрия не развалилась и не превратилась в какую-то неузнаваемую теорию, является так называемая «аксиома параллельных прямых».

Часто ее еще называют «пятый постулат Евклида». Формулируем:

Аксиома параллельных прямых

Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.

Смотри: через любую точку   проходит только одна прямая  , которая параллельна  , все остальные будут пересекать прямую  .

Казалось бы: чего проще – ну , одна так одна… Но ты себе просто не представляешь, сколько споров вели математики на протяжении прямо-таки тысячелетий, прежде чем осознали истинную роль этой аксиомы о параллельных прямых. В конце концов , уже в 19-м веке, после открытий Лобачевского, Гаусса и других ученых стало ясно, что можно построить и другие виды геометрии, в которых не выполняется аксиома параллельных прямых, в которых ее можно выбросить, но эти геометрии уже оказываются не геометриями плоскости, а геометриями на каких-то хитрых поверхностях.

А наша привычная плоскость оттого и называется евклидовой, что при построении геометрии на ней, при решении всех задачек и доказательстве теорем мы считаем этот многострадальный пятый постулат Евклида выполнимым.

Ну вот, а теперь возникает два вопроса:

1. Если где-то в задаче даны или оказались параллельными две какие-то прямые, то что? Как это использовать?
2. А как вообще узнать, что какие-то прямые параллельны?

• Ответ на первый вопрос называется «свойства параллельных прямых», а ответ на второй вопрос называется «признаки параллельных прямых».
• Но прежде нам понадобится много названий, которые нужно запомнить, как таблицу умножения.
• Итак, ситуация: две прямые пересечены третьей (она называется секущей)

Получается куча углов. Целых   штук.

Приняты такие названия этих углов:

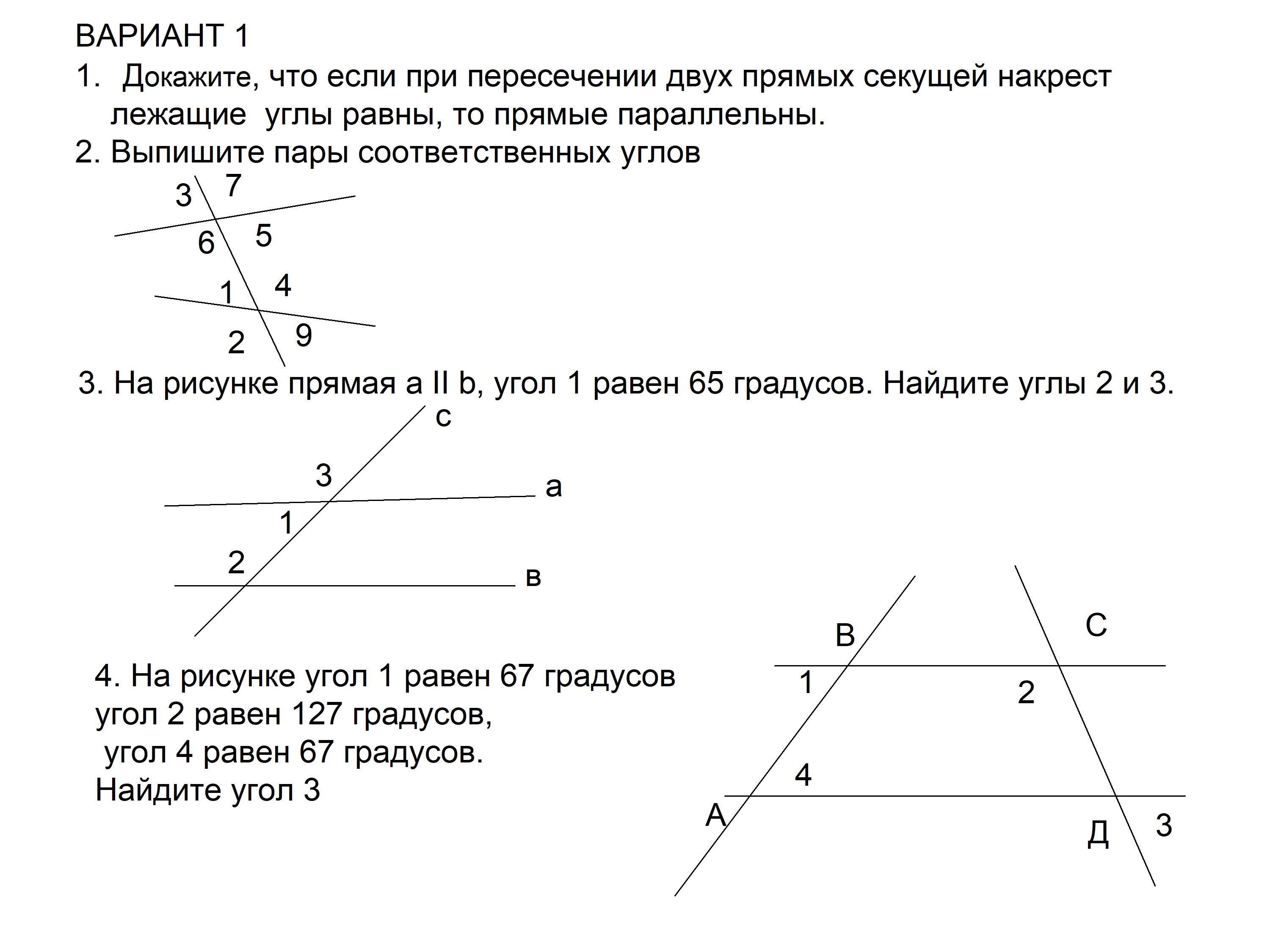и   называются внутренними накрест лежащими углами    и   – тоже внутренние накрест лежащие углы.

Название говорит само за себя:   и  , так же, как и   и   лежат «накрест» — по разные стороны от секущей и «внутри», между прямыми   и  .

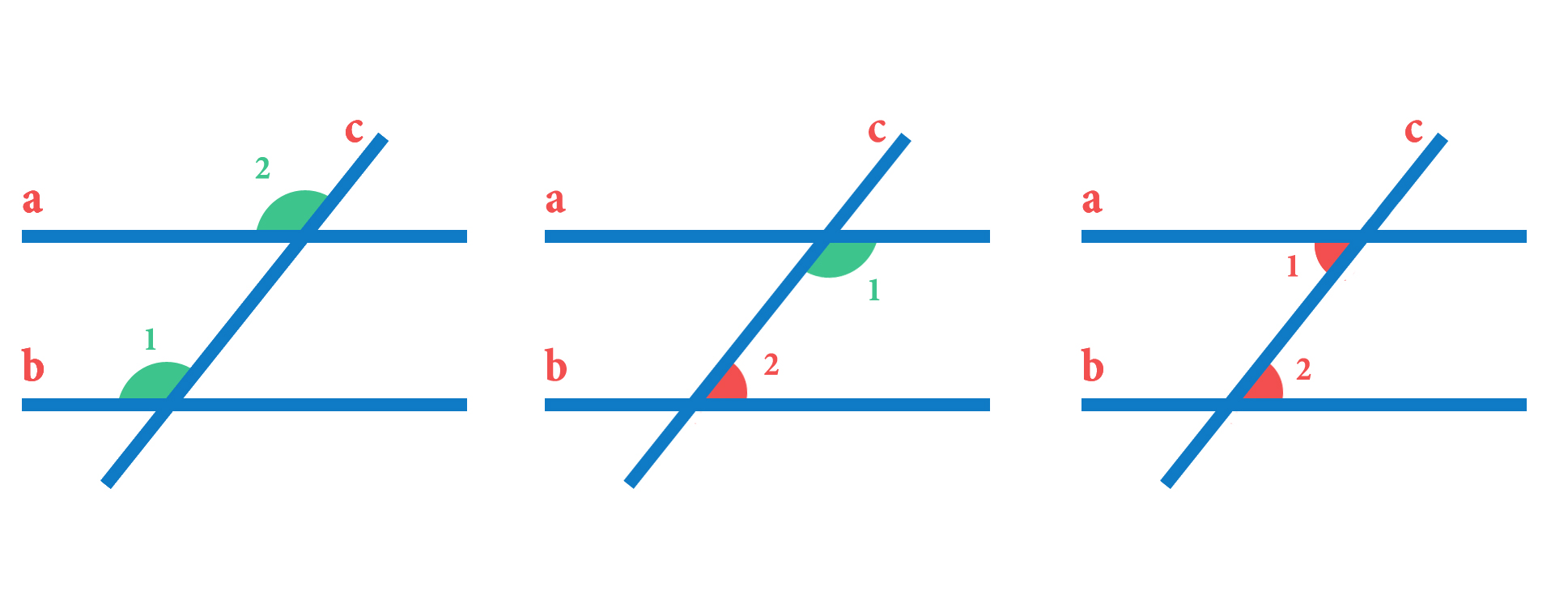и   (а еще   и  ) называются внутренними односторонними углами. Они лежат с одной стороны от секущей и «внутри» между прямыми   и  .

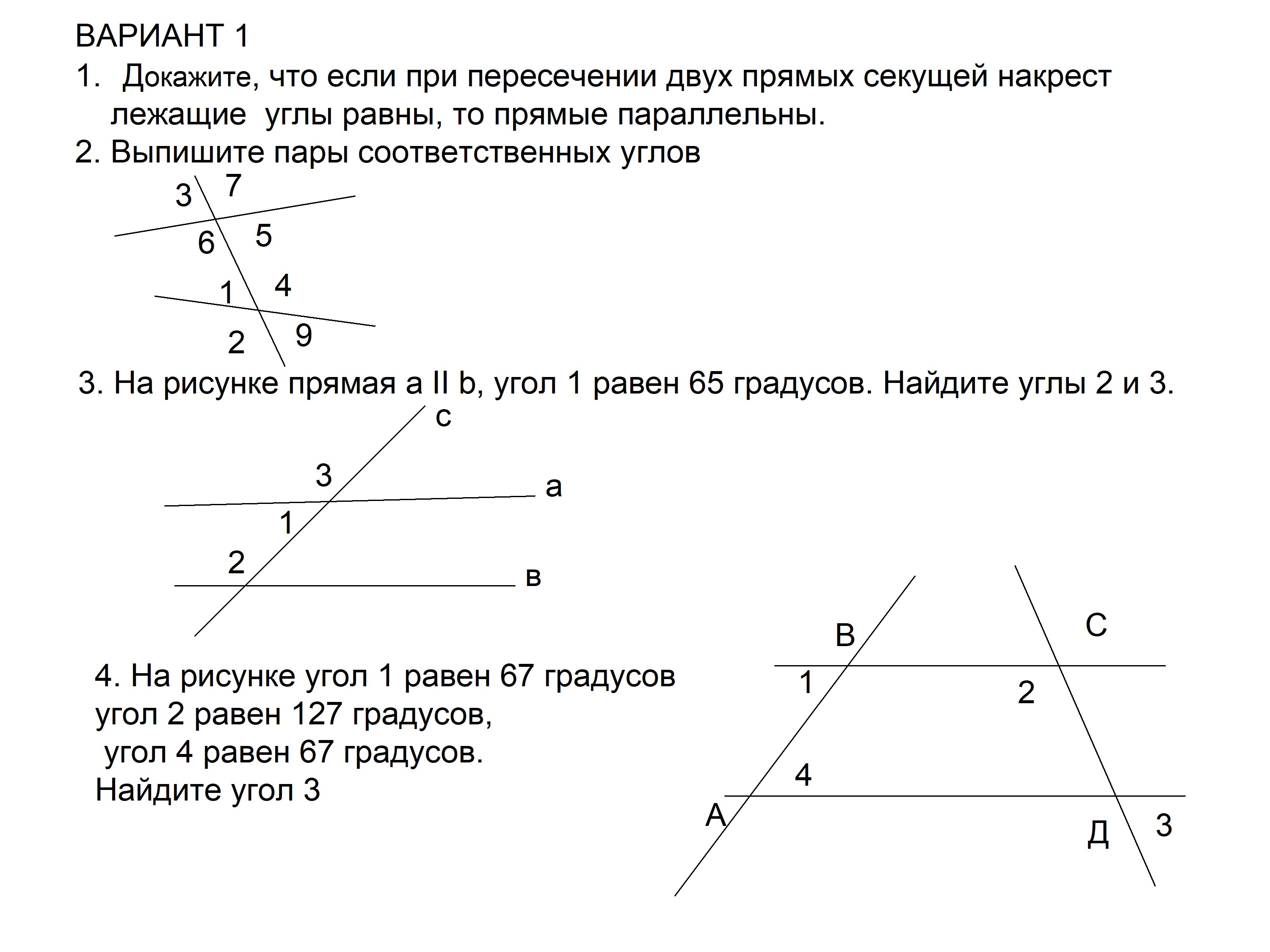и   (а еще   и  ) называются внешними односторонними углами (ты уже догадался, почему?)

И последнее название: соответственные углы.

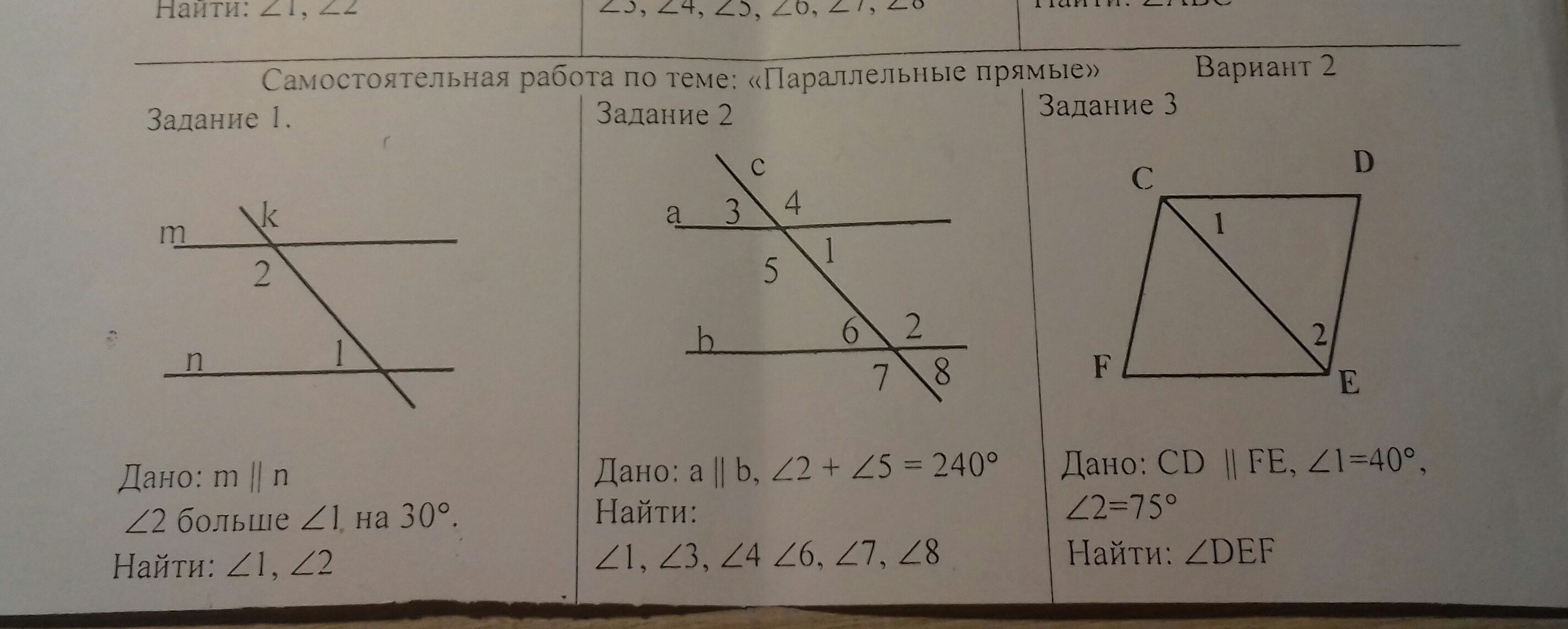Это пары углов:

Обрати внимание,   и   лежат в одинаковых «соответственных» местах около точек   и  . То же можно сказать и об остальных перечисленных парах – посмотри на рисунок.

Свойства параллельных прямых

Напоминаем (а то отвлеклись на названия), что пытаемся ответить на вопрос: если  , то что?

И вот что:

Если две параллельные прямые пересечены третьей (секущей) прямой, то: Внутренние накрест лежащие углы равны Соответственные углы равны Сумма любых двух внутренних односторонних равна

Запомни – все задачи с участием слова «параллельность» решаются с помощью этой теоремы о свойствах параллельных прямых.

А теперь, наоборот, признаки параллельных прямых.

Признаки параллельных прямых

То есть, как бы узнать, что прямые – параллельны?

Если две прямые (  и  ) пересечены третьей и оказалось, что Какие-нибудь два накрест лежащих угла равны ИЛИ Какие нибудь два соответственных угла равны ИЛИ Сумма хоть каких-то двух внутренних односторонних равна   ИЛИ Сумма хоть каких – то двух внешних односторонних равна  , то прямые   и   – параллельны

1. Заметь, что для того, чтобы установить параллельность прямых, достаточно выяснить, скажем, равенство всего двух углов (или накрест лежащих, или соответственных), а уже все остальное окажется , так сказать, бонусом.
2. Смотри-ка, вот схема:

Параллельные прямые. коротко о главном

• Параллельные прямые — это прямые, которые лежат в одной плоскости и не пересекаются, сколько бы их не продолжали:  .
• Секущая — прямая, пересекающая две параллельные прямые:  .
• Аксиома параллельных прямых: через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.

и  ,   и   — внутренние накрест лежащие углы;   и  ,   и   — внутренние односторонние углы;   и  ,   и   — внешние односторонние углы;   и  ,   и  ,   и  ,   и   — соответственные углы.

Свойства параллельных прямых:

Если две параллельные прямые пересечены третьей (секущей) прямой, то:

• внутренние накрест лежащие углы равны:  ,  ;
• соответственные углы равны:  ,  ,  ,  ;
• сумма любых двух внутренних односторонних углов равна  :  ,  ;
• сумма любых двух внешних односторонних углов равна  :  ,  .

Признаки параллельных прямых:

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

1. Стать учеником YouClever,
2. Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц», 
3. А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.

можно кликнув по этой ссылке.

 

Источник: https://youclever.org/book/parallelnye-pryamye-1

Параллельные прямые, признаки и условия параллельности прямых, две прямые параллельны если

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Параллельные прямые: основные сведения

Определение 1

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

Определение 2

Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Чтобы обозначить параллельность прямых, общепринято использовать символ ∥. Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b. Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b, или прямая b параллельна прямой а.

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Аксиома

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Теорема 1

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10-11 классов).

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Определение 3

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

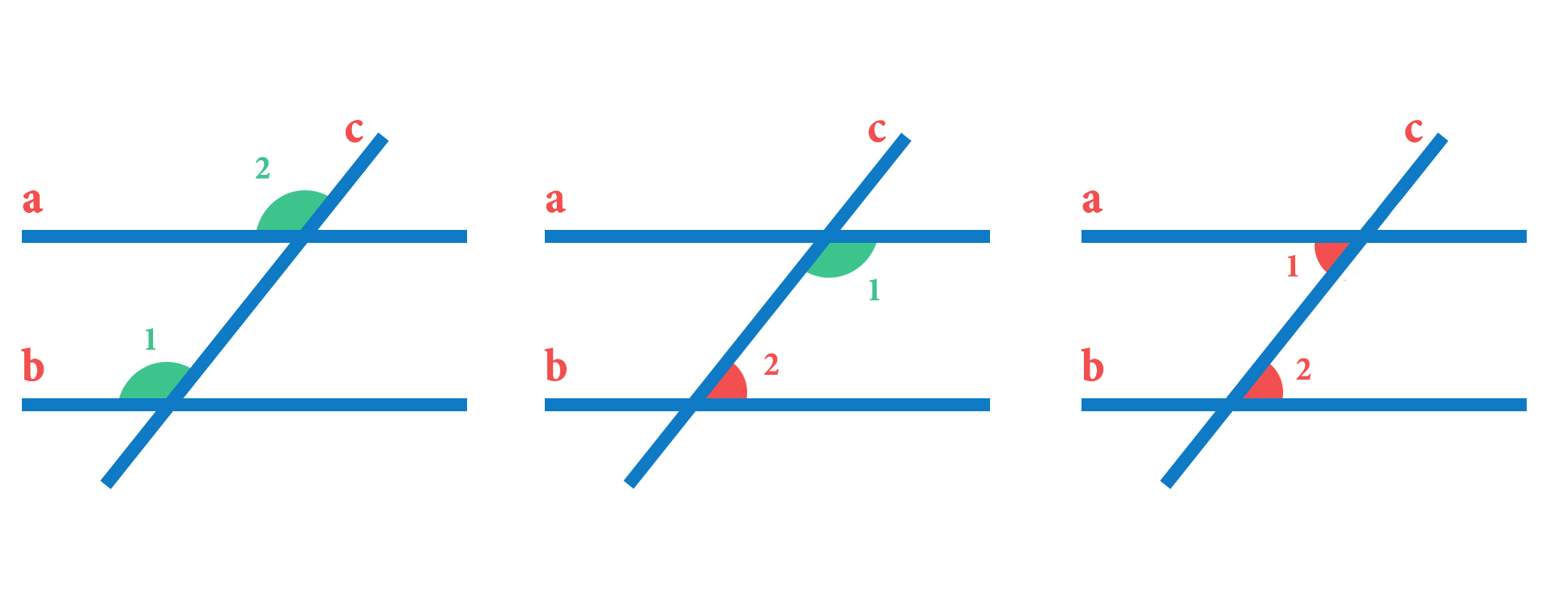
Теорема 2

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

• Доказательство указанных условий присутствует в программе геометрии за 7-9 классы.
• В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
• Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

Теорема 3

На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

Теорема 4

В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

Теорема 5

На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

Теорема 6

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Проиллюстрируем:

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е.

, чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д.

Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Теорема 7

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a→=(ax, ay) и b→=(bx, by) являются направляющими векторами прямых a и b;

и nb→=(nbx, nby) являются нормальными векторами прямых a и b, то указанное выше необходимое и достаточное условие запишем так: a→=t·b→⇔ax=t·bxay=t·by или na→=t·nb→⇔nax=t·nbxnay=t·nby или a→, nb→=0⇔ax·nbx+ay·nby=0, где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.

1. Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A1x+B1y+C1=0; прямая b  — A2x+B2y+C2=0. Тогда нормальные векторы заданных прямых будут иметь координаты (А1, В1) и (А2, В2) соответственно. Условие параллельности запишем так:

A1=t·A2B1=t·B2

1. Прямая a описывается уравнением прямой с угловым коэффициентом вида y=k1x+b1. Прямая b — y=k2x+b2. Тогда нормальные векторы заданных прямых будут иметь координаты (k1, -1) и (k2, -1) соответственно, а условие параллельности запишем так:

k1=t·k2-1=t·(-1)⇔k1=t·k2t=1⇔k1=k2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны.

И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

1. Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x-x1ax=y-y1ay и x-x2bx=y-y2by или параметрическими уравнениями прямой на плоскости: x=x1+λ·axy=y1+λ·ay и x=x2+λ·bxy=y2+λ·by.

1. Тогда направляющие векторы заданных прямых будут: ax, ay и bx, by соответственно, а условие параллельности запишем так:
2. ax=t·bxay=t·by
3. Разберем примеры.

Пример 1

Заданы две прямые: 2x-3y+1=0 и x12+y5=1. Необходимо определить, параллельны ли они.

• Решение
• Запишем уравнение прямой в отрезках в виде общего уравнения:
• x12+y5=1⇔2x+15y-1=0
• Мы видим, что na→=(2, -3) — нормальный вектор прямой 2x-3y+1=0, а nb→=2, 15- нормальный вектор прямой x12+y5=1.

Полученные векторы не являются коллинеарными, т.к. не существует такого значения t, при котором будет верно равенство:

1. 2=t·2-3=t·15⇔t=1-3=t·15⇔t=1-3=15
2. Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
3. Ответ: заданные прямые не параллельны.

Пример 2

Заданы прямые y=2x+1и x1=y-42. Параллельны ли они?

• Решение
• Преобразуем каноническое уравнение прямой x1=y-42 к уравнению прямой с угловым коэффициентом:
• x1=y-42⇔1·(y-4)=2x⇔y=2x+4
• Мы видим, что уравнения прямых y = 2x + 1 и y = 2x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2x + 1, например, (0, 1), координаты этой точки не отвечают уравнению прямой x1=y-42, а значит прямые не совпадают.

1. Следующим шагом определим выполнение условия параллельности заданных прямых.
2. Нормальный вектор прямой y = 2x + 1 это вектор na→=(2, -1), а направляющий вектором второй заданной прямой является b→=(1, 2). Скалярное произведение этих векторов равно нулю:
3. na→, b→=2·1+(-1)·2=0

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Теорема 8

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

Иначе говоря, если a→=(ax, ay, az) и b→=(bx, by, bz)являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t, чтобы выполнялось равенство:

a→=t·b→⇔ax=t·bxay=t·byaz=t·bz

Пример 3

Заданы прямые x1=y-20=z+1-3 и x=2+2λy=1z=-3-6λ. Необходимо доказать параллельность этих прямых.

Решение

Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a→ и b→ заданных прямых имеют координаты: (1, 0, -3) и (2, 0, -6).

• Так как:
• 1=t·20=t·0-3=t·-6⇔t=12, то a→=12·b→.
• Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
• Ответ: параллельность заданных прямых доказана.

Источник: https://Zaochnik.com/spravochnik/matematika/prjamaja-ploskost/parallelnye-prjamye-priznaki-i-uslovija-parallelno/

Свойства параллельных прямых. Аксиома параллельных прямых — урок. Геометрия, 7 класс

Признаки, которые мы рассматривали в первой части теории, и свойства, которые будем рассматривать в этой части, доказываем разными способами.

Признак — это некоторый факт, благодаря которому мы устанавливаем справедливость интересующего нас суждения о некотором объекте.

Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти две прямые параллельны.

Свойство — если мы уверены в справедливости суждения, мы формулируем свойство объекта.

Если две прямые параллельны, то при пересечении их с третьей секущей накрест лежащие углы равны.

Аксиома, в свою очередь — такая истина, которую не надо доказывать. В каждой науке есть свои аксиомы, на справедливости которых строят все дальнейшие суждения и их доказательства.

Аксиома параллельных прямых.

В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.

Иногда эту аксиому называют как одно из свойств параллельных прямых, но на справедливости этой аксиомы строятся многие доказательства в геометрии.

Другие свойства параллельных прямых.

1. Если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.

2. Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.

Эти свойства в отличие от аксиомы нужно доказать.

Докажем 1. Свойство.  

Даны две параллельные прямые (a) и (b). Верно ли, что если прямая (c) параллельна прямой (a), то она параллельна и прямой (b)?

 

Используем противоположное суждение.

Допустим, что возможна ситуация, когда прямая (c) параллельна одной из параллельных прямых — прямой (a) — пересекает другую прямую (b) в некоторой точке (K).

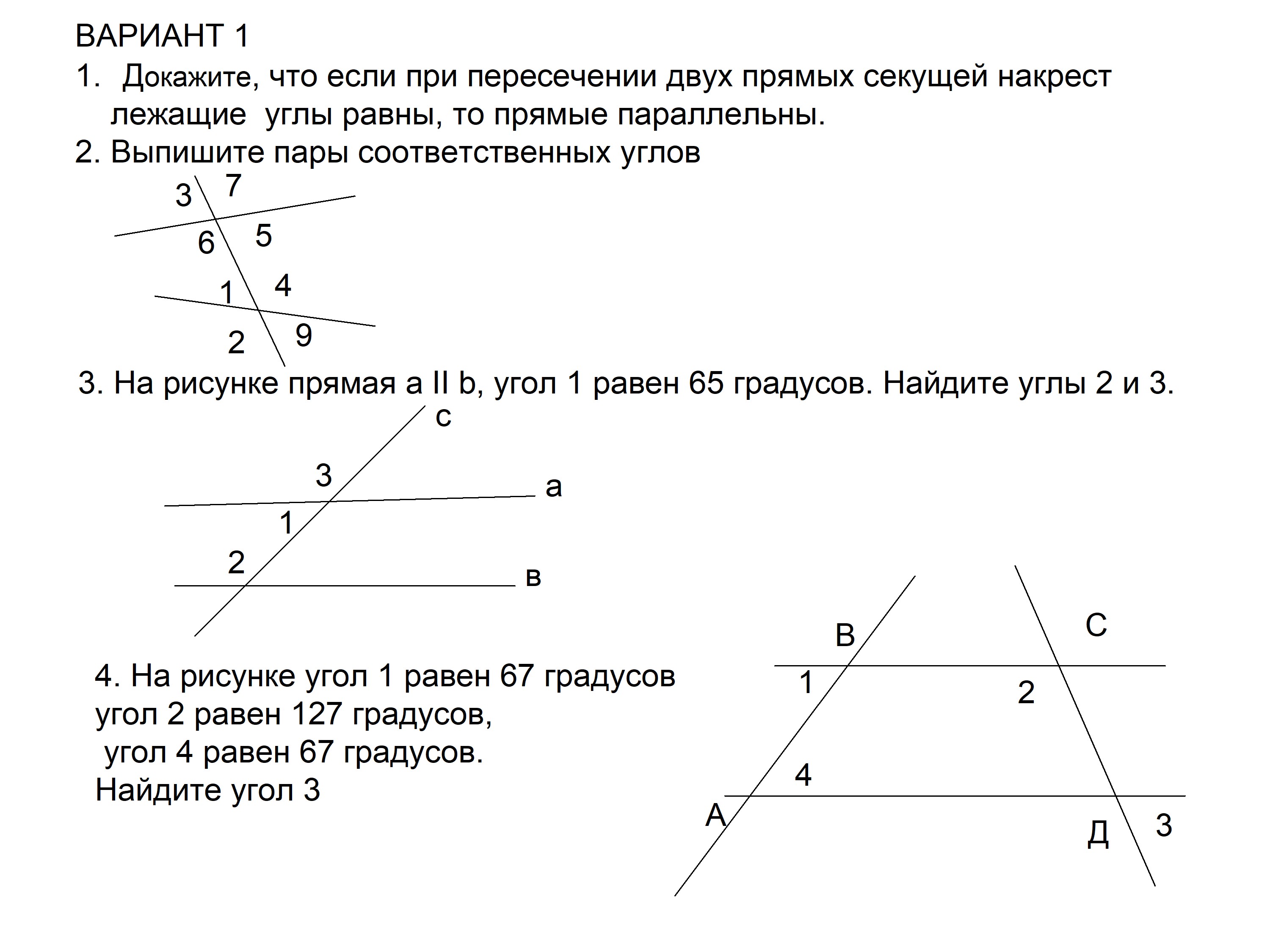
Получается противоречие с аксиомой параллельных прямых. Мы имеем ситуацию, когда через точку проходят две пересекающиеся прямые, которые параллельны одной и той же прямой (a). Такого не может быть, значит, прямые (b) и (c) пересекаться не могут.

Мы доказали, что верно: если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.

Попробуй доказать самостоятельно 2. Свойство.

Если некая прямая (c) пересекает одну из двух параллельных прямых (a), то она пересекает и вторую параллельную прямую (b).

Таким же методом от противоположного суждения попробуй представить, что возможна ситуация, когда прямая пересекает одну из параллельных прямых, но не пересекает другую.

Свойства углов, которые образуются при пересечении двух параллельных прямых с третьей секущей, мы уже назвали в первой части теории.

При пересечении двух параллельных прямых третьей секущей:

• — накрест лежащие углы равны,
• — соответственные углы равны,
• — сумма односторонних углов равна (180°).

Источник: https://www.yaklass.ru/p/geometria/7-klass/parallelnye-priamye-9124/priznaki-parallelnosti-dvukh-priamykh-aksioma-parallelnykh-priamykh-9228/re-4ba7ee5b-3478-495b-b7eb-3e4eeb2d9b4c

Свойства параллельных прямых

Сначала рассмотрим разницу между понятиями признак, свойство и аксиома.

Определение 1

Признаком называют некий факт, по которому можно определить истинность суждения об интересующем объекте.

Пример 1

Прямые являются параллельными, если их секущая образует равные накрест лежащие углы.

Определение 2

Свойство формулируется в том случае, когда есть уверенность в справедливости суждения.

Пример 2

При параллельных прямых их секущая образует равные накрест лежащие углы.

Определение 3

Аксиомой называют такое утверждение, которое не требует доказательства и принимается как истина без него.

Каждая наука имеет аксиомы, на которых строятся последующие суждения и их доказательства.

Аксиома параллельных прямых

Иногда аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.

Теорема 1

Через точку, которая не лежит на заданной прямой, на плоскости можно провести лишь одну прямую, которая будет параллельной заданной.

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

Аксиома доказательства не требует.

Теорема 2

Свойство1. Свойство транзитивности параллельности прямых:

Когда одна из двух параллельных прямых является параллельной третьей, то и вторая прямая будет ей параллельна.

Свойства требуют доказательств.

Доказательство:

Пусть имеются две параллельные прямые $a$ и $b$. Прямая $с$ параллельна прямой $а$. Проверим, будет ли в таком случае прямая $с$ параллельна и прямой $b$.

Для доказательства будем пользоваться противоположным суждением:

Представим, что возможен такой вариант, при котором прямая $c$ параллельна одной из прямых, например, прямой $a$, а другую – прямую $b$ – пересекает в некоторой точке $K$.

Получаем противоречие согласно аксиоме параллельных прямых. Получается ситуация, при которой в одной точке пересекаются две прямые, к тому же параллельные одной и той же прямой $a$. Такая ситуация невозможна, следовательно, прямые $b$ и $c$ пересекаться не могут.

Таким образом, доказано, что если одна из двух параллельных прямых является параллельной третьей прямой, то и вторая прямая параллельна третьей прямой.

Теорема 3

Свойство 2.

Если одна из двух параллельных прямых пересекается третьей, то ею будет пересекаться и вторая прямая.

Доказательство:

Построим доказательство методом от противного.

Представим, что прямая $с$ не пересекает прямую $b$. Тогда через точку $К$ проходят две прямые $а$ и $с$, которые не пересекают прямую $b$, т. е. являются параллельными ей. Но такая ситуация противоречит аксиоме параллельных прямых. Значит, предположение было неверным и прямая $с$ пересечет прямую $b$.

Теорема доказана.

Свойства углов, которые образуют две параллельные прямые и секущая:
накрест лежащие углы равны,
соответственные углы равны,
* сумма односторонних углов равна $180^{circ}$.

Пример 3

Даны две параллельные прямые и третья прямая, перпендикулярная одно из них. Доказать, что эта прямая перпендикулярна и другой из параллельных прямых.

• Доказательство.
• Пусть имеем прямые $а parallel b$ и $с perp а$.
• Поскольку прямая $с$ пересекает прямую $а$, то согласно свойству параллельных прямых она будет пересекать и прямую $b$.
• Секущая $с$, пересекая параллельные прямые $а$ и $b$, образует с ними равные внутренние накрест лежащие углы.

Т.к. $с perp а$, то углы будут по $90^{circ}$.

Следовательно, $с perp b$.

Доказательство завершено.

Источник: https://spravochnick.ru/matematika/parallelnye_pryamye/svoystva_parallelnyh_pryamyh/

Признаки параллельности двух прямых

Рассмотрим две прямые и , которые пересекает в двух точках третья прямая (Рис.1). Прямая называется секущей по отношению к прямым и .

При пересечении прямых и секущей образуется восемь углов, которые обозначены цифрами на Рис.2. 

• Некоторые пары из этих углов имеют специальные названия:
• накрест лежащие углы: 3 и 5, 4 и 6;
• односторонние углы:4 и 5, 3 и 6;
• соответственные углы:1 и 5, 4 и 8, 2 и 6, 3 и 7.

1. Теорема

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Дано: прямые и , АВ — секущая, 1 и 2 — накрест лежащие, 1 = 2 (Рис.3).

1. Доказать: .
2. Доказательство:
3. 1 случай

Предположим, что 1 = 2 = 900, т.е. эти углы прямые, получим АВ и АВ (Рис.4), следовательно, (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны).

2 случай

Предположим, что 1 и2 — не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой и продолжим его до пересечения с прямой , точку пересечения ОН с прямой обозначим Н1 (Рис. 5).

Получим ОНА = ОН1В по 2 признаку равенства треугольников (углы3 и 4 вертикальные, т.к.

получены при пересечении двух прямых АВ и НН1, а вертикальные углы равны друг другу, т.е. 3 = 4, АО = ОВ, т.к.

О — середина АВ, 1 = 2 по условию), следовательно, 5 =6, значит, 6 — прямой, также как и 5 (т.к по построению ОН ).

Получаем, НН1 и НН1, значит  (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны). Что и требовалось доказать.

2. Теорема

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Дано: прямые и , АВ — секущая, 1 и 2 — соответственные, 1 = 2 (Рис.6).

• Доказать: .
• Доказательство:

По условию 1 = 2 и 2 = 3, т.к.они вертикальные, откуда 1 = 3, при этом углы 1 и 3 накрест лежащие, следовательно,  (см. теорему 1). Что и требовалось доказать.

3. Теорема

Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.

Дано: прямые и , АВ — секущая, 1 и 2 — односторонние, 1 + 2 = 1800 (Рис.7).

1. Доказать: .
2. Доказательство:

Углы 3 и 2 — смежные, значит по свойству смежных углов 3 + 2 = 1800, откуда 3 = 1800 — 2, при этом 1 + 2 = 1800, откуда 1 = 1800 — 2, тогда 1 = 3, а углы 1 и 3 накрест лежащие, следовательно, (см. теорему 1). Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

• Параллельные прямые
• Практические способы построения параллельных прямых
• Аксиомы геометрии
• Аксиома параллельных прямых
• Теорема о накрест лежащих углах
• Теорема о соответственных углах
• Теорема об односторонних углах
• Теорема об углах с соответственно параллельными сторонами
• Теорема об углах с соответственно перпендикулярными сторонами
• Параллельные прямые

Правило встречается в следующих упражнениях:

1. 7 класс
2. Задание 189, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
3. Задание 192, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
4. Задание 193, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
5. Задание 211, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
6. Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
7. Задание 233, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8. Задание 297, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
9. Задание 399, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
10. Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
11. Задание 1270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

• © budu5.com, 2020
• Пользовательское соглашение
• Copyright
• Нашли ошибку?
• Связаться с нами

Источник: https://budu5.com/manual/chapter/3387

3 признака параллельности двух прямых на плоскости: доказательство

В этой статье будет предоставлена информация о признаках параллельности прямых на плоскости. Смотрите доказательства параллельности прямых, представленные примеры и рисунки для наглядного пояснения данной темы.

Из учебника по геометрии следует, что параллельными прямыми на плоскости считаются прямые, что не имеют общих точек пересечения. Если же трактовать правило в трехмерном пространстве, то параллельными прямыми считают такие две линии, которые расположены на одной плоскости и, опять-таки, не имеют общих точек.

У параллельности линий есть признаки, аксиомы, свойства. Далее подробней изучим 3 признака параллельности двух прямых на плоскости.

Признаки параллельности двух прямых на плоскости: что такое признаки, аксиомы, свойства?

Сначала рассмотрим, какая разница между понятиями: признак, свойство и аксиома. Это позволит не путаться в дальнейшем, что очень важно для точных наук:

• Признаки – это некие факты, именно по признакам и можно установить истинное ли суждение об интересующих предметах или нет.
• Свойства – это точные формулировки (правила), которые невозможно опровергнуть.
• Аксиома – это должное утверждение, совершенно не требующее доказательств. Именно на аксиомах и строятся, в частности в геометрии, доказательства признаков и свойств.

Что такие термины: аксиома, теорема, следствие

Как видите, понятия имеют отличия друг от друга. Дальше больше изучим 3 признака параллельности двух прямых на плоскости, чтобы доказать признаки, придется применять аксиомы, свойства.

Признаки параллельности двух прямых на плоскости: определение

Из геометрии известно, что существует 3 признака параллельности двух прямых на плоскости. Это изучалось в седьмом классе.

Признаки

Признаки параллельности двух прямых – 7 класс:

1. В первом признаке речь идет о том, что когда две линии перпендикулярны третьей, то они между собой не имеют никаких общих точек пересечения, и они параллельные.
2. Во втором признаке упоминается об углах. Точнее, если две линии пересекает третья, накрест лежащие углы, образовавшиеся в результате пересечения равные, или же соответственные углы равные – линии (||) параллельные.
3. Сумма односторонних углов равная 180º, то эти линии (||) между собой параллельные.

ВАЖНО: Существуют обратные признаки параллельности линий. Они трактуются в обратной очередности. Точнее, две линии считаются параллельными. Об этом будет говориться в последнем пункте.

Первый признак параллельности двух прямых на плоскости — доказательство

Признаки параллельности двух прямых на плоскости очень часто применяются для решения разнообразных геометрических задач, потому нужно не только знать, как его формулировать, а еще уметь и доказать данное утверждение.

Еще раз повторим – первый признак звучит так:

Когда две линии перпендикулярны третьей, то они между собой не имеют общих точек пересечения и параллельны. К данному изречению следует добавить, если линии лежат в одной плоскости, так как в трехмерном пространстве данное утверждение не совсем верно.

Доказательство признака:

Доказать признак можно легко. Для наглядности ниже представлен рисунок:

Чертеж первого признака о параллельности двух линий

• Существует аксиома, что к линии на плоскости можно провести перпендикулярную прямую из заданной точки, что не принадлежит линии, и причем только одну.

Представьте себе, что из одной точки можно провести две линии от другой линии. Но тогда не получится прямых углов, соответственно последнее утверждение не верное, а признак является верным.

Второй признак параллельности двух прямых – доказательство

Все признаки параллельности двух прямых на плоскости не так сложно и запомнить, но вот второй является самым сложным в плане доказательств.

Когда две линии пересекает косая, накрест лежащие углы равные, или же соответственные углы равные, то линии между собой (||) параллельные.

Смотрите изображение далее, здесь подробно описано, какие образуются углы при пересечении линией двух прямых:

Наименования углов

Доказательство:

Пусть дано: ∠ACK=∠KDB (накрест лежащие углы ∠ACK, ∠KDB равны), то линия b||a.

Второй признак параллельности двух линий

• Итак, точки C, D – это точки пересечений двух линий a, b. Вначале на отрезке путем несложных вычислений находим среднюю точку отрезка DC.
• Это будет K, необходимо через середину отрезка (через точку K) провести линию ⊥ к b.
• Углы в вершине с точкой K будут равны друг другу, потому что они вертикальные, а по условию задано, что ∠ACK=∠KDB. Еще и CK=KD. Из этого следует, что треугольники, образовавшиеся в результате пересечения двух линий, равны.
• Угол CAK равен 90º по условию, поскольку линия AB перпендикулярна прямой a. Значит и углы, образованные линией AB с прямыми a, b, равны 90º и треугольники CAK и KBD прямоугольные.
• А по первому признаку перпендикуляр можно провести только к двум параллельным линиям.

Доказательство:

Когда соответственные углы образованные линиями у основания равны, то линия a||b.

• Опять-таки, первое, что следует сделать провести перпендикуляр к линии a.
• Из равенства треугольников CAK и KBD вытекает, что:
• Угол у основания будет равен 90º по условию и соответственный ∠KBD=90º.
• Значит линия BA является перпендикуляром и для линии a, и для прямой b.

Вывод: прямые (||) параллельные.

Третий признак параллельности двух прямых – доказательство

Третье утверждение – когда сумма (∑) односторонних углов равная 180º, значит эти линии (||) параллельны, доказать очень просто.

• Нужно провести перпендикулярную линию к прямой a, углы, образовавшиеся у основания на линии a, будут равны 90º и 90º=180º.
• Углы в вершине с точкой K будут равны друг другу, потому что они вертикальные. Еще и CK=KD по условию. Из этого следует, что треугольники образовавшиеся в результате пересечения двух линий, равны.
• Значит линия BA является перпендикуляром и для линии a, и для линии b.

Признаки параллельности двух линий на одной поверхности

Исходя из рисунка, ∠1 и ∠4 смежные. Как мы уже знаем, сумма смежных углов (∠1+∠4) равна 180º. При этом ∠1=∠2, как накрест лежащие.

Отсюда вывод: сумма односторонних углов равна 180º(∠2+∠4=180º).

Обратные признаки параллельности двух прямых на плоскости

Еще существуют обратные признаки параллельности двух линий на одной плоскости. И их утверждения звучат с точностью до наоборот:

1. Линии считаются (||) параллельными, когда к ним можно провести одну общую перпендикулярную линию.
2. Две линии на одной поверхности параллельные, когда у них накрест лежащие углы между собой равны или же они прямые.
3. Две линии на одной поверхности считаются (||) параллельными, когда соответственные углы у оснований равные.
4. Две линии на одной поверхности (||) параллельные, когда сумма (∑ ) односторонних углов равняется 180º.

Обратные признаки

Далее в видео будут представлены наглядные доказательства признаков параллельности двух линий в одной плоскости.

Ниже предоставлены статьи на тему образования детей в школе, если вам интересно можете обратить внимание на них:

Видео: Признаки параллельности двух прямых

Источник: https://heaclub.ru/3-priznaka-parallelnosti-dvuh-pryamyh-na-ploskosti-dokazatelstvo