Экстремумы функции, максимум и минимум

Содержание

Что будем изучать:

1. Введение.
2. Точки минимума и максимума.
3. Экстремум функции.
4. Как вычислять экстремумы?
5. Примеры.

Введение в экстремумы функций

Ребята, давайте посмотрим на график некоторой функции:

Заметит, что поведение нашей функции y=f (x) во многом определяется двумя точками x1 и x2. Давайте внимательно посмотрим на график функции в этих точках и около них.

До точки x2 функция возрастает, в точке x2 происходит перегиб, и сразу после этой точки функция убывает до точки x1. В точке x1
функция опять перегибается, и после этого — опять возрастает.

Точки x1 и x2 пока так и будем называть точками перегиба. Давайте проведем касательные в этих точках:

Касательные в наших точках параллельны оси абсцисс, а значит, угловой коэффициент касательной равен нулю. Это значит, что и производная нашей функции в этих точках равна нулю.

Посмотрим на график вот такой функции:

Касательные в точках x2 и x1 провести невозможно. Значит, производной в этих точках не существует. Теперь посмотрим опять на наши точки на двух графиках. Точка x2 — это точка, в которой функция достигает наибольшего значения в некоторой области (рядом с точкой x2). Точка x1 — это точка, в
которой функция достигает своего наименьшего значения в некоторой области (рядом с точкой x1).

Точки минимума и максимума

Определение: Точку x= x0 называют точкой минимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≥ f(x0).
Определение: Точку x=x0 называют точкой максимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≤ f(x0).
Ребята, а что такое окрестность?
Определение: Окрестность точки — множество точек, содержащее нашу точку, и близкие к ней.

Окрестность мы можем задавать сами. Например, для точки x=2, мы можем определить окрестность в виде точек 1 и 3.

Вернемся к нашим графикам, посмотрим на точку x2, она больше всех других точек из некоторой окрестности, тогда по определению — это точка максимума. Теперь посмотрим на точку x1, она меньше всех других точек из некоторой окрестности, тогда по определению — это точка минимума.

Ребята, давайте введем обозначения:

ymin — точка минимума,
ymax — точка максимума.

Важно! Ребята, не путайте точки максимума и минимума с наименьшим и наибольшим значение функции. Наименьшее и наибольшее значения ищутся на всей области определения заданной функции, а точки минимума и максимума в некоторой окрестности.

Экстремумы функции

Для точек минимума и максимума есть общей термин – точки экстремума.

Экстремум (лат. extremum – крайний) – максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума.

Соответственно, если достигается минимум – точка экстремума называется точкой минимума, а если максимум – точкой максимума.

Как же искать экстремумы функции?

Давайте вернемся к нашим графикам. В наших точках производная либо обращается в нуль (на первом графике), либо не существует (на втором графике).

Тогда можно сделать важное утверждение: Если функция y= f(x) имеет экстремум в точке x=x0, то в этой точке производная функции либо равна нулю, либо не существует.
Точки, в которых производная равна нулю называются стационарными.
Точки, в которых производной функции не существует, называются критическими.

Как вычислять экстремумы?

Ребята, давайте опять вернемся к первому графику функции:

Анализируя этот график, мы говорили: до точки x2 функция возрастает, в точке x2 происходит перегиб, и после этой точки функция убывает до точки x1. В точке x1 у функции опять перегибается, и после этого
функция опять возрастает.

На основании таких рассуждений, можно сделать вывод, что функция в точках экстремума меняет характер монотонности, а значит и производная функция меняет знак. Вспомним: если функция убывает, то производная меньше либо равно нулю, а если функция возрастает, то производная больше либо равна нулю.

Обобщим полученные знания утверждением:

Теорема: Достаточное условие экстремума: пусть функция y=f(x) непрерывна на некотором промежутке Х и имеет внутри промежутка стационарную или критическую точку x= x0. Тогда:

Если у этой точки существует такая окрестность, в которой при x < x0 выполняется f’(x) < 0, а при x > x0 выполняется f’(x)>0, то точка x0 – точка минимума функции y= f(x).

Если у этой точки существует такая окрестность, в которой при x < x0 выполняется f ’(x)>0, а при x> x0 выполняется f’(x)Если у этой точки существует такая окрестность, в которой и слева и справа от точки x0 знаки производной одинаковы, то в точке x0 экстремума нет.

Для решении задач запомните такие правила: Если знаки производных определены то:

Алгоритм исследования непрерывной функции y= f(x) на монотонность и экстремумы:

Найти производную y’.
Найти стационарные(производная равна нулю) и критические точки (производная не существует).
Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
По указанным выше утверждениям сделать вывод о характере точек экстремума.

Примеры нахождения точки экстремумов

1) Найти точки экстремума функции и определить их характер: y= 7+ 12*x — x3

Решение: Наша функция непрерывна, тогда воспользуемся нашим алгоритмом:
а) y'= 12 — 3×2,
б) y'= 0, при x= ±2,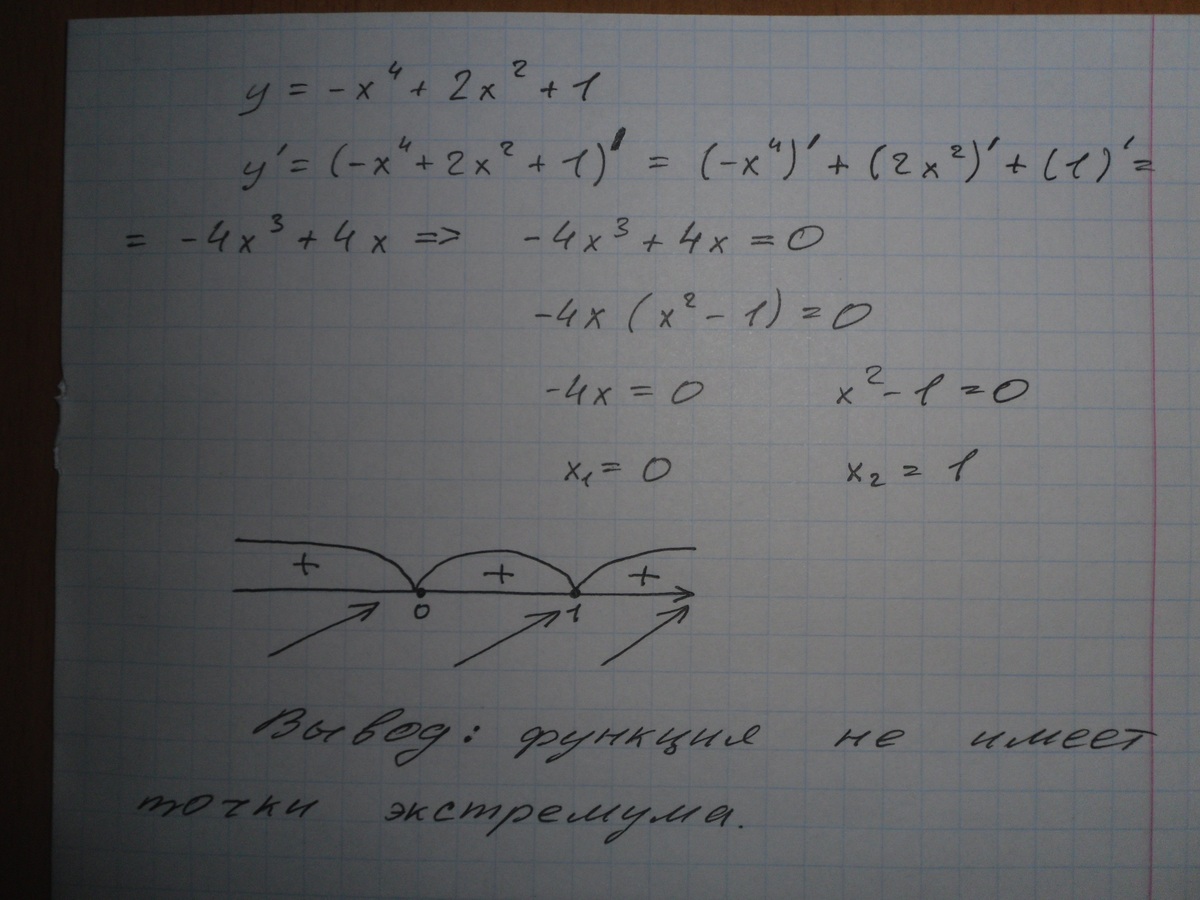
г) посмотрим на наш рисунок, где изображены правила определения экстремумов. Точка x= -2 — точка минимума функции, точка x= 2 — точка максимума функции.
Ответ: x= -2 — точка минимума функции, x= 2 — точка максимума функции.

2) Найти точки экстремума функции и определить их характер.

Решение: Наша функция непрерывна. Воспользуемся нашим алгоритмом:
а)
б) в точке x= 2 производная не существует, т.к. на нуль делить нельзя,

Область определения функции: [2; +∞], в этой точки экстремума нет, т.к. окрестность точки не определена. Найдем значения, в которой производная равна нулю:

в) Отметим стационарные точки на числовой прямой и определим знаки производной:

г) посмотрим на наш рисунок, где изображены правила определения экстремумов. Точка x= 3 — точка минимума функции.
Ответ: x= 3 — точка минимума функции.

3) Найти точки экстремума функции y= x — 2cos(x) и определить их характер, при -π ≤ x ≤ π.
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
4) Найти точки экстремума функции и определить их характер:

Решение: Наша функция непрерывна, воспользуемся нашим алгоритмом:
а) y'= 1 + 2sin(x),
б) найдем значения в которой производная равна нулю: 1 + 2sin(x)= 0, sin(x)= -1/2, т.к. -π ≤ x ≤ π, то: x= -π/6, -5π/6,
Точка x= -5π/6 — точка максимума функции.
Точка x= -π/6 — точка минимума функции.
Ответ: x= -5π/6 — точка максимума функции, x= -π/6 — точка минимума функции.

Решение: Наша функция имеет разрыв только в одной точке x= 0. Воспользуемся алгоритмом:
а)
б) найдем значения в которой производная равна нулю: y'= 0 при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 точка минимума функции.
Точка x= 2 — точка минимума функции. В точке x= 0 функция не существует.
Ответ: x= ±2 — точки минимума функции.

Задачи для самостоятельного решения

а) Найти точки экстремума функции и определить их характер: y= 5×3 — 15x — 5.
б) Найти точки экстремума функции и определить их характер:

в) Найти точки экстремума функции и определить их характер: y= 2sin(x) — x при π ≤ x ≤ 3π.

г) Найти точки экстремума функции и определить их характер:

Источник: https://mathematics-tests.com/algebra-10-klass-urok-ekstremumy-funktsii

Значения функции и точки максимума и минимума

Неопубликованная запись

Наменьшее значение функции
Точки max
Точки min

Как говорил крестный отец: «Ничего личного». Только производные!

Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.

12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.

12 задание бывает двух видов:

Найти точку максимума / минимума (просят найти значения «x»).
Найти наибольшее / наименьшее значение функции (просят найти значения «y»).

Как же действовать в этих случаях?

Найти точку максимума / минимума

Взять производную от предложенной функции.
Приравнять ее к нулю.
Найденный или найденные «х» и будут являться точками минимума или максимума.
Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.

Задания с ЕГЭ:

Найдите точку максимума функции

Приравняем ее к нулю:
Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):

Все верно, сначала функция возрастает, затем убывает — это точка максимума!

Ответ: −15

Найдите точку минимума функции

Преобразуем и возьмем производную:

Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.

Отлично! Сначала функция убывает, затем возрасает — это точка минимума!

Ответ: −2

Найти наибольшее / наименьшее значение функции

Взять производную от предложенной функции.
Приравнять ее к нулю.
Найденный «х» и будет являться точкой минимума или максимума.
Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.

Задания с ЕГЭ:
Найдите наибольшее значение функции на отрезке [−4; −1]

Преобразуем и возьмем производную:
«3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?

Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:

Ответ: −6
Найдите наибольшее значение функции на отрезке [0; 1,5π]

Берем производную:
Находим, чему равняется sin(x):
Но такое невозможно! Sin(x)…
Получается, что уравнение не имеет решения, и в таких ситуациях нужно подставлять крайние значения промежутка в первоначальное уравнение:

Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».

Ответ: 11

Выводы:

70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.

Будь в курсе новых статеек, видео и легкого математического юмора.

Источник: https://ik-study.ru/ege_math/znachieniia_funktsii_i_tochki_max_i_min0

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

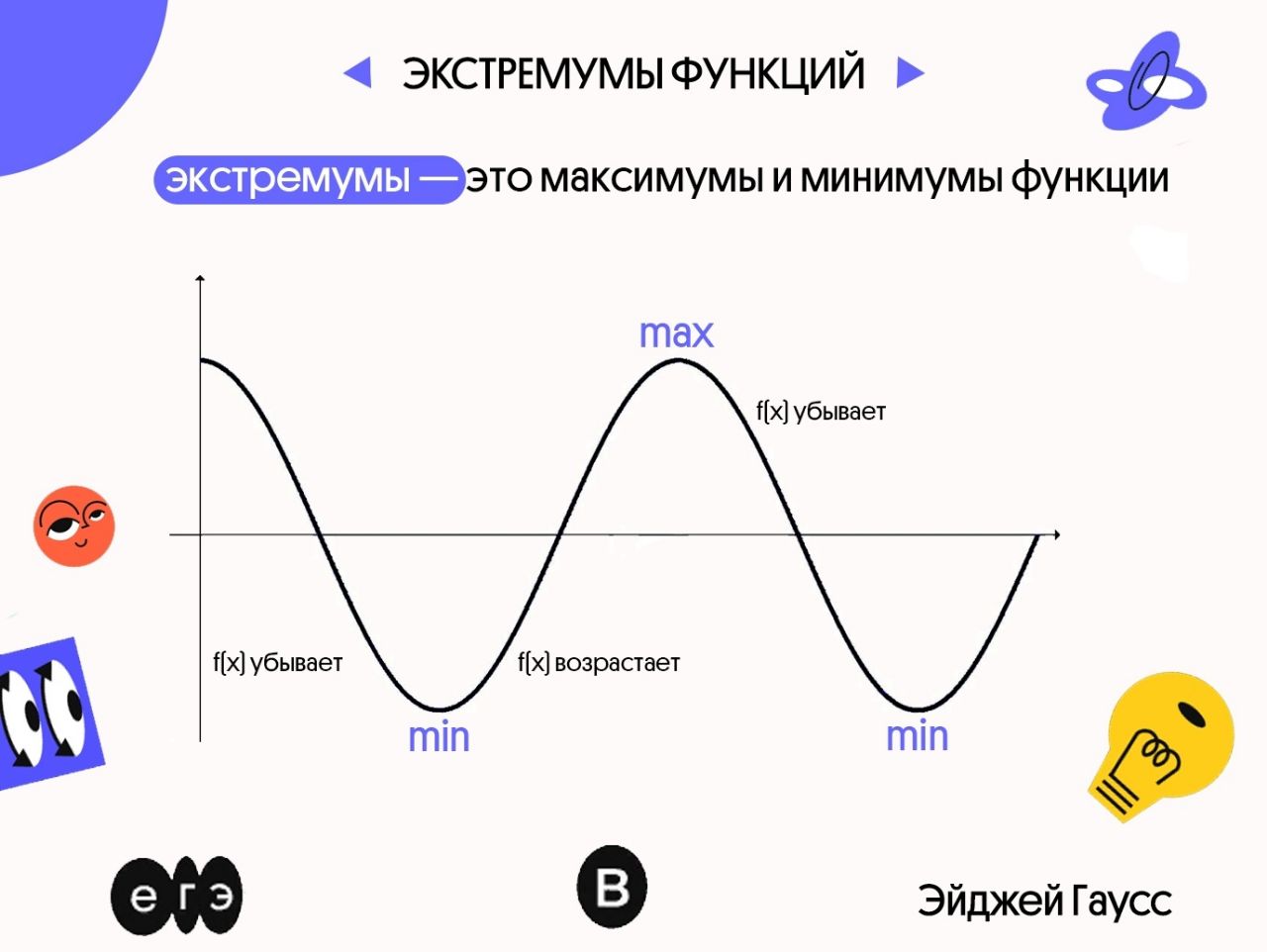
Минимумы и максимумы вместе именуют экстремумами функции

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает. — Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус. — Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Найдите производную функции (f'(x)).
Найдите корни уравнения (f'(x)=0).
Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2: — если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума; — если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54). Решение: 1. Найдем производную функции: (y'=15x^4-60x^2).

2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15) (x^4-4x^2=0) (x^2 (x^2-4)=0) (x=0) (x^2-4=0)
(x=±2)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Источник: http://cos-cos.ru/math/327/

Урок алгебры в 11 классе Максимум и минимум функции

Урок №33. Алгебра и НМА в 11 классе. Дата 06.11.18 г.

Учитель математики Абкелямова З.Н.

Тема урока: Анализ контрольной работы.Максимум и минимум функции.

Цели: изучить понятие максимума и минимума функции;
Составить алгоритм нахождения максимального и минимального значения функции.
Мотивация: на успешность подготовки к ЕГЭ по математике.
Ход урока.
Русский математик XIX века Чебышев говорил , что « особенную важность имеют методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды.»

Подготовка к изучению новой темы.

При исследовании поведения функции вблизи точки удобно пользоваться понятием окрестности.

Окрестностью точки а называется любой интервал , содержащий эту точку.

Определение. Точка х0 называется точкой максимума функции f(х), если существует такая окрестность точки х, что для всех х≠х0 из этой окрестности выполняется неравенство f(x) f(x0).

Пусть график некоторой функции имеет вот такой вид.

а) Если рассмотреть значение функции в точкехна этом графике то оно будет наибольшим (максимальным), чем в любой другой точке из близлежащей окрестности. В этом случае говорят, чтох0 — точка максимума (max).

Точках из области определения функции называется точкой максимума, если длялюбого из окрестноститочки хвыполняется неравенство f(x).

Максимум и минимум функции объединяют словом экстремум( с латинского — крайний), а точки максимума и минимума называют точками экстремума (экстремальными точками)Изучая график можно прийти к выводу, что наиболее «заметными» точками области определения являются какие точки Х, в которых возрастание функции сменяется убыванием (х=-6; х=2; х=7), или, наоборот убывание сменяется возрастанием (х=-7,5; х=-1,5; х=4). Эти точки называются соответственно точками максимума хmax=-6 хmax=2 хmax=7 и минимума хmin=-7,5; хmin=2; хmin=7.

Точку отрезка [а;в], в которой функция достигает наибольшего значения на отрезке называют точкой максимума на отрезке.
Значение функции в этой точке и есть максимум функции на отрезке.
Точку отрезка [а;в], в которой функция достигает наименьшего значения на отрезке называют точкой минимума на отрезке.
Значение функции в этой точке и есть минимум функции на отрезке.
Названия и обозначения максимума и минимума происходит от латинских слов maximum ( наибольшее) minimum ( наименьшее).

На рисунке изображён график непрерывной функции на отрезке [а;в]

2,5 – точка максимума на отрезке [-3;5] .

0– точка минимума на отрезке [-3;5] .

Для точек максимума и минимума принято общее название . Их называют точками экстремума: хmax и хmin.

Значения функции в этих точках называют соответственно максимума и минимума функции уmax, ymin.

Пусть надо найти наибольшее и наименьшее значение функции на отрезке [а;в] и имеющей производную на интервале (а,в). Важную роль при нахождении наибольшего и наименьшего значения функции , при построении графика играют критические точки.

Определение. Внутренние точки области определения , в которых производная равна нулю или не существуют называются критическими точками.

Найти критические точки функции

№5.6 а), в), №5.7 а),в).

№5.6 а) у= 2х3-3х2 [-3;3] .

у ʹ=6х2-6х у ʹ=0 х= 0, х=1- критические точки
в) у=3х4+х3+7 [-3;2]
у ʹ=12х3+3х2 у ʹ=0 х=0, х=-1 –критические точки
№5.7 а) у= [-1;1]
у ʹ= у ʹ=0 х=0 производная не существует, следовательно
х=0 критическая точка
6) В ЕГЭ В11 нахождение наибольшего и наименьшего значения функции.
Алгоритм нахождения точек экстремума

Найти производную функции.
Решить уравнение f ´(х)=0, и найти тем самым стационарные точки или критические точки
Найти критические точки функции на интервале (а,в);
Вычислить значения функции в найденных точках, принадлежащих интервалу (а,в);
Вычислить значения функции на концах отрезка, т.е. в точках х=а, х=в;
Среди всех вычисленных значений функции выбрать наибольшее и наименьшее.

Замечания.

Если функция у=f(x) на [а;в], имеет точку максимума (минимума), то в этой точке функция принимает наибольшее или наименьшее значение.
Если функция у=f(x) на [а;в] не имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение функция принимает на одном конце отрезка, а наименьшее на другом.

Найти наибольшее и наименьшее значение функции f(x)=3х2+4х3+1 на отрезке [-2;1] . (Решает учитель)

fʹʹ(x)=(3х2+4х3+1) ʹ=6х+12х2. Для любого хЄR найдем производную f(x)
fʹʹ(x)=0
6х+12х2=0
Х( 6+12х)=0
Х=0 или 6+12х=0
Х= —
Х=0 и х= — критические точки, принадлежат заданному отрезку.
0Є[-2;1], — Є[-2;1],
Найдем значения функции в заданных точках.
f(0)=1
f(- =1,25
f(-2)=-11
f(1)=8 сравнив значения функций, выбираем наибольшее и наименьшее значение функции на отрезке.
max f(x)= f(1) =8
min f(x)= f(-2)=-11
Ответ : 8,11.
Г) № 5.10 а) в) ( для тех кто работает быстро, за каждый верно выполненный пример ученик получает +, три + «5» в журнал)
№5.11 а)в)

Домашнее задание №5.10 (в,г) 5.14 стр 120.

дополнительное задание.Найти наибольшее значение функции у= 12 cosх+6х-2+6 на отрезке [0;].

Тема урока: Максимум и минимум функции.
Цели: закрепить навык нахождения наибольшего и наименьшего значения функции на отрезке путем решения разнообразных задач.
Ход урока.

Проверка домашнего задания.

№5.6 б) f(х) =5х3-15х на отрезке [-2;2]

f' (х) =15х2 -15 f(х) =0 х=1 х=-1 критические точки
г) у=х4-4х2 на отрезке [-4;4]
у'=4х3 -8х у'=0 х1=0 х2= х=- критические точки
№ 5.7 б) у= на отрезке
У'= у'=0 х=0 производная не существует, следовательно, х=0 критическая точка
г) у= 2 -х на промежутке (0; 2]
У'= у'=0 х=0 производная не существует, следовательно
Х=0 критическая точка.
№ 5.8 б) у=ех-хе на отрезке [-2;2]
У'= ех-х у'=0 ех-е=0
Х=1
г) у= cos2х +х на отрезке [- π; π]
у'= -2sin 2х+1 у'=0 -2sin 2х+1=0
х= (-1)к +к, кЄZ
х= ; π ; Є [- π; π]
№ 5.10 б) у= х3+ 3х на отрезке [-1;2]
У'= 3х2+3 у=0 3х2+3=0
Критических точек нет , значит функция достигает свое наибольшее и наименьшее значение на концах отрезка.
У(-1)=-4
У(2)=14 Г) у= х3- 3х на отрезке [-1;2]
У'=3х2-3 у=0 3х2-3=0
Х=-1 х=1 -1;1 Є [-1;2]
У(-1)=0 у(3)=18 у(1)=-2 у(-2)=-2
Наибольшее значение 18, наименьшее значение -2.

№ 5.11 б) наибольшее значение 3, наименьшее значение -3.

(Два ученика на обратной стороне доски)

Взять производные функций
Cos3х, ех, (х-14)ех-13, ln(2х+3), tg2х
Класс делает в тетрадях и потом проверяем.

Верно ли , что если функция у= f(x) непрерывна на отрезке[а;в] , то существуют точки этого отрезка, в которых функция принимает свое наибольшее и наименьшее значение. (да)
Какую точку отрезка [а;в] называют точкой максимума и минимума функции у= f(x); точкой минимума функции у= f(x).
Как называются значения функции в этих точках?
Какие точки отрезка [а;в] называются критическими точками функции? Как найти эти точки?
Как найти максимум и минимум функции на отрезке?

Работа по графику .
Указать точки максимума и минимума функции.
Назвать максимум и минимум функции на отрезке.

Работа с классом.

Найдите наибольшее значение функции у=-х2 +10х на отрезке [0;7].

( У(0)=0, у(7)=21, у(15)=25)

Найдите наименьшее значение функции у=(х-21)ех-20 на отрезке

[19;21].

У(19)= у(20)=-1 у(21)=0

Найдите наибольшее значение функции у= 7 cosх+7х-на отрезке [0;].

У() =16 у(0)= 7- +9 у(=

Аналогично определяется максимум и минимум функции на интервале и полуинтервале.

-14-

Хmax=-5,5 ymin=4

Хmin- нет, т.к. х=3 не входит в (-5,5;3)

Работа с классом. ( у доски работает ученик)
Найти наибольшее значение функции у= -2х2 на промежутке (-2;2).
Решение.
У`= х3-4х у=0 х=0 х=2 х=-2 критические точки , но х=2 и х=-2 не входят в данный промежуток.

Найдем значение функции у(0)=0, а у= (х2-8) 0 при каждом х, таком , что 0х|, то на интервале (-2;2) функция имеет максимум в точке х=0.

На интервале (-2;2) функция не имеет минимума, так как у= -2х2 -4при каждом х, таком, что |х|2 и -2 не принадлежат (-2;2), следовательно у=0 максимум функции.

Обучающая самостоятельная работа.

найдите наибольшее значение функции у=(х-8)ех-7 на отрезке [6;8].
найдите наибольшее значение функции у=7х-6sinх+8 на отрезке [].

3) найти наименьшее значение функции у=х2-3х+lnх+3 на отрезке [;]

На задания даётся 15 минут. С помощью проектора ученики проверяют решение.

Решение.

у=(х-8)ех-7 на отрезке[6;8].

у'=ех-7(х-7) у'=0 х=7 критическая точка
у(6)= у(7)=-1 у(8)=0
наибольшее значение функции равно 0

у=7х-6sinх+8 на отрезке [].

у'=7- 6cosх у'=0 6cosх=7 х= критических точек нет
у(-=14 у(0)=8
наибольшее значение функции равно 8
3) у=х2-3х+lnх+3 на отрезке [;] ОДЗ: х
у'=2х-3+ у'=0 2х2-3х+1=0
х=1 х= не принадлежит [;]
у(1)=1 у()= ln+3 у()= ln +3
наименьшее значение функции равно1.
Домашнее задание: рассмотреть из открытого банка заданий — 5 функций.

Источник: https://infourok.ru/urok-algebri-v-klasse-maksimum-i-minimum-funkcii-3350394.html

Урок 16. экстремумы функции — Алгебра и начала математического анализа — 11 класс — Российская электронная школа

Алгебра и начала математического анализа, 11 класс

Урок № 16. Экстремумы функции.

Перечень вопросов, рассматриваемых в теме
1) Определение точек максимума и минимума функции
2) Определение точки экстремума функции
3) Условия достаточные для нахождения точек экстремума функции
Глоссарий по теме

Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Максимум функции. Значение функции в точке максимума называют максимумом функции
Минимум функции. Значение функции в точке минимума называют минимумом функции
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).

Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .

Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .

Точки экстремума функции. Точки минимума и максимума называют точками экстремума.

Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Алгоритм исследования функции на монотонность и экстремумы:
1) Найти область определения функции D(f)
2) Найти f' (x).
3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
существует) точки функции y = f(x).
4) Отметить стационарные и критические точки на числовой
прямой и определить знаки производной на получившихся
промежутках.
5) Сделать выводы о монотонности функции и точках ее
экстремума.
Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.

Точку х = х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x0).
Точку х = х0 называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x0).

Точки максимума и минимума – точки экстремума.
Функция может иметь неограниченное количество экстремумов.
Критическая точка – это точка, производная в которой равна или не существует.
Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
Алгоритм нахождения максимума/минимума функции на отрезке:

найти экстремальные точки функции, принадлежащие отрезку,
найти значение функции в экстремальных точках из пункта 1 и в концах отрезка,
выбрать из полученных значений максимальное и минимальное.

Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежуток монотонности функции у=х2 -8х +5
Решение: Найдем производную заданной функции: у’=2x-8
2x-8=0

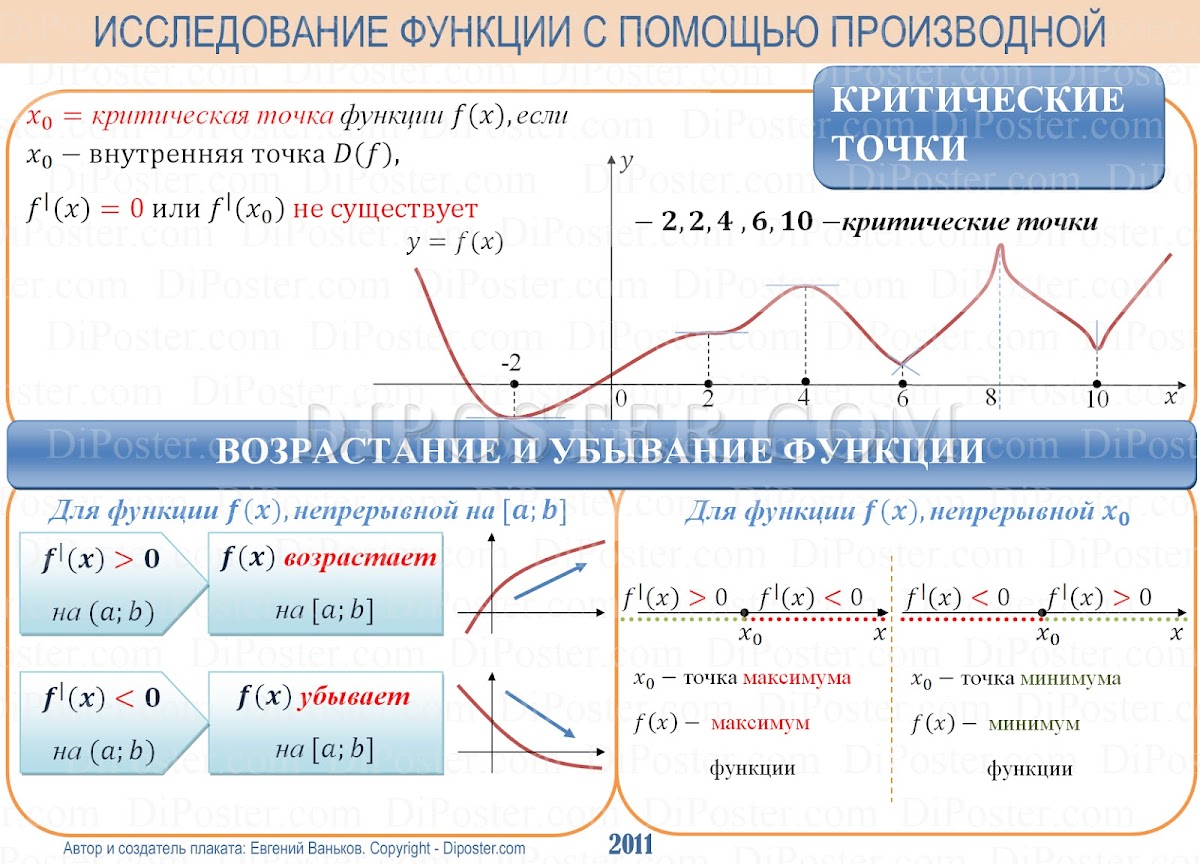
х=4
Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
№2. Найдите точку минимума функции у= 2х-ln(х+3)+9

х=-2,5

Определим знаки производной функции и изобразим на рисунке поведение функции:

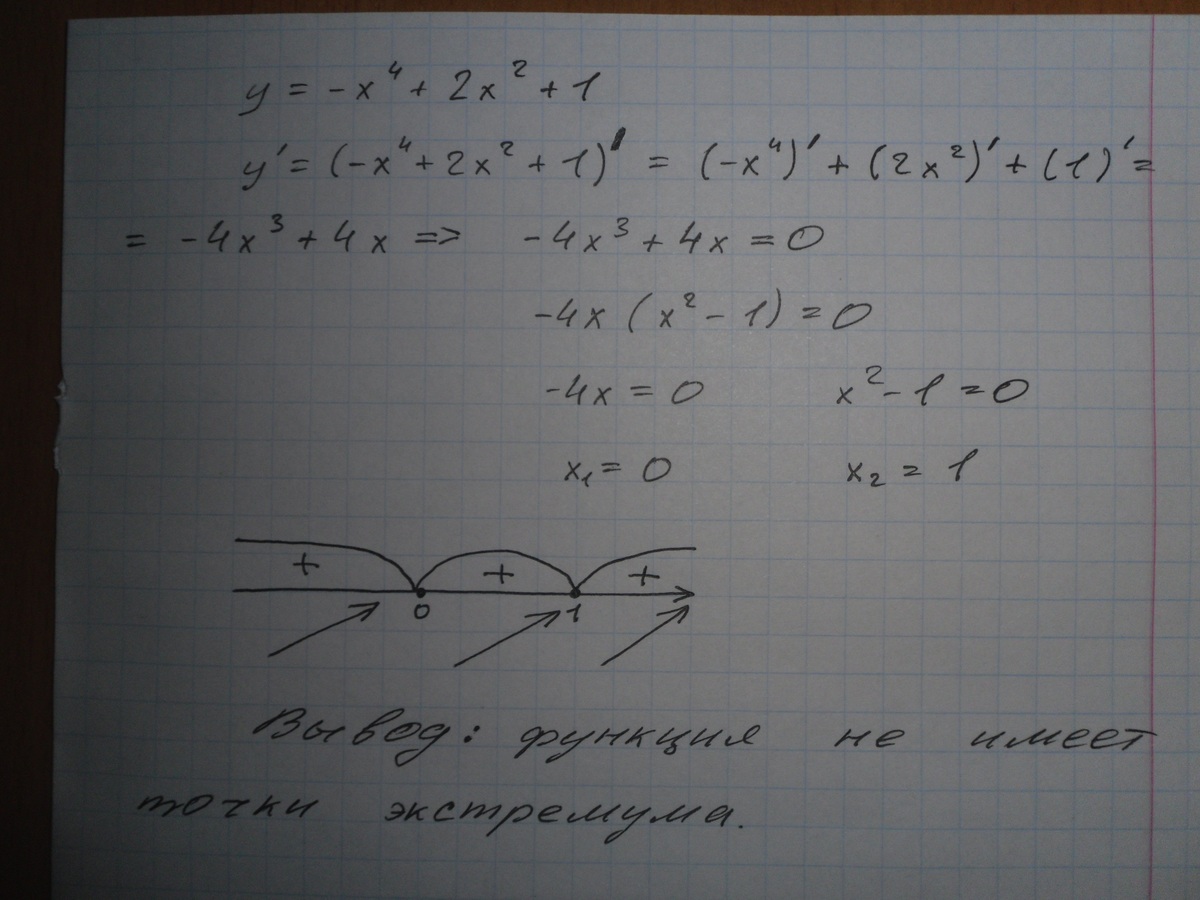
Ответ: -2,5 точка min

№3. Материальная точка движется прямолинейно по закону x(t) = 10t2 − 48t + 15, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.

Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.

V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 мc

Ответ: V=12 мc

№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.

Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3

Ответ: 3

Источник: https://resh.edu.ru/subject/lesson/3987/conspect/

Конспект по «Машинному обучению». Математический анализ. Градиентный спуск

Вспомним математический анализ

Непрерывность функции и производная

Пусть , — предельная точка множества (т.е. ), .

Определение 1 (предел функции по Коши):
Функция стремится к при , стремящемся к , если

Обозначение: . Определение 2:

Интервалом называется множество ;
Интервал, содержащий точку , называется окрестностью этой точки.
Проколотой окрестностью точки называется окрестность точки, из которой исключена сама эта точка.

Обозначение:

или — окрестность точки ;
— проколотая окрестность точки ;

Определение 3 (предел функции через окрестности): Определения 1 и 3 равносильны.

Определение 4 (непрерывность функции в точке):

непрерывна в
непрерывна в

Из определений 3 и 4 видно, что

( непрерывна в , где — предельная точка )

Определение 5:
Функция называется непрерывной на множестве , если она непрерывна в каждой точке множества .
Определение 6:

Функция , определённая на множестве , называется дифференцируемой в точке , предельной для множества , если существует такая линейная относительно приращения аргумента функция [дифференциал функции в точке ], что приращение функции представляется в виде
Величина называется производной функции в точке .

Также

Определение 7:

Точка называется точкой локального максимума (минимума), а значение функции в ней — локальным максимумом (минимумом) функции , если :
Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них — локальными экстремумами функции.
Точка экстремума функции называется точкой внутреннего экстремума, если является предельной точкой как для множества , так и для множества .

Лемма 1 (Ферма):

Если функция дифференцируема в точке внутреннего экстремума , то её производная в этой точке равна нулю: .

Утверждение 1 (теорема Ролля):

Если функция непрерывна на отрезке , дифференцируема в интервале и , то найдётся точка такая, что .

Теорема 1 (теорема Лагранжа о конечном приращении):
Если функция непрерывна на отрезке и дифференцируема в интервале , то найдётся точка такая, что

Следствие 1 (признак монотонности функции): Если в любой точке некоторого интервала производная функции неотрицательная (положительная), то функция не убывает (возрастает) на этом интервале.

Следствие 2 (критерий постоянства функции):

Непрерывная на отрезке функция постоянна не нём тогда и только тогда, когда её производная равна нулю в любой точке отрезка (или хотя бы интервала ).

Частная производная функции многих переменных

Через обозначают множество:

Определение 8:
Функция , определённая на множестве , называется дифференцируемой в точке , предельной для множества , если

где — линейная относительно функция [дифференциал функции в точке (обозн.

или )], а при .

Соотношение (1) можно переписать в следующем виде:

или Если перейти к координатной записи точки , вектора и линейной функции , то равенство (1) выглядит так где — связанные с точкой вещественные числа. Необходимо найти эти числа.

Обозначим

где — базис в .

При из (2) получаем
Из (3) получаем

Определение 9: Предел (4) называется частной производной функции в точке по переменной . Обозначается:

Пример 1:

Градиентный спуск

Пусть , где .

Определение 10:
Градиентом функции называется вектор, -й элемент которого равен :

Градиент — это то направление, в котором функция быстрее всего возрастает. А значит, направление, в котором она быстрее всего убывает, — это и есть направление, обратное градиенту, то есть .

Целью метода градиентного спуска является поиск точки экстремума (минимума) функции.
Обозначим через вектор параметров функции на шаге . Вектор обновления параметров на шаге :

В формуле выше параметр — это скорость обучения, которая регулирует размер шага, который мы делаем в направлении склона-градиента.

В частности, могут возникать две противоположные друг другу проблемы:

если шаги будут слишком маленькими, то обучение будет слишком долгим, и повышается вероятность застрять в небольшом неудачном локальном минимуме по дороге (первое изображение на картинке ниже);
если слишком большие, можно бесконечно прыгать через искомый минимум взад-вперёд, но так и не прийти в самую нижнюю точку (третье изображение на картинке ниже).

Пример: Рассмотрим пример работы метода градиентного спуска в простейшем случае (). То есть . Пусть . Тогда: В случае, когда , получается ситуация, как на третьем изображении картинки выше. Мы постоянно перепрыгиваем точку экстремума. Пусть . Тогда: Видно, что итеративно мы приближаемся к точке экстремума. Пусть . Тогда: Точка экстремума найдена за 1 шаг.

Список используемой литературы:

«Математический анализ. Часть 1», В.А. Зорич, Москва, 1997;
«Глубокое обучение. Погружение в мир нейронных сетей», С. Никуленко, А. Кадурин, Е. Архангельская, ПИТЕР, 2018.

Источник: https://habr.com/post/474338/

Необходимые и достаточные условия существования экстремумов. Примеры

Экстремумом функции называется максимальное (минимальное) значение функции на заданном множестве. Точка, в которой достигается экстремум называется точкой экстремума.
Точка называется точкой локального максимума функции , если выполняется условие:
Аналогично точка называется точкой локального минимума функции , если выполняется условие:

Точки, в которых производная равна нулю, называются стационарными точками.Точки, в которых функция непрерывна, а её производная либо равна нулю, либо не существует, называются критическими точками.

Теорема (необходимое условие экстремума)

Если точка — точка экстремума функции , то она критическая.

Доказательство

По условию точка — точка экстремума функции по теореме Ферма производная точка является критической.

Пример:

Найти экстремум функции .
Найдем производную этой функции: критические точки задаются уравнением . Корни этого уравнения и .

Как видно по рисунку функция имеет максимум в точке 1, а минимум в точке 3. Подставим эти значения чтобы убедиться в исходную функцию: и в точке функция имеет минимум, равный -4, а в точке функция имеет максимум, равный 0.

Замечания:

Не всякая критическая точка является точкой экстремума.

Пример:

Рассмотрим функцию . Построим график этой функции:
Производная данной функции в точке по определению является критической точкой, однако в этой точке функция не имеет экстремума.

Теорема (первое достаточное условие экстремума в терминах первой производной)

Пусть функция определена и дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки и непрерывна в этой точке. Тогда:

Если производная меняет знак с «-» на «+» при переходе через точку : и , то — точка строго минимума функции
Если производная меняет знак с «+» на «-» при переходе через точку : и , то — точка строго максимума функции

Доказательство

Пусть, например, меняет знак с «-» на «+». Рассмотрим точку на сегменте Воспользуемся теоремой о конечных приращениях Лагранжа: , . Поскольку при переходе через точку функция меняет знак с «-» на «+», то и , то
Аналогично рассмотрим сегмент , получим
— точка строгого минимума функции.

Замечания:

Если — точка строго экстремума, то из этого не следует, что производная меняет знак при переходе через точку

Теорема (второе достаточное условие строгого экстремума в терминах второй производной)

Пусть дана функция , она определена в некоторой окрестности точки , ее первая производная и пусть , тогда:

Если , то точка — точка строгого минимума;
Если , то точка — точка строгого максимума.

Доказательство

Докажем теорему для первого случая, когда . По скольку непрерывна, то на достаточно малом интервале , т.к , то возрастает в этом интервале. , значит на интервале и на интервале .
Таким образом функция убывает на интервале и возрастает на интервале по первому достаточному условию экстремума функция в точке имеет минимум.
Аналогично доказывается второй случай теоремы.

Замечания:

Если и , то функция может и не иметь экстремум в точке

Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше двух)

Пусть функция определена в некоторой окрестности точки , и в этой точке существуют производные до n-го порядка пусть , и , Тогда:

Если (т.е — четное), то — точка экстремума:
- если , то — точка локального максимума;
- если , то — точка локального минимума;
Если (т.е — нечетное), то — не является точкой экстремума.

Доказательство

Воспользуемся формулой Тейлора в окрестности точки с остатком в форме Пеано: .
По скольку все производные до порядка включительно равны нулю получим: Запишем полученное выражение в виде: . Выражение . Пусть , . Отсюда следует, что сохранение или изменение знака приращения функции во время перехода через точку зависит от четности . Последний факт и доказывает теорему.

Список литературы:

максимум из 4 баллов Место Имя Записано Баллы Результат

Таблица загружается

Нет данных

Источник: https://ib.mazurok.com/2013/05/17/extremum-of-the-function/